初中数学几何最值问题典型例题精修订
(完整版)初中数学《几何最值问题》典型例题
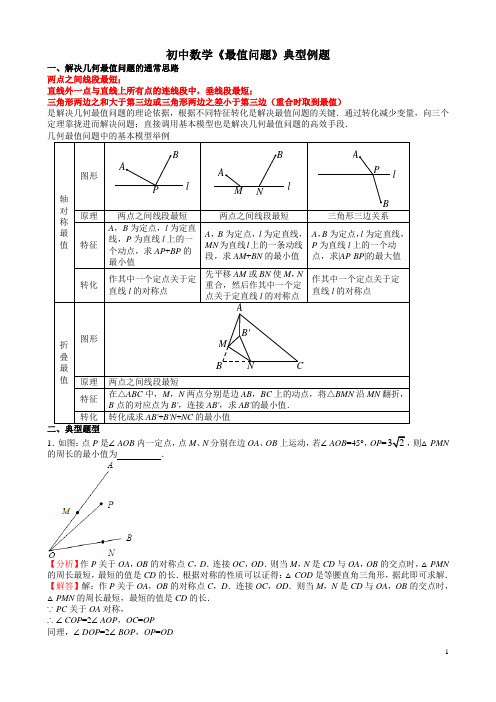
初中数学《最值问题》典型例题一、解决几何最值问题的通常思路两点之间线段最短；直线外一点与直线上所有点的连线段中，垂线段最短；三角形两边之和大于第三边或三角形两边之差小于第三边（重合时取到最值）是解决几何最值问题的理论依据，根据不同特征转化是解决最值问题的关键．通过转化减少变量，向三个定理靠拢进而解决问题；直接调用基本模型也是解决几何最值问题的高效手段．轴对称最值图形lPBANM lBAAPBl 原理两点之间线段最短两点之间线段最短三角形三边关系特征A，B为定点，l为定直线，P为直线l上的一个动点，求AP+BP的最小值A，B为定点，l为定直线，MN为直线l上的一条动线段，求AM+BN的最小值A，B为定点，l为定直线，P为直线l上的一个动点，求|AP-BP|的最大值转化作其中一个定点关于定直线l的对称点先平移AM或BN使M，N重合，然后作其中一个定点关于定直线l的对称点作其中一个定点关于定直线l的对称点折叠最值图形B'NMCAB原理两点之间线段最短特征在△ABC中，M，N两点分别是边AB，BC上的动点，将△BMN沿MN翻折，B点的对应点为B'，连接AB'，求AB'的最小值．转化转化成求AB'+B'N+NC的最小值1．如图：点P是∠AOB内一定点，点M、N分别在边OA、OB上运动，若∠AOB=45°，OP=32，则△PMN 的周长的最小值为．【分析】作P关于OA，OB的对称点C，D．连接OC，OD．则当M，N是CD与OA，OB的交点时，△PMN 的周长最短，最短的值是CD的长．根据对称的性质可以证得：△COD是等腰直角三角形，据此即可求解．【解答】解：作P关于OA，OB的对称点C，D．连接OC，OD．则当M，N是CD与OA，OB的交点时，△PMN的周长最短，最短的值是CD的长．∵PC关于OA对称，∴∠COP=2∠AOP，OC=OP同理，∠DOP=2∠BOP，OP=OD∴∠COD=∠COP+∠DOP=2（∠AOP+∠BOP）=2∠AOB=90°，OC=OD．∴△COD是等腰直角三角形．则CD=2OC=2×32=6．【题后思考】本题考查了对称的性质，正确作出图形，理解△PMN周长最小的条件是解题的关键．2．如图，当四边形P ABN的周长最小时，a=．【分析】因为AB，PN的长度都是固定的，所以求出P A+NB的长度就行了．问题就是P A+NB什么时候最短．把B点向左平移2个单位到B′点；作B′关于x轴的对称点B″，连接AB″，交x轴于P，从而确定N点位置，此时P A+NB最短．设直线AB″的解析式为y=kx+b，待定系数法求直线解析式．即可求得a的值．【解答】解：将N点向左平移2单位与P重合，点B向左平移2单位到B′（2，﹣1），作B′关于x轴的对称点B″，根据作法知点B″（2，1），设直线AB″的解析式为y=kx+b，则123k bk b=+⎧⎨-=+⎩，解得k=4，b=﹣7．∴y=4x﹣7．当y=0时，x=74，即P（74，0），a=74．故答案填：74．【题后思考】考查关于X轴的对称点，两点之间线段最短等知识．3．如图，A 、B 两点在直线的两侧，点A 到直线的距离AM =4，点B 到直线的距离BN =1，且MN =4，P 为直线上的动点，|P A ﹣PB |的最大值为．D PB′N MA【分析】作点B 于直线l 的对称点B ′，则PB =PB ′因而|P A ﹣PB |=|P A ﹣PB ′|，则当A ，B ′、P 在一条直线上时，|P A ﹣PB |的值最大．根据平行线分线段定理即可求得PN 和PM 的值然后根据勾股定理求得P A 、PB ′的值，进而求得|P A ﹣PB |的最大值．【解答】解：作点B 于直线l 的对称点B ′，连AB ′并延长交直线l 于P ． ∴B ′N =BN =1，过D 点作B ′D ⊥AM ， 利用勾股定理求出AB ′=5 ∴|P A ﹣PB |的最大值=5．【题后思考】本题考查了作图﹣轴对称变换，勾股定理等，熟知“两点之间线段最短”是解答此题的关键．4．动手操作：在矩形纸片ABCD 中，AB =3，AD =5．如图所示，折叠纸片，使点A 落在BC 边上的A ′处，折痕为PQ ，当点A ′在BC 边上移动时，折痕的端点P 、Q 也随之移动．若限定点P 、Q 分别在AB 、AD 边上移动，则点A ′在BC 边上可移动的最大距离为 ．【分析】本题关键在于找到两个极端，即BA ′取最大或最小值时，点P 或Q 的位置．经实验不难发现，分别求出点P 与B 重合时，BA ′取最大值3和当点Q 与D 重合时，BA ′的最小值1．所以可求点A ′在BC 边上移动的最大距离为2．【解答】解：当点P 与B 重合时，BA ′取最大值是3， 当点Q 与D 重合时（如图），由勾股定理得A ′C =4，此时BA ′取最小值为1． 则点A ′在BC 边上移动的最大距离为3﹣1=2． 故答案为：2【题后思考】本题考查了学生的动手能力及图形的折叠、勾股定理的应用等知识，难度稍大，学生主要缺乏动手操作习惯，单凭想象造成错误．5．如图，直角梯形纸片ABCD ，AD ⊥AB ，AB =8，AD =CD =4，点E 、F 分别在线段AB 、AD 上，将△AEF 沿EF 翻折，点A 的落点记为P ．当P 落在直角梯形ABCD 内部时，PD 的最小值等于 ．【分析】如图，经分析、探究，只有当直径EF最大，且点A落在BD上时，PD最小；根据勾股定理求出BD的长度，问题即可解决．【解答】解：如图，∵当点P落在梯形的内部时，∠P=∠A=90°，∴四边形PF AE是以EF为直径的圆内接四边形，∴只有当直径EF最大，且点A落在BD上时，PD最小，此时E与点B重合；由题意得：PE=AB=8，由勾股定理得：BD2=82+62=80，∴BD=45，∴PD=458 ．【题后思考】该命题以直角梯形为载体，以翻折变换为方法，以考查全等三角形的判定及其性质的应用为核心构造而成；解题的关键是抓住图形在运动过程中的某一瞬间，动中求静，以静制动．6．如图，∠MON=90°，矩形ABCD的顶点A、B分别在边OM，ON上，当B在边ON上运动时，A随之在OM上运动，矩形ABCD的形状保持不变，其中AB=2，BC=1，运动过程中，点D到点O的最大距离为．【分析】取AB的中点E，连接OD、OE、DE，根据直角三角形斜边上的中线等于斜边的一半可得OE=AB，利用勾股定理列式求出DE，然后根据三角形任意两边之和大于第三边可得OD过点E时最大．【解答】解：如图，取AB的中点E，连接OD、OE、DE，∵∠MON=90°，AB=2∴OE=AE=12AB=1，∵BC=1，四边形ABCD是矩形，∴AD，∴DE2，根据三角形的三边关系，OD＜OE+DE，∴当OD过点E是最大，最大值为2+1．故答案为：2+1．【题后思考】本题考查了矩形的性质，直角三角形斜边上的中线等于斜边的一半的性质，三角形的三边关系，勾股定理，确定出OD过AB的中点时值最大是解题的关键．7．如图，线段AB的长为4，C为AB上一动点，分别以AC、BC为斜边在AB的同侧作等腰直角△ACD 和等腰直角△BCE，那么DE长的最小值是．【分析】设AC=x，BC=4﹣x，根据等腰直角三角形性质，得出CD=22x，CD′=22（4﹣x），根据勾股定理然后用配方法即可求解．【解答】解：设AC=x，BC=4﹣x，∵△ABC，△BCD′均为等腰直角三角形，∴CD=22x，CD′=22（4﹣x），∵∠ACD=45°，∠BCD′=45°，∴∠DCE=90°，∴DE2=CD2+CE2=12x2+12（4﹣x）2=x2﹣4x+8=（x﹣2）2+4，∵根据二次函数的最值，∴当x取2时，DE取最小值，最小值为：4．故答案为：2．【题后思考】本题考查了二次函数最值及等腰直角三角形，难度不大，关键是掌握用配方法求二次函数最值．8．如图，菱形ABCD中，AB=2，∠A=120°，点P，Q，K分别为线段BC，CD，BD上的任意一点，则PK+QK 的最小值为．【分析】根据轴对称确定最短路线问题，作点P关于BD的对称点P′，连接P′Q与BD的交点即为所求的点K，然后根据直线外一点到直线的所有连线中垂直线段最短的性质可知P′Q⊥CD时PK+QK的最小值，然后求解即可．【解答】解：如图，∵AB=2，∠A=120°，∴点P′到CD的距离为2×33∴PK+QK3故答案为：3．【题后思考】本题考查了菱形的性质，轴对称确定最短路线问题，熟记菱形的轴对称性和利用轴对称确定最短路线的方法是解题的关键．9．如图所示，正方形ABCD的边长为1，点P为边BC上的任意一点（可与B、C重合），分别过B、C、D作射线AP的垂线，垂足分别为B′、C′、D′，则BB′+CC′+DD′的取值范围是．【分析】首先连接AC，DP．由正方形ABCD的边长为1，即可得：S△ADP=12S正方形ABCD=12，S△ABP+S△ACP=S△ABC=12S正方形ABCD=12，继而可得12AP•（BB′+CC′+DD′）=1，又由1≤AP≤2，即可求得答案．【解答】解：连接AC，DP．∵四边形ABCD是正方形，正方形ABCD的边长为1，∴AB=CD，S正方形ABCD=1，∵S△ADP=12S正方形ABCD=12，S△ABP+S△ACP=S△ABC=12S正方形ABCD=12，∴S△ADP+S△ABP+S△ACP=1，∴12AP•BB′+12AP•CC′+12AP•DD′=12AP•（BB′+CC′+DD′）=1，则BB′+CC′+DD′=2 AP，∵1≤AP≤2，∴当P当P与C重合时，有最小值2．∴2≤BB′+CC′+DD′≤2．故答案为：2≤BB′+CC′+DD′≤2．【题后思考】此题考查了正方形的性质、面积及等积变换问题．此题难度较大，解题的关键是连接AC，DP，根据题意得到S△ADP+S△ABP+S△ACP=1，继而得到BB′+CC′+DD′=2 AP．10．如图，菱形ABCD中，∠A=60°，AB=3，⊙A、⊙B的半径分别为2和1，P、E、F分别是边CD、⊙A 和⊙B上的动点，则PE+PF的最小值是．【分析】利用菱形的性质以及相切两圆的性质得出P与D重合时PE+PF的最小值，进而求出即可．【解答】解：由题意可得出：当P与D重合时，E点在AD上，F在BD上，此时PE+PF最小，连接BD，∵菱形ABCD中，∠A=60°，∴AB=AD，则△ABD是等边三角形，∴BD=AB=AD=3，∵⊙A、⊙B的半径分别为2和1，∴PE=1，DF=2，∴PE+PF的最小值是3．故答案为：3．【题后思考】此题主要考查了菱形的性质以及相切两圆的性质等知识，根据题意得出P点位置是解题关键．。
(完整)初中数学《几何最值问题》典型例题
初中数学《最值问题》典型例题一、解决几何最值问题的通常思路两点之间线段最短；直线外一点与直线上所有点的连线段中，垂线段最短；三角形两边之和大于第三边或三角形两边之差小于第三边（重合时取到最值）是解决几何最值问题的理论依据，根据不同特征转化是解决最值问题的关键．通过转化减少变量，向三个定理靠拢进而解决问题；直接调用基本模型也是解决几何最值问题的高效手段．几何最值问题中的基本模型举例轴对称最值图形lPBANM lBAAPBl原理两点之间线段最短两点之间线段最短三角形三边关系特征A，B为定点，l为定直线，P为直线l上的一个动点，求AP+BP的最小值A，B为定点，l为定直线，MN为直线l上的一条动线段，求AM+BN的最小值A，B为定点，l为定直线，P为直线l上的一个动点，求|AP-BP|的最大值转化作其中一个定点关于定直线l的对称点先平移AM或BN使M，N重合，然后作其中一个定点关于定直线l的对称点作其中一个定点关于定直线l的对称点折叠最值图形B'NMCAB原理两点之间线段最短特征在△ABC中，M，N两点分别是边AB，BC上的动点，将△BMN沿MN翻折，B点的对应点为B'，连接AB'，求AB'的最小值．转化转化成求AB'+B'N+NC的最小值二、典型题型1．如图：点P是∠AOB内一定点，点M、N分别在边OA、OB上运动，若∠AOB=45°，OP=32，则△PMN 的周长的最小值为．【分析】作P关于OA，OB的对称点C，D．连接OC，OD．则当M，N是CD与OA，OB的交点时，△PMN 的周长最短，最短的值是CD的长．根据对称的性质可以证得：△COD是等腰直角三角形，据此即可求解．【解答】解：作P关于OA，OB的对称点C，D．连接OC，OD．则当M，N是CD与OA，OB的交点时，△PMN的周长最短，最短的值是CD的长．∵PC关于OA对称，∴∠COP=2∠AOP，OC=OP同理，∠DOP=2∠BOP，OP=OD∴∠COD=∠COP+∠DOP=2（∠AOP+∠BOP）=2∠AOB=90°，OC=OD．∴△COD是等腰直角三角形．则CD=2OC=2×32=6．【题后思考】本题考查了对称的性质，正确作出图形，理解△PMN周长最小的条件是解题的关键．2．如图，当四边形P ABN的周长最小时，a=．【分析】因为AB，PN的长度都是固定的，所以求出P A+NB的长度就行了．问题就是P A+NB什么时候最短．把B点向左平移2个单位到B′点；作B′关于x轴的对称点B″，连接AB″，交x轴于P，从而确定N点位置，此时P A+NB最短．设直线AB″的解析式为y=kx+b，待定系数法求直线解析式．即可求得a的值．【解答】解：将N点向左平移2单位与P重合，点B向左平移2单位到B′（2，﹣1），作B′关于x轴的对称点B″，根据作法知点B″（2，1），设直线AB″的解析式为y=kx+b，则123k bk b=+⎧⎨-=+⎩，解得k=4，b=﹣7．∴y=4x﹣7．当y=0时，x=74，即P（74，0），a=74．故答案填：74．【题后思考】考查关于X轴的对称点，两点之间线段最短等知识．3．如图，A 、B 两点在直线的两侧，点A 到直线的距离AM =4，点B 到直线的距离BN =1，且MN =4，P 为直线上的动点，|P A ﹣PB |的最大值为 ．D PB′N BMA【分析】作点B 于直线l 的对称点B ′，则PB =PB ′因而|P A ﹣PB |=|P A ﹣PB ′|，则当A ，B ′、P 在一条直线上时，|P A ﹣PB |的值最大．根据平行线分线段定理即可求得PN 和PM 的值然后根据勾股定理求得P A 、PB ′的值，进而求得|P A ﹣PB |的最大值．【解答】解：作点B 于直线l 的对称点B ′，连AB ′并延长交直线l 于P ． ∴B ′N =BN =1，过D 点作B ′D ⊥AM ， 利用勾股定理求出AB ′=5 ∴|P A ﹣PB |的最大值=5．【题后思考】本题考查了作图﹣轴对称变换，勾股定理等，熟知“两点之间线段最短”是解答此题的关键．4．动手操作：在矩形纸片ABCD 中，AB =3，AD =5．如图所示，折叠纸片，使点A 落在BC 边上的A ′处，折痕为PQ ，当点A ′在BC 边上移动时，折痕的端点P 、Q 也随之移动．若限定点P 、Q 分别在AB 、AD 边上移动，则点A ′在BC 边上可移动的最大距离为 ．【分析】本题关键在于找到两个极端，即BA ′取最大或最小值时，点P 或Q 的位置．经实验不难发现，分别求出点P 与B 重合时，BA ′取最大值3和当点Q 与D 重合时，BA ′的最小值1．所以可求点A ′在BC 边上移动的最大距离为2．【解答】解：当点P 与B 重合时，BA ′取最大值是3， 当点Q 与D 重合时（如图），由勾股定理得A ′C =4，此时BA ′取最小值为1． 则点A ′在BC 边上移动的最大距离为3﹣1=2． 故答案为：2【题后思考】本题考查了学生的动手能力及图形的折叠、勾股定理的应用等知识，难度稍大，学生主要缺乏动手操作习惯，单凭想象造成错误．5．如图，直角梯形纸片ABCD ，AD ⊥AB ，AB =8，AD =CD =4，点E 、F 分别在线段AB 、AD 上，将△AEF 沿EF 翻折，点A 的落点记为P ．当P 落在直角梯形ABCD 内部时，PD 的最小值等于 ．【分析】如图，经分析、探究，只有当直径EF最大，且点A落在BD上时，PD最小；根据勾股定理求出BD的长度，问题即可解决．【解答】解：如图，∵当点P落在梯形的内部时，∠P=∠A=90°，∴四边形PF AE是以EF为直径的圆内接四边形，∴只有当直径EF最大，且点A落在BD上时，PD最小，此时E与点B重合；由题意得：PE=AB=8，由勾股定理得：BD2=82+62=80，∴BD=45，∴PD=458 ．【题后思考】该命题以直角梯形为载体，以翻折变换为方法，以考查全等三角形的判定及其性质的应用为核心构造而成；解题的关键是抓住图形在运动过程中的某一瞬间，动中求静，以静制动．6．如图，∠MON=90°，矩形ABCD的顶点A、B分别在边OM，ON上，当B在边ON上运动时，A随之在OM上运动，矩形ABCD的形状保持不变，其中AB=2，BC=1，运动过程中，点D到点O的最大距离为．【分析】取AB的中点E，连接OD、OE、DE，根据直角三角形斜边上的中线等于斜边的一半可得OE=AB，利用勾股定理列式求出DE，然后根据三角形任意两边之和大于第三边可得OD过点E时最大．【解答】解：如图，取AB的中点E，连接OD、OE、DE，∵∠MON=90°，AB=2∴OE=AE=12AB=1，∵BC=1，四边形ABCD是矩形，∴AD，∴DE2，根据三角形的三边关系，OD＜OE+DE，∴当OD过点E是最大，最大值为2+1．故答案为：2+1．【题后思考】本题考查了矩形的性质，直角三角形斜边上的中线等于斜边的一半的性质，三角形的三边关系，勾股定理，确定出OD过AB的中点时值最大是解题的关键．7．如图，线段AB的长为4，C为AB上一动点，分别以AC、BC为斜边在AB的同侧作等腰直角△ACD 和等腰直角△BCE，那么DE长的最小值是．【分析】设AC=x，BC=4﹣x，根据等腰直角三角形性质，得出CD=22x，CD′=22（4﹣x），根据勾股定理然后用配方法即可求解．【解答】解：设AC=x，BC=4﹣x，∵△ABC，△BCD′均为等腰直角三角形，∴CD=22x，CD′=22（4﹣x），∵∠ACD=45°，∠BCD′=45°，∴∠DCE=90°，∴DE2=CD2+CE2=12x2+12（4﹣x）2=x2﹣4x+8=（x﹣2）2+4，∵根据二次函数的最值，∴当x取2时，DE取最小值，最小值为：4．故答案为：2．【题后思考】本题考查了二次函数最值及等腰直角三角形，难度不大，关键是掌握用配方法求二次函数最值．8．如图，菱形ABCD中，AB=2，∠A=120°，点P，Q，K分别为线段BC，CD，BD上的任意一点，则PK+QK 的最小值为．【分析】根据轴对称确定最短路线问题，作点P关于BD的对称点P′，连接P′Q与BD的交点即为所求的点K，然后根据直线外一点到直线的所有连线中垂直线段最短的性质可知P′Q⊥CD时PK+QK的最小值，然后求解即可．【解答】解：如图，∵AB=2，∠A=120°，∴点P′到CD的距离为2×33∴PK+QK3故答案为：3．【题后思考】本题考查了菱形的性质，轴对称确定最短路线问题，熟记菱形的轴对称性和利用轴对称确定最短路线的方法是解题的关键．9．如图所示，正方形ABCD的边长为1，点P为边BC上的任意一点（可与B、C重合），分别过B、C、D作射线AP的垂线，垂足分别为B′、C′、D′，则BB′+CC′+DD′的取值范围是．【分析】首先连接AC，DP．由正方形ABCD的边长为1，即可得：S△ADP=12S正方形ABCD=12，S△ABP+S△ACP=S△ABC=12S正方形ABCD=12，继而可得12AP•（BB′+CC′+DD′）=1，又由1≤AP≤2，即可求得答案．【解答】解：连接AC，DP．∵四边形ABCD是正方形，正方形ABCD的边长为1，∴AB=CD，S正方形ABCD=1，∵S△ADP=12S正方形ABCD=12，S△ABP+S△ACP=S△ABC=12S正方形ABCD=12，∴S△ADP+S△ABP+S△ACP=1，∴12AP•BB′+12AP•CC′+12AP•DD′=12AP•（BB′+CC′+DD′）=1，则BB′+CC′+DD′=2 AP，∵1≤AP≤2，∴当P与B重合时，有最大值2；当P与C重合时，有最小值2．∴2≤BB′+CC′+DD′≤2．故答案为：2≤BB′+CC′+DD′≤2．【题后思考】此题考查了正方形的性质、面积及等积变换问题．此题难度较大，解题的关键是连接AC，DP，根据题意得到S△ADP+S△ABP+S△ACP=1，继而得到BB′+CC′+DD′=2 AP．10．如图，菱形ABCD中，∠A=60°，AB=3，⊙A、⊙B的半径分别为2和1，P、E、F分别是边CD、⊙A 和⊙B上的动点，则PE+PF的最小值是．【分析】利用菱形的性质以及相切两圆的性质得出P与D重合时PE+PF的最小值，进而求出即可．【解答】解：由题意可得出：当P与D重合时，E点在AD上，F在BD上，此时PE+PF最小，连接BD，∵菱形ABCD中，∠A=60°，∴AB=AD，则△ABD是等边三角形，∴BD=AB=AD=3，∵⊙A、⊙B的半径分别为2和1，∴PE=1，DF=2，∴PE+PF的最小值是3．故答案为：3．【题后思考】此题主要考查了菱形的性质以及相切两圆的性质等知识，根据题意得出P点位置是解题关键．。
中考数学几何最值问题(习题及答案)
几何最值问题（习题）➢例题示范例1：如图，已知∠AOB 的大小为α，P 是∠AOB 内部的一个定点，且OP=2，E，F 分别是OA，OB 边上的动点．若△PEF 周长的最小值为2，则α=（）A．30°B．45°C．60°D．90°思路分析：1.分析定点、动点．定点：P动点（定直线）：E（射线OA），F（射线OB）和最小（周长最小）对称到异侧2.根据不变特征分析判断属于轴对称最值问题，可调用轴对称最值问题的处理方式：作点P 关于OA 的对称点P′，点P 关于OB 的对称点P′′，连接P′P′′，交OA 于点E，交OB 于点F，此时△PEF 的周长取得最小值．3.设计算法．如图，由题意得OP′=OP′′=P′P′′=2，所以△OP′P′′是等边三角形，故α=30°．13➢巩固练习1.如图，在平面直角坐标系xOy 中，Rt△OAB 的直角顶点A 在x 轴的正半轴上，顶点B 的坐标为(3，)，P 为斜边OB 上一动点．若点C 的坐标为(1，0)，则PA+PC 的最小值为（）2A．132B．312C．3 192D．22.如图，已知A，B 两点在直线l 的异侧，A 到直线l 的距离AM=4，B 到直线l 的距离BN=1，且MN=4．若点P 在直线l 上运动，则PA -A．5PB 的最大值为（）B．41 C．3 415D．63.已知点A，B 均在由面积为1 的相同小长方形组成的网格的格点上，建立如图所示的平面直角坐标系，若P 是x 轴上使得PA+PB 的值最小的点，Q 是y 轴上使得QA -QB 的值最大的点，则OP·OQ= ．2第1 题图第2 题图74.如图1，A，B 两个单位位于一条封闭街道的两旁（直线l1，l2分别是街道的两边），现准备合作修建一座过街人行天桥．图1 图2 （1）天桥建在何处才能使由A 经过天桥走到B 的路程最短？在图2 中作出此时桥PQ 的位置．（注：桥的宽度忽略不计，桥必须与街道垂直）（2）根据图1 中提供的数据计算由A 经过天桥走到B 的最短路程．（单位：米）5.如图，已知正方形ABCD 的边长为2，当点A 在x 轴上运动时，点D 随之在y 轴上运动，则在运动过程中，点B 到原点O 的最大距离为．3【参考答案】➢巩固练习1. B2. A3. 34. （1）略（2）由A 经过天桥走到 B 的最短路程是85 米55. 1+4。
初中数学几何最值专题1：蚂蚁行程(最全修正版)
蚂蚁行程【例题精讲】例1、如图，一只螳螂在一圆柱形松树树干的A点处，发现它的正上方B点处有一只小虫子，螳螂想捕到这只虫子，但又怕被发现，于是准备按如图所示的路线，绕到虫子后面吃掉它．已知树干的周长为40cm，A，B两点间的距离为30cm．若螳螂想吃掉B点处的小虫子，螳螂绕行的最短路程为cm。
解析提示：总结：例2、如图，台阶阶梯每一层高20cm，宽30cm，长50cm，一只蚂蚁从A点爬到B点，最短路程是。
解析提示：总结：例3、如图所示的圆锥底面半径OA＝2cm，高PO＝4cm，一只蚂蚁由A点出发绕侧面一周后回到A点处，则它爬行的最短路程为。
解析提示：总结：针对训练1、如图，已知圆柱的底面周长为6，高AB＝3，小虫在圆柱表面爬行，从C点爬到对面的A点，然后再沿另一面爬回C点，则小虫爬行的最短路程为．2、如图，有一圆柱，其高为14cm，它的底面周长为10cm，在圆柱下底面A处有一只蚂蚁，它想得到上面B 处的食物，其中B离上沿2cm，则蚂蚁经过的最短路程为．3、如图，桌面上的长方体长为8，宽为6，高为4，B为CD的中点．一只蚂蚁从A点出发沿长方体的表面到达B点，则它运动的最短路程为。
4、如图，圆柱体的高为4cm，底面周长为6cm，小蚂蚁在圆柱表面爬行，从A点到B点，路线如图所示，则最短路程为．5、如图，桌面上的正方体的棱长为2，B为一条棱的中点．已知蚂蚁沿正方体的表面从A点出发，到达B 点，则它运动的最短路程为（）6、有一圆柱体油罐，已知油罐底面周长是12m，高AB是5m，要从点A处开始绕油罐一周建造房子，正好到达A点的正上方B处，问梯子最短有多长？7、（1）如图1，长方体的长为4cm，宽为3cm，高为12cm．求该长方体中能放入木棒的最大长度；（2）如图2，长方体的长为4cm，宽为3cm，高为12cm．现有一只蚂蚁从点A处沿长方体的表面爬到点G 处，求它爬行的最短路程．（3）若将题中的长方体换成透明圆柱形容器（容器厚度忽略不计）的高为12cm，底面周长为10cm，在容器内壁离底部3cm的点B处有一饭粒，此时一只蚂蚁正好在容器外壁且离容器上沿3cm的点A处．求蚂蚁吃到饭粒需要爬行的最短路程是多少？8、李老师在与同学进行“蚂蚁怎样爬最近”的课题研究时设计了以下三个问题：（1）如图1，正四棱柱的底面边长为5cm，侧棱长为6cm，一只蚂蚁从正四棱柱底面上的点A沿着棱柱表面爬到C1处，那么蚂蚁需要爬行的最短路程的长是cm；（2）如图2，一个圆柱形食品盒，它的高为10cm，底面圆的周长为32cm．（先画出示意图，再写出解答过程）①点A位于盒外底面的边缘，如果在A处有一只蚂蚁，它想吃到盒外表面对侧中点B处的食物请求出蚂蚁需要爬行的最短路程；②将图2改为一个无盖的圆柱形食品盒，点C距离下底面3cm，此时蚂蚁从C处出发，爬到盒内表面对侧中点B处（如图3）．那么蚂蚁爬行的最短路程是多少？课堂精练1、如图，圆柱体的高为8cm，底面周长为4cm，小蚂蚁在圆柱表面爬行，从A点到B点，路线如图，则最短路程为．2、如图，有一圆锥形粮堆，其正视图是边长为6m的正三角形ABC，粮堆母线AC的中点P处有一老鼠正在偷吃粮食，此时，小猫正在B处，它要沿圆锥侧面到达P处捕捉老鼠，则小猫所经过的最短路程是（）m．3、如图是放在地面上的一个长方体盒子，其中AB＝18cm，BC＝12cm，BF＝10cm，点M在棱AB上，且AM＝6cm，点N是FG的中点，一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N，它需要爬行的最短路程是多少？4、如图，圆柱的底面周长为6cm，AC是底面圆的直径，高BC＝6cm，P是BC上一点且PC＝BC．一只蚂蚁从点A出发沿着圆柱的侧面爬行到点P，求爬行的最短路程是多少．。
初中数学最值问题典型例题(含答案分析)
考查知识点：1、“两点之间线段最短”（2、代数计算最值问题 问题原型：饮马问题造桥选址问题（完全平方公式 出题背景变式：角、三角形、菱形、矩形、正方形、梯形、 解题总思路：找点关于线的对称点实现“折”转“直” 几何基本模型： 条件 问题 方法 中考数学最值问题总结 ,“垂线段最短”，“点关于线对称”，“线段的平移”。
3、二次函数中最值问题） 配方求多项式取值 二次函数顶点）圆、坐标轴、抛物线等。
如下左图， A 、B 是直线I 同旁的两个定点.在直线I 上确定一点P ，使PA PB 的值最小. 作点 A 关于直线I 的对称点A ，连结AB 交I 于 点P ，则PA PB AB 的值最小 例1、如图，四边形 ABCD 是正方形，△ ABE 是等边三 角形，M 为对角线BD （不含B 点） 上任意一点，将 BM 绕点B 逆时针旋转60°得到BN ，连接 EN 、AM 、CM . (1) 求证：△ AMB ENB ; (2) ①当M 点在何处时，AM+CM 的值最小;②当 M 点在何处时，AM+BM+CM 的值最小，并说明理由;(3) 当AM+BM+CM 的最小值为 ■■ ■■■ I 时，求正方形的边长。
例2、如图13,抛物线y=ax2+ bx + c（a丰（的顶点为（1,4 ）,交x轴于A B,交y轴于D, 其中B点的坐标为（3,0 ）（1）求抛物线的解析式（2）如图14,过点A的直线与抛物线交于点E，交y轴于点F，其中E点的横坐标为2，若直线PQ为抛物线的对称轴，点G为PQ上一动点，则x轴上是否存在一点H，使D、G、F、H四点围成的四边形周长最小•若存在，求出这个最小值及G、H的坐标；若不存在，请说明理由•（3）如图15,抛物线上是否存在一点T，过点T作x的垂线，垂足为M，过点M作直线MN// BD,交线段AD于点N,连接MD使厶DN WA BMD若存在，求出点T的坐标；若不存在，说明理由.例3、如图1，四边形AEFG与ABCD都是正方形，它们的边长分别为a,b(b >2a且点F在AD上(以下问题的结果可用a,b表示)(1) 求DBF;(2) 把正方形AEFG绕点A逆时针方向旋转45°得图2,求图2中的S^DBF;(3) 把正方形AEFG绕点A旋转任意角度，在旋转过程中DBF是否存在最大值，最小值？如果存在，试求出最大值、最小值；如果不存在，请说明理由。
初中数学几何最值专题33：点与圆之“一箭穿心”(最全修正版)
初中数学几何最值专题33：点与圆之“一箭穿心”(最全修正版)一箭穿心介绍】本文主要介绍一种几何问题——一箭穿心，即求解一个动点在平面内移动时，与固定点和固定直线的连线长度最短的问题。
例题精讲】例1、在平面直角坐标系中，点A的坐标为（4，0），点B是第一象限内的一个动点并且使∠OBA＝90°，点C的坐标为（0，3），则BC的最小值为多少？解析提示：根据勾股定理可得，AB的长度为4，由于∠OBA＝90°，所以OB为BC的最小值。
因此，BC的最小值为3.例2、在半圆O的直径AB上，点D到A的距离为20，到B的距离为4，点C在弧BD上移动，求BH的最小值。
解析提示：根据勾股定理可得，AD的长度为20，AB的长度为4，所以BD的长度为√396.由于BCD构成等腰三角形，所以∠BCD＝∠CBD，因此BH为CD的中线，所以BH的长度为√196＋（√396÷2）²＝5.因此，BH的最小值为5.例3、在平面直角坐标系中，已知点A（0，1）、点B（t，1+t）、C（－t，1－t）（t＞0），点P在以D（3，3）为圆心，1为半径的圆上运动，且始终满足∠BPC＝90°，则t的最小值是多少？解析提示：根据勾股定理可得，BP²＝PC²＋BC²。
由于∠BPC＝90°，所以BP²＝BC²＋1.代入坐标可得（t－3）²＋(2t－2)²＝(t＋3)²＋(2t)²＋1.化简可得t＝√2.因此，t的最小值为√2.例4、在平面直角坐标系中，圆心M的坐标为（3，4），⊙M的半径为2，点P是⊙M上的任意一点，PA⊥PB，且PA、PB与x轴分别交于A、B两点，若点A、点B关于原点O对称，则AB的最小值为多少？解析提示：根据勾股定理可得，PA²＝PM²－AM²，PB²＝PM²－BM²。
题型六 几何最值(专题训练)(解析版)
题型六几何最值（专题训练）1.如图，△ABC 中，AB ＝AC ＝10，tanA ＝2，BE ⊥AC 于点E ，D 是线段BE 上的一个动点，则CD BD +的最小值是( )【答案】B【详解】如图，作DH ⊥AB 于H ，CM ⊥AB 于M ．∵BE ⊥AC ，∴∠AEB=90°，∵tanA=BE AE=2，设AE=a ，BE=2a ，则有：100=a 2+4a 2，∴a 2=20，∴，∴，∵AB=AC ，BE ⊥AC ，CM ⊥AB ，∴（等腰三角形两腰上的高相等））∵∠DBH=∠ABE ，∠BHD=∠BEA ，∴sin DH AE DBH BD AB Ð===，∴BD ，∴BD=CD+DH ，∴CD+DH ≥CM ，∴BD ≥∴BD 的最小值为故选B ．2.如图，在Rt ABC D 中，90°Ð=C ，4AC =，3BC =，点O 是AB 的三等分点，半圆O 与AC 相切，M ，N 分别是BC 与半圆弧上的动点，则MN 的最小值和最大值之和是（ ）A ．5B ．6C ．7D ．8【答案】B【详解】如图，设⊙O 与AC 相切于点D ，连接OD ，作OP BC ^垂足为P 交⊙O 于F ，此时垂线段OP 最短，PF 最小值为OP OF -，∵4AC =，3BC =，∴5AB =∵90OPB °Ð=，∴OP ACP ∵点O 是AB 的三等分点，∴210533OB =´=，23OP OB AC AB ==，∴83OP =，∵⊙O 与AC 相切于点D ，∴OD AC ^，∴OD BC ∥，∴13OD OA BC AB ==，∴1OD =，∴MN 最小值为85133OP OF -=-=，如图，当N 在AB 边上时，M 与B 重合时，MN 经过圆心，经过圆心的弦最长，MN 最大值1013133=+=，513+=633,∴MN 长的最大值与最小值的和是6．故选B ．3.如图，在矩形纸片ABCD 中，2AB =，3AD =，点E 是AB 的中点，点F 是AD 边上的一个动点，将AEF V 沿EF 所在直线翻折，得到'A EF V ，则'A C 的长的最小值是( )A B ．3C 1-D 1-【答案】D【详解】以点E 为圆心，AE 长度为半径作圆，连接CE ，当点A'在线段CE 上时，A'C 的长取最小值，如图所示，根据折叠可知：1A'E AE AB 12===．在Rt BCE V 中，1BE AB 12==，BC 3=，B 90Ð=o ，CE \==，A'C \的最小值CE A'E 1=-=．故选D ．4.如图，四边形ABCD 是菱形，AB=4，且∠ABC=∠ABE=60°，G 为对角线BD （不含B 点）上任意一点，将△ABG 绕点B 逆时针旋转60°得到△EBF ，当AG+BG+CG 取最小值时EF 的长（ ）A ．B ．C ．D ．【答案】D【详解】解：如图，∵将△ABG 绕点B 逆时针旋转60°得到△EBF ，∴BE=AB=BC ，BF=BG ，EF=AG ，∴△BFG 是等边三角形．∴BF=BG=FG ，．∴AG+BG+CG=FE+GF+CG ．根据“两点之间线段最短”，∴当G 点位于BD 与CE 的交点处时，AG+BG+CG 的值最小，即等于EC 的长，过E 点作EF ⊥BC 交CB 的延长线于F ，∴∠EBF=180°-120°=60°，∵BC=4，∴BF=2，，在Rt △EFC 中，∵EF 2+FC 2=EC 2，∴．∵∠CBE=120°，∴∠BEF=30°，∵∠EBF=∠ABG=30°，∴EF=BF=FG ，∴EF=13故选：D ．5.如图，Rt ABC △中，AB BC ^，6AB =，4BC =，P 是ABC △内部的一个动点，且满足90PAB PBA °Ð+Ð=，则线段CP 长的最小值为________.【答案】2：【详解】∵∠PAB+∠PBA=90°∴∠APB=90°∴点P 在以AB 为直径的弧上（P 在△ABC 内）设以AB 为直径的圆心为点O ，如图接OC ，交☉O 于点P ，此时的PC 最短∵AB=6，∴OB=3∵BC=4∴5OC ===∴PC=5-3=26.如图，正方形ABCD 的边长为4，E 为BC 上一点，且BE=1，F 为AB 边上的一个动点，连接EF ，以EF 为边向右侧作等边△EFG ，连接CG ，则CG 的最小值为 ．【分析】同样是作等边三角形，区别于上一题求动点路径长，本题是求CG 最小值，可以将F 点看成是由点B 向点A 运动，由此作出G 点轨迹：考虑到F 点轨迹是线段，故G 点轨迹也是线段，取起点和终点即可确定线段位置，初始时刻G 点在1G 位置，最终G 点在2G 位置（2G 不一定在CD 边），12G G 即为G点运动轨迹．CG 最小值即当CG ⊥12G G 的时候取到，作CH ⊥12G G 于点H ，CH 即为所求的最小值．根据模型可知：12G G 与AB 夹角为60°，故12G G ⊥1EG ．过点E 作EF ⊥CH 于点F ，则HF=1G E =1，CF=1322CE =，所以CH=52，因此CG 的最小值为52．GA B CDE F27.如图，矩形ABCD 中，4AB =，6BC =，点P 是矩形ABCD 内一动点，且D D =PAB PCD S S ，则PC PD +的最小值为_____．【答案】【详解】ABCD Q 为矩形，AB DC\=又=V V Q PAB PCDS S \点P 到AB 的距离与到CD 的距离相等，即点P 线段AD 垂直平分线MN 上，连接AC ，交MN 与点P ，此时PC PD +的值最小，且PC PD AC +=====故答案为：8.如图，在△ABC 中，∠ACB ＝90°，∠A ＝30°，AB ＝5，点P 是AC 上的动点，连接BP ，以BP 为边作等边△BPQ ，连接CQ ，则点P 在运动过程中，线段CQ 长度的最小值是2______．【答案】54．【详解】解：如图，取AB的中点E，连接CE，PE．∵∠ACB=90°，∠A=30°，∴∠CBE=60°，∵BE=AE，∴CE=BE=AE，∴△BCE是等边三角形，∴BC=BE，∵∠PBQ=∠CBE=60°，∴∠QBC=∠PBE，∵QB=PB，CB=EB，∴△QBC≌△PBE（SAS），∴QC=PE，∴当EP⊥AC时，QC的值最小，在Rt△AEP中，∵AE=52，∠A=30°，∴PE=12AE=54，∴CQ的最小值为54．故答案为：549.如图，在正方形ABCD 中，AB ＝8，AC 与BD 交于点O ，N 是AO 的中点，点M 在BC 边上，且BM ＝6．P 为对角线BD 上一点，则PM ﹣PN 的最大值为 ．【答案】2【分析】作以BD 为对称轴作N 的对称点N'，连接PN'，MN'，依据PM ﹣PN ＝PM ﹣PN'≤MN'，可得当P ，M ，N'三点共线时，取“＝”，再求得//AN CN BM CM =＝31，即可得出PM ∥AB ∥CD ，∠CMN'＝90°，再根据△N'CM 为等腰直角三角形，即可得到CM ＝MN'＝2．【解答】解：如图所示，作以BD 为对称轴作N 的对称点N'，连接PN'，MN'，根据轴对称性质可知，PN ＝PN'，∴PM ﹣PN ＝PM ﹣PN'≤MN'，当P ，M ，N'三点共线时，取“＝”，∵正方形边长为8，∴AC ＝2AB ＝28，∵O 为AC 中点，∴AO ＝OC ＝24，∵N 为OA 中点，∴ON ＝22，∴ON'＝CN'＝22，∴AN'＝26，∵BM ＝6，∴CM ＝AB ﹣BM ＝8﹣6＝2，∴//AN CN BM CM =＝31∴PM ∥AB ∥CD ，∠CMN'＝90°，∵∠N'CM ＝45°，∴△N'CM 为等腰直角三角形，∴CM ＝MN'＝2，即PM ﹣PN 的最大值为2，故答案为：2．【点评】本题主要考查了正方形的性质以及最短路线问题，凡是涉及最短距离的问题，一般要考虑线段的性质定理，结合轴对称变换来解决，多数情况要作点关于某直线的对称点．10.如图，ABC V 是等边三角形，6AB =，N 是AB 的中点，AD 是BC 边上的中线，M 是AD 上的一个动点，连接,BM MN ，则BM MN +的最小值是________．【答案】【分析】根据题意可知要求BM+MN 的最小值，需考虑通过作辅助线转化BM ，MN 的值，从而找出其最小值，进而根据勾股定理求出CN ，即可求出答案．【解析】解：连接CN ，与AD 交于点M ，连接BM ．（根据两点之间线段最短；点到直线垂直距离最短），AD 是BC 边上的中线即C 和B 关于AD 对称，则BM+MN=CN ，则CN 就是BM+MN 的最小值．∵ABC V 是等边三角形，6AB =，N 是AB 的中点，∴AC=AB=6,AN=12AB=3, CN AB ^,∴CN ====即BM+MN的最小值为故答案为：【点睛】本题考查的是轴对称-最短路线问题，涉及到等边三角形的性质，勾股定理，轴对称的性质，等腰三角形的性质等知识点的综合运用．11.如图，在中，∠ACB=90°，BC=12，AC=9，以点C 为圆心，6为半径的圆上有一个动点D ．连接AD 、BD 、CD ，则2AD+3BD 的最小值是 ．【分析】首先对问题作变式2AD+3BD=233AD BD æö+ç÷èø，故求23AD BD +最小值即可．考虑到D 点轨迹是圆，A 是定点，且要求构造23AD ，条件已经足够明显．当D 点运动到AC 边时，DA=3，此时在线段CD 上取点M 使得DM=2，则在点D 运动过程中，始终存在23DM DA =．ABC D A BCD问题转化为DM+DB 的最小值，直接连接BM ，BM 长度的3倍即为本题答案．12.如图，四边形ABCD 中，AB ∥CD ，∠ABC ＝60°，AD ＝BC ＝CD ＝4，点M 是四边形ABCD 内的一个动点，满足∠AMD ＝90°，则点M 到直线BC 的距离的最小值为_____．【答案】2-【解析】【分析】取AD 的中点O ，连接OM ，过点M 作ME ⊥BC 交BC 的延长线于E ，点点O 作OF ⊥BC 于F ，交CD 于G ，则OM+ME ≥OF ．求出OM ，OF 即可解决问题．【详解】解：取AD 的中点O ，连接OM ，过点M 作ME ⊥BC 交BC 的延长线于E ，点点O 作OF ⊥BC 于F ，交CD 于G ，则OM+ME ≥OF ．∵∠AMD＝90°，AD＝4，OA＝OD，∴OM＝12AD＝2，∵AB∥CD，∴∠GCF＝∠B＝60°，∴∠DGO＝∠CGE＝30°，∵AD＝BC，∴∠DAB＝∠B＝60°，∴∠ADC＝∠BCD＝120°，∴∠DOG＝30°＝∠DGO，∴DG＝DO＝2，∵CD＝4，∴CG＝2，∴OG＝，GF，OF＝，∴ME≥OF﹣OM＝﹣2，∴当O，M，E共线时，ME的值最小，最小值为2．【点睛】本题考查解直角三角形，垂线段最短，直角三角形斜边中线的性质等知识，解题的关键是学会用转化的思想思考问题，属于中考常考题型．13.如图，四边形ABCD是菱形，A B=6，且∠ABC=60° ，M是菱形内任一点，连接AM，BM，CM，则AM+BM+CM 的最小值为________．【答案】【详解】将△BMN 绕点B 顺时针旋转60度得到△BNE ，∵BM=BN ，∠MBN=∠CBE=60°，∴MN=BM ∵MC=NE ∴AM+MB+CM=AM+MN+NE ．当A 、M 、N 、E 四点共线时取最小值AE ．∵AB=BC=BE=6，∠ABH=∠EBH=60°，∴BH ⊥AE ，AH=EH ，∠BAH=30°，∴BH=12AB=3，BH=AE=2AH=故答案为14.如图，在矩形ABCD 中，E 为AB 的中点，P 为BC 边上的任意一点，把PBE △沿PE 折叠，得到PBE △，连接CF ．若AB ＝10，BC ＝12，则CF 的最小值为_____．【答案】8【解析】【分析】点F 在以E 为圆心、EA 为半径的圆上运动，当E 、F 、C 共线时时，此时FC 的值最小，根据勾股定理求出CE ，再根据折叠的性质得到BE ＝EF ＝5即可．【详解】解：如图所示，点F在以E为圆心EA为半径的圆上运动，当E、F、C共线时时，此时CF的值最小，根据折叠的性质，△EBP≌△EFP，∴EF⊥PF，EB＝EF，∵E是AB边的中点，AB＝10，∴AE＝EF＝5，∵AD＝BC＝12，∴CE＝13，∴CF＝CE﹣EF＝13﹣5＝8．故答案为8．【点睛】本题考查了折叠的性质、全等三角形的判定与性质、两点之间线段最短的综合运用，灵活应用相关知识是解答本题的关键．15、如图，△ABC中，∠BAC＝30°且AB＝AC，P是底边上的高AH上一点．若AP+BP+CP的最小值为，则BC＝_____．-【详解】如图将△ABP绕点A顺时针旋转60°得到△AMG．连接PG，CM．∵AB=AC ，AH ⊥BC ，∴∠BAP=∠CAP ，∵PA=PA ，∴△BAP ≌△CAP （SAS ），∴PC=PB ，∵MG=PB ，AG=AP ，∠GAP=60°，∴△GAP 是等边三角形，∴PA=PG ，∴PA+PB+PC=CP+PG+GM ，∴当M ，G ，P ，C 共线时，PA+PB+PC 的值最小，最小值为线段CM 的长，∵AP+BP+CP 的最小值为，∴，∵∠BAM=60°，∠BAC=30°，∴∠MAC=90°，∴AM=AC=2，作BN ⊥AC 于N ．则BN=12AB=1，，，∴16.如图所示，30AOB Ð=o ，点P 为AOB Ð内一点，8OP =，点,M N 分别在,OA OB 上，求PMN D 周长的最小值_____．【答案】PMN D 周长的最小值为8【详解】如图，作P 关于OA 、OB 的对称点12P P 、，连结1OP 、2OP ，12PP 交OA 、OB 于M 、N ，此时PMN D 周长最小，根据轴对称性质可知1PM PM =，2P N PN =，1212PM N PM M N PN PP \D =++=，且1A O P A O P Ð=Ð，2BO P BO P Ð=Ð，12260POP AOB Ð=Ð=°，128O P O P O P ===，12PPO D 为等边三角形，1218PP OP ==即PMN D 周长的最小值为8.17.在正方形ABCD 中，点E 为对角线AC （不含点A ）上任意一点，AB=；（1）如图1，将△ADE 绕点D 逆时针旋转90°得到△DCF ，连接EF ；①把图形补充完整（无需写画法）； ②求2EF 的取值范围；(2)如图2，求BE+AE+DE 的最小值．【答案】（1）①补图见解析；②2816EF ££；（2）2+【详解】（1）①如图△DCF 即为所求；②∵四边形ABCD 是正方形，∴BC ＝AB ＝，∠B ＝90°，∠DAE ＝∠ADC ＝45°，∴AC AB ＝4，∵△ADE 绕点D 逆时针旋转90°得到△DCF ，∴∠DCF ＝∠DAE ＝45°，AE ＝CF ，∴∠ECF ＝∠ACD ＋∠DCF ＝90°，设AE ＝CF ＝x ，EF 2＝y ，则EC ＝4−x ，∴y ＝（4−x ）2＋x 2＝2x 2−8x ＋160（0＜x ≤4）．即y ＝2（x −2）2＋8，∵2＞0，∴x ＝2时，y 有最小值，最小值为8，当x ＝4时，y 最大值＝16，∴8≤EF 2≤16．（2）如图中，将△ABE 绕点A 顺时针旋转60°得到△AFG ，连接EG ，DF ．作FH ⊥AD 于H ．由旋转的性质可知，△AEG 是等边三角形，∴AE ＝EG ，∵DF ≤FG ＋EG ＋DE ，BE ＝FG ，∴AE ＋BE ＋DE 的最小值为线段DF 的长．在Rt △AFH 中，∠FAH ＝30°，AB ＝=AF ，∴FH ＝12AF ，AH ，在Rt △DFH 中，DF =＝2+，∴BE ＋AE ＋ED 的最小值为2．。
初中数学最值问题典型例题(含答案解析分析)
中考数学最值问题总结考查知识点：1、“两点之间线段最短”，“垂线段最短”，“点关于线对称”，“线段的平移”。
（2、代数计算最值问题 3、二次函数中最值问题）问题原型：饮马问题造桥选址问题（完全平方公式配方求多项式取值二次函数顶点）出题背景变式：角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等。
解题总思路：找点关于线的对称点实现“折”转“直”几何基本模型：条件：如下左图，A、B是直线l同旁的两个定点．问题：在直线l上确定一点P，使PA PB+的值最小．方法：作点A关于直线l的对称点A'，连结A B'交l于点P，则PA PB A B'+=的值最小例1、如图，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM．（1）求证：△AMB≌△ENB；（2）①当M点在何处时，AM+CM的值最小；②当M点在何处时，AM+BM+CM的值最小，并说明理由；（3）当AM+BM+CM的最小值为时，求正方形的边长。
ABA'′Pl例2、如图13，抛物线y=ax2＋bx＋c(a≠0)的顶点为（1,4），交x轴于A、B，交y轴于D，其中B点的坐标为（3,0）（1）求抛物线的解析式（2）如图14，过点A的直线与抛物线交于点E，交y轴于点F，其中E点的横坐标为2，若直线PQ为抛物线的对称轴，点G为PQ上一动点，则x轴上是否存在一点H，使D、G、F、H 四点围成的四边形周长最小.若存在，求出这个最小值及G、H的坐标；若不存在，请说明理由.（3）如图15，抛物线上是否存在一点T，过点T作x的垂线，垂足为M，过点M作直线MN ∥BD，交线段AD于点N，连接MD，使△DNM∽△BMD，若存在，求出点T的坐标；若不存在，说明理由.例3、如图1，四边形AEFG与ABCD都是正方形，它们的边长分别为a,b(b≥2a),且点F在AD上（以下问题的结果可用a,b表示）（1）求S△DBF;(2) 把正方形AEFG绕点A逆时针方向旋转450得图2,求图2中的S△DBF;(3) 把正方形AEFG绕点A旋转任意角度,在旋转过程中,S△DBF是否存在最大值,最小值?如果存在,试求出最大值、最小值；如果不存在，请说明理由。
初中数学几何最值专题39：定边定角之直角隐圆(最全修正版)
隐圆------定边对直角知识回顾：直径所对的圆周角是直角．构造思路：一条定边所对的角始终为直角，则直角顶点轨迹是以定边为直径的圆或圆弧．【例题精讲】解析提示：总结：例2、在Rt △ABC 中，∠C ＝90°，AC ＝10，BC ＝12，点D 为线段BC 上一动点．以CD 为⊙O 直径，作AD 交⊙O 于点E ，连BE ，则BE 的最小值为 。
解析提示：总结：A B例3、如图，在△ABC中，∠ABC＝90°，AB＝6，点P是AB边上的一个动点，以BP为直径的圆交CP于点Q，若线段AQ长度的最小值是3，则△ABC的面积为。
解析提示：总结：例4、如图，在Rt△ABC中，∠ACB＝90°，BC＝4，AC＝10，点D是AC上的一个动点，以CD为直径作圆O，连接BD交圆O于点E，则AE的最小值为。
解析提示：总结：例5、如图，以G（0，1）为圆心，半径为2的圆与x轴交于A、B两点，与y轴交于C，D两点，点E为⊙O上一动点，CF⊥AE于F，当点E在⊙O的运动过程中，线段FG的长度的最小值为。
解析提示：总结：针对训练1、如图，△ABC 是边长为2的等边三角形，D 是边BC 上的动点，BE ⊥AD 于E ，则CE 的最小值为 。
2、已知正方形ABCD 边长为2，E 、F 分别是BC 、CD 上的动点，且满足BE=CF ，连接AE 、BF ，交点为P 点，则PD 的最小值为 。
3、如图，已知正方形ABCD 的边长为6，点E 是正方形内部一点，连接BE ，CE ，且∠ABE=∠BCE ，点P 是AB 边上一动点，连接PD ，PE ，则PD+PE 的长度最小值为 。
4、如图， AB 是半圆O 的直径，点C 在半圆O 上，AB=5，AC=4．D是弧BC 上的一个动点，连接AD ，过点C 作CE ⊥AD 于E ，连接BE ．在点D 移动的过程中，BE 的最小值为 。
E FA B CDPB5、如图，AC ＝3，BC ＝5，且∠BAC ＝90°，D 为AC 上一动点，以AD 为直径作圆，连接BD 交圆于E 点，连CE ，则CE 的最小值为 。
初中数学几何最值专题51：米勒最大张角(最全修正版)
米勒最大张角【例题精讲】例1、已知A（2，0），B（4，0）是x轴上的两点，点C是y轴上的动点，当∠ ACB最大时，则点C的坐标为。
解析提示：总结：例2、如图，某大楼上装有一块长方形广告牌，上下边相距6m下底边距地面11.6m，如果人的眼部高度是1.6m，那么从远处正对广告牌走进市，在何处看广告牌效果最好。
此时人距广告牌的距离是解析提示：总结：例3、如图，在Rt△ABC中，AB=3，BC=4，D为BC中点，P为AC上的动点，tan∠BPD的最大时值为，解析提示：总结：例4、（1）如图①，AB是⊙O的弦，点C是⊙O上的一点，在直线AB上方找一点D，使得∠ADB＝∠ACB，画出∠ADB，并说明理由；（2）如图②，AB是⊙O的弦，点C是⊙O上的一点，在过点C的直线l上找一点P，使得∠APB＜∠ACB，画出∠APB，并说明理由；问题解决：（3）如图③，已知足球球门宽AB约为5米，一球员从距B点5米的C点（点A、B、C均在球场底线上），沿与AC成45°角的CD方向带球．试问，该球员能否在射线CD上找到一点P，使得点P为最佳射门点（即∠APB最大）？若能找到，求出这时点P与点C的距离；若找不到，请说明理由．解析提示：总结针对训练1、已知点A、B的坐标分别是（0，1）、（0，3），点C是x轴正半轴上一动点，当∠ ACB最大时，点C的坐标为____2、如图，在平面直角坐标系中，已知A（2，0），B（8，0），点P是y轴上的一个动点，当∠AOB度数最大时，求P点坐标。
3、足球射门，不考虑其他因素，仅考虑射点到球门AB的张角大小时，张角越大，射门越好，已知在正方形网格中（每个正方形单位长度都为1），点A，B，C，D，E均在格点上，球员带球沿CD方向进攻，如图建立直角坐标系，则：（1）在C、D、E三点中，到球门AB张角相等的两个点是；（2）在CD上，射门最好的点的坐标为．4、发现问题：（1）如图1，AB为⊙O的直径，请在⊙O上求作一点P，使∠ABP＝45°．（不必写作法）问题探究：（2）如图2，等腰直角三角形△ABC中，∠A＝90°，AB＝AC＝3，D是AB上一点，AD＝2，在BC边上是否存在点P，使∠APD＝45°？若存在，求出BP的长度，若不存在，请说明理由．问题解决：（3）如图3，为矩形足球场的示意图，其中宽AB＝66米、球门EF＝8米，且EB＝FA．点P、Q分别为BC、AD上的点，BP＝7米，∠BPQ＝135°，一位左前锋球员从点P处带球，沿PQ方向跑动，球员在PQ上的何处才能使射门角度（∠EMF）最大？求出此时PM的长度．5、【概念认识】自一点引出的两条射线分别经过已知线段的两端，则这两条射线所成的角称为该点对已知线段的视角，如图①，∠APB是点P对线段AB的视角．【数学理解】如图②，已知线段AB与直线l，在直线l上取一点P，使点P对线段AB的视角最大．（1）过A、B两点，作⊙O使其与直线l相切，切点为P，则点P对线段AB的视角最大，即∠APB最大．为了证明点P的位置即为所求，不妨在直线l上另外任取一点Q，连接AQ、BQ，证明：∠APB＞∠AQB即可，请完成这个证明．【问题解决】在足球电子游戏中，足球队球门的视角越大，越容易被踢进，如果一名球员沿直线带球前进，那么他应当在哪个地方射门，才能使进球的可能性最大？（2）如图③，A、B是足球门的两端，线段AB是球门的宽，CD是球场边线，∠ADC是直角．①若该球员沿边线CD带球前进，记足球所在的位置为点P，在图③中，用直尺和圆规在线段CD上求作点P，使点P对AB的视角最大（不写作法，保留作图痕迹）．②若M是线段CD上一点，∠CMN＝60°，该球员沿射线MN带球前进（如图④），记足球所在的位置为点P，已知AB＝4，BD＝9，DM＝，求点P对AB的最大视角．（1）如图1，AB是⊙O的弦，直线l与O相交于点M、N两点，M1，M2是直线l上异于点M，N的两个点，则∠AMB ∠AM1B（用＞，＜或＝连接）．（2）如图2，AB是⊙O的弦，直线l与⊙O相切于点M，点M1是直线l上异于点M的任意一点，请在图2中画出图形，试判断∠AMB，∠AM1B的大小关系，并证明．【解决问题】（3）某游乐园的平面图如图3所示，场所保卫人员想在线段OD上的点M处安装监控装置，用来监控OC边上的AB段，为了让监控效果达到最佳，必须要求∠AMB最大．已知∠DOC＝60°，OA＝400米，AB＝200米，问在线段OD上是否存在一点M，使得∠AMB最大，若存在，请求出此时OM的长和∠AMB的度数，如果不存在，请说明理由．（1）如图①，在矩形ABCD中，AB＝2AD，P为CD边上的中点，试比较∠APB和∠ADB的大小关系，并说明理由；（2）如图②，在正方形ABCD中，P为CD上任意一点，试问当P点位于何处时∠APB最大？并说明理由；问题解决（3）某儿童游乐场的平面图如图③所示，场所工作人员想在OD边上点P处安装监控装置，用来监控OC边上的AB段，为了让监控效果最佳，必须要求∠APB最大，已知：∠DOC＝60°，OA＝400米，AB＝200米，问在OD边上是否存在一点P，使得∠APB最大，若存在，请求出此时OP的长和∠APB的度数；若不存在，请说明理由．8、如图，在每一个四边形ABCD中，均有AD∥BC，CD⊥BC，∠ABC＝60°，AD＝8，BC＝12．（1）如图①，点M是四边形ABCD边AD上的一点，则△BMC的面积为；（2）如图②，点N是四边形ABCD边AD上的任意一点，请你求出△BNC周长的最小值；（3）如图③，在四边形ABCD的边AD上，是否存在一点P，使得cos∠BPC的值最小？若存在，求出此时cos∠BPC的值；若不存在，请说明理由．。
(完整版)中考复习：几何图形中的最值问题
中考复习：几何图形中的最值问题几何图形中的最值问题★1.如图，在Rt△ABC中，∠ACB＝90°，AB＝5，BC＝3.若点D是AB边上任意一点，且不与点A、B重合，连接CD.将△BCD沿着CD 所在的直线翻折，使得点B落在点B′处，连接AB′，则AB′的最小值为________．第1题图1【解析】在Rt△ABC中，根据勾股定理可得：AC＝AB2－BC2＝52－32＝4，由对称性可知：BC＝B′C＝3，∵B′C的长度固定，∴当AB′＋B′C的值最小时，AB′的值最小，根据“两点之间，线段最短”可知当A、B′、C三点共线时，AB′最小，∴AB′＝AC－B′C＝4－3＝1. ★2.如图，在菱形ABCD中，AB＝43，∠ABC＝60°，点M、N分别是BC、CD上任意一点，点P是BD上一点，连接PM、PN，则PM ＋PN的最小值为________．第2题图第2题解图6【解析】如解图，作点N关于BD对称的点N′，根据菱形的对称性可知点N′在AD上，又由两平行线之间，垂线段最短，过点N′作1 / 7N ′M ⊥BC 于点M ，故MN ′与BD 的交点P 即满足PM ＋PN 的值最小，故MN ′＝AB ·sin ∠ABC ＝43×32＝6.★3.如图，在矩形ABCD 中，AB ＝9，BC ＝12，点E 是BC 中点，点F 是边CD 上的任意一点，当△AEF 的周长最小时，则DF 的长为________．第3题图 第3题解图 6 【解析】如解图，作点E 关于直线CD 的对称点E ′，连接AE ′交CD 于点F ，∵在矩形ABCD 中，AB ＝9，BC ＝12，点E 是BC 中点，∴BE ＝CE ＝CE ′＝6，∵AB ⊥BC ，CD ⊥BC ，∴CE ′BE ′＝CF AB ，即612＋6＝CF9，解得CF ＝3，∴DF ＝CD －CF ＝9－3＝6.★4.如图，在Rt △ABO 中，∠AOB ＝90°，AO ＋BO ＝5，延长AO 到C ，使OC ＝3，延长BO 到D ，使OD ＝4，连接BC 、CD 、DA ，则四边形ABCD 面积的最大值为________．第4题图18 【解析】设OA ＝x ，OB ＝y ，∵AO ＋BO ＝5，∴x ＋y ＝5，∵延中考复习：几何图形中的最值问题 3 / 7 长AO 到C ，OC ＝3，延长BO 到D ，OD ＝4，连接BC 、CD 、DA ，∠AOB ＝90°，∴S 四边形ABCD ＝S △ACD ＋S △ABC ＝12AC ·OD ＋12AC ·OB ＝12AC ·(OD ＋OB )＝12AC ·BD ＝12(x ＋3)(y ＋4)，∵x ＋y ＝5，∴S四边形ABCD ＝12(x ＋3)(5－x ＋4)＝12(x ＋3)(9－x )＝－12(x －3)2＋18. ∴四边形ABCD 的最大面积为18.★5.如图，已知四边形ABCD ，∠BAD ＝120°，CB ⊥AB ，CD ⊥AD ，且AB ＝AD ＝3，点E 、F 分别是BC 、CD 边上的动点，那么△AEF 周长的最小值是________．第5题图 第5题解图 63 【解析】如解图，延长AB 至点M ，使BM ＝AB ，延长AD 至点N ，使DN ＝AD ，连接MN ，交BC 于点E ，交DC 于点F .∵CB ⊥AB ，CD ⊥AD ，∴BC 、CD 是AM 、AN 的垂直平分线，∴AE ＝ME ，AF ＝FN .∵△AEF 的周长＝AE ＋EF ＋AF ＝ME ＋EF ＋FN ＝MN ，∴此时△AEF 的周长为线段MN 的长．∵AB ＝AD ＝3，∴AM ＝AN ＝6，∵∠BAD ＝120°，∴∠M ＝∠N ＝30°，∴MN ＝2AM ·cos30°＝12×32＝6 3.★6.如图，在Rt△ABC中，AB⊥BC，AB＝6，BC＝4，P是△ABC内部的一个动点，且满足∠P AB＝∠PBC，则线段CP长的最小值为________．第6题图第6题解图2【解析】如解图，∵∠P AB＝∠PBC，∠ABC＝90°，∴∠BAP＋∠PBA ＝90°，∴∠APB＝90°，∴点P始终在以AB的中点O为圆心，以OA ＝OB＝OP＝12AB＝3为半径的圆上，由解图知，只有当在点P在OC 与⊙O的交点处时，PC的长最小．在Rt△OBC中，OC＝OB2＋BC2＝32＋42＝5，∴P′C＝OC－OP′＝5－3＝2，∴线段CP长的最小值为2.★7.如图，在矩形ABCD中，AD＝2，AB＝3，点E是AD边的中点，点F是射线AB上的一动点，将△AEF沿EF所在直线翻折得到△A′EF，连接A′C，则A′C的最小值为________．第7题图第7题解图10－1【解析】如解图，∵点E是AD的中点，∴根据翻折性质得中考复习：几何图形中的最值问题 5 / 7 A ′E ＝AE ＝DE ＝12AD ＝12×2＝1，∵点F 为动点，∴随着点F 的运动，点A ′的运动轨迹是以点E 为圆心，AE 为半径在矩形ABCD 内的圆弧，当E 、A ′、C 不在同一直线上时，则CA ′、A ′E 和CE 围成三角形，根据三角形的三边关系，即A ′C >CE －A ′E ，当E 、A ′、C 在同一直线上时，即A ′C ＝CE －A ′E ，综上所述A ′C ≥CE －A ′E ，∴当E 、A ′、C 在同一直线上时，A ′C 有最小值，∵在Rt △CDE 中，CD ＝3，DE ＝1，∴CE ＝CD 2＋DE 2＝32＋1＝10，∴A ′C 的最小值为CE －DE ＝10－1.★8.如图，正方形ABCD 的边长为4，∠DAC 的平分线交DC 于点E .若点P 、Q 分别是AD 和AE 上的动点，则DQ ＋PQ 的最小值是________．第8题图 第8题解图 22 【解析】如解图，作D 关于AE 的对称点D ′，DD 交AE 于F ，再过D ′作D ′P ⊥AD 于P ，∵DD ′⊥AE ，∴∠AFD ＝∠AFD ′，∵AF ＝AF ，∠DAE ＝∠CAE ，∴△ADF ≌△AD ′F ，∴AD ′＝AD ＝4，∵D ′与D 关于AE 对称，∴QD ＝QD ′，∴DQ ＋PQ ＝QD ′＋PQ ＝PD ′，∴D ′P ′即为DQ ＋PQ 的最小值，∵四边形ABCD 是正方形，∴∠DAD ′＝45°，∴AP ＝PD ′，∴在Rt △APD ′中，PD ′2＋AP 2＝AD ′2，即2P ′D 2＝16，∴PD ′＝22，即DQ ＋PQ 的最小值为2 2.★9.如图，点P 为边长为2的正方形ABCD 外一动点，且P A ⊥PB ，连接AC 、PC ，则△P AC 的最大面积为________．第9题图 第9题解图 2＋1 【解析】如解图，作出以AB 为直径的⊙O 交线段AC 于点E ，连接PE 、OE 、BE ，由AC 为正方形的对角线及⊙O 的直径为AB ，可得△AEB 为等腰直角三角形，则点E 为AC 的中点，∴S △APC ＝2S △APE ，∴要使得△APC 的面积最大，只需使得△APE 面积最大即可．∵AE长度为定值，∴只需使△APE 中AE 边上的高最大即可，∵AE ＝12AC＝12AB 2＋BC 2＝2，OA ＝OB ＝OE ＝1，∴△AOE 是等腰直角三角形，∴Rt △AOE 中，利用等面积法求得AE 边上的高为OA ·OE AE ＝1×12＝22，∴△APE 中AE 边上的高的最大值为1＋22，∴△APE 面积的最大值为12×(1＋22)×2＝22＋12，∴△P AC 的最大面积为2×(22＋12)＝2＋1.★10.如图，在四边形ABDE 中，C 是BD 边的中点，BD ＝8，AB ＝2，中考复习：几何图形中的最值问题DE＝8.若∠ACE＝135°，则线段AE长度的最大值是________．第10题图10＋42【解析】如解图①，分别将△ABC、△CDE沿AC、CE翻折，则点B落到点F处，点D落在点G处，连接AG、FG.由“两点之间线段最短”可知AG≤AF＋FG，AE≤AG＋EG，∴AE≤AF＋FG＋EG，∴如解图②所示，当点A、F、G、E四点共线时，AE最大，此时，AE＝AF＋FG＋EG，由翻折可证△ACB≌△ACF，∴CB＝CF，AB＝AF，∠ACB＝∠ACF.同理，△CDE≌△CGE，CD＝CG，DE＝GE，∠ECD＝∠ECG.∵∠ACE＝135°，∴∠ACB＋∠ECD＝45°＝∠ACF＋∠ECG，∴∠FCG＝90°.又∵BC＝DC，∴FC＝GC，∴△FCG 是等腰直角三角形．∵BD＝8，AB＝2，DE＝8，∴AF＝AB＝2，EG ＝DE＝8，由勾股定理得FG＝42＋42＝42，∴AE＝AF＋FG＋EG ＝10＋4 2.即AE的最大值为10＋4 2.第10题解图①第10题解图②7 / 7。
初中数学《几何最值问题》典型例题精编版
初中数学《最值问题》典型例题一、解决几何最值问题的通常思路两点之间线段最短；直线外一点与直线上所有点的连线段中，垂线段最短；三角形两边之和大于第三边或三角形两边之差小于第三边（重合时取到最值）是解决几何最值问题的理论依据，根据不同特征转化是解决最值问题的关键．通过转化减少变量，向三个定理靠拢进而解决问题；直接调用基本模型也是解决几何最值问题的高效手段．几何最值问题中的基本模型举例轴对称最值图形lPBANM lBAAPBl 原理两点之间线段最短两点之间线段最短三角形三边关系特征A，B为定点，l为定直线，P为直线l上的一个动点，求AP+BP的最小值A，B为定点，l为定直线，MN为直线l上的一条动线段，求AM+BN的最小值A，B为定点，l为定直线，P为直线l上的一个动点，求|AP-BP|的最大值转化作其中一个定点关于定直线l的对称点先平移AM或BN使M，N重合，然后作其中一个定点关于定直线l的对称点作其中一个定点关于定直线l的对称点折叠最值图形B'NMCAB原理两点之间线段最短特征在△ABC中，M，N两点分别是边AB，BC上的动点，将△BMN沿MN翻折，B点的对应点为B'，连接AB'，求AB'的最小值．转化转化成求AB'+B'N+NC的最小值二、典型题型1．如图：点P是∠AOB内一定点，点M、N分别在边OA、OB上运动，若∠AOB=45°，OP=32，则△PMN 的周长的最小值为．【分析】作P关于OA，OB的对称点C，D．连接OC，OD．则当M，N是CD与OA，OB的交点时，△PMN 的周长最短，最短的值是CD的长．根据对称的性质可以证得：△COD是等腰直角三角形，据此即可求解．【解答】解：作P关于OA，OB的对称点C，D．连接OC，OD．则当M，N是CD与OA，OB的交点时，△PMN的周长最短，最短的值是CD的长．∵PC关于OA对称，∴∠COP=2∠AOP，OC=OP同理，∠DOP=2∠BOP，OP=OD∴∠COD=∠COP+∠DOP=2（∠AOP+∠BOP）=2∠AOB=90°，OC=OD．∴△COD是等腰直角三角形．则CD=2OC=2×32=6．【题后思考】本题考查了对称的性质，正确作出图形，理解△PMN周长最小的条件是解题的关键．2．如图，当四边形P ABN的周长最小时，a=．【分析】因为AB，PN的长度都是固定的，所以求出PA+NB的长度就行了．问题就是P A+NB什么时候最短．把B点向左平移2个单位到B′点；作B′关于x轴的对称点B″，连接AB″，交x轴于P，从而确定N点位置，此时PA+NB最短．设直线AB″的解析式为y=kx+b，待定系数法求直线解析式．即可求得a的值．【解答】解：将N点向左平移2单位与P重合，点B向左平移2单位到B′（2，﹣1），作B′关于x轴的对称点B″，根据作法知点B″（2，1），设直线AB″的解析式为y=kx+b，则123k bk b，解得k=4，b=﹣7．∴y=4x﹣7．当y=0时，x=74，即P（74，0），a=74．故答案填：74．【题后思考】考查关于X轴的对称点，两点之间线段最短等知识．3．如图，A、B两点在直线的两侧，点A到直线的距离AM=4，点B到直线的距离BN=1，且MN=4，P为直线上的动点，|P A﹣PB|的最大值为．D PB ′N BMA【分析】作点B 于直线l 的对称点B ′，则PB=PB ′因而|P A ﹣PB|=|PA ﹣PB ′｜，则当A ，B ′、P 在一条直线上时，|P A ﹣PB|的值最大．根据平行线分线段定理即可求得PN 和PM 的值然后根据勾股定理求得P A 、PB ′的值，进而求得|P A ﹣PB|的最大值．【解答】解：作点B 于直线l 的对称点B ′，连AB ′并延长交直线l 于P ．∴B ′N=BN=1，过D 点作B ′D ⊥AM ，利用勾股定理求出AB ′=5∴|PA ﹣PB|的最大值=5．【题后思考】本题考查了作图﹣轴对称变换，勾股定理等，熟知“两点之间线段最短”是解答此题的关键．4．动手操作：在矩形纸片ABCD 中，AB=3，AD =5．如图所示，折叠纸片，使点A 落在BC 边上的A ′处，折痕为PQ ，当点A ′在BC 边上移动时，折痕的端点P 、Q 也随之移动．若限定点P 、Q 分别在AB 、AD 边上移动，则点A ′在BC 边上可移动的最大距离为．【分析】本题关键在于找到两个极端，即BA ′取最大或最小值时，点P 或Q 的位置．经实验不难发现，分别求出点P 与B 重合时，BA ′取最大值3和当点Q 与D 重合时，BA ′的最小值1．所以可求点A ′在BC 边上移动的最大距离为2．【解答】解：当点P 与B 重合时，BA ′取最大值是3，当点Q 与D 重合时（如图），由勾股定理得A ′C=4，此时BA ′取最小值为1．则点A ′在BC 边上移动的最大距离为3﹣1=2．故答案为： 2【题后思考】本题考查了学生的动手能力及图形的折叠、勾股定理的应用等知识，难度稍大，学生主要缺乏动手操作习惯，单凭想象造成错误．5．如图，直角梯形纸片ABCD ，AD ⊥AB ，AB=8，AD=CD =4，点E 、F 分别在线段AB 、AD 上，将△AEF 沿EF 翻折，点A 的落点记为P ．当P 落在直角梯形ABCD 内部时，PD 的最小值等于．【分析】如图，经分析、探究，只有当直径EF最大，且点A落在BD上时，PD最小；根据勾股定理求出BD的长度，问题即可解决．【解答】解：如图，∵当点P落在梯形的内部时，∠P=∠A=90°，∴四边形PFAE是以EF为直径的圆内接四边形，∴只有当直径EF最大，且点A落在BD上时，PD最小，此时E与点B重合；由题意得：PE=AB=8，由勾股定理得：BD2=82+62=80，∴BD=45，∴PD=458．【题后思考】该命题以直角梯形为载体，以翻折变换为方法，以考查全等三角形的判定及其性质的应用为核心构造而成；解题的关键是抓住图形在运动过程中的某一瞬间，动中求静，以静制动．6．如图，∠MON=90°，矩形ABCD的顶点A、B分别在边OM，ON上，当B在边ON上运动时，A随之在OM上运动，矩形ABCD的形状保持不变，其中AB=2，BC=1，运动过程中，点D到点O的最大距离为．【分析】取AB的中点E，连接OD、OE、DE，根据直角三角形斜边上的中线等于斜边的一半可得OE=AB，利用勾股定理列式求出DE，然后根据三角形任意两边之和大于第三边可得OD过点E时最大．【解答】解：如图，取AB的中点E，连接OD、OE、DE，∵∠MON=90°，AB=2∴OE=AE=12AB=1，∵BC=1，四边形ABCD是矩形，∴AD=BC=1，∴DE=2，根据三角形的三边关系，OD＜OE+DE，∴当OD过点E是最大，最大值为2+1．故答案为：2+1．【题后思考】本题考查了矩形的性质，直角三角形斜边上的中线等于斜边的一半的性质，三角形的三边关系，勾股定理，确定出OD过AB的中点时值最大是解题的关键．7．如图，线段AB的长为4，C为AB上一动点，分别以AC、BC为斜边在AB的同侧作等腰直角△ACD 和等腰直角△BCE，那么DE长的最小值是．【分析】设AC=x，BC=4﹣x，根据等腰直角三角形性质，得出CD=22x，CD′＝22（4﹣x），根据勾股定理然后用配方法即可求解．【解答】解：设AC=x，BC=4﹣x，∵△ABC，△BCD′均为等腰直角三角形，∴CD=22x，CD′＝22（4﹣x），∵∠ACD=45°，∠BCD′=45°，∴∠DCE=90°，∴DE2=CD2+CE2=12x2+12（4﹣x）2=x2﹣4x+8=（x﹣2）2+4，∵根据二次函数的最值，∴当x取2时，DE取最小值，最小值为：4．故答案为：2．【题后思考】本题考查了二次函数最值及等腰直角三角形，难度不大，关键是掌握用配方法求二次函数最值．8．如图，菱形ABCD中，AB=2，∠A=120°，点P，Q，K分别为线段BC，CD，BD上的任意一点，则PK+QK 的最小值为．【分析】根据轴对称确定最短路线问题，作点P关于BD的对称点P′，连接P′Q与BD的交点即为所求的点K，然后根据直线外一点到直线的所有连线中垂直线段最短的性质可知P′Q⊥CD时PK+QK的最小值，然后求解即可．【解答】解：如图，∵AB=2，∠A=120°，∴点P′到CD的距离为2×32=3，∴PK+QK的最小值为3．故答案为：3．【题后思考】本题考查了菱形的性质，轴对称确定最短路线问题，熟记菱形的轴对称性和利用轴对称确定最短路线的方法是解题的关键．9．如图所示，正方形ABCD 的边长为1，点P 为边BC 上的任意一点（可与B 、C 重合），分别过B 、C 、D 作射线AP 的垂线，垂足分别为B ′、C ′、D ′，则BB ′＋CC ′+DD ′的取值范围是．【分析】首先连接AC ，DP ．由正方形ABCD 的边长为1，即可得：S △ADP =12S 正方形ABCD =12，S △ABP +S △ACP =S △ABC =12S 正方形ABCD =12，继而可得12AP?（BB ′＋CC ′＋DD ′）=1，又由1≤AP ≤2，即可求得答案．【解答】解：连接AC ，DP ．∵四边形ABCD 是正方形，正方形ABCD 的边长为1，∴AB=CD ，S 正方形ABCD =1，∵S △ADP =12S正方形ABCD =12，S △ABP +S △ACP =S △ABC =12S正方形ABCD =12，∴S △ADP +S △ABP +S △ACP =1，∴12AP ?BB ′＋12AP ?CC ′＋12AP?DD ′＝12AP?（BB ′＋C C ′＋DD ′）=1，则BB ′＋CC ′＋DD ′＝2AP，∵1≤AP ≤2，∴当P 与B 重合时，有最大值2；当P 与C 重合时，有最小值2．∴2≤BB ′＋CC ′＋DD ′≤２．故答案为：2≤BB ′＋CC ′＋DD ′≤２．【题后思考】此题考查了正方形的性质、面积及等积变换问题．此题难度较大，解题的关键是连接AC ，DP ，根据题意得到S △ADP +S △ABP +S △ACP =1，继而得到BB ′＋CC ′＋D D ′=2AP．10．如图，菱形ABCD中，∠A=60°，AB=3，⊙A、⊙B的半径分别为2和1，P、E、F分别是边CD、⊙A 和⊙B上的动点，则PE+PF的最小值是．【分析】利用菱形的性质以及相切两圆的性质得出P与D重合时PE+PF的最小值，进而求出即可．【解答】解：由题意可得出：当P与D重合时，E点在AD上，F在BD上，此时PE+PF最小，连接BD，∵菱形ABCD中，∠A=60°，∴AB=AD，则△ABD是等边三角形，∴BD=AB=AD=3，∵⊙A、⊙B的半径分别为2和1，∴PE=1，DF=2，∴PE+PF的最小值是3．故答案为：3．【题后思考】此题主要考查了菱形的性质以及相切两圆的性质等知识，根据题意得出P点位置是解题关键．。
初中数学最值问题典型例题(含答案分析)
中考数学最值问题总结考查知识点：1、“两点之间线段最短”，“垂线段最短”，“点关于线对称”，“线段的平移”。
（2、代数计算最值问题 3、二次函数中最值问题） 问题原型：饮马问题 造桥选址问题 （完全平方公式 配方求多项式取值 二次函数顶点） 出题背景变式：角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等。
解题总思路:找点关于线的对称点实现“折”转“直” 几何基本模型： 条件：如下左图,A 、B 是直线l 同旁的两个定点． 问题：在直线l 上确定一点P ，使PA PB +的值最小． 方法：作点A 关于直线l 的对称点A ',连结A B '交l 于 点P ，则PA PB A B '+=的值最小例1、如图，四边形ABCD 是正方形，△ABE 是等边三角形，M 为对角线BD （不含B 点)上任意一点，将BM 绕点B 逆时针旋转60°得到BN ，连接EN 、AM 、CM ．（1）求证：△AMB ≌△ENB ；(2）①当M 点在何处时，AM+CM 的值最小；②当M 点在何处时，AM+BM+CM 的值最小，并说明理由；（3）当AM+BM+CM 的最小值为 时,求正方形的边长。
AB A '′Pl例2、如图13，抛物线y=ax2＋bx＋c（a≠0)的顶点为（1，4），交x轴于A、B，交y轴于D，其中B点的坐标为(3，0）（1)求抛物线的解析式（2）如图14，过点A的直线与抛物线交于点E，交y轴于点F，其中E点的横坐标为2，若直线PQ为抛物线的对称轴，点G为PQ上一动点，则x轴上是否存在一点H,使D、G、F、H四点围成的四边形周长最小.若存在,求出这个最小值及G、H的坐标；若不存在，请说明理由.(3）如图15，抛物线上是否存在一点T，过点T作x的垂线，垂足为M，过点M作直线M N∥BD,交线段AD于点N,连接MD，使△DNM∽△BMD，若存在，求出点T的坐标;若不存在，说明理由.例3、如图1,四边形AEFG与ABCD都是正方形，它们的边长分别为a，b(b≥2a),且点F在AD上（以下问题的结果可用a,b表示）（1)求S△DBF；(2）把正方形AEFG绕点A逆时针方向旋转450得图2,求图2中的S△DBF;(3) 把正方形AEFG绕点A旋转任意角度,在旋转过程中，S△DBF是否存在最大值，最小值?如果存在,试求出最大值、最小值；如果不存在，请说明理由。
(完整word版)初中几何最值问题
初中几何最值问题例题精讲一、三点共线1、构造三角形【例 1】在锐角VABC中， AB=4，BC=5，∠ ACB=45°，将△ABC 绕点 B 按逆时针方向旋转，获取△A1BC1．点E 为线段 AB 中点，点 P 是线段 AC 上的动点，在△ABC 绕点 B 按逆时针方向旋转过程中，点P 的对应点是点 P1，求线段 EP1长度的最大值与最小值．C1P1 AEPA 1B C 【牢固】以平面上一点O 为直角极点，分别画出两个直角三角形，记作△AOB和△COD，其中∠ ABO=∠DCO =30 °．如图，若 BO= 3 3，点 N 在线段 OD 上，且 NO=2．点 P 是线段 AB 上的一个动点，在将△AOB 绕点 O 旋转的过程中，线段 PN 长度的最小值为 _______，最大值为 _______．AO P OBN NC DC D备用图【例 2】如图，MON 90°，矩形ABCD 的极点 A． B 分别在边OM ， ON 上，当 B 在边 ON 上运动时， A 随之在边 OM 上运动，矩形ABCD 的形状保持不变，其中AB=2， BC=1，运动过程中，点 D 到点O 的最大距离为 __________【牢固】已知：△AOB 中， AB OB 2 ，△COD 中，CD OC 3 ,∠ABO ∠DCO .连接AD 、BC ，点 M 、N、 P 分别为OA、OD、BC的中点.若 A 、O、C三点在同素来线上，且∠ ABO 2 ，固定△AOB ，将△ COD 绕点 O 旋转，则PM的最大值为____________B AMOP NDC【牢固】在平面直角坐标系xOy 中，点 A 、 B 分别在x轴、y轴的正半轴上，点M为线段AB的中点．点D 、E 分别在x轴、y轴的负半轴上，且DE AB 10 ．以 DE 为边在第三象限内作正方形DGFE ，央求出线段MG 长度的最大值，并直接写出此时直线MG 所对应的函数的剖析式．yBMD O A xGEF【例 3 】如图，已知 A( 1, y ) ，B(2, y 2 ) 为反比率函数1P(x,0) 在x正半轴上运y图像上的两点，动点2 1 x动，当线段AP与线段BP之差达到最大时，点P的坐标是 _________yABO P x2、轴对称【例 1】求x 3 2 2 1 的最小值4x【例 2】ABE ,CD CD 是半径为5的MN 于点F，P为e O 的两条弦，EF 上任意一点，则AB 8 ，PA+PCCD 6 ，的最小值为MN 为直径，_________AB MN 于点ACM NE O P FDB【牢固】设半径为 1 的半圆的圆心为O ，直径为AB , C、 D 是半圆上两点，若弧AC 的度数为96 °，弧 BD的度数为36°，动点P在直径AB上，则CP+PD的最小值是 _______【牢固】设正三角形 ABC 的边长是2， M 是 AB 边上的中点， P 是边 BC 上任意一点，则PA+PM 的最大值为 _______,最小值为 ________【例 3】如图，已知等边△ABC 的边长为1， D、E、 F 分别是 AB、 BC、 AC 边上的点（均不与点A、 B、 C 重合），记△ DEF的周长为p .若D、E、F分别是AB、BC、AC边上任意点，则p的取值范围是.ADFB EC【例 4】如图 1，在平面直角坐标系中，抛物线y＝— x2＋ 2x＋ 3 与 x 轴交于 A．B 两点，与y 轴交于点C，点D 是抛物线的极点．（1）求直线 AC 的剖析式及 B． D 两点的坐标；（ 2）请在直线AC 上找一点M，使△BDM 的周长最小，求出点M 的坐标．图 1【例 5】如图，直线y 3 分别交 x 轴、 y 轴于 C、A 两点，将射线 AM 绕点 A 顺时针旋转 45°获取射x 23线A N， D 为 AM 上的动点， B 为 AN 上的动点，点 C 在∠ MAN 的内部．（1）当 AM∥ x 轴，且四边形 ABCD 为梯形时，求△ BCD 的面积；（2）求△BCD 周长的最小值；（ 3）当△BCD 的周长获取最小值，且BD 5 2时，求△ BCD 的面积．3yA yAyA2 2 2D1 M 1 1O 123C 4x O 123C 4x O 12 3 C 4x BN备用图备用图【例 6】在直角坐标系中， A 1, 2 ， B 4, 1 ， C m,0 ， D n, n 为四边形的 4 个极点，当四边形ABCD 的周长最短时，m_________nyODC xBA【牢固】如图1，抛物线 y＝ ax2＋ bx＋ c（ a≠0）的极点为 C（ 1， 4），交 x 轴于 A、 B 两点，交 y 轴于点 D，其中点 B 的坐标为（ 3， 0）。
初中数学几何最值专题16：加权费马点(最全修正版)
加权费马点
【例题精讲】
例1、在△ABC中，BC=4.AC=3√2,∠ACB=45°，P为三角形ABC内部一点，求AP+BP+√2PC的最小值
解析提示：
总结：
例2、（1）问题提出：如图1，已知等边△ABC的边长为2，D为BC的中点，P是AD上一动点，则BP+AP 的最小值为．
（2）问题探究：如图2，在Rt△ABC中，∠BAC＝90°，∠ABC＝30°，AC＝，在三角形内有一点P满足∠APB＝∠BPC＝120°，求PA+PB+PC的值．
（3）问题解决：如图3，某地在脱贫攻坚乡村振兴中因地制宜建造了3个特色农产品种植基地A，B，C．现需根据产品中转点P修建通往种植基地A，B，C的道路PA，PB，PC，方便农产品的储藏运输，根据地质设计，PB路段每米造价是PA的倍，PC路段每米造价是PA的2倍．已知AB＝BC＝2000米，∠ABC＝30°，要使修建3条道路费用最小，即求PA+PB+2PC的最小值．
解析提示：
总结：
针对训练
1、在等边三角形ABC中，边长为4，P为三角形ABC内部一点，求AP+BP+√2PC的最小值
2、如图，在△ABC中，∠ACB=30°，BC=6，AC=5，在△ABC内部有一点P，连接PA、PB、PC。
求：（1）PA+PB+PC的最小值；
（2）PA+PB+√2PC的最小值；
（3）PA+PB+√3PC的最小值；
（4）PA+2PB+√3PC的最小值；
（5）2PA+PB+√3PC的最小值；
（6）3PA+4PB+5PC的最小值；。
初中数学几何最值专题37：圆切线的转化(最全修正版)
切线长最值【例题精讲】例1、如图，点A的坐标为（﹣3，﹣2），⊙A的半径为1，P为x轴上一动点，PQ切⊙A于点Q，则当PQ 最小值时，点P的坐标为。
解析提示：总结：例2、如图，在平面直角坐标系xOy中，直线AB过点A（﹣3，0），B（0，3），⊙O的半径为1（O 为坐标原点），点P在直线AB上，过点P作⊙O的一条切线PQ，Q为切点，则切线长PQ的最小值为。
解析提示：总结：例3、如图，在△ABC中，AC＝4，AB＝5，BC＝6，⊙A的半径为2，点P是BC边上的动点，过点P作⊙A的一条切线PQ（其中点Q为切点），则线段PQ长度的最小值为。
解析提示：总结：例4、如图，直线y＝x+1与x轴、y轴分别相交于A、B两点，P是该直线上的任一点，过点D（3，0）向以P为圆心，AB为半径的⊙P作两条切线，切点分别为E、F．则四边形PEDF面积的最小值为。
解析提示：总结：例5、如图，AB为⊙O的直径，C为半圆的中点，⊙C的半径为2，AB＝8，点P是直径AB上的一动点，PM解析提示：总结：例6、如图，已知A、B两点的坐标分别为(2，0)、(0，2)，⊙C的圆心坐标为（－1，0），半径为1．若D 是⊙C上的一个动点，线段DA与y轴交于点E，则△ABE面积的最小值是。
解析提示：总结：针对训练1、如图，在Rt△AOB中，OA＝OB＝O的半径为1，点P是AB边上的动点，过点P作⊙O的一条切线PQ(点Q为切点)，则切线PQ的最小值为。
2、如图，⊙O的半径为1，点P（a，a﹣4）为⊙O外一点，过点P作⊙O的两条切线，切点分别为点A和点B，则四边形PBOA面积的最小值是。
3、如图，⊙O的半径为2，点O到直线l距离为3，点P是直线l上的一个动点，PQ切⊙O于点Q，则PQ 的最小值为。
4、如图，已知线段OA交⊙O于点B，且OB=AB，点P是⊙O上的一个动点，那么∠OAP的最大值是。
5、阅读理解：如图1，在纸面上画出了直线l与⊙O，直线l与⊙O相离，P为直线l上一动点，过点P作⊙O的切线PM，切点为M，连接OM、OP，当△OPM的面积最小时，称△OPM为直线l与⊙O的“最美三角形”．解决问题：（1）如图2，⊙A的半径为1，A（0，2），分别过x轴上B、O、C三点作⊙A的切线BM、OP、CQ，切点分别是M、P、Q，下列三角形中，是x轴与⊙A的“最美三角形”的是．（填序号）①△ABM；②△AOP；③△ACQ（2）如图3，⊙A的半径为1，A（0，2），直线y＝kx（k≠0）与⊙A“最美三角形”的面积为，求k的值．（3）点B在x轴上，以B为圆心，为半径画⊙B，若直线y＝x+3与⊙B的“最美三角形”的面积小于，请直接写出圆心B的横坐标x B的取值范围．课堂精炼1、如图，点A的坐标为（﹣3，﹣2），⊙A的半径为1，P为x轴上一动点，PQ切⊙A于点Q，则当PQ最小值时，点P的坐标为。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
初中数学几何最值问题典型例题GE GROUP system office room 【GEIHUA16H-GEIHUA GEIHUA8Q8-初中数学《最值问题》典型例题一、解决几何最值问题的通常思路两点之间线段最短；直线外一点与直线上所有点的连线段中，垂线段最短；三角形两边之和大于第三边或三角形两边之差小于第三边（重合时取到最值）是解决几何最值问题的理论依据，根据不同特征转化是解决最值问题的关键．通过转化减少变量，向三个定理靠拢进而解决问题；直接调用基本模型也是解决几何最值问题的高效手段．几何最值问题中的基本模型举例二、典型题型1．如图：点P是∠AOB内一定点，点M、N分别在边OA、OB上运动，若∠AOB=45°，OP=PMN的周长的最小值为．【分析】作P关于OA，OB的对称点C，D．连接OC，OD．则当M，N是CD与OA，OB的交点时，△PMN的周长最短，最短的值是CD的长．根据对称的性质可以证得：△COD是等腰直角三角形，据此即可求解．【解答】解：作P关于OA，OB的对称点C，D．连接OC，OD．则当M，N是CD与OA，OB的交点时，△PMN的周长最短，最短的值是CD的长．∵PC关于OA对称，∴∠COP=2∠AOP，OC=OP同理，∠DOP=2∠BOP，OP=OD∴∠COD=∠COP+∠DOP=2（∠AOP+∠BOP）=2∠AOB=90°，OC=OD．∴△COD是等腰直角三角形．则CD OC=6．【题后思考】本题考查了对称的性质，正确作出图形，理解△PMN周长最小的条件是解题的关键．2．如图，当四边形PABN的周长最小时，a= ．【分析】因为AB，PN的长度都是固定的，所以求出PA+NB的长度就行了．问题就是PA+NB什么时候最短．把B点向左平移2个单位到B′点；作B′关于x轴的对称点B″，连接AB″，交x轴于P，从而确定N点位置，此时PA+NB最短．设直线AB″的解析式为y=kx+b，待定系数法求直线解析式．即可求得a的值．【解答】解：将N点向左平移2单位与P重合，点B向左平移2单位到B′（2，﹣1），作B′关于x轴的对称点B″，根据作法知点B″（2，1），设直线AB″的解析式为y=kx+b，则123k bk b=+⎧⎨-=+⎩，解得k=4，b=﹣7．∴y=4x﹣7．当y=0时，x=74，即P（74，0），a=74．故答案填：74．【题后思考】考查关于X轴的对称点，两点之间线段最短等知识．3．如图，A、B两点在直线的两侧，点A到直线的距离AM=4，点B到直线的距离BN=1，且MN=4，P为直线上的动点，|PA﹣PB|的最大值为．【分析】作点B于直线l的对称点B′，则PB=PB′因而|PA﹣PB|=|PA﹣PB′|，则当A，B′、P在一条直线上时，|PA﹣PB|的值最大．根据平行线分线段定理即可求得PN和PM的值然后根据勾股定理求得PA、PB′的值，进而求得|PA﹣PB|的最大值．【解答】解：作点B于直线l的对称点B′，连AB′并延长交直线l于P．∴B′N=BN=1，过D点作B′D⊥AM，利用勾股定理求出AB′=5∴|PA﹣PB|的最大值=5．【题后思考】本题考查了作图﹣轴对称变换，勾股定理等，熟知“两点之间线段最短”是解答此题的关键．4．动手操作：在矩形纸片ABCD中，AB=3，AD=5．如图所示，折叠纸片，使点A落在BC边上的A′处，折痕为PQ，当点A′在BC边上移动时，折痕的端点P、Q也随之移动．若限定点P、Q分别在AB、AD边上移动，则点A′在BC边上可移动的最大距离为．【分析】本题关键在于找到两个极端，即BA′取最大或最小值时，点P或Q的位置．经实验不难发现，分别求出点P与B重合时，BA′取最大值3和当点Q与D重合时，BA′的最小值1．所以可求点A′在BC边上移动的最大距离为2．【解答】解：当点P与B重合时，BA′取最大值是3，当点Q与D重合时（如图），由勾股定理得A′C=4，此时BA′取最小值为1．则点A′在BC边上移动的最大距离为3﹣1=2．故答案为：2【题后思考】本题考查了学生的动手能力及图形的折叠、勾股定理的应用等知识，难度稍大，学生主要缺乏动手操作习惯，单凭想象造成错误．5．如图，直角梯形纸片ABCD，AD⊥AB，AB=8，AD=CD=4，点E、F分别在线段AB、AD上，将△AEF沿EF翻折，点A的落点记为P．当P落在直角梯形ABCD内部时，PD的最小值等于．【分析】如图，经分析、探究，只有当直径EF最大，且点A落在BD上时，PD最小；根据勾股定理求出BD的长度，问题即可解决．【解答】解：如图，∵当点P落在梯形的内部时，∠P=∠A=90°，∴四边形PFAE是以EF为直径的圆内接四边形，∴只有当直径EF最大，且点A落在BD上时，PD最小，此时E与点B重合；由题意得：PE=AB=8，由勾股定理得：BD2=82+62=80，∴BD=45，∴PD=458．【题后思考】该命题以直角梯形为载体，以翻折变换为方法，以考查全等三角形的判定及其性质的应用为核心构造而成；解题的关键是抓住图形在运动过程中的某一瞬间，动中求静，以静制动．6．如图，∠MON=90°，矩形ABCD的顶点A、B分别在边OM，ON上，当B在边ON 上运动时，A随之在OM上运动，矩形ABCD的形状保持不变，其中AB=2，BC=1，运动过程中，点D到点O的最大距离为．【分析】取AB的中点E，连接OD、OE、DE，根据直角三角形斜边上的中线等于斜边的一半可得OE=AB，利用勾股定理列式求出DE，然后根据三角形任意两边之和大于第三边可得OD过点E时最大．【解答】解：如图，取AB的中点E，连接OD、OE、DE，∵∠MON=90°，AB=2∴OE =AE =12AB =1， ∵BC =1，四边形ABCD 是矩形，∴AD =BC =1，∴DE根据三角形的三边关系，OD ＜OE +DE ，∴当OD 过点E ．故答案为：+1．【题后思考】本题考查了矩形的性质，直角三角形斜边上的中线等于斜边的一半的性质，三角形的三边关系，勾股定理，确定出OD 过AB 的中点时值最大是解题的关键．7．如图，线段AB 的长为4，C 为AB 上一动点，分别以AC 、BC 为斜边在AB 的同侧作等腰直角△ACD 和等腰直角△BCE ，那么DE 长的最小值是 ．【分析】设AC =x ，BC =4﹣x ，根据等腰直角三角形性质，得出CD =2x ，CD ′=2（4﹣x ），根据勾股定理然后用配方法即可求解． 【解答】解：设AC =x ，BC =4﹣x ，∵△ABC ，△BCD ′均为等腰直角三角形，∴CD =2x ，CD ′=2（4﹣x ）， ∵∠ACD =45°，∠BCD ′=45°，∴∠DCE =90°，∴DE 2=CD 2+CE 2=12x 2+12（4﹣x ）2=x 2﹣4x +8=（x ﹣2）2+4， ∵根据二次函数的最值，∴当x 取2时，DE 取最小值，最小值为：4．故答案为：2．【题后思考】本题考查了二次函数最值及等腰直角三角形，难度不大，关键是掌握用配方法求二次函数最值．8．如图，菱形ABCD 中，AB =2，∠A =120°，点P ，Q ，K 分别为线段BC ，CD ，BD 上的任意一点，则PK +QK 的最小值为 ．【分析】根据轴对称确定最短路线问题，作点P 关于BD 的对称点P ′，连接P ′Q 与BD 的交点即为所求的点K ，然后根据直线外一点到直线的所有连线中垂直线段最短的性质可知P ′Q ⊥CD 时PK +QK 的最小值，然后求解即可．【解答】解：如图，∵AB=2，∠A=120°，∴点P′到CD的距离为∴PK+QK．故答案为：．【题后思考】本题考查了菱形的性质，轴对称确定最短路线问题，熟记菱形的轴对称性和利用轴对称确定最短路线的方法是解题的关键．9．如图所示，正方形ABCD的边长为1，点P为边BC上的任意一点（可与B、C重合），分别过B、C、D作射线AP的垂线，垂足分别为B′、C′、D′，则BB′+CC′+DD′的取值范围是．【分析】首先连接AC，DP．由正方形ABCD的边长为1，即可得：S△ADP=12S正方形ABCD =12，S△ABP+S△ACP=S△ABC=12S正方形ABCD=12，继而可得12AP（BB′+CC′+DD′）=1，又由1≤AP，即可求得答案．【解答】解：连接AC，DP．∵四边形ABCD是正方形，正方形ABCD的边长为1，∴AB=CD，S正方形ABCD=1，∵S△ADP=12S正方形ABCD=12，S△ABP+S△ACP=S△ABC=12S正方形ABCD=12，∴S△ADP+S△ABP+S△ACP=1，∴12APBB′+12APCC′+12APDD′=12AP（BB′+CC′+DD′）=1，则BB′+CC′+DD′=2AP，∵1≤AP∴当P与B重合时，有最大值2；当P与C．≤BB′+CC′+DD′≤2．故答案为：≤BB′+CC′+DD′≤2．【题后思考】此题考查了正方形的性质、面积及等积变换问题．此题难度较大，解题的关键是连接AC，DP，根据题意得到S△ADP+S△ABP+S△ACP=1，继而得到BB′+CC′+DD′=2AP．10．如图，菱形ABCD中，∠A=60°，AB=3，⊙A、⊙B的半径分别为2和1，P、E、F分别是边CD、⊙A和⊙B上的动点，则PE+PF的最小值是．【分析】利用菱形的性质以及相切两圆的性质得出P与D重合时PE+PF的最小值，进而求出即可．【解答】解：由题意可得出：当P与D重合时，E点在AD上，F在BD上，此时PE+PF最小，连接BD，∵菱形ABCD中，∠A=60°，∴AB=AD，则△ABD是等边三角形，∴BD=AB=AD=3，∵⊙A、⊙B的半径分别为2和1，∴PE=1，DF=2，∴PE+PF的最小值是3．故答案为：3．【题后思考】此题主要考查了菱形的性质以及相切两圆的性质等知识，根据题意得出P点位置是解题关键．。