河北大学数字电路2011年考研专业课初试真题
2011年考研计算机学科专业基础综合考试真题及答案详解

40.主机甲与主机乙之间已建立一个 TCP 连接,主机甲向主机乙发送了 3 个连续的 TCP 段,
分别包含 300 字节、400 字节和 500 字节的有效载荷,第 3 个段的序号为 900。若主机
乙仅正确接收到第 1 和第 3 个段,则主机乙发送给主机甲的确认序号是
A 300
B 500
C 1200
A.进程 P 的代码段B.进程 P 中打开的文件
C.进程 P 的全局变量
D.进程 P 中某线程的栈指针
26.用户程序发出磁盘 I/O 请求后,系统的正确处理流程是
A.用户程序→系统调用处理程序→中断处理程序→设备驱动程序
B.用户程序→系统调用处理程序→设备驱动程序→中断处理程序
C.用户程序→设备驱动程序→系统调用处理程序→中断处理程序
A.仅 II
B.仅 、II
C.仅 III
D.仅 、III
9.为提高散列(Hash)表的查找效率,可以采取的正确措施是
增大装填(载)因子
II 设计冲突(碰撞)少的散列函数 III.处理冲突(碰撞)时避免产生聚集(堆积)现象
您所下载的资料来源于 获取更多考研资料,请访问
考研资料下载中心
A.仅 I
B.仅 II
素和队尾元素。若初始时队列为空,且要求第 1 个进入队列的元素存储在 A[0]处,则初
始时 front 和 rear 的值分别是
A 0, 0
B 0, n-1
C n-1, 0
D n-1, n-1
4.若一棵完全二叉树有 768 个结点,则该二叉树中叶结点的个数是
A 257
B 258
C 384
D 385
5.若一棵二叉树的前序遍历序列和后序遍历序列分别为 1, 2, 3, 4 和 4, 3, 2, 1,则该二叉树
河北大学(已有10试题)

河北大学电子信息工程学院电路分析根底2021电路分析技术2007电路分析2021-2021模拟电子技术根底2021——2021-2021电子技术根底2007——2021-2021数字信号处理2021——2021-2021半导体物理学2005高等数学2006——2021控制理论与数学电子根底2006通信原理2005,2007——2021-2021通信原理、信号与系统2006微电子学根底2007微电子技术根底2006,2021自动控制理论2007——2021-2021自动控制原理2005传感器技术2007——2021-2021电磁学2007——2021-2021管理学院财政学、社会保障2007——2021电子商务2007专业综合〔行政管理专业〕2021——2021-2021 公共管理学2007——2021-2021公共管理学〔单独考试〕2007管理学2021——2021-2021行政管理综合2007西方经济学2005——2021-2021管理信息系统2007财政学2006财政学、劳动经济学2005微观经济学、管理学2005——2006会计学综合2005——2021-2021企业管理综合2007——2021-2021劳动和社会保障2006社会保障学2005信息检索2021——2021-2021情报学根底2021-2021图书馆学根底2005——2006,2021-2021信息资源建设2005——2006信息资源管理2007——2021档案学根底2021-2021公共财政与社会保障2021-2021化学与环境科学学院高等数学2007——2021高分子化学与物理2005——2006高分子化学2021-2021化学综合2006——2021〔注:2006年的试卷共7页,缺P7〕环境化学2005——2006,2021——2021-2021环境监测2021——2021-2021环境监测与环境工程2006无机化学2005——2021-2021物理化学2005——2021-2021物理化学〔结构化学〕2005——2006有机化学2005——2007,2021-2021分析化学2005,2007——2021-2021机械与建筑工程学院材料力学2021——2021-2021工程力学2006理论力学2005教育学院教育学专业根底综合〔全国统考试卷〕2007——2021-2021〔2007——2021-2021有答案〕心理学专业根底综合〔全国统考试卷〕2007——2021-2021〔2007——2021-2021有答案〕教与学的根本理论2007——2021-2021比拟教育学2005开展与教育心理学专业综合考试2005教育管理学2005教育技术学2005——2021-2021教育学〔比拟教育学专业〕2005教育学〔教育史专业〕2005教育学〔教育原理专业〕2005教育学综合2006教育原理2005心理学概论2005——2006,2021——2021-2021心理学研究方法2006,2021——2021-2021信息技术教育应用2005中外教育史2005——2006经济学院人口学2021人口学理论2005——2007,2021-2021统计学2005人口统计学2005〔注:本试卷共2页,缺P2〕西方经济学2005——2021-2021政治经济学与西方经济学2007——2021-2021西方经济学与政治经济学2005——2006政经与西经2005货币银行学2005人口、资源与环境经济学2005社会学理论2007人文学院语言学根底2007——2021文学根底2007——2021-2021汉语言根底2021-2021古代汉语2006古代汉语〔汉语言文字学专业〕2005,2021-2021〔注:2005共2页,缺P1〕古代汉语〔中国古典文献学专业〕2005古代汉语、现代汉语2006古代汉语与文献2006,2021-2021古代文学与外国文学2005文学批评2005文艺理论2005——2006文学理论2021-2021现代汉语与古代汉语2005〔注:本卷共2页,缺P1〕现代汉语与语言理论2005——2006语言学理论2005中国古代文学2006,2021-2021中国现当代文学2005——2006,2021-2021中国文学史〔中国古代文学专业〕2005中国文学史〔中国古典文献学专业〕2005综合〔中国古代文学专业〕2005〔注:本卷共2页,缺P1〕综合课〔中国语言文学所有专业〕2006历史学专业根底〔全国统考试卷〕2007——2021历史学根底2021-2021史学概论2005历史综合〔中国近现代史专业〕2006历史综合〔专门史专业〕2006古代汉语〔历史学、中国古代史专业〕2005中国古代史2005——2006中国近代史2005中国近现代史2006中国通史2005——2006中国现代史2005东北亚国际关系史2003年复试试卷宋辽夏金史方向2003年复试试卷中国古代经济史方向2003年复试试卷中国古代政法史方向2003年复试试卷中国古代史专业同等学力考生加试题2003年复试试卷中国古代史专业2003年复试试卷中国古代史专业同等学力考生加试?中国通史?试卷中国古代史专业同等学力考生加试?史学导论?试卷中国近现代史专业2003年复试试卷生命科学学院生态学2006——2021-2021生物化学2005——2021-2021生物学综合2006——2021-2021微生物学2005,2007——2021〔注:2005年试卷共2页,缺P2〕细胞生物学2005植物生物学2005动物生态学2005普通动物学2005普通昆虫学2005有机化学2005——2021数学与计算机学院高等代数与解析几何2005——2021-2021数学分析2005——2021-2021数据结构与操作系统2005——2021外国语学院二外法语2005——2021-2021二外日语2005——2021-2021英语语言技能综合2007——2021-2021英语语言知识综合2021——2021-2021英语知识综合2007语言学根底2021——2021-2021语言学根底理论2007根底英语2005——2006翻译与写作2005——2006二外英语2005,2007——2021-2021日语综合2021——2021-2021〔2021-2021缺第三页〕日本语知识综合2007日语技能综合2021日语语言技能综合2007根底日语2005综合日语2005——2006物理科学与技术学院电动力学2006——2021-2021高等数学2005——2021-2021光学2005——2021-2021量子力学2005——2021-2021电磁学2007——2021-2021普通物理2021-2021新闻传播学院文史综合2005——2021〔2021为回忆版〕传播理论与实务2005新闻传播学〔传播学〕2006新闻传播综合2006——2021〔2021为回忆版〕新闻学综合2005药学学院分析化学2005,2007——2021-2021药物分析2005,2007——2021-2021药物化学2007,2021-2021有机化学2006——2021-2021〔2021-2021共4页缺2页〕综合化学2005生物化学〔药〕2021-2021艺术学院中外美术史2007——2021-2021美学2005——2021-2021设计学概论2005,2021——2021-2021艺术概论2007——2021-2021艺术设计概论2007艺术设计理论2005——2006,2021——2021-2021艺术设计史2006——2007艺术学2005——2021-2021音乐技术理论2006——2021音乐理论2005音乐学理论2006——2021影视艺术教育2007——2021-2021视听语言2007——2021-2021政法学院政治学原理2007——2021-2021专业综合〔政治学专业〕2021法律根底2005法学根底2005伦理学2005马克思主义开展史2007马克思主义根本原理2007——2021-2021马克思主义原理2005——2006马克思主义哲学2006——2007,2021-2021马克思主义哲学〔哲学学科、马克思主义哲学专业〕2005 马克思主义哲学〔中国哲学专业〕2005马克思主义哲学原理2021毛泽东思想与邓小平理论概论2005——2006,2021-2021 邓小平理论与毛泽东思想概论2021邓小平理论与毛泽东思想2007当代中国政治与政府,政治社会学2007民商法2005诉讼法2005宪法与行政法2005行政法与行政诉讼法学2006法学综合二〔含刑法、刑事诉讼法、经济法〕2021——2021-2021法学综合一〔含法理、宪法学、民法〕2021——2021-2021理论法学〔法理学、宪法学〕2006——2007应用法学〔民法、刑法〕〔法学理论、宪法学与行政法学、民商法学、刑法学、经济法学、诉讼法学专业〕2007〔本卷共3页,缺P3〕应用法学〔法学、民商法专业〕2006应用法学〔诉讼法专业〕2006逻辑学2021——2021-2021哲学史〔马克思主义哲学、中国哲学、伦理学专业〕2007哲学史〔伦理学专业〕2005哲学史〔哲学学科、马克思主义哲学专业〕2005中西哲学史2021中国哲学史2005哲学综合2021-2021综合考试〔西方哲学局部〕2006社会学理论2007——2021-2021社会学研究方法2007——2021-2021公共管理学2007——2021-2021公共管理学〔单独考试〕2007专业根底课〔法律硕士〕2007综合课〔法律硕士〕2007当代中国政治与政府政治社会学2021-2021质检学院传感器技术2007——2021-2021电子技术根底2007——2021-2021。
2010-2011数字电子技术A卷及答案

2011~2012学年度第二学期《数字电子技术基础》试卷(A 卷)适用年级专业:2010级电子信息工程、自动化 考 试 形 式:( )开卷、(√)闭卷二级学院: 行政班级: 学 号:教 学 班: 任课教师: 姓 名:注:学生在答题前,请将密封线外各项内容准确填写,填写不清者,将不计成绩。
一、填空题(本大题共10小题,每空格1分,共10分)请在每小题的空格中填上正确答案。
错填、不填均无分。
1.对于十进制数83,它对应的十六进制数表示是。
2.逻辑代数的基本逻辑运算有 、或、非3种。
3.将变量的全部最小项分别用一个小方块表示,并使具有逻辑相邻性的最小项在几何位置上也相邻地排列在一起而得到的图形称为 。
4.现有一个存储容量为256k ×4位的RAM 存储器,则该存储器RAM 的地址线有 根。
5.图1所示为某计数器的时序图,由此可判定该计数器是 进制计数器。
FAB CPQ 0Q 1Q 2图1 图26.某一门电路的工作波形如图2所示,其中A 、B 是输入端,F 是输出端。
则F 的逻辑表达式为 。
7. 可编程阵列逻辑PAL 是一种与阵列可编程、或阵列 的可编程逻辑器件。
8.将模拟信号转化为数字信号,需要采用A/D 转换器。
实现A/D 转换一般要经过采样、保持、量化和 等4个过程。
9.如果用ROM 实现将8位二进制数转换成十进制数(用BCD 码表示)的转换电路,其所需容量为。
10.图3所示的门电路为集电极开路的TTL 电路,则可写出输出信号的表达式Y = 。
A +0.3VB+3.6VY图3二、选择题(本大题共10小题,每小题2分,共20分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
11.十进制数87所对应的十六进制数和8421BCD 码分别为 。
【 】A .87H ,(10000111)8421BCDB .57H ,(10000111)8421BCDC .A7H ,(10100111)8421BCD D .57H ,(01010111)8421BCD12.设某函数的表达式为)(E D C B A F+=,则F= 。
十四套名校数电考研真题、答案与详解

十四套名校数电考研真题、答案与详解网学天地()出品版权所有!目 录1华中科技大学2008年《电子技术基础》考研真题与答案 (1)2电子科技大学2010年《数字电路》考研真题与答案 (6)3浙江大学2011年《信号系统与数字电路》考研真题与答案 (14)4吉林大学2010年《电子技术》考研真题与答案 (20)5南开大学2011年《电子综合基础》考研真题与答案 (23)6华南理工大学2011年《电子技术基础》考研试题 (27)7哈尔滨工业大学2010年《电子技术基础》考研真题与答案 (33)8哈尔滨工业大学2010年《电路与数字电子技术》考研真题与答案 (39)9哈尔滨工业大学2010年《信号与系统、数字电路》考研真题与答案 (40)10复旦大学2009年《电子线路与集成电路设计》考研真题与答案 (48)11东南大学2008年《信号与系统、数字电路》考研真题与答案 (52)12深圳大学2011年《数字电路与专业综合》考研真题与答案 (60)13重庆大学2010年《电子技术一》考研真题与答案 (67)14北京邮电大学2009年《电子电路》考研真题与答案 (71)网学天地( )出品 版权所有! 11 华中科技大学2008年《电子技术基础》考研真题与答案数字电子技术部分一、填空题(每空1分,共20分)4.数字电路中的三极管一般工作于________区和________区。
答案:截止 饱和5.(63)O 的二进制补码是________,格雷码是________。
答案:(101100)B (101010)B6.四个逻辑变量的最小项最多有________个,任意两个最小项之积为________。
答案:16 07.触发器是对脉冲________敏感的存储单元电路,锁存器是对脉冲________敏感的存储电源电路。
答案:边沿 电平8.对于一个含有逻辑变量A 的逻辑表达式L ,当其他变量用0或1代入后,表达式可化简为:L =________或________时,会产生竞争冒险。
十四套名校数电考研真题、答案与详解

十四套名校数电考研真题、答案与详解网学天地()出品版权所有!目 录1华中科技大学2008年《电子技术基础》考研真题与答案 (1)2电子科技大学2010年《数字电路》考研真题与答案 (6)3浙江大学2011年《信号系统与数字电路》考研真题与答案 (14)4吉林大学2010年《电子技术》考研真题与答案 (20)5南开大学2011年《电子综合基础》考研真题与答案 (23)6华南理工大学2011年《电子技术基础》考研试题 (27)7哈尔滨工业大学2010年《电子技术基础》考研真题与答案 (33)8哈尔滨工业大学2010年《电路与数字电子技术》考研真题与答案 (39)9哈尔滨工业大学2010年《信号与系统、数字电路》考研真题与答案 (40)10复旦大学2009年《电子线路与集成电路设计》考研真题与答案 (48)11东南大学2008年《信号与系统、数字电路》考研真题与答案 (52)12深圳大学2011年《数字电路与专业综合》考研真题与答案 (60)13重庆大学2010年《电子技术一》考研真题与答案 (67)14北京邮电大学2009年《电子电路》考研真题与答案 (71)网学天地( )出品 版权所有! 11 华中科技大学2008年《电子技术基础》考研真题与答案数字电子技术部分一、填空题(每空1分,共20分)4.数字电路中的三极管一般工作于________区和________区。
答案:截止 饱和5.(63)O 的二进制补码是________,格雷码是________。
答案:(101100)B (101010)B6.四个逻辑变量的最小项最多有________个,任意两个最小项之积为________。
答案:16 07.触发器是对脉冲________敏感的存储单元电路,锁存器是对脉冲________敏感的存储电源电路。
答案:边沿 电平8.对于一个含有逻辑变量A 的逻辑表达式L ,当其他变量用0或1代入后,表达式可化简为:L =________或________时,会产生竞争冒险。
2011考研数学一真题及答案解析

2011年全国硕士研究生入学统一考试数学一试题一、选择题:1~8小题,每小题4分,共32分,下列每题给出的四个选项中,只有一个选项符合题目要求,请将所选项前的字母填在答题纸...指定位置上. (1) 曲线234(1)(2)(3)(4)y x x x x =−−−−的拐点是( )(A) (1,0). (B) (2,0). (C) (3,0). (D) (4,0). (2) 设数列{}n a 单调减少,lim 0n n a →∞=,1(1,2,)nn kk S an ===∑ 无界,则幂级数1(1)nn n a x ∞=−∑的收敛域为( )(A) (1,1]−. (B) [1,1)−. (C) [0,2). (D) (0,2]. (3) 设函数()f x 具有二阶连续导数,且()0f x >,(0)0f '=,则函数()ln ()z f x f y =在点(0,0)处取得极小值的一个充分条件是( )(A) (0)1f >,(0)0f ''>. (B) (0)1f >,(0)0f ''<. (C) (0)1f <,(0)0f ''>. (D) (0)1f <,(0)0f ''<.(4) 设4ln sin I x dx π=⎰,40ln cot J x dx π=⎰,40ln cos K x dx π=⎰,则,,I J K 的大小关系是( )(A) I J K <<. (B) I K J <<. (C) J I K <<. (D) K J I <<.(5) 设A 为3阶矩阵,将A 的第2列加到第1列得矩阵B ,再交换B 的第2行与第3行得单位矩阵,记1100110001P ⎛⎫ ⎪= ⎪ ⎪⎝⎭,2100001010P ⎛⎫ ⎪= ⎪ ⎪⎝⎭,则A =( ) (A) 12PP . (B) 112P P −. (C) 21P P . (D) 121P P −.(6) 设1234(,,,)A αααα=是4阶矩阵,*A 为A 的伴随矩阵,若(1,0,1,0)T是方程组0Ax =的一个基础解系,则*0A x =的基础解系可为( )(A) 13,αα. (B) 12,αα. (C) 123,,ααα. (D) 234,,ααα.(7) 设1()F x ,2()F x 为两个分布函数,其相应的概率密度1()f x ,2()f x 是连续函数,则必为概率密度的是( )(A)12()()f x f x . (B)212()()f x F x .(C)12()()f x F x . (D)1221()()()()f x F x f x F x +.(8) 设随机变量X 与Y 相互独立,且()E X 与()E Y 存在,记{}max ,U X Y =,{}min ,V X Y =则()E UV =( )(A)()()E U E V ⋅. (B)()()E X E Y ⋅. (C)()()E U E Y ⋅. (D)()()E X E V ⋅.二、填空题:9~14小题,每小题4分,共24分,请将答案写在答题纸...指定位置上. (9) 曲线0tan (0)4π=≤≤⎰xy tdt x 的弧长s = .(10) 微分方程cos xy y e x −'+=满足条件(0)0y =的解为y = .(11) 设函数2sin (,)1xytF x y dt t =+⎰,则222x y F x ==∂=∂ .(12) 设L 是柱面方程221x y +=与平面=+z x y 的交线,从z 轴正向往z 轴负向看去为逆时针方向,则曲线积分22L y xzdx xdy dz ++=⎰ .(13) 若二次曲面的方程22232224x y z axy xz yz +++++=,经过正交变换化为221144y z +=,则a = .(14) 设二维随机变量(),X Y 服从正态分布()22,;,;0N μμσσ,则()2E X Y = .三、解答题:15~23小题,共94分.请将解答写在答题纸...指定的位置上.解答应写出文字说明、证明过程或演算步骤.(15)(本题满分10分)求极限110ln(1)lim()x e x x x−→+.(16)(本题满分9分)设函数(,())z f xy yg x =,其中函数f 具有二阶连续偏导数,函数()g x 可导且在1x =处取得极值(1)1g =,求211x y zx y==∂∂∂.(17)(本题满分10分)求方程arctan 0k x x −=不同实根的个数,其中k 为参数.(18)(本题满分10分)(Ⅰ)证明:对任意的正整数n ,都有111ln(1)1n n n<+<+ 成立. (Ⅱ)设111ln (1,2,)2n a n n n=+++−=,证明数列{}n a 收敛.(19)(本题满分11分)已知函数(,)f x y 具有二阶连续偏导数,且(1,)0f y =,(,1)0f x =,(,)Df x y dxdy a =⎰⎰,其中{}(,)|01,01D x y x y =≤≤≤≤,计算二重积分''(,)xy DI xy f x y dxdy =⎰⎰.(20)(本题满分11分)设向量组123(1,0,1)(0,1,1)(1,3,5)T T T ααα===,,,不能由向量组1(1,1,1)T β=,2(1,2,3)T β=,3(3,4,)T a β=线性表示.(I) 求a 的值;(II) 将123,,βββ由123,,ααα线性表示.(21)(本题满分11分)A 为三阶实对称矩阵,A 的秩为2,即()2r A =,且111100001111A −⎛⎫⎛⎫ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪−⎝⎭⎝⎭.(I) 求A 的特征值与特征向量; (II) 求矩阵A . (22)(本题满分11分)设随机变量X 与Y且{}221P X Y ==.(I) 求二维随机变量(,)X Y 的概率分布; (II) 求Z XY =的概率分布; (III) 求X 与Y 的相关系数XY ρ.(23)(本题满分 11分) 设12,,,n X X X 为来自正态总体20(,)μσN 的简单随机样本,其中0μ已知,20σ>未知.X 和2S 分别表示样本均值和样本方差.(I) 求参数2σ的最大似然估计量2σ∧; (II) 计算2()E σ∧和2()D σ∧.2011年全国硕士研究生入学统一考试数学一试题答案一、选择题:1~8小题,每小题4分,共32分,下列每题给出的四个选项中,只有一个选项符合题目要求,请将所选项前的字母填在答题纸...指定位置上. (1)【答案】(C).【解析】记1111,1,0y x y y '''=−==,2222(2),2(2),2,y x y x y '''=−=−= 32333(3),3(3),6(3),y x y x y x '''=−=−=− 432444(4),4(4),12(4),y x y x y x '''=−=−=− (3)()y x P x ''=−,其中(3)0P ≠,30x y =''=,在3x =两侧,二阶导数符号变化,故选(C).(2)【答案】(C).【解析】观察选项:(A),(B),(C),(D)四个选项的收敛半径均为1,幂级数收敛区间的中心在1x =处,故(A),(B)错误;因为{}n a 单调减少,lim 0n n a →∞=,所以0n a ≥,所以1nn a∞=∑为正项级数,将2x =代入幂级数得1nn a∞=∑,而已知S n =1nkk a=∑无界,故原幂级数在2x =处发散,(D)不正确.当0x =时,交错级数1(1)nn n a ∞=−∑满足莱布尼茨判别法收敛,故0x =时1(1)nn n a ∞=−∑收敛.故正确答案为(C).(3)【答案】(A). 【解析】(0,0)(0,0)|()ln ()|(0)ln (0)0zf x f y f f x∂''=⋅==∂, (0,0)(0,0)()|()|(0)0,()z f y f x f y f y '∂'=⋅==∂故(0)0f '=, 2(0,0)(0,0)2|()ln ()|(0)ln (0)0,zA f x f y f f x∂''''==⋅=⋅>∂22(0,0)(0,0)()[(0)]|()|0,()(0)z f y f B f x x y f y f ''∂'==⋅==∂∂222(0,0)(0,0)22()()[()][(0)]|()|(0)(0).()(0)z f y f y f y f C f x f f y f y f ''''∂−''''==⋅=−=∂ 又22[(0)]ln (0)0,AC B f f ''−=⋅>故(0)1,(0)0f f ''>>.(4)【答案】(B). 【解析】因为04x π<<时, 0sin cos 1cot x x x <<<<,又因ln x 是单调递增的函数,所以ln sin ln cos ln cot x x x <<. 故正确答案为(B). (5)【答案】 (D).【解析】由于将A 的第2列加到第1列得矩阵B ,故100110001A B ⎛⎫ ⎪= ⎪ ⎪⎝⎭, 即1AP B =,11A BP −=.由于交换B 的第2行和第3行得单位矩阵,故100001010B E ⎛⎫⎪= ⎪ ⎪⎝⎭, 即2,P B E =故122B P P −==.因此,121A P P −=,故选(D).(6)【答案】(D).【解析】由于(1,0,1,0)T 是方程组0Ax =的一个基础解系,所以(1,0,1,0)0TA =,且()413r A =−=,即130αα+=,且0A =.由此可得*||A A A E O ==,即*1234(,,,)A O =αααα,这说明1234,,,αααα是*0A x =的解.由于()3r A =,130αα+=,所以234,,ααα线性无关.又由于()3r A =,所以*()1r A =,因此*0A x =的基础解系中含有413−=个线性无关的解向量.而234,,ααα线性无关,且为*0A x =的解,所以234,,ααα可作为*0A x =的基础解系,故选(D).(7)【答案】(D). 【解析】选项(D)1122()()()()f x F x f x F x dx +∞−∞⎡⎤+⎣⎦⎰2211()()()()F x dF x F x dF x +∞−∞⎡⎤=+⎣⎦⎰21()()d F x F x +∞−∞⎡⎤=⎣⎦⎰12()()|F x F x +∞−∞=1=. 所以1221()()f F x f F x +为概率密度.(8)【答案】(B).【解析】因为 {},,max ,,,X X Y U X Y Y X Y ≥⎧==⎨<⎩ {},,min ,,Y X Y V X Y X X Y ≥⎧==⎨<⎩.所以,UV XY =,于是()()E UV E XY = ()()E X E Y =.二、填空题:9~14小题,每小题4分,共24分,请将答案写在答题纸...指定位置上. (9)【答案】(ln 1+.【解析】选取x 为参数,则弧微元sec ds xdx ===所以440sec ln sec tan ln(1s xdx x x ππ==+=+⎰. (10)【答案】sin xy e x −=.【解析】由通解公式得(cos )dx dxx y e e x e dx C −−⎰⎰=⋅+⎰(cos )x e xdx C −=+⎰(sin )xe x C −=+.由于(0)0,y =故C =0.所以sin xy e x −=.(11)【答案】4. 【解析】2sin 1()F xy y x xy ∂=⋅∂+, 22222cos sin 2[1()]F y xy xy xy y x xy ∂−⋅=⋅∂+, 故2(0,2)2|4Fx∂=∂. (12)【答案】π.【解析】取22:0,1S x y z x y +−=+≤,取上侧,则由斯托克斯公式得,原式=22SS dydz dzdx dxdyydydz xdzdx dxdy x y z y xzx∂∂∂=++∂∂∂⎰⎰⎰⎰.因'',1, 1.x y z x y z z =+==由转换投影法得221[(1)(1)1]Sx y ydydz xdzdx dxdy y x dxdy +≤++=⋅−+−+⎰⎰⎰⎰.221(1)x y x y dxdy π+≤=−−+=⎰⎰221x y dxdy π+≤==⎰⎰.(13)【答案】1a =.【解析】由于二次型通过正交变换所得到的标准形前面的系数为二次型对应矩阵A 的特征值,故A 的特征值为0,1,4.二次型所对应的矩阵1131111a A a ⎛⎫ ⎪= ⎪ ⎪⎝⎭,由于310ii A λ===∏,故113101111a a a =⇒=.(14)【答案】()22μμσ+.【解析】根据题意,二维随机变量(),X Y 服从()22,;,;0N μμσσ.因为0xy ρ=,所以由二维正态分布的性质知随机变量,X Y 独立,所以2,X Y .从而有()()()()()()22222E XY E X E Y D Y E Y μμμσ⎡⎤==+=+⎣⎦. 三、解答题:15~23小题,共94分.请将解答写在答题纸...指定的位置上.解答应写出文字说明、证明过程或演算步骤.(15)(本题满分10分)【解析】110ln(1)lim[]x e x x x−→+0ln(1)1lim[1].1x x x x e e →+−−=2ln(1)limx x xx e →+−=22201()2lim x x x o x x x e→−+−=22201()2lim x x o x x e→−+=12e −=.(16)(本题满分9分) 【解析】[],()z f xy yg x =[][]12,(),()()zf xy yg x y f xy yg x yg x x∂'''=⋅+⋅∂ [][]211112,()(,())(,())()zf xy yg x y f xy yg x x f xy yg x g x x y∂'''''=++∂∂ []{}21222(),()()[,()][,()]()g x f xy yg x yg x f xy yg x x f xy yg x g x '''''''+⋅+⋅+. 因为()g x 在1x =可导,且为极值,所以(1)0g '=,则21111121|(1,1)(1,1)(1,1)x y d zf f f dxdy =='''''=++. (17)(本题满分10分)【解析】显然0x =为方程一个实根. 当0x ≠时,令(),arctan xf x k x=−()()22arctan 1arctan xx x f x x −+'=. 令()2arctan 1x g x x x R x =−∈+,()()()222222211220111x x x x g x x x x +−⋅'=−=>+++, 即(),0x R g x '∈>. 又因为()00g =,即当0x <时,()0g x <; 当0x >时,()0g x >. 当0x <时,()'0f x <;当0x >时,()'0f x >.所以当0x <时,()f x 单调递减,当0x >时,()f x 单调递增 又由()00lim lim1arctan x x xf x k k x→→=−=−,()lim lim arctan x x xf x k x→∞→∞=−=+∞, 所以当10k −<时,由零点定理可知()f x 在(,0)−∞,(0,)+∞内各有一个零点; 当10k −≥时,则()f x 在(,0)−∞,(0,)+∞内均无零点.综上所述,当1k >时,原方程有三个根.当1k ≤时,原方程有一个根.(18)(本题满分10分)【解析】(Ⅰ)设()()1ln 1,0,f x x x n ⎡⎤=+∈⎢⎥⎣⎦显然()f x 在10,n⎡⎤⎢⎥⎣⎦上满足拉格朗日的条件,()1111110ln 1ln1ln 1,0,1f f n n n n n ξξ⎛⎫⎛⎫⎛⎫⎛⎫−=+−=+=⋅∈ ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭所以10,n ξ⎛⎫∈ ⎪⎝⎭时, 11111111101n n n nξ⋅<⋅<⋅+++,即:111111n n n ξ<⋅<++, 亦即:111ln 11n n n⎛⎫<+< ⎪+⎝⎭. 结论得证.(II )设111111ln ln 23nn k a n n n k==++++−=−∑. 先证数列{}n a 单调递减.()111111111ln 1ln ln ln 1111n n n n k k n a a n n k k n n n n ++==⎡⎤⎡⎤⎛⎫⎛⎫−=−+−−=+=−+ ⎪ ⎪⎢⎥⎢⎥+++⎝⎭⎝⎭⎣⎦⎣⎦∑∑,利用(I )的结论可以得到11ln(1)1n n <++,所以11ln 101n n ⎛⎫−+< ⎪+⎝⎭得到1n n a a +<,即数列{}n a 单调递减.再证数列{}n a 有下界.1111ln ln 1ln nnn k k a n n k k ==⎛⎫=−>+− ⎪⎝⎭∑∑,()11112341ln 1ln ln ln 1123nnk k k n n k k n ==++⎛⎫⎛⎫⎛⎫+==⋅⋅=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∑∏,()1111ln ln 1ln ln 1ln 0nnn k k a n n n n k k ==⎛⎫=−>+−>+−> ⎪⎝⎭∑∑.得到数列{}n a 有下界.利用单调递减数列且有下界得到{}n a 收敛.(19)(本题满分11分) 【解析】11''(,)xy I xdx yf x y dy =⎰⎰11'0(,)x xdx ydf x y =⎰⎰()()111'000,|,x x xdx yf x y f x y dy ⎡⎤'=−⎢⎥⎣⎦⎰⎰ ()11''0(,1)(,)x x xdx f x f x y dy =−⎰⎰.因为(,1)0f x =,所以'(,1)0x f x =.11'(,)xI xdx f x y dy =−⎰⎰11'0(,)x dy xf x y dx =−⎰⎰111000(,)|(,)dy xf x y f x y dx ⎡⎤=−−⎢⎥⎣⎦⎰⎰1100(1,)(,)dy f y f x y dx ⎡⎤=−−⎢⎥⎣⎦⎰⎰ Dfdxdy =⎰⎰a =.(20)(本题满分11分)【解析】(I)由于123,,ααα不能由123,,βββ线性表示,对123123(,,,,,)βββααα进行初等行变换:123123113101(,,,,,)12401313115a ⎛⎫ ⎪= ⎪⎪⎝⎭βββααα113101011112023014a ⎛⎫ ⎪→− ⎪ ⎪−⎝⎭113101011112005210a ⎛⎫ ⎪→− ⎪ ⎪−−⎝⎭. 当5a =时,1231231(,,)2(,,,)3r r ββββββα=≠=,此时,1α不能由123,,βββ线性表示,故123,,ααα不能由123,,βββ线性表示.(II)对123123(,,,,,)αααβββ进行初等行变换:123123101113(,,,,,)013124115135⎛⎫ ⎪= ⎪ ⎪⎝⎭αααβββ101113013124014022⎛⎫ ⎪→ ⎪ ⎪⎝⎭101113013124001102⎛⎫ ⎪→ ⎪ ⎪−−⎝⎭ 1002150104210001102⎛⎫ ⎪→ ⎪ ⎪−−⎝⎭, 故112324βααα=+−,2122βαα=+,31235102βααα=+−.(21)(本题满分11分)【解析】(I)由于111100001111A −⎛⎫⎛⎫⎪ ⎪= ⎪ ⎪ ⎪ ⎪−⎝⎭⎝⎭,设()()121,0,1,1,0,1T T αα=−=,则()()1212,,A αααα=−,即1122,A A αααα=−=,而120,0αα≠≠,知A 的特征值为121,1λλ=−=,对应的特征向量分别为()1110k k α≠,()2220k k α≠.由于()2r A =,故0A =,所以30λ=.由于A 是三阶实对称矩阵,故不同特征值对应的特征向量相互正交,设30λ=对应的特征向量为()3123,,Tx x x α=,则13230,0,T T⎧=⎨=⎩αααα即13130,0x x x x −=⎧⎨+=⎩. 解此方程组,得()30,1,0Tα=,故30λ=对应的特征向量为()3330k k α≠.(II) 由于不同特征值对应的特征向量已经正交,只需单位化:))()3121231231,0,1,1,0,1,0,1,0T T Tαααβββααα==−====. 令()123,,Q βββ=,则110TQ AQ −⎛⎫⎪=Λ= ⎪ ⎪⎝⎭, TA Q Q =Λ22122001102201022⎛−⎛⎫⎪ ⎪−⎛⎫⎪ ⎪⎪= ⎪ ⎪⎪⎪ ⎪⎪⎝⎭⎪ ⎪− ⎪⎪⎝⎭ ⎪⎝⎭220012200000002210001022⎛−⎛⎫− ⎪ ⎪⎛⎫⎪ ⎪ ⎪==⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎪ ⎪⎪ ⎪⎝⎭ ⎪⎝⎭.(22)(本题满分11分)【解析】(I)因为{}221P X Y==,所以{}{}222210≠=−==P X Y P X Y.即{}{}{}0,10,11,00P X Y P X Y P X Y==−=======.利用边缘概率和联合概率的关系得到{}{}{}{}1 0,000,10,13P X Y P X P X Y P X Y====−==−−===;{}{}{}11,110,13P X Y P Y P X Y==−==−−==−=;{}{}{}11,110,13P X Y P Y P X Y====−===.即,X Y的概率分布为(II)Z的所有可能取值为1,0,1−.{}{}111,13P Z P X Y=−===−=.{}{}111,13P Z P X Y=====.{}{}{}101113P Z P Z P Z==−=−=−=.Z XY=的概率分布为(III)因为XY Cov XY E XY E X E Y ρ−⋅==其中()()1111010333E XY E Z ==−⋅+⋅+⋅=,()1111010333E Y =−⋅+⋅+⋅=.所以()()()0−⋅=E XY E X E Y ,即X ,Y 的相关系数0ρ=XY . (23)(本题满分 11分)【解析】因为总体X 服从正态分布,故设X 的概率密度为202()2()x f x μσ−−=,x −∞<<+∞.(I) 似然函数22002211()()22222211()(;)](2)ni i i x nnnx i i i L f x eμμσσσσπσ=−−−−−==∑===∏∏;取对数:222021()ln ()ln(2)22ni i x n L μσπσσ=−=−−∑; 求导:22022221()ln ()()22()ni i x d L nd μσσσσ=−=−+∑2202211[()]2()nii x μσσ==−−∑.令22ln ()0()d L d σσ=,解得22011()n i i x n σμ==−∑. 2σ的最大似然估计量为02211()ni i X n σμ∧==−∑.(II) 方法1:20~(,)μσi X N ,令20~(0,)i i Y X N μσ=−,则2211n i i Y n σ=∧=∑.2212221()()()()[()]n i i i i i E E Y E Y D Y E Y n σσ=∧===+=∑.2222212221111()()()()n i n i i D D Y D Y Y Y D Y n nnσ∧===+++=∑442244112{()[()]}(3)σσσ=−=−=i i E Y E Y n n n. 方法2:20~(,)μσi X N ,则~(0,1)i X N μσ−,得到()2201~ni i X Y n μχσ=−⎛⎫= ⎪⎝⎭∑,即()2201ni i Y X σμ==−∑.()()222222011111()n i i E E X E Y E Y n n n n n μσσσσσ=∧⎛⎫⎡⎤=−===⋅= ⎪⎢⎥⎣⎦⎝⎭∑.()()22444022222111112()2n i i D D X D Y D Y n nn n n n μσσσσσ=∧⎛⎫⎡⎤=−===⋅= ⎪⎢⎥⎣⎦⎝⎭∑.。
河北大学初试数字电路

数字电路
【适用专业】电路与系统、通信与信息系统、微电子学与固体电子学、电子与通信工程、控制工程、集成电路工程
【参考教材】《数字电子技术基础》张锁良北京邮电大学出版社
《数字电子技术基础简明教程》余孟尝高等教育出版社
【命题范围】
一、逻辑代数基础
1.掌握常用数制、码制及其相互转换。
2.熟练掌握逻辑代数的基本公式和定理。
3.掌握逻辑函数的表示方法及相互转换。
4.熟练掌握逻辑函数的化简方法。
二、门电路
1. 了解高低电平、正负逻辑、集成度等基本概念。
2. 掌握半导体二极管、三极管和MOS管的结构及开关特性。
3. 了解TTL门电路和MOS门电路的电路结构、工作原理及主要特性与参数。
4. 熟悉各种门电路的外特性。
三、组合逻辑电路
1. 熟练掌握组合逻辑电路的基本分析方法和设计方法。
2. 掌握常用组合逻辑电路的功能、原理和设计方法。
3. 熟悉用中规模集成电路实现组合逻辑函数。
4. 了解竞争冒险。
四、触发器
1.熟悉触发器的电路结构及特点。
2. 掌握各种功能触发器的逻辑符号、逻辑功能。
3. 了解触发器的电气特性。
五、时序逻辑电路
1.了解时序逻辑电路的特点、分类及功能表示。
2.熟练掌握时序逻辑电路的基本分析方法。
3.熟练掌握计数器的分析、设计。
4.了解一般时序逻辑电路的设计。
5.熟练掌握典型中规模集成计数器应用,利用集成计数器构成任意进制计数器。
6.了解寄存器和读写存储器的电路组成、工作原理及特点。
河北大学2011年考研参考书目
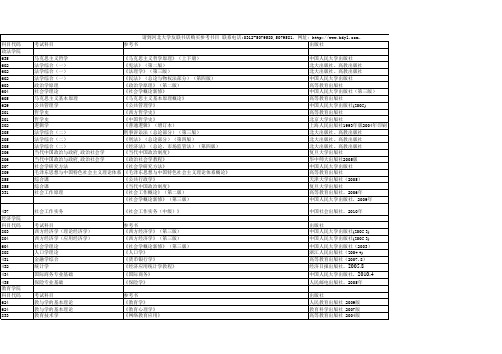
考试科目 理科数学 普通物理 普通物理 普通物理 量子力学 电动力学 电磁学 数字电路 光学 光学 光电技术 考试科目 理科数学 物理化学 统计物理 无机化学
827 828 829 830 830 830 838 839 879 880 生命学院 科目代码 623 626 627 628 831 832 842 633 634 873 874 339 340 875 876 877 878 建工学院 科目代码 845 电信学院 科目代码 601 835 835 844 848 849
翻译硕士英语 英语翻译基础 翻译硕士俄语 俄语翻译基础 翻译硕士日语 日语翻译基础 汉语写作与百科知识
《美国文学史及作品选读》 《英汉汉英翻译教程》 《新编语言学教程》 《英语写作教程》 《语言学教程》 《日本文学史》 《日本文化》 《日语语法研究》 (初级上、下, 中级上册) 《语言学概论》 《西方语言与流派》
高等教育出版社,2007版 科学出版社09版 北京师范大学出版社 浙江教育出版社 人民教育出版社 浙江教育出版社 北京师范大学出版社 北京师范大学出版社 北京师范大学出版社 2008年版 科学出版社09版 教育科学出版社,2007年版 科学出版社,2009年版 出版社 复旦大学出版社2006年版 复旦大学出版社 中山大学出版社2006版 高等教育出版社(增订三版) 高等教育出版社2005年第二版 复旦大学出版社 高等教育出版社 中山大学出版社2006版 高等教育出版社 北京大学出版社 中华书局 中华书局 出版社 商务印书馆 不限编者 外语教学与研究出版社 外语教学与研究出版社 上海外语教研社 外研社 外语教学与研究出版社 上海外语教育出版社 电子工业出版社 北京大学出版社(2005) 不限编者
外研社1995 外研社2002 清华大学出版社2008 外研社1996 外研社2006 外研社1981 上海外语教育出版社1986 外研社2006 外研社2004 东南大学出版社2005 西南师范大学出版社2008
