2013年七年级数学11月期中试题 (新人教版第8套)

合集下载

2013新课标人教版七年级数学上册期中考试试卷及答案

21. (本题9分)观察一列数：1、2、4、8、16、…我们发现，这一列数从
第二项起，每一项与它前一项的比都等于2.一般地，如果一列数从第二
项起，每一项与它前一项的比都等于同一个常数，这一列数就叫做等比
数列，这个常数就叫做等比数列的公比.
（1）等比数列5、-15、45、…的第4项是_________.（2分）
依题意有：50+0.4t=0.6t
………………………………３分
解得t=250
………………………………4分
（2）若小敏的爸爸预计一个月内使用本地通话费180元,则使用全球
通有：
50+0.4t=180 ∴=325
………………………………6分
若小敏的爸爸预计一个月内使用本地通话费180元,则使用神州行
(A) (B) (C)2
(D) -2
2．武汉长江二桥是世界上第一座弧线形钢塔斜拉桥，该桥全长
16800m，用科学记数法表示这个数为（）.
(A)1.68×104m
(B)16.8×103 m
(C)0.168×104m
(D)1.68×103m
3．如果收入15元记作+15元，那么支出20元记作（）元.
(A)+5
即运动1.8秒时，原点恰好处在A、B两点的正中间
………………8分
（3）设运动y秒时，点B追上点A
根据题意,得4y-y=15,
解之得
y=5
………………10分
即点B追上点A共用去5秒,而这个时间恰好是点C从开始运动到停
止运动所花的时间,因此点C行驶的路程为:20×5=100(单位长度) ………………12分
（2）如果一列数是等比数列，且公比为.那么有：，，。

2013人教版七下数学期中试卷

7、如图所示，在△ABC中，CD、BE分别是 AB、AC边上的
高，并且 CD、BE （）
交于点 P，若∠A=50°，则 ∠BPC等于
A、90°
B、130° C、100°
பைடு நூலகம்
D、150°
8、如果甲图形上的点 P(-2,4)经平移变换后是 Q(3,-2),则甲图上的点 M(1,-2)经这样平移后的对应
点的坐标是(
) A、(6,-8) B、(-4,4)
C、(5,3 )
D、(3,-5)
9．如图，一条公路修到湖边时，需拐弯绕湖而过，如果第一次拐的角∠Ａ是 120°，第二次拐的角
∠Ｂ是 150°，第三次拐的角是∠Ｃ，这时的道路恰好和第一次拐弯之前的道路平行，则∠Ｃ是（）
Ａ、150°Ｂ、140°Ｃ、130° Ｄ、120°
4、如图，PO⊥OR，OQ⊥PR，则点 O 到 PR所在的直线的距离是线段（）
A、PO B、RO C、OQ D、PQ
5、若 x 轴上的点 P 到 y 轴的距离为 3，则点 P 的坐标为（）
A、(0,3) B、(0,3)或(0,-3) C、(3,0) D、(3,0)或(-3,0)
6、一个正方形在平面直角坐标系中三个顶点的坐标为（－2，－3），（－2， 1），（2，1），则第四个顶点的坐标为（） A、（2，2）； B、（3，2）； C、（2，－3）； D、（2，3）
2013人教版七下数学期中试卷
一、选择题 1、点 P（1，-5）所在的象限是（）Ａ、第一象限Ｂ、第二象限Ｃ、第三象限 2、下面四个图形中，∠1 与∠2 是对顶角的图形（
Ｄ、第四象限）
3、如图，直线 a∥b，直线 c 是截线，如果∠1=50°，那么∠2 等于(

新人教版七年级下册数学期中试卷及答案doc人教 (8)

新人教版七年级下册数学期中试卷及答案doc 人教一、选择题1．14的算术平方根为（） A ．116 B ．12± C ．12D ．12- 2．下列生活现象中，不是平移现象的是( ) A ．人站在运行着的电梯上B ．推拉窗左右推动C ．小明在荡秋千D ．小明躺在直线行驶的火车上睡觉 3．在平面直角坐标系中，点()2,1-位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 4．下列命题是假命题．．．的是（）． A ．同一平面内，两直线不相交就平行 B ．对顶角相等C ．互为邻补角的两角和为180°D ．相等的两个角一定是对顶角 5．直线12//l l ，125A ∠=︒，85B ∠=︒，115∠=︒，则2∠=（）A ．15°B ．25°C ．35D ．20° 6．下列说法正确的是（）A ．a 2的正平方根是aB ．819=±C ．﹣1的n 次方根是1D ．321a --一定是负数7．如图，在//AB CD 中，∠AEC ＝50°，CB 平分DCE ∠，则ABC ∠的度数为（）A ．25°B ．30°C ．35°D ．40°8．如图，动点P 在平面直角坐标系xOy 中，按图中箭头所示方向运动，第1次从原点运动到点()1,2，第2次接着运动到点()20,，第3次接着运动到点()3,1，第4次接着运动到点()4,0，……，按这样的运动规律，经过第2021次运动后，动点P 的坐标是（）A ．()2020,0B ．()2020,1C ．()2021,1D ．()2021,2二、填空题9．比较大小，请在横线上填“＞”或“＜”或“＝”9________327.10．在平面直角坐标系中，点(,)M a b 与点(3,1)N -关于x 轴对称，则a b +的值是_____． 11．如图，在ABC 中，90C ∠=︒，30B ∠=︒，AD 是ABC 的角平分线，DE AB ⊥，垂足为E ，1DE =，则BC =__________．12．如图，已知AB //EF ，∠B =40°，∠E =30°，则∠C -∠D 的度数为________________．13．将一条长方形纸带按如图方式折叠，若1108∠=︒，则2∠的度数为________°．14．a ※b 是新规定的这样一种运算法则：a ※b=a+2b ，例如3※（﹣2）=3+2×（﹣2）=﹣1．若（﹣2）※x=2+x ，则x 的值是_____．15．在平面直角坐标系中，已知线段3,AB =且//AB x 轴，且点A 的坐标是()1,2,则点B 的坐标是____．16．在平面直角坐标系中，对于点P (x ，y )，我们把点P ′(－y ＋1，x ＋1)叫做点P 的幸运点．已知点A 1的幸运点为A 2，点A 2的幸运点为A 3，点A 3的幸运点为A 4，…，这样依次得到点A 1，A 2，A 3，…，A n ．若点A 1的坐标为(3，1)，则点A 2020的坐标为_______．三、解答题17．计算：（1）3981++- （2）23427(3)+---（3）2(23)+（4）353325-++18．求下列各式中的x 值:（1）16（x +1）2＝25; （2）8（1﹣x ）3＝12519．阅读并完成下列的推理过程．如图，在四边形ABCD 中，E 、F 分别在线段AB 、AD 上，连结ED 、EF ，已知∠AFE ＝∠CDF ，∠BCD +∠DEF ＝180°．证明BC ∥DE ；证明：∵∠AFE ＝∠CDF （已知）∴EF ∥CD （）∴∠DEF ＝∠CDE （）∵∠BCD +∠DEF ＝180°（）∴ （）∴BC ∥DE （）20．如图，在平面直角坐标系中，三角形ABC 三个顶点的坐标分别为()()()2,2,3,1,0,2A B C --．点P (,)a b 是三角形ABC 的边AC 上任意一点，三角形ABC 经过平移后得到三角形A B C '''，已知点P 的对应点P '()2,3a b -+．（1）在图中画出平移后的三角形A B C '''，并写出点,,A B C '''的坐标；（2）求三角形ABC 的面积．21．已知某正数的两个不同的平方根是3a ﹣14和a +2；b +11的立方根为﹣3；c 6的整数部分；（1）求a +b +c 的值；（2）求3a ﹣b +c 的平方根．22．如图，纸上有五个边长为1的小正方形组成的图形纸，我们可以把它剪开拼成一个正方形．（1）拼成的正方形的面积与边长分别是多少？（2）如图所示，以数轴的单位长度的线段为边作一个直角三角形，以数轴的-1点为圆心，直角三角形的最大边为半径画弧，交数轴正半轴于点A ，那么点A 表示的数是多少？点A 表示的数的相反数是多少？（3）你能把十个小正方形组成的图形纸，剪开并拼成正方形吗？若能，请画出示意图，并求它的边长23．如图①，将一张长方形纸片沿EF 对折，使AB 落在''A B 的位置；（1）若1∠的度数为a ，试求2∠的度数（用含a 的代数式表示）；（2）如图②，再将纸片沿GH 对折，使得CD 落在''C D 的位置．①若//'EF C G ，1∠的度数为a ，试求3∠的度数（用含a 的代数式表示）；②若''B F C G ⊥，3∠的度数比1∠的度数大20︒，试计算1∠的度数．24．如图，两个形状，大小完全相同的含有30°、60°的三角板如图放置，PA 、PB 与直线MN 重合，且三角板PAC ，三角板PBD 均可以绕点P 逆时针旋转．（1）①如图1，∠DPC ＝度．②我们规定，如果两个三角形只要有一组边平行，我们就称这两个三角形为“孪生三角形”，如图1，三角板BPD 不动，三角板PAC 从图示位置开始每秒10°逆时针旋转一周（0°<旋转<360°），问旋转时间t为多少时，这两个三角形是“孪生三角形”．（2）如图3，若三角板PAC的边PA从PN处开始绕点P逆时针旋转，转速3°/秒，同时三角板PBD的边PB从PM处开始绕点P逆时针旋转，转速2°/秒，在两个三角板旋转过程中，（PC转到与PM重合时，两三角板都停止转动）．设两个三角板旋转时间为t秒，以下两个结论：①CPDBPN∠∠为定值；②∠BPN+∠CPD为定值，请选择你认为对的结论加以证明．【参考答案】一、选择题1．C解析：C【分析】根据算术平方根的定义求解.【详解】解：因为211 24⎛⎫=⎪⎝⎭，所以14的算术平方根为12.故选C.【点睛】本题主要考查算术平方根的定义，解决本题的关键是要熟练掌握算术平方根的定义. 2．C【分析】根据平移是某图形沿某一直线方向移动一定的距离，平移不改变图形的形状和大小，解答即可．【详解】解：根据平移的性质，A、B、D都正确，而C小明在荡秋千，荡秋千的运动过程中，方向不断的发解析：C【分析】根据平移是某图形沿某一直线方向移动一定的距离，平移不改变图形的形状和大小，解答即可．【详解】解：根据平移的性质，A、B、D都正确，而C小明在荡秋千，荡秋千的运动过程中，方向不断的发生变化，不是平移运动．故选：C．【点睛】本题考查了图形的平移，解题的关键是掌握图形的平移只改变图形的位置，而不改变图形的形状和大小．3．B【分析】根据平面直角坐标系的四个象限内的坐标特征回答即可．【详解】解：解：在平面直角坐标系中，点P（−2，1）位于第二象限，故选：B．【点睛】本题考查了点的坐标，横坐标小于零，纵坐标大于零的点在第二象限．4．D【分析】根据相交线、对顶角以及邻补角的有关性质对选项逐个判断即可．【详解】解：A：同一平面内，两条不相交的直线平行，选项正确，不符合题意；B：对顶角相等，选项正确，不符合题意；C：互为邻补角的两角和为180°，选项正确，不符合题意；D：相等的两个角不一定是对顶角，选项错误，符合题意；故答案选D．【点睛】此题主要考查了相交线、对顶角以及邻补角的有关性质，熟练掌握相关基本性质是解题的关键．5．A【分析】分别过A、B作直线1l的平行线AD、BC，根据平行线的性质即可完成．【详解】分别过A、B作直线1l∥AD、1l∥BC，如图所示，则AD∥BC∵1l ∥2l∴2l ∥BC∴∠CBF =∠2∵1l ∥AD∴∠EAD =∠1=15゜∴∠DAB =∠EAB -∠EAD =125゜-15゜=110゜∵AD ∥BC∴∠DAB +∠ABC =180゜∴∠ABC =180゜-∠DAB =180゜-110゜=70゜∴∠CBF =∠ABF -∠ABC =85゜-70゜=15゜∴∠2=15゜故选：A ．【点睛】本题考查了平行线的性质与判定等知识，关键是作两条平行线．6．D【分析】根据平方根、算术平方根、立方根的定义判断A 、B 、D ，根据乘方运算法则判断C 即可．【详解】A ：a 2的平方根是a ±，当0a ≥时，a 2的正平方根是a ，错误；B 819，错误；C ：当n 是偶数时，()1=1n - ；当n 时奇数时，()1=-1n -，错误；D ：∵210a --< ，∴321a --【点睛】本题考查平方根、算术平方根、立方根的定义以及乘方运算，掌握相关的定义与运算法则是解题关键．7．A【分析】根据平行线的性质得到∠ABC =∠BCD ，∠ECD =∠AEC =50°再根据角平分线的定义得到∠BCE =∠BCD =12∠ECD =25°，由此即可求解．【详解】解：∵AB ∥CD ，∴∠ABC=∠BCD，∠ECD=∠AEC=50°∵CB平分∠DCE，∠ECD=25°∴∠BCE=∠BCD =12∠ABC=∠BCD=25°故选A．【点睛】本题考查了平行线的性质，角平分线的定义，掌握平行线的性质：两直线平行，内错角相等是解题的关键．8．D【分析】根据已知提供的数据从横纵坐标分别分析得出横坐标为运动次数，纵坐标为2，0，1，0，2，0，1，0…，每4次一轮这一规律，进而求出即可．【详解】解：由图可知：横坐标1，2，3，4…依解析：D【分析】根据已知提供的数据从横纵坐标分别分析得出横坐标为运动次数，纵坐标为2，0，1，0，2，0，1，0…，每4次一轮这一规律，进而求出即可．【详解】解：由图可知：横坐标1，2，3，4…依次递增，则第2021个点的横坐标为2021；纵坐标2，0，1，0，2，0，1，0…4个一循环，2021÷4=505…1，∴经过第2021次运动后，P（2021，2）．故选D．【点睛】此题主要考查了点的坐标规律，培养学生观察和归纳能力，从所给的数据和图形中寻求规律进行解题是解答本题的关键．二、填空题9．＝【分析】先根据算数平方根和立方根的定义进行化简，再根据实数大小的比较方法进行比较即可【详解】解：∵，∴=故答案为：＝【点睛】本题考查的是实数的大小比较以及算数平方根、立方根，熟练掌解析：＝【分析】先根据算数平方根和立方根的定义进行化简，再根据实数大小的比较方法进行比较即可【详解】解：∵∴故答案为：＝【点睛】本题考查的是实数的大小比较以及算数平方根、立方根，熟练掌握相关的知识是解答此题的关键．10．4【分析】根据关于x 轴对称的两点的横坐标相同，纵坐标互为相反数求得a 、b 的值即可求得答案.【详解】点与点关于轴对称，，，则a+b 的值是：,故答案为．【点睛】本题考查了关于x 轴对称的解析：4【分析】根据关于x 轴对称的两点的横坐标相同，纵坐标互为相反数求得a 、b 的值即可求得答案.【详解】点(,)M a b 与点(3,1)M -关于x 轴对称，3a ∴=，1b =，则a+b 的值是：4,故答案为4．【点睛】本题考查了关于x 轴对称的点的坐标特征，熟练掌握关于坐标轴对称的点的坐标特征是解此类问题的关键.11．【解析】已知∠C=90°，AD是△ABC的角平分线，DE⊥AB，根据角平分线的性质可得DC=DE=1；因，根据30°直角三角形的性质可得BD=2DE=2，所以BC=CD+DB=1+2=3.解析：【解析】已知∠C=90°，AD是△ABC的角平分线，DE⊥AB，根据角平分线的性质可得DC=DE=1；因∠=︒⊥，，根据30°直角三角形的性质可得BD=2DE=2，所以BC=CD+DB=1+2=3.B DE AB3012．10°【分析】过点C作CG∥AB，过点D作DH∥EF，根据平行线的性质可得AB∥CG∥DH∥EF，从而可得∠BCG=∠B=40°，∠EDH=∠E=30°，∠DCG=∠CDH，即可求解．【详解】解析：10°【分析】过点C作CG∥AB，过点D作DH∥EF，根据平行线的性质可得AB∥CG∥DH∥EF，从而可得∠BCG=∠B=40°，∠EDH=∠E=30°，∠DCG=∠CDH，即可求解．【详解】解：如图，过点C作CG∥AB，过点D作DH∥EF，∵AB//EF，∴AB∥CG∥DH∥EF，∵∠B=40°，∠E=30°，∴∠BCG=∠B=40°，∠EDH=∠E=30°，∠DCG=∠CDH，∴∠BCD-∠CDE=∠BCG-∠EDH=40°-30°=10°．故答案为：10°．【点睛】本题主要考查了平行线的性质，准确作出辅助线是解题的关键．13．36【分析】根据平行线的性质、折叠的性质即可解决．【详解】∵AB ∥CD ，如图∴∠GEC=∠1=108゜由折叠的性质可得：∠2=∠FED∵∠2+∠FED+∠GEC=180゜∴∠2=解析：36【分析】根据平行线的性质、折叠的性质即可解决．【详解】∵AB ∥CD ，如图∴∠GEC =∠1=108゜由折叠的性质可得：∠2=∠FED∵∠2+∠FED +∠GEC =180゜∴∠2=11(180)(180108)3622GEC ︒-∠=⨯︒-︒=︒ 故答案为：36【点睛】本题考查了平行线的性质、折叠的性质、平角的概念，关键是掌握折叠的性质． 14．4【解析】根据题意可得（﹣2）※x=﹣2+2x ，进而可得方程﹣2+2x=2+x ，解得：x=4.故答案为：4．点睛：此题是一个阅读理解型的新运算法则题，解题关键是明确新运算法则的特点，然后直接根解析：4【解析】根据题意可得（﹣2）※x=﹣2+2x ，进而可得方程﹣2+2x=2+x ，解得：x=4. 故答案为：4．点睛：此题是一个阅读理解型的新运算法则题，解题关键是明确新运算法则的特点，然后直接根据新定义的代数式计算即可.15．或【分析】设点B 的坐标为，然后根据轴得出B 点的纵坐标，再根据即可得出B 点的横坐标．【详解】设点B 的坐标为，∵轴，点A （1，2）∴B 点的纵坐标也是2，即．∵，或，解得或，∴点解析：()4,2或()2,2-【分析】设点B 的坐标为(,)a b ，然后根据//AB x 轴得出B 点的纵坐标，再根据3,AB =即可得出B 点的横坐标．【详解】设点B 的坐标为(,)a b ，∵//AB x 轴，点A （1，2）∴B 点的纵坐标也是2，即2b = ．∵3AB =，13a ∴-=或13a -= ，解得4a =或2a =- ，∴点B 的坐标为()4,2或()2,2-．故答案为：()4,2或()2,2-．【点睛】本题主要考查平行于x 轴的线段上的点的特点，掌握平行于x 轴的线段上的点的特点是解题的关键．16．(0，-2)【分析】根据伴随点的定义，罗列出部分点A 的坐标，根据点A 的变化找出规律“A4n+1（3，1），A4n+2（0，4），A4n+3（-3，1），A4n+4（0，-2）（n 为自然数）”，根解析：(0，-2)【分析】根据伴随点的定义，罗列出部分点A 的坐标，根据点A 的变化找出规律“A 4n +1（3，1），A 4n +2（0，4），A 4n +3（-3，1），A 4n +4（0，-2）（n 为自然数）”，根据此规律即可解决问题．【详解】解：观察，发现规律：A1（3，1），A2（0，4），A3（-3，1），A4（0，-2），A5（3，1），…，∴A4n+1（3，1），A4n+2（0，4），A4n+3（-3，1），A4n+4（0，-2）（n为自然数）．∵2020=4×504+4，∴点A2020的坐标为（0，-2）．故答案为：(0，-2)．【点睛】本题考查了规律型中的点的坐标，解题的关键是发现规律“A4n+1（3，1），A4n+2（0，4），A4n+3（-3，1），A4n+4（0，-2）（n为自然数）”．三、解答题17．（1）6；（2）-4；（3）；（4）.【分析】（1）利用算术平方根和立方根、绝对值化简，再进一步计算即可；（2）利用算术平方根和立方根化简，再进一步计算即可；（3）类比单项式乘多项式展开计算解析：（1）6；（2）-4；（3）2+；（4）【分析】（1）利用算术平方根和立方根、绝对值化简，再进一步计算即可；（2）利用算术平方根和立方根化简，再进一步计算即可；（3）类比单项式乘多项式展开计算；（4）利用绝对值的性质化简，再进一步合并同类二次根式．【详解】解：（11-=3+2+1=6；（2=2-3-3=-4；（33)=2+；（4+=故答案为（1）6；（2）-4；（3）2+4）【点睛】本题考查立方根和算术平方根，实数的混合运算，先化简，再进一步计算，注意选择合适的方法简算．18．（1）或；（2）【分析】（1）根据平方根，即可解答；（2）根据立方根，即可解答．【详解】解：（1）等式两边都除以16，得.等式两边开平方，得.所以，得.所以，解析：（1）14x =或94x =-；（2）3.2x =- 【分析】（1）根据平方根，即可解答；（2）根据立方根，即可解答．【详解】解：（1）等式两边都除以16，得()225116x +=. 等式两边开平方，得514x +=±. 所以，得5511-44x x +=+=或. 所以，19-44x =或（2）等式两边都除以8，得()31251-8x =. 等式两边开立方，得51-2x =. 所以，3.2x =- 【点睛】本题考查平方根、立方根，解题关键是熟记平方根、立方根．.19．同位角相等，两直线平行；两直线平行，内错角相等；已知；∠BCD+∠CDE ＝180°；等量代换；同旁内角互补，两直线平行．【分析】根据平行线的性质与判定填空即可【详解】证明：∵∠AFE ＝∠CD解析：同位角相等，两直线平行；两直线平行，内错角相等；已知；∠BCD +∠CDE ＝180°；等量代换；同旁内角互补，两直线平行．【分析】根据平行线的性质与判定填空即可【详解】证明：∵∠AFE ＝∠CDF （已知）∴EF ∥CD （同位角相等，两直线平行）∴∠DEF ＝∠CDE （两直线平行，内错角相等）∵∠BCD +∠DEF ＝180°（已知）∴∠BCD +∠CDE ＝180°（等量代换）∴BC ∥DE （同旁内角互补，两直线平行）故答案为：同位角相等，两直线平行；两直线平行，内错角相等；已知；∠BCD +∠CDE ＝180°；等量代换；同旁内角互补，两直线平行【点睛】本题考查了平行线的性质与判定，掌握平行线的性质与判定是解题的关键．20．（1）作图见解析，；（2）7【分析】（1）直接利用P 点平移变化规律得出A′、B′、C′的坐标；直接利用得出各对应点位置进而得出答案；（2）利用三角形ABC 所在矩形面积减去周围三角形面积进而得出解析：（1）作图见解析，()()()4,1,1,4,2,5A B C '--；（2）7【分析】（1）直接利用P 点平移变化规律得出A ′、B ′、C ′的坐标；直接利用得出各对应点位置进而得出答案；（2）利用三角形ABC 所在矩形面积减去周围三角形面积进而得出答案．【详解】解：（1）∵P (,)a b 到点P 的对应点P '()2,3a b -+，横坐标向左平移了两个单位，纵坐标向上平移了3个单位．∵()()()2,2,3,1,0,2A B C --，∴()()()4,1,1,4,2,5A B C '--，如图所示，三角形A ′B ′C ′即为所求，（2）三角形ABC的面积为：4×5−12×1×3−12×2×4−12×3×5＝7．【点睛】此题主要考查了平移变换以及三角形面积求法，正确得出对应点位置是解题关键．21．（1）-33；（2）【分析】（1）由平方根的性质知3a-14和a+2互为相反数，可列式，解之可得a=3，根据立方根定义可得b的值，根据可得c的值；（2）分别将a，b，c的值代入3a-b+c，可解析：（1）-33；（2）7±【分析】（1）由平方根的性质知3a-14和a+2互为相反数，可列式，解之可得a=3，根据立方根定义可得b的值，根据263<<可得c的值；（2）分别将a，b，c的值代入3a-b+c，可解答．【详解】解：（1）∵某正数的两个平方根分别是3a-14和a+2，∴（3a-14）+（a+2）=0，∴a=3，又∵b+11的立方根为-3，∴b+11=(-3)3=-27，∴b=-38，又∵469<<，∴263<，又∵c6的整数部分，∴c=2；∴a+b+c=3+(-38)+2=-33；（2）当a=3，b=-38，c=2时，3a-b+c=3×3-(-38)+2=49，∴3a-b+c的平方根是±7．本题主要考查了立方根、平方根及无理数的估算，解题的关键是熟练掌握平方根和立方根的定义．22．（1）5；；（2）；；（3）能，．【分析】（1）易得5个小正方形的面积的和，那么就得到了大正方形的面积，求得面积的算术平方根即可为大正方形的边长．（2）求出斜边长即可．（3）一共有10个小正解析：（1）5；5；（2）51-；（3）能，10．-；15【分析】（1）易得5个小正方形的面积的和，那么就得到了大正方形的面积，求得面积的算术平方根即可为大正方形的边长．（2）求出斜边长即可．（3）一共有10个小正方形，那么组成的大正方形的面积为10，边长为10的算术平方根，画图．【详解】试题分析：解：（1）拼成的正方形的面积与原面积相等1×1×5=5，边长为5，如图（1）（2）斜边长=22+=，2222故点A表示的数为：222-；点A表示的相反数为：222-（3）能，如图拼成的正方形的面积与原面积相等1×1×10=1010考点：1．作图—应用与设计作图；2．图形的剪拼．23．（1）；（2）① ；②(1)由平行线的性质得到，由折叠的性质可知，∠2=∠BFE ，再根据平角的定义求解即可；(2) ①由（1）知，，根据平行线的性质得到，再由折叠的性质及平角的定义解析：（1）1902a ︒- ；（2）①1454a ︒+ ；②50︒ 【分析】(1)由平行线的性质得到4'B FC a ∠=∠=，由折叠的性质可知，∠2=∠BFE ，再根据平角的定义求解即可；(2) ①由（1）知，1902BFE a ∠=︒-，根据平行线的性质得到1BFE C'GB 902a ∠=∠=︒- ，再由折叠的性质及平角的定义求解即可；②由（1）知，∠BFE = 19012EFB '∠=︒-∠，由''B F C G ⊥可知：''90B FC FGC ∠+∠=︒，再根据条件和折叠的性质得到''11402190B FC FGC +=∠+∠=∠︒-∠︒，即可求解．【详解】解：（1）如图，由题意可知'//'A E B F ，∴14a ∠=∠=，∵//AD BC ，∴4'B FC a ∠=∠=，180BFB a '∴∠=︒-，∴由折叠可知1129022BFE BFB a '∠=∠=∠=︒-．（2）①由题（1）可知1902BFE a ∠=︒- ， ∵//'EF C G ，1902BFE C'GB a ∴∠=∠=︒-，再由折叠可知：113180*********HGC C GB a a ⎛⎫∠+∠=︒-∠=︒-︒-=︒+ ⎪⎝⎭'， 13454HGC a ∴∠=∠=︒+；②由''B F C G ⊥可知：''90B FC FGC ∠+∠=︒，由（1）知19012BFE ∠=︒-∠， 11802180290112B FC BFE ⎛⎫'∴∠=︒-∠=︒-︒-∠=∠ ⎪⎝⎭，又3∠的度数比1∠的度数大20︒，∴3=1+20∠∠︒，()18023180212014021FGC '∴∠=︒-∠=︒-∠+︒=︒-∠，''11402190B FC FGC +=∴∠+∠=∠︒-∠︒，1=50∴∠︒．【点睛】此题考查了平行线的性质，属于综合题，有一定难度，熟记“两直线平行，同位角相等”、“两直线平行，内错角相等”及折叠的性质是解题的关键．24．（1）①90；②t 为或或或或或或；（2）①正确，②错误，证明见解析．【分析】（1）①由平角的定义，结合已知条件可得：从而可得答案；②当时，有两种情况，画出符合题意的图形，利用平行线的性质与角的和解析：（1）①90；②t 为3s 或6s 或9s 或18s 或21s 或24s 或27s ；（2）①正确，②错误，证明见解析．【分析】（1）①由平角的定义，结合已知条件可得：180,DPC CPA DPB ∠=︒-∠-∠从而可得答案；②当//BD PC 时，有两种情况，画出符合题意的图形，利用平行线的性质与角的和差求解旋转角，可得旋转时间；当//PA BD 时，有两种情况，画出符合题意的图形，利用平行线的性质与角的和差关系求解旋转角，可得旋转时间；当//AC DP 时，有两种情况，画出符合题意的图形，利用平行线的性质与角的和差关系求解旋转角，可得旋转时间；当//AC BD 时，画出符合题意的图形，利用平行线的性质与角的和差关系求解旋转角，可得旋转时间；当//AC BP 时的旋转时间与//PA BD 相同；（2）分两种情况讨论：当PD 在MN 上方时，当PD 在MN 下方时，①分别用含t 的代数式表示,CPD BPN ∠∠，从而可得CPD BPN∠∠的值；②分别用含t 的代数式表示,CPD BPN ∠∠，得到BPN CPD ∠+∠是一个含t 的代数式，从而可得答案．【详解】解：（1）①∵∠DPC＝180°﹣∠CPA﹣∠DPB，∠CPA＝60°，∠DPB＝30°，∴∠DPC＝180﹣30﹣60＝90°，故答案为90；②如图1﹣1，当BD∥PC时，∵PC∥BD，∠DBP＝90°，∴∠CPN＝∠DBP＝90°，∵∠CPA＝60°，∴∠APN＝30°，∵转速为10°/秒，∴旋转时间为3秒；如图1﹣2，当PC∥BD时，PC BD∠PBD＝90°，∵//,∴∠CPB＝∠DBP＝90°，∵∠CPA＝60°，∴∠APM＝30°，∵三角板PAC绕点P逆时针旋转的角度为180°+30°＝210°，∵转速为10°/秒，∴旋转时间为21秒，如图1﹣3，当PA∥BD时，即点D与点C重合，此时∠ACP＝∠BPD＝30°，则AC∥BP，∵PA∥BD，∴∠DBP＝∠APN＝90°，∴三角板PAC绕点P逆时针旋转的角度为90°，∵转速为10°/秒，∴旋转时间为9秒，如图1﹣4，当PA∥BD时，∵∠DPB＝∠ACP＝30°，∴AC∥BP，∵PA∥BD，∴∠DBP＝∠BPA＝90°，∴三角板PAC绕点P逆时针旋转的角度为90°+180°＝270°，∵转速为10°/秒，∴旋转时间为27秒，如图1﹣5，当AC∥DP时，∵AC∥DP，∴∠C＝∠DPC＝30°，∴∠APN＝180°﹣30°﹣30°﹣60°＝60°，∴三角板PAC绕点P逆时针旋转的角度为60°，∵转速为10°/秒，∴旋转时间为6秒，AC DP时，如图1﹣6，当////AC DP ，90DPA PAC ∴∠=∠=︒，1803090240DPN DPA ∠+∠=︒-︒+︒=︒，∴三角板PAC 绕点P 逆时针旋转的角度为240︒，∵转速为10°/秒，∴旋转时间为24秒，如图1﹣7，当AC ∥BD 时，∵AC ∥BD ，∴∠DBP ＝∠BAC ＝90°，∴点A 在MN 上，∴三角板PAC 绕点P 逆时针旋转的角度为180°，∵转速为10°/秒，∴旋转时间为18秒，当//AC BP 时，如图1-3，1-4，旋转时间分别为：9s ，27s ．综上所述：当t 为3s 或6s 或9s 或18s 或21s 或24s 或27s 时，这两个三角形是“孪生三角形”；（2）如图，当PD 在MN 上方时，①正确，理由如下：设运动时间为t 秒，则∠BPM ＝2t ，∴∠BPN ＝180°﹣2t ，∠DPM ＝30°﹣2t ，∠APN ＝3t ．∴∠CPD ＝180°﹣∠DPM ﹣∠CPA ﹣∠APN ＝90°﹣t ，21802,BPN CPD t ∴∠=∠=︒- ∴1.2CPD BPN ∠=∠ ②∠BPN +∠CPD ＝180°﹣2t +90°﹣t ＝270°﹣3t ，可以看出∠BPN +∠CPD 随着时间在变化，不为定值，结论错误．当PD 在MN 下方时，如图，①正确，理由如下：设运动时间为t 秒，则∠BPM ＝2t ，∴∠BPN ＝180°﹣2t ，∠DPM ＝230,t -︒ ∠APN ＝3t ．∴∠CPD ＝360CPA APN DPB BPN ︒-∠-∠-∠-∠()360603301802t t =︒-︒--︒-︒-=90t ︒-21802,BPN CPD t ∴∠=∠=︒- ∴1.2CPD BPN ∠=∠ ②∠BPN +∠CPD ＝180°﹣2t +90°﹣t ＝270°﹣3t ，可以看出∠BPN +∠CPD 随着时间在变化，不为定值，结论错误．综上：①正确，②错误．【点睛】本题考查的是角的和差倍分关系，平行线的性质与判定，角的动态定义（旋转角）的理解，掌握分类讨论的思想是解题的关键．。

七年级下学期数学期中考试试卷第8套真题

七年级下学期数学期中考试试卷一、单选题1. 如图所示的图案分别是三菱、大众、奥迪、奔驰汽车的车标，其中可以看着是由“基本图案”经过平移得到的是（）A . 奥迪B . 本田C .大众D . 铃木2. 下列各式中计算正确的是A . = x5B .C .D .3. 流感病毒的直径为0.00000012m，该数值用科学记数法表示为（）A . mB . mC . mD .m4. 下列从左到右的变形，是因式分解的是（）A .B .C .D .5. 如图，点E 在BC 的延长线上，下列条件中能判断AB//CD的是（）A . ∠3=∠4B . ∠D=∠DCEC . ∠B=∠DD . ∠1=∠26. 若多项式a2+kab+4b2是完全平方式，则常数k的值为（）A . 2B . 4C . ±2D . ±47. 方程组的解满足方程x＋y－a=0，那么a的值是（）A . 5B . -5C . 3D . -38. 如图，在边长为a的正方形上剪去一个边长为b的小正方形（a＞b），把剩下的部分剪拼成一个梯形，分别计算这两个图形阴影部分的面积，由此可以验证的等式是（）A . （a﹣b）2=a2﹣2ab+b2B . （a+b）2=a2+2ab+b2C . a2﹣b2=（a+b）（a﹣b）D . a2﹣ab=a（a﹣b）9. 李明同学早上骑自行车上学，中途因道路施工步行一段路，到学校共用时15分钟．他骑自行车的平均速度是250米/分钟，步行的平均速度是80米/分钟．他家离学校的距离是2900米．如果他骑车和步行的时间分别为x、y分钟，列出的方程是（）A .B .C .D .10. 如图，△ABC的角平分线CD、BE相交于F，∠A=90°，EG∥BC，且CG⊥EG 于G，下列结论：①∠CEG=2∠DCB；②∠DFB= ∠CGE；③∠ADC=∠GCD；④CA平分∠BCG．其中正确的个数是（）A . 1B . 2C . 3D . 4二、填空题11. 计算：________.12. n边形的外角和是________．13. 在△ABC中，若∠A﹣∠B=∠C，则此三角形是________三角形．14. 如果，是方程组的解，则________.15. 已知，则________.16. 计算：________.17. 如图，两个正方形的边长分别为a、b，如果a＋b＝7，ab＝10，则阴影部分的面积为________.18. 如图，在△ABC中，∠C=90°，BC=8cm，AC=6cm，点E是BC的中点，动点P从A点出发以每秒2cm的速度沿A→C→B运动，设点P运动的时间是t秒，那么当t=________，△APE的面积等于6.三、解答题19. 计算或化简:（1）；（2）；（3）；（4） .20. 因式分解:（1）；（2） .21. 解方程组：．22. 如图，每个小正方形的边长为1个单位，每个小方格的顶点叫格点.（1 ）画出△ABC向右平移4个单位后得到的△A1B1C1；（2 ）图中AC与A1C1的关系是：_▲_.（3 ）画出△ABC的AB边上的高CD；垂足是D；（4 ）图中△ABC的面积是_▲_.23. 已知的结果中不含关于字母的一次项.先化简，再求：的值.24. 关于x、y的两个方程组和具有相同的解，则a、b的值是多少？25. 填写下列空格完成证明：如图，EF∥AD ，∠1 = ∠2 ，∠BAC = 70° ，求∠AGD .解：∵ EF∥AD ，∴ ∠2 = ▲ .（）∵ ∠1 = ∠2 ，∴ ∠1 = ∠3.（）∴▲∥ ▲ .（）∴ ∠BAC + ▲ = 180° .（）∵ ∠BAC = 70° ，∴ ∠AGD =▲ ° .26. 我市某农场有A、B两种型号的收割机共20台，每台A型收割机每天可收大麦100亩或者小麦80亩，每台B型收割机每天可收大麦80亩或者小麦60亩，该农场现有19 000亩大麦和11 500亩小麦先后等待收割．先安排这20台收割机全部收割大麦，并且恰好10天时间全部收完.（1）问A、B两种型号的收割机各多少台？（2）由于气候影响，要求通过加班方式使每台收割机每天多完成10%的收割量，问这20台收割机能否在一周时间内完成全部小麦收割任务？27. “a2≥0”这个结论在数学中非常有用，有时我们需要将代数式配成完全平方式.例如：x2+4x+5＝x2+4x+4+1＝（x+2）2+1，∵（x+2）2≥0，∴（x+2）2+1≥1，∴x2+4x+5≥1.试利用“配方法”解决下列问题：（1）填空：x2﹣4x+5＝（x________）2+________；（2）已知x2﹣4x+y2+2y+5＝0，求x+y的值；（3）比较代数式：x2﹣1与2x﹣3的大小.28. 如图，AD∥BC，∠B＝∠D＝50°，点E、F在BC上，且满足∠CAD＝∠CAE，AF平分∠BAE.（1）∠CAF＝________°；（2）若平行移动CD，那么∠ACB与∠AEB度数的比值是否随之发生变化？若变化，试说明理由；若不变，求出这个比值；（3）在平行移动CD的过程中，是否存在某种情况，使∠AFB＝∠ACD？若存在，求出∠ACD度数；若不存在，说明理由.。

七年级下学期期中数学试卷第8套真题

七年级下学期期中数学试卷一、精心选一选1. 下列各图中，∠1与∠2是对顶角的是（）A .B .C .D .2. 在平面直角坐标系中，点P（﹣2，3）向右平移3个单位长度后的坐标为（）A . （3，6）B . （1，3）C . （1，6）D . （6，6）3. 如图，下列条件中，不能判断直线a∥b的是（）A . ∠1=∠3B . ∠2=∠3C . ∠4=∠5D . ∠2+∠4=180°4. 已知：直线l1∥l2，一块含30°角的直角三角板如图所示放置，∠1=25°，则∠2等于（）A . 30°B . 35°C . 40°D . 45°5. 16的平方根是（）A . 2B . 4C . ﹣2或2D . ﹣4或46. 若a是（﹣3）2的平方根，则等于（）A . ﹣3B .C . 或﹣D . 3或﹣37. 已知下列命题：①相等的角是对顶角；②互补的角就是平角；③互补的两个角一定是一个锐角，另一个为钝角；④平行于同一条直线的两条直线平行；⑤邻补角的平分线互相垂直．其中真命题的个数为（）A . 3个B . 2个C . 1个D . 0个8. 在数﹣3.14，，0，π，，0.1010010001…中无理数的个数有（）A . 3个B . 2个C . 1个D . 4个9. 以二元一次方程组的解为坐标的点（x，y）在平面直角坐标系的（）A . 第一象限B . 第二象限C . 第三象限D . 第四象限10. 点M（2，﹣3）到x轴的距离是（）A . 2B . ﹣3C . 3D . 以上都不对二、认真的填一填11. 若直线a∥b，b∥c，则________，其理由是________．12. 如图，要把池中的水引到D处，可过D点作CD⊥AB于C，然后沿CD开渠，可使所开渠道最短，试说明设计的依据：________．13. 点P（﹣7，3）是由点M先向左平移动3个单位，再向下平移动3个单位而得到，则M的坐标为________．14. 若点M（a+5，a﹣3）在y轴上，则点M的坐标为________，到x轴的距离为________．15. 把命题“等角的补角相等”改写成“如果…那么…”的形式是________．16. 若+|b2﹣9|=0，则ab=________．17. 的平方根是________，81的算术平方根是________，=________．18. 若一个二元一次方程组的解为则这个方程组可以是________．三、解答题19. 解方程组：（1）（2）．20. 已知：如图，∠1=∠2．求证：∠3+∠4=180°证明：∵∠1=∠2（已知）∴a∥b（________）∴∠3+∠5=180°（两直线平行，同旁内角互补）又∵∠4=∠5（________）∴∠3+∠4=180°（等量代换）21. 如图所示，已知∠1+∠2=180°，∠3=∠B，试判断∠AED与∠C的大小关系，并对结论进行说理．22. 一个正数x的两个不同的平方根是3a﹣4和1﹣6a，求a及x的值．23. 已知是关于x，y的二元一次方程3x=y+a的解，求a（a ﹣1）的值．24. 已知关于x，y的方程组与有相同的解，求a，b的值．25. 如图，直角坐标系中，△ABC的顶点都在网格点上，其中，C点坐标为（1，2）．（1）写出点A、B的坐标：A（________，________）、B（________，________）（2）将△ABC先向左平移2个单位长度，再向上平移1个单位长度，得到△A′B′C′，则A′B′C′的三个顶点坐标分别是A′（________，________）、B′（________，________）、C′（________，________）．（3）△ABC的面积为________．26. 在“五一”期间，小明、小亮等同学随家长一同到某公园游玩，下面是购买门票时，小明与他爸爸的对话（如图），试根据图中的信息，解答下列问题：（1）他们共去了几个成人，几个学生？（2）请你帮助算算，用哪种方式购票更省钱？。

2013版新人教版七年级下数学期中综合测试卷及答案(pdf版)

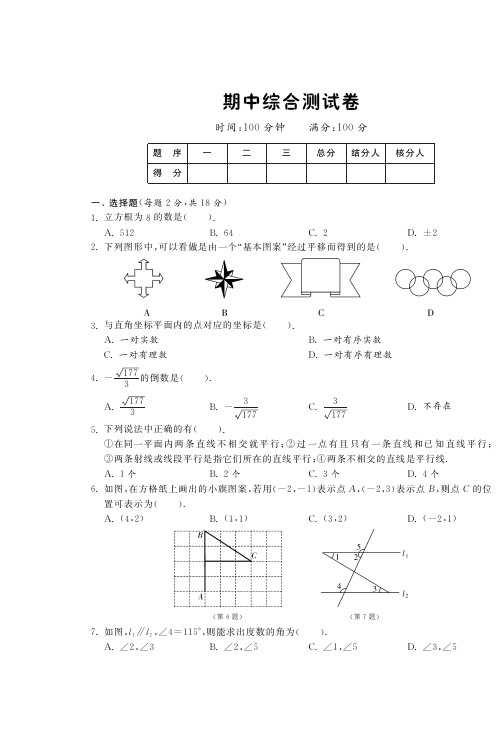
期中综合测试卷时间:１００分钟㊀㊀满分:１００分题㊀序一二三总分结分人核分人得㊀分一㊁选择题(每题２分,共１８分)１．立方根为８的数是(㊀㊀)．A．５１２B．６４C．２D．ʃ２２．下列图形中,可以看做是由一个基本图案经过平移而得到的是(㊀㊀)．３．与直角坐标平面内的点对应的坐标是(㊀㊀)．A．一对实数B．一对有序实数C．一对有理数D．一对有序有理数４．－１７７３的倒数是(㊀㊀)．A．１７７３B．－３１７７C．３１７７D．不存在５．下列说法中正确的有(㊀㊀)．①在同一平面内两条直线不相交就平行;②过一点有且只有一条直线和已知直线平行;③两条射线或线段平行是指它们所在的直线平行;④两条不相交的直线是平行线．A．１个B．２个C．３个D．４个６．如图,在方格纸上画出的小旗图案,若用(－２,－１)表示点A,(－２,３)表示点B,则点C的位置可表示为(㊀㊀)．A．(４,２)B．(１,１)C．(３,２)D．(－２,１)(第６题)㊀㊀㊀㊀(第７题)７．如图,l１ʊl２,ø４＝１１５ʎ,则能求出度数的角为(㊀㊀)．A．ø２,ø３B．ø２,ø５C．ø１,ø５D．ø３,ø５８．下列命题:①无理数可分为正无理数㊁零㊁负无理数;②数轴上的每一个点都与实数一一对应;③若实数a 有立方根,则a 为非负数;④立方根与平方根相等的数是１．其中正确命题的个数是(㊀㊀)．A．０B ．１C ．２D．３９．如果A (１－a ,b ＋１)在第三象限,那么点B (a ,b )在(㊀㊀)．A．第一象限B ．第二象限C ．第三象限D．第四象限二㊁填空题(每题２分,共２２分)１０．若数轴上一个点到原点的距离为２,则这个数为㊀㊀㊀㊀．１１．某数的一个平方根是－３,则它的另一个平方根是㊀㊀㊀㊀,这个数是㊀㊀㊀㊀．１２．一个正数x 的平方根分别是a －１和a ＋３,则a ＝㊀㊀㊀㊀,x ＝㊀㊀㊀㊀．１３．命题等角的补角相等的题设是㊀㊀㊀㊀㊀㊀㊀,结论是㊀㊀㊀㊀㊀㊀㊀．１４．已知点P (x ,y )在第四象限,且|x ＋１|＝２,|y －２|＝３,则点P 的坐标为㊀㊀㊀㊀．(第１５题)１５．如图,C D 平分øA C B ,A E ʊC D ,交B C 的延长线于E ,øA C B ＝５０ʎ,则øE ＝㊀㊀㊀㊀,øC A E ＝㊀㊀㊀㊀．１６．用不等号连接下列各数:(１)１７㊀㊀㊀㊀４．２;(２)－２０㊀㊀㊀㊀－５．１７．已知,直线A B 与C D 相交于点O ,O E ʅC D ,垂足为O ,则图中øA O E 与øDO B 的关系是㊀㊀㊀㊀．(第１７题)㊀㊀㊀(第１８题)㊀㊀㊀(第１９题)１８．如图所示,O P ʊQ R ʊS T ,若ø２＝１１０ʎ,ø３＝１２０ʎ．则ø１＝㊀㊀㊀㊀．１９．如图,将直尺与三角尺叠放在一起,在图中标记的所有角中,与ø２互余的角是㊀㊀㊀㊀．２０．已知点P 在第四象限,它的横坐标与纵坐标的和为１,则点P 的坐标可以是㊀㊀㊀㊀．三㊁解答题(第２１~２４题每题７分,２５~２８每题８分,共６０分)２１．计算:(１)ʃ５２＋１２２;(２)３２６２７－１＋１－５４æèçöø÷２．２２．在正方形网格中,每个小正方形的边长均为１个单位长度,әA B C的三个顶点的位置如图所示,现将әA B C平移,使点A变换为点Aᶄ,点Bᶄ㊁Cᶄ分别是B㊁C的对应点．(１)请画出平移后的әAᶄBᶄCᶄ,并求әAᶄBᶄCᶄ的面积;(２)若连接A Aᶄ㊁C Cᶄ,则这两条线段之间的关系是㊀㊀㊀㊀．(第２２题)２３．已知一立方体纸盒的体积比棱长是６c m的立方体体积大１２７c m３,求该立方体纸盒的棱长．２４．计算下列各题:(１)４的平方根与８的立方根的和;(２)３与１２的积的算术平方根与－２１６的立方根的和．２５．某计算装置有一数据入口A和一运算结果的出口B,下表给出的是小红输入的数字及所得的运算结果:A０１４９１６２５３６B－１０１２３４５若小红输入的数为４９,则输出的结果应为多少?若小红输入的数字为a,你能用a表示输出结果吗?２６．如图,已知点D㊁E㊁F和点A㊁B㊁C分别在同一直线上,若ø１＝ø２,øC＝øD,试探究øA 与øF的关系,并说明理由．(第２６题)２７．已知直线A BʊC D,E为A B㊁C D间的一点,连接E A㊁E C．(第２７题)(１)如图(１),若øA＝２０ʎ,øC＝４０ʎ,则øA E C＝㊀㊀㊀㊀ʎ;(２)如图(２),若øA＝xʎ,øC＝yʎ,则øA E C＝㊀㊀㊀㊀ʎ;(３)如图(３),若øA＝α,øC＝β,则α,β与øA E C之间有何等量关系?并简要说明．２８．如图所示,大圆圈O内有一小圆圈O１,小圆圈O１从现在的位置沿O１O的方向平移４个单位后,得到小圆圈O２,已知小圆圈半径为１．求:(１)大圆圈的面积;(２)小圆圈在平移过程中扫过的面积．(第２８题)期中综合测试卷１．A㊀２．D㊀３．B㊀４．B㊀５．A㊀６．B㊀７．B㊀８．B ９．D㊀１０．２或－２㊀１１．３㊀９㊀１２．－１㊀４１３．两个角相等㊀它们的补角相等㊀１４．(１,－１)１５．２５ʎ㊀２５ʎ㊀１６．＜㊀＞㊀１７．互余㊀１８．５０ʎ１９．ø４,ø５,ø６２０．答案不唯一,比如:(１．５,－０．５)２１．(１)ʃ１３㊀(２)－１１２２２．(１)如图㊀３．５㊀(２)平行且相等(第２２题)２３．７c m㊀２４．(１)０或４㊀(２)０２５．若小红输入的数为４９,则输出的结果应为６．若小红输入的数字为a,则用a表示的输出结果是a－１(aȡ０)．２６．øA＝øF．理由如下:ȵ㊀ø１＝ø２,ø１＝ø３,ʑ㊀ø２＝ø３．ʑ㊀B DʊC E．ʑ㊀øC＝øA B D．ȵ㊀øC＝øD,ʑ㊀øD＝øA B D．ʑ㊀A CʊD F．ʑ㊀øA＝øF．２７．(１)６０㊀(２)３６０－x－y(３)øA E C＝１８０ʎ－α＋β．理由如下:过点E作E FʊA B．ȵ㊀A BʊC D,ʑ㊀E FʊC D．ʑ㊀α＋øA E F＝１８０ʎ,β＝øC E F．ʑ㊀øA E F＝１８０ʎ－α,øC E F＝β．ʑ㊀øA E C＝øA E F＋øC E F＝１８０ʎ－α＋β．２８．(１)ȵ㊀小圆圈O１从现在的位置沿O１O的方向平移４个单位后,得到小圆圈O２,ʑ㊀O１O２＝４,故大圆圈半径为３．ʑ㊀S＝πr２＝９π．(２)小圆圈在平移过程扫过的面积是矩形的面积为４ˑ２＝８．。

七年级下册数学期中试卷及答案人教 (8)

七年级下册数学期中试卷及答案人教一、选择题 1．4的平方根是（）A ．2B ．2±C ．2D ．2±2．在下面的四幅图案中，能通过图案（1）平移得到的是（）A ．B ．C ．D ． 3．点(﹣4，2)所在的象限是（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 4．命题：①对顶角相等；②同旁内角互补；③如果两条直线垂直于同一条直线，那么这两条直线互相平行；④过一点有且只有一条直线与已知直线平行；⑤平行于同一条直线的两条直线互相平行．其中是真命题的有（）A ．5个B ．4个C ．3个D ．2个5．如图，直线12//l l ，23216∠+∠=°，则1∠的度数为（）A ．216︒B ．36︒C ．44︒D ．18︒6．下列说法正确的是（）A ．一个数的立方根有两个，它们互为相反数B ．负数没有立方根C ．任何一个数都有平方根和立方根D ．任何数的立方根都只有一个7．如图，已知////AB CD EF ，FC 平分AFE ∠，26C ∠=︒，则A ∠的度数是（）A ．35︒B ．45︒C ．50︒D ．52︒8．如图，在平面直角坐标系中，(1,1)A ，(1,1)B -，(1,2)C --，(1,2)D -，把一条长为2018个单位长度且没有弹性的细线（线的粗细忽略不计）的一端固定在点A 处，并按A B C D A →→→→…的规律绕在四边形ABCD 的边上，则细线另一端所在位置的点的坐标是（）A ．(1,0)-B ．(1,2)-C ．(1,1)-D ．(0,2)-二、填空题9．36的平方根是_________10．点(m ，1)和点(2，n)关于x 轴对称，则mn 等于_______.11．若(,)A a b 在第一、三象限的角平分线上,a 与b 的关系是_________.12．如图，点D 、E 分别在AB 、BC 上，DE ∥AC ，AF ∥BC ，∠1＝70°，则∠2＝_____°．13．如图，在△ABC 中，将∠B 、∠C 按如图所示的方式折叠，点B 、C 均落于边BC 上的点Q 处，MN 、EF 为折痕，若∠A=82°，则∠MQE= _________14．实数a 、b 在数轴上所对应的点如图所示，则|3﹣b |+|a +3|+2a 的值_____．15．若点P(2-m ，m+1)在x 轴上，则P 点坐标为_____．16．如图，已知A 1（1，2），A 2（2，2），A 3（3，0），A 4（4，﹣2），A 5（5，﹣2），A 6（6，0），…，按这样的规律，则点A 2021的坐标为 ____________．三、解答题17．计算：（1）3-(-5)+(-6)（2）()211162--⨯ 18．求下列各式中x 的值：（1）24241x -=；（2）()38127x -=．19．完成下面的证明：如图，点D 、E 、F 分别是三角形ABC 的边BC 、CA 、AB 上的点，连接DE ，DF ，//DE AB ，BFD CED ∠=∠，连接BE 交DF 于点G ，求证：180EGF AEG ∠+∠=︒．证明：∵//DE AB （已知）∴A CED ∠=∠（_______________）又∵BFD CED ∠=∠（已知）∴A BFD ∠=∠（______________）∴//DF AC （_____________）∴180EGF AEG ∠+∠=︒（______________）20．已知在平面直角坐标系中有三点A （﹣2，1）、B （3，1）、C （2，3）．请回答如下问题：（1）在坐标系内描出点A 、B 、C 的位置；（2）求出以A 、B 、C 三点为顶点的三角形的面积；（3）在y 轴上是否存在点P ，使以A 、B 、P 三点为顶点的三角形的面积为10，若存在，请直接写出点P 的坐标；若不存在，请说明理由．21．已知：31a +的立方根是2-，21b -的算术平方根3，c 是43的整数部分．（1）求,,a b c 的值；（2）求922a b c -+的平方根． 22．小丽想用一块面积为400cm 2的正方形纸片,沿着边的方向裁处一块面积为300cm 2的长方形纸片.(1)请帮小丽设计一种可行的裁剪方案；(2)若使长方形的长宽之比为3:2,小丽能用这块纸片裁处符合要求的纸片吗？若能,请帮小丽设计一种裁剪方案,若不能，请简要说明理由.23．如图，直线//PQ MN ，点C 是PQ 、MN 之间（不在直线PQ ，MN 上）的一个动点．（1）如图1，若1∠与2∠都是锐角，请写出C ∠与1∠，2∠之间的数量关系并说明理由；（2）把直角三角形ABC 如图2摆放，直角顶点C 在两条平行线之间，CB 与PQ 交于点D ，CA 与MN 交于点E ，BA 与PQ 交于点F ，点G 在线段CE 上，连接DG ，有BDF GDF ∠=∠，求AEN CDG ∠∠的值；（3）如图3，若点D 是MN 下方一点，BC 平分PBD ∠， AM 平分CAD ∠，已知25PBC ∠=︒，求ACB ADB ∠+∠的度数．24．如图1，点O 在MN 上，90,,AOB AOM m OCQ n ∠=︒∠=︒∠=︒，射线OB 交PQ 于点C ，已知m ，n 满足：220(70)0m n -+-=．（1）试说明MN //PQ 的理由；（2）如图2，OD 平分AON ∠，CF 平分OCQ ∠，直线OD 、CF 交于点E ，则OEF ∠=______︒；（3）若将AOB ∠绕点O 逆时针旋转()090αα<<︒，其余条件都不变，在旋转过程中，OEF ∠的度数是否发生变化？请说明你的结论．【参考答案】一、选择题1．D解析：D【分析】依据平方根的定义、算术平方根的定义进行解答即可．【详解】解：∵42=， ∴42 故选D.【点睛】本题主要考查的是算术平方根、平方根的定义，熟练掌握相关概念是解题的关键． 2．C【分析】平移前后形状与大小没有改变，并且对应点的连线平行且相等的图形即可．【详解】解：A 、对应点的连线相交，不能通过平移得到，不符合题意；B 、对应点的连线相交，不能通过平移得到，不符合题解析：C【分析】平移前后形状与大小没有改变，并且对应点的连线平行且相等的图形即可．【详解】解：A 、对应点的连线相交，不能通过平移得到，不符合题意；B 、对应点的连线相交，不能通过平移得到，不符合题意；C 、可通过平移得到，符合题意；D、对应点的连线相交，不能通过平移得到，不符合题意；故选：C．【点睛】本题考查了平移变换，解题的关键是熟练掌握平移变换的性质，属于中考常考题型．3．B【分析】根据第二象限的点的横坐标是负数，纵坐标是正数解答．【详解】解：点（-4，2）所在的象限是第二象限．故选：B．【点睛】本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．4．D【分析】根据对顶角的概念、平行线的性质、平行公理、平行线的判定定理判断即可．【详解】解：①对顶角相等，①是真命题，故①正确；②两直线平行，同旁内角互补，②是假命题，故②错误；③在同一平面内，如果两条直线垂直于同一条直线，那么这两条直线互相平行，③是假命题，故③是错误；④过直线外一点有且只有一条直线与已知直线平行，④是假命题，故④错误；⑤平行于同一条直线的两条直线互相平行，⑤是真命题，故⑤正确；综上所述，真命题有①⑤，有2个．故选：D．【点睛】本题主要考查了对顶角的概念、平行线的性质、平行公理、平行线的判定定理，解题的关键是熟练掌握相关知识点．5．B【分析】记∠1顶点为A，∠2顶点为B，∠3顶点为C，过点B作BD∥l1，由平行线的性质可得∠3+∠DBC=180°，∠ABD+(180°－∠1)=180°，由此得到∠3+∠2+(180°－∠1)=360°，再结合已知条件即可求出结果．【详解】如图，过点B作BD∥l1，∵12//l l ，∴BD ∥l 1∥l 2，∴∠3+∠DBC =180°，∠ABD +(180°－∠1)=180°，∴∠3+∠DBC +∠ABD +(180°－∠1)=360°，即∠3+∠2+(180°－∠1)=360°，又∵∠2+∠3=216°，∴216°+(180°－∠1)=360°，∴∠1=36°．故选：B ．【点睛】本题考查了平行线的性质，正确作出辅助线，熟练掌握平行线性质是解题的关键． 6．D【分析】根据负数没有平方根，一个正数的平方根有两个且互为相反数，一个数的立方根只有一个，结合选项即可作出判断．【详解】A 、一个数的立方根只有1个，故本选项错误；B 、负数有立方根，故本选项错误；C 、负数只有立方根，没有平方根，故本选项错误；D 、任何数的立方根都只有一个，故本选项正确．故选：D ．【点睛】本题考查了平方根、算术平方根、立方根的概念，解决本题的关键是熟记平方根、算术平方根、立方根的概念．7．D【分析】由题意易得26EFC C ∠=∠=︒，则有52EFA ∠=︒，然后根据平行线的性质可求解．【详解】解：∵//CD EF ，26C ∠=︒，∴26EFC C ∠=∠=︒，∵FC 平分AFE ∠，∴26EFC CFA ∠=∠=︒，∴52EFA ∠=︒，∵//AB CD ，∴52A EFA ∠=∠=︒；故选D．【点睛】本题主要考查平行线的性质及角平分线的定义，熟练掌握平行线的性质及角平分线的定义是解题的关键．8．C【分析】先求出四边形ABCD的周长为10，得到2018÷10的余数为8，由此即可解决问题．【详解】解：∵A（1，1），B（−1，1），C（−1，−2），D（1，−2），∴AB＝1−（−1解析：C【分析】先求出四边形ABCD的周长为10，得到2018÷10的余数为8，由此即可解决问题．【详解】解：∵A（1，1），B（−1，1），C（−1，−2），D（1，−2），∴AB＝1−（−1）＝2，BC＝1−（−2）＝3，CD＝1−（−1）＝2，DA＝1−（−2）＝3，∴绕四边形ABCD一周的细线长度为2＋3＋2＋3＝10，2018÷10＝201…8，∴细线另一端在绕四边形第202圈的第8个单位长度的位置，即细线另一端所在位置的点在D处上面1个单位的位置，坐标为（1，−1）．故选：C．【点睛】本题利用点的坐标考查了数字变化规律，根据点的坐标求出四边形ABCD一周的长度，从而确定2018个单位长度的细线的另一端落在第几圈第几个单位长度的位置是解题的关键．二、填空题9．．【详解】【分析】先确定，再根据平方根定义可得的平方根是±.【详解】因为，6的平方根是±，所以的平方根是±.故正确答案为±.【点睛】此题考核算术平方根和平方根定义.此题关键要看清符号所表示解析：【详解】=.6=，6的平方根是6故正确答案为.【点睛】此题考核算术平方根和平方根定义.此题关键要看清符号所表示的意义.10．-2【分析】直接利用关于x轴对称点的性质得出m，n的值进而得出答案．【详解】∵点A（m，1）和点B（2，n）关于x轴对称，∴m＝2，n＝-1，故mn＝−2．故填：-2.【点睛】此题解析：-2【分析】直接利用关于x轴对称点的性质得出m，n的值进而得出答案．【详解】∵点A（m，1）和点B（2，n）关于x轴对称，∴m＝2，n＝-1，故mn＝−2．故填：-2.【点睛】此题主要考查了关于x轴对称点的性质，正确掌握关于x轴对称点的性质是解题关键．11．a=b．【详解】根据第一、三象限的角平分线上的点的坐标特征，易得a=b.解析：a=b．【详解】根据第一、三象限的角平分线上的点的坐标特征，易得a=b.12．70【分析】根据两直线平行，同位角相等可得∠C=∠1，再根据两直线平行，内错角相等可得∠2=∠C．【详解】∵DE∥AC，∴∠C＝∠1＝70°，∵AF∥BC，∴∠2＝∠C＝70°．故答解析：70【分析】根据两直线平行，同位角相等可得∠C=∠1，再根据两直线平行，内错角相等可得∠2=∠C ．【详解】∵DE ∥AC ，∴∠C ＝∠1＝70°，∵AF ∥BC ，∴∠2＝∠C ＝70°．故答案为70．【点睛】本题考查了平行线的性质，熟记性质并准确识图是解题的关键．13．【分析】根据折叠的性质得到，，再根据的度数即可求出的度数，再根据求解即可．【详解】解：∵折叠，∴，，∵，∴，∴．故答案是：．【点睛】本题考查折叠问题，解题的关键是掌握折叠的性质解析：82︒【分析】根据折叠的性质得到B MQN ∠=∠，C EQF ∠=∠，再根据A ∠的度数即可求出MQN EQF ∠+∠的度数，再根据()180MQE MQN EQF ∠=︒-∠+∠求解即可．【详解】解：∵折叠，∴B MQN ∠=∠，C EQF ∠=∠，∵82A ∠=︒，∴1808298MQN EQF B C ∠+∠=∠+∠=︒-︒=︒，∴()1801809882MQE MQN EQF ∠=︒-∠+∠=︒-︒=︒．故答案是：82︒．【点睛】本题考查折叠问题，解题的关键是掌握折叠的性质．14．﹣2a﹣b【分析】直接利用数轴结合绝对值以及平方根的性质化简得出答案．【详解】解：由数轴可得：a＜﹣，0＜b＜，故|﹣b|+|a+|+＝﹣b﹣（a+）﹣a＝﹣b﹣a﹣﹣a＝﹣2a﹣b解析：﹣2a﹣b【分析】直接利用数轴结合绝对值以及平方根的性质化简得出答案．【详解】解：由数轴可得：a0＜b故b|+|ab﹣（a ab﹣a a＝﹣2a﹣b．故答案为：﹣2a﹣b．【点睛】此题主要考查了实数的运算以及实数与数轴，正确化简各式是解题关键．15．（3，0）【分析】根据x轴上的点的坐标纵坐标为0列方程可求出m的值，即可得出点P坐标．【详解】∵点P(2-m，m+1)在x轴上，∴m+1=0，解得：m=-1，∴2-m=3，∴P点坐标解析：（3，0）【分析】根据x轴上的点的坐标纵坐标为0列方程可求出m的值，即可得出点P坐标．【详解】∵点P(2-m，m+1)在x轴上，∴m+1=0，解得：m=-1，∴2-m=3，∴P点坐标为（3，0），故答案为：（3，0）【点睛】本题考查了点的坐标，熟记x轴上的点的纵坐标等于0是解题的关键．16．（2021，﹣2）【分析】观察发现，每6个点形成一个循环，再根据点A6的坐标及2021÷6所得的整数及余数，可计算出点A2021的横坐标，再根据余数对比第一组的相应位置的数可得其纵坐标．【详解解析：（2021，﹣2）【分析】观察发现，每6个点形成一个循环，再根据点A6的坐标及2021÷6所得的整数及余数，可计算出点A2021的横坐标，再根据余数对比第一组的相应位置的数可得其纵坐标．【详解】解：观察发现，每6个点形成一个循环，∵A6（6，0），∴OA6＝6，∵2021÷6＝336…5，∴点A2021的位于第337个循环组的第5个，∴点A2021的横坐标为6×336+5＝2021，其纵坐标为：﹣2，∴点A2021的坐标为（2021，﹣2）．故答案为：（2021，﹣2）．【点睛】此题主要考查坐标的规律探索，解题的关键是根据图形的特点发现规律进行求解．三、解答题17．（1）2；（2）-1【分析】(1)利用加减法法则计算即可得到结果；(2)先算乘方和平方根，再算乘法，最后进行加减计算即可得到结果．【详解】（1）解：3-(-5)+(-6)=3+5-6解析：（1）2；（2）-1【分析】(1)利用加减法法则计算即可得到结果；(2)先算乘方和平方根，再算乘法，最后进行加减计算即可得到结果．【详解】（1）解：3-(-5)+(-6)=3+5-6=2（2）解：(-1)21 2=1-4× 1 2=1-2=-1【点睛】此题考查了实数的运算，熟练掌握运算法则是解本题的关键．18．（1）；（2）【分析】（1）先移项，然后运用直接开平方法，即可求出的值；（2）方程两边同时除以8，然后计算立方根，即可得到答案．【详解】解：（1）∴，∴，∴；（2），∴，∴，解析：（1）52x=±；（2）52x=【分析】（1）先移项，然后运用直接开平方法，即可求出x的值；（2）方程两边同时除以8，然后计算立方根，即可得到答案．【详解】解：（1）24241x-=∴2425x=，∴2254x=，∴52x=±；（2）()38127x -=，∴()32718x -=， ∴312x -=， ∴52x =；【点睛】本题考查了直接开平方法、开立方根法求方程的解，解题的关键是熟练掌握直接开平方法、开立方根法进行解题．19．两直线平行，同位角相等；等量代换；同位角相等，两直线平行；两直线平行，同旁内角互补【分析】根据平行线的性质与判定进行证明即可得到答案．【详解】证明：∵（已知）∴（两直线平行，同位角相等）解析：两直线平行，同位角相等；等量代换；同位角相等，两直线平行；两直线平行，同旁内角互补【分析】根据平行线的性质与判定进行证明即可得到答案．【详解】证明：∵//DE AB （已知）∴A CED ∠=∠（两直线平行，同位角相等）又∵BFD CED ∠=∠（已知）∴A BFD ∠=∠（等量代换）∴//DF AC （同位角相等，两直线平行）∴180EGF AEG ∠+∠=．（两直线平行，同旁内角互补）【点睛】本题主要考查了平行线的性质与判定，解题的关键在于能够熟练掌握相关知识进行求解．20．（1）见解析；（2）S△ABC＝5；（3）存在，P点的坐标为（0，5）或（0，﹣3）．【分析】（1）根据点的坐标，直接描点；（2）根据点的坐标可知，ABx轴，且AB＝3﹣（﹣2）＝5，点C到线解析：（1）见解析；（2）S△ABC＝5；（3）存在，P点的坐标为（0，5）或（0，﹣3）．【分析】（1）根据点的坐标，直接描点；（2）根据点的坐标可知，AB//x轴，且AB＝3﹣（﹣2）＝5，点C到线段AB的距离3﹣1＝2，根据三角形面积公式求解；（3）因为AB＝5，要求ABP的面积为10，只要P点到AB的距离为4即可，又P点在y 轴上，满足题意的P点有两个．【详解】解：（1）描点如图；（2）依题意，得AB//x轴，且AB＝3﹣（﹣2）＝5，∴S△ABC＝1×5×2＝5；2（3）存在；∵AB＝5，S△ABP＝10，∴P点到AB的距离为4，又点P在y轴上，∴P点的坐标为（0，5）或（0，﹣3）．【点睛】本题考查了点的坐标的表示方法，能根据点的坐标表示三角形的底和高并求三角形的面积．21．（1）；（2）其平方根为．【分析】（1）根据立方根，算术平方根，无理数的估算即可求出的值；（2）将（1）题求出的值代入，求出值之后再求出平方根．【详解】解：（1）由题得．．又，解析：（1）3,5,6a b c =-==；（2）其平方根为4±．【分析】（1）根据立方根，算术平方根，无理数的估算即可求出,,a b c 的值；（2）将（1）题求出的值代入922a b c -+，求出值之后再求出平方根．【详解】解：（1）由题得318,219a b +=--=．3,5a b ∴=-=．<67∴<．6c ∴=．3,5,6a b c ∴=-==．（2）当3,5,6a b c =-==时，()99223561622a b c -+=⨯--+⨯=． ∴其平方根为4±．【点睛】本题考查了立方根，平方根，无理数的估算．正确把握相关定义是解题的关键． 22．（1）可以以正方形一边为长方形的长，在其邻边上截取长为15cm 的线段作为宽即可裁出符合要求的长方形；（2）不能，理由见解析.【解析】（1）解：设面积为400cm2的正方形纸片的边长为a cm∴解析：（1）可以以正方形一边为长方形的长，在其邻边上截取长为15cm 的线段作为宽即可裁出符合要求的长方形；（2）不能，理由见解析.【解析】（1）解：设面积为400cm 2的正方形纸片的边长为a cm∴a 2=400又∵a ＞0∴a =20又∵要裁出的长方形面积为300cm 2∴若以原正方形纸片的边长为长方形的长，则长方形的宽为：300÷20=15（cm ）∴可以以正方形一边为长方形的长，在其邻边上截取长为15cm 的线段作为宽即可裁出符合要求的长方形（2）∵长方形纸片的长宽之比为3：2∴设长方形纸片的长为3x cm，则宽为2x cm∴6x 2=300∴x 2=50又∵x＞0∴x=52∴长方形纸片的长为152又∵()2152=450＞202即：152＞20∴小丽不能用这块纸片裁出符合要求的纸片23．（1）见解析；（2）；（3）75°【分析】（1）根据平行线的性质、余角和补角的性质即可求解．（2）根据平行线的性质、对顶角的性质和平角的定义解答即可．（3）根据平行线的性质和角平分线的定义以；（3）75°解析：（1）见解析；（2）12【分析】（1）根据平行线的性质、余角和补角的性质即可求解．（2）根据平行线的性质、对顶角的性质和平角的定义解答即可．（3）根据平行线的性质和角平分线的定义以及三角形内角和解答即可．【详解】解：（1）∠C=∠1+∠2，证明：过C作l∥MN，如下图所示，∵l∥MN，∴∠4=∠2（两直线平行，内错角相等），∵l∥MN，PQ∥MN，∴l∥PQ，∴∠3=∠1（两直线平行，内错角相等），∴∠3+∠4=∠1+∠2，∴∠C=∠1+∠2；（2）∵∠BDF=∠GDF，∵∠BDF =∠PDC ，∴∠GDF =∠PDC ，∵∠PDC +∠CDG +∠GDF =180°，∴∠CDG +2∠PDC =180°，∴∠PDC =90°-12∠CDG ，由（1）可得，∠PDC +∠CEM =∠C =90°，∴∠AEN =∠CEM ， ∴190(90)90122CDG AEN CEM PDC CDG CDG CDG CDG ︒-︒-∠∠∠︒-∠====∠∠∠∠，（3）设BD 交MN 于J ．∵BC 平分∠PBD ，AM 平分∠CAD ，∠PBC =25°，∴∠PBD =2∠PBC =50°，∠CAM =∠MAD ，∵PQ ∥MN ，∴∠BJA =∠PBD =50°，∴∠ADB =∠AJB -∠JAD =50°-∠JAD =50°-∠CAM ，由（1）可得，∠ACB =∠PBC +∠CAM ，∴∠ACB +∠ADB =∠PBC +∠CAM +50°-∠CAM =25°+50°=75°．【点睛】本题考查了平行线的性质、余角和补角的性质，解题的关键是根据平行找出角度之间的关系．24．（1）见解析；（2）45；（3）不变，见解析；【分析】（1）由可求得m 及n ，从而可求得∠MOC=∠OCQ ，则可得结论；（2）易得∠AON 的度数，由两条角平分线，可得∠DON ，∠OCF 的度数，也解析：（1）见解析；（2）45；（3）不变，见解析；【分析】（1）由220(70)0m n -+-=可求得m 及n ，从而可求得∠MOC =∠OCQ ，则可得结论；（2）易得∠AON 的度数，由两条角平分线，可得∠DON ，∠OCF 的度数，也易得∠COE 的度数，由三角形外角的性质即可求得∠OEF 的度数；（3）不变，分三种情况讨论即可．【详解】（1）∵200m -≥，2(70)0n -≥，且220(70)0m n -+-=∴200m -=，2(70)0n -=∴m =20，n =70∴∠MOC =90゜－∠AOM =70゜∴∠MOC =∠OCQ =70゜∴MN ∥PQ（2）∵∠AON =180゜－∠AOM =160゜又∵OD 平分AON ∠，CF 平分OCQ ∠∴1802DON AON ∠=∠=︒，1352OCF OCQ ∠=∠=︒∵80MOE DON ∠=∠=︒∴10COE MOE MOC ∠=∠-∠=︒∴∠OEF =∠OCF +∠COE =35゜+10゜=45゜故答案为：45．（3）不变，理由如下：如图，当0゜<α<20゜时，∵CF 平分∠OCQ∴∠OCF =∠QCF设∠OCF =∠QCF =x则∠OCQ =2x∵MN ∥PQ∴∠MOC =∠OCQ =2x∵∠AON =360゜－90゜—(180゜－2x )=90゜+2x ，OD 平分∠AON∴∠DON =45゜+x∵∠MOE =∠DON =45゜+x∴∠COE =∠MOE －∠MOC =45゜+x －2x =45゜－x∴∠OEF =∠COE +∠OCF =45゜－x +x =45゜当α=20゜时，OD 与OB 共线，则∠OCQ =90゜，由CF 平分∠OCQ 知，∠OEF =45゜当20゜<α<90゜时，如图∵CF 平分∠OCQ∴∠OCF =∠QCF设∠OCF =∠QCF =x则∠OCQ =2x∵MN ∥PQ∴∠NOC=180゜－∠OCQ=180゜－2x∵∠AON=90゜+(180゜－2x)=270゜－2x，OD平分∠AON∴∠AOE=135゜－x∴∠COE=90゜－∠AOE=90゜－(135゜－x)=x－45゜∴∠OEF=∠OCF－∠COE=x－(x－45゜)=45゜综上所述，∠EOF的度数不变．【点睛】本题主要考查了角平分线的定义，平行线的判定与性质，角的和差关系，注意分类讨论，引入适当的量便于运算简便．。

人教版2013年七年级下期中考试数学试卷及答案

勐捧中学2013学年度下学期七年级期中学业水平检测数学试卷（考试时间：120分钟分数：100分）一、填空题：（每题2分，共20分）1.已知P （4，-2），则点P 在第象限。

2． 2)5(±的算术平方根是，36的平方根是 . 327-=3．如图，a 、b 直线相交，∠1=60０，则∠3=________，∠2=__________．4．如图，直线AB 、CD 、EF 相交于点O ，则∠AOC 的对顶角是_____________，∠AOD 的对顶角是_____________．5．如图，要从小河a 引水到村庄A ，请设计并作出一条最佳路线，理由是： _______________ ． 6． 37-的相反数是 , 绝对值等于3的数是7．把命题“等角的余角相等”改写成“如果……那么………”的形式是。

8．将点P （-2，-1）向左平移2个单位得A ′，A ′的坐标是．9．23- 23-; 10．在同一平面内，两条直线的位置关系只有两种： _________ 、 _________．二、选择：（每题2分，共20分）11．16的算术平方根为（）A 、4B 、4±C 、2D 、2±12．下列语句中，正确的是（） A 、无理数都是无限小数 B 、无限小数都是无理数 C 、带根号的数都是无理数 D 、不带根号的数都是无理数13．在实数70107.081221.03、、、、－。

π中，其中无理数的个数为（）A 、1B 、2C 、3D 、414．如图，∠ADE 和∠CED 是（）A ．同位角B ．内错角C ．同旁内角D ．互为补角15．在下图中，∠1，∠2是对顶角的图形是（）16．下列各点中，在第二象限的点是（） A ．（2，3） B ．(2,－3) C ．(－2,3) D ．(－2, －3)17．2)2(-的平方根是（） A ．±2 B. ±1.414 C. ±2 D.－218.下列式子中，正确的是（） A ．3355-=- B.6.06.3-=- C. 13)13(2-=- D. 636±= 19.－27的立方根与81的平方根之和为（） A.0 B.6 C.0或-6 D.0或620．在△ABC 中，∠A=20 o ,∠B=50 o,则∠C = ( )A 、60°B 、70°C 、110°D 、120° 三、计算题: （每题5分，共10分）21、 22、第（11）题E DCBA第14题四、解答题：(共50分)23、（8分）如图，AB ∥CD ，∠1=45°，∠D =∠C ，求∠D 、∠C 、∠B 的度数．1AB CD24．（8分）如图，∠5=∠CDA =∠ABC ，∠1=∠4，∠2=∠3，∠BAD +∠CDA =180°，填空：∵∠5=∠CDA （已知）∴ // （） ∵∠5=∠ABC （已知）∴ // （） ∵∠2=∠3（已知）∴ // （）∵∠BAD +∠CDA =180°（已知）∴ // （） 25．（7分）如图，OA ⊥OB ，OC ⊥OD ，∠BOC =30°，求∠AOD 的度数．26.（8分）平面直角坐标系中,顺次连结A(-2,1),B(-2,-1),C(2,-2),D(2,3)各点, 你会得到一个什么图形?试求出该图形的面积.27．（7分）如图，直线l n l m ⊥⊥,，∠1=∠2，求证∠3=∠4．28、（12分）.如图,AB ∥CD,分别探讨下面四个图形中∠APC 与∠PAB,∠PCD 的关系,请你从所得的关系中任选一个关系加以说明.(1)PDC BA (2)PD C BA(3)P C BA(4)PDC BA勐捧中学2013学年度下学期七年级期中学业水平检测数学参考答案一、填空：（每题2分，共20分）1、第四象限2、5 ；或-； -33、∠3=60０ ,∠2=120０4、∠BOD ；∠BOC5、作图略，垂线段最短。

新人教版2013年七年级下数学期中考试卷(包含答案)

2014年七年级第二学期数学期中考试卷（总分：120分时间：90分钟）一、选择题（每小题3分，共30分） 1、下面说法正确的是（）A ．过一点有且只有一条直线与已知直线垂直。

B ．同一平面内，过一点有且只有一条直线与已知直线平行。

C ．平行于同一条直线的两条直线互相平行。

D ．垂直于同一条直线的两条直线互相垂直。

2、两条平行直线被第三条直线所截，同位角的平分线( ) A.互相重合 B.互相平行 C.互相垂直 D.相交3、如图，若AB ∥CD ，则∠A 、∠E 、∠D 之间的关系是( ) A.∠A +∠E +∠D =180° B.∠A －∠E +∠D =180° C.∠A +∠E －∠D =180° D.∠A +∠E +∠D =270°4、点P 为直线l 外一点，点A 、B 、C 为直线l 上三点，PA = 4 cm ，PB = 5 cm ，PC = 2 cm ，则点到直线l 的距离是（） A . 2cm B . 小于2cm C . 不大于2cm D . 4cm5、（1）无理数就是开方开不尽的数；（2）无理数包括正无理数、零、负无理数；（3）无理数是无限不循环小数；（4）无理数都可以用数轴上的点来表示。

上面正确的说法的个数是（）A ．1B ．2C ．3D ．46、若a 为实数，则下列式子中一定是负数的是（）A . 2a -B . 2)1(+-aC . 2a -D . )1(+--a 7、下列式子中，正确的是（）A ．3355-=- B.6.06.3-=- C. 13)13(2-=- D. 636±= 8、将点P （－3，y ）向下平移3个单位长度，再向右平移2个单位长度后得到点Q （x ,-1）,则（）A . x=2 ，y=-3B . x=-1 ，y=2C . x=-1 ，y=2D . x=2 ，y=1 9、点A （m ＋3,m ＋1）到x 轴的距离为3，则m 的值为（）A . 0B . 2C . 0或-6D . 2或-410、小明家的坐标为(1，2)，小丽家的坐标为(4，－1)，如果规定向上为正北方向，则小丽家在小明家的( )A ．东南方向B ．东北方向C ．西南方向D ．西北方向二、填空题（每空3分，共30分）学校：班级：姓名：座号：图2 图3 图411、如图2，直线AB 、CD 相交于点O ，EF ⊥AB ，且∠COE=50°，则∠BOD= 12、如图3，AB ∥CD, EG•平分∠BEF,若∠1=72°,则∠2=____ ___13、如图4，AB ∥CD ，∠B=60°，CM 平分∠BCE ，∠MCN=90°，则∠DCN= 14、已知一个正数的平方根为1523-+a a 和，则这个数的是 15、化简：2)3(17ππ-+-= 1610.1==17、如果点A 的坐标为(a +1，－1－3a )，那么点A 在第象限. 18、点P 在第二象限内，点P 到x 轴的距离是3，到y 轴的距离是5，那么点P 的坐标为19、已知AB∥x 轴，点A （2，3），并且AB ＝4，则点B 的坐标为 20、已知点()2,3-P ，点A 与点P 关于y 轴对称，则点A 的坐标是 ______ 三、解答题。

2013年秋人教版七年级数学期中考试测试题

马场中学2013年秋七年级数学期中考试测试题(本大题共10小题，每小题3分，共30分）、－3的倒数是（）．－3 B ．3 C ．31 D ．31－、如果0<a 时，1+aa 的值是（）A. 0B. 1C. 2D. 不能确定、用四舍五入法按要求对1.804分别取近似值，其中错误的是（） A ．1.8（精确到0.1） B ．1.80（精确到百分位）C ．2（精确到个位）D ．1.8（精确到0.01）、下列各式中，正确的是( )A ．y x y x y x 2222-=-B ．ab b a 532=+C ．437=-ab abD ．523a a a =+ 、a-b 的相反数是（）A ．a-bB . b - aC .- a-bD 、不能确定、两个有理数的积为负数，和也为负数，那么这两个数（）A ．都是负数B ．绝对值较大的数是正数，另一个是负数C ．互为相反数D ．绝对值较大的数是负数，另一个是正数、已知496b a -和445b a n 是同类项，则代数式1012-n 的值是（）A ．17B ．37C ．–17D ．98 、下列说法中①－a 一定是负数；②|－a|一定是正数；③倒数等它本1；④绝对值等于它本身的数是1。

其中正确的个数是（）A ．1个B ．2个C ．3个D ．4个、有理数a b ，在数轴上的位置如图所示，下列各式不正确的是（） A 、0<+b a B 、0<abC 、0<baD 、0<-b a、已知代数式y x 2+的值是3，则代数式142++y x 的值是( )A ．1B ．4C ．7D ．不能确定二、填空题(本大题共10小题，每小题2分，共20分) 11、倒数等于其本身的数是 .12、计算（－1）2007＋（－0.125×8）2006＝．13、用四舍五入法将数897654321精确到千万位是。

14、单项式33y x -的系数是_____ 次数是15、一个单项式加上22x y +-后等于22y x +，则这个单项式为 16、北京冬季里某一天的气温为-3℃～3℃，这一天北京的温差是 ℃. 17、若m 、n 满足2)3(2++-n m =0，则.__________=m n18.若单项式33y x m 与52n x y -是同类项，则=+n m ____________ 19.现定义一种新运算 “*”，对于任意两个整数 1a b a b *=⨯-，则8*2的结果是。

2013年人教版初一下册数学期中试卷(带答案)

2013年人教版初一下册数学期中试卷（带答案）2012-2013学年度第二学期七年级期中质量检测数学试卷（完卷时间：120分钟满分：100分）题号一二三总分1819202122232425得分一、选择题：（选一个正确答案的序号填入括号内，每小题2分，共20分）1．下面的四个图形中，∠1与∠2是对顶角的是（）。

A．B．C．D．2．的平方根是（）。

A．B．C．D．3．下列式子正确的是（）。

A．B．C．D．4．如图，已知AB⊥CD，垂足为O，EF为过O点的一条直线，则∠1与∠2的关系一定成立的是（）。

A．相等C．互补B．互余D．互为对顶角5．下列说法正确的是（）。

A．无限小数都是无理数C．无理数是无限不循环小数B．带根号的数都是无理数D.实数包括正实数、负实数6．已知点P(m，1)在第二象限，则点Q(－m，3)在（）。

A．第一象限B．第二象限C．第三象限D．第四象限7．已知在同一平面内三条直线a、b、c，若a‖c，b‖c，则a与b的位置关系是（）。

A．a⊥bB．a⊥b或a‖bC．a‖bD．无法确定8．如图，把一块含有45°角的直角三角尺的两个顶点放在直尺的对边上，如果∠1＝20°，那么∠2的度数是（）。

A．30°C．20°B．25°D．15°9．一个正数x的平方根是2a－3与5－a，则x的值是（）。

A．64B．36C．81D．4910．在平面直角坐标系中，已知点A（－4，0）和B（0，2）,现将线段AB沿着直线AB平移，使点A与点B重合，则平移后点B坐标是（）。

A．（0，－2）B．（4，2）C．（4，4）D．（2，4）二、填空题：（每小题3分，共21分）11.的相反数是，绝对值是。

12.如果，，那么0.0003的平方根是。

13.命题“同角的余角相等”改写成“如果……那么……”的形式是。

14.如图所示，想在河的两岸搭建一座桥，搭建方式最短的是，理由是15.小刚在小明的北偏东60°方向的500m处，则小明在小刚的。

2013年下期七年级期中考试数学试卷.doc

2013年下期七年级期中考试数学试卷满分 100分时间 90分钟一、选择题（共24分，每小题3分）1. －2的相反数是（）A ．2B ．－2C ．21 D ． 21- 2. 一个数和它的倒数相等，则这个数是（）A ．1B ．1-C ．±1D ．±1和0 3. 零是（）A 正有理数B 正数C 非正数D 有理数 4. 下列各组数中，数值相等的是（）A ．33)2(2--和 B ．22)2(2--和 C ．2332--和 D ．1010)1(1--和5. 在三个连续的奇数中，最大的一个是1＋2n ，那么最小的一个是（） A 、2n －1 B 、2n －3 C 、2(n －1) D 、2（n －2）6. 下列式子中错误的是（） A 、x 的21倍与y 的3倍的和是y x 321+ B 、a 的31与b 的和的平方是2)31(b a +C 、两数的平方和加上它们的积的2倍是ab b a 2)(2++ D 、三个数的积减去7是7-abc 7. 买了5千克橘子，花了 m 元，则这种橘子的单价是（）． A ．m 5元 B ．5m元 C ．5m 元 D ．（m －5）元 8. 下列各组中，不是同类项的是（）A 、2235.0ab b a 与 B 、y x y x 2222-与 C 、315与 D 、mm x x 32--与二、填空题（共24分，每小题3分）9. 绝对值等于10的数是．10. 若0)5b (2a 2=-++，则a b的值是 .11. 用科学记数法表示13 040 000，应记作_______________.班次考号姓名12. 在数轴上与-3距离四个单位的点表示的数是__________. 13. 213R π的系数是_____，次数是_____． 14. 比较大小 -87 -76 15. 我校七年级学生在今年植树节中栽了m 棵树，若八年级学生栽树比七年级多n 棵，则两个年级共载树＿＿＿＿棵。

2013年七年级数学期中考试试卷.doc

荷花中学2012年七年级数学期中测试试卷姓名______________班级______________计分______________一、精心选一选（ 12×3分=36分） 1、13的相反数是( ) A .3 B .3- C .13 D .13-2、下列计算正确的是( )2.(1)(1)0A --+-= 2.237B -+-=3.(2)8C --= 111.()11222D -+--=-3、一个数的绝对值是5，则这个数是( )A. 5±B.5C. －5D.25 4、单项式233xy z π-的系数和次数分别是 ( )A.－π，5B.－1，6C. －3，7D.－3π，65、在22-，2(2)-，(2)--，(2)-+，2--，2-中，负数的个数为（）A. 1个B. 2个C. 3个D. 4个6、长城总长约为6700000米，用科学记数法表示为（） A ．6.7510⨯米 B ．6.7610⨯米 C ．6.7710⨯米 D ．6.7810⨯米 7、下列去括号正确的是( )A.()5252+-=+-x xB.()222421+-=--x x C.()n m n m +=-323231D.x m x m 232232+-=⎪⎭⎫⎝⎛--8、下列运算正确的是（） A 、422=-B 、4)2(2-=- C 、6)2(3-=- D 、9)3(2=-9 买一个足球需要m 元，买一个篮球需要n 元，则买4个足球、7个篮球共需要( ) A. )47(n m +元 B.mn 28元 C.)74(n m + 元 D.mn 11元10、两个有理数a ,b 在数轴上的位置如图，下列四个式子中运算结果为正数的式子是( )A 、a+bB 、a －bC 、abD 、ba 11、、已知3||=x ，2||=y ，且x ·y ＜0，则x+y 的值等于（）A 、5或－5B 、1或－1C 、5或1D 、－5或－112、有一列数n a a a a , , , ,321 ，从第二个数开始，每一个数都等于1与它前面那个数的倒数的差，若12a =，则2011a 为A ．2011B ．2C ．－1D ．12二、细心填一填（8×3分=24分） 13、多项式53124232--+c ab a a 是_____次_____项式，常数项是_____。

(完整版)人教版七年级数学下册期中试卷及答案人教 (8)

(完整版)人教版七年级数学下册期中试卷及答案人教一、选择题1．1.96的算术平方根是（） A ．0.14B ．1.4C ．0.14-D ．±1.42．下列各组图形可以通过平移互相得到的是（） A ．B ．C ．D ．3．在平面直角坐标系中，点P （5，﹣1）在（） A ．第一象限B ．第二象限C ．第三象限D ．第四象限4．下列命题中，假命题是（）A ．如果两条直线都与第三条直线平行，那么这两条直线也互相平行B ．在同一平面内，过一点有且只有一条直线与已知直线垂直C ．两条直线被第三条直线所截，同旁内角互补D ．两点的所有连线中，线段最短5．如图，直线//a b ，三角板的直角顶点在直线b 上，已知125∠=︒，则2∠等于（）．A ．25°B ．55°C ．65°D ．75°6．下列说法正确的是（）A ．a 2的正平方根是aB 819=±C ．﹣1的n 次方根是1D 321a --7．在同一平面内，若∠A 与∠B 的两边分别平行，且∠A 比∠B 的3倍少40°，则∠A 的度数为（） A ．20°B ．55°C ．20°或125°D ．20°或55°8．如图，在平面直角坐标系xOy 中，点()1,0P ．点P 第1次向上跳动1个单位至点()11,1P ，紧接着第2次向左跳动2个单位至点()21,1P -，第3次向上跳动1个单位至点3P ，第4次向右跳动3个单位至点4P ，第5次又向上跳动1个单位至点5P ，第6次向左跳动4个单位至点6P ，……．照此规律，点P 第200次跳动至点200P 的坐标是（）A ．()51,100B ．()26,50C ．()26,50-D ．()51,100-二、填空题9．若102.0110.1=，则± 1.0201=_________．10．已知点,A a b （）在第四象限，||5,||3a b ==，则点A 关于y 轴对称的坐标是__________.11．三角形ABC 中，∠A=60°，则内角∠B ，∠C 的角平分线相交所成的角为_____． 12．如图，//AB EF ，设90C ∠=︒，那么x ，y ，z 的关系式______．13．如图，四边形ABCD 中，点M 、N 分别在AB 、BC 上，将△BMN 沿MN 翻折，得△FMN ，若MF ∥AD ，FN ∥DC ，则∠D 的度数为 ___．14．材料：一般地，n 个相同因数a 相乘：n a a a a a⋅⋅⋅⋅⋅个记为n a ．如328=，此时3叫做以2为底的8的对数，记为2log 8（即2log 83=）．那么3log 9=_____，()2231log 16log 813+=_____． 15．P （2m -4，1-2m ）在y 轴上，则m =__________．16．如图，在平面直角坐标系中，一动点从原点O 出发，按向上，向右，向下，向右的方向不断移动，每移动一个单位，得到点1(0,1)A ，()21,1A ，()31,0A ，()42,0A ，…，那么点2021A 的坐标为__________．三、解答题17．计算：(1)()4129-⨯- (2)()432054⎛⎫-⨯- ⎪⎝⎭18．（1）已知a m ＝3，a n ＝5，求a 3m ﹣2n 的值．（2）已知x ﹣y ＝35，xy ＝1825，求下列各式的值：①x 2y ﹣xy 2； ②x 2＋y 2.19．完成下面的证明．如图，AB ∥CD ，∠B +∠D ＝180°，求证：BE ∥DF ．分析：要证BE ∥DF ，只需证∠1＝∠D ．证明：∵AB ∥CD （已知） ∴∠B +∠1＝180°（） ∵∠B +∠D ＝180°（已知） ∴∠1＝∠D （） ∴BE ∥DF （）20．在平面直角坐标系中，已知O ，A ，B ，C 四点的坐标分别为O （0，0），A （0，3），B （－3，3），C （－3，0）．（1）在平面直角坐标系中，描出O ，A ，B ，C 四点；（2）依次连接OA ，AB ，BC ，CO 后，得到图形的形状是___________．21．阅读下面的文字，解答问题，例如：479<<,即273<<,7∴的整数部分是2，小数部分是72-；（1）试解答：17的整数部分是____________，小数部分是________（2）已知917-小数部分是m ，917+小数部分是n ，且()21x m n +=+，请求出满足条件的x 的值．22．如图，这是由8个同样大小的立方体组成的魔方，体积为64．（1）求出这个魔方的棱长；（2）图中阴影部分是一个正方形ABCD ，求出阴影部分的边长．23．已知：直线AB ∥CD ，直线MN 分别交AB 、CD 于点E 、F ，作射线EG 平分∠BEF 交CD 于G ，过点F 作FH ⊥MN 交EG 于H ．（1）当点H 在线段EG 上时，如图1 ①当∠BEG ＝36︒时，则∠HFG ＝．②猜想并证明：∠BEG 与∠HFG 之间的数量关系．（2）当点H 在线段EG 的延长线上时，请先在图2中补全图形，猜想并证明：∠BEG 与∠HFG 之间的数量关系．24．[感知]如图①，//40130AB CD AEP PFD ∠=︒∠=︒，，，求EPF ∠的度数．小乐想到了以下方法，请帮忙完成推理过程．解：（1）如图①，过点P 作//PM AB ． ∴140AEP ∠=∠=︒（_____________）， ∴//AB CD ，∴//PM ________（平行于同一条直线的两直线平行）， ∴_____________（两直线平行，同旁内角互补）， ∴130PFD ∠=︒， ∴218013050︒︒∠=-=︒，∴12405090︒∠=+︒+∠=︒，即90EPF ∠=︒．[探究]如图②，//,50,120AB CD AEP PFC ∠=︒∠=︒，求EPF ∠的度数；[应用]（1）如图③，在[探究]的条件下，PEA ∠的平分线和PFC ∠的平分线交于点G ，则G ∠的度数是_________º．（2）已知直线//a b ，点A ，B 在直线a 上，点C ，D 在直线b 上（点C 在点D 的左侧），连接AD BC ，，若BE 平分ABC DE ∠，平分ADC ∠，且BE DE ，所在的直线交于点E ．设(),ABC ADC αβαβ∠=∠=≠，请直接写出BED ∠的度数（用含,αβ的式子表示）．【参考答案】一、选择题1．B解析：B【分析】根据算术平方根的定义：一般地，如果一个正数x的平方等于a，即x2=a，那么这个正数x 叫做a的算术平方根即可得出答案．【详解】解：∵2，1.4 1.96∴1.96的算术平方根是1.4，故选：B．【点睛】本题考查了算术平方根，掌握算术平方根的定义是解题的关键，如果一个正数x的平方等于a，即x2=a，那么这个正数x叫做a的算术平方根．2．C【分析】根据平移不改变图形的形状和大小，进而得出答案．【详解】解：观察图形可知选项C中的图案通过平移后可以得到．故选：C．【点睛】本题考查了图形的平移，正确掌握平移的性质是解题关键．解析：C【分析】根据平移不改变图形的形状和大小，进而得出答案．【详解】解：观察图形可知选项C中的图案通过平移后可以得到．故选：C．【点睛】本题考查了图形的平移，正确掌握平移的性质是解题关键．3．D【分析】根据点的横纵坐标的符号可得所在象限．【详解】解：∵点P的横坐标是正数，纵坐标是负数，∴点P（5，-1）在第四象限，故选：D．【点睛】本题主要考查点的坐标，熟练掌握各象限内点的坐标的特点是解本题的关键，第一、二、三、四象限内的点的坐标符号分别是（+，+）、（-，+）、（-，-）、（+，-）．4．C【分析】分析是否为真命题，需要分别分析各题设是否能推出结论，从而利用排除法得出答案．【详解】A.如果两条直线都与第三条直线平行，那么这两条直线也互相平行，选项A是真命题，故不符合题意；B.在同一平面内，过一点有且只有一条直线与已知直线垂直，选项B是真命题，故不符合题意；C.两条直线被第三条直线所截，同旁内角不一定互补，选项C是假命题，故符合题意；D. 两点的所有连线中，线段最短，选项D是真命题，故不符合题意．故选：C．【点睛】本题主要考查了命题的真假判断，属于基础题，正确的命题叫真命题，错误的命题叫做假命题，判断命题的真假关键是要熟悉课本中的性质定理．5．C【分析】利用平行线的性质，可证得∠2=∠3，利用已知可证得∠1+∠3=90°，求出∠3的度数，进而求出∠2的度数．【详解】解：如图∵a//b∴∠2=∠3，∵∠1+∠3=180°-90°=90°∴∠3=90°-∠1=90°-25°=65°∴∠2=65°．故选C．【点睛】本题主要考查了平行线的性质，灵活运用“两直线平行、同位角相等”是解答本题的关键．6．D【分析】根据平方根、算术平方根、立方根的定义判断A、B、D，根据乘方运算法则判断C即可．【详解】A ：a 2的平方根是a ±，当0a ≥时，a 2的正平方根是a ，错误；B ：819=，错误；C ：当n 是偶数时，()1=1n- ；当n 时奇数时，()1=-1n-，错误； D ：∵210a --< ，∴321a --一定是负数，正确【点睛】本题考查平方根、算术平方根、立方根的定义以及乘方运算，掌握相关的定义与运算法则是解题关键． 7．C 【分析】根据∠A 与∠B 的两边分别平行，可得两个角大小相等或互补，因此分两种情况，分别求∠A 得度数．【详解】解：∵两个角的两边分别平行， ∴这两个角大小相等或互补， ①这两个角大小相等，如下图所示：由题意得，∠A =∠B ，∠A =3∠B -40°， ∴∠A =∠B =20°，②这两个角互补，如下图所示：由题意得，180A B ∠+∠=︒，340A B ∠=∠-︒， ∴55B ∠=︒，125A ∠=︒，综上所述，∠A 的度数为20°或125°，故选：C ．【点睛】本题考查了平行线的性质，解题的关键是根据平行线的性质找出图中角度之间的关系．8．A 【分析】设第n 次跳动至点Pn ，根据部分点An 坐标的变化找出变化规律P4n （n + 1，2n），Pn+1（n + 1，2n + 1），P4n+2（-n-1，2n+ 1），P4n+3（-n-1，2解析：A【分析】设第n次跳动至点P n，根据部分点A n坐标的变化找出变化规律P4n（n + 1，2n），P n+1（n + 1，2n + 1），P4n+2（-n-1，2n+ 1），P4n+3（-n-1，2n +2），依此规律结合200 = 50 ×4，即可得出点P200的坐标．【详解】解：设第n次跳动至点P n，观察发现：P（1，0），P1（1，1），P2（-1，1），P3（-1，2），P4（2，2），P5（2，3），P6（-2，3），P7（-2，4），P8（3，4），P9（3，5），...，∴P4n+1（n + 1，2n +1），P4n+2（-n-1，2n+ 1），P4n+3（-n-1，2n+2），P4n（n + 1，2n），（n为自然数），∵200 = 50 × 4，∴P200（50+1 ，50×2），即（51，100）．故选A．【点睛】本题考查了规律型中点的坐标，解题的关键是准确找到点的坐标变化规律．二、填空题9．±1.01【分析】根据算术平方根的意义，把被开方数的小数点进行移动（每移动两位，结果移动一位），进行填空即可．【详解】解：∵，∴，故答案为±1.01．【点睛】本题考查了算术平方根的移解析：±1.01【分析】根据算术平方根的意义，把被开方数的小数点进行移动（每移动两位，结果移动一位），进行填空即可．【详解】解：∵10.1=，∴ 1.01=±，故答案为±1.01．【点睛】本题考查了算术平方根的移动规律的应用，能根据移动规律填空是解此题的关键．10．【分析】由第四象限点的坐标符号是（+，-），可得，关于y 轴对称的点，纵坐标相同，横坐标互为相反数，即可求解．【详解】解：因为在第四象限，则，所以，又因为关于y 轴对称，x 值相反，y 值不变，解析：53--（，）【分析】由第四象限点的坐标符号是（+，-），可得53A -（，），关于y 轴对称的点，纵坐标相同，横坐标互为相反数，即可求解．【详解】解：因为,A a b （）在第四象限，则00a b ><，，所以53A -（，），又因为53A -（，）关于y 轴对称，x 值相反，y 值不变，所以点A 关于y 轴对称点坐标为53--（，）. 故答案为53--（，）. 【点睛】本题考查点的坐标的意义和对称的特点．关键是掌握点的坐标的变化规律．11．120°和60° 【详解】试题分析：因为三角形的内角和是180度，所以∠B+∠C=180°-∠A=180°-60°=120°，又因为∠DFE=∠BFC ，∠BFC=180°-（∠FBC+∠FCB ），解析：120°和60° 【详解】试题分析：因为三角形的内角和是180度，所以∠B+∠C=180°-∠A=180°-60°=120°，又因为∠DFE=∠BFC ，∠BFC=180°-（∠FBC+∠FCB ），因为角平分线CD 、EF 相交于F ，所以∠FBC+∠FCB=（∠B+∠C ）÷2=120°÷2=60°，再代入∠DFE=∠BFC=180°-（∠FBC+∠FCB ），即可解答．试题解析：∠B+∠C=180°-∠A=180°-60°=120°，又因为∠DFE=∠BFC ，∠BFC=180°-（∠FBC+∠FCB ），因为角平分线CD 、EF 相交于F ，所以∠FBC+∠FCB=（∠B+∠C ）÷2=120°÷2=60°， ∠DFE=180°-（∠FBC+∠FCB ）， =180°-60°， =120°；∠DFE 的邻补角的度数为：180°-120°=60°．考点：角的度量．12．【分析】过作，过作，根据平行线的性质可知，然后根据平行线的性质即可求解；【详解】如图，过作，过作，∴，∴，，，∵，∴，∴，∴，∴，∴．故答案为：．【点睛】本题考查了平解析：90x y z +-=︒【分析】过C 作//CN AB ，过D 作//DM AB ，根据平行线的性质可知//////AB CN DM EF ，然后根据平行线的性质即可求解；【详解】如图，过C 作//CN AB ，过D 作//DM AB ，∴//////AB CN DM EF ，∴1x =∠，23∠∠=，4z ∠=，∵90BCD ∠=︒，∴1290∠+∠=︒，∴390x +∠=︒，∴3490x z +∠+∠=︒+，∴90x y z +=︒+，∴90x y z +-=︒．故答案为：90x y z +-=︒．【点睛】本题考查了平行线的性质，两直线平行同位角相等，两直线平行内错角相等，正确理解平行线的性质是解题的关键；13．95°【分析】首先利用平行线的性质得出∠BMF＝100°，∠FNB＝70°，再利用翻折变换的性质得出∠FMN＝∠BMN＝50°，∠FNM＝∠MNB＝35°，进而求出∠B的度数以及得出∠D的度数．解析：95°【分析】首先利用平行线的性质得出∠BMF＝100°，∠FNB＝70°，再利用翻折变换的性质得出∠FMN＝∠BMN＝50°，∠FNM＝∠MNB＝35°，进而求出∠B的度数以及得出∠D的度数．【详解】解：∵MF∥AD，FN∥DC，∠A＝100°，∠C＝70°，∴∠BMF＝100°，∠FNB＝70°，∵将△BMN沿MN翻折，得△FMN，∴∠FMN＝∠BMN＝50°，∠FNM＝∠MNB＝35°，∴∠F＝∠B＝180°−50°−35°＝95°，∴∠D＝360°−100°−70°−95°＝95°．故答案为：95°．【点睛】此题主要考查了平行线的性质以及多边形内角和定理以及翻折变换的性质，得出∠FMN＝∠BMN，∠FNM＝∠MNB是解题关键．14．3；．【分析】由可求出，由，可分别求出，，继而可计算出结果．【详解】解：（1）由题意可知：，则，（2）由题意可知：，，则，，∴，故答案为：3；．【点睛】本题主解析：3；1 173．【分析】由239=可求出2log 93=，由4216=，43=81可分别求出2log 164=，3log 814=，继而可计算出结果．【详解】解：（1）由题意可知：239=，则2log 93=，（2）由题意可知：4216=，43=81，则2log 164=，3log 814=， ∴223141(log 16)log 811617333+=+=，故答案为：3；1173．【点睛】本题主要考查定义新运算，读懂题意，掌握运算方法是解题关键．15．2【分析】根据y 轴上的点的横坐标是0列式计算即可得到m 的值．【详解】∵点P （2m-4，1-2m ）在y 轴上，∴2m-4=0，解得m=2．故答案为：2．【点睛】此题考查点的坐标，熟记y解析：2【分析】根据y 轴上的点的横坐标是0列式计算即可得到m 的值．【详解】∵点P （2m -4，1-2m ）在y 轴上，∴2m -4=0，解得m=2．故答案为：2．【点睛】此题考查点的坐标，熟记y 轴上的点的横坐标为0是解题的关键．16．【分析】由题意可知，每隔四次移动重复一次，继续得出A5，A6，A7，A8，…，归纳出点An 的一般规律，从而可求得结果．【详解】∵，，，∴根据点的平移规律，可分别得：，，，，，，，，…，，，解析：()1010,1【分析】由题意可知，每隔四次移动重复一次，继续得出A 5，A 6，A 7，A 8，…，归纳出点A n 的一般规律，从而可求得结果．【详解】∵1(0,1)A ，()21,1A ，()31,0A ，()42,0A∴根据点的平移规律，可分别得：()52,1A ，()63,1A ，()73,0A ，()84,0A ，()94,1A ，()105,1A ，()115,0A ，()126,0A ，…，()4322,1n A n --，()4221,1n A n --，()4121,0n A n --，()42,0n A n∵2021=505×4+1∴2021A 的横坐标为2×505=1010，纵坐标为1即2021(1010,1)A故答案为：()1010,1【点睛】本题考查了平面直角坐标系中点的坐标的规律问题，点平移的坐标特征，体现了由特殊到一般的数学思想，关键是由前面若干点的的坐标寻找出规律．三、解答题17．(1)-1；(2)-1【分析】（1）根据乘方及二次根式的化简即可求解；（2）根据乘法的分配率计算即可.【详解】（1）（2）【点睛】本题考查的是实数的运算，掌握运算法则及乘法的分配率是解析：(1)-1；(2)-1【分析】（1）根据乘方及二次根式的化简即可求解；（2）根据乘法的分配率计算即可.【详解】（1）()412-⨯（2）()()()434320=-20--20=-1615=-15454⎛⎫-⨯-⨯⨯+ ⎪⎝⎭【点睛】本题考查的是实数的运算，掌握运算法则及乘法的分配率是关键.18．（1）；（2）①；②【分析】（1）逆向运用同底数幂的除法法则以及幂的乘方运算法则计算即可；（2）①利用提公因式法因式分解解答即可；②根据完全平方公式计算即可．【详解】解：（1），，解析：（1）2725；（2）①54125；②95 【分析】（1）逆向运用同底数幂的除法法则以及幂的乘方运算法则计算即可；（2）①利用提公因式法因式分解解答即可；②根据完全平方公式计算即可．【详解】解：（1）3m a =，5n a =，32m n a -∴ 32m n a a =÷32()()m n a a =÷3235=÷2725=；（2）①35x y -=，1825xy =， 22x y xy ∴-183()255xy x y =-=⨯ 54125=； ②35x y -=，1825xy =， 22x y ∴+2()2x y xy =-+23182525⎛⎫=+⨯ ⎪⎝⎭ 9362525=+9．5【点睛】本题考查了完全平方公式，同底数幂的除法，提公因式法因式分解以及幂的乘方，熟记相关公式与运算法则是解答本题的关键．19．两直线平行，同旁内角互补；同角的补角相等；同位角相等，两直线平行【分析】要证BE∥DF，只需证∠1＝∠D，由AB∥CD可知∠B+∠1＝180°，又有∠B+∠D ＝180°，由此即可证得．【详解】解析：两直线平行，同旁内角互补；同角的补角相等；同位角相等，两直线平行【分析】要证BE∥DF，只需证∠1＝∠D，由AB∥CD可知∠B+∠1＝180°，又有∠B+∠D＝180°，由此即可证得．【详解】证明：∵AB∥CD（已知）∴∠B+∠1＝180°（两直线平行，同旁内角互补）∵∠B+∠D＝180°（已知）∴∠1＝∠D（同角的补角相等），∴BE∥DF（同位角相等，两直线平行）故答案为：两直线平行，同旁内角互补；同角的补角相等；同位角相等，两直线平行．【点睛】本题主要考查了平行线的性质与判定，解题的关键在于能够熟练掌握相关知识进行求解．20．（1）见解析；（2）正方形【分析】（1）根据平面直角坐标系找出各点的位置即可；（2）观察图形可知四边形ABCO是正方形．【详解】解：（1）如图．（2）四边形ABCO是正方形．【点睛】解析：（1）见解析；（2）正方形【分析】（1）根据平面直角坐标系找出各点的位置即可；（2）观察图形可知四边形ABCO 是正方形．【详解】解：（1）如图．（2）四边形ABCO 是正方形．【点睛】本题考查了坐标与图形性质，能够准确在平面直角坐标系中找出点的位置是解题的关键． 21．（1）4，；（2）【分析】（1）根据夹逼法可求的整数部分和小数部分；（2）首先估算出m ，n 的值，进而得出m+n 的值，可求满足条件的x 的值．【详解】（1）∵，即，∴的整数部分是4，小数部分解析：（1）4174；（2）122,0x x =-=【分析】（117（2）首先估算出m ，n 的值，进而得出m+n 的值，可求满足条件的x 的值．【详解】（1）∵161725<4175<， ∴174174，故答案是：4174；（2）∵4175<<， ∴5174-<--，∴95994-<-，∴94，小数部分是945m ==∵45<，∴94995+<+，∴913，小数部分是9134n ==，∵2(1)541x m n +=+==所以11x +=±解得：122,0x x =-=．【点睛】本题考查了估算无理数的大小，无理数的整数部分及小数部分的确定方法：设无理数为m ，m 的整数部分a 为不大于m 的最大整数，小数部分b 为数m 减去其整数部分，即b=m-a ；理解概念是解题的关键．22．（1）棱长为4；（2）边长为：（或）【分析】（1）由立方体的体积为棱长的立方可以得到答案；（2）用勾股定理直接计算得到答案．【详解】解：（1）设正方体的棱长为，则，所以，即正方体的棱长为4．解析：（1）棱长为4；（2【分析】（1）由立方体的体积为棱长的立方可以得到答案；（2）用勾股定理直接计算得到答案．【详解】解：（1）设正方体的棱长为x ，则364x =，所以4x =，即正方体的棱长为4．（2）因为正方体的棱长为4，所以AB =【点睛】本题考查的是立方根与算术平方根的理解与计算，由实际的情境去理解问题本身就是求一个数的立方根与算术平方根是关键．23．（1）①18°；②2∠BEG+∠HFG=90°，证明见解析；（2）2∠BEG-∠HFG=90°证明见解析部【分析】（1）①证明2∠BEG+∠HFG=90°，可得结论．②利用平行线的性质证明即可．解析：（1）①18°；②2∠BEG +∠HFG =90°，证明见解析；（2）2∠BEG -∠HFG =90°证明见解析部【分析】（1）①证明2∠BEG +∠HFG =90°，可得结论．②利用平行线的性质证明即可．（2）如图2中，结论：2∠BEG-∠HFG=90°．利用平行线的性质证明即可．【详解】解：（1）①∵EG平分∠BEF，∴∠BEG=∠FEG，∵FH⊥EF，∴∠EFH=90°，∵AB∥CD，∴∠BEF+∠EFG=180°，∴2∠BEG+90°+∠HFG=180°，∴2∠BEG+∠HFG=90°，∵∠BEG=36°，∴∠HFG=18°．故答案为：18°．②结论：2∠BEG+∠HFG=90°．理由：∵EG平分∠BEF，∴∠BEG=∠FEG，∵FH⊥EF，∴∠EFH=90°，∵AB∥CD，∴∠BEF+∠EFG=180°，∴2∠BEG+90°+∠HFG=180°，∴2∠BEG+∠HFG=90°．（2）如图2中，结论：2∠BEG-∠HFG=90°．理由：∵EG平分∠BEF，∴∠BEG=∠FEG，∵FH⊥EF，∴∠EFH=90°，∵AB∥CD，∴∠BEF+∠EFG=180°，∴2∠BEG+90°-∠HFG=180°，∴2∠BEG-∠HFG=90°．【点睛】本题考查平行线的性质，角平分线的定义等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．24．[感知]见解析；[探究]70°；[应用]（1）35；（2）或【分析】[感知]过点P 作PM ∥AB ，根据平行线的性质得到∠1=∠AEP ，∠2+∠PFD=180°，求出∠2的度数，结合∠1可得结果；解析：[感知]见解析；[探究]70°；[应用]（1）35；（2）2αβ+或2βα-【分析】[感知]过点P 作PM ∥AB ，根据平行线的性质得到∠1=∠AEP ，∠2+∠PFD =180°，求出∠2的度数，结合∠1可得结果；[探究]过点P 作PM ∥AB ，根据AB ∥CD ，PM ∥CD ，进而根据平行线的性质即可求∠EPF 的度数；[应用]（1）如图③所示，在[探究]的条件下，根据∠PEA 的平分线和∠PFC 的平分线交于点G ，可得∠G 的度数；（2）画出图形，分点A 在点B 左侧和点A 在点B 右侧，两种情况，分别求解．【详解】解：[感知]如图①，过点P 作PM ∥AB ，∴∠1=∠AEP =40°（两直线平行，内错角相等）∵AB ∥CD ，∴PM ∥CD （平行于同一条直线的两直线平行），∴∠2+∠PFD =180°（两直线平行，同旁内角互补），∴∠PFD =130°（已知），∴∠2=180°-130°=50°，∴∠1+∠2=40°+50°=90°，即∠EPF =90°；[探究]如图②，过点P 作PM ∥AB ，∴∠MPE =∠AEP =50°，∵AB ∥CD ，∴PM ∥CD ，∴∠PFC =∠MPF =120°，∴∠EPF =∠MPF -∠MPE =120°-50°=70°；[应用]（1）如图③所示，∵EG 是∠PEA 的平分线，FG 是∠PFC 的平分线，∴∠AEG =12∠AEP =25°，∠GFC =12∠PFC =60°，过点G 作GM ∥AB ，∴∠MGE =∠AEG =25°（两直线平行，内错角相等）∵AB ∥CD （已知），∴GM ∥CD （平行于同一条直线的两直线平行），∴∠GFC =∠MGF =60°（两直线平行，内错角相等）．∴∠G =∠MGF -∠MGE =60°-25°=35°．故答案为：35．（2）当点A 在点B 左侧时，如图，故点E 作EF ∥AB ，则EF ∥CD ，∴∠ABE =∠BEF ，∠CDE =∠DEF ，∵BE 平分ABC DE ∠，平分ADC ∠，,ABC ADC αβ∠=∠=，∴∠ABE =∠BEF =12α，∠CDE =∠DEF =12β， ∴∠BED =∠BEF +∠DEF =2αβ+；当点A 在点B 右侧时，如图，故点E 作EF ∥AB ，则EF ∥CD ，∴∠DEF =∠CDE ，∠ABG =∠BEF ，∵BE 平分ABC DE ∠，平分ADC ∠，,ABC ADC αβ∠=∠=，∴∠DEF =∠CDE =12β，∠ABG =∠BEF =12α， ∴∠BED =∠DEF -∠BEF =2βα-；综上：∠BED 的度数为2αβ+或2βα-．【点睛】本题考查了平行线的判定与性质、平行公理及推论，角平分线的定义，解决本题的关键是熟练运用平行线的性质．。

数学七年级下册数学期中试卷及答案人教 (8)

数学七年级下册数学期中试卷及答案人教一、选择题1．9的平方根是（）A ．3B ．3±C ．3D ．3± 2．下列现象属于平移的是（） A ．投篮时的篮球运动B ．随风飘动的树叶在空中的运动C ．刹车时汽车在地面上的滑动D ．冷水加热过程中小气泡变成大气泡 3．在平面直角坐标系中，下列各点位于第三象限的是（） A ．(0,3) B ．(2,1)- C ．(1,2)- D ．(1,1)-- 4．给出以下命题：①对顶角相等；②在同一平面内，垂直于同一条直线的两条直线平行；③相等的角是对顶角；④内错角相等．其中假命题有（）A ．1个B ．2个C ．3个D ．4个5．如图，直线a ，b 被直线c ，d 所截，若12∠=∠，3125∠=︒，则4∠的度数是（）A ．65︒B ．60︒C ．55︒D ．75︒ 6．若a 2＝16，3b ＝2，则a +b 的值为（） A ．12B ．4C ．12或﹣4D ．12或4 7．一副直角三角板如图所示摆放，它们的直角顶点重合于点O ，//CO AB ，则BOD ∠=（）A ．30B ．45︒C ．60︒D ．90︒8．在平面直角坐标系中，点A （1，0）第一次向左跳动至A 1（﹣1，1），第二次向右跳至A 2（2，1），第三次向左跳至A 3（﹣2，2），第四次向右跳至A 4（3，2），…，按照此规律，点A 第2021次跳动至A 2021的坐标是（）A ．（﹣1011，1011）B ．（1011，1010）C ．（﹣1010，1010）D ．（1010，1009）二、填空题9．1x -8，则x 的值是________________．10．点(,1)a 关于x 轴的对称点的坐标为(5,)b ，则+a b 的值是______．11．如图，在△ABC 中，∠ABC ，∠ACB 的角平分线相交于O 点．如果∠A=α，那么∠BOC 的度数为____________.12．如图，AD 是∠EAC 的平分线，AD ∥BC ，∠B ＝40°，则∠DAC 的度数为____．13．如图，点E 、点G 、点F 分别在AB 、AD 、BC 上，将长方形ABCD 按EF 、EG 翻折，线段EA 的对应边EA '恰好落在折痕EF 上，点B 的对应点B '落在长方形外，B 'F 与CD 交于点H ，已知∠B 'HC ＝134°，则∠AGE ＝_____°．14．已知57+的小数部分是a ，57-的小数部分是b ，则2019()a b +=________． 15．若点P (3,1)m m +-在x 轴上，则点P 的坐标为____．16．如图，点()00,0A ，()11,2A ，()22,0A ，()33,2A -，()44,0A ，……根据这个规律，探究可得点2021A 的坐标是________．三、解答题17．计算：（1）23272-；（2）432+-．18．求下列各式中的x 值．（1）2164x -=（2）()318x -=19．请补全推理依据：如图，已知：12180∠+∠=︒，3A ∠=∠，求证：B C ∠=∠．证明：∵12180∠+∠=︒（已知）∴//AD EF （）∴3D ∠=∠（）又∵3A ∠=∠（已知）∴D A ∠=∠（）∴//AB CD （）∴B C ∠=∠（）20．如图，在平面直角坐标系中，A （﹣1，﹣2），B （﹣2，﹣4），C （﹣4，﹣1）．△ABC 中任意一点P （x 0，y 0）经平移后对应点为P 1（x 0+2，y 0+4），将△ABC 作同样的平移得到△A 1B 1C 1．（1）请画出△A 1B 1C 1并写出点A 1，B 1，C 1的坐标；（2）求△A 1B 1C 1的面积；21．已知：a 是93+的小数部分，b 是93-的小数部分．（1）求a b 、的值；（2）求445a b ++的平方根．22．（1）如图1，分别把两个边长为1cm 的小正方形沿一条对角线裁成4个小三角形拼成一个大正方形，则大正方形的边长为______cm ；（2）若一个圆的面积与一个正方形的面积都是22πcm ，设圆的周长为C 圆．正方形的周长为C 正，则C 圆______C 正（填“=”，或“<”，或“>”）（3）如图2，若正方形的面积为2900cm ，李明同学想沿这块正方形边的方向裁出一块面积为2740cm 的长方形纸片，使它的长和宽之比为5:4，他能裁出吗？请说明理由？23．如图，已知直线12//l l ，点A B 、在直线1l 上，点C D 、在直线2l 上，点C 在点D 的右侧，()80,2,ADC ABC n BE ∠=︒∠=︒平分,ABC DE ∠平分ADC ∠，直线BE DE 、交于点E ．（1）若20n =时，则BED ∠=___________；（2）试求出BED ∠的度数（用含n 的代数式表示）；（3）将线段BC 向右平行移动，其他条件不变，请画出相应图形，并直接写出BED ∠的度数．（用含n 的代数式表示）24．已知两条直线l 1，l 2，l 1∥l 2，点A ，B 在直线l 1上，点A 在点B 的左边，点C ，D 在直线l 2上，且满足115ADC ABC ∠=∠=o ．（1）如图①，求证：AD ∥BC ；（2）点M ，N 在线段CD 上，点M 在点N 的左边且满足MAC BAC ∠=∠，且AN 平分∠CAD ；（Ⅰ）如图②，当30ACD ∠=o 时，求∠DAM 的度数；（Ⅱ）如图③，当8CAD MAN ∠=∠时，求∠ACD 的度数．【参考答案】一、选择题1．B解析：B【分析】直接根据平方根的定义进行解答即可．【详解】解：∵(±3)2=9，∴9的平方根是±3．故选：B．【点睛】本题考查的是平方根的定义，即如果一个数的平方等于a，这个数就叫做a的平方根，也叫做a的二次方根．2．C【分析】判断是否是平移现象，要根据平移的性质进行，即图形平移前后的形状和大小没有变化，只是位置发生变化．【详解】解：A. 投篮时的篮球运动，不是沿直线运动，此选项不是平移现象；B解析：C【分析】判断是否是平移现象，要根据平移的性质进行，即图形平移前后的形状和大小没有变化，只是位置发生变化．【详解】解：A. 投篮时的篮球运动，不是沿直线运动，此选项不是平移现象；B. 随风飘动的树叶在空中的运动，在空中不是沿直线运动，此选项不是平移现象；C. 刹车时汽车在地面上的滑动，此选项是平移现象；D. 冷水加热过程中小气泡变成大气泡，大小发生了变化，此选项不是平移现象．故选：C．【点睛】本题考查的知识点是平移的概念，掌握平移的性质是解此题的关键．3．D【分析】根据各象限内点的坐标特征对各选项分析判断后利用排除法求解．【详解】解：A、(0，3)在y轴上，故本选项不符合题意；B、(−2，1)在第二象限，故本选项不符合题意；C、(1，−2)在第四象限，故本选项不符合题意；D、(-1，-1)在第三象限，故本选项符合题意．故选：D．【点睛】本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解题的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．4．B【分析】根据对顶角的性质、平行线的判定和性质进行判断即可．【详解】解：①对顶角相等，是真命题；②在同一平面内，垂直于同一条直线的两条直线平行，是真命题；③相等的角不一定是对顶角，原命题是假命题；④两直线平行，内错角相等，原命题是假命题．故选：B．【点睛】考查了命题与定理的知识，解题的关键是了解对顶角的性质、平行线的判定和性质，难度较小．5．C【分析】首先证明a∥b，推出∠4＝∠5，求出∠5即可．【详解】解：∵∠1＝∠2，∴a∥b，∴∠4＝∠5，∵∠5＝180°﹣∠3＝55°，∴∠4＝55°，故选：C．【点睛】本题考查平行线的判定和性质，解题的关键是熟练掌握基本知识，属于中考常考题型．6．D【分析】根据平方根和立方根的意义求出a、b即可．【详解】解：∵a2＝16，∴a＝±4，∵2，∴b＝8，∴a+b＝4+8或﹣4+8，即a+b＝12或4．故选：D．【点睛】本题考查了平方根和立方根以及有理数加法，解题关键是明确平方根和立方根的意义，准确求出a、b的值，注意：一个正数的平方根有两个．7．C【分析】由AB//CO得出∠BAO=∠AOC，即可得出∠BOD．【详解】AB CO，解：//∴∠=∠=︒60OAB AOC∴∠=︒+︒=︒BOC6090150∠+∠=∠+∠=︒AOC DOA DOA BOD90∴∠=∠=︒AOC BOD60故选：C．【点睛】本题考查两直线平行内错角相等的知识点，掌握这一点才能正确解题．8．A【分析】根据图形观察发现，第偶数次跳动至点的坐标，横坐标是次数的一半加上1，纵坐标是次数的一半，奇数次跳动与该偶数次跳动的横坐标的相反数加上1，纵坐标相同，然后写出即可．【详解】解：如图，解析：A【分析】根据图形观察发现，第偶数次跳动至点的坐标，横坐标是次数的一半加上1，纵坐标是次数的一半，奇数次跳动与该偶数次跳动的横坐标的相反数加上1，纵坐标相同，然后写出即可．【详解】解：如图，观察发现，第2次跳动至点的坐标是（2，1），第4次跳动至点的坐标是（3，2），第6次跳动至点的坐标是（4，3），第8次跳动至点的坐标是（5，4），…第2n次跳动至点的坐标是（n+1，n），则第2020次跳动至点的坐标是（1011，1010），第2021次跳动至点A2021的坐标是（﹣1011，1011）．故选：A．【点睛】本题考查了规律型：点的坐标，坐标与图形的性，结合图形得到偶数次跳动的点的横坐标与纵坐标的变化情况是解题的关键．二、填空题9．65【解析】【分析】根据算术平方根的定义确定x-1的值，解方程即可.【详解】∵＝8∴x-1=64x=65故答案为65【点睛】本题考查了算术平方根的定义，掌握算术平方根的定义是关键解析：65【解析】【分析】根据算术平方根的定义确定x-1的值，解方程即可.【详解】∵1x 8∴x-1=64x=65故答案为65【点睛】本题考查了算术平方根的定义，掌握算术平方根的定义是关键.10．4【分析】根据横坐标不变，纵坐标相反，确定a,b的值，计算即可．【详解】∵点关于轴的对称点的坐标为，∴a=5，b= -1，∴a+b= 5-1=4，故答案为：4．【点睛】本题考查了坐解析：4【分析】根据横坐标不变，纵坐标相反，确定a,b的值，计算即可．【详解】∵点(,1)a关于x轴的对称点的坐标为(5,)b，∴a=5，b= -1，∴a+b= 5-1=4，故答案为：4．【点睛】本题考查了坐标系中轴对称问题，熟练掌握轴对称的坐标变化特点是解题的关键．11．90°+【解析】∵∠ABC、∠ACB的角平分线相交于点O，∴∠OBC=∠ABC，∠OCB=∠ACB，∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°-∠A)=90°-∠A，解析：90°+1 2【解析】∵∠ABC、∠ACB的角平分线相交于点O，∴∠OBC=12∠ABC，∠OCB=12∠ACB，∴∠OBC+∠OCB=12(∠ABC+∠ACB)=12(180°-∠A)=90°-12∠A，∵在△OBC中，∠BOC=180°-∠OBC-∠OCB，∴∠BOC=180°-（90°-12∠A）=90°+12∠A=90°+12.12．40°【分析】根据平行线的性质可得∠EAD=∠B，根据角平分线的定义可得∠DAC=∠EAD，即可得答案．【详解】∵AD∥BC，∠B＝40°，∴∠EAD=∠B=40°，∵AD是∠EAC的平解析：40°【分析】根据平行线的性质可得∠EAD=∠B，根据角平分线的定义可得∠DAC=∠EAD，即可得答案．【详解】∵AD∥BC，∠B＝40°，∴∠EAD=∠B=40°，∵AD是∠EAC的平分线，∴∠DAC=∠EAD=40°，故答案为：40°【点睛】本题考查平行线的性质及角平分线的定义，两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补；熟练掌握平行线的性质是解题关键．13．11【分析】由外角的性质和平行线的性质求出的度数，即可求出的度数，进而求出的度数，求得的度数，即可求出的度数．【详解】解：如图，，，，，折叠，，，，，故答案为：11．解析：11【分析】由外角的性质和平行线的性质求出IEB ∠的度数，即可求出FEB ∠的度数，进而求出AEF ∠的度数，求得AEG ∠的度数，即可求出AGE ∠的度数．【详解】解：如图，134B HC '∠=︒，1349044B IH B HC B '''∴∠=∠-∠=︒-︒=︒，//CD AB ，44IEB B IH '∴∠=∠=︒，折叠，1222BA F B IH ''∴∠=∠=︒， 18022158AEA '∴∠=︒-︒=︒，1792AEG AEA '∴∠=∠=︒， 180907911AGE ∴∠=︒-︒-︒=︒，故答案为：11．【点睛】本题考查了角之间的计算，解题的关键是理解折叠就是轴对称，利用轴对称的性质求解． 14．1【分析】根据4＜7＜9可得，2＜＜3，从而有7＜5+＜8，由此可得出5+的整数部分是7，小数部分a 用5+减去其整数部分即可，同理可得b 的值，再将a ，b 的值代入所求式子即可得出结果．【详解】解析：1【分析】根据4＜7＜9可得，2＜3，从而有7＜＜8，由此可得出7，小数部分a用b的值，再将a，b的值代入所求式子即可得出结果．【详解】解：∵4＜7＜9，∴23，∴-3＜＜-2，∴7＜＜8，2＜3，∴7，2，∴，∴2019+=12019=1．a b()故答案为：1．【点睛】此题主要考查了估算无理数的大小，正确得出各数的小数部分是解题关键．15．（4，0）．【分析】根据x轴上点的纵坐标为0列方程求出m的值，再求解即可．【详解】∵点P（m+3，m-1）在x轴上，∴m-1=0，解得m=1，所以，m+3=1+3=4，所以，点P的坐解析：（4，0）．【分析】根据x轴上点的纵坐标为0列方程求出m的值，再求解即可．【详解】∵点P（m+3，m-1）在x轴上，∴m-1=0，解得m=1，所以，m+3=1+3=4，所以，点P的坐标为（4，0）．故答案为：（4，0）．【点睛】本题考查了点的坐标，熟记x轴上点的纵坐标为0是解题的关键．16．【分析】由图形得出点的横坐标依次是0、1、2、3、4、、，纵坐标依次是0、2、0、、0、2、0、、，四个一循环，继而求得答案．【详解】解：观察图形可知，点的横坐标依次是0、1、2、3、4、2021,2解析：()【分析】由图形得出点的横坐标依次是0、1、2、3、4、⋯、n，纵坐标依次是0、2、0、2-、0、2、0、2-、⋯，四个一循环，继而求得答案．【详解】解：观察图形可知，点的横坐标依次是0、1、2、3、4、⋯、n，纵坐标依次是0、2、0、2-、0、2、0、2-、⋯，四个一循环，÷=⋯，202145051A坐标是(2021,2)．故点2021故答案是：(2021,2)．【点睛】本题考查了规律型：点的坐标，学生的观察图形的能力和理解能力，解此题的关键是根据图形得出规律．三、解答题17．（1）-1；（2）．【分析】（1）按照立方根的定义与平方的含义分别计算，再求差即可；（2）按照算术平方根的含义与绝对值的应用先化简，再合并即可．【详解】解：（1）原式．（2）原式．【点解析：（1）-1；（2）4．【分析】（1）按照立方根的定义与平方的含义分别计算，再求差即可；（2）按照算术平方根的含义与绝对值的应用先化简，再合并即可．【详解】=-=-．解：（1）原式341（2）原式224=+【点睛】本题考查的是立方根，乘方，算术平方根，绝对值的运算，实数的加减运算，掌握运算法则是解题关键．18．（1）；（2）．【分析】（1）首先求出的值是多少，然后根据平方根的含义和求法，求出x的值即可．（2）根据立方根的含义和求法，可得x-1=2，据此求出x的值是多少即可．【详解】（1）解解析：（1）52x=±；（2）3x=．【分析】（1）首先求出2x的值是多少，然后根据平方根的含义和求法，求出x的值即可．（2）根据立方根的含义和求法，可得x-1=2，据此求出x的值是多少即可．【详解】（1）2164x-=2254x=解得：52 x=±故答案为：52 x=±（2）()318x-=12x-=解得：3x=故答案为：3x=【点睛】本题考查了平方根的含义和求法，立方根的含义和求法．19．同旁内角互补，两直线平行；两直线平行，同位角相等；等量代换；内错角相等，两直线平行；两直线平行，内错角相等【分析】根据平行线的判定定理以及性质定理证明即可．【详解】证明：∵∠1＋∠2＝180解析：同旁内角互补，两直线平行；两直线平行，同位角相等；等量代换；内错角相等，两直线平行；两直线平行，内错角相等【分析】根据平行线的判定定理以及性质定理证明即可．【详解】证明：∵∠1＋∠2＝180°（已知），∴AD∥EF（同旁内角互补，两直线平行），∴∠3＝∠D（两直线平行，同位角相等），又∵∠3＝∠A（已知），∴∠D＝∠A（等量代换），，∴AB∥CD（内错角相等，两直线平行），∴∠B＝∠C（两直线平行，内错角相等）．故答案为：同旁内角互补，两直线平行；两直线平行，同位角相等；等量代换；内错角相等，两直线平行；两直线平行，内错角相等．【点睛】本题主要考查了平行线的判定与性质，熟记平行线的判定定理与性质定理是解本题的关键．20．（1）画图见解析，A1（1，2），B1（0，0），C1（-2，3）；（2）【分析】（1）分别作出A，B，C的对应点A1，B1，C1，从而可得坐标．（2）利用分割法求解即可．【详解】解：（1解析：（1）画图见解析，A1（1，2），B1（0，0），C1（-2，3）；（2）7 2【分析】（1）分别作出A，B，C的对应点A1，B1，C1，从而可得坐标．（2）利用分割法求解即可．【详解】解：（1）如图，A1B1C1并写即为所求作，A1（1，2），B1（0，0），C1（-2，3）．（2）△A1B1C1的面积=3×3-12×3×2-12×1×2-12×1×3=72．【点睛】本题考查作图-平移变换，三角形的面积等知识，解题的关键是理解题意，灵活运用所学知识解决问题．21．（1），；（2）±3．【分析】（1）首先得出1＜＜2，进而得出a ，b 的值；（2）根据平方根即可解答．【详解】（1）∵1＜＜2∴10＜＜11，7＜＜8∴的整数部分为10，的整数部分为7，解析：（1）31a ，2b =2）±3．【分析】（1）首先得出12，进而得出a ，b 的值；（2）根据平方根即可解答．【详解】（1）∵12∴10＜911，7＜98∴910，97，910,97a b ∴=+=+，1a ∴=，2b = （2）原式()45a b =++415=⨯+9=9∴的平方根为：3±．【点睛】此题主要考查了估算无理数的大小，正确得出a ，b 的值是解题关键．22．（1）；（2）＜；（3）不能，理由见解析【分析】（1）根据所拼成的大正方形的面积为2即可求得大正方形的边长；（2）由圆和正方形的面积公式可分别求的圆的半径及正方形的边长，进而可求得圆和正方形的解析：（12）＜；（3）不能，理由见解析【分析】（1）根据所拼成的大正方形的面积为2即可求得大正方形的边长；（2）由圆和正方形的面积公式可分别求的圆的半径及正方形的边长，进而可求得圆和正方形的周长，利用作商法比较这两数大小即可；（3）利用方程思想求出长方形的长边，与正方形边长比较大小即可；【详解】解：（1）∵小正方形的边长为1cm ，∴小正方形的面积为1cm 2，∴两个小正方形的面积之和为2cm 2，即所拼成的大正方形的面积为2 cm 2，设大正方形的边长为x cm ，∴22x = ， ∴x∴；（2）设圆的半径为r ，∴由题意得22r ππ=， ∴r = ∴=22C r π=圆设正方形的边长为a∵22a π=， ∴a∴=4C a =正∴1C C ===<圆正故答案为：＜；（3）解：不能裁剪出，理由如下：∵正方形的面积为900cm 2，∴正方形的边长为30cm∵长方形纸片的长和宽之比为5:4，∴设长方形纸片的长为5x ，宽为4x ，则54740x x ⋅=，整理得：237x =，∴22(5)252537925900x x ==⨯=>，∴22(5)30x >，∴530x >，∴长方形纸片的长大于正方形的边长，∴不能裁出这样的长方形纸片．【点睛】本题通过圆和正方形的面积考查了对算术平方根的应用，主要是对学生无理数运算及比较大小进行了考查．23．（1）60°；（2）n°+40°；（3）n°+40°或n°-40°或220°-n°【分析】（1）过点E 作EF ∥AB ，然后根据两直线平行内错角相等，即可求∠BED 的度数；（2）同（1）中方法求解解析：（1）60°；（2）n°+40°；（3）n°+40°或n°-40°或220°-n°【分析】（1）过点E作EF∥AB，然后根据两直线平行内错角相等，即可求∠BED的度数；（2）同（1）中方法求解即可；（3）分当点B在点A左侧和当点B在点A右侧，再分三种情况，讨论，分别过点E作EF∥AB，由角平分线的定义，平行线的性质，以及角的和差计算即可．【详解】解：（1）当n=20时，∠ABC=40°，过E作EF∥AB，则EF∥CD，∴∠BEF=∠ABE，∠DEF=∠CDE，∵BE平分∠ABC，DE平分∠ADC，∴∠BEF=∠ABE=20°，∠DEF=∠CDE=40°，∴∠BED=∠BEF+∠DEF=60°；（2）同（1）可知：∠BEF=∠ABE=n°，∠DEF=∠CDE=40°，∴∠BED=∠BEF+∠DEF=n°+40°；（3）当点B在点A左侧时，由（2）可知：∠BED=n°+40°；当点B在点A右侧时，如图所示，过点E作EF∥AB，∵BE平分∠ABC，DE平分∠ADC，∠ABC=2n°，∠ADC=80°，∴∠ABE=12∠ABC=n°，∠CDG=12∠ADC=40°，∵AB∥CD∥EF，∴∠BEF=∠ABE=n°，∠CDG=∠DEF=40°，∴∠BED=∠BEF-∠DEF=n°-40°；如图所示，过点E 作EF ∥AB ，∵BE 平分∠ABC ，DE 平分∠ADC ，∠ABC =2n °，∠ADC =80°，∴∠ABE =12∠ABC =n °，∠CDG =12∠ADC =40°，∵AB ∥CD ∥EF ，∴∠BEF =180°-∠ABE =180°-n °，∠CDE =∠DEF =40°，∴∠BED =∠BEF +∠DEF =180°-n °+40°=220°-n °；如图所示，过点E 作EF ∥AB ，∵BE 平分∠ABC ，DE 平分∠ADC ，∠ABC =n °，∠ADC =70°，∴∠ABG =12∠ABC =n °，∠CDE =12∠ADC =40°，∵AB ∥CD ∥EF ，∴∠BEF =∠ABG =n °，∠CDE =∠DEF =40°，∴∠BED =∠BEF -∠DEF =n °-40°；综上所述，∠BED 的度数为n °+40°或n °-40°或220°-n °．【点睛】此题考查了平行线的判定与性质，以及角平分线的定义，正确应用平行线的性质得出各角之间关系是解题关键．24．（1）证明见解析；（2）（Ⅰ）；（Ⅱ）．【分析】（1）先根据平行线的性质可得，再根据角的和差可得，然后根据平行线的判定即可得证；（2）（Ⅰ）先根据平行线的性质可得，从而可得，再根据角的和差可得解析：（1）证明见解析；（2）（Ⅰ）5DAM ∠=︒；（Ⅱ）25ACD ∠=︒．【分析】（1）先根据平行线的性质可得65BAD ∠=︒，再根据角的和差可得180BAD ABC ∠+∠=︒，然后根据平行线的判定即可得证；（2）（Ⅰ）先根据平行线的性质可得30BAC ACD ∠=∠=︒，从而可得30MAC ∠=︒，再根据角的和差可得35DAC ∠=︒，然后根据DAM DAC MAC ∠=∠-∠即可得；（Ⅱ）设MAN x ∠=，从而可得8CAD x ∠=，先根据角平分线的定义可得142CAN CAD x ∠=∠=，再根据角的和差可得5BAC MAC x ∠=∠=，然后根据65CAD BAC BAD ∠+∠=∠=︒建立方程可求出x 的值，从而可得BAC ∠的度数，最后根据平行线的性质即可得．【详解】（1）12//,115l l ADC ∠=︒，18065BAD ADC ∴∠=︒-∠=︒，又115ABC ∠=︒，180BAD ABC ∴∠+∠=︒，//AD BC ∴；（2）（Ⅰ）12//,30l l ACD ∠=︒，30BAC ACD ∴∠=∠=︒，MAC BAC ∠=∠，30MAC ∴∠=︒，由（1）已得：65BAD ∠=︒，35DAC BAD BAC ∴∠=∠-∠=︒，35305DAM DAC MAC ∴∠=∠-∠=︒-︒=︒；（Ⅱ）设MAN x ∠=，则8CAD x ∠=， AN 平分CAD ∠，142CAN CAD x ∴∠=∠=， 5MAC CAN MAN x ∴∠=∠+∠=，MAC BAC ∠=∠，5BAC x ∴∠=，由（1）已得：65BAD ∠=︒，65CAD BAC BAD ∴∠+∠=∠=︒，即8565x x +=︒，解得5x =︒，525BAC x ∴∠==︒，又12//l l ，25ACD BAC ∴∠=∠=︒．【点睛】本题考查了平行线的判定与性质、角的和差、角平分线的定义、一元一次方程的几何应用等知识点，熟练掌握平行线的判定与性质是解题关键．。

七年级数学11月期中试题 (新人教版第8套)

北京市第七中学～第一学期期中检测试卷七年级数学试卷满分：100 分考试时间：100分钟一．选择题（本大题共10小题，每小题2分，共20分，在每小题的四个选项中，只有一个符合题目要求）1．下列各数中，是负分数的是（）A ． 45 B ．6 C ．0 D ．－3.12．下列各数中，的相反数．．．是（） A ．3 B ． C ．D ． 3．下列说法中正确的是（）A ．0既不是整数也不是分数B ．整数和分数统称有理数C ．一个数的绝对值一定是正数D ．绝对值等于本身的数是0和1 4．已知，两数在数轴上对应的点如图所示，下列结论正确的是（）A ．B ．C ．D ．5．我国领土面积大约是9600000平方公里，用科学记数法应记为（）A ．平方公里B ．平方公里C ．平方公里D ．平方公里6．下列各组数中，运算结果相等的是（）A ．与B ．与C ．与D ．与7．下列式子中，是单项式的是（）A ．B ．C ．D ． 8．下列各式中，运算错误．．的是（） A ． B ．3-3-3131-a b b a <0>ab 0<+b a 0>ba71096.0⨯6106.9⨯51096⨯5106.9⨯232⎪⎭⎫ ⎝⎛32222-()22-()71--71-()35-35-2321yz x -y x -22n m -x1x x x 325=-055=-nm mn a0 bC ．D ．9．一种商品，降价10﹪后的售价是元,则原价为 ( )A ．元B ．元C ．元D ．元10. 不相等的有理数在数轴上的对应点分别为A,B,C ，如果，那么点A,B,C 在数轴上的位置关系是（）A ．点A 在点B,C 之间B ．点B 在点A,C 之间C ．点C 在点A,B 之间D ．以上三种情况均有可能二．填空题（本大题共10小题，每小题2分，共20分）1．如果火车向东开出500千米记作＋500千米，那么向西开出1000千米记作千米。

2013人教版七级下册数学期中试卷

2013人教版七年级下册数学期中试卷一、耐心填一填，一锤定音!(每小题3分，共27分)1、把命题平行于同一条直线的两条直线平行改写为如果那么的形式是2、如图1，直线a、b相交，1=36，则2=。

3、绝对值是，-343的立方根是，的平方根是4、如图2，AB∥EF，BC∥DE，则B的度数为.5、最大的负整数是，最小的正整数是，绝对值最小的实数是，6、如图4，△ABC平移到△，则图中与线段平行的有;与线段相等的有。

7、已知=0，则=.8、如图5，直线a∥b，且1=28，2=50，则ABC=9、已知一个正数的两个平方根是和，则=，=.二、精心选一选慧眼识金!(每小题3分，共30分)10、下列各式中无意义的是()A.B.C.D.11、下列说法中正确的是()A.立方根是它本身的数只有1和0B.算数平方根是它本身的数只有1和0C.平方根是它本身的数只有1和0D.绝对值是它本身的数只有1和012、的立方根是()A.B.C.D.13、如图7，以下说法错误的是()A、与是内错角B、与是同位角C、与是内错角D、与是同旁内角14、实数，-2，-3的大小关系是()A.B.C.D.15、三条直线相交于一点，构成的对顶角共有()A、3对B、4对C、5对D、6对16、下列所示的四个图形中，和是同位角的是()A、②③B、①②③C、①②④D、①④17、在下列说法中：10的平方根是-2是4的一个平方根;的平方根是;④0.01的算术平方根是0.1;⑤，其中正确的有()A.1个B.2个C.3个D.4个18、点P为直线l外一点，点A、B、C为直线l上三点，PA=4cm，PB=5cm，PC=2cm，则点P到直线l的距离是()A、2cmB、小于2cmC、不大于2cmD、4cm19、如图10，直线a、b都与直线c相交，给出下列条件：①2;②6;③7=180④8=180。

其中能判断a∥b的条件是()A、①②B、②④C、①③④D、①②③④三、作图题(每小题8分，共16分)20、读句画图：如图，直线CD与直线AB相交于C，根据下列语句画图(1)过点P作PQ∥CD，交AB于点Q(2)过点P作PRCD，垂足为R21、在下图中平移三角形ABC，使点A移到点，点B和点C应移到什么位置?请在图中画出平移后图形(保留作图痕迹)。