杠杆滑轮计算题练习(打印版)
杠杆与滑轮练习题

杠杆与滑轮练习题杠杆与滑轮练习题杠杆与滑轮是物理学中常见的两种简单机械。
它们在日常生活中的应用广泛,不仅在工程领域中发挥着重要作用,也在我们的日常活动中起到了便利和辅助的作用。
本文将通过一些练习题来帮助读者更好地理解和应用杠杆与滑轮的原理。
一、杠杆练习题1. 一个杠杆的长度为2米,杠杆的一端放置了一个质量为10千克的物体,另一端放置了一个质量为5千克的物体。
如果杠杆平衡,求两个物体之间的距离。
解析:根据杠杆平衡条件,杠杆两端所受的力矩相等。
设两个物体之间的距离为x,则有10 * (2 - x) = 5 * x。
解得x = 1.33米。
2. 一个杠杆的长度为3米,杠杆的一端放置了一个质量为20千克的物体,另一端放置了一个质量为15千克的物体。
如果杠杆平衡,求两个物体之间的距离。
解析:同样根据杠杆平衡条件,设两个物体之间的距离为x,则有20 * (3 - x) = 15 * x。
解得x = 1.8米。
以上两个练习题展示了杠杆平衡的基本原理,即力矩相等。
通过解方程可以求得两个物体之间的距离,这对于平衡杠杆的设计和应用有着重要意义。
二、滑轮练习题1. 一个滑轮组由两个滑轮组成,滑轮A的半径为10厘米,滑轮B的半径为20厘米。
如果滑轮A的线速度为2米/秒,求滑轮B的线速度。
解析:滑轮的线速度与滑轮半径之间成反比关系。
设滑轮B的线速度为v,则有2 * 10 = v * 20。
解得v = 1米/秒。
2. 一个滑轮组由三个滑轮组成,滑轮A的半径为5厘米,滑轮B的半径为10厘米,滑轮C的半径为15厘米。
如果滑轮A的线速度为3米/秒,求滑轮C的线速度。
解析:同样根据滑轮的线速度与滑轮半径之间的关系,设滑轮C的线速度为v,则有3 * 5 = v * 15。
解得v = 1米/秒。
通过以上滑轮练习题,我们可以看到滑轮的线速度与滑轮半径之间成反比关系。
这个关系在实际应用中非常重要,例如在起重机的设计中,通过合理选择滑轮的半径可以实现不同的力比。
杠杆与滑轮练习题

杠杆与滑轮练习题一、选择题1. 杠杆的五要素包括:A. 支点、力臂、动力、阻力、杠杆B. 支点、力臂、动力、阻力、平衡C. 支点、力臂、动力、阻力、作用点D. 支点、力臂、动力、阻力、力矩2. 以下哪种情况,杠杆处于平衡状态?A. 动力臂大于阻力臂B. 动力小于阻力C. 动力臂等于阻力臂D. 动力等于阻力3. 滑轮组中,动滑轮的作用是:A. 改变力的方向B. 改变力的大小C. 同时改变力的方向和大小D. 增加摩擦力4. 使用定滑轮时,以下说法正确的是:A. 可以省力B. 可以改变力的方向C. 不能省力,但可以改变力的方向D. 不能省力,也不能改变力的方向5. 以下哪种滑轮是省力杠杆?A. 定滑轮B. 动滑轮C. 滑轮组D. 以上都不是二、填空题6. 杠杆的平衡条件是_________。
7. 一个杠杆的动力臂是阻力臂的两倍,那么动力是阻力的_________。
8. 滑轮组由_________和_________组成。
9. 使用动滑轮可以省力,但需要_________。
10. 定滑轮实质上是一个等臂杠杆,它的作用是_________。
三、判断题11. 动力臂大于阻力臂的杠杆是省力杠杆。
()12. 滑轮组的省力情况取决于动滑轮的数量。
()13. 定滑轮不能省力,但可以改变力的方向。
()14. 动滑轮的实质是一个动力臂是阻力臂两倍的省力杠杆。
()15. 杠杆的分类是根据动力臂和阻力臂的相对大小来划分的。
()四、简答题16. 简述杠杆的分类及其特点。
17. 解释为什么使用滑轮组可以省力。
18. 描述定滑轮和动滑轮在实际应用中的区别。
五、计算题19. 假设有一个杠杆,其动力臂是阻力臂的3倍,动力是200N,求阻力的大小。
20. 如果使用一个动滑轮,已知施加的力是100N,物体的重力是500N,计算物体被提升的高度。
六、应用题21. 某工厂需要提升一个重1000N的货物,使用一个由两个动滑轮和一个定滑轮组成的滑轮组,求需要施加的最小力是多少?22. 描述在建筑工地上,如何利用杠杆原理来移动一块重物。
初三物理杠杆滑轮练习题

初三物理杠杆滑轮练习题在初三物理学习中,杠杆和滑轮是非常重要的两个概念。
它们在解决物理问题中起到了至关重要的作用。
下面将提供一些物理杠杆和滑轮的练习题,以帮助学生深入理解这两个概念并提高解决问题的能力。
练习题1:杠杆问题1. 在一个平衡杠杆上,两个物体分别位于杠杆的两端。
左端的质量为2kg,距离支点的距离为4m。
右端的质量为5kg,距离支点的距离为x米。
求x的值。
解析:根据杠杆的平衡条件,左端的力矩等于右端的力矩,即2kg* 4m = 5kg * x。
解得x = 1.6m。
练习题2:滑轮问题2. 在一个滑轮系统中,两个物体分别悬挂在两个滑轮的两端。
左侧滑轮的半径为0.5m,右侧滑轮的半径为1m。
左侧物体的质量为4kg,左右两侧绳子不可伸长或收缩。
求右侧物体的质量。
解析:根据滑轮的性质,相连的物体悬挂在不可伸长或收缩的绳子上,左右两侧的拉力相等。
由于左侧滑轮的半径是右侧滑轮的二倍,根据力矩平衡条件,可得4kg * g * 0.5m = M * g * 1m,解得右侧物体的质量M为2kg。
练习题3:杠杆和滑轮混合问题3. 在一个杠杆和滑轮组成的复杂系统中,左端悬挂着一个重锤,右端悬挂着一个物体。
左端重锤的质量为8kg,右端物体的质量为4kg。
左杠杆臂的长度为2m,右杠杆臂的长度为4m。
右侧滑轮的半径为0.5m。
系统处于平衡状态,求右侧滑轮的拉力。
解析:首先根据杠杆的平衡条件,左边的力矩等于右边的力矩。
即8kg * g * 2m = 4kg * g * 4m + T * 0.5m,其中T表示右侧滑轮的拉力。
解得T = 48N。
通过以上这些练习题,我们可以看到杠杆和滑轮在物理学习中的重要性。
掌握了杠杆和滑轮的原理和运用,不仅能够很好地解决物理问题,还可以通过它们来解释和理解自然界中的现象。
然而,这些习题只是一部分,初三物理杠杆和滑轮的知识还远远不止于此。
在未来的学习中,同学们还需要进一步学习相关的公式和定律,并进行更加复杂的问题解析和应用。
物理杠杆滑轮练习题含答案-打印 (科组教研精品 低碳排版)

6.(佛山市)如图所示的简单机械,在使用中属于费力杠杆的是()解析:判断一个杠杆是什么类型的杠杆,通常采用比较杠杆动力臂和阻力臂长短。
动力臂比阻力臂长的是省力杠杆,反之是费力杠杆。
镊子是费力杠杆,羊角锤、瓶起子是省力杠杆,托盘天平是等臂杠杆。
答案:B25.(佛山市)如图所示,甲是我们常使用的指甲钳,乙是它的示意图。
请细心观察,此钳哪些部位分别应用了哪些物理知识及原理,请你写出二个应用不同原理的例子。
答案:钳口D很锋利——压力一定时,减小受力面积可增加压强;钳柄(AC)上有粗糙的刻纹——增大摩擦;指甲钳的CBA部分——省力杠杆17.(广州)在图中用线代表绳子,将两个滑轮连成省力的滑轮组,要求人用力往下拉绳使重物升起.解析:理论上吊起动滑轮绳子股数越多,越省力,但由于人站在地面上向下拉,有两股绳子吊起动滑轮,根据“奇动偶定”的方法,绳子起点定在定滑轮上。
所以画出如图所示的绕线。
答案:如图所示。
5.(成都)如图所示的简单工具在使用过程中,不能省力的是()解析:定滑轮不能省力,但能改变施力的方向。
答案:D5.( 成都)在抗震救灾中,为了从垮塌的建筑中尽快地实施救援,营救生命,使用到了大量的汽车起重机。
正在家中复习的小陈同学看到救灾现场的救援画面后,在感动之余,找来了一台玩具汽车起重机,进行了探究。
小陈要探究的问题是,起重机吊起的重物静止在空中时:①支撑臂对起重臂的作用力大小;②水平地面受到的起重机的压强。
为此,小陈除起重机外,还准备了以下器材:重物、弹簧测力计、棉线、面积足够大的坐标纸、墨水、毛笔、复写纸。
(1)要完成他的探究,上述器材中还应该增加的是_________________________________。
(2)为完成问题①的探究,需要测量力臂。
请你在图18中作出支撑臂CD 对起重臂AB 的作用力F的力臂,其中O 点是支点。
(3)在问题②的探究中,针对接触面积的测量中遇到的困难,小陈设计了两套实验方案。
杠杆滑轮练习44题

《杠杆和滑轮》练习班级姓名家长签字______________一、知识点:(必须要熟记)1.杠杆:在力的作用下绕固定点转动的硬棒,杠杆可直可弯。
2.力臂:是支点到力的作用线的垂直距离。
3.杠杆的平衡条件:杠杆处于静止或缓慢匀速转动状态,平衡条件是F1×L1=F2×L2。
4.杠杆的应用:省力杠杆,L1<L2;费力杠杆,L1>L2;等臂杠杆,L1=L2;5.滑轮和滑轮组:定滑轮相当于等臂杠杆,不省力但可改变力的方向;动滑轮相当于动力臂为阻力臂二倍的杠杆,可省一半力,但不能改变力的方向。
滑轮组即可以省力又可以改变力的方向,但却不能同时省距离。
6.对于滑轮或滑轮组,S= h;若不计摩擦绳重和动滑轮重有F= ;若不计摩擦绳重有F=二、巩固题1.如图1所示,轻质杠杆支点为O,在已调平的杠杆两端分别挂上一些钩码,每一个钩码的质量相等,杠杆恰好在水平位置平衡,如果两边各拿走一个钩码,杠杆将 ( ) A.仍保持平衡并静止B.不平衡,向顺时针方向转动C.不平衡,向逆时针方向转动D.仍保持平衡,但要转动2.图2中属费力杠杆的是()3.下列说法正确的是()A.杠杆一定能够省力B.定滑轮既能省力又能改变力的方向C.动滑轮既能省力又能改变力的方向D.滑轮组既能省力又能改变力的方向4.家用的手摇晾衣架如图所示,它实际是由定滑轮和动滑轮组成的滑轮组。
假设衣服和晾衣架的总重为100N,则静止时绳子自由端的拉力为(不计动滑轮重及摩擦)()A、100NB、50NC、25ND、20N5.用如图所示的装置提升同一物体,在滑轮重及摩擦不计的情况下最省力的是()6.一辆汽车不小心陷进泥潭后,司机按图所示的甲、乙两种方法安装滑轮,均可将汽车从泥潭中匀速拉出。
比较这两个装置,下列说法正确的是()A.甲、乙安装的都是动滑轮,都能省力 B.甲、乙安装的都是定滑轮,都不能省力C.甲安装的是动滑轮,能省力 D.乙安装的是动滑轮,能省力7.如图所示,一名同学在做俯卧撑,如果把人的躯干看作一个杠杆,这是一个________(填“省力”或“费力”)杠杆,该杠杆的支点是________(填图中字母)。
杠杆、滑轮作图专题训练word版

一、杠杆作图1、如图所示,一杠杆在力F1的作用下处于静止状态,请画出它的力臂L1。
2、杠杆在我国古代就有了许多巧妙的应用,护城河上安装的吊桥(如图)就是一个杠杆,它的支点是C 点,画出绳对吊桥的拉力及拉力的力臂。
3、如图,画出人对杠杆作用力F的力臂L和物体A所受重力G的示意图。
4、如图所示,请画出动力的力臂L。
5、如图所示的组合机械,请在图中画出杠杆OA的动力臂L和所挂重物G的重力示意图.6、请作出图中:①物体A所受重力G的示意图;②力F的力臂L。
7、杠杆OA可绕O点转动,受力情况如图所示。
请作出力F的力臂L。
8、曲杆可绕固定点O转动,在一个最小的拉力F的作用下,在图所示位置保持静止,请在图乙中画出:①拉力F的力臂和拉力F的示意图;②所挂物体受到重力的示意图。
9、在图中,O是杠杆的支点,请在图中画出能使杠杆平衡的最小的力F1的示意图及其力臂L1。
10、如图所示,轻质杠杆可绕O转动,杠杆上吊一重物G,在动力F1作用下杠杆静止在水平位置,l为动力F1的力臂,请在图中作出动力F1和阻力F2的示意图。
11、如图所示杠杆OA处于静止状态,L2是力F2的力臂.请在图中画出力F1的力臂L1和力F2的示意图.12、如图所示,轻质杠杆AOB处于静止状态,作出作用在A点的最小力F和力臂l。
二、滑轮作图1、按要求连接滑轮组2、画出右图中最省力的绳子的绕线方法3、小红借助滑轮组提升重物,请画出最省力的绕线方法。
4、图中的定滑轮和动轮绕制滑组,要能够改变力的方向。
5、如图,站在地面上的人通过滑轮组提升物体,请画出滑轮组的绕线。
6、如图所示,某人站在A处通过一根绳和两个滑轮匀速提起物体B,所用的拉力F=100N,物体B重300N,(不计滑轮重、绳重及摩擦力),画出滑轮组的绕线。
7、建筑工地上,工人师傅将如图丙所示的滑轮装配成最省力的滑轮组,利用它站在地面上向下拉绳提升重物,请在图中画出滑轮组的绕线。
9、根据题中所给出的滑轮组,请在图中画出省力的绕法(要求所给的滑轮都利用)。
杠杆、滑轮及机械效率练习题

杠杆、滑轮及机械效率练习题(总4页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--杠杆专项练习一、下列杠杆中,O是支点,在图上画出F1、F2的力臂,并且用L1、L2表示它们:二、应用杠杆原理F1l1=F2l2解决杠杆问题:1、在均匀铁条的中点O处用线将其悬挂起来,铁条水平平衡,如图5(a)所示。
若将OB弯折,如图(b)所示,则铁条将[ ]A.A端下降,C端上升 B.A端上升,C端下降C.仍然平衡 D.无法判断2、在图2中,能够平衡的杠杆是图[ ]3、一根不均匀木棒长1米,当用力F1=6牛竖直向上作用在它的A端时,刚能抬起A端,当用力F2=12牛竖直向上作用在它的B端,刚能抬起它的B端,求此棒的重力和重心距A端的距离。
4、一根扁担长,前后两筐内分别装有300N和400N的货物。
问:人肩挑处离前筐多远才能平衡(不计扁担及筐的质量)5、一根杠杆长1米,支点O在它的最左端,现将一G为90牛顿的重物放在距O点20厘米处,若使杠杆处于水平静止状态,则动力作用在杠杆最右端时,应向____时(左,中,右),动力最小,且动力的大小是______牛顿。
6、杠杆两端各挂有重力不相等的两块同种材料做成的实心金属块A、B,已知G A<G B,此时杠杆平衡,如图4所示。
当把A、B金属块都浸没在水中时,杠杆将 [ ]A.失去平衡,A端向下倾斜 B.失去平衡,B端向下倾斜C.仍然保持平衡 D.条件不足,无法判断7、一把杆秤不计自重,提纽到秤钩距离是4cm,秤砣质量250g。
用来称质量是2kg的物体,秤砣应离提纽多远,秤杆才平衡若秤杆长60cm,则这把秤最大能称量多少千克的物体8、身高几乎相同的兄弟二人,用长米的扁担抬一桶水,水桶挂在距哥哥肩米处的扁担上,桶和水共重300牛,问兄弟二人肩上各负担多大的力(不计扁担重)9、一根轻质杠杆AB 长,当A 点挂质量为的实心铝块,B 端挂重物P 为9N 时,杠杆能平衡。
杠杆滑轮计算题练习(打印版)
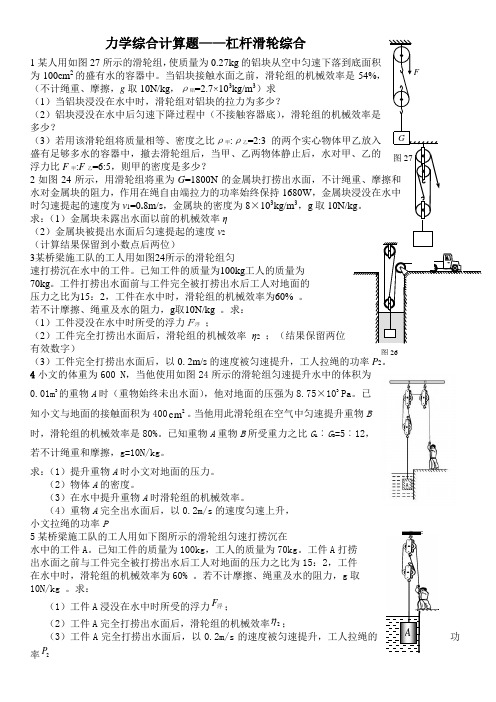
力学综合计算题——杠杆滑轮综合1某人用如图27所示的滑轮组,使质量为0.27kg 的铝块从空中匀速下落到底面积为100cm 2的盛有水的容器中。
当铝块接触水面之前,滑轮组的机械效率是54%,(不计绳重、摩擦,g 取10N/kg ,ρ铝=2.7×103kg/m 3)求(1)当铝块浸没在水中时,滑轮组对铝块的拉力为多少?(2)铝块浸没在水中后匀速下降过程中(不接触容器底),滑轮组的机械效率是多少?(3)若用该滑轮组将质量相等、密度之比ρ甲:ρ乙=2:3的两个实心物体甲乙放入盛有足够多水的容器中,撤去滑轮组后,当甲、乙两物体静止后,水对甲、乙的浮力比F 甲:F 乙=6:5,则甲的密度是多少?2如图24所示,用滑轮组将重为G =1800N 的金属块打捞出水面,不计绳重、摩擦和水对金属块的阻力,作用在绳自由端拉力的功率始终保持1680W ,金属块浸没在水中时匀速提起的速度为v 1=0.8m/s ,金属块的密度为8×103kg/m 3,g 取10N/kg 。
求:(1)金属块未露出水面以前的机械效率η(2)金属块被提出水面后匀速提起的速度v 2(计算结果保留到小数点后两位)3某桥梁施工队的工人用如图24所示的滑轮组匀速打捞沉在水中的工件。
已知工件的质量为100kg 工人的质量为70kg 。
工件打捞出水面前与工件完全被打捞出水后工人对地面的压力之比为15:2,工件在水中时,滑轮组的机械效率为60% 。
若不计摩擦、绳重及水的阻力,g 取10N/kg 。
求:(1)工件浸没在水中时所受的浮力F浮 ;(2)工件完全打捞出水面后,滑轮组的机械效率η2 ;(结果保留两位有效数字) (3)工件完全打捞出水面后,以0.2m/s 的速度被匀速提升,工人拉绳的功率P 2。
4小文的体重为600 N ,当他使用如图24所示的滑轮组匀速提升水中的体积为0.01m 3的重物A 时(重物始终未出水面),他对地面的压强为8.75×103 Pa 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
力学综合计算题——杠杆滑轮综合08年丰台区二模:某人用如图27所示的滑轮组,使质量为0.27kg的铝块从空中匀速下落到底面积为100cm2的盛有水的容器中。
当铝块接触水面之前,滑轮组的机械效率是54%,(不计绳重、摩擦,g取10N/kg,ρ铝=2.7×103kg/m3)求(1)当铝块浸没在水中时,滑轮组对铝块的拉力为多少?(2)铝块浸没在水中后匀速下降过程中(不接触容器底),滑轮组的机械效率是多少?(3)若用该滑轮组将质量相等、密度之比ρ甲:ρ乙=2:3的两个实心物体甲乙放入盛有足够多水的容器中,撤去滑轮组后,当甲、乙两物体静止后,水对甲、乙的浮力比F甲:F乙=6:5,则甲的密度是多少?08年石景山区一模:如图24所示,用滑轮组将重为G=1800N的金属块打捞出水面,不计绳重、摩擦和水对金属块的阻力,作用在绳自由端拉力的功率始终保持1680W,金属块浸没在水中时匀速提起的速度为v1=0.8m/s,金属块的密度为8×103kg/m3,g取10N/kg。
求:(1)金属块未露出水面以前的机械效率η(2)金属块被提出水面后匀速提起的速度v2(计算结果保留到小数点后两位)08年怀柔区二模:某桥梁施工队的工人用如图24所示的滑轮组匀速打捞沉在水中的工件。
已知工件的质量为100kg工人的质量为70kg。
工件打捞出水面前与工件完全被打捞出水后工人对地面的压力之比为15:2,工件在水中时,滑轮组的机械效率为60% 。
若不计摩擦、绳重及水的阻力,g取10N/kg 。
求:(1)工件浸没在水中时所受的浮力F浮;(2)工件完全打捞出水面后,滑轮组的机械效率η2;(结果保留两位有效数字)(3)工件完全打捞出水面后,以0.2m/s的速度被匀速提升,工人拉绳的功率P2。
图26图27F09年崇文区一模:小文的体重为600 N ,当他使用如图24所示的滑轮组匀速提升水中的体积为0.01m 3的重物A 时(重物始终未出水面),他对地面的压强为8.75×103 Pa 。
已知小文与地面的接触面积为4002cm 。
当他用此滑轮组在空气中匀速提升重物B 时,滑轮组的机械效率是80%。
已知重物A 重物B 所受重力之比G A ︰G B =5︰12,若不计绳重和摩擦,g=10N/kg 。
求:(1)提升重物A 时小文对地面的压力。
(2)物体A 的密度。
(3)在水中提升重物A 时滑轮组的机械效率。
(4)重物A 完全出水面后,以0.2m/s 的速度匀速上升,小文拉绳的功率P 。
09年顺义区一模:某桥梁施工队的工人用如下图所示的滑轮组匀速打捞沉在 水中的工件A 。
已知工件的质量为100kg ,工人的质量为70kg 。
工件A 打捞出水面之前与工件完全被打捞出水后工人对地面的压力之比为15:2,工件在水中时,滑轮组的机械效率为60% 。
若不计摩擦、绳重及水的阻力,g 取10N/kg 。
求:(1)工件A 浸没在水中时所受的浮力浮F ;(2)工件A 完全打捞出水面后,滑轮组的机械效率2 ;(3)工件A 完全打捞出水面后,以0.2m/s 的速度被匀速提升,工人拉绳的功率2P 。
09海淀区一模:如图23所示,质量为70kg 的工人站在岸边通过一滑轮组打捞一块沉没在水池底部的石材,3.09年海淀区一模:该滑轮组中动滑轮质量为5kg 。
当工人用120N 的力拉滑轮组的绳端时,石材仍沉在水底不动。
工人继续增大拉力将石材拉起,在整个提升过程中,石材始终以0.2m/s 的速度匀速上升。
在石材还没有露出水面之前滑轮组的机械效率为η1,当石材完全露出水面之后滑轮组的机械效率为η2。
在石材脱离水池底部至完全露出水面的过程中,地面对人的支持力的最大值与最小值之比为29:21。
绳重及滑轮的摩擦均可忽略不计,石材的密度ρ石=2.5×103kg/m 3,取g =10N/kg ,求:(1)与打捞前相比,当人用120N 的力拉绳端时,水池底部对石材的支持力变化了多少;(2)η1与η2的比值;(3)当石材完全露出水面以后,人拉绳子的功率。
图2309年怀柔区一模:如图21所示,某工地用固定在水平工作台上的卷扬机(其内部有电动机提供动力)通过滑轮组匀速提升货物,已知卷扬机的总质量为120kg ,工作时拉动绳子的功率恒为400W 。
第一次提升质量为320kg 的货物时,卷扬机对绳子的拉力为F 1,对工作台的压力为N 1;第二次提升质量为240kg 的货物时,卷扬机对绳子的拉力为F 2,对工作台的压力为N 2。
已知N 1与N 2之比为25:23,取g=10N/kg ,绳重及滑轮的摩擦均可忽略不计。
求:(1)卷扬机对绳子的拉力F 1的大小; (2)第一次提升货物过程中滑轮组的机械效率;(3)前后两次提升货物过程中货物竖直向上运动的速度之比。
09年平谷一模:体重为510N 的人,站在水平地面上对地面的压强为p 1, .如图3所示,用滑轮组拉物体A 沿水平方向做匀速运动,此时人对地面的压强为p 2,压强变化了2750pa 。
已知人一只脚的面积是200cm 2,滑轮组的机械效率为80%。
(不计绳重和摩擦,地面上的定滑轮与物体A 相连的绳子沿水平方向,地面上的定滑轮与动滑轮相连的绳子沿竖直方向,人对绳子的拉力与对地面的压力始终竖直向下且在同一直线上,)。
求:(1)绳对人的拉力; (2)物体A 与地面的摩擦力;(3)若在物体A 上再放一个物体B,滑动摩擦力增大了30N,此时该装置的机械效率是多少?(7分)09年西城区二模:工人利用滑轮组按照图25所示的方式提升货箱。
工人的体重为G 人=800N 。
提升第一个货箱时,工人用F 0=500N 的竖直向下的力拉绳时,没有提起货箱。
工人用F 1=600N 的竖直向下的力拉绳时,货箱恰能以0.2m/s 的速度匀速上升。
此时工人提升货箱的效率为62.5%。
第二个货箱比第一个货箱重500N ,工人仍能提起第二个货箱并使第二个货箱以0.1m/s的速度匀速上升。
求:⑴第一个货箱未被拉动时,水平地面对货箱的支持力;⑵工人提升第一个货箱和第二个货箱做功功率变化量的大小。
09年丰台区二模:如图18所示,金鹏同学为他的妈妈设计了一款颈椎拉伸器,左边滑轮下端是由密度为3×103kg/m 3的圆柱体合金块充当配重,它的底面积为5dm 2,高为4dm 。
右边自由端安放颈圈套在患者的颈部。
当颈部承受拉力为55N 时,配重对地面的压强为p 1,当颈部承受的拉力为105N 时,配重对地面的压强为p ’1,已知p 1:p ’1‘=2:1,妈妈重600N ,忽略绳重和摩擦,g =10N/kg ,求:(1)配重单独放置时对地面的压强;(2)动滑轮自重;(3)当配重与地面的压强为零时,妈妈对地面的压力为多少。
图 3 图2109年宣武区一模:如图25所示,是一个上肢力量健身器示意图。
配重A受到的重力为350N,其底面积为5×10-2m2。
B、C都是定滑轮,D是动滑轮;杠杆EH可绕O点在竖直平面内转动,OE=3OH。
小明受到的重力为500N,当他通过细绳在H点分别施加竖直向下的拉力T1、T2时,杠杆两次都在水平位置平衡,小明对地面的压力分别为F1、F2,配重A受到的拉力分别为F A1、F A2,配重A对地面的压强分别为p1、p2,且两次A对地面的压强相差2×103Pa。
已知F1∶F2=4∶3,p1∶p2=3∶2 。
杠杆EH和细绳的质量及滑轮组装置的摩擦力均忽略不计。
求:(1) 拉力F A2与F A1之差;(2) 小明对地面的压力F1;(3)当小明通过细绳在H点施加竖直向下的拉力T 3时,配重A匀速上升2cm,此时滑轮组的机械效率η。
(请画出相关..受力分析图.....)09年怀柔区二模:某校科技小组的同学设计了一个从水中打捞物体的模型,如图22所示其中D、E、G、H都是定滑轮,M是动滑轮,杠杆BC可绕O点在竖直平面内转动,OC∶OB=3∶4。
杠杆BC和细绳的质量均忽略不计。
人站在地面上通过拉绳子提升水中的物体A,容器的底面积为300 cm2,人的质量是70 kg,通过细绳施加竖直向下的拉力时, A始终以0.6m/s的速度匀速上升。
当杠杆到达水平位置时物体A总体积的五分之三露出液面,液面下降了50cm,此时的拉力为F1 ,它的功率为P1,地面对他的支持力是N1;当物体A完全离开液面时,此时通过细绳施加竖直向下的拉力为F2 ,它的功率为P2,地面对人的支持力是N2。
已知A的质量为75kg,N1∶N2=2∶1,忽略细绳与滑轮的摩擦以及水对物体的阻力,g取10N/kg。
求:⑴当物体露出液面为总体积的五分之三时,物体所受的浮力;⑵动滑轮M受到的重力;⑶P1∶P2的值。
09年西城区一模:在图23所示装置中,甲物重G甲=10N,乙物重G乙是动滑轮重G轮的8倍。
物体乙跟地面的接触面积为1.5×10-2m2。
轻杆AB可以绕O点转动,且OA∶OB=2∶1。
不计轴摩擦,装置如图所示处于平衡状态时,乙对水平地面的压强P=2×103Pa。
求:此时动滑轮对物体乙的拉力F拉;若在物体甲下面再加挂物体丙,恰使物体乙对地面的压强为零。
求:丙的物重G丙。
图25图2309年门头沟二模:火车道口处设置人工控制的栏杆,图25是栏杆的示意图。
密度和粗细均匀的栏杆全长6m ,质量为40kg 。
栏杆的重心位于P 点,栏杆可绕O 点在竖直平面内无摩擦转动。
栏杆的H 端通过滑轮组来提升栏杆,其中A 、B 、D 、E 、都是定滑轮,C 是动滑轮,T 为固定在水平地面上的挂钩。
当火车通过岔道口后, 管理人员用力F 1竖直向下拉绳子, 栏杆恰好在水平位置平衡。
管理人员为了减轻自己的工作强度,他在H 端下方的绳子上加挂了一个质量为10kg 的重物,用力F 2以0.2m/s 的速度匀速拉动绳子使栏杆逆时针转动45°角时车辆放行。
此时管理人员将绳端固定在挂钩T 上。
已知:F 1∶F 2=17∶15;OH=1m, 忽略细绳与滑轮的摩擦。
g 取10N/kg 。
求:⑴动滑轮C 的重力; ⑵F 1的大小; ⑶F 2的功率;08年中考题:如图是一个上肢力量健身器示意图。
配重A 受到的重力为1200N ,其底面积为5×10-2m2. B 、C 都是定滑轮,D 是动滑轮;杠杆EH 可绕O 点在竖直平面内转动,OE :0H =2:5。
小成受到的重力为600N ,他通过细绳在H 点施加竖直向下的拉力为T1时,杠杆在水平位置平衡,小成对地面的压力为F1,配重A 受到的拉力为FA1,配重A 对地面的P1为6×103pa 。
小成在H 点施加竖直向下的拉力为T2时,杠杆仍在水平位置平衡,小成对地面的压力为F2,配重A 受到的拉力为FA2,配重A 对地面的压强P2为4×103pa 。
