QR码纠错码原理及实现
QR码编码原理二(编码)
编码就是把常见的数字、字符等转换成QR码的方法。
说具体的编码之前,先说一下QR码的最大容量问题。
一、最大容量QR码的最大容量取决于选择的版本、纠错级别和编码模式(Mode:数字、字符、多字节字符等)。
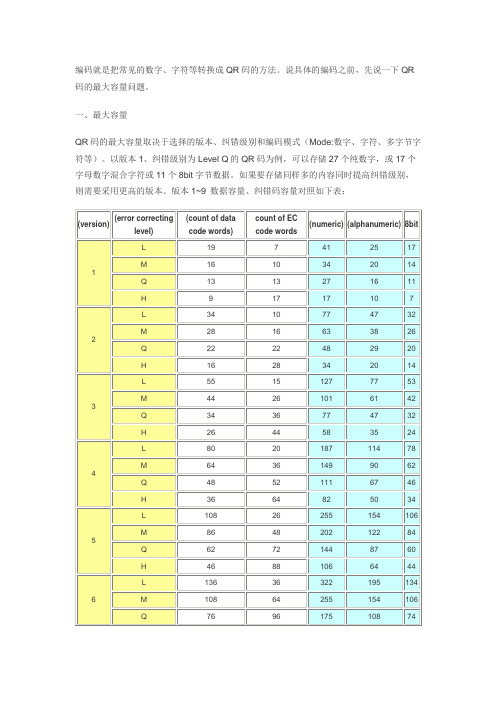
以版本1、纠错级别为Level Q的QR码为例,可以存储27个纯数字,或17个字母数字混合字符或11个8bit字节数据。
如果要存储同样多的内容同时提高纠错级别,则需要采用更高的版本。
版本1~9 数据容量、纠错码容量对照如下表:下面,就举例说明将“ABCDE123”转换成为版本1、Level H的QR码转换方法。
二、模式标识符(Mode Indicator)QR码的模式(Mode)就是前文提到的数字、字符、8bit 字节码、多字节码等。
对于不同的模式,都有对应的模式标识符(Mode Indicator)来帮助解码程序进行匹配,模式标识符是4bit 的二进制数:1、数字模式(numeric mode ): 00012、混合字符模式(alphanumeric mode): 00103、8bit byte mode: 01004、日本汉字(KANJI mode): 10005、中国汉字(GB2312):1101由于示例文本串是混合字符,因此将选择alphanumeric mode,其标识码为:0010三、文本串计数标识符(Character count indicator)文本串计数标识符用来存储源内容字符串的长度,在版本1-9的QR码中,文本串长度标识符自身的长度被定义为:数字 : 10bit混合字符: 9bit8bit 字节码: 8bit多字节码: 8bit在本例中,源文本串的长度为8个字符,混合字符的长度为9bit,因此将字符个数8编码为9位二进制表示:000001000加上混合字符模式标识码,总的编码为0010 000001000四、数据内容编码1、数字模式下的编码在数字模式下,数据被限制为3个数字一段,分成若干段。
QR码纠错编码

Ie wrs Q c e Re- l r aot ; o fl Eoc r tg Ky o I R o ; d o n nl r m Glse ; r rcncd d d e S oo g i h ai d r - ei o r o e
条码技术是在计算机技术与信息技术基础 卜 发展起来的 们 集编码、印刷、i别、数据采集和处理于一 t : 体的新兴技 术。由J传统的 一 l 维条码信息容量很小, 信息的详细描述要 依赖数据库提供,囚而使其应用受到了一 定的限制。土世纪
G()的 元 另 求 成多 式 也 用 域 素 Fa 域 素, 外, 生 项 时 要 到 元 2上 a 因 , 们 求 G( 的 个 元 。 伽 华 的 , 此 我 先 出 F0 各 域 素 由 罗 域 2 )
性 知, a G() 本 元素, G() 每一 质可 若 是 F 的 原域 丫 则F 中 元 f
a (x( + 7 +a。 p6 6 ( 5 ( (+ (= x i a: ( )7 + )' a 1 ) ) 3 x ( X+ +
5 ( + t 4 ( + 3 ( + ) + )+ x a; ( ) + 5 3 “: ( ) + X i 3 “2 ( 、 x 1 之
( I pI ( n p0 a + ) a x 十 + ) 可见,两元素的相加的和就是对应多项式的系数相加后 所得的多项式。山 于系数取自 F ) 。与 ,校2 G ( ,故 1R是 相加, 2
第2卷 ,
V1 9 b. 2
第1 期
No了
计
算
机
工
程
2 )年1 (3 月 K
C mpt E g er g o ue ni ei r n n
文童编号:10-12( 0) - 03 1 01 48 03 1 - 9-f 1 2 0 0 〕 文献标识码:A
qr code 原理

qr code 原理
QR码的原理是利用二维编码来存储和传输信息。
它由黑白方块组成,可以被红外线扫描仪、激光扫描仪或手机相机等设备扫描并解码。
QR码的生成过程具体如下:首先,将需要编码的数据(例如文本、网址或其他信息)转换成二进制形式。
接下来,将二进制数据按照一定规律分配给QR码中的黑白方块,形成一个特定的二维编码模式。
每个方块代表一个数据单元,可以存储0或1的二进制值。
QR码的结构设计上采用了一种巧妙的纠错技术,即在编码中加入冗余信息,使得即使在一定程度的损坏或污损情况下,扫描仪仍然能够正确识别和解码信息。
这种纠错技术称为“Reed-Solomon”纠错码。
在扫描QR码时,扫描设备通过光源照射到码上,并接收反射回来的光信号。
然后,扫描设备解码接收到的信号,将其转换成二进制数据。
最后,通过解码软件将二进制数据解析为原始信息,例如网址、文本或其他数据。
由于QR码具有高密度存储信息、快速读取、纠错能力强等特点,广泛应用于商品包装、广告宣传、移动支付、票务管理等领域。
基于Reed_Solomon算法的QR码纠错编码

+α 2 x 2 +α 1 x+α 0
β(x)=β 7 x 7 +β 6 x 6 +β 5 x5 +β 4 x4 +β 3 x3
+β 2 x 2 +β 1 x+β 0 如元素10011010可表示为x 7 + x 4 + x 3 + x,则α,β
k-1
dk-1x +...+d
2
2x +d1x+d0,
则
可
用
多
项
式d(x)
表
示
待
编
码
的
数据。在编码中,我们要用到生成多项式的概念,由生成多
项式生成我们所要的编码。对于循环码的编码,有以下定
理: 定 理 1:GF(2m)上的[n,k]循环码中,存在唯一的n-k次
首 一 多 项 式g(x),每一码多项式 C(x)都是 g(x)的 倍 式 , 且 每
第 29卷 第 1期 Vol.29 № 1
计 算 机 工 程 Computer Engineering
2003年 1月 January 2003
·基金项目论文·
文章编号: 1000— 3428(2003)01 — 0093—03
文献标识码:A
中 图 分 类 号 : TP391.1
基于Reed-Solomon算法的QR码纠错编码
一个次数小于或等于n-1 的g(x)的倍式一定是码多项式(证明
参见参考文献2)。 我们所要进行的 Reed-Solomon编码是循环码的一种,因
此,我们可以这样构造生成多项式:设a∈GF(2m) 是 本 原 域 元素,mi (x)是ai 的最小多项式(I=0,1,...,r-1),则生成多项式
qr 编码逻辑 -回复

qr 编码逻辑-回复关于QR编码逻辑[qr 编码逻辑],指的是QR编码的原理和逻辑。
QR码(Quick Response code)是一种二维码,被广泛应用于商业和个人领域,方便快捷地扫描和解码。
本文将一步一步回答有关QR编码逻辑的问题,包括QR码的构成、编码方式、解码原理和应用等内容。
首先,我们来了解QR码的构成。
QR码由黑白方格组成,每个方格被称为一个模块。
QR码可以根据需求扩展到不同的尺寸,最小的QR码为21x21模块,最大的QR码可达177x177模块。
QR码中有三个特殊的模块:定位模块、对齐模块和校准模块。
定位模块用于确定QR码的位置和方向,对齐模块用于帮助解码器自动识别QR码的位置,而校准模块则用于对图像进行纠偏。
QR码的编码方式有多种,最常用的是数值、字母和字符的混合编码。
具体而言,QR码可以包含数字(0-9)、大写字母(A-Z)、ASCII字符和中文汉字等数据。
不同数据的编码方式也不同,数字使用4位二进制表示一个数字,字母使用11位二进制表示一个字母,而汉字使用13位二进制表示一个汉字。
编码后的数据以一定的格式和规则组织在QR码中,以实现正确的解码。
接下来,我们来探讨QR码的解码原理。
QR码的解码过程主要分为图像处理、数据提取和错误纠正三个步骤。
首先,需要对QR码的图像进行处理,包括二值化、去噪声和纠偏等操作,以提高解码的准确性。
然后,从处理后的图像中提取出QR码的模块,并计算模块的大小和位置关系,以确定QR码的结构。
最后,对提取出的模块进行解码,根据编码规则将模块的数据转换为原始数据,即可获得QR码中所含信息。
QR码的应用非常广泛,涵盖了商业和个人领域。
在商业方面,QR码可以用于商品标签、广告宣传、支付码等场景。
通过扫描QR码,用户可以获取商品信息、参与活动或完成支付等操作。
在个人领域,QR码可以用于个人名片、电子门票、WiFi连接等场景。
用户可以通过扫描QR码,轻松地获取联系方式、入场许可或快速连接到WiFi网络。
纠错编码的基本原理与性能

纠错编码的基本原理与性能
1.分组码的基本原理
(1)分组码的定义
分组码是指将信息码分组,为每组信码附加若干监督码(即差错控制码)的编码方式。
(2)分组码的结构
分组码一般用符号(n,k)表示,其中n是码组的总位数,又称码组的长度(码长),k 是码组中信息码元的数目,n-k=r为码组中的监督码元数目,又称监督位数目。
图11-1 分组码的结构
(3)分组码的参量
①码重
码重是指分组码中“1”的个数目。
②码距
码距是指两个码组中对应位上数字不同的位数,又称汉明距离。
③最小码距
最小码距是指编码中各个码组之间距离的最小值。
2.纠错编码的基本原理
最小码距d0的大小直接关系编码的检错和纠错能力:
(1)为检测e个错码,要求最小码距
(2)为纠正t个错码,要求最小码距
(3)为纠正t个错码,同时检测e个错码,要求最小码距
码距与纠错和检错能力的关系如图11-2所示。
图11-2 码距与检错和纠错能力的关系
纠错编码的性能
1.误码率的改善
采用纠错编码,误码率得到很大改善,改善的程度和所用的编码有关。
2.信噪比的改善
对于给定的传输系统,为
式中,R B为码元速率。
3.带宽增大
监督码元加入,发送序列增长,冗余度增大,若保持信息码元速率不变,则传输速率增大,系统带宽增大。
QR二维码的原理与识别方法

QR二维码的原理与识别方法一、QR码的原理:1.数据编码:QR码将信息编码为一系列黑白方块的模式。
它将输入的信息进行分段,并将每个字符转换为相应的二进制码,然后通过一系列的编码规则生成QR码的编码区域。
2. 误差校正:QR码通过内置的校验码来检测和纠正数据的错误。
它在编码区域中添加了一些特殊的模块,并使用Reed-Solomon纠错码来计算校验码,从而可以在一定程度上恢复和纠正编码中的错误。
3.定位模块:QR码中包含了多个定位模块,用来标识QR码的边界并帮助解码。
定位模块的位置和大小是固定的,解码器通过检测定位模块的位置和模式来确定QR码的边界。
4.数据密度:QR码的数据密度非常高,可以存储更多的信息。
通过增加编码区域的大小和模块的个数,可以有效提高QR码的存储容量和密度。
二、QR码的识别方法:2.定位模块检测:在图像中定位QR码的位置是识别QR码的重要步骤。
通常可以使用图像处理的方法,如边缘检测、轮廓检测等技术来检测QR码的定位模块,从而确定QR码的边界和角度。
4.数据解析与提取:在解码和校验码之后,可以将二进制数据转换为文本、数字或链接等特定的信息。
根据QR码的编码规则,将每个字符的二进制数据映射为相应的字符,从而提取和解析出最终的数据。
总结:QR码的原理是通过在二维平面上的黑白方块编码来存储信息,同时利用校验码和定位模块等机制来实现数据的校验和解析。
识别QR码的方法包括图像扫描、定位模块检测、解码校验码和数据解析与提取等步骤。
QR码已经在各个领域广泛应用,方便了信息的传递和存储。
纠错编码的方法

纠错编码的方法纠错编码(Error Correction Code,ECC)是一种在数字通信中用于检测和纠正错误的技术。
在数字通信中,由于噪声、干扰或其他原因,数据可能会发生错误。
纠错编码通过添加冗余信息来提高数据传输的可靠性,从而实现错误的检测和纠正。
1. 纠错编码的基本原理纠错编码的基本原理是通过在待传输数据中添加额外的冗余信息,并将这些冗余信息与原始数据一起传输。
接收方根据冗余信息对接收到的数据进行校验,并尝试恢复出原始数据。
常用的纠错编码方法包括海明码(Hamming Code)、卷积码(Convolutional Code)、低密度奇偶校验(Low-Density Parity Check, LDPC)等。
这些方法采用不同的算法和策略来实现错误检测和纠正。
2. 海明码海明码是一种最早被广泛应用于纠错编码中的方法。
它通过在待传输数据中添加冗余位来实现错误检测和纠正。
海明码采用了一种特殊的生成矩阵和校验矩阵来计算校验位,并将其添加到待传输数据中。
接收方根据接收到的数据和校验位计算出错误位,并进行纠正。
海明码的一个重要特点是可以检测和纠正多个错误。
通过添加足够数量的校验位,海明码能够检测到并纠正多达两个比特的错误。
3. 卷积码卷积码是一种基于状态机的纠错编码方法,它采用了一种特殊的编码器来生成冗余信息。
卷积码的编码器使用一个或多个移位寄存器和一个组合逻辑电路来生成冗余信息。
待传输数据经过编码器后,会产生一系列冗余比特,这些比特与原始数据一起传输。
接收方使用最大似然译码算法对接收到的数据进行解码,并根据冗余比特计算出错误位,并尝试进行纠正。
卷积码具有较高的编解码性能,但其复杂度较高。
为了降低复杂度,常常采用迭代译码算法(如Turbo译码)来提高性能。
4. 低密度奇偶校验低密度奇偶校验(LDPC)是一种近年来得到广泛关注和应用的纠错编码方法。
它采用了一种特殊的校验矩阵来生成冗余信息。
LDPC码的校验矩阵是一个稀疏矩阵,其中每一行和每一列的1的数量较少。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
增刊 1
冯汉禄等: QR 码纠错码原理及实现
41
原始 信 息 v( x) 在 传 输 的 过 程 中 受 到 的 错 误 影 响 为 E( X) , 则实际接收到的信号 R( x) = v( x) + E( x) , 则原始信 息 v( x) = R( x) - E( x) , 设接收到的码字多项式为:
[4 ] r
σ( x) =
∏ ( 1 - x x) ; 0 ≤ r ≤ t
i i =1
( 7)
把 σ( x) 展开: σ ( x ) = ( 1 - x1 x ) ( 1 - x2 x ) ( 1 - x3 x ) … ( 1 - x t x ) = 1 - ( x1 + x2 + … + x t ) x + ( x1 x2 + x1 x3 + … + x t - 1 x t ) x2 - … + ( - 1 ) t x1 x2 … x t 令 σ1 = - ( x 1 + x 2 + … + x t ) ( 8)
1
RS 码编译算法
域是能够进行加与乘两种运算的非空元素的集合 。 伽罗 GF) 是一个有限域, 瓦域( Galois Field, 以素数 q 为模的整数 构成 q 阶的伽罗瓦域为 GF( q) 。 在 GF( q) 中, 某一个元素 a 满 q -1 a = 1 , a GF ( q ) 。 GF 足 称 为 的本原元 在任何 ( q) 中都能找 到一个本原元, 能够用它的幂次表示所有 q - 1 个非零元素, 0 a1 , a2 , a3 , a4 , …, a q -1 ,其 中 从而组 成 一 个 循 环 群 G( a) : a , q -1 a = 1。 [3 ] 可以纠正 t 个错误的 RS 码的生成多项式 为: 2 2t 2t g ( x ) = ( x - a ) ( x - a ) … ( x - a ) = x + g2 t - 1 x 2 t - 1 + g2 t - 2 x n - 2 + … + g1 x + g0 ( 1) 1, 2, …, 2 t - 1 ) 是 GF( q) 中元素, a 为 GF( q) 其中: g i ( i = 0 , 中的一个本原元。 1 2 若原始信息的多项式为 d( x) = d0 + d1 x + d2 x + … +
中很容易受到污染、 涂痕、 撕裂等各种形式的破坏, 直接影响 因此采用一种好的检错与纠错算法尤为重要 。 目前在 识别, Solomon ) 错误控 二维条码中应用的最为广泛的是 RS ( ReedSolomon 码是一种重要的循环码, 制码。Reed是分组中纠错 能力最强的一种码, 在 QR 码中利用 RS 纠错码, 最高纠错等 [2 ] Solomon 码编译码 级能纠错 30% 的错误码字 。 但是 Reed算法比较复杂, 本文对 RS 纠错码算法在 QR 码中的应用进行 了相关研究。
n -1
R( x) =
∑r x
i i =0
i
= r0 x0 + r1 x1 + r2 x2 + … + r n - 2 x n - 2 + ( 3)
S3 … Sr S1 S2 S2 S3 S4 … S r + 1 T , B =[ 其中 A = σ x σ x -1 …σ t] S r S r + 1 S r + 2 … S2 r - 1 因此, 译码的关键是求解 σ( x) , 从而求出错误位置的值 。 系数 矩阵的行列式不为零时, 求解方程, 错误值的个数即为矩阵的 [5 ] 译码流程如图 2 。 秩 ,
S = Y1 ( X1 ) 2 + Y2 ( X2 ) 2 + … + Y r ( X r ) 2 2 S3 = Y1 ( X1 ) 3 + Y2 ( X2 ) 3 + … + Y r ( X r ) 3 S = Y ( X ) 2t + Y ( X ) 2t + …Y ( X ) 2t 2t 1 1 2 2 r r
S j = R( a j ) = C( a j ) + E( a j ) = E( a j ) =
t
∑Y X
i i =1
li
= ( 5)
图2
RS 码译码流程
∑Y a
i i =1
li
2
RS 码在 QR 码中的编码过程
l 2, …, r) , 令 Xi = X i ( i = 1, 于是有 S1 = Y1 X1 + Y2 X2 + … + Yr Xr 。 同理用 a 的各次幂, 即式( 1 ) 的各个零点, 对差错 多项式( 5 ) 求值, 可得到 2 t 个方程的方程组。 S1 = Y1 X1 + Y2 X2 + … + Y r X r
∑Y X
i i =1
li
( 4)
l 其中 Y i ∈ GF( q) ,X i 称为错误位置, 说明错误发生在 R( x) n -1 中的第 n - l i ( x 的系数算第一位) 位, 错误值是 Y i 。 j 2, …, 2t) 对 用纠错码生成多项式 g( x) 的各个零点 a ( j = 1, j R( x) 求值, 其结果定义为伴随多项式 Sj 。 因为 C( a ) = 0, 故 t
0
引言
QR 二维条码又称为快速响应矩阵码, 相比于一维条码 它具有数据量大、 不依赖数据库、 应用方便、 纠错能力强等特 [1 ] 点 。也正因为二维条码的这些特点, 使二维条码比一维条 码的编码与解码技术更为复杂 。本文在对国内外的二维条码 进行对比研究之后, 论述了 QR 二维条码的编码与解码原理, Solomon 的原理。 并详尽阐述了二维码中所应用的 ReedQR 码如图 1 所示, 由正方形模块组成的一个正方形矩阵 列构成, 它包括编码区、 功能图形和空白区三部分 。编码区是 由文本信息转化的二进制码组成, 它包括格式信息、 版本信 息、 数据和纠错码字。功能图形包括位置探测图形 、 位置探测 定位图形和校正图形。 图形分隔符、
r n -1 x n -1
n -1 + e n - 2 x n - 2 + … + e1 x1 + e0 。 错误多项式 E( x) = e n -1 x 如果含有 r( 0 ≤ r ≤ t) 个错误, 它们发生在未知错误位置 i1 , i2 , …, i r 上, 则 t
E ( x ) = Y t X l t + Y t - 1 X l t - 1 + … + Y 1 X l1 =
第 31 卷增刊 1 2011 年 6 月 文章编号: 1001 - 9081 ( 2011 ) S1 - 0040 - 03
计算机应用 Journal of Computer Applications
Vol. 31 Suppl. 1 June 2011
QR 码纠错码原理及实现
冯汉禄, 黄颖为, 牛晓娇, 钱银超
摘
Principle and implementation of error correcting coding of QR code
FENG Hanlu, HUANG Yingwei, NIU Xiaojiao, QIAN Yinchao
( Faculty of Printing and Packaging Engineering,Xi'an University of Technology, Xi'an Shaanxi 710048,China)
σ t = ( - 1 ) x1 x2 … x t 则式( 8 ) 变为:
r 2 t σ t = 1 + σ1 x + σ2 x + … + σ t x = σ ( x ) =
{
QR 码多项式算法用位的模 2 算法和字节的模 100011101 算 8 8 4 3 这是伽罗华域 2 以 100011101 表示模块多项式: x + x + x + 法, 2 [7 ] x +1 。 数据码字为多项式各项的系数, 第一个数据码字为 最高次项的系数, 第一个纠错码字前的最后一个数据码字是 最低项的系数。 纠错码字是数据码字被纠错码字多项式 g( x) 除得的余 数。 余数的最高次系数为第一个纠错码字, 最低次项系数为最 后个纠错码字, 也是整个块的最后一个码字 。 格式信息是由 5 个数据位和 10 个纠错位组成的一个 15 QR 码中用 BCH( 15 , 5 ) 码纠错, 位序列, 以数据位串为系数的 [6 ] 10 8 G ( x ) = x + x + x5 + x4 + x2 + x + 1 多项式被生成多项式 除, 所得的剩余多项式的系数串追加到系数串上形成 ( 15 , 5 ) BCH 码字符串。 最后通过用 101010000010010 对位串进行 异或运算掩模, 来保证掩模图形和纠错等级的任意组合的格 式信息不全为 0 。 例: 纠错等级 M; 掩模图形参考 101 00101 二进制字符串: x2 + 1 生成多项式: 5 位信息组位长( 15 - 5) : x12 + x10 将次数升 15 位码字总长度, 10 8 5 4 2 2 7 被 G( x) 除后: = ( x + x + x + x + x + x + 1) x + ( x + 6 4 3 2 x +x +x +x ) 把上面的剩余多项式的系数字符串附加至格式信息数据串 00101 + 0011011100 → 001010011011100
