编译原理第4章作业答案
编译原理-第4章 语法分析--习题答案

第4章语法分析习题答案1.判断(1)由于递归下降分析法比较简单,因此它要求文法不必是LL(1)文法。
(× )LL(1)文法。
(× )(3)任何LL(1)文法都是无二义性的。
(√)(4)存在一种算法,能判定任何上下文无关文法是否是LL(1) 文法。
(√)(× )(6)每一个SLR(1)文法都是LR(1)文法。
(√)(7)任何一个LR(1)文法,反之亦然。
(× )(8)由于LALR是在LR(1)基础上的改进方法,所以LALR(× )(9)所有LR分析器的总控程序都是一样的,只是分析表各有不同。
(√)(10)算符优先分析法很难完全避免将错误的句子得到正确的归约。
(√)2.文法G[E]:E→E+T|TT→T*F|FF→(E)|i试给出句型(E+F)*i的短语、简单短语、句柄和最左素短语。
答案:画出语法树,得到:短语: (E+F)*i ,(E+F) ,E+F ,F ,i简单短语: F ,i句柄: F最左素短语: E+F3.文法G[S]:S→SdT | TT→T<G | GG→(S) | a试给出句型(SdG)<a的短语、简单短语、句柄和最左素短语。
答案:画出语法树,得到:短语:(SdG)<a 、(SdG) 、SdG 、G 、a简单(直接)短语:G 、a句柄:G最左素短语:SdG4.对文法G[S]提取公共左因子进行改写,判断改写后的文法是否为LL(1)文法。
S→if E then S else SS→if E then SS→otherE→b答案:提取公共左因子;文法改写为:S→if E then S S'|otherS'→else S|E→bLL(1)文法判定:① 文法无左递归② First(S)={if,other}, First(S')={else, }First(E)={b}Follow(S)= Follow(S')={else,#}Follow(E)={then}First(if E then S S')∩First(other)=First(else S)∩First( )=③First(S')∩Follow(S')={else}不为空集故此文法不是LL(1)文法。
编译基础学习知识原理第4章规范标准答案
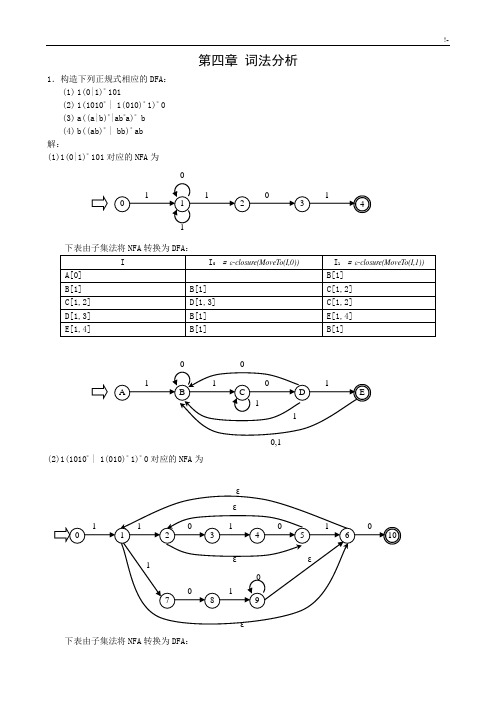
第四章 词法分析1.构造下列正规式相应的DFA :(1) 1(0|1)*101(2) 1(1010* | 1(010)* 1)*(3) a((a|b)*|ab *a)*b(4) b((ab)* | bb)*ab 解:(1)1(0|1)*101对应的NFA 为下表由子集法将NFA 转换为DFA :(2)1(1010* | 1(010)* 1)*0对应的NFA 为下表由子集法将NFA 转换为DFA :(3)a((a|b)*|ab*a)* b (略)(4)b((ab)* | bb)* ab (略)2.已知NFA=({x,y,z},{0,1},M,{x},{z})其中:M(x,0)={z},M(y,0)={x,y},M(z,0)={x,z},M(x,1)={x}, M(y,1)=φ,M(z,1)={y},构造相应的DFA。
解:根据题意有NFA图如下0,1 下表由子集法将NFA转换为DFA:下面将该DFA最小化:(1)首先将它的状态集分成两个子集:P1={A,D,E},P2={B,C,F}(2)区分P2:由于F(F,1)=F(C,1)=E,F(F,0)=F并且F(C,0)=C,所以F,C等价。
由于F(B,0)=F(C,0)=C,F(B,1)=D,F(C,1)=E,而D,E不等价(见下步),从而B与C,F可以区分。
有P21={C,F},P22={B}。
(3)区分P1:由于A,E输入0到终态,而D输入0不到终态,所以D与A,E可以区分,有P11={A,E},P12={D}。
(4)由于F(A,0)=B,F(E,0)=F,而B,F不等价,所以A,E可以区分。
(5)综上所述,DFA可以区分为P={{A},{B},{D},{E},{C,F}}。
所以最小化的DFA如下:3.将图4.16确定化:图4.16解:下表由子集法将NFA转换为DFA:14.把图4.17的(a)和(b)分别确定化和最小化:(a) (b)解: (a):可得图(a1),由于F(A,b)=F(B,b)=C,并且F(A,a)=F(B,a)=B,所以A,B 等价,可将DFA 最小化,即:删除B ,将原来引向B 的引线引向与其等价的状态A ,有图(a2)。
编译原理第4章习题答案

S-> S’ S’->(S)SS’| First( (S)SS’) = { ( } Follow(S)=Follow(S’)= { (, ),$ }
预测分析表
非终结符 S ( S->S’ ) S->S’ $ S->S’
S’
S’->(S)SS’
S’->
S’->
S’->
冲突
仔细分析后,发现该文法 S->S(S)S| 是二义性文法。 二义性文法不可能是LL(1)文法。 例如:( ) ( )
S->aS’ S’->aS’AS’|Ɛ A->+|*
First(S) = First(aS’)={a} First(S’)= First(aS’AS’) ∪ First(Ɛ)= {a} ∪{Ɛ}= {a, Ɛ} First(A) = { +,*}
Follow(S) ={$} 因为 S->aS’,所以把Follow(S)加入到Follow(S’)中。 因为 S’->aS’AS’的第一个S’ ,所以把First(AS’)={+,*}加入到Follow(S’)中。 因为 S’->aS’AS’的第二个S’ ,所以Follow(S)加入到Follow(S’)中。 所以,Follow(S’)= {$, +,*} 对 S’->aS’AS’的A ,当A后面的S’推导出非空时,把First(S’)-{Ɛ}={a}加入到Follow(A)中。 对 S’->aS’AS’的A ,当A后面的S’推导出空时,把Follow(S’)={$,+,*}加入到Follow(A)中。 所以,Follow(A)= {a, +,*,$} 对于S’->aS’AS’|Ɛ,因为First(aS’AS’) ∩Follow(S’)={a} ∩{$,+,*}=空集,所以没有冲突。 对于A->+|*,因为First(+) ∩First(*)={+} ∩{*}=空集,所以没有冲突。 所以该文法是LL(1)文法。
蒋立源编译原理第三版第四章习题与答案.docx

第五章习题5-1设有文法G[S] :S→A/A→aA∣ AS∣/(1)找出部分符号序偶间的简单优先关系。
(2)验证 G[S] 不是简单优先文法。
5-2对于算符文法G[S] :S→E E→ E-T∣ T T→T*F∣F F→ -P∣P P→ (E)∣i(1)找出部分终结符号序偶间的算符优先关系。
(2)验证 G[S] 不是算符优先文法。
5-3 设有文法G′[E] :E→E E→E+T |T1T →T T→T*F|F F→(E)|i11111其相应的简单优先矩阵如题图5-3所示,试给出对符号串(i+i )进行简单优先分析的过程。
题图 5-3 文法 G′ [E] 的简单优先矩阵5-4设有文法G[E]:E→E+T|TT→T*F|FF→(E)|i其相应的算符优先矩阵如题图5-4 所示。
试给出对符号串(i+i )进行算符优先分析的过程。
(i*+)#(○○○○○<<<<=i○○○○>>>>○○○○○○*<<>>>>○○○○○○+<<<>>>○○○○)>>>>○○○○#<<<<题图 5-4文法 G[E] 的算符优先矩阵5-5对于下列的文法,试分别构造识别其全部可归前缀的DFA和 LR(0) 分析表,并判断哪些是LR(0) 文法。
(1)S →aSb∣ aSc∣ ab(2)S →aSSb∣ aSSS∣c(3)S →AA→Ab∣ a5-6下列文法是否是SLR(1)文法?若是,构造相应的SLR(1) 分析表,若不是,则阐明其理由。
(1) S →Sab∣ bR R→S∣a(2) S →aSAB∣ BA A→aA∣ B B→ b(3) S →aA∣bB A→cAd∣εB→cBdd∣ε5-7对如下的文法分别构造LR(0) 及 SLR(1) 分析表,并比较两者的异同。
S→cAd∣ b A→ASc∣a5-8对于文法G[S]:S→A A→BA∣εB→ aB∣ b(1)构造 LR(1) 分析表;(2)给出用LR(1)分析表对输入符号串abab 的分析过程。
编译原理课后习题答案ch4

注意:本题应该理解为对图(a)进行确定化和对图(b)进行最小化。提供的答案没有对图(a)确 定化。
盛威网()专业的计算机学习网站 14
《编译原理》课后习题答案第四章
第5题 构造一个 DFA,它接收 Σ={0,1}上所有满足如下条件的字符串:每个 1 都有 0 直接跟在 右边。并给出该语言的正规式。 答案: 按题意相应的正规表达式是(0*10)*0*, 或 0*(0 | 10)*0* 构造相应的 DFA, 首先构造 NFA 为
7
《编译原理》课后习题答案第四章
注意:这个题,也可以这样构造 NFA(用最少的ε,但注意不能出错) :
a,b 0 a a 2 a,b 1 a b 3
盛威网()专业的计算机学习网站
8
《编译原理》课后习题答 ε X b A ε F B a C b ε b G b H ε ε D ε E a I b Y
除 X,A 外,重新命名其他状态,令 AB 为 B、AC 为 C、ABY 为 D,因为 D 含有 Y(NFA 的终态),所以 D 为终态。 . X A B C D DFA 的状态图:: 0 . A C A C 1 A B B D B
(2)先构造 NFA: 0 ε X 1 A ε ε F B 1 C 1 0 ε 0 D 1 E 1 0 ε 用子集法将 NFA 确定化 ε X T0=X A T1= ABFL Y CG T2= Y T3= CGJ DH K T4= DH EI T5= ABFKL T6= ABEFIL EJY T7= ABEFGJLY EHY CGK T8= ABEFHLY EY CGI T9= ABCFGJKL DHY T10= ABEFLY T11= CGJI DHJ T12= DHY T13= DHJ EIK T14= ABEFIKL ABEFIKL EJY CG DHJ ?正确 DHJG EI EIK DHY EY DHJ CG K ABEFLY CGJI DHY CGK ABEFHLY ABCFGJKL EY CGI ABEFGJLY EHY CGK ABEFIL Y EJY CG CG DH ABFKL EI DH K Y CGJ ABFL Y CG X A 0 1 1 ε L ε K ε J 0 Y
编译原理第四章参考答案

编译原理第四章参考答案1.1考虑下⾯⽂法G1S->a|^|(T)T->T,S|S消去G1的左递归。
然后对每个⾮终结符,写出不带回溯的递归⼦程序。
答::(1)消除左递归:S->a|^|(T)T-> ST’T’->,S T’|ε(2)first(S)={ a , ^ , ( } first(T)= { a , ^ , ( } first(T’)={ , ε}First(a)={a},First(^)={^},First( (T) )={ ( }S的所有候选的⾸符集不相交First(,ST’)={,} ,First(ε)={ε},T’的所有候选的⾸符集不相交Follow(T’)=Follow(T)={ )}first(T’)∩Follow(T’)={}所以改造后的⽂法为LL(1)⽂法。
不带回溯的递归⼦程序如下:S( ){if (lookahead=’a’) advance;Else if(lookahead=’^’) advance;Else if(lookahead=’(’){advance;T();if(lookahead=’)’) advance;else error();}Else error();}T( ){S( );T’( ):}T’->,S T’|εT’( ){if (lookahead=’,’){advance;T’();}Else if(lookahead=Follow(T’)) advance;Else error;}有⽂法G(S):S→S+aF|aF|+aFF→*aF|*a(1)改写⽂法为等价⽂法G[S’],消除⽂法的左递归和回溯(2)构造G[S’]相应的FIRST和FOLLOW集合;(3)构造G[S’]的预测分析表,以此说明它是否为LL(1)⽂法。
(4)如果是LL(1)⽂法,请给出句⼦a*a+a*a*a的预测分析过程该⽂法为LL(1)⽂法,因为它的预测分析表中⽆冲突项。
编译原理 龙书答案

第四章部分习题解答Aho:《编译原理技术与工具》书中习题(Aho)4.1 考虑文法S → ( L ) | aL → L, S | Sa)列出终结符、非终结符和开始符号解:终结符:(、)、a、,非终结符:S、L开始符号:Sb)给出下列句子的语法树i)(a, a)ii)(a, (a, a))iii)(a, ((a, a), (a, a)))c)构造b)中句子的最左推导i)S(L)(L, S) (S, S) (a, S) (a, a)ii)S(L)(L, S) (S, S) (a, S) (a, (L)) (a, (L, S)) (a, (S, S)) (a, (a, S) (a, (a, a))iii)S(L)(L, S) (S, S) (a, S) (a, (L)) (a, (L, S)) (a, (S, S)) (a, ((L), S)) (a, ((L, S), S)) (a, ((S, S), S)) (a, ((a, S), S))(a, ((a, a), S)) (a, ((a, a), (L))) (a, ((a, a), (L, S))) (a, ((a, a), (S, S))) (a, ((a, a), (a, S))) (a, ((a, a), (a, a)))d)构造b)中句子的最右推导i)S(L)(L, S) (L, a) (S, a) (a, a)ii)S(L)(L, S) (L, (L)) (L, (L, S)) (L, (L, a)) (L, (S, a)) (L, (a, a)) (S, (a, a)) (a, (a, a))iii)S(L)(L, S) (L, (L)) (L, (L, S)) (L, (L, (L))) (L, (L, (L, S))) (L, (L, (L, a))) (L, (L, (S, a))) (L, (L, (a, a))) (L, (S,(a, a))) (L, ((L), (a, a))) (L, ((L, S), (a, a))) (L, ((L, a), (a,a))) (L, ((S, a), (a, a))) (L, ((a, a), (S, S))) (S, ((a, a), (a,a))) (a, ((a, a), (a, a)))e)该文法产生的语言是什么解:设该文法产生语言(符号串集合)L,则L = { (A1, A2, …, A n) | n是任意正整数,A i=a,或A i∈L,i是1~n之间的整数}(Aho)4.2考虑文法S→aSbS | bSaS |a)为句子构造两个不同的最左推导,以证明它是二义性的S aSbS abS abaSbS ababS ababS aSbS abSaSbS abaSbS ababS ababb)构造abab对应的最右推导S aSbS aSbaSbS aSbaSb aSbab ababS aSbS aSb abSaSb abSab ababc)构造abab对应语法树d)该文法产生什么样的语言?解:生成的语言:a、b个数相等的a、b串的集合(Aho)4.3 考虑文法bexpr→bexpr or bterm | btermbterm→bterm and bfactor | bfactorbfactor→not bfactor | ( bexpr ) | true | falsea)试为句子not ( true or false)构造分析树解:b)试证明该文法产生所有布尔表达式证明:一、首先证明文法产生的所有符号串都是布尔表达式变换命题形式——以bexpr、bterm、bfactor开始的推导得到的所有符号串都是布尔表达式最短的推导过程得到true、false,显然成立假定对步数小于n的推导命题都成立考虑步数等于n 的推导,其开始推导步骤必为以下情况之一bexpr bexpr or btermbexpr btermbterm bterm and bfactorbexpr bfactorbfactor not bfactorbfactor ( bexpr )而后继推导的步数显然<n,因此由归纳假设,第二步句型中的NT推导出的串均为布尔表达式,这些布尔表达式经过or、and、not运算或加括号,得到的仍是布尔表达式因此命题一得证。
编译原理第4章答案

第四章 词法分析1.构造下列正规式相应的DFA :(1) 1(0|1)*101(2) 1(1010*| 1(010)*1)*0 (3) a((a|b)*|ab *a)*b (4) b((ab)*| bb)*ab 解:(1)1(0|1)*101对应的NFA 为下表由子集法将NFA 转换为DFA :(2)1(1010*| 1(010)*1)*0对应的NFA 为 10,1下表由子集法将NFA转换为DFA:(3)a((a|b)*|ab *a)*b (略) (4)b((ab)*| bb)*ab (略)2.已知NFA=({x,y,z},{0,1},M,{x},{z})其中:M(x,0)={z},M(y,0)={x,y},M(z,0)={x,z},M(x,1)={x}, M(y,1)=φ,M(z,1)={y},构造相应的DFA 。
解:根据题意有NFA 图如下下表由子集法将NFA 转换为DFA :0,1下面将该DFA最小化:(1)首先将它的状态集分成两个子集:P1={A,D,E},P2={B,C,F}(2)区分P2:由于F(F,1)=F(C,1)=E,F(F,0)=F并且F(C,0)=C,所以F,C等价。
由于F(B,0)=F(C,0)=C,F(B,1)=D,F(C,1)=E,而D,E不等价(见下步),从而B与C,F可以区分。
有P21={C,F},P22={B}。
(3)区分P1:由于A,E输入0到终态,而D输入0不到终态,所以D与A,E可以区分,有P11={A,E},P12={D}。
(4)由于F(A,0)=B,F(E,0)=F,而B,F不等价,所以A,E可以区分。
(5)综上所述,DFA可以区分为P={{A},{B},{D},{E},{C,F}}。
所以最小化的DFA如下:3.将图确定化:1101111解:下表由子集法将NFA 转换为DFA :4.把图的(a)和(b)分别确定化和最小化:(a) (b)解: (a):下表由子集法将NFA 转换为DFA :0,1a可得图(a1),由于F(A,b)=F(B,b)=C,并且F(A,a)=F(B,a)=B,所以A,B 等价,可将DFA 最小化,即:删除B ,将原来引向B 的引线引向与其等价的状态A ,有图(a2)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
编译原理第4章作业
答案
本页仅作为文档封面,使用时可以删除
This document is for reference only-rar21year.March
第四章
习题4.2.1:考虑上下文无关文法: S->S S +|S S *|a 以及串aa + a*
(1)给出这个串的一个最左推导
S -> S S *
-> S S + S *
-> a S + S *
-> a a + S *
-> aa + a*
(3)给出这个串的一棵语法分析树
习题4.3.1:下面是一个只包含符号a和b的正则表达式的文法。
它使用+替代表示并运算的符号|,以避免和文法中作为元符号使用的竖线相混淆:
rexpr→ rexpr + rterm | rterm
rterm→rterm rfactor | rfactor
rfactor→ rfactor * | rprimary
rprimary→a | b
1)对这个文法提取公因子
2)提取公因子的变换使这个文法适用于自顶向下的语法分析技术吗?
3)提取公因子之后,原文法中消除左递归
4)得到的文法适用于自顶向下的语法分析吗?
解
1)提取左公因子之后的文法变为
rexpr→ rexpr + rterm | rterm
rterm→rterm rfactor | rfactor
rfactor→ rfactor * | rprimary
rprimary→a | b
2)不可以,文法中存在左递归,而自顶向下技术不适合左递归文法
3)消除左递归后的文法
rexpr -> rterm rexpr’
rexpr’-> + rterm rexpr’|ε
rterm-> rfactor rterm’
rterm’-> rfactor rterm’|ε
rfactor-> rprimay rfactor’
rfactor’-> *rfactor’|ε
rprimary-> a | b
4)该文法无左递归,适合于自顶向下的语法分析
习题4.4.1:为下面的每一个文法设计一个预测分析器,并给出预测分析表。
可能要先对文法进行提取左公因子或消除左递归
(3)S->S(S)S|ε
(5)S->(L)|a L->L,S|S
解
(3)
①消除该文法的左递归后得到文法
S->S’
S’->(S)SS’|ε
②计算FIRST和FOLLOW集合
FIRST(S)={(,ε} FOLLOW(S)={),$}
FIRST(S’)={(,ε} FOLLOW(S’)={),$}
③构建预测分析表
①消除该文法的左递归得到文法 S->(L)|a
L->SL’
L’->,SL’|ε
②计算FIRST与FOLLOW集合
FIRST(S)={(,a} FOLLOW(S)={ ),, ,$}
FIRST(L)={(,a} FOLLOW(L)={ ) }
FIRST(L’)={,,ε} FOLLOW(L’)={ ) }
③构建预测分析表
习题4.4.4 计算练习4.2.2的文法的FIRST和FOLLOW集合3)S S(S)S|ε
5)S→(L)|a,L→L,S|S
解:
3)FIRST(S)={ ,( } FOLLOW(S)={ (,),$ }
5)FIRST(S)={ (,a } FOLLOW(S)={ ),,,$ }
FIRST(L)={ (,a } FOLLOW(L)={ ),, }
习题4.6.2为练习4.2.1中的增广文法构造SLR项集,计算这些项集的GOTO 函数,给出这个文法的语法分析表。
这个文法是SLR文法吗?
S SS+|SS*|a
解:
①构造该文法的增广文法如下
S’->S
S->SS+
S->SS*
S->a
②构造该文法的LR(0)项集如下
③GOTO函数如下
GOTO(I0,S)=I1 GOTO(I0,a)=I2
GOTO(I1,S)=I3 GOTO(I1,a)=I2 GOTO(I1,$)=acc
GOTO(I3,S)=I3 GOTO(I3,+)=I4 GOTO(I3,*)=I5 GOTO(I3,a)=I2 ④构造该文法的语法分析表
注:FOLLOW(S’)=FOLLOW(S)={+,*,a,$}
这个文法是SLR文法,因为语法分析表中没有重复的条目
习题4.6.6说明下面文法
S→SA|A
A→a
是SLR(1)的,而不是LL(1)的。
证明:
1)可以求得FIRST(SA)=FIRST(A)={a},故该文法不是LL(1)文法
2)构造该文法的增广文法的语法分析表如下
①构造增广文法
S’->S
S->SA
S->A
A->a
②构造LR(0)项集族
③GOTO函数如下
GOTO(I0,S)=I1 GOTO(I0,A)=I2 GOTO(I0,a)=I3
GOTO(I1,A)=I4 GOTO(I1,a)=I3 GOTO(I1,$)=acc
④构建语法分析表如下(FOLLOW(A)=FOLLOW(S)={a,$})
可以看到该语法分析表中没有重复的条目故该文法是SLR(1)文法
习题4.7.4说明下面的文法
S->Aa|bAc|dc|bda
A->d
是LALR(1)的,但不是SLR(1)的证明:
1、构造该文法的SLR(1)语法分析表
①构造增广文法
S’->S
S->Aa
S->bAc
S->dc
S->bda
A->d
②构造LR(0)项集族
③GOTO函数
GOTO(I0,S)=I1 GOTO(I0,A)=I2 GOTO(I0,b)=I3 GOTO(I0,d)=I4 GOTO(I1,$)=acc GOTO(I2,a)=I5 GOTO(I3,A)=I6 GOTO(I3,d)=I7 GOTO(I4,c)=I8 GOTO(I6,c)=I9 GOTO(I7,a)=I10
④构建SLR语法分析表如下(FOLLOW(A)={a,c})
可以看到在图中存在二义性的条目,故该文法不是SLR(1)文法
2、构造该文法的LALR(1)语法分析表
①构造该增广文法的LR(1)项集族如下
②项集合并:没有可以合并的项集
③GOTO函数
GOTO(I0,S)=I1 GOTO(I0,A)=I2 GOTO(I0,b)=I3 GOTO(I0,d)=I4 GOTO(I1,$)=acc GOTO(I2,a)=I5 GOTO(I3,A)=I6 GOTO(I3,d)=I7 GOTO(I4,c)=I8 GOTO(I6,c)=I9 GOTO(I7,a)=I10
④构造LALR(1)分析表如下
可见该分析表中不存在二义性的条目,故该文法是LALR(1)文法
习题4.7.5说明下面的文法
S->Aa|bAc|Bc|bBa
A->d
B->d
是LR(1)的,但不是LALR(1)的
证明:
1、构造该文法的LR(1)语法分析表
①构造该文法的增广文法
S’->S
S->Aa
S->bAc
S->Bc
S->bBa
A->d
B->d
②构造该增广文法的LR(1)项集族如下
②项集合并:没有可以合并的项集 ③GOTO 函数
GOTO(I0,S)=I1 GOTO(I0,A)=I2 GOTO(I0,b)=I3 GOTO(I0,B)=I4 GOTO(I0,d)=I5
GOTO(I1,$)=acc GOTO(I2,a)=I6 GOTO(I3,A)=I7 GOTO(I3,B)=I8 GOTO(I3,d)=I9
GOTO(I4,c)=I10 GOTO(I7,c)=I11 GOTO(I8,a)=I12 ④构造LR(1)分析表如下
可见该分析表中不存在二义性的条目,故该文法是LR(1)文法
2、 构造该文法的LALR(1)语法分析表
①合并LR(1)项集族
I5和I9可以合并为
②构造LALR(1)语法分析表如下
可见该语法分析表中存在有二义性的条目,故该文法不是LALR(1)文法。
