中科大_盲信号处理_第3章1
现代信号处理盲

SCA利用信号的稀疏性进行盲信号处理,通过寻找观测信号中的稀疏 成分来恢复源信号。
非负矩阵分解(NMF)
NMF是一种基于非负性约束的矩阵分解方法,可用于盲信号处理和特 征提取。
深度学习
近年来,深度学习在盲信号处理领域取得了显著进展,通过训练深度 神经网络模型来实现盲信号处理和源信号分离。
01
信号处理基础
信号定义与分类
信号定义
信号是传递信息的物理量,可以 是电信号、光信号、声信号等。 在信号处理中,主要研究电信号 的处理。
信号分类
根据信号的性质和特征,信号可 分为模拟信号和数字信号、连续 时间信号和离散时间信号、确定 性信号和随机信号等。
线性时不变系统
线性系统
线性时不变系统的性质
线性系统是指系统的输出与输入之间满 足线性叠加原理,即输出的总响应等于 各输入单独作用时产生的响应之和。
线性时不变系统具有稳定性、因果性、 可逆性、可交换性等性质,这些性质 在信号处理中具有重要意义。
时不变系统
时不变系统是指系统特性不随时间变 化,即输入信号的时移不会导致输出 信号的时移。
频域分析与变换
REPORT
THANKS
感谢观看
CATALOG
DATE
ANALYSIS
SUMMAR Y
信号失真比(SDR) 反映输出信号相对于原始信号的失真程度,值越 高表示分离效果越佳。
3
源信号与估计信号的相关系数
通过计算源信号与估计信号之间的相关系数,评 估分离算法对源信号的恢复程度。
计算复杂度评估
算法运算量
统计算法在执行过程中所需的乘法、加法等基本运算次数,以评 估其计算复杂度。
算法执行时间
盲信号处理ch2-3

2004-10-632004-10-62004-10-6Where is the phase?Channel 12004-10-6channel 22004-10-6channel 32004-10-6Same Amplitude2004-10-6Different Phasechannel 12004-10-6Channel 22004-10-6channel 32004-10-6Same Auto-correlation2004-10-6Different TOM(Channel1)2004-10-6Different TOM(Channel 2)2004-10-6Different TOM(Channel 3)2004-10-6Amplitude of TOM2004-10-6Phase of TOM (Channel 1)2004-10-6Phase of TOM (Wavelet2)2004-10-6Phase of TOM (Wavelet3)2004-10-6Same cross-correlationDifferent TOCMTOCM of x1 and x2TOCM of y1 and y22004-10-6222004-10-6232004-10-6242004-10-6252004-10-6262004-10-6高阶统计量和二阶统计量对于非高斯信号,仅用二阶统计量来描述是不够的,因为其高阶统计量并不为零。
信道估计中,信道的二阶统计量丢失了相位信息,而高阶统计量保留了相位信息。
高阶统计量高阶矩高阶累计量高阶矩谱高阶累计量谱2004-10-62004-10-6312004-10-632高阶矩和高阶累计量关系高阶矩2004-10-634 2004-10-6352004-10-62004-10-6372004-10-6确定性信号的高阶谱2004-10-62004-10-6422004-10-6432004-10-6442004-10-645累计量投影性质2004-10-647三阶累计量支撑域信道的阶数决定其高阶累计量的支撑域。
中科大_盲信号处理_第3章1

H (y ) H (x) log | det( W ) |
故有
(3-8)
I (y ) H ( yi ) H (x) log | det( W ) |
i 1
N
(3-9)
H (x) 与 W 的选择无关,故 I (y ) 的极小化等价于
N min I (y ) min H ( yi ) log | det( W ) | W W i 1
(3-6)
ˆ ,s ˆ 是真实 s 0 ˆ) S , 盲源分离的目标就是在 “辨识空间 S ” 中找到一个解 (H 则认为该 s
的一个“好”的估计;或者等价地说: (1)从混合信号中恢复出了“源信号的波形”; (2)分离出的信号与源信号之间有“波形保持关系”。 注:由于盲源分离问题中存在着固有的 “幅度的不确定性”,因此通常假设 s 0 的每个 分量的方差为 1。 三.ICA 解的存在性 (3-3)式的信号模型中,应该需要什么样的条件才能保证找到的解在子空间 S 中?关 于这个问题,有如下的存在性定理。 定理:对于(3-3)式的信号模型,如果 (1)混合矩阵 H 是列满秩的,即 rank(H ) N (2)s 零均值的平稳随机向量过程,各个分量之间相互统计独立,且其分量信 号中至多有一个服从高斯分布 则存在解混矩阵 W ,使得 y Wx WHs 的各个分量相互独立,且混合-分离复合 矩阵 C WH PD 。 几点说明: 条件(1)意味着 M N ,即观测到的混合分量信号的个数不少于待分离的源信 号的个数,即混合系统是超定系统( M N )或正定系统( M N )。 通过一些降维处理,总可以将“超定系统”转换为“正定系统”,所以通常在 讨论问题时,都假设 M N ,此时 H 是一个非奇异矩阵。 在条件(2)中,如果 s 中高斯分布的分量个数多于一个时,则只能将非高斯的分 离信号从混合信号中分离出来。
盲信号处理

盲信号处理简介盲信号处理是一种信号处理技术,用于从未知信号中提取有用的信息,而无需先对信号进行先验模型假设或知识。
它在许多领域中都有广泛的应用,包括通信、图像处理和信号分析等。
盲信号处理的基本原理盲信号处理的基本原理是通过对未知信号进行适当的变换,将其转化为已知的形式,从而可以利用已有的信号处理技术进行进一步分析或处理。
常用的盲信号处理方法包括独立成分分析(ICA)、盲源分离(BSS)和盲降噪等。
独立成分分析(ICA)独立成分分析是一种用于从多个相互混合的信号中恢复原始信号的方法。
它基于统计模型假设,将混合信号看作多个相互独立成分的线性加权和。
通过寻找一个线性变换,使得变换后的信号趋于相互独立,从而可以分离出原始信号。
ICA广泛应用于语音分离、图像分离和脑电图分析等领域。
在语音分离中,ICA可以将多个说话者的混合音频信号分离出来,实现单独的语音信号提取。
盲源分离(BSS)盲源分离是一种用于从混合信号中分离出各个源信号的方法。
与ICA类似,盲源分离也是通过对混合信号进行适当的变换,使得各个源信号能够被分离出来。
不同的是,盲源分离不需要假设源信号之间的独立性,只需要假设它们之间的统计特性不同。
盲源分离广泛应用于音频信号处理、图像分析和信号源检测等领域。
在音频信号处理中,盲源分离可以将多个乐器的混音音频信号分离出来,实现对每个乐器的单独处理。
盲降噪盲降噪是一种用于从含噪信号中提取出原始信号的方法。
它常用于信号增强和去噪等应用场景。
盲降噪不需要事先知道噪声的统计特性,而是通过估计信号和噪声之间的相关性,将噪声部分从含噪信号中减去,从而得到清晰的原始信号。
盲降噪主要应用于语音识别、图像增强和音频修复等领域。
在语音识别中,盲降噪可以去除背景噪声,提高语音识别的准确率。
盲信号处理的应用盲信号处理在许多领域中都有广泛的应用。
通信在通信领域,盲信号处理可以用于信道均衡和多用户检测等。
通过对接收到的信号进行盲源分离或盲降噪,可以提高信号的质量和可靠性,从而改善通信系统的性能。
盲信号总结

盲分离研究背景与数学模型简介:盲信号分离是当前信号处理领域最热门的技术之一。
由于其重要的理论价值和广泛的应用前景 ,盲信号分离在近 20 年引起了广泛的重视和研究。
盲信号分离起源于鸡尾酒会议问题 ,即在很多人同时说话的情况下(通常包含噪声),怎样从多个声音采集设备(如麦克风)采集到的声音信号中分离出所需要的各个说话者的声音?在这个过程中,各个信号源未知,信号混叠参数即传输信道的先验知识也未知,因此我们称这个过程是“盲”的。
目前,以盲信号分离为核心的盲信号处理技术已经成为重要的研究课题,并在许多领域,特别是在语音信号分离与识别、生物信号(如脑电图、心电图)处理、雷达、声纳、遥感、通信系统、噪声控制等领域,吸引了大量的研究和重视。
盲信号分离:是指在不知道源信号和传输信道特性的情况下,从一个传感器阵列的输出信号(也叫观测信号,混叠信号)中分离或估计出源信号的波形。
目标是如何最大化分离信号的独立性。
观测数据:是一组传感器的输出,其中每个传感器接收到的是源信号的不同混合。
源信号混合方式:有线性和非线性两种方式。
当混叠模型为非线性时,一般很难从混叠数据中恢复源信号,除非对信号和混叠模型有进一步的先验知识。
线性模型有三种:(1)线性瞬时混叠(2)延迟无回声混叠(3)回声混叠1,线性瞬时混叠模型:目前主要采用的工具是稀疏成分分析。
2,延迟无回声混叠模型:即每个传感器仅接收到每个源一次。
由于传输距离的远近及传输介质的影响,源信号到达每个传感器的时刻可能并不是同时的。
3,回声混叠:各个传感器不仅直接接收到每个源信号,而且还接收到每个源信号的回声信号。
根据混叠方式对盲信号分离进行分类:如果根据传感器个数M 和源信号个数N 来分类,则把M > N称为超定模型,M = N为适定模型,M < N称为欠定模型。
欠定模型比适定模型和超定模型更难求解。
对适定或者超定模型,只要能够估计出混叠矩阵,就能恢复源信号。
●按照未知信号源的混合形式,可以将盲处理分为线性混合和非线性混合两种类型,其中线性混合包括瞬时混合和卷积混合。
中国科技大学数字信号处理2复习总结资料

有关通知考试时间:2015-12-30(星期三)下午3:00---5:00地点:3B215教室第〇章绪论主要掌握有关的基本基本概念:数字信号,数字信号处理,现代数字信号处理的主要内容,DSP应用实例与面临的挑战。
➢数字信号:时间和幅度均离散➢数字信号处理:以一定目的通过数字运算的方式将数字信号从一种形式转换为另一种形式➢数字信号处理(I):数字滤波和数字谱分析理论和算法---(确定信号)➢现代数字信号处理:自适应数字滤波和功率谱估计理论和算法---(非确定信号)➢应用实例:视听数字化(CD,MP3,数字VIDEO等),数字广播,多媒体技术等➢挑战:信号压缩、自适应信号处理---非平稳时变信号的处理、分类和识别第一章自适应滤波引言一线性滤波概念理解滤波器的概念及线性滤波、最优滤波、维纳滤波、卡尔曼滤波的概念➢滤波器:一个器件(硬件或软件),它对混有噪声的数据序列过滤或估计,达到提取有用信号的目的。
●滤波:使用小于等于t的数据=> t时刻有用信息(因果)●平滑:使用小于等于t和大于等于t的数据=>t时刻有用信号(非因果)τ>)时刻有用信息(因果)●预测:使用小于等于t的数据=>t+τ(0➢线性滤波:滤波器的输入(被滤波,平滑,预测的输出量)是其输入数据的线性加权。
➢最优滤波:指在已知输入信号的某些统计特性的条件下,滤波的结果是有用信号(被估计量,需提取的量)按某一准则的最优估计➢维纳滤波:在信号平稳,已知统计特性的先验知识下,采用最小均方误差准则的线性最优滤波➢卡尔曼滤波:信号非平稳,已知状态和观察方程的先验知识下,采用最小均方误差准则的线性最优滤波➢自适应滤波:当滤波器的系数或参数可随新的数据获取而按某一预定准则而变化时,称之为自适应滤波二维纳滤波(Weiner Filtering)掌握:维纳滤波问题, Weiner-Hopf方程,FIR维纳滤波计算及其最小均方误差计算方法,掌握正交原理,去相关滤波的概念, 了解最优滤波与一般线性滤波的比较。
盲信号处理ch1-1

ICA原理
尽管混合矩阵 A 未知,但假设其可逆
s1(t) = w11x1(t) + w12 x2 (t) + w13x3 (t) s2 (t) = w21x1(t) + w22 x2 (t) + w23x3 (t) s3 (t) = w31x1(t) + w32 x2 (t) + w33x3 (t)
10
图象重构
9
最近邻 插值
4幅图 象重构
双线性 插值
图c去 模糊
资料来源
Profs. Juha Karhunen and Erkki Oja at the Helsinki University of Technology http://www.cis.hut.fi/projects/ica/book/
应用领域
石油勘探(地震波场分离) 通信信号处理(多用户检测) 语音分离 生物信号分离 经济数据分析 图象分离 …..
脑磁信号分离
8
Event-related potentials (ERP)
和一个特定事件的相关联的脑电波(EEG) 变化
信号重构(Signal Reconstruction)
等价性 需要源信号的概率分布函数(pdf)信息
目标函数
非高斯性 基于高阶统计量的目标函数(Higher order statistics,HOS) 负熵(Negentropy)
等价性 不需要源信号的概率分布函数(pdf)信息
优化算法
梯度法(Gradient) 定点优化(Fixed point methods)
信号处理 傅立叶变换、滤波器组、小波和小波包, 信号稀疏表达
数学表达式为:
盲信号处理
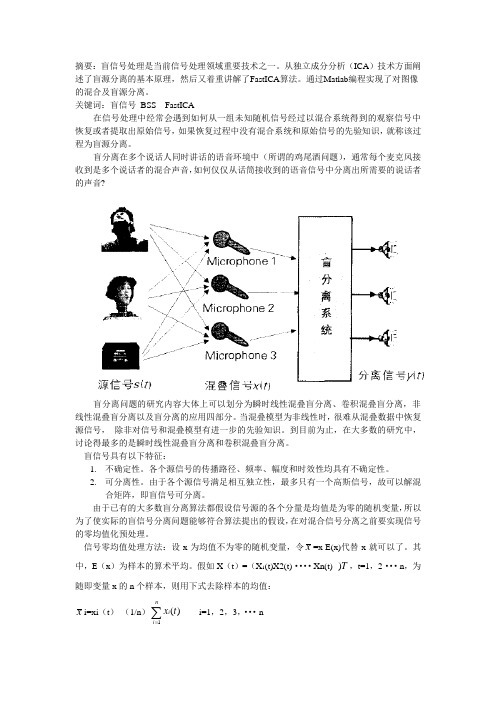
摘要:盲信号处理是当前信号处理领域重要技术之一。
从独立成分分析(ICA )技术方面阐述了盲源分离的基本原理,然后又着重讲解了FastICA 算法。
通过Matlab 编程实现了对图像的混合及盲源分离。
关键词:盲信号 BSS FastICA在信号处理中经常会遇到如何从一组未知随机信号经过以混合系统得到的观察信号中恢复或者提取出原始信号,如果恢复过程中没有混合系统和原始信号的先验知识,就称该过程为盲源分离。
盲分离在多个说话人同时讲话的语音环境中(所谓的鸡尾酒问题),通常每个麦克风接收到是多个说话者的混合声音,如何仅仅从话筒接收到的语音信号中分离出所需要的说话者的声音?盲分离问题的研究内容大体上可以划分为瞬时线性混叠盲分离、卷积混叠盲分离,非线性混叠盲分离以及盲分离的应用四部分。
当混叠模型为非线性时,很难从混叠数据中恢复源信号, 除非对信号和混叠模型有进一步的先验知识。
到目前为止,在大多数的研究中,讨论得最多的是瞬时线性混叠盲分离和卷积混叠盲分离。
盲信号具有以下特征:1. 不确定性。
各个源信号的传播路径、频率、幅度和时效性均具有不确定性。
2. 可分离性。
由于各个源信号满足相互独立性,最多只有一个高斯信号,故可以解混合矩阵,即盲信号可分离。
由于已有的大多数盲分离算法都假设信号源的各个分量是均值是为零的随机变量,所以为了使实际的盲信号分离问题能够符合算法提出的假设,在对混合信号分离之前要实现信号的零均值化预处理。
信号零均值处理方法:设x 为均值不为零的随机变量,令x =x-E(x)代替x 就可以了。
其中,E (x )为样本的算术平均。
假如X (t )=(X 1(t)X2(t)····Xn(t) T ),t=1,2···n ,为随即变量x 的n 个样本,则用下式去除样本的均值:x i=xi (t )-(1/n ))(1∑=ni i t x i=1,2,3,···n另外在实际中,信号在传输接收中混合信号的各个分量之间难免有一些相关成分,这时零均值x 的协方根矩阵}{T xx E Rxx 不是对角阵。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
( f Px ) ( f x ) ;
2. ( f x ) 的值与随机向量 x 各个分量的绝对幅度无关, 即对任意的满秩对角矩阵 D 有
( f Dx ) ( f x ) ;
3. 若随机向量 x 的各个分量统计独立,则对于任意的可逆矩阵 A 有: ( f x ) ( f Ax ) ; 4. 若随机向量 x 的各个分量统计独立,当且仅当矩阵 A 存在分解 A PD 时( P 为排 列矩阵, D 为满秩对角矩阵),有: ( f Ax ) ( f x ) 。 可见, 只要找到一个合适的对照函数并对其进行最小化就可以实现随机向量的独立分 量分析,同时也就实行了信号源的分离。 由于随机向量的概率密度函数是未知的,只能通过一定的方法进行估计。因此,除了 满足上述的四个条件外,实际的对照函数还应该便于估计、近似,以及易于进行优化处 理。 二、基于互信息极小化(MMI)代价函数 解混系统 W 的输出为 y Wx ,寻找一个合适的 W 使 y 的各个分量相互独立,就实现 了混合信号的分离。
号“排列顺序不确定性(模糊性)”。 所以,可接受的 M 要满足 M PD ,此时
ˆ PDs 0 s ˆ 的每个分量信号与 s 0 中的某个分量信号的波形相同! 即s
令 S 是“辨识空间 S ”中的一个特定子空间,即
(3-5)
S {H 0 D1P 1 , PDs 0 }
其中 P 为任意的置换矩阵, D 是任意的非奇异的对角矩阵。
(3-2)
H 是 M N 的 常 数 矩 阵 , 其 元 素 为 hij ; s(t ) [ s1 (t ), s2 (t ),, sN (t )]T ,
x(t ) [ x1 (t ), x2 (t ),, xM (t )]T , n(t ) [n1 (t ), n2 (t ),, nM (t )]T 都是零均值的随机向量。
第二节
一些典型的度量独立性的对照函数(代价函数)
一、对照函数(代价函数)的选取原则 记 F { f x , x R M } 为所有的 M 维随机向量的概率密度函数的集合, 则 ICA 问题中的 对照函数 () 为一个 F R 的映射,并且满足下列条件: 1. ( f x ) 的值与随机向量 x 各个分量的排列顺序无关,即对任意的排列矩阵 P 有
只要解混后的向量 y 的各个分量信号相互统计独立,就能实现源信号的盲分离。 关于 ICA 问题的模糊性、存在性等详细分析和描述,请阅读下列的文献:
[1] Cao X. R., Liu R.W., General Approach to Blind source Separation, IEEE Trans. on Signal Processing, 1996, 44(3): 562~571 [2] Comon P., Independent Component Analysis, A New Concept ? Signal Processing, 1994, 36: 287~314 [3] Comon P., Blind Separation of Sources, Part II: Problems Statement. Signal Processing, 1991, 24:11~20 [4] Lang T., Yujiro Inouye, Liu R. W., Waveform-Preserving Blind Estimation of Multiple Independent Sources, IEEE Trans. on Signal Processing, 1993, 41(7): 2461~2470
H 0 s 0 相同输出的 H 和 s 的全体,称为(3-3)式信号模型的“辨识空间”,即 S {(H, s); Hs H 0s 0 }
1
(3-4)
如果 ( H 0 , s 0 ) S , 则对于任意的非奇异矩阵 M , 都有 ( H 0M , Ms 0 ) S 。 这表明, 在只给定 x 的情况下,(3-3)式的解是不唯一的! 2. 解的不确定性 在辨识空间中,什么样的解是 H 0 和 s 0 的“好”的估计呢?或者说,什么样的 M 是 可以接受的? 从实际应用的角度来考虑:
(3-6)
ˆ ,s ˆ 是真实 s 0 ˆ) S , 盲源分离的目标就是在 “辨识空间 S ” 中找到一个解 (H 则认为该 s
的一个“好”的估计;或者等价地说: (1)从混合信号中恢复出了“源信号的波形”; (2)分离出的信号与源信号之间有“波形保持关系”。 注:由于盲源分离问题中存在着固有的 “幅度的不确定性”,因此通常假设 s 0 的每个 分量的方差为 1。 三.ICA 解的存在性 (3-3)式的信号模型中,应该需要什么样的条件才能保证找到的解在子空间 S 中?关 于这个问题,有如下的存在性定理。 定理:对于(3-3)式的信号模型,如果 (1)混合矩阵 H 是列满秩的,即 rank(H ) N (2)s 零均值的平稳随机向量过程,各个分量之间相互统计独立,且其分量信 号中至多有一个服从高斯分布 则存在解混矩阵 W ,使得 y Wx WHs 的各个分量相互独立,且混合-分离复合 矩阵 C WH PD 。 几点说明: 条件(1)意味着 M N ,即观测到的混合分量信号的个数不少于待分离的源信 号的个数,即混合系统是超定系统( M N )或正定系统( M N )。 通过一些降维处理,总可以将“超定系统”转换为“正定系统”,所以通常在 讨论问题时,都假设 M N ,此时 H 是一个非奇异矩阵。 在条件(2)中,如果 s 中高斯分布的分量个数多于一个时,则只能将非高斯的分 离信号从混合信号中分离出来。
在确定了目标函数之后, 需要考虑采用什么样的算法来优化目标函数, 使其达到极值 (极大或极小)。优化目标函数的算法可以分为两大类,即批处理(Batch Processing) 算法和自适应处理(Adaptive Processing)算法。 “批处理算法”的含义是:已经获得了 K 个观测向量 x(0), x(1), , x(i ), , x( K ) ,同时 利用这 K 个观测向量来求出 W 或 U 。而“自适应处理”的含义是:每次只对一个观测向 量 x(i ) 进行处理,得到 W (i ) 或 U(i ) 的估计,而且随着观测向量的不断输入,以迭代方式 更新 W (i ) 或 U(i ) , 即 W (i 1) W (i ) W(i ) 或 U(i 1) U(i ) U(i ) , 直至迭代更新过 程收敛。 本章的后续部分将介绍目标函数的选择以及各种优化实现算法。
H (y ) H (x) log | det( W ) |
故有
(3-8)
I (y ) H ( yi ) H (x) logH (x) 与 W 的选择无关,故 I (y ) 的极小化等价于
N min I (y ) min H ( yi ) log | det( W ) | W W i 1
y 的互信息为:
I (y ) I [ p (y ), p( yi )] H ( yi ) H (y )
i 1 i 1
N
N
(3-7)
I (y ) 0 ,当且仅当 y 中的各个分量互相独立时, I (y ) 0 。据此得到基于“互信息极
小化(Minimization of Mutual Information)”判断独立性的准则及其代价函数。 准则:选择矩阵 W ,使得 I (y ) 最小,即使得式(3-7)所示的代价函数极小。应该注意 到, I (y ) 满足对照函数的四个基本要求。 由于
ˆ, 1)源信号的信息主要是存在于信号的波形中,所以,如果我们得到 s 的一个估计 s
其波形与真实 s 0 的波形相同,对于大多数应用来说,这应该是可以接受的;此时有
ˆ Ds0 , D 是任意的非奇异的对角矩阵。也就是说,s ˆ 相对于 s 0 存在着“幅度不确定性 s
(模糊性)”。
ˆ 的各个分量的排列顺序与 s 0 的各个分量的排列顺序不同,这也应该是 2)如果只是 s ˆ Ps 0 , P 是任意的置换矩阵。也就是说, s ˆ 相对于 s 0 存在着分量信 可接受的;此时有 s
z (t )
Q
W UQ
U
y (t )
H
3-2
二步法求解过程示意图
采用二步求解法时,其第一步“球化(空间白化)”是求出球化矩阵 Q ,使得 z (t ) 的各 个分量的方差为 1,而且互不相关(不是相互独立);第二步“正交变换”是求一个正交矩 阵 U ,使得 y (t ) 的各个分量的方差保持为 1,同时相互独立。注意到,第一步的输出 z (t ) 的各个分量已经满足了独立性对二阶统计特性的要求,所以在第二步求 U 时只要考虑三 阶以上的统计量(通常为三阶和四阶统计量)。 不管是一步求解法还是二步求解法,都需要利用 y (t ) 的各个分量的“相互独立”这一 条件来确定 W 或 U 。因此,在 ICA 求解时,选择合适的度量 y (t ) 的各个分量相互独立程 度的判据(准则)是重要一个环节,这些度量独立性的判据通常称为“对照函数(contrast function)”、“代价函数(cost function)”、或“目标函数(objective function)”。
第三章
独立分量分析(ICA)
第一节 问题描述
一.信号模型 考虑如图 3-1 所示的信号混合系统。
s1
s2
sn
x1
图 3-1
x2
源信号线性瞬时混合示意图
xm
N 个信号源 s1 , s2 , , s N 所发出的信号被 M 个传感器(如天线、麦克风等) 接收后输出 M 个混合信号 x1 , x2 , , xM 。假设不同源信号到达各个传感器的时间 差可以忽略不计,并且传感器的输出是各个源信号的线性瞬时混合,即
四.ICA 问题的求解 为什么只考虑求解W而不考虑求解H呢? 按照求解的步骤,ICA 问题的求解可以分为“一步求解法”和“二步求解法”。 “一步求解法”是直接求解解混矩阵(系统) W ,而“二步求解法”是将解混过程分解 为“球化”和“正交变换”两个步骤来完成,如图 3-2 所示。
