电路分析中回路分析法和割集分析法 ppt课件
割集分析法

i4
2V I
i4 = i1 + i2 = – 0.25 + 0.85 = 0.6A
II
i5 = 3A(已知), i7 = i1 = – 0.25A
以上各式中,u1、u2、u3分别为支路 1、支路 2 和支路 3 的 电压。
电路分析基础——第一部分:2-5
例2-16 电路如图2-37(a),试求ux。
致,则互电导为正,否则为负;
电流输送:is11、is22、is33 。该基本割集上电流源输 送电流的代数和,电流源电流方向与割
集方向相反者为正,否则为负。
ut1、…、uti、…、ut(n-1):在确定基本割集顺序后, 每个基本割集上的树支电压;
电路分析基础——第一部分:2-5
17/23
注意:在用割集分析时,往往把感兴趣的支路选为树支,使其 电压成为直接求解对象。电路中的电压源支路都应尽量选为树 支,因为电压源是已知的,可以减少未知独立变量的个数。
例如:在图(b)中,切割用虚线表
1
2
示,例如切割II使节点1、3与节点2、 I
3
4分为两个分离部分,所切割的支路 G3、G4、G1和电流源支路的集合就 是割集II。
割集的多样性:一个连通图可以有许
II
4
III
1
2
3
多不同的割集,图(b)中就表明了
三种不同的割集。
4
电路分析基础——第一部分:2-5
7/23
电路分析基础——第一部分:2-5
21/23
i2 =
u2 0.5
=
– ut6 – ut5 – ut4 0.5
= – 2(2–2.75+ 0.326) = 0.85A
电路电路分析方法PPT课件

树
树支:构成树的支路
连支:属于G而不属于T的支路
特点
1)对应一个图有很多的树 2)树支的数目是一定的:
bt n 1
连支数: bl b bt b (n 1)
第6页/共48页
回路 (Loop):
L是连通图的一个子图,构成一条闭合路径,并满足: (1)连通(2)每个节点关联2条支路
123 75
支路电流法的特点:
支路法列写的是 KCL和KVL方程, 所以方程列写方便、直观,但 方程数较多,宜于在支路数不多的情况下使用。
第16页/共48页
例1.
I1 7
+ 70V
–
求各支路电流及电压源各自发出的功率。
a
I2
1 +
6V –
11 2
b
解
(1) n–1=1个KCL方程:
I3
节点a:–I1–I2+I3=0
选取独立回路,使理想电流源支路仅仅属于一个回路, 该回路电流即 IS 。
例
R1
R2
RS
+
i1
iS i2
US _
R4
i3
R3
第28页/共48页
与电阻并联的电流源,可做电源等效变换
I
º
IS
转换
R
º
4.受控电源支路的处理
I
+
º
RIS _
R º
对含有受控电源支路的电路,可先把受控源看作独立电源按上述方法 列方程,再将控制量用回路电流表示。
列方程
节点电压法列写的是结点上的KCL方程,独立方 程数为:
(n 1)
与支路电流法相比,方程数减少b-(n-1)个。
大学物理电路分析精品课程 第三章 电路的一般分析方法

I S I4 I1 0
I
1
I3
I2
0
I
4
I3
I5
0
U 4 U S1 U 3 U1 0 U1 U 2 U 0 U 3 U S1 U 5 U S 2 U 2 0
I1R1 U1
I I
2 3
R2 R3
U2 U3
I
4
R4
U4
I 5 R5 U 5
支路电流法(1B法)
1) U 2
2
添加以下方程:
2U 23 2(U 2 U 3 ) 4U 43 4(U 4 U 3 ) U1 U 4
例题3——割集分析法
5 + 19V - 2
I1 +
30V _
4A 1.5I1
4
+ 25V
_
选树如图所示,则只需要对2、4支路 (树支)所决定的基本割集列写方程即可
(5 2 4) I1 (2 4) 4 4 1.5I1 30 25 19
I S
U4 R4
U1 R1
0
UR11
U3 R3
U2 R2
0
U
4
U3
U5
0
R4 R3 R5
3-3 节点法与割集法
一、节点法
1 .方法
任选电路中某一节点为参考节点, 其他节点与此参考节点间的电压称为 “节点电压”。节点法是以节点电压作 为独立变量,对各个独立节点列写KCL 电流方程,得到含(n-1)个变量的(n-1)个 独立电流方程,从而求解电路中待求量。
第三章 电路的一般分析方法
❖重点 1、支路法 2、节点法 3、网孔法
❖难点 1、改 拓扑术语
支路 节点 回路 网孔 基本回路 割集 基本割集
割集分析法

§3-6 割 集 分 析 法一、割集与基本割集1)、割集 割集是支路的集合,它必须满足以下两个条件: (1) 移去该集合中的所有支路,则图被分为两部分。
(2) 当少移去该集合中的任何一条支路,则图仍是连通的。
需要说明的是,在移去支路时,与其相连的结点并不移去。
图G 是一个连通图,如图3-26(a)所示,支路集合{1,5,2}、{1,5,3,6}、{2,5,4,6}均为图G 割集。
将以上割集的支路用虚线表示,分别如图3-26(b)、(c)、(d)所示,不难看出,去掉虚线支路后,各图均被分成了两部分,但是图3-26 图G 及其割集(a)(b)(c)(d)只要少去掉其中的一条虚线支路,图仍然是连通的,故满足割集所要求的条件。
而支路集合{1,5,4,6}、{1,2,3,4,5}不是图G 的割集。
将集合中的支路用虚线表示后如图3-27(a)和(b)所示。
对于图3-27(a)来说,移去支路1、5、4、6后,图虽说被分为两部分(结点①为其中的一部分),但如不移去支路5,图仍被分为两部分;而对于图3-27(b)来说,将支路1、2、3、4、5移去后,图则被分成了三部分,故以上两种支路集合不是割集。
2)、作高斯面确定割集在图G 上作一个高斯面(闭合面),使其包围G 的某些节点,而每条支路只能被闭合面切割一次,去掉与闭合面相切割的支路,图G 将被分为两部分,那么这组支路集合即为图G 的一个割集。
在图G 上画高斯面(闭合面)C 1、C 2、(a)(b)图3-27 非割集说明①②③①②C 3如图3-28所示,对应割集C 1、C 2、C 3的支路集合为{1,5,2}、{1,5,3,6}、{2,5,4,6}。
3)、基本割集基本割集又称单树支割集,即割集中只含一条树支,其余均为连支。
如选支路1、5、3为树支,如图3-29所示,则割集C 1,C 2,C 3为基本割集,基本割集的方向与树支的参考方向一致。
当树选定后,对应的基本割集是唯一确定的。
电路分析电路分析方法PPT课件

+ US1
–
iA
i5 R5
iB
+ –US2
网孔电流是一组彼此独 立无关的变量。
.
− US4+ R4
i4 iC
R6
i6
+− US3
R3 i3 5
例1:试列写下图所示电路的网孔方程组
解:
+ US1
–
Байду номын сангаас
R1
R4
R3I1
R5 R6 I2
IS
(R1 + R3 + R5) I1-R5 I2-R3I3= US1
US2 +–
§2-1 网孔分析法
网孔分析法是以网孔电流为未知量,利用KVL 定律列出方程组,进而求得电路响应的分析方法。
网孔分析法只适用于求解平面电路。
求解量 (未知数):网孔电流
求解量数目(方程数):网孔数 m 列方程依据: KVL定律
网孔电流是一组完备的变量: i1 R1
R2 i2
求出网孔电流,即可方 便地求得各支路电流。
求解量数目(方程数):节点数 n− 1
列方程依据: KCL定律 节点电压是一组完备的变量:
1
i1
i5
G5 2
i3 3
求出节点电压,即可方
G1
i2 G3 i4
便地求得各支路电压。 节点电压是一组彼此独
iS G2
G4
立无关的变量。
.
4
12
[例] 列出图示电路的节点电位方程组。
R3
解:选d点作为参考点,有Vd = 0
+
uo
u–
uo 非线性区
uo
实
UOM
电路分析基础线性电路的一般分析方法精品PPT课件

+
US4 -
R6 i3
+ US1 R2 + R4
im1
-
US3 im2
R3
i5
i2
R5
+
US2 -
UUSS31RR42((iimm21
im3 ) im3)
US3 R5im
R3(im1 im2 ) 2 US 2 R3 (im2
R1im1 im1)
0 0
US 4 R6im3 R4 (im3 im2 ) R2 (im3 im1) 0
网孔电流的方向可任意假定
网孔电流一旦求得,所有支路电 流即可求出
+
US4 -
R6 i3
+ US1
-
R1
i4
im3
i6
i1 R2 + R4
im1
-
US3 im2
R3
i5
i2
R5
+
US2 -
设平面连通电路,有m个网孔, 且每个网孔就是一个独立回路,各网 孔KVL方程相互独立。所以可分别在 m个网孔中利用KVL和支路伏安关系 得到一组以m个网孔电流为变量的方 程。方程个数与待求解变量(即网孔 电流)数目相同,且相互独立。该组 方程就是网孔方程。
线性电路的一般分析方法有支路电流法、网孔分析法、节 点分析法、回路分析法和割集分析法等。这些分析方法都 是建立在基尔霍夫定律、欧姆定律及网络图论的基础上, 它们都能利用系统的方法列出描述电路的方程,进行一般 性的分析。其中网孔分析法和节点分析法列写方程步骤简 单、规律明显、易于掌握,是电路分析中常用的方法。本 章主要讨论这两种分析方法。
①如果电路中电流源两端并有电阻,可利用等效变换,将电 流源等效为电压源。
②如果电流源两端没有并电阻,又可分为两种情况处理
电路分析课件(回路分析法)
节点电压:u1,u2; u1, u2自动满足KVL
(电位单值性) 是一组完备的独立变量。
+ us1 - R1 i1
R3 1
i2 R2
3
i3
2 i5
i4
R5
R4
+
us2
-
电路原理
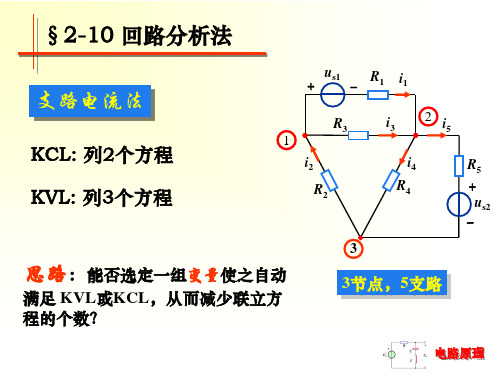
§2-10 回路分析法·回路电流
回路分析法
关键:回路电流
+ us1 - R1 i1
il1 R3
i3
2 i5
回路中独占支路的电流就为该回路的回路电流;
回路共有支路的电流就为流过该支路的回路电流
i4 R4 il3
R5
+ us2
-
叠加。
方向:指定的回路电流参考方向
3
(独立)回路电流数=支路数-节点数+1=支路数-独立节点数
求解3个变量 列写3个独立方程 ?
电路原理
§2-10 回路分析法 ·回路电流 + us1 - R1 i1
+ us1 - R1 i1
il1 R3 1
(R1 R3 )il1 R3il2 us1
i2
il2
R2
R3il1 (R2 R3 R4 )il2 R4il3 0
i3
2 i5
i4 R4 il3
R5
+ us2
-
R4il2 (R4 R5 )il3 us2
3
电路原理
§2-10 回路分析法 ·物理意义
1
KVL:ub 0
(b-n+1)个
i2
il2
R2
i4 R4 il3
R5
+ us2
-
《基本割集的找法》课件

注意事项和技巧
1 各个割集间不能重合
2 尝试不同的顺序
3 练习,练习,再练习
所有的割集都必须是不重叠 的,否则计算就会出现问题。
如果不使用适当的顺序来排 除其他可以组合得到的割集, 您可能无法找到正确的基本 割集。
只有通过练习,才能真正掌 握基本割集的找法。使用各 种图形进行练习,以更好地 理解基本割集。
找到基本割集的步骤
1
排除那些可以由其他割集组合得到
2
的割集
接下来,根据每个割集是否可以由其他割集
组合得到,来筛选掉那些不是基本割集的割
3
集。
确定图形的割集
首先需要确定图形中所有的割集,这些割集 可以是任意大小的区域。
剩下来的就是基本割集
那些不能被其他割集组合得到的割集就是基 本割集。现在您已经掌握了如何找到图形的 基本割集的方法。
基本割集的找法
欢迎来到《基本割集的找法》PPT课件!在本课件中,我们将学习如何定义基 本割集、找到基本割集的步骤,以及它们的应用场景。
基本割集的定义
1 什么是基本割集?
2 为什么我们需要基本割集?
基本割集是一种小的、不可再分的割集,用于将 图形划分成两个部分。它们是割集树状结构中的 最底层。
在分析独立不相关的事件时,我们可以使用基本 割集,它们可以使得分析更容易。
示例演示:找到一个割集的基本割集
割集
这个图形被分成了4部分:上、下、左和右。
两两相交的割集
现在,判断那些割集是两两相交的。这里,我们发现 只有两个相交:左下和右上。
剩下来的就是基本割集
左下和右上被分解成许多小的基本割集,这里显示了
示例演示:找到多个割集的基本割集
图形的割集
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
称为树支,连接树支的支路称为连支。由b条支路和n个结点
构成的连通图有n-1条树支和b-n+1条连支。 2.割集(cut set)是图论的另一个重要概念,它是连通图中满足
以下两个条件的支路集合
1) 移去全部支路,图不再连通。
2) 恢复任何一条支路,图必须连通。
2020/11/13
2
精品资料
• 你怎么称呼老师?
• 如果老师最后没有总结一节课的重点的难点,你 是否会认为老师的教学方法需要改进?
• 你所经历的课堂,是讲座式还是讨论式? • 教师的教鞭
• “不怕太阳晒,也不怕那风雨狂,只怕先生骂我 笨,没有学问无颜见爹娘 ……”
• “太阳当空照,花儿对我笑,小鸟说早早早……”
KCL可以用割集来陈述:在集总参数电路中,任一时刻, 与任一割集相关的全部支路电流的代数和为零。
2020/11/13
14
例3-18用割集分析法重解图3-11电路,只列一个方程求电压 u2。
图3-22
解: 为了求得电压u2,作一个封闭面与支路2及其它电阻支 路和电流源支路相交,如图所示,这几条支路构成一个割
集,列出该割集的KCL方程
i4i5i2i33A
2020/11/13
15
i4i5i2i33A
练习题:选择1,5,6为树支,2,3,4为连支,写出基本割集 和基本回路。
2020/11/13
基本割集:{1,4,2},{5,2,4,3},{6,2,3}
基本回路:{2,1,5,6},{4,5,1},{3,5,6}
8
二、回路分析法
与网孔分析法相似,也可用(b-n+1)个独立回路电 流作变量,来建立回路方程。由于回路电流的选择有 较大灵活性,当电路存在m个电流源时,假如能够让 每个电流源支路只流过一个回路电流,就可利用电流 源电流来确定该回路电流,从而可以少列写m个回路 方程。网孔分析法只适用平面电路,回路分析是更普 遍的分析方法。
与结点分析法用n-1个结点电压作为变量来建立电 路方程类似,也可以用n-1个树支电压作为变量来建立 割集的KCL方程。由于选择树支电压有较大的灵活性, 当电路存在m个独立电压源时,其电压是已知量,若 能选择这些树支电压作为变量,就可以少列m个电路 方程。结点分析法只适用连通电路,而割集分析是更 普遍的分析方法。
例如,按照图示割集可以写出以下KCL方程
i4i5i2i33A
2020/11/13
5
由一条树支和几条连支构成的割集,称为基本割集。
基本割集:{2,4,1},{5,1,3},{6,1,3,4}
基本割集的KCL方程是一组线性无 关的方程组
2,5,6为树支,1,3,4为连支
i2 i4 i1 0 i5 i3 i1 0 i6 i3 i4 i1 0
求解方程得到电流i2
i223 V 058V 11 V3A
2020/11/13
12
练习题1:选择图示电路的i3,i4和i5作为三个回路电流, 只用一个回路方程求出电流i5;
练习题2:选择选择图示电路的i3,i4和i6作为三个回路 电流,只用一个回路方程求出电流i6。
2020/11/13
13
三、割集分析法
连支电流 i1,i3 , i4 是一组独立电流变量
i2i4i1 0 i2 i1i4
i5i3i1 0 i5 i1i3
2020/11/13
i6i3i4i1 0i6 i1i3i4
6
由一条连支和几条树支构成的回路,称为基本回路。 基本回路:{1,2,6,5},{3,5,6} ,{4,6,2} 基本回路的KVL方程是一组线性无 关的方程组Βιβλιοθήκη u1 u2 u6 u5 0
2,5,6为树支,1,3,4为连支
u3 u5 u6 0 u4 u6 u2 0
树支电压u2,u5 , u6 是是一组独立电压变量。
u1u2u6u50u1u5u6u2
u3u5u60 u3u6u5
u4u6u20 u4u2u6
2020/11/13
7
可以证明,n-1条树支电压是一组独立电压变量(它们不构 成回路),由此可以导出割集分析法。b-n+1条连支电流是一组 独立电流变量(它们不构成割集),由此可以导出回路分析法。
§3-4 回路分析法和割集分析法
本节先介绍利用独立电流或独立电压作 变量来建立电路方程的另外两种方法--回 路分析法和割集分析法,然后对各种电路 分析方法作个总结。
2020/11/13
1
一、图论的几个名词
先介绍图论的几个名词。
1.树(tree)是图论的一个重要概念。图由结点和支路组成,树
是连通图中连通全部结点而不形成回路的子图。构成树的支路
2i102的0/11回/13路方程
10
图3-21
用观察法列出电流i1的回路方程
( 5 3 1 ) i 1 ( 1 3 ) i 3 ( 5 3 ) i 4 2 V 0
代入i3=2A, i4=1A,求得电流i1 2V 08V8V
i15314A 根据支路电流与回路电流的关系可以求得其它支路电流
代入用电压u2表示电阻电流的VCR方程
i42 u 4 21 (1V 4u28V) i51 u 5 11 (1V 4u2) i22 u 2 i31 u 3 11 (8Vu2)
得到以下方程
1
1
11
2 ( 1 V 4 u 2 8 V ) 1 ( 1 V 4 u 2 ) 2 u 2 1 ( 8 V u 2 ) 3 A
2020/11/13
9
例3-17 用回路分析法重解图3-5电路,只列一个方程求电流 i1和i2。
图3-21
解: 为了减少联立方程数目,让1A和2A电流源支路只流过
一个回路电流。例如图3-21(a)和(b)所选择的回路电流都
符合这个条件。假如选择图3-21(a)所示的三个回路电流i1,
i3和i4,则i3=2A, i4=1A成为已知量,只需用观察法列出电流
20i 22 0/1 1/13i 1 i 4 3 A i 5 i 1 i 3 2 A i 6 i 1 i 3 i 4 1 A 11
假如选择图3-21(b)所示的三个回路电流i2,i3和i4,由于 i3=2A, i4=1A成为已知量,只需用观察法列出电流i2的回路方程
( 3 5 1 ) i 2 ( 1 3 ) 2 ( A ) 1 1 2 A V 0
