第6章 立体几何初步 6.1 空间的几何体
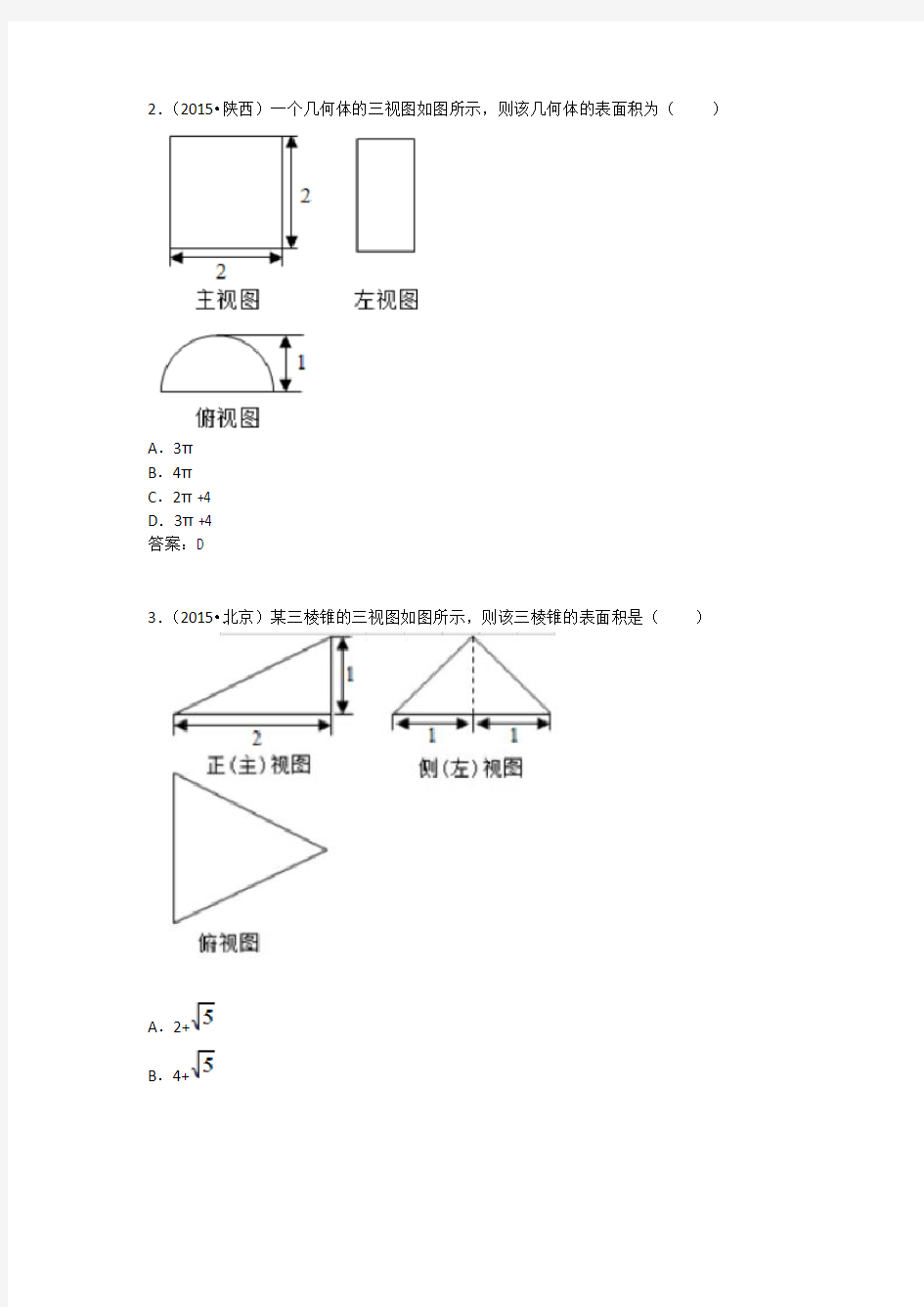

2.(2015?陕西)一个几何体的三视图如图所示,则该几何体的表面积为()
A.3π
B.4π
C.2π+4
D.3π+4
答案:D
3.(2015?北京)某三棱锥的三视图如图所示,则该三棱锥的表面积是()
A.2+
B.4+
C.2+2
D.5
答案:C
4.(2015?浙江)某几何体的三视图如图所示(单位:cm),则该几何体的体积是()
A.8cm3
B.12cm3
C.
D.
答案:C
5.(2015?新课标II)一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为()
A.
B.
C.
D.
答案:D
6.(2015?河北)圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r=()
A.1
B.2
C.4
D.8
答案:B
7.(2015?安徽)一个四面体的三视图如图所示,则该四面体的表面积是()
A.1+
B.2+
C.1+2
D.2
答案:B
8.(2015?北京)某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为()
A.1
B.
C.
D.2
答案:C
9.(2015?福建)某几何体的三视图如图所示,则该几何体的表面积等于()
A.8+2
B.11+2
C.14+2 D.15 答案:B
中职数学试卷:立体几何
江苏省洪泽中等专业学校数学单元试卷(立体几何) 时间120分钟 满分150分 一.选择题(每题5分,共50分) 1、一条直线和直线外两点可确定平面的个数是( ) A 、1 B 、2 C 、3 D 、1或2 2、若直线L ⊥平面a ,直线m ?a ,则L 与的关系是( )。 A 、L ⊥m B 、L ∥m C 、L 与m 异面 D 、无法确地 3、如果空间中两条直线互相垂直,那么它们( ) A 、一定相交 B 、是异面直线 C 、是共面直线 D 、一定不平行 4、.棱长都是1的三棱锥的表面积为( ) A. 3 B. 23 C. 33 D.4 3 5、两个球的表面积之比为1:4,则它们的体积之比是( )。 A 、1:64 B 、1:16 C 、1:8 D 、1:32 6、正方体的全面积是18,则正方体的体积是( )。 A 、9 3 B 、9 C 、33 D 、27 7、正方体1111ABCD A B C D -中,上底面对角线11A C 与侧面对角线1B C 所成的角为( )。 A 、30° B 、45° C 、60° D 、90° 8、圆锥的轴截面是一个等腰直角三角形,母线长为2,则它的侧面积为( )。 A 、4π B 、22π C 、4 2 π D 、8π 9、长方体1111ABCD A B C D -中,AB=3,BC=3,AA 1=4,则二面角D 1-AB-D 的余弦值是( )。 A 、53 B 、54 C 、22 D 、4 3 10、正三棱锥中,底面边长为33,侧棱长为5,则它的高为是( )。 A 3 B 、4 C 、26 D 、23 二、填空题(每题5分,共30分)
立体几何空间角
D C 1 A 1 B 1 C 1 D B C A D 立体几何专题----空间角 知识点归纳 1、异面直线所成的角 异面直线所成角的定义: 如图,已知两条异面直线 a , b , 经过空间任一点O作直线 a′∥a , b ′∥b 则把 a ′ 与 b ′所成的锐角(或直角)叫做异面直线所成的角(或夹角). a b 注1:异面直线所成的角的范围( 0O , 90O ] 注2:如果两条异面直线 a , b 所成的角为直角,我们就称这两条直线互相垂直 , 记为a ⊥ b 注3:在求作异面直线所成的角时,O点常选在其中的一条直线上(如线段的端点,线段的中点等) 2 、直线与平面所成的角 平面的一条斜线和它在平面内的射影所成的锐角,叫做这条直线和这个平面所成的角 (1)一条直线垂直于平面,它们所成的角是直角 (2)一条直线和平面平行,或在平面内,它们所成的角是0 ?的角 (3)直线和平面所成角的范围是[0?,90?] 3、二面角: 如右图在二面角的棱l取一点O,以点O为垂足,在半平面α和β内分别作垂直于棱l的射线OA和OB,则 叫做二面角的平面角. 注:①二面角的平面角的大小与O点位置_____ _。 ②二面角的平面角的范围是_______ 。 ③平面角为______的二面角叫做直二面角。 试题探究: 1、如图:表示正方体 1 1 1 1 D C B A ABCD-, 求异面直线 1 1 CC BA和所成的角。 2、空间四边形ABCD中,2 AD BC ==,,E F分别是, AB CD的中点,3 EF=, 求异面直线, AD BC所成的角。 3、在单位正方体 1111 ABCD A B C D -中,试求直线 1 BD与平面ABCD所成的角. 4、在单位正方体 1111 ABCD A B C D -中,求直线 11 A C与截面 11 ABC D所成的角. 5、将一副三角板如图拼接,∠BAC=∠BCD=90°,AB=AC,∠BDC=60°,且平面ABC⊥平面BCD, (1)求证:平面ABD⊥平面ACD;(2)求二面角A-BD-C的正切值;(3)求异面直线AD与BC所成角的余弦值. a′O b′ a P α O A O A B D C A 1 B 1 C 1 D A F E D B A B D B 1 A 1 C 1 D 1
立体几何初步空间几何体
立体几何初步---空间几何体 1、空间几何体的结构---柱、锥、台、球的结构特征 (1)棱柱: 定义:有两个面互相平行,其余各面都是四边形,且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫棱柱。 不在同一个面上的两个顶点的连线叫做棱柱的对角线 两个互相平行的面叫做棱柱的底 其余各面叫做棱柱的侧面 侧面与底面的公共顶点叫做棱柱的顶点 两个侧面的公共边叫做棱柱的侧棱 两个面的公共边叫做棱柱的棱 棱柱的性质及几何特征: 侧棱都相等,侧面都是平行四边形。 直棱柱的各个侧面都是矩形; 正棱柱的各个侧面都是全等的矩形。 两个底面与平行于底面的平面的截面是全等的多边形。 过不相邻的两条侧棱的截面是平行四边形。 分类:以底面多边形的边数作为分类的标准分为三棱柱、四棱柱、五棱柱等。 按侧棱是否和底面垂直分类:斜棱柱,直棱柱。直棱柱又分为正棱柱与其它直棱柱。 表示:用各顶点字母,如五棱柱或用对角线的端点字母,如五棱柱 (2)棱锥 定义:有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的几何体叫棱锥。 如果一个棱锥的底面是正多边形,并且顶点在底面的射影是底面中心,这样的棱锥叫做正棱锥。 分类:以底面多边形的边数作为分类的标准分为三棱锥、四棱锥、五棱锥等 表示:用各顶点字母,如五棱锥 几何特征:侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方。 性质: Ⅰ、正棱锥的性质 (1)各侧棱相等,各侧面都是全等的等腰三角形。 (2)棱锥的高、斜高和斜高在底面上的射影组成一个直角三角形;棱锥的高、侧棱和侧棱在 底面上的射影也组成一个直角三角形。 (3)顶点在底面正多边形的射影是底面的中心
文科立体几何面角二面角专题-带答案
文科立体几何线面角二面角专题 学校:___________姓名:___________班级:___________考号:___________ 一、解答题 1.如图,在三棱锥中,,,为的中点.(1)证明:平面; (2)若点在棱上,且二面角为,求与平面所成角的正弦值. 2.如图,在三棱锥中,,,为的中点.(1)证明:平面; (2)若点在棱上,且,求点到平面的距离. 3.(2018年浙江卷)如图,已知多面体ABCA1B1C1,A1A,B1B,C1C均垂直于平面ABC,∠ABC=120°,A1A=4,C1C=1,AB=BC=B1B=2.
(Ⅰ)证明:AB1⊥平面A1B1C1; (Ⅱ)求直线AC1与平面ABB1所成的角的正弦值. 4.如图,在三棱柱中,点P,G分别是,的中点,已知⊥平面 ABC,==3,==2. (I)求异面直线与AB所成角的余弦值; (II)求证:⊥平面; (III)求直线与平面所成角的正弦值. 5.如图,四棱锥,底面是正方形,,,,分别是,的中点.
(1)求证; (2)求二面角的余弦值. 6.如图,三棱柱中,侧棱底面,且各棱长均相等.,,分别为棱,,的中点. (1)证明:平面; (2)证明:平面平面; (3)求直线与直线所成角的正弦值. 7.如图,在四边形ABCD中,AB//CD,∠AB D=30°,AB=2CD=2AD=2,DE⊥平面ABCD,EF//BD,且BD=2EF. (Ⅰ)求证:平面ADE⊥平面BDEF; (Ⅱ)若二面角C BF D的大小为60°,求CF与平面ABCD所成角的正弦值. 8.如图,在四棱锥中,平面,,,
,点是与的交点,点在线段上,且. (1)证明:平面; (2)求直线与平面所成角的正弦值. 9.在多面体中,底面是梯形,四边形是正方形,,,,, (1)求证:平面平面; (2)设为线段上一点,,求二面角的平面角的余弦值. 10.如图,在多面体中,四边形为等腰梯形,,已知,,,四边形为直角梯形,,. (1)证明:平面,平面平面;
理科数学2010-2019高考真题分类训练专题八立体几何第二十二讲空间几何体的三视图、表面积和体积答案
专题八 立体几何初步 第二十二讲 空间几何体的三视图、表面积和体积 答案部分 2019年 1.解析 该模型为长方体1111ABCD A B C D -,挖去四棱锥O EFGH -后所得的几何体,其中O 为长方体的中心,E ,F ,G ,H ,分别为所在棱的中点,6cm AB BC ==, 14cm AA =, 所以该模型体积为: 1111311 664(46432)314412132(cm )32 ABCD A B C D O EFGH V V ---=??-??-????=-=, 3D 打印所用原料密度因为为30.9g /cm ,不考虑打印损耗, 所以制作该模型所需原料的质量为:1320.9118.8(g)?=. 2.解析 因为长方体1111ABCD A B C D -的体积是120,E 为1CC 的中点, 所以11111120ABCD A B C D V AB BC DD -=??=,所以三棱锥E BCD -的体积: 111332E BCD BCD V S CE BC DC CE -=??=????=V 11 1012 AB BC DD ???=. 3.解析 由题可知,四棱锥底面正方形的对角线长为2,且垂直相交平分,由勾股定理得,正四棱锥的高为2. 因为圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,则圆柱的上底面直径为底面正方形对角线的一半等于1,即半径等于 1 2 ,由相似比可得圆柱的高为正四棱锥高的一半,为1. 所以该圆柱的体积为2 1124V Sh π?? ==π?= ??? . 4.解析:由PA PB PC ==及ABC △是边长为2的正三角形可知,三棱锥P ABC -为正三棱锥,
立体几何空间距离问题
空间距离问题 (专注高三数学辅导:) 空间中距离的求法是历年高考考查的重点,其中以点与点、点到线、点到面的距离为基础,求其他几种距离一般化归为这三种距离. ●难点磁场 (★★★★)如图,已知ABCD是矩形,AB=a,AD=b,PA⊥平面ABCD,PA=2c,Q 是PA的中点. 求:(1)Q到BD的距离; (2)P到平面BQD的距离. 。 P为RT△ABC所在平面α外一点,∠ACB=90°(如图) (1)若PC=a,∠PCA=∠PCB=60°,求P到面α的距离及PC和α所成的角 (2)若PC=24,P到AC,BC的距离都是6√10,求P到α的距离及PC和α所成角 (3)若PC=PB=PA,AC=18,P到α的距离为40,求P到BC的距离
●案例探究 [例1]把正方形ABCD 沿对角线AC 折起成直二面角,点E 、F 分别是AD 、BC 的中点,点O 是原正方形的中心,求: (1)EF 的长; (2)折起后∠EOF 的大小. 命题意图:考查利用空间向量的坐标运算来解决立体几何问题,属★★★★级题目. < 知识依托:空间向量的坐标运算及数量积公式. 错解分析:建立正确的空间直角坐标系.其中必 须保证x 轴、y 轴、z 轴两两互相垂直. 技巧与方法:建系方式有多种,其中以O 点为原点,以OB 、OC 、OD 的方向分别为x 轴、y 轴、z 轴的正方向最为简单. 解:如图,以O 点为原点建立空间直角坐标系O —xyz ,设正方形ABCD 边长为a ,则A (0,-22a ,0),B (2 2 a ,0,0),C (0, 2 2 a ,0),D (0,0, 22a ),E (0,-4 2a , a ),F ( 42a , 4 2 a ,0) 21| |||,cos ,2||,2||8042)42)(42(420) 0,4 2 ,42(),42,42,0()2(23 ,43)420()4242()042(||)1(2 2222-=>=<== - =?+-+?=?=-==∴=-+++-=OF OE OF OE OF OE a OF a OE a a a a a OF OE a a OF a a OE a EF a a a a a EF ∴∠EOF =120° [例2]正方体ABCD —A 1B 1C 1D 1的棱长为1,求异面直线A 1C 1与AB 1间的距离. 命题意图:本题主要考查异面直线间距离的求法,属★★★★级题目. 知识依托:求异面直线的距离,可求两异面直线的公垂线,或转化为求线面
职高数学——立体几何
平面的基本性质 一、高考要求: 理解平面的基本性质. 二、知识要点: 1.平面的表示方法:平面是无限延展的,是没有边界的.通常用平行四边形表示平面,平面一般用希腊字母α、β、γ、…来命名,还可以用表示平行四边形的对角顶点的字母来命名. 2.平面的基本性质: (1)如果一条直线上的两点在一个平面内,那么这条直线上的所有 点都在这个平面内.这时我们说,直线在平面内或平面经过直线.用符 号语言表示为:如果A∈a,B∈a,且A∈α,B∈α,则a?α. (2)经过不在同一条直线上的三点,有且只有一个平面.也可简单地 说成,不共线的三点确定一个平面.它有三个推论: 推论1:经过一条直线和直线外的一点,有且只有一个平面; 推论2:经过两条相交直线,有且只有一个平面; ; 推论3:经过两条平行直线,有且只有一个平面. (3)如果两个平面有一个公共点,那么它们就有另外的公共点,并且 这些公共点的集合是经过这个点的一条直线.这时我们称这两个平面相交. 用符号语言表示为:如果A∈α,A∈β,则α∩β= ,且A∈ . 3.有关概念:如果空间内的几个点或几条直线都在同一平面内,那么我们就说它们共面;如果构成图形的所有点都在同一平面内,则这类图形叫做平面图形;如果构成图形的点不全在同一平面内,则这类图形叫做立体图形.直线和平面都是空间的子集,直线又是平面的子集. 三、典型例题: 例1:已知E、F、G、H分别是空间四边形ABCD各边AB、AD、BC、CD上的点,且EF与GH 相交于点P.求证:点B、D、P在同一直线上. 证明: ∵E∈AB, F∈AD又AB∩AD=A ∴E、F∈平面ABD ∴EF?平面ABD 同理GH?平面CBD ∵EF与GH相交于点P $ ∴P∈平面ABD,P∈平面CBD, 又平面ABD∩平面ABD=BD ∴P∈BD即点B、D、P在同一直线上. 例2:如图,已知直线a∥b,直线m与a、b分别交于点A、B, 求证:a、b、m三条直线在同一平面内.
空间立体几何归纳
空间立体几何归纳一、考点分析 基本图形 1棱柱一一有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。 ”斜棱柱 ①棱柱棱垂直于底面正棱柱★ ---------- 、直棱柱\ 洪他棱柱III ②四棱柱I底面为平行四边形平行六面体I 侧棱垂直于底面I直平行六面体底面为矩形 正四棱柱 长方体底面为正方形侧棱与底面边长相等.正方体
2.棱锥 棱锥一一有一个面是多边形, 其余各面是有一个公共顶点的三角形, 由这些面所围成的几何 体叫做棱锥。 ★正棱锥——如果有一个棱锥的底面是正多边形,并且顶点在底面的射影是底面的中心, 这样的棱锥叫做正棱锥。 3.球 球的性质: ①球心与截面圆心的连线垂直于截面; ★②r 二?、R 2 -d 2 (其中,球心到截面的距离为 注:球的有关问题转化为圆的问题解决 d 、球的半径为 R 、截面的半径为r ) ★球与多面体的组合体: 球与正四面体,球与长 方体,球与正方体等的内接与外切 轴 0'1 B A
平行垂直基础知识网络★★★ 平行与垂直关系可互相转化 异面直线所成的角,线面角,二面角的求法★★★ 1求异面直线所成的角 〔三[0 ,90 1: 解题步骤:一找(作):利用平移法找出异面直线所成的角; (1)可固定一条直线平移 另一条与其相交;(2 )可将两条一面直线同时平移至某一特殊位置。常用中位线平移法 证:证明所找(作)的角就是异面直线所成的角(或其补角) 。常需要证明线线平行; 三计算:通过解三角形,求出异面直线所成的角; 2求直线与平面所成的角 v 0 ,90 1:关键找“两足”:垂足与斜足 解题步骤:一找:找(作)出斜线与其在平面内的射影的夹角 (注意三垂线定理的应用) 二证:证明所找(作)的角就是直线与平面所成的角(或其补角) (常需证明线面垂直); 计算:常通过解直角三角形,求出线面角。 3求二面角的平面角 "〔0,二丨 解题步骤:一找: 根据二面角的平面角的定义,找(作)出二面角的平面角; 二证: 证明所找(作)的平面角就是二面角的平面角 (常用定义法,三垂线法,垂面法);三计算: 通过解三角形,求出二面角的平面角。 平行关系 垂直关系 平面几何知识 平面几何知识 * 线线平行 线线垂直 判定推论 ? 线面垂直 ■ ? ----- 面面垂直 1. a | ,b . :? = a 〃 b 2. a 丨 *,a 〃b= b _ :? 3. a |「,,a . - =■ :- // - 4. :? 〃 :, a . := a _ : 5. 】// :, __' : __ ' 判定 判定 线面平行 面面平行 判 义 质
立体几何及解题技巧以及空间距离专题复习
立体几何及解题技巧以及空间距离专题复习
知识点整理 (一)平行与垂直的判断 ⑴平行:设,的法向量分别为U,V ,贝U 直线l,m 的方向向量分 别为a,b ,平面 线线平行i // m a 〃 b a 诂;线面平行i // a u a u 0 ; 面面平行// u // v u J. ⑵ 垂直:设直线l ,m 的方向向量分别为a,b ,平面,的法向量 分别为u,v ,则 线线垂直I 丄m a 丄b ab 0 ;线面垂直I 丄 a // u a ku 「; 面面垂直丄 u 丄v u v 0. (二)夹角与距离的计算 注意:以下公式可以可以在非正交 基底下用,也可以在正交基底下用坐标运算 (1)夹角:设直线l ,m 的方向向量分别为,平面,的法向量 分别为u ,v ,则 ①两直线I ,m 所成的角为 (2)空间距离 ②直线I 与平面 ③二面角一I 的大小为(0< < ),cos cos (0< =2),sin 所成的角为
点、直线、平面间的距离有种.点到平面的距离是重点,两异面直线间的距离是难 ①点到平面的距离h:(定理)如图,设n是是平 面的法向量,AP是平面的一条斜线,其中A 则点P到平面的距离 uuu uu ②h 1 Auur n |(实质是AP在法向量n 方向上的投影的绝对值) |n| uuu ur ③异面直线l i,l2间的距离d: d AB JC』1( 11,12的公垂向量为 |n| ' n, C、D分别是h,l2上任一点). 题型一:非正交基底下的夹角、的计算 例1.如图,已知二面角-I - 点 A , B , A C I于点C, 且 AC=CD=DB=1. 求:(1) A、B两点间的距离; (2)求异面直线AB和CD勺所成的角(3) AB与CD勺距 离. 解:设AC a,CD b,DB c,则 |a| |b| |c| 1, a,b b,c 900, a,c 60°, 2 ? ? 2 ?? 2 ■■ 2 |AB | a b c . a b c 2a b 2b c 2c a 2 A、B两点间的距离为2. (2)异面直线AB和CD的所成的角为60°
建立空间直角坐标系-解立体几何题
建立空间直角坐标系,解立体几何高考题 立体几何重点、热点: 求线段的长度、求点到平面的距离、求直线与平面所成的夹角、求两异面直线的夹角、求二面角、证明平行关系和垂直关系等. 常用公式: 1 、求线段的长度: 222z y x AB ++==()()()2 12212212z z y y x x -+-+-= 2、求P 点到平面α的距离: PN = ,(N 为垂足,M 为斜足,为平面α的法向量) 3、求直线l 与平面α所成的角:|||||sin |n PM ?= θ,(l PM ?,α∈M ,为α的法向量) 4、求两异面直线AB 与CD 的夹角:cos = θ 5、求二面角的平面角θ:|||||cos |21n n ?= θ,( 1n ,2n 为二面角的两个面的法向量) 6、求二面角的平面角θ:S S 射影 = θ cos ,(射影面积法) 7、求法向量:①找;②求:设, 为平面α内的任意两个向量,)1,,(y x =为α的法向量, 则由方程组?????=?=?0 n b n a ,可求得法向量.
