KMP算法详解
KMP讲解

有了覆盖函数,那么实现kmp算法就是很简单的了,我们的原则还是从左向右匹配,但是当失配发生时,我们不用把target_index向回移动,target_index前面已经匹配过的部分在pattern自身就能体现出来,只要动pattern_index就可以了。
当发生在j长度失配时,只要把pattern向右移动j-overlay(j)长度就可以了。
说了这么半天那么这种方法是什么呢,这种方法是就大名鼎鼎的确定的有限自动机(Deterministic finite state automaton DFA),DFA可识别的文法是3型文法,又叫正规文法或是正则文法,既然可以识别正则文法,那么识别确定的字串肯定不是问题(确定字串是正则式的一个子集)。对于如何构造DFA,是有一个完整的算法,这里不做介绍了。在识别确定的字串时使用DFA实在是大材小用,DFA可以识别更加通用的正则表达式,而用通用的构建DFA的方法来识别确定的字串,那这个overhead就显得太大了。
{
index = overlay_value[index];
}
if(pattern[index+1]==pattern[i])
{
overlay_value[i] = index +1;
KMP 算法可在O(n+m)时间内完成全部的串的模式匹配工作。
ok,最后给出KMP算法实现的c++代码:
#include<iostream>
#include<string>
#include<vector>
using namespace std;
int kmp_find(const string& target,const string& pattern)
kmp

2 KMP算法:KMP算法是由D.E.Knuth(克努特),J.H.Morris(莫里斯),V.R.Pratt(普拉特)等人共同提出的,该算法主要消除了主串指针(i指针)的回溯,利用已经得到的部分匹配结果将模式串右滑尽可能远的一段距离再继续比较,从而使算法效率有某种程度的提高,O(n+m)。
先从例子入手(p82):按Brute-Force算法i=i-j+2=2-2+2=2,j=1按Brute-Force算法i=i-j+2=2-1+2=3,j=1按Brute-Force算法i=i-j+2=8-6+2=4,j=1,但从已匹配的情况看,模式串在t[6]即“c”前的字符都是匹配的,再看已匹配的串“abaab”,t[1]t[2]与t[4]t[5]相同,那么,因为t[4]t[5]与原串s[6]s[7]匹配,所以t[1]t[2]必然与原串s[6]s[7]匹配,因此说t[3]可以直接与s[8]匹配,按KMP 算法i=8,j=3匹配成功。
从上例看出在匹配不成功时,主串指针i不动,j指针也不回到第一个位置,而是回到一个恰当的位置,如果这时让j指针回到第一个位置,就可能错过有效的匹配,所以在主串指针i不动的前提下,j指针回到哪个位置是问题的关键,既不能将j右移太大,而错过有效的匹配,另一方面,又要利用成功的匹配,将j右移尽可能地大,而提高匹配的效率,因此问题的关键是寻找模式串自身的规律。
//////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////。
和直接比较若不满足和直接比较所以:满足:,设1i i 12112111112121s ),2(;s )1(""")"2(""")"1(""""t t j k t t t t t t t t s s t t t t s s s s k j k j k j k j i j i m n <<====-+-+----+-////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////设s=” s 1 s 2 ... s n ”, t=” t 1 t 2 ... t m ”,在匹配过程中,当s i ≠ t j (1≤i ≤n-m+1,1≤j ≤m)时,存在(前面的j-1个字符已匹配):” s i-j+1 ... s i-1 ” =” t 1 t 2 ... t j-1 ” (1) 若模式中存在可互相重叠的最长的真子串,满足: ” t 1 t 2 ... t k-1 ”=”t j-k+1 t j-k+2 ... t j-1 ” (2) 其中真子串最短可以是t 1 ,即 t 1。
kmp的nextval数组

kmp的nextval数组【KMP算法之NextVal数组】KMP算法是一种高效的字符串匹配算法,其核心思想是利用已经匹配的部分字符来跳过不必要的比较,以达到快速匹配的目的。
其中一个重要的优化是使用nextval数组,用于在失配时找到下一次需要比较的位置。
1. KMP算法简介:KMP算法由Knuth、Morris和Pratt三人提出,其核心思想是根据模式串(pattern)自身的特点,预先计算出一个nextval 数组,用于在匹配过程中跳过不必要的比较。
KMP算法的时间复杂度为O(m+n),其中m和n分别为主串(target)和模式串(pattern)的长度。
2. NextVal数组的定义:NextVal数组是在求解next数组时的一种优化,其定义与next 数组略有不同。
NextVal数组的值nextval[i]表示,当模式串的第i个字符与主串的第i个字符失配时,下一个需要比较的位置在哪里。
3. NextVal数组的求解:(1)定义一个辅助数组next[],用于存储当前位置之前的最大相同前后缀长度。
(2)对模式串进行遍历,计算next数组的值:a. 初始化next[0] = -1,next[1] = 0;b. 使用两个指针i和j,分别指向模式串的第i个字符和第j个字符,初始值为i=2,j=0;c. 若p[i-1] == p[j],则next[i] = j + 1,同时i++,j++;d. 若p[i-1] != p[j],则在j = next[j]的基础上,继续比较,直到p[i-1] == p[j]或者j = 0;e. 若j = 0,则next[i] = 0,同时i++;f. 重复步骤c~e,直到遍历完整个模式串。
(3)通过next数组求解nextval数组:a. 初始化nextval[1] = 0;b. 遍历next数组,对于next[i] >= 0的位置,若p[i] ==p[next[i]],则nextval[i+1] = next[i] + 1;c. 若p[i] != p[next[i]],则继续在next数组中找到next[next[i]],直到找到p[i] == p[next[next[i]]]或者next[i] = -1;d. 若找到p[i] == p[next[next[i]]],则nextval[i+1] =next[next[i]] + 1;e. 若next[i] = -1,则nextval[i+1] = 0。
实验04:串应用KMP算法PPT课件

在生物信息学中的应用
在生物信息学中,KMP算法被广泛应用于基因序列的比对和拼接,以及蛋白质序列 的匹配和比对。
通过构建基因序列或蛋白质序列的索引表,KMP算法可以在O(n+m)的时间复杂度 内完成序列的比对和拼接,提高了比对和拼接的准确性和效率。
KMP算法在生物信息学中的应用有助于深入了解基因和蛋白质的结构和功能,为生 物医学研究和疾病诊断提供了有力支持。
06 实验总结与展望
KMP算法的优缺点
优点
高效:KMP算法在匹配失败时能跳过 尽可能多的字符,减少比较次数,从
而提高匹配效率。
适用范围广:KMP算法适用于各种模 式串匹配问题,不受模式串长度的限 制。
缺点
计算量大:KMP算法需要计算和存储 部分匹配表,对于较长的模式串,计 算量较大。
不适合处理大量数据:KMP算法在处 理大量数据时可能会占用较多内存, 导致性能下降。
匹配失败的处理
当模式串中的某个字符与主串中的对应字符不匹配时,模式串向右 滑动,与主串的下一个字符重新对齐,继续比较
next[ j]表示当模式串中第j个字符与主 串中的对应字符不匹配时,模式串需 要向右滑动的位置。
next数组的构建
next数组的作用
在匹配过程中,通过next数组可以快 速确定模式串需要滑动到哪个位置, 从而提高了匹配效率。
通过已知的next值,递推计算出next 数组中其他位置的值。
KMP算法的时间复杂度
01
02
03
04
时间复杂度分析
KMP算法的时间复杂度取决 于模式串在主串中出现的次数 以及每次匹配所花费的时间。
最佳情况
当模式串在主串中连续出现时 ,KMP算法的时间复杂度为
KMP算法计算next值和nextVal值
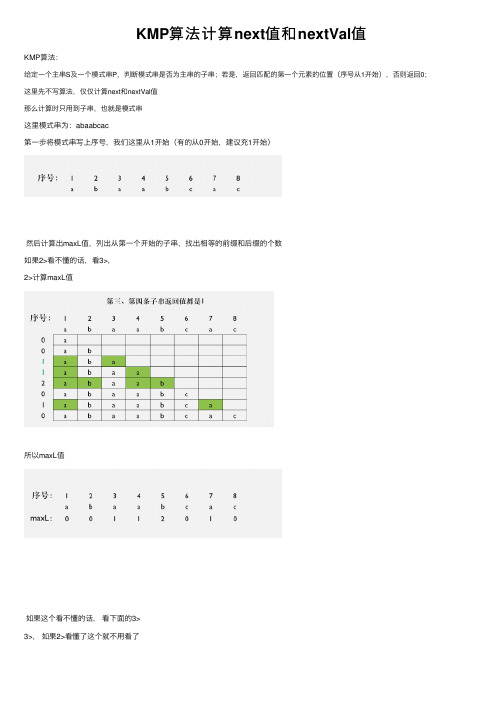
KMP算法计算next值和nextVal值
KMP算法:
给定⼀个主串S及⼀个模式串P,判断模式串是否为主串的⼦串;若是,返回匹配的第⼀个元素的位置(序号从1开始),否则返回0;这⾥先不写算法,仅仅计算next和nextVal值
那么计算时只⽤到⼦串,也就是模式串
这⾥模式串为:abaabcac
第⼀步将模式串写上序号,我们这⾥从1开始(有的从0开始,建议充1开始)
然后计算出maxL值,列出从第⼀个开始的⼦串,找出相等的前缀和后缀的个数
如果2>看不懂的话,看3>,
2>计算maxL值
所以maxL值
如果这个看不懂的话,看下⾯的3>
3>,如果2>看懂了这个就不⽤看了
依次类推4>计算next值
接下来将maxL复制⼀⾏,去掉最后⼀个数,在开头添加⼀个-1,向右平移⼀个格,然后每个值在加1的到next值
5>计算nextVal值,⾸先将第⼀个为0,然后看next和maxL是否相等(先计算不相等的)
当next和maxL不相等时,将next的值填⼊
当next和maxL相等时,填⼊对应序号为next值得nextVal值
所以整个nextVal值为:。
严蔚敏 数据结构 kmp算法详解

当此集合非空时
next[j]= -1 0 当j=0时 其他情况
t=“abab”对应的next数组如下:
j t[j] next[j] 0 a -1 1 b 0 2 a 0 3 b 1
void GetNext(SqString t,int next[]) { int j,k; j=0;k=-1;next[0]=-1; while (j<t.len-1)
既然如此,回溯到si-j+1开始与t匹配可以不做。那 么,回溯到si-j+2 开始与t匹配又怎么样?从上面推理 可知,如果 "t0t1…tj-2"≠"t2t3…tj"
仍然有
"t0t1…tj-2"≠"si-j+2si-j+3…si"
这样的比较仍然“失配”。依此类推,直到对于 某一个值k,使得: "t0t1…tk-2"≠" tj-k+1tj-k+2…tj-1"
b 3
第 1 次匹配
第 2 次匹配
s=aaabaaaa b t=aaaab
第 3 次匹配
s=aaabaaaa b t=aaaab
第 4 次匹配
s=aaabaaaa b t=aaaab
第 5 次匹配
s=aaabaaaa b t=aaaab
上述定义的next[]在某些情况下尚有缺陷。 例如,模式“aaaab”在和主串“aaabaaaab”匹配时, 当i=3,j=3时,s.data[3]≠t.data[3],由next[j]的指示还需 进行i=3、j=2,i=3、j=1,i=3、j=0等三次比较。实际上, 因为模式中的第1、2、3个字符和第4个字符都相等, 因此,不需要再和主串中第4个字符相比较,而可以将模 式一次向右滑动4个字符的位置直接进行i=4,j=0时的 字符比较。
KMP算法(改进的模式匹配算法)——next函数

KMP算法(改进的模式匹配算法)——next函数KMP算法简介KMP算法是在基础的模式匹配算法的基础上进⾏改进得到的算法,改进之处在于:每当匹配过程中出现相⽐较的字符不相等时,不需要回退主串的字符位置指针,⽽是利⽤已经得到的部分匹配结果将模式串向右“滑动”尽可能远的距离,再继续进⾏⽐较。
在KMP算法中,依据模式串的next函数值实现字串的滑动,本随笔介绍next函数值如何求解。
next[ j ]求解将 j-1 对应的串与next[ j-1 ]对应的串进⾏⽐较,若相等,则next[ j ]=next[ j-1 ]+1;若不相等,则将 j-1 对应的串与next[ next[ j-1 ]]对应的串进⾏⽐较,⼀直重复直到相等,若都不相等则为其他情况题1在字符串的KMP模式匹配算法中,需先求解模式串的函数值,期定义如下式所⽰,j表⽰模式串中字符的序号(从1开始)。
若模式串p 为“abaac”,则其next函数值为()。
解:j=1,由式⼦得出next[1]=0;j=2,由式⼦可知1<k<2,不存在k,所以为其他情况即next[2]=1;j=3,j-1=2 对应的串为b,next[2]=1,对应的串为a,b≠a,那么将与next[next[2]]=0对应的串进⾏⽐较,0没有对应的串,所以为其他情况,也即next[3]=1;j=4,j-1=3 对应的串为a,next[3]=1,对应的串为a,a=a,所以next[4]=next[3]+1=2;j=5,j-1=4 对应的串为a,next[4]=2,对应的串为b,a≠b,那么将与next[next[4]]=1对应的串进⾏⽐较,1对应的串为a,a=a,所以next[5]=next[2]+1=2;综上,next函数值为 01122。
题2在字符串的KMP模式匹配算法中,需先求解模式串的函数值,期定义如下式所⽰,j表⽰模式串中字符的序号(从1开始)。
若模式串p为“tttfttt”,则其next函数值为()。
KMP算法详解

KMP算法详解KMP 算法详解KMP 算法是⼀个⼗分⾼效的字符串查找算法,⽬的是在⼀个字符串 s 中,查询 s 是否包含⼦字符串 p,若包含,则返回 p 在 s 中起点的下标。
KMP 算法全称为 Knuth-Morris-Pratt 算法,由 Knuth 和 Pratt 在1974年构思,同年 Morris 也独⽴地设计出该算法,最终由三⼈于1977年联合发表。
举⼀个简单的例⼦,在字符串 s = ababcabababca 中查找⼦字符串 p = abababca,如果暴⼒查找,我们会遍历 s 中的每⼀个字符,若 s[i] = p[0],则向后查询p.length() 位是否都相等。
这种朴素的暴⼒的算法复杂度为O(m×n),其中m和n分别是 p 和 s 的长度。
KMP 算法可以⽅便地简化这⼀查询的时间复杂度,达到O(m+n)。
1. PMT 序列PMT 序列是 KMP 算法的核⼼,即 Partial Match Table(部分匹配表)。
举个例⼦:char a b a b a b c aindex01234567PMT00123401PMT 的值是字符串的前缀集合与后缀集合的交集中最长元素的长度。
PMT[0] = 0: 字符串 a 既没有前缀,也没有后缀;PMT[1] = 0: 字符串 ab 前缀集合为 {a},后缀集合为 {b},没有交集;PMT[2] = 1: 字符串 aba 前缀集合为 {a, ab},后缀集合为 {ba, a},交集为 {a},交集元素的最长长度为1;PMT[3] = 2: 字符串 abab 前缀集合为 {a, ab, aba},后缀集合为 {bab, ab, b},交集为 {ab},交集元素的最长长度为2;…… 以此类推。
2. 算法主体现在我们已经知道了 PMT 序列的含义,那么假设在 PMT 序列已经给定的情况下,如何加速字符串匹配算法?tar 存储 s 的下标,从 0 开始,若 tar > s.length() - 1,代表匹配失败;pos 存储 p 的下标,从 0 开始,若 s[tar] != p[pos],则 pos ⾛到下⼀个可能匹配的位置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
KMP算法详解
KMP算法即Knuth-Morris-Pratt算法,是模式匹配的一种改进算法,因为是名字中三人同时发现的,所以称为KMP算法。
因为偶然接触到有关KMP的问题,所以上网查了一下next数组和 nextval数组的求法,却没有找到,只有在CSDN的资料文件里找到了next数组的简单求法(根据书上提供的程序也可以求到,但一般在课堂讲解的时候,学生难以理解,所以希望以更容易理解的形式来讲解),那位高人说时间关系,先讲到这里,于是讲完了next数组就功成身退了。
BS的同时,自己研究了下nextwal数组,发现了其中的简易规律,并写了出来,希望能对需要快速理解KMP中nextval的求法的朋友有所帮助。
int get_nextval(SString T,int &nextval[ ]){
//求模式串T的next函数修正值并存入数组nextval。
i=1; nextval[1]=0; j=0;
while(i<T[0]){
if(j==0||T[i]==T[j]){
++i;++j;
if (T[i]!=T[j]) nextval[i]=j;
else nextval[i]=nextval[j];
}
else j=nextval[j];
}
}//get_nextval
根据这段程序来求nextval的值是可以方便计算出来,但如果是应付考研试题或者期末考试就有点麻烦了。
而如果记住我推荐的方法,那么任何时候都可以很方便地求解nextval 了。
首先看看next数组值的求解方法。
例如:
next数组的求解方法是:第一位的next值为0,第二位的next值为1,后面求解每一位的next值时,根据前一位进行比较。
首先将前一位与其 next值对应的内容进行比较,如果相等,则该位的next值就是前一位的next值加上1;如果不等,向前继续寻找next 值对应的内容来与前一位进行比较,直到找到某个位上内容的next值对应的内容与前一位相等为止,则这个位对应的值加上1即为需求的next值;如果找到第一位都没有找到与前一位相等的内容,那么需求的位上的next值即为1。
看起来很令人费解,利用上面的例子具体运算一遍。
1.前两位必定为0和1。
2.计算第三位的时候,看第二位b的next值,为1,则把b和1对应的a进行比较,不同,则第三位a的next的值为1,因为一直比到最前一位,都没有发生比较相同的现象。
3.计算第四位的时候,看第三位a的next值,为1,则把a和1对应的a进行比较,
相同,则第四位a的next的值为第三位a的next值加上1。
为2。
因为是在第三位实现了其next值对应的值与第三位的值相同。
4.计算第五位的时候,看第四位a的next值,为2,则把a和2对应的b进行比较,不同,则再将b对应的next值1对应的a与第四位的a进行比较,相同,则第五位的next 值为第二位b的next值加上1,为2。
因为是在第二位实现了其next值对应的值与第四位的值相同。
5.计算第六位的时候,看第五位b的next值,为2,则把b和2对应的b进行比较,相同,则第六位c的next值为第五位b的next值加上1,为3,因为是在第五位实现了其next值对应的值与第五位相同。
6.计算第七位的时候,看第六位c的next值,为3,则把c和3对应的a进行比较,不同,则再把第3位a的next值1对应的a与第六位c比较,仍然不同,则第七位的next 值为1。
7.计算第八位的时候,看第七位a的next值,为1,则把a和1对应的a进行比较,相同,则第八位c的next值为第七位a的next值加上1,为2,因为是在第七位和实现了其next值对应的值与第七位相同。
在计算nextval之前要先弄明白,nextval是为了弥补next函数在某些情况下的缺陷而产生的,例如主串为“aaabaaaab”、模式串为“aaaab”那么,比较的时候就会发生一些浪费的情况:比较到主串以及模式串的第四位时,发现其值并不相等,据我们观察,我们可以直接从主串的第五位开始与模式串进行比较,而事实上,却进行了几次多余的比较。
使用nextval可以去除那些不必要的比较次数。
求nextval数组值有两种方法,一种是不依赖next数组值直接用观察法求得,一种方法是根据next数组值进行推理,两种方法均可使用,视更喜欢哪种方法而定。
我们使用例子“aaaab”来考查第一种方法。
1.试想,在进行模式匹配的过程中,将模式串“aaaab”与主串进行匹配的时候,如果第一位就没有吻合,即第一位就不是a,那么不用比较了,赶快挪到主串的下一位继续与模式串的第一位进行比较吧,这时,模式串并没有发生偏移,那么,模式串第一位a的nextval 值为0。
2.如果在匹配过程中,到第二位才发生不匹配现象,那么主串的第一位必定是a,而第二位必定不为a,既然知道第二位一定不为a,那么主串的第一、二两位就没有再进行比较的必要,直接跳到第三位来与模式串的第一位进行比较吧,同样,模式串也没有发生偏移,第二位的nextval值仍然为0。
3.第三位、第四位类似2的过程,均为0。
4.如果在匹配过程中,直到第五位才发生不匹配现象,那么主串的第一位到第四位必定为a,并且第五位必定不为b,可是第五位仍然有可能等于a。
如果万一第五位为a,那么既然前面四位均为a,所以,只要第六位为b,第一个字符串就匹配成功了。
所以,现在的情况下,就是看第五位究竟是不是a了。
所以发生了下面的比较:
前面的三个a都不需要进行比较,只要确定主串中不等于b的那个位是否为a,即可以进行如下的比较:如果为a,则继续比较主串后面一位是否为b;如果不为 a,则此次比较结束,继续将模式串的第一位去与主串的下一位进行比较。
由此看来,在模式串的第五位上,进行的比较偏移了4位(不进行偏移,直接比较下一位为0),故第五位b的nextval值为4。
我们可以利用第一个例子“abaabcac”对这种方法进行验证。
a的nextval值为0,因为如果主串的第一位不是a,那么没有再比较下去的必要,直接比较主串的第二位是否为a。
如果比较到主串的第二位才发生错误,则主串第一位肯定为a,第二位肯定不为b,此时不能直接跳到第三位进行比较,因为第二位还可能是a,所以对主串的第二位再进行一次比较,偏移了1位,故模式串第二位的nextval值为1。
以此类推,nextval值分别为:01021302。
其中第六位的nextval之所以为3,是因为,如果主串比较到第六位才发生不匹配现象,那么主串的前五位必定为“abaab”且第六位必定不是“c”,但第六位如果为“a”的话,那么我们就可以从模式串的第四位继续比较下去。
所以,这次比较为:
而不是:
因为前两位a和b已经确定了,所以不需要再进行比较了。
所以模式串第六位的nextval 值为这次比较的偏移量3。
再来看求nextval数组值的第二种方法。
1.第一位的nextval值必定为0,第二位如果于第一位相同则为0,如果不同则为1。
2.第三位的next值为1,那么将第三位和第一位进行比较,均为a,相同,则,第三位的nextval值为0。
3.第四位的next值为2,那么将第四位和第二位进行比较,不同,则第四位的nextval 值为其next值,为2。
4.第五位的next值为2,那么将第五位和第二位进行比较,相同,第二位的next值为
1,则继续将第二位与第一位进行比较,不同,则第五位的nextval值为第二位的next值,为1。
5.第六位的next值为3,那么将第六位和第三位进行比较,不同,则第六位的nextval 值为其next值,为3。
6.第七位的next值为1,那么将第七位和第一位进行比较,相同,则第七位的nextval 值为0。
7.第八位的next值为2,那么将第八位和第二位进行比较,不同,则第八位的nextval 值为其next值,为2。
在“aaaab”内进行验证。
