2019年浙江版中考数学§9_4 操作探究型问题(试题部分)
2019年浙江省绍兴市中考数学试题(word版,含答案)

浙江省2019年初中学业水平考试绍兴市试卷数学试题卷考生须知:1.本试卷共6页,有三个大题,24小题,全卷满分150分,考试时间120分钟.2.答案必须写在答题纸相应的位置上,写在本试卷、草稿纸上均无效.3.答题前认真阅读答题纸上的“注意事项”,按规定答题,本次考生不能使用计算器.参考公式:抛物线)0(2≠++=a c bx ax y 的顶点坐标是)44,2(2ab ac a b --.卷I (选择题)一、选择题(本大题共10个小题,每小题4分,共40分,请选出每小题中一个最符合题意的选项,不选、多选、错选均不给分) 1. 5-的绝对值是 A.5 B.-5 C.51 D.51- 2.某市决定为全市中小学生教室安装空调,今年预计投入资金126 000 000元,其中数字126 000 000用科学记数法可表示为A.7106.12⨯ B.81026.1⨯ C.91026.1⨯ D.1010126.0⨯ 3.如图的几何体由6个相同的小正方体搭成,它的主视图是4.为了解某地区九年级男生的身高情况,随机抽取了该地区100名九年级男生,他们的身高x (cm )统计如下:根据以上结果,抽查该地区一名九年级男生,估计他的身高不低于180cm 的概率是 A.0.85 B. 0.57 C. 0.42 D.0.155.如图,墙上钉着三根木条a,b,c ,量得∠1=70°,∠2=100°,那么木条a,b 所在直线所夹的锐角是A.5°B.10°C.30°D.70°6.若三点(1,4),(2,7),(a ,10)在同一直线上,则a 的值等于A. -1B. 0C. 3D. 47.在平面直角坐标系中,抛物线)3)(5(-+=x x y 经过变换后得到抛物线)5)(3(-+=x x y ,则这个变换可以是A.向左平移2个单位B.向右平移2个单位C.向左平移8个单位D.向右平移8个单位8.如图,△ABC 内接于圆O ,∠B=65°,∠C=70°,若BC=22,则弧BC 的长为 A.π B.π2 C.π2 D.π229.正方形ABCD 的边AB 上有一动点E ,以EC 为边作矩形ECFG ,且边FG 过点D ,在点E 从点A 移动到点B 的过程中,矩形ECFG 的面积A.先变大后变小B.先变小后变大C.一直变大D.保持不变10.如图1,长、宽均为3,高为8的长方体容器,放置在水平桌面上,里面盛有水,水面高为6,绕底面一棱长进行旋转倾斜后,水面恰好触到容器口边缘,图2是此时的示意图,则图2中水面高度为 A.524 B.532 C.173412 D.173420卷II (非选择题)二、填空题(本大题有6个小题,每小题5分,共30分)11.因式分解:=-12x ▲ . 12.不等式423≥-x 的解为 ▲ .13.我国的《洛书》中记载着世界最古老的一个幻方:将1~9这九个数字填入3×3的方格中,使三行、三列、两对角线上的三个数之和都相等,如图的幻方中,字母m 所表示的数是 ▲ .14.如图,在直线AP 上方有一个正方形ABCD ,∠PAD=30°,以点B 为圆心,AB 为半径作弧,与AP 交于点A,M ,分别以点A,M 为圆心,AM 长为半径作弧,两弧交于点E ,连结ED ,则∠ADE 的度数为 ▲ .15.如图,矩形ABCD 的顶点A,C 都在曲线xky =(常数0,0>≥x k )上,若顶点D 的坐标为(5,3),则直线BD 的函数表达式是 ▲ .16.把边长为2的正方形纸片ABCD 分割成如图的四块,其中点O 为正方形的中心,点E,F 分别是AB,AD 的中点,用这四块纸片拼成与此正方形不全等的四边形MNPQ (要求这四块纸片不重叠无缝隙),则四边形MNPQ 的周长是 ▲ .三、解答题(本大题有8小题,17~20题每小题8分,第21题10分,第22,23小题每小题12分,第24小题14分,共80分,解答需要写出必要的文字说明、演算步骤或证明过程) 17.(1)计算:12)21()2(60sin 42----+︒-π(2)x 为何值时,两个代数式14,12++x x 的值相等?18.如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量y (千瓦时)关于已行驶路程x (千米)的函数图象.(1)根据图象,直接写出蓄电池剩余电量为35千瓦时时汽车已行驶的路程,当1500≤≤x 时,求1千瓦时的电量汽车能行驶的路程;(2)当200150≤≤x 时求y 关于x 的函数表达式,并计算当汽车已行驶180千米时,蓄电池的剩余电量.19.小明、小聪参加了100m 跑的5期集训,每期集训结束市进行测试,根据他们的集训时间、测试成绩绘制成如下两个统计图:根据图中信息,解答下列问题:(1)这5期的集训共有多少天?小聪5次测试的平均成绩是多少?(2)根据统计数据,结合体育运动的实际,从集训时间和测试成绩这两方面,说说你的想法.20.如图1,为放置在水平桌面l 上的台灯,底座的高AB 为5cm 。
2019年浙江省中考数学精编试卷附解析

2019年浙江省中考数学精编试卷学校:__________ 姓名:__________ 班级:__________ 考号:__________注意事项: 1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上一、选择题1.如图,一个小球从A 点沿制定的轨道下落,在每个交叉口都有向左或向右两种机会均等的结果,小球最终到达 H 点的概率是( ) A .12B .14C .16D .182.如图,在△ABC 中,DE ∥BC ,DE 分别与AB 、AC 相交于点D 、E ,若AD=4,DB=2,则DE ∶BC 的值为( ) A .32 B .21 C .43 D .53 3.在△ABC 中,E 是 AB 上一点,AE=2,BE=3,AC= 4,在 AC 上取一点 D ,使△ADE ∽△ABC ,则 AD 的值是( )A .85B .52C .85或52D .85或254.如图,在平行四边形ABCD 中,CE ⊥AB ,E 为垂足.如果∠A=125°,则∠BCE=( )A .55°B .35°C .25°D .30°5.下列语句中,属于命题的是 ( ) A .直线AB 与CD 垂直吗B 过线段AB 的中点C 画AB 的垂线 C .同旁内角不互补,两直线不平行D .连结A ,B 两点6.如图,下列不等式一定能成立的是( ) A .∠5>∠3B .∠4>∠3C .∠6>∠2D .∠5>∠67.如图,AB ∥EF ∥DC ,EG ∥DB ,则图中与∠1相等的角(∠1除外)共有( ) A .6个B .5个C .4个D .2个8.一个三角形的两条边分别为1和2,若要使这个三角形成为直角三角形,则应满足下列各个条件中的( )BCDEA.第三边长为3 B.第三边的平方为3 C.第三边的平方为5 D.第三边的平方为3或59.下列关于分式263xχ--的说法,正确的()A.当3x=时,分式有意义B.当3x≠时,分式没有意义C.当3x=时,分式的值为零D.分式的值不可能为零10.方程组525x yx y=+⎧⎨-=⎩的解满足方程0x y a++=,那么a的值是()A.5 B.-5 C.3 D.-311.如图所示,线段AB上有C和D两个点,则图中共有线段()A. 3条B. 4条C.5条D.6 条二、填空题12.如图,点D在⊙O的直径 AB 的延长线上,且 BD=BC,若 CD 切⊙O于点 C,则∠CAB 的度教为.13.把命题“两个奇数的和必为偶数”改写成“如果…那么…”的形式为 . 14.当 m 时,关于x的方程2(2)530m x x m-++=是一元二次方程.15.将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三角形,……如此继续下去,结果如下表:所剪次数1234…n正三角形个数471013…a n则n解答题16.方程48x=有个解,不等式48x<的解集是.17.如图的方格纸中,左边图形到右边图形的变换是 .18.用加减法解方程组335532x yx y+=⎧⎨-=⎩,把两个方程的两边,直接消去未知数得到的一元一次方程是.19.从 1,2,3,4,5 中任选两个数,这两个数的和恰好等于7 有种可能.20.如图,若把△ABC绕A点旋转一定角度就得到△ADE,那么对应边AB= , AC= ,BC= ;对应角∠CAB= ,∠B= ,∠C= .21.如图所示,点P关于OA、OB的对称点分别是P1,P2,P1P2分别交OA,OB于C,D两点, P1P2=6 cm,则△PCD的周长为.解答题22.如图所示,∠1= .23.看图填空.(A、0、B在一条直线上)(1)∠AOD= + =∠AOE- ;(2)∠BOE+∠EOC= ;(3)∠EOA-∠AOD= ;(4)∠AOC+ = 180°;(5)若0C平分∠AOD,0E平分∠BOD,则∠AOD=2 =2 .∠BOE= =12.24.如果2x =,3y =,且20xy<,那么x y += . 三、解答题25.一个盒子中装有白色的小塑料球.为了估计这袋有多少小球,小明将形状、大小都相同的红色小球 1000 个混入其中,摇匀后任意取出 100 粒,发现红色小塑料球有 4 个,你能估计出自塑料球的个数吗?26.如图,梯形ABCD 中,AB ∥CD ,且AB =2CD ,E ,F 分别是AB ,BC •的中点,EF 与BD 相交于点M . (1)求证:△EDM ∽△FBM ;(2)若DB =9,求BM .27.如图,五边形ABCDE ∽五边形 RSTUV ,求∠R 的度数和RS 的长.28.如图,在□ABCD 中,BC =2AB ,E 为BC 的中点. (1)求证:AE 平分∠BAD ; (2)求∠AED 的度数.29.写出下列命题的逆命题,并判断逆命题的真假,如果是假命题请反举例说明. (1)对顶角相等;(2)等腰三角形的两底角的平分线相等; (3)在三角形中,钝角所对的边最大.30.先化简,再求值. 22222222(22)[(33)(33)]x y xy x y x y x y xy ---++-,其中12x =-,2y =.【参考答案】学校:__________ 姓名:__________ 班级:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题1.B2.A3.C4.B5.C6.A7.B8.D9.D10.A11.D二、填空题12.30°13.如果两个数是奇数,那么它们的和必为偶数14.2≠15.3n+116.1,x<217.以AB为对称轴作轴对称图形,再向右平移8格18.相加,y,8x=719.220.AD,AE,DE,∠EAD,∠D,∠E21.6 cm22.120°23.(1)∠AOC,∠COD,∠DOE (2)∠BOC (3)∠DOE (4)∠COB (5)∠AOC,∠COD,∠DOE,∠BOD24.1或-1三、解答题25.设白塑料球有x个,则4100010010000x=+,解得x= 24000(个)答:估计白塑料球有 24000 个26.(1)略(2)3.27.∵五边形 ABCDE∽五边形RSTUV,∴∠R=∠A= 128°.∴RS RVAB AE=,即446RS=,∴83RS=28.提示:(1)由AB=BE,推出∠BAE=∠AEB,由AD∥BC,推出∠DAE=∠AEB;(2)同理DE平分∠ADC,所以∠AED=90°.29.(1)逆命题:相等的角是对顶角,是假命题,举例略;(2)逆命题:若一个三角形有两个角的平分线相等,则这个三角形是等腰三角形,是真命题;(3)逆命题:在三角形中,最大边所对的角是钝角,是假命题.如直角三角形30.22 x y xy -+ ,1 22 -。
2019浙江省杭州市中考数学试题(含答案)[真题]
![2019浙江省杭州市中考数学试题(含答案)[真题]](https://img.taocdn.com/s3/m/3e4794acbd64783e08122b6f.png)
浙江省杭州市2019年中考数学试题一、选择题:本大题有10小题,每小题3分,共30分.在每小题所给出的四个选项中,只有一项符合题目要求的.1.计算下列各式,值最小的是( )A.9102-+⨯B.2+0×1-9C.2+0-1+9D.2+0+1-92.在平面直角坐标系中,点A (m ,2)与点B (3,n )关于y 轴对称,则( )A.m=3,n=2B.m= - 3,n=2C.m=2,n=3D.m= - 2,n=33.如图,P 为圆O 外一点,PA ,PB 分别切圆O 于A ,B 两点,若PA=3,则PB=( ) A.2 B.3 C.4 D.54.已知九年级某班30名学生种树72棵,男生每人种3棵树,女生每人种2棵树,设男生有x 人,则( )A.30)72(32=-+x xB.30)72(23=-+x xC.72)30(32=-+x xD.72)30(23=-+x x5.点点同学对数据26,36,36,46,5■,52进行统计分析,发现其中一个两位数的个位数字被墨水涂污看不到了,则计算结果与被涂污数字无关的是( )A.平均数B.中位数C.方差D.标准差6.如图,在△ABC 中,点D,E 分别在AB 和AC 边上,DE ∥BC ,M 为BC 边上一点(不与点B,C 重合),连接AM 交DE 于点N ,则( ) A.AE AN AN AD = B.CE MN MN BD = C. MC NE BM DN = D.BMNE MC DN =7.在△ABC 中,点D,E 分别在ABC 中,若一个内角等于另两个内角的差,则( )A.必有一个内角等于30°B.必有一个内角等于45°C.必有一个内角等于60°D.必有一个内角等于90°8.已知一次函数b ax y +=1和)(2b a a bx y ≠+=,函数1y 和2y 的图象可能是( )9.如图,一块矩形木板ABCD 斜靠在墙边(OC ⊥OB ,点A,B,C,D,O 在同一平面内).已知AB=a ,AD=b ,∠BCO=x ,则点A 到OC 的图象与x 轴有N 个交点,则( )A.x b x a sin sin +B.x b x a cos cos +C.x b x a cos sin +D.x b x a sin cos +10.在平面直角坐标系,已知b a ≠,设函数))((b x a x y ++=的图象与x 轴有M 个交点,函数)1)(1(++=bx ax y 的图象与x 轴有N 个交点,则( )A.M=N-1或M=N+1B.M=N-1或M=N+2C.M=N 或M=N+1D.M=N 或M=N-1二、填空题:本大题有6小题,每小题4分,共24分11.因式分解:=-21x .12.某计算机程序第一次算得m 个数据的平均数为x ,第二次算得另外n 个数据的平均数为y ,则这m+n 个数据的平均数等于 .13.如图是一个圆锥形冰淇淋外壳(不计厚度),已知其母线长为12cm ,底面圆半径为3cm ,则这个冰淇淋外壳的侧面积等于 cm 2(结果精确到个位).14.在直角三角形ABC 中,若2AB=AC ,则cosC= .15.某函数满足当自变量1=x 时,函数值0=y ;当自变量0=x 时,函数值1=y ,写出一个满足条件的函数表达式 .16.如图,把某矩形纸片ABCD 沿EF 、GH 折叠(点E 、H 在AD 边,点E,G 在BC 边上),使点B 和点C 落在AD 边上同一点P 处,A 点的对称点为A '点,D 点的对称点为D '点,若∠FPG=90°,△A 'EP 的面积为4,△PH D '的面积为1,则矩形ABCD 的面积等于 .三、解答题:本大题有7个小题,共66分.17.(本题6分) 化简:122442----x x x . 圆圆的解答如下:x x x x x x x x 2)4()2(2412244222+-=--+-=---- 圆圆的解答正确吗?如果不正确,写出正确的解答.18.(本题8分)称量五框水果的质量,若每框以50kg 为基准,超过基准部分的千克数记为正数,不足基准部分的千克数记为负数,甲组为实际称量读数,乙组为记录数据,并把所得数据整理成如下统计表和未完成的统计图(单位:kg ).(1)补充完整乙组数据的折线统计图;(2)①甲、乙两组数据的平均数分别为甲x 、乙x ,写出甲x 和乙x 之间的等量关系;②甲、乙两组数据的方差分别为2甲S 、2乙S ,比较2甲S 和2乙S 的大小,并说明理由.19.(本题8分)如图,在△ABC 中,BC AB AC <<.(1)已知线段AB 的垂直平分线与BC 边交于点P ,连接AP ,求证:∠APC=2∠B ;(2)以点B 为圆心,线段AB 长为半径画弧,与BC 边交于点Q ,连接AQ ,若∠AQC=3∠B ,求∠B 的度数.20.(本题8分)方方驾驶小汽车匀速地从A 地行驶到B 地,行驶里程为480千米,设小汽车行驶时间为t (单位:小时),行驶速度为v (单位:千米/小时),且全程速度限定为不超过120千米/小时.(1)求v 关于t 的函数表达式;(2)方方上午8点驾驶小汽车从A 地出发:①方方需在当天12点48分至14点(含12点48分和14点)间到达B 地,求小汽车行驶速度v 的范围; ②方方能否在当天11点30分前到达B 地?说明理由.21.(本题10分)如图,已知正方形ABCD 的边长为1,正方形CEFG 的面积为1S ,点E 在DC 边上,点G 在BC 的延长线上,设线段AD 和DE 为邻边的矩形的面积为2S ,且1S =2S .(1)求线段CE 的长;(2)若点H 为BC 边的中点,连接HD ,求证:DH=GH.22.(本题12分)设二次函数2121,)()((x x x x x x y --=是实数).(1)甲求得当0=x 时,0=y ;当1=x 时,0=y ;乙求得当21=x 时,21-=y ,若甲求得的结果都正确,你认为乙求得的结果正确吗?说明理由.(2)写出二次函数图象的对称轴,并求该函数的最小值(用含21,x x 的代数式表示).(3)已知二次函数的图象经过(0,m )和(1,n )两点(m,n 是实数),当1021<<<x x 时,求证:1610<<mn .23.(本题12分)如图,已知锐角三角形ABC 内接于圆O ,OD 、BC 交于点D ,连接OA.(1)若∠BAC=60°,①求证:OD=21OA ; ②当OA=1时,求△ABC 面积的最大值.(2)点E 在线段OA 上,OE=OD ,连接DE ,设∠ABC=m ∠OED ,∠ACB=n ∠OED (m,n 是正数),若∠ABC <∠ACB ,求证:02=+-n m .。
【中考真题】浙江省杭州市2019年中考数学试题(解析版)word【推荐】

浙江省杭州市2019年中考数学试题(解析版)浙江省杭州市2019年中考数学试卷一、选择题(本大题有10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一个符合题目要求)1.计算下列各式,值最小的是()A. B. C. D.【答案】A【解析】【分析】根据实数的运算法则,遵循先乘除后加减的运算顺序即可得到答案.【详解】根据实数的运算法则可得:A.;B.;C.;D.;故选A.【点睛】本题考查实数的混合运算,掌握实数的混合运算顺序和法则是解题的关键..2.在平面直角坐标系中,点与点关于y轴对称,则()A. ,B. ,C. ,D. ,【答案】B【解析】【分析】根据点关于y轴对称,其横坐标互为相反数,纵坐标相同即可得到答案.【详解】A,B关于y轴对称,则横坐标互为相反数,纵坐标相同,故选B【点睛】本题考查点坐标的轴对称,解题的关键熟练掌握点坐标的轴对称.3.如图,P为⊙外一点,PA、PB分别切⊙于A、B两点,若,则()A. 2B. 3C. 4D. 5【答案】B【解析】【分析】根据切线长定理即可得到答案.【详解】因为PA和PB与⊙相切,根据切线长定理,所以PA=PB=3,故选B.【点睛】本题考查切线长定理,解题的关键是熟练掌握切线长定理.4.已知九年级某班30位同学种树72棵,男生每人种3棵,女生每人种2棵,设男生x人,则()A. B. C. D.【答案】D【解析】【分析】先设男生x人,根据题意可得.【详解】设男生x人,则女生有(30-x)人,由题意得:,故选D.【点睛】本题考查列一元一次方程,解题关键是读懂题意,得出一元一次方程.5.点点同学对数据26,36,36,46,5■,52进行统计分析,发现其中一个两位数被墨水涂污看不到了,则计算结果与被涂污数字无关的是()A. 平均数B. 中位数C. 方差D. 标准差【答案】B【解析】【分析】根据平均数、中位数、方差和标准差的概念,结合题意即可解答.【详解】因为这组数据的中位数是36和46的平均数,则这组数据中的中位数是41,与涂污数字无关,故选B.【点睛】本题考查平均数、中位数、方差和标准差,解题的关键是熟悉平均数、中位数、方差和标准差的相关计算.6.如图,在中,D、E分别在AB边和AC边上,,M为BC边上一点(不与B、C重合),连结AM交DE于点N,则()A. B. C. D.【答案】C【分析】根据平行线性质和相似三角形的判定可得△ADN∽△ABM,△ANE∽△AMC,再根据相似三角形的性质即可得到答案.【详解】∵,∴△ADN∽△ABM,△ANE∽△AMC,∴,故选C.【点睛】本题考查平行线的性质、相似三角形的判定和性质,解题的关键是熟练掌握平行线的性质、相似三角形的判定和性质.7.在中,若一个内角等于另外两个角的差,则()A. 必有一个角等于B. 必有一个角等于C. 必有一个角等于D. 必有一个角等于【答案】D【解析】【分析】先设三角形的两个内角分别为x,y,则可得(180°-x-y),再分三种情况讨论,即可得到答案.【详解】设三角形的一个内角为x,另一个角为y,则三个角为(180°-x-y),则有三种情况:①②③综上所述,必有一个角等于90°故选D.【点睛】本题考查三角形内角和的性质,解题的关键是熟练掌握三角形内角和的性质,分情况讨论.8.已知一次函数和,函数和的图象可能是()A. B. C. D.【答案】A【解析】根据一次函数图形的性质,结合题意和,即可得到答案.【详解】①当,、的图象都经过一、二、三象限②当,、的图象都经过二、三、四象限③当,的图象都经过一、三、四象限,的图象都经过一、二、四象限④当,的图象都经过一、二、四象限,的图象都经过一、三、四象限满足题意的只有A.故选A.【点睛】本题考查一次函数图像,解题的关键是熟练掌握一次函数图像的性质.9.如图,一块矩形木板ABCD斜靠在墙边,(,点A、B、C、D、O在同一平面内),已知,,.则点A到OC的距离等于()A. B. C. D.【答案】D【解析】【分析】根据矩形的性质可得BC=AD=b,∠ABC=90°,再根据三角函数可得答案.【详解】过点A作AE⊥OB于点E,因为四边形ABCD是矩形,且AB=a,AD=b所以BC=AD=b,∠ABC=90°所以∠ABE=∠BCO=x因为,所以,所以点A到OC的距离故选D.【点睛】本题考查矩形的性质和三角函数,解题的关键是熟练掌握矩形的性质和三角函数.10.在平面直角坐标系中,已知,设函数的图像与x轴有M个交点,函数的图像与x轴有N个交点,则()A. 或B. 或C. 或D. 或【答案】C【解析】【分析】先根据函数的图像与x轴有M个交点解得,再对a,b分情况讨论,求得答案.【详解】对于函数,当时,函数与x轴两交点为(-a,0)、(-b,0),∵,所以有2个交点,故对于函数①,交点为,此时②,交点为,此时③,交点为,此时综上所述,或故选C.【点睛】本题考查二次函数与坐标轴的交点,解题的关键是分情况讨论a,b.二、填空题(本大题有6小题,每小题4分,共24分)11.因式分解:________.【答案】(1+x)(1-x)【解析】【分析】根据平方差公式即可得到答案.【详解】对用平方差公式,得【点睛】本题考查因式分解,解题的关键是熟练掌握因式分解的方法.12.某计算机程序第一次算得m个数据的平均数为x,第二次算得另外n个数据的平均数为y,则这个数据的平均数等于______.【答案】.【解析】【分析】根据加权平均数的基本求法,平均数等于总和除以个数,即可得到答案.【详解】平均数等于总和除以个数,所以平均数.【点睛】本题考查求加权平均数,解题的关键是掌握加权平均数的基本求法.13.如图,一个圆锥形冰激凌外壳(不计厚度).已知其母线长为,底面圆半径为,则这个冰激凌外壳的侧面积等于______(计算结果精确到个位).【答案】113.【解析】【分析】根据圆锥侧面积公式,代入题中数据,即可得到答案.【详解】根据题中数据,结合圆锥侧面积公式得:【点睛】本题考查求圆锥侧面积,解题的关键是熟练掌握圆锥侧面积公式.14.在直角三角形ABC中,若,则_______.【答案】或.【解析】【分析】对AC分两种情况讨论,根据三角函数即可得到答案.【详解】如图所示,分两种情况讨论,AC可以是直角边,也可以是斜边①当AC是斜边,设AB=x,则AC=2x,由勾股定理可得:BC=x,则②当AC是直角边,设AB=x,则AC=2x,由勾股定理可得:BC=x,则综上所述,或.【点睛】本题考查三角函数,解题的关键是对AC分情况讨论.15.某函数满足当自变量时,函数值;当自变量时,函数值,写出一个满足条件的函数表达式_____.【答案】或或等.【解析】【分析】由于题中没有指定是什么具体的函数,可以从一次函数,二次函数等方面考虑,只要符合题中的两个条件即可.【详解】符合题意的函数解析式可以是或或等,(本题答案不唯一)故答案为:如或或等.【点睛】本题考查一次函数、二次函数的解析式,解题的关键是知道一次函数、二次函数的定义.16.如图,把某矩形纸片ABCD沿EF、GH折叠(点E、H在AD边上,点F、G在BC边上),使得点B、点C落在AD边上同一点P处,A点的对称点为点,D点的对称点为点,若,的面积为4,的面积为1,则矩形ABCD的面积等于_____.【答案】.【解析】【分析】根据相似三角形的判断得到△A'EP~△D'PH,由三角形的面积公式得到S△A'EP,再由折叠的性质和勾股定理即可得到答案.【详解】∵A'E∥PF∴∠A'EP=∠D'PH又∵∠A=∠A'=90°,∠D=∠D'=90°∴∠A'=∠D'∴△A'EP~△D'PH又∵AB=CD,AB=A'P,CD=D'P∴A'P= D'P设A'P=D'P=x∵S△A'EP:S△D'PH=4:1∴A'E=2D'P=2x∴S△A'EP=∵∴∴A'P=D'P=2∴A'E=2D'P=4∴∴∴∴∴∴【点睛】本题考查矩形的性质、折叠的性质,解题的关键是掌握矩形的性质、折叠的性质.三、解答题(本大题有7个小题,共66分)17.化简:圆圆的解答如下:圆圆的解答正确吗?如果不正确,写出正确的解答.【答案】圆圆的解答不正确.正确解为,解答见解析.【解析】【分析】根据完全平方差公式先对分式进行通分,再化简,即可得到答案.【详解】圆圆的解答不正确.正确解答如下:原式.【点睛】本题考查分式化简,解题的关键是掌握完全平方差公式.18.称重五筐水果的质量,若每筐以50千克为基准,超过基准部分的千克数记为正数,不足基准部分的千克数记为负数,甲组为实际称重读数,乙组为记录数据,并把所得数据整理成如下统计表和未完成的统计图(单位:千克)实际称量读数折线统计图 记录数据折线统计图⑴补充完整乙组数据的折线统计图; ⑵①甲、乙两组数据的平均数分别为、,写出与之间的等量关系; ②甲、乙两组数据的平均数分别为、,比较与的大小,并说明理由.【答案】(1)补全折线统计图,如图所示.见解析;(2)①,②,理由见解析.【解析】【分析】(1)根据统计表中的信息即可得出答案;(2)①先求出甲、乙的平均数,即可得出与之间的等量关系; ②先计算、,再对与的大小进行比较.【详解】(1)补全折线统计图,如图所示.(2)①. ②,理由如下: 因为222221[(4850)(5250)(4750)(4950)(5450)]5x x x x x =--+--+--+--+--乙乙乙乙乙, 所以 【点睛】本题结合折线统计图和统计表考查平均数和方差,解题的关键是读懂题中统计图表所给出的信息.19.如图,在中,.⑴已知线段AB的垂直平分线与BC边交于点P,连结AP,求证:;⑵以点B为圆心,线段AB的长为半径画弧,与BC边交于点Q,连结AQ,若,求的度数.【答案】(1)见解析;(2)∠B=36°.【解析】【分析】(1)根据垂直平分线的性质,得到PA=PB,再由等腰三角形的性质得到∠PAB=∠B,从而得到答案;(2)根据等腰三角形的性质得到∠BAQ=∠BQA,设∠B=x,由题意得到等式∠AQC=∠B+∠BAQ=3x,即可得到答案.【详解】(1)证明:因为点P在AB的垂直平分线上,所以PA=PB,所以∠PAB=∠B,所以∠APC=∠PAB+∠B=2∠B.(2)根据题意,得BQ=BA,所以∠BAQ=∠BQA,设∠B=x,所以∠AQC=∠B+∠BAQ=3x,所以∠BAQ=∠BQA=2x,在△ABQ中,x+2x+2x=180°,解得x=36°,即∠B=36°.【点睛】本题考查垂直平分线的性质、等腰三角形的性质,解题的关键是掌握垂直平分线的性质、等腰三角形的性质.20.方方驾驶小汽车匀速地从A地行使到B地,行驶里程为480千米,设小汽车的行使时间为t(单位:小时),行使速度为v(单位:千米/小时),且全程速度限定为不超过120千米/小时.⑴求v关于t的函数表达式;⑵方方上午8点驾驶小汽车从A出发①方方需在当天12点48分至14点(含12点48分和14点)间到达B地,求小汽车行驶速度v范围.②方方能否在当天11点30分前到达B地?说明理由.【答案】(1);(2)①,②方方不能在11点30分前到达B地.【解析】【分析】(1)根据题意,得,由题意,得,从而得到答案;(2)①根据一元一次不等式,结合题意即可得到答案;②根据不等式,即可求解答案.【详解】(1)根据题意,得,所以,因为,所以当时,,所以(2)①根据题意,得,因为,所以,所以②方方不能在11点30分前到达B地.理由如下:若方方要在11点30分前到达B地,则,所以,所以方方不能在11点30分前到达B地.【点睛】本题考查反比例函数的解析式、一元一次不等式,解题的关键是掌握反比例函数、一元一次不等式.21.如图,已知正方形ABCD的边长为1,正方形CEFG的面积为,点E在CD边上,点G 在BC的延长线上,设以线段AD和DE为邻边的矩形的面积为,且.⑴求线段CE的长;⑵若点H为BC边的中点,连结HD,求证:.【答案】(1)CE=;(2)见解析.【解析】【分析】根据正方形的性质,(1)先设CE=x(0<x<1),则DE=1-x,由S1=S2,列等式即可得到答案.(2)根据勾股定理得到HD,再由H,C,G在同一直线上,得证HD=HG.【详解】根据题意,得AD=BC=CD=1,∠BCD=90°.(1)设CE=x(0<x<1),则DE=1-x,因为S1=S2,所以x2=1-x,解得x=(负根舍去),即CE=(2)因为点H为BC边的中点,所以CH=,所以HD=,因为CG=CE=,点H,C,G在同一直线上,所以HG=HC+CG=+=,所以HD=HG【点睛】本题考查正方形的性质、勾股定理和一元二次函数,解题的关键是根据题意列出一元二次函数.22.设二次函数(、是实数).⑴甲求得当时,;当时,,乙求得当时,.若甲求得的结果都正确,你认为乙求得的结果正确吗?说明理由;⑵写出二次函数的对称轴,并求出该函数的最小值(用含、的代数式表示);⑶已知二次函数的图像经过,两点(m、n是实数),当时,求证:.【答案】(1)乙求得的结果不正确,理由见解析;(2)对称轴为,;(3)见解析.【解析】【分析】(1)将当时,;当时,的数据代入二次函数,列方程得到二次函数解析式,再代入乙得数据,即可得出答案;(2)根据二次函数轴对称公式,判断函数最低点,即可解答;(3)由题意得到,,则得到的等式,由,并结合函数的图象,得到.【详解】(1)乙求得的结果不正确,理由如下:根据题意,知图象经过点(0,0),(1,0),所以,当时,,所以乙求得的结果不正确.(2)函数图象的对称轴为,当时,函数有最小值M,(3)因为,所以,,所以因为,并结合函数的图象,所以,所以,因为,所以【点睛】本题考查二次函数综合,解题的关键是熟练掌握二次函数的相关概念和计算.23.如图,已知锐角内接于⊙O,于点D,连结AO.⑴若.①求证:;②当时,求面积的最大值;⑵点E在线段OA上,,连接DE,设,(m、n是正数),若,求证:【答案】(1)①见解析;②△ABC面积的最大值是;(2)见解析.【解析】【分析】(1)①连接OB,OC,由圆的性质可得答案;②先作AF⊥BC,垂足为点F,要使得面积最大,则当点A,O,D在同一直线上时取到再根据三角形的面积公式即可得到答案;(2)先设∠OED=∠O DE=α,∠COD=∠BOD=β,由锐角三角形性质得到即,再结合题意及三角形内角和的性质得到两式联立即可得到答案.【详解】(1)①证明:连接OB,OC,因为OB=OC,OD⊥BC,所以∠BOD=∠BOC=×2∠BAC=60°,所以OD=OB=OA②作AF⊥BC,垂足为点F,所以AF≤AD≤AO+OD=,等号当点A,O,D在同一直线上时取到由①知,BC=2BD=,所以△ABC的面积即△ABC面积的最大值是(2)设∠OED=∠ODE=α,∠COD=∠BOD=β,因为△ABC是锐角三角形,所以∠AOC+∠AOB+2∠BOD=360°,即(*)又因为∠ABC<∠ACB,所以∠EOD=∠AOC+∠DOC因为∠OED+∠ODE+∠EOD=180°,所以(**)由(*),(**),得,即【点睛】本题综合考查圆的性质、三角形内角和的性质勾股定理,解题的关键是熟练掌握圆的性质、三角形内角和的性质勾股定理.2019年浙江省杭州市中考语文试题()浙江省杭州市2019年中考语文试题一、积累(20分)阅读下面的文字,完成1—3题。
2019年浙江省绍兴市中考数学试题(word版,含答案)

浙江省2019年初中学业水平考试绍兴市试卷数学试题卷考生须知:1.本试卷共6页,有三个大题,24小题,全卷满分150分,考试时间120分钟.2.答案必须写在答题纸相应的位置上,写在本试卷、草稿纸上均无效.3.答题前认真阅读答题纸上的“注意事项”,按规定答题,本次考生不能使用计算器. 参考公式:抛物线)0(2≠++=a c bx ax y 的顶点坐标是)44,2(2a b ac a b --. 卷I (选择题)一、选择题(本大题共10个小题,每小题4分,共40分,请选出每小题中一个最符合题意的选项,不选、多选、错选均不给分)1. 5-的绝对值是A.5B.-5C.51D.51- 2.某市决定为全市中小学生教室安装空调,今年预计投入资金126 000 000元,其中数字126 000 000用科学记数法可表示为A.7106.12⨯B.81026.1⨯C.91026.1⨯D.1010126.0⨯3.如图的几何体由6个相同的小正方体搭成,它的主视图是4.为了解某地区九年级男生的身高情况,随机抽取了该地区100名九年级男生,他们的身高x (cm )统计如下:根据以上结果,抽查该地区一名九年级男生,估计他的身高不低于180cm 的概率是A.0.85B. 0.57C. 0.42D.0.155.如图,墙上钉着三根木条a,b,c ,量得∠1=70°,∠2=100°,那么木条a,b 所在直线所夹的锐角是A.5°B.10°C.30°D.70°6.若三点(1,4),(2,7),(a ,10)在同一直线上,则a 的值等于A. -1B. 0C. 3D. 47.在平面直角坐标系中,抛物线)3)(5(-+=x x y 经过变换后得到抛物线)5)(3(-+=x x y ,则这个变换可以是A.向左平移2个单位B.向右平移2个单位C.向左平移8个单位D.向右平移8个单位8.如图,△ABC 内接于圆O ,∠B=65°,∠C=70°,若BC=22,则弧BC 的长为 A.π B.π2 C.π2 D.π229.正方形ABCD 的边AB 上有一动点E ,以EC 为边作矩形ECFG ,且边FG 过点D ,在点E 从点A 移动到点B 的过程中,矩形ECFG 的面积A.先变大后变小B.先变小后变大C.一直变大D.保持不变10.如图1,长、宽均为3,高为8的长方体容器,放置在水平桌面上,里面盛有水,水面高为6,绕底面一棱长进行旋转倾斜后,水面恰好触到容器口边缘,图2是此时的示意图,则图2中水面高度为A.524B.532 C.173412 D.173420 卷II (非选择题)二、填空题(本大题有6个小题,每小题5分,共30分)11.因式分解:=-12x ▲ .12.不等式423≥-x 的解为 ▲ .13.我国的《洛书》中记载着世界最古老的一个幻方:将1~9这九个数字填入3×3的方格中,使三行、三列、两对角线上的三个数之和都相等,如图的幻方中,字母m 所表示的数是 ▲ .14.如图,在直线AP 上方有一个正方形ABCD ,∠PAD=30°,以点B 为圆心,AB 为半径作弧,与AP 交于点A,M ,分别以点A,M 为圆心,AM 长为半径作弧,两弧交于点E ,连结ED ,则∠ADE 的度数为 ▲ .15.如图,矩形ABCD 的顶点A,C 都在曲线xk y =(常数0,0>≥x k )上,若顶点D 的坐标为(5,3),则直线BD 的函数表达式是 ▲ . 16.把边长为2的正方形纸片ABCD 分割成如图的四块,其中点O 为正方形的中心,点E,F 分别是AB,AD 的中点,用这四块纸片拼成与此正方形不全等的四边形MNPQ (要求这四块纸片不重叠无缝隙),则四边形MNPQ 的周长是 ▲ .三、解答题(本大题有8小题,17~20题每小题8分,第21题10分,第22,23小题每小题12分,第24小题14分,共80分,解答需要写出必要的文字说明、演算步骤或证明过程)17.(1)计算:12)21()2(60sin 420----+︒-π(2)x 为何值时,两个代数式14,12++x x 的值相等?18.如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量y (千瓦时)关于已行驶路程x (千米)的函数图象.(1)根据图象,直接写出蓄电池剩余电量为35千瓦时时汽车已行驶的路程,当1500≤≤x 时,求1千瓦时的电量汽车能行驶的路程;(2)当200150≤≤x 时求y 关于x 的函数表达式,并计算当汽车已行驶180千米时,蓄电池的剩余电量.19.小明、小聪参加了100m 跑的5期集训,每期集训结束市进行测试,根据他们的集训时间、测试成绩绘制成如下两个统计图:根据图中信息,解答下列问题:(1)这5期的集训共有多少天?小聪5次测试的平均成绩是多少?(2)根据统计数据,结合体育运动的实际,从集训时间和测试成绩这两方面,说说你的想法.20.如图1,为放置在水平桌面l 上的台灯,底座的高AB 为5cm 。
2019浙江杭州_中考_数学_试题卷及答案共6页word资料
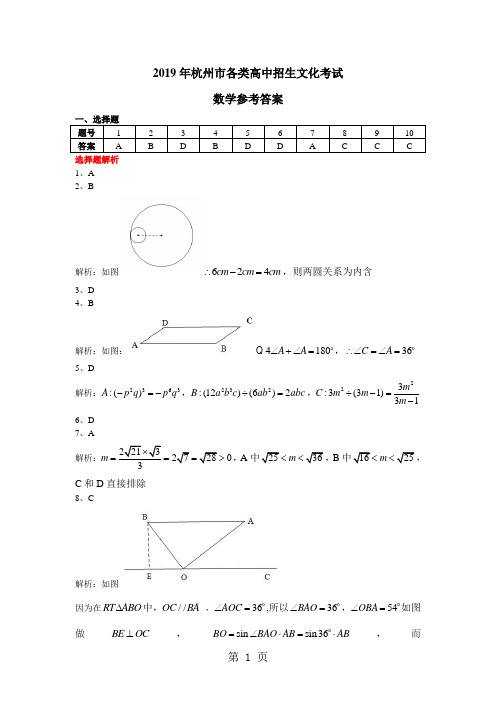
2019年杭州市各类高中招生文化考试数学参考答案一、选择题 题号 12 3 4 5 6 7 8 9 10 答案ABDBDDACCC选择题解析 1、A 2、B解析:如图624cm cm cm ∴-=,则两圆关系为内含3、D4、B解析:如图:4180A A ∠+∠=o Q ,36C A ∴∠=∠=o5、D解析:2363:()A p q p q -=-,232:(12)(6)2B a b c ab abc ÷=,223:3(31)31m C m m m ÷-=-6、D7、A 解析:2213272803m ⨯===>,A 中2536m <<,B 中1625m <<,C 和D 直接排除8、C解析:如图因为在RT ABO ∆中,//OC BA ,36AOC ∠=o,所以36BAO ∠=o,54OBA ∠=o如图做BE OC ⊥,sin sin36BO BAO AB AB=∠⋅=⋅o ,而sin sin 54BE BOE OB OB =∠⋅=⋅o ,而1AB =,sin36sin54BE ∴=o o ,即点A 到OC 的距离。
9、C解析:如图由所给的抛物线解析式可得A ,C 为定值(1,0)A -,(0,3)C -则10AC =,而3(,0)B k , ⑴ 0k >,则可得① AC BC =,则有223()310k +=,可得3k =② AC AB =,则有3110k +=,可得3101k =-, ③ AB BC =,则有23319()k k +=+,可得34k =⑵ 0k <,B 只能在A 的左侧④ 只有AC AB =,则有3110k --=,可得3101k =-+10、C解析:对方程组进行化简可得211x a y a =+⎧⎨=-⎩①31a -≤≤Q ,5213a ∴-≤+≤,仅从x 的取值范围可得知①错误②当2a =-时,33x y =-⎧⎨=⎩,则,x y 的值互为相反数,则②正确③当1a =时,30x y =⎧⎨=⎩,而方程43x y a +=-=,则,x y 也是此方程的解,则③正确⑤ 1x ≤,则211a +≤,则0a ≤,而题中所给31a -≤≤,则30a -≤≤,114a ≤-≤ 则14y ≤≤,选项④正确二、填空题11、2,1; 12、43m +,1; 13、6.56; 14、232b -≤≤; 15、15,1或9; 16、(1,1),(2,3),(0,2),(2,2)-----填空题解析 11、(1)2,(2)112、(1)43m +,(2)1解析:原代数式=(4)(4)43(4)3m m m m +-+=-,代入1m =-得原式=113、6.56解析:设年利率为%x ,由题可得不等式1000(1%)1065.6x +≥,解得 6.56x ≥ 解析:因为0a > 则0a >,而要使得不等式的值小于0,则只有30a -<,所以可得03a <<,可得2322a -<-<,则232b -≤≤14、 (1)15,(2)1或9解析:由题意可知, V Sh =,代入可易得下底面积为215cm而2200cm 为总的侧面积,则每一条底边所在的侧面积为250cm ,因为高为10cm ,所以菱形底边长为5cm ,而底面积为215cm ,所以高3AE cm =① 如图,E 在菱形内部EC BC BE =-,222594BE AB BE =-=-=,所以1EC =② 如图,E 在菱形外部EC BC BE =+,9EC =解析:如图三、解答题17、解:原式=2222232()()2228m m m m m m m m m m m -++---=-⨯⋅=-观察38m -,则原式表示一个能被8整除的数18、 解:k 只能-1,当1k =,函数为44y x =-+,是一次函数,一次函数无最值, 当2k =,函数为243y x x =-+,为二次函数,而此函数开口向上, 则无最大值当1k =-,函数为2246y x x =--+,为二次函数,此函数开口向下,有最大值,变形为22(1)8y x =-++,则当1x =-时,max 8y =19、解:(1)作图略(2)如图作外接圆由题可得,222(3)(4)(5)a a a +=, 222AB BC AC ∴+=,则ABC ∆为直角三角形,而=90ABC ∠o ,则AC 为外接圆的直径2=62ABC AB BC S a ∆⋅=,而2225=()24AC S aππ=圆 20、解:(1)第三边长为6,(212<<边长中,任意整数边长即可);(2)设第三边长为L ,由三角形的性质可得7575L -<<+,即212L <<,而组中最多有n 个三角形 =34567891011L ∴,,,,,,,,,则=9n ;(3)在这组三角形个数最多时,即=9n ,而要使三角形周长为偶数,且两条定边的和为12, 则第三边也必须为偶数, 则=46810L ,,,21、解:(1)在梯形ABCD 中,AD//BC ,AB CD =,而在正ABE ∆和正DCF ∆中,AB AE =,DC DF =且60BAE CDF ∠=∠=oAE DF ∴=且EAD FDA ∠=∠且AD 公共(2)如图作BH AD ⊥,CK AD ⊥,则有BC HK =同理22CD CK KD ==而234AEB DCF S S a ∆∆==而由题得AEB DCF S S S ∆∆+=梯22、解:(1)当2k =-时,(1,2)A -A Q 在反比例函数图像上∴设反比例函数为ky x =, 代入A 点坐标可得2k =-(2)要使得反比例函数与二次函数都是y 随着x 的增大而增大, 而对于二次函数2y kx kx k =+-,其对称轴为12x =-,要使二次函数满足上述条件,在0k <的情况下, 则x 必须在对称轴的左边,即12x <-时,才能使得y 随着x 的增大而增大∴ 综上所述,则0k <,且12x <-(3)由(2)可得15(,)24Q k --ABQ ∆Q 是以AB 为斜边的直角三角形A Q 点与B 点关于原点对称,所以原点O 平分AB 又Q 直角三角形中斜边上的中线是斜边的一半 作AD OC ⊥,QC OC ⊥ 而2221OA AD OD k =+=+则233k =,或233k =- 23、解:(1)OB AT ⊥Q ,且AE CE ⊥Q∴在CAE ∆和COB ∆中,90AEC CBO ∠=∠=o(图为一种可能的情况)而BCO ACE ∠=∠(2)33AE =Q ,30A ∠=o连结OM在MOB ∆中,OM R =,222MNMB ==, 而在COB ∆中,332BO BC OC == 又OC EC OM R +==Q 整理得2181150R R +-=23R ∴=-(不符合题意,舍去),或5R = 则5R =(3)在EF 同一侧,COB ∆经过平移、旋转和相似变换(无轴对称变换)后这样的三角形有3个,如图, 顶点在圆上的三角形如图所示,连结FO 过圆心交O e 于D ,连结DE 5EF =Q ,直径10FD =,可得30FDE ∠=o53ED ∴=,则510531553EFD C ∆=++=+ 由(2)可得33COB C ∆=+,1553533EFD OBC C C ∆∆+∴==+ (此问也可以通过相似比得出答案)。
2019年浙江省中考数学试卷(附答案与解析)
第2页(共24页)123如图的几何体由六个相同的小正方体搭成,它的主视图是()4C .0.42D .0.15,C ,量得170∠︒=,2100∠︒=,那么木条a ,b 所在()第5题图C .30︒D .70︒10)在同一直线上,则a 的值等于()C .3D .4()()53x x +-=经变换后得到抛物线(3)(5)y x x =+-,()B .向右平移2个单位D .向右平移8个单位65︒=,70C ∠︒=.若BC =则»BC的长为()第8题图C .2πD .E ,以EC 为边作矩形ECFG ,且边FG 过点D .在ECFG 的面积()第9题图B .先变小后变大毕业学校_____________姓名________________考生号_____________________________________________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷第3第4页(共24页)C .一直变大D .10.如图1,长、宽均为3,高为8面高为6意图,则图2中水面高度为图1第10题图A .245B .325C卷Ⅱ二、填空题(本大题有6小题,每小题5分,共3011.因式分解:21x -=.12.不等式324x-≥的解为.13.所表示的数是.第13题图14.如图,在直线AP 上方有一个正方形ABCD ,∠半径作弧,与AP 交于点A ,M ,分别以点A ,M 交于点E ,连结ED ,则ADE ∠的度数为.题14题图C 都在曲线ky x =(常数0k >,0x >)上,若顶点D的函数表达式是.第15题图分割成如图的四块,其中点O 为正方形的中心,点.用这四块纸片拼成与此正方形不全等的四边形MNPQ ,则四边形MNPQ 的周长是.第16题图17~20小题每小题8分,第21小题10分,第22,14分,共80分.解答需写出必要的文字说明、演算212-⎛⎫--- ⎪⎝⎭21x +,41x +的值相等?数学试卷第5页(共第6页(共24页)18.路程x (千米)的函数图象.(1)根据图象,直接写出蓄电池剩余电量为0150x ≤≤时,求1(2)当150200x ≤≤时,求y 关于x 蓄电池的剩余电量.19.小明、小聪参加了100 m 跑的5期集训,时间、测试成绩绘制成如下两个统计图.第19题图根据图中信息,解答下列问题:(1)这5期的集训共有多少天?小聪5(2底座的高AB 为5cm ,长度均为20cm 的连杆.BCD 成平角,150ABC ∠︒=,如图2,求连杆端点D C 逆时针旋转,使165BCD ∠︒=,如图3,问此时0.1cm ,参考数据:2 1.41≈,3 1.73≈)图2图3第20题图AB 的长为2,过点C 的切线交AB 的延长线于点D ..30D ∠︒=,求AD 的长.请你解答.AD 的长30A ∠︒=,连结OC ,就可以证明ACB V 与DCO V ,并解答.第21题图-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------毕业学校_____________姓名________________考生号_____________________________________________数学试卷第7第8页(共24页)22.有一块形状如图的五边形余料ABCDE ,AB =135C ∠︒=,90E ∠︒>并使所截矩形材料的面积尽可能大.(1)若所截矩形材料的一条边是BC 或AE (2)能否截出比(1最大值;如果不能,说明理由.23.(12分)如图1是实验室中的一种摆动装置,BC 的等腰直角三角形,摆动臂AD 可绕点A 旋转,10DM =.(1)在旋转过程中,①当A ,D ,M 三点在同一直线上时,求AM ②当A ,D ,M (2)若摆动臂AD 顺时针旋转90°,点D 2D 处,连结12D D ,如图2,此时2135AD C ∠︒=,260CD =,求2BD 的长.图1a ,BCb =,点M ,N 分别在边AB ,CD 上,点E ,FEF 交于点P ,记k MN EF =:.EF ⊥时,求k 的值..60MPE ∠︒=,3MP EF PE ==时,求:a b 第24题图数学试卷第9页(共第10页(共24页)浙江省绍兴市2019卷Ⅰ一、选择题1.【答案】A【解析】根据绝对值的性质求解.解:根据负数的绝对值等于它的相反数,得|5|5-=.故选:A.【考点】绝对值2.【答案】B【解析】科学记数法的表示形式为10na ⨯值时,要看把原数变成a 数相同.当原数绝对值1>时,n 解:数字126000000科学记数法可表示为81.2610⨯故选:B.【考点】科学计数法3.【答案】A个正方形,故A 符合题意,故选:A.【考点】三视图4.【答案】D【解析】先计算出样本中身高不低于180 cm 解:样本中身高不低于180 cm 的频率150.15100==,所以估计他的身高不低于180 cm 的概率是0.15.故选:D.【考点】统计,等可能事件的概率,根据三角形内角和定理计算,得到答案.1801007010︒︒︒︒=--=,180°再将点(,10)a 代入解析式即可;y kx b +=,;.,顶点坐标是(1,16)--.(1,16)-.2个单位长度得到抛物线(3)(5)y x x =+-,数学试卷第1112页(共24页)8.【答案】A【解析】连接OB ,OC .首先证明OBC △解:连接OB ,OC .∵180180657045A ABC ACB ∠=-∠-∠=-︒-︒=︒︒︒∴90BOC ︒∠=∴BC =∴2OB OC ==∴»BC的长为2902360ππ⋅⋅=,故选:A.【考点】三角形内角和,圆周角,圆心角,弧长公式9.【答案】D【解析】由BCE FCD △∽△,即可得矩形ECFG 与正方形ABCD 的面积相等.解:∵正方形ABCD 和矩形ECFG 中,90DCB FCE ︒∠=∠=,90F B ︒∠=∠=,∴DCF ECB ∠=∠,∴BCE FCD △∽△,∴CF CDCB CE=,∴CF CE CB CD ⋅⋅=,∴矩形ECFG 与正方形ABCD 的面积相等.故选:D.【考点】正方形,矩形,相似三角形10.【答案】A【解析】设DE x =,则8AD x -=,BG 于F ,由CDE BCF △∽△的比例线段5=,数学试卷第13页(共第14页(共24页)解:原式(1)(1)x x =+-.故答案为:(1)(1)x x +-.【考点】因式分解,平方差公式12.【答案】2x ≥【解析】先移项,再合并同类项,把x 的系数化为1解:移项得,342x +≥,合并同类项得,36x ≥,把x 的系数化为1得,2x ≥.故答案为:2x ≥.【考点】一元一次不等式13.【答案】4【解析】根据“解:根据“上的三个数之和都等于15,∴第一列第三个数为:15258--=,∴15834m =--=.故答案为:4【考点】一元一次方程14.【答案】15°或45°【解析】分点E 与正方形ABCD 的直线AP 解:∵四边形ABCD 是正方形,∴AD AE =,90DAE ∠=︒,∴180903060BAM ∠=︒-︒-︒=︒,AD AB =,当点E 与正方形ABCD 的直线AP ∴45ADE ∠=︒,当点E 与正方形ABCD 的直线AP ∴AE M '△为等边三角形,∴60E AM ∠'=︒,︒,,33k A ⎛⎫ ⎪⎝⎭,5,5k C ⎛⎫ ⎪⎝⎭,BD 的解析式.,35n k n +=+=,解得350m n ⎧=⎪⎨⎪=⎩,数学试卷第15第16页(共24页)16.【答案】6+或10或8+解:如图所示:图1的周长为1236+++=+;图2的周长为141410+++=;图3的周长为358++=+故四边形MNPQ 的周长是6+或10或8+故答案为:6+或10或8+三、解答题17.【答案】解:(1)原式341432=⨯+--=-.(2)2141x x +=+,240x x -=,(4)0x x -=,10x =,24x =.【解析】(1)根据实数运算法则解答;(2)利用题意得到2141x x +=+因式分解18.【答案】解:(115066035=-千米;,(200,10)代入,20=,0.5110y x =-+,当汽车已行驶180千米时,蓄.35千瓦时时汽车已行驶了150千米,据x 的函数表达式,再把180x =代入即可求出当汽车已.5710142056++++=(天),11.7611.6111.5311.62)511.68++++÷=(秒),5次测试的平均成绩是11.68秒;4期出现,建议集训时间定为14天.5期的集训共有多少天和小聪5次测试的平均.DE ⊥于O .数学试卷第17页(共第18页(共24页)图2∵90OEA BOE BAE∠=∠=∠=︒,∴四边形ABOE是矩形,∴90OBA=︒∠,∴1509060DBO∠=︒-︒=︒,∴sin60OD BD︒=⋅=,∴539.6(cm)DF OD OE OD AB=+=+=≈.(2)作DF l⊥于F,CP DF⊥于P,BG DF⊥于是矩形,图3∵60CBH∠=︒,90CHB∠=︒,∴30BCH∠=︒,∵165BCD∠=︒,45DCP∠=︒,∴sin60CH BC︒=⋅=,sin45DP CD︒=⋅∴DF DP PG GF DP CH AB=++=++=5 3.2(cm)-=.DE于O.解直角三角形求出OD即可解决问题.P,BG DF⊥于G,CH BG⊥于H.则四边形PCHG-DE即可解决问题.90DCB+∠=︒90OCD∠=︒,再根据含30度的直角2,然后计算OA OD+即可;的长,利用圆周角定理得到90ACB∠=︒,再证明数学试卷第19第20页(共24页)30A DCB∠=∠=︒,然后根据含3022.【答案】(1)①若所截矩形材料的一条边是BC 过点C 作CF AE ⊥于F ,16530S AB BC =⋅=⨯=;②若所截矩形材料的一条边是AE ,如图2所示:过点E 作EF AB ∥交CD 于F ,FG AB ⊥于G ,过点则四边形AEFG 为矩形,四边形BCHG 为矩形,∵135C ∠=︒,∴45FCH ∠=︒,∴CHF △为等腰直角三角形,∴6AE FG ==,5HG BC ==,BG CH FH ==,∴651BG CH FH FG HG ===-=-=,∴615AG AB BG =-=-=,∴*26530S AE AG ==⨯=;(2)能;理由如下:在CD 上取点F ,过点F 作FM AB ⊥于M ,FN ⊥则四边形ANFM 为矩形,四边形BCGM 为矩形,∵135C ∠=︒,∴45FCG ∠=︒,∴CGF △为等腰直角三角形,∴5MG BC ==,BM CG =,FG DG =,设AM x =,则6BM x =-,∴11FM GM FG GM CG BC BM x =+=+=+=-,∴22(11)11( 5.5)S AM FM x x x x x =⨯=-=-+=-+∴当 5.5x =时,S 的最大值为30.25.图1图2图3BC ,过点C 作CF AE ⊥于F ,得出,过点E 作EF AB ∥交CD 于F ,FG AB ⊥于G ,过AEFG 为矩形,四边形BCHG 为矩形,证出CHF △6FG ==,5HG BC ==,BG CH FH ==,求出1=,5AG AB BG =-=,得出26530S AE AG =⋅=⨯=;FM AB ⊥于M ,FN AE ⊥于N ,过点C 作CG FM⊥四边形BCGM 为矩形,证出CGF △为等腰三角形,CG ,FG DG =,设AM x =,则6BM x =-,11BC BM x=+=-,得出211x x +,由二次函数的性质即可得出结果.40DM +=,或20.AM AD DM =-=22223010800DM -=-=,.22230101000DM +=+=,.或.数学试卷第21页(共第22页(共24页)由题意:1290D AD ∠=︒,1230AD AD ==,∴2145AD D ︒∠=,12302D D =,∵2135AD C ︒∠=,∴1290CD D ︒∠=,∴221212306CD CD D D =+=∵2190BAC A AD ∠=∠=︒,∴2212BAC CAD D AD CAD ∠-∠=∠-∠,∴12BAD CAD ∠=∠,∵AB AC =,21AD AD =,∴21()BAD CAD SAS V V ≌,∴21306BD CD ==【解析】(1)①分两种情形分别求解即可.②显然MAD ∠不能为直角.当AMD ∠为直角时,根据222AM AD DM =-,计算即可,当90ADM ∠=︒时,根据222AM AD DM =+,计算即可.(2)连接CD .首先利用勾股定理求出1CD ,再利用全等三角形的性质证明21BD CD =即可.【考点】线段、角的和差,勾股定理,等腰直角三角形,全等三角24.【答案】(1)如图1中,Q ,设EF 交MN 于点O .1+80CEO ∠=︒, ,k 的值最大,最大值,k 的值最小,最小值为5.第24页(共24页)∴3MN EFPM PE==,∴2PN PFPM PE==,∵FPN EPM∠=∠,∴PNF PMEV V∽,∴2NF PNME PM==,//NFME设2PE m=,则4PF m=,6MP m=,12NP m=,①如图2中,当点N与点D重合时,点M恰好与B图2∵60MPE FPH∠=∠=︒,∴2PH m=,FH=,10PH m=,∴35a AB FHb AD HD===②如图3中,当点N与C重合,作EH MN⊥于H.图3∴13HC PH PC m=+=,∴tan13MB HEHCEBC HC∠=--,∵ME FC∥,∴MEB FCB CFD∠=∠=∠,MQ CD⊥于Q,设EF交MN于点O.证明.,当MN的长取最大时,EF取最短,此的最短时,EF的值取最大,此时k的值最小,3PE=,推出=3MN EFPM PE-,推出2PN PFPM PE==,2PNPM==,ME NF∥,设2PE m=,则4PF m=,2中,当点N与点D重合时,点N与C重合,分别求解即可.数学试卷第23。
2019年浙江版中考数学§9.2 旋转操作型问题(试题部分)

解析 ∵在△AOB中,∠AOB=90°,AO=3 cm,BO=4 cm,
∴AB= OA2 OB2 =5 cm, ∵点D为AB的中点,
∴OD= 12 AB=2.5 cm.
∵将△AOB绕顶点O按顺时针方向旋转到△A1OB1处, ∴OB1=OB=4 cm, ∴B1D=OB1-OD=1.5 cm. 故答案为1.5. 思路分析 先在直角△AOB中利用勾股定理求出AB的长,再利用直角三角形斜边上的中线等
如图1,若AD=AB,求证:①△BCE≌△ACF;②AE+AF=AC. (2)类比发现 如图2,若AD=2AB,过点C作CH⊥AD于点H,求证:AE=2FH. (3)深入探究
如图3,若AD=3AB,探究得: AE 3AF 的值为常数t,则t=
.
AC
解析 (1)证明:①∵平行四边形ABCD中,∠BAD=120°, ∴∠D=∠B=60°. ∵AD=AB,∴△ABC和△ACD为正三角形, ∴∠B=∠CAD=60°,∠ACB=60°,BC=AC. (2分) ∵∠ECF=60°,∴∠BCE+∠ACE=∠ACF+∠ACE=60°, ∴∠BCE=∠ACF, (3分) ∴△BCE≌△ACF(ASA). (4分) ②∵△BCE≌△ACF, ∴BE=AF,∴AE+AF=AE+BE=AB=AC. (5分) (2)证明:设DH=x,由已知,得CD=2x,CH= 3 x, ∴AD=2AB=4x,∴AH=AD-DH=3x. ∵CH⊥AD,∴AC= AH 2 CH 2 =2 3 x, ∴AC2+CD2=AD2,∴∠ACD=90°, ∴∠BAC=∠ACD=90°, (6分)
∴ CC ' = AC = 74 . BB ' AB 5
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
30°,∴BC=B'C= AB ' =8.
cos 30
图④ 综上所述,BC的长度为4或6或8或12.
2.(2017岳阳,23,10分)问题背景:已知∠EDF的顶点D在△ABC的边AB上(不与A,B重合).DE交 AC所在直线于点M,DF交BC所在直线于点N.记△ADM的面积为S1,△BND的面积为S2.
的仍是轴对称图形,则小红折叠的矩形纸片的长宽之比为
;
拓展应用
(4)在图2中,若∠B=30°,AB=4 3 ,当△AB'D恰好为直角三角形时,BC的长度为
.
解析 解决问题 (1)①B'D∥AC(互相平行). ②菱形. (2)结论仍成立. ①∵∠DAC=∠BCA,∠BCA=∠ACB', ∴∠ACB'=∠DAC,∴AE=CE. ∵B'C=AD,AE=CE, ∴B'E=DE, ∴∠CB'D=∠ADB'.
∴ AH =3,
CH
设CH=x, ∴BH=AH=3x, ∵BC=4,
∴3x+x=4, ∴x=1, ∴AH=3,CH=1, 由旋转知,∠EHF=∠BHD=∠AHC=90°,EH=AH=3,CH=DH=FH,
∴∠EHA=∠FHC, EH = FH =1,
AH HC
∴△EHA∽△FHC, ∴∠EAH=∠C, ∴tan∠EAH=tan C=3, ∴HP=3AP,∵AH=EH,∴AE=2AP, 在Rt△AHP中,AP2+HP2=AH2, 即AP2+(3AP)2=9,
解析 (1)证明:在Rt△AHB中,∠ABC=45°, ∴AH=BH,
BH AH,
在△BHD和△AHC中, BHD AHC 90,∴△BHD≌△AHC(SAS),
DH CH ,
∴BD=AC. (2)(i)如图,过点H作HP⊥AE于点P. 在Rt△AHC中, ∵tan C=3,
拓展应用
(4)4或6或8或12(答对一个得1分). 详解:如图①,当∠B'AD=90°时,∠B=∠AB'E=∠ADC=30°,AB'=AB=CD, 在△B'AE和△CDE中,∠AB'E=∠EDC,∠B'EA=∠DEC,∴∠DCE=∠B'AE=90°,∴AE=AB'tan 30°
=4,ED= CD =8,∴BC=AD=AE+ED=12.
cos 30
图①
如图②,当∠B'AD=90°时,∵CD∥AB,AD∥BC,∴∠B+∠BAD=180°,∴∠BAD=150°,∴∠BAB'=
60°,∴∠BAC=∠B'AC=30°,∵∠ACD=∠BAC=30°,∴AE=CE,∴B'E=ED,∴AE= 1 ED= 1 CD=
23
4 3 ,∴BC=AD= AE =4.
在Rt△AMG中,MG=AM·sin A= 3 AM,∴S1= 1 AD·MG= 3 AM.同理,S2= 3 BN,∴S1·S2=3 AM·BN=
2
2
2
2
12.
(3)(i)过M,N分别作MG⊥AB,NH⊥AB,垂足为G,H.
由(2)可知, AD = AM ,
BN BD
∴BN·AM=ab,∵MG=AM·sin α,∴S1=1 AD·MG=1 a·AM·sin α.
∴AP= 3 10 , 10
∴AE= 3 10 . 5
(ii)EF=2HG.理由如下: 由(i)知,△AEH和△FHC都为等腰三角形, ∴∠GAH=∠HCG=30°,设CG与AH交点为Q, ∴△AGQ∽△CHQ,
∴ AQ = GQ , CQ HQ
∴ AQ = CQ , GQ HQ
∵∠AQC=∠GQH, ∴△AQC∽△GQH,
解决问题
(1)在图1中,
①B'D和AC的位置关系为
;
②将△AEC剪下后展开,得到的图形是
;ห้องสมุดไป่ตู้
(2)若图1中的矩形变为平行四边形时(AB≠BC),如图2所示,结论①和结论②是否成立,若成立,
请挑选其中的一个结论加以证明,若不成立,请说明理由;
(3)小红沿对角线折叠一张矩形纸片,发现所得图形是轴对称图形,沿对称轴再次折叠后,得到
2
2
同理,S2= 12 b·BN·sin α,
∴S1·S2=
1 4
a2b2
sin2α.
(ii)S1·S2= 1 a2b2 sin2α.
4
3.(2016成都,27,10分)如图①,在△ABC中,∠ABC=45°,AH⊥BC于点H,点D在AH上,且DH=CH, 连接BD.
(1)求证:BD=AC; (2)将△BHD绕点H旋转,得到△EHF(点B,D分别与点E,F对应),连接AE. (i)如图②,当点F落在AC上时(F不与C重合),若BC=4,tan C=3,求AE的长; (ii)如图③,当△EHF是由△BHD绕点H逆时针旋转30°得到时,设射线CF与AE相交于点G,连接 GH,试探究线段GH与EF之间满足的等量关系,并说明理由.
∵∠AEC=∠B'ED,∠ACB'=∠CAD, ∴∠ADB'=∠DAC, ∴B'D∥AC. ②如图所示,设展开后点E的对应点为F(由题意知F在BC上). ∵四边形ABCD是平行四边形, ∴CF∥AE, ∴∠DAC=∠ACF, 由折叠可得,∠ACE=∠ACF,CE=CF, ∴∠DAC=∠ACE, ∴AE=CE, ∴AE=CF,
∴ EF = AC = CQ = 1 =2, HG GH QH sin 30
即EF=2HG.
中考数学 (浙江专用)
第九章 实验操作型专题
§9.4 操作探究型问题
好题精练
1.(2018黑龙江齐齐哈尔,23)综合与实践 折纸是一项有趣的活动,同学们小时候都玩过折纸,可能折过小动物、小花、飞机、小船
等,折纸活动也伴随着我们初中数学的学习. 在折纸过程中,我们可以通过研究图形的性质和运动、确定图形位置等,进一步发展空间观念, 在经历借助图形思考问题的过程中,我们会初步建立几何直观.折纸往往从矩形纸片开始,今 天,就让我们带着数学的眼光来玩一玩折纸,看看折叠矩形的对角线之后能得到哪些数学结论. 实践操作 如图1,将矩形纸片ABCD沿对角线AC翻折,使点B'落在矩形ABCD所在平面内,B'C和AD相交于 点E,连接B'D.
3
tan 30
图② 如图③,当∠ADB'=90°时,∵B'D∥AC,∴∠DAC+∠ADB'=180°,∴∠DAC=90°,∵∠ADC=∠B=30°, ∴BC=AD=CD·cos 30°=6.
图③ 如图④,当∠AB'D=90°时,∵B'D∥AC,∴∠B'AC+∠AB'D=180°,∴∠B'AC=90°,∵∠AB'E=∠B=
解析 (1)12. (2)过M,N分别作MG⊥AB,NH⊥AB,垂足为G,H. ∵∠ADM+∠MDN+∠NDB=180°, ∠ADM+∠A+∠DMA=180°,∠EDF=∠A, ∴∠NDB=∠DMA,又∵∠A=∠B,
∴△NDB∽△DMA,∴ AD = AM .
BN BD
∵AB=6,AD=4,∴BD=2, ∴BN·AM=AD·BD=8.
(1)初步尝试:如图①,当△ABC是等边三角形,AB=6,∠EDF=∠A,且DE∥BC,AD=2时,则S1·S2= ;
(2)类比探究:在(1)的条件下,先将点D沿AB平移,使AD=4,再将∠EDF绕点D旋转至如图②所示
位置,求S1·S2的值; (3)延伸拓展:当△ABC为等腰三角形时,设∠B=∠A=∠EDF=α. (i)如图③,当点D在线段AB上运动时,设AD=a,BD=b,求S1·S2的表达式(用a,b和α 的三角函数表 示). (ii)如图④,当点D在BA的延长线上运动时,设AD=a,BD=b,直接写出S1·S2的表达式,不必写出解 答过程.
∴四边形AECF是菱形. (3)1∶1或 3 ∶1(答对一个得1分,写成“1或 3 ”也正常给分) 详解:如图,沿对角线AC折叠时,当AB在射线AD上时,可得∠BAC=∠DAC=45°,AB=AD,四边形 ABCD是正方形,矩形长宽之比为1∶1;
如图,沿对角线AC折叠时,当AB不在射线AD上时,依题意得∠DAC=∠FAE=30°,设EF=ED=a,则 AF=AB= 3 a,AE=2a,所以AD=AE+ED=3a,矩形长宽之比为 3∶1.
