玻色分布和费米分布
波色统计和费米统计
A为常数,著名的斯特藩-玻尔兹曼定律
b
11
物理意义: 单位体积的辐射能只与温度有关, 与温度的四次方成正比。
b
12
适用量子分布的理想气体称之为简并气体。
1.费米分布 (适用自旋为1/2的电子系统)
FFD
1 e( )/kT
1
常记为 f ,称为费米能级
b
2
费米分布的性质
别:
b
3
费米能级的具体表示:
其中:n N 表示单位体积的自由电子数 V
b
4
f
f
0
1
2
8
Tc
2 2
mk
(N 2.612V
)2/3
玻色子的质量和粒子数密度决定。
b
7
物理意义:
超导体的正常态转化到超导态可用玻色凝聚解释
b
8
光子气体
平衡系统特点: 高频光子和低频光子总在不停地转换,因而光子数 量也在不断变化,系统中光子数不守恒。
b
9
上式称之为普朗克辐射公式。
b
10
上式为著名的维恩位移定律。 该定律可以用于确定很多星体表面的温度。
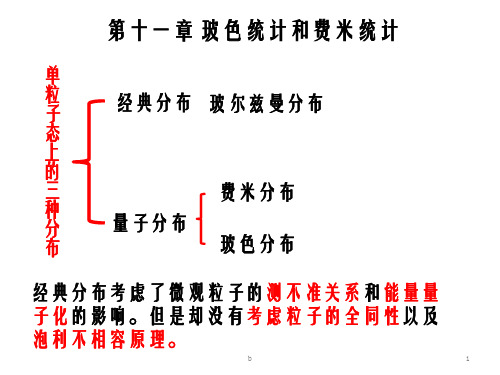
第十一章 玻色统计和费米统计
单
粒 子
经典分布 玻尔兹曼分布
态
上
的
三
费米分布
种 分 布
量子分布 玻色分布
经典分布考虑了微观粒子的测不准关系和能量量
子化的影响。但是却没有考虑粒子的全同性以及
泡利不相容原理。
b
1
粒子全同性的微观解释: 微观粒子具有波动性,它们在运动时无轨道可言, 因而无法用编号的方法追踪它们的运动,它们是 不可分辨的。 或者说,粒子的互换不产生新的微观态。
玻色分布和费米分布

玻色分布和费米分布现对费米分布推导如下 : 对 ()∏-=Ωl l l l l D F a a !!!..ωω 取对数得:()[]∑---=Ωl l l l l D F a !ln !ln !ln ln ..εωω N>>1,若假设a l >>1 , ωl >>1可得到:()()[]∑----=Ωll l l l l l l l D F a a a a ωωωωln ln ln ln ..约束条件:∑=llN a;∑=lll E a ε为求在此约束条件下的最大值,使用拉格朗日乘数法,取未定因子为α和β则拉格朗日函数为:l l l l l lD F a a aE N δβεαωβδαδδ∑⎪⎪⎭⎫ ⎝⎛++--=--Ωln ln .. 若令上式为零,则有:0ln=++-l l l l a a βεαω , 即上式给出了费米系统粒子的最概然分布,称为费米——狄拉克分布。
玻色分布的推导作为练习,请同学们课后自己推导. 6.8 三种分布的关系 1 、由∑=llN a∑=lll E aε确定拉氏乘子a 和β的值.在许多实际问题中,也往往将β看作由实验确定的已知参量而由∑=l ll aεE 确定系统的内能.或将a 和β都当作由实验确定的已知参量,而由∑=llN a∑=lll E aε确定系统的平均总粒子数和内能.2 、能级的εl 有ωl 个量子态处在其中任何一个量子态上的平均粒子数应该是相同的,因此处在能量为εS 的量子态S 上的平均粒子数为: sss a f ω=即: sss a f ω=定域系统 :seβεα--费米系统:11++se βεα 玻色系统:11++seβεα总粒子数和能量可分别表示为: N =∑ssf定域系统 =∑--sSe βεα“+”费米系统 “-”玻色系统 =∑±+sSe 11βεαE =∑sss f ε定域系统 =∑--ss Se βεαε“+”费米系统 “-”玻色系统 =∑±+ssSe 1βεαε(式中εs 为粒子的所有量子状态求和 )3 、若α满足 1>>αe , 则 有: ss e e a lll βεαβεαωω++≈±=1这时玻色分布和费米分布都过渡到玻耳兹曼分布,由上式可知:11<<=+le a llβεαω(对所有l )这时任一量子态上的平均粒子数都远小于1,这个式子就是前边提到的所谓的非简并性条件,当非简并条件满足时,费米分布和玻色分布都过渡到玻耳兹曼分布. 4 、在推导最概然分布时,应用了l >>1 , ωl >>1, al -ωl >>1等条件,这些条件实际上是不满足的,这是推导过程的一个严重的缺点,我们将在后边的学习中用巨正则系统求平均分布的方法严格地导出这些分布.5 、定域系统和满足经典极限条件的玻色(费米)系统虽然遵从同样的分布,但它们的微观状态数是不同的.前者为ΩM.B.,后者为ΩM.B ./N!因此对那些直接由分布函数导出的热力学量,两者具有相同的统计表达式.然而,对于例如熵和自由能等与微观状态有关的热力学量,两者的统计表达式有差异.6最可几分布的推导也可以推广到含有多个组元的情况。
玻尔兹曼系统、玻色子系统、费米子系统的区别及统计规律

玻尔兹曼系统、玻色子系统、费米子系统的区别及统计规律当描述粒子行为时,玻尔兹曼系统、玻色子系统和费米子系统有着不同的特点和统计规律。
下面对它们进行详细说明:玻尔兹曼系统:描述:玻尔兹曼系统适用于经典粒子,如分子和原子等。
这些粒子之间可以相互交换位置和能量,且粒子可以具有任意能量。
玻尔兹曼系统假设粒子之间是无差别可区分的。
统计规律:玻尔兹曼系统中的粒子遵循玻尔兹曼分布。
玻尔兹曼分布描述了粒子在可分辨的能级上的分布情况,其表达式为:P(E) ∝exp(-E/kT),其中P(E)表示具有能量E的粒子的概率,k是玻尔兹曼常数,T是系统的温度。
玻色子系统:描述:玻色子是具有整数自旋的粒子,如光子和声子等。
玻色子系统中的粒子可以占据相同的量子态,即多个粒子可以处于同一个量子态。
这种行为被称为玻色统计。
统计规律:玻色子系统中的粒子遵循玻色-爱因斯坦统计。
根据玻色-爱因斯坦分布,粒子的分布可以是任意整数,不受限制。
这意味着在低温条件下,大量玻色子可以集中在系统的最低能级,形成所谓的玻色-爱因斯坦凝聚。
费米子系统:描述:费米子是具有半整数自旋的粒子,如电子和中子等。
费米子系统中的粒子由于遵循泡利不相容原理,每个量子态只能被一个粒子占据。
这意味着费米子之间无法处于同一个量子态,也无法彼此交换位置。
统计规律:费米子系统中的粒子遵循费米-狄拉克统计。
根据费米-狄拉克分布,每个量子态最多只能被一个粒子占据。
在多粒子费米子系统中,由于每个量子态只能占据一个粒子,系统的能级填充依次递增,满足所谓的泡利不相容原理。
总结:玻尔兹曼系统适用于经典粒子,粒子之间无限制;玻色子系统适用于具有整数自旋的粒子,允许多个粒子占据同一个量子态;费米子系统适用于具有半整数自旋的粒子,每个量子态最多只能有一个粒子占据。
玻尔兹曼系统服从玻尔兹曼分布,玻色子系统服从玻色-爱因斯坦统计,费米子系统服从费米-狄拉克统计。
这些统计规律决定了粒子在不同系统中的分布特征和行为方式。
凝聚态物理学中的玻色子与费米子

凝聚态物理学中的玻色子与费米子凝聚态物理学是研究物质在宏观尺度上的性质和行为的领域。
在这个领域中,玻色子和费米子是两个重要的概念。
本文将探讨这两种粒子在凝聚态物理学中的重要性和应用。
玻色子和费米子是基本粒子的分类方式之一。
前者是具有整数自旋的粒子,如光子、声子、玻色-爱因斯坦凝聚(Bose-Einstein Condensate)中的粒子等;后者则是具有半整数自旋的粒子,如电子、质子和中子等。
这两种粒子的行为和性质有着显著的差异。
首先,玻色子和费米子的最显著区别之一是它们服从的统计分布。
根据玻色-爱因斯坦统计,多个玻色子可以占据同一个量子态,这就导致了Bose-Einstein凝聚的产生,其中所有粒子都处于同一个量子态,表现出量子相干性。
而根据费米-狄拉克统计,费米子不允许多个粒子处于同一个态,这也是为什么我们不能在同一时刻在同一个位置找到两个电子的原因。
这两种统计分布的不同给玻色子和费米子带来了截然不同的行为。
在凝聚态物理学中,玻色子和费米子有着不同的物理性质和相互作用。
作为最重要的实例之一,玻色-爱因斯坦凝聚是玻色子行为的一个突出例证。
在极低温度下,玻色子可以凝聚成一个巨大的波函数,而不再是彼此独立的实体。
这种凝聚体现了量子力学的特性,如相干性和波动性,是研究玻色子集体行为的有力工具。
与此相反,由于费米-狄拉克统计的限制,费米子之间的相互作用具有独特的属性。
著名的是,费米子统计下的电子导致了电子波函数的空间分布,进而导致了周期性的晶体结构。
这就是凝聚态物理学中晶体的形成原理之一。
费米子之间的排斥效应也导致了材料的稳定性,使得粒子之间不能靠得太近,从而形成凝聚态物质的基本结构。
除了上述的基本性质之外,玻色子和费米子在凝聚态物理学中还有广泛的应用。
玻色子激发态在超导体中扮演着重要的角色,通过与声子相互作用来传导电子。
费米子的行为则解释了诸如半导体和绝缘体等材料的电子结构,为材料的性质和行为提供了重要的基础。
冷原子物理学中的费米气体和玻色气体

冷原子物理学中的费米气体和玻色气体费米气体和玻色气体是冷原子物理学中两个重要的概念。
它们是描述冷原子系统中粒子行为的理论模型,对于研究凝聚态物理和量子信息等领域具有重要意义。
本文将对费米气体和玻色气体的特点、性质以及在研究中的应用进行探讨。
首先,费米气体和玻色气体的区别在于粒子的统计特性。
费米气体中的粒子遵循费米-狄拉克统计,即每个量子态只能被一个粒子占据,而且不同粒子之间不能占据相同的量子态。
这样的性质导致费米气体中的粒子更趋于分散分布,且有一定的排斥效应,使得费米气体表现出了一些与能带结构相关的特征。
相比之下,玻色气体中的粒子遵循玻色-爱因斯坦统计,不同粒子可以占据相同的量子态,且可以在低能态中集体聚集,形成玻色凝聚。
这两种不同的统计特性决定了费米气体和玻色气体在性质上的差异。
在冷原子物理学中,费米气体和玻色气体被广泛研究。
对于费米气体而言,一个重要的问题是费米子间的相互作用和凝聚性质。
由于费米气体中粒子之间的排斥效应,费米子一般不会形成玻色凝聚,但可以通过调控外界条件和相互作用来研究费米子的配对、多体效应和超流等现象。
这对于理解高温超导和凝聚态物理中的一些基本问题具有重要意义。
相比之下,玻色气体的研究重点在于玻色凝聚和量子相干性。
玻色凝聚是玻色气体中粒子在低温下集体同一量子态的现象,也被称为玻色-爱因斯坦凝聚。
这种凝聚态具有超流性质,能够产生相干的粒子流动。
对玻色凝聚的研究不仅对于理解凝聚态物理和相干性有重要意义,还有助于开发原子激光、量子计算和量子通信等领域的应用。
近年来,随着冷原子技术的发展,对费米气体和玻色气体的研究取得了许多重要成果。
科学家们利用光腔技术、强磁场和激光冷却等手段,成功地制备出了超冷原子气体,并通过精确控制粒子间的相互作用和外场条件,实现了一些新奇的量子现象。
例如,在费米气体中观察到了花式的BCS-BEC跨越,而在玻色气体中实现了有序的Bose-Einstein凝聚和超流态。
玻色子 费米子 声速

玻色子费米子声速玻色子(Boson)和费米子(Fermion)是量子力学中两种重要的粒子类型,它们具有不同的行为特征和统计规律。
声速则是介质中传播声波的速度,它与介质的物理性质和分子结构有关。
本文将探讨玻色子和费米子的特点,并介绍它们在声速中的应用。
一、玻色子(Boson)玻色子是一类自旋量子数为整数的粒子,它们遵循玻色-爱因斯坦统计。
根据波尔兹曼分布和玻色子的能级分布形式,我们可以得到以下玻色子的特点:1. 非排斥性:玻色子之间不具有排斥力,多个玻色子可以占据同一个量子态。
例如,光子就是一种玻色子,多个光子可以处于同一个能级。
2. Bose-Einstein凝聚:当低温下玻色子数目越来越多时,它们会聚集到最低能级,形成Bose-Einstein凝聚。
这种凝聚相态的产生使得玻色子具有特殊的量子统计行为,如超流和超导。
3. 玻色-爱因斯坦统计:根据玻色-爱因斯坦统计,玻色子的分布遵循玻尔兹曼分布,其能级上粒子的平均数为玻色-爱因斯坦分布函数。
玻色子在声速中的应用:玻色子在声学中的应用可以追溯到声子理论,它描述了晶体中声波的传播行为。
声子可以看作是晶体中的一种玻色子,它们的存在导致晶格在振动时不同原子之间的相互作用。
根据声子理论,声速与晶格的弹性性质和原子间力常数有关。
二、费米子(Fermion)费米子是一类自旋量子数为半整数的粒子,它们遵循费米-狄拉克统计。
根据波尔兹曼分布和费米子的能级分布形式,我们可以得到以下费米子的特点:1. 排斥性:费米子之间具有排斥力,根据泡利不相容原理,每个量子态最多只能被一个费米子占据。
例如,电子就是一种费米子,保证了原子内电子壳层填充的稳定性。
2. 费米-狄拉克统计:费米子的分布遵循费米-狄拉克统计,其能级上粒子的分布满足费米-狄拉克分布函数。
费米子在声速中的应用:费米子在声学中的应用较少,在固体物理中更为重要。
例如,费米子的行为解释了金属电导和半导体的性质。
电子作为一种费米子,在导体中由于费米能级的存在,只有能量小于费米能级的电子参与导电,这解释了金属的高电导性质。
玻色分布和费米分布

但遗憾的是,众多的实验物理 学家将自旋极化的氢原子气体降温, 并未观察到BEC现象。于是 Wieman和Cornell开始将兴趣转向 碱金属原 子气体,1995年,他们 将铷原子限制在磁阱中进行激光冷 却首次成功 的观察到原子气的 BEC现象。同年,MIT的Ketterle 也在钠原子气中实 现了BEC。 BEC的实现不仅在基础研究方面具 有重大意义,还可能在 “原子芯 片”和量子计算机等方面有广泛的 应用前景。因此2001年的诺 贝尔 物理学奖授予Wieman、Cornell和 Ketterle以表彰他们在BEC实验 方 面的开创性工作。
第八章 玻色统计和费米统计
在第六章,我们用最概然方法导出了这两种系统的 统计分布规律,本章将进一步介绍这两种分布在辐射场 和金属电子气体中的应用。
§8.1 热力学量的统计表达式
一、玻色分布和费米分布
玻色分布和费米分布可写为
2020年6月11日星期四
第八章 玻色统计和费米统计
al
l
e l
1
(8.1.1)
1 g
N V
h2
2 mkT
3/
2
2020年6月11日星期四
第八章 玻色统计和费米统计
Hale Waihona Puke U3 2NkT
1
1 23/ 2
1 g
N V
h2
2 mkT
3/ 2
讨论:
➢上式第一项是根据玻耳兹曼分布得到的内能; 第二项是由量子统计关联导致的附加能量,与微 观粒子的全同性原理有关。
➢费米气体的附加能量为正,费米子间表现出排 斥作用;玻色气体的附加能量为负,玻色子间表 现出吸引作用;
2020年6月11日星期四
第八章 玻色统计和费米统计
热力学 统计物理:第八章 玻色统计和费米统计

y
y l
e l • ( ) • ( l )
1
[ y
l
l
ln(1 e l
)]
1
l
l
y 1 e l
l
l l
e l 1 y
Y 1 ln p 1 ln
y
V
N ln
U ln
Y 1 ln
y
dN d ( ln )
dU d ( ln )
Ydy 1 ln dy
U ln ln[ (1 e l )l ]
l
[
l
l ln(1 e l )]
l
l
e l • ( l )
1 e l
l
ll
e l 1
广义力Y是 l 的统计平均值:
y
Y
l
l
y
al
l
l l
e l 1 y
Y也可通过配分函数求得:
Y 1 ln 1 ln[ (1 e l )l ]
y
(dU Ydy dN ) d ( ln ) ln dy d ( ln )
y
(dU Ydy dN ) d ( ln ) ln dy d ( ln )
y
d ( ln ) ln • d ln • d ln dy d ( ln ) ln • d ln • d
e l 1
在实际应用中,两种分布的区别在于将和看作已知常量(开系条件
的平均分布),还是将N和U看作已知常量(孤立系统的最概然分布)。
说明: 本节推导玻色系统和费米系统热力学量的 统计表达式时,采用平均分布观点,也就
是将、和y(粒子能量含外参量y)看作 已知参量,而将热力学量表达为、和y的
函数。
回顾:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
玻色分布和费米分布
现对费米分布推导如下 : 对 ()∏-=Ωl l l l l D F a a !
!!
..ωω 取对数得:()[]
∑---=Ωl l l l l D F a !ln !ln !ln ln ..εωω N>>1
,
若假设a l >>1 , ωl >>1可得到:
()()[]∑----=Ωl
l l l l l l l l D F a a a a ωωωωln ln ln ln ..
约束条件:
∑=l
l
N a
;
∑=l
l
l E a ε
为求在此约束条件下的最大值,使用拉格朗日乘数法,取未定因子为α和β则拉格朗
日函数为:l l l l l l
D F a a a
E N δβεαωβδαδδ∑⎪⎪⎭
⎫ ⎝⎛++--=--Ωln ln .. 若令上式为零,则有:0ln
=++-l l l l a a βεαω , 即
上式给出了费米系统粒子的最概然分布,称为费米——狄拉克分布。
玻色分布的推导作为练习,请同学们课后自己推导. 6.8 三种分布的关系 1 、由
∑=l
l
N a
∑=l
l
l E a
ε确定拉氏乘子a 和β的值.
在许多实际问题中,也往往将β看作由实验确定的已知参量而由∑=l l
l a
εE 确定系统的内
能.或将a 和β都当作由实验确定的已知参量,而由
∑=l
l
N a
∑=l
l
l E a
ε确定系统的平均
总粒子数和内能.
2 、能级的εl 有ωl 个量子态处在其中任何一个量子态上的平均粒子数应该是相同的,因此处在能量为εS 的量子态S 上的平均粒子数为: s
s
s a f ω=
即: s
s
s a f ω=
定域系统 :s
e
βεα--
费米系统:11++s
e βεα 玻色系统:
1
1
++s
e
βεα
总粒子数和能量可分别表示为: N =
∑s
s
f
定域系统 =
∑--s
S
e βεα
“+”费米系统 “-”玻色系统 =
∑±+s
S
e 1
1
βεα
E =
∑s
s
s f ε
定域系统 =
∑--s
s S
e βεα
ε
“+”费米系统 “-”玻色系统 =∑±+s
s
S
e 1
βεα
ε(式中εs 为粒子的所有量子状态求
和 )
3 、若α满足 1>>α
e , 则 有: s
s e e a l
l
l βεαβεαωω++≈
±=
1
这时玻色分布和费米分布都过渡到玻耳兹曼分布,由上式可知:
11<<=
+l
e a l
l
βεαω(对所有l )
这时任一量子态上的平均粒子数都远小于1,这个式子就是前边提到的所谓的非简并性
条件,当非简并条件满足时,费米分布和玻色分布都过渡到玻耳兹曼分布. 4 、在推导最概然分布时,应用了l >>1 , ωl >>1, al -ωl >>1等条件,这些条件实际上是不满足的,这是推导过程的一个严重的缺点,我们将在后边的学习中用巨正则系统求平均分布的方法严格地导出这些分布.
5 、定域系统和满足经典极限条件的玻色(费米)系统虽然遵从同样的分布,但它们的微观状态数是不同的.前者为ΩM.B.,后者为ΩM.B ./N!因此对那些直接由分布函数导出的热力学量,两者具有相同的统计表达式.然而,对于例如熵和自由能等与微观状态有关的热力学量,两者的统计表达式有差异.
6最可几分布的推导也可以推广到含有多个组元的情况。
