SPSS分析中学生成绩
SPSS教程-简单回归分析-案例及结果解释
案例:
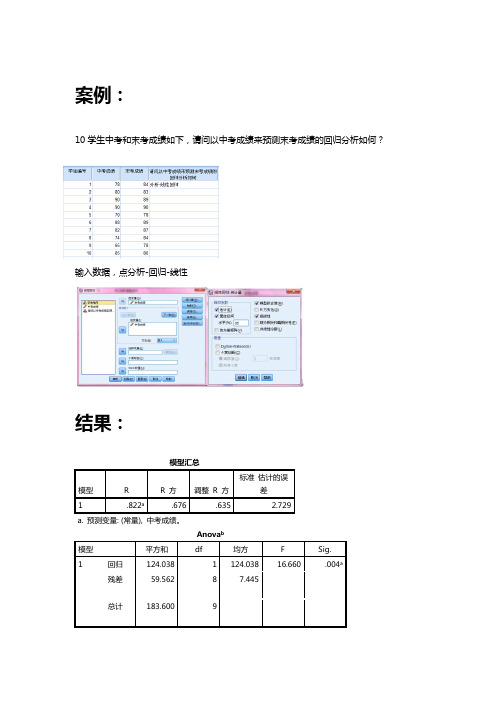
10学生中考和末考成绩如下,请问以中考成绩来预测末考成绩的回归分析如何?输入数据,点分析-回归-线性
结果:
模型汇总
模型R R 方调整R 方标准估计的误
差
1 .822a.676 .635 2.729
a. 预测变量: (常量), 中考成绩。
Anova b
模型平方和df 均方 F Sig.
1 回归124.038 1 124.038 16.660 .004a
残差59.562 8 7.445
总计183.600 9
R平方的F检验为16.660,达显著水平。
系数估计:个别变量,B,beta及显著性检验。
中考变量beta为0.822,达显著水平。
结果分析:
以中考成绩预测末考成绩,为单一回归分析,由于数学基础相同,简单回归与相关分析的主要结果相同。
Pearson相关系数、Multiple R与Beta皆为0.822,这几个系数的检验值均相同,达显著水平。
R平方则提供回归变异量,显示中考成绩预测末考成绩有63.5%的解释力,F(1,8)=16.66,p=0.004,显示该解释力具有统计上的意义。
系数估计的结果指出,中考成绩能够有效预测末考成绩,beta系数达0.822(t=4.082, p=0.004), 表示中考成绩越高,末考成绩越好。
用spss对学生成绩进行分析

vvSPSS统计分析软件>>课程设计报告班级___________________姓名___________________学号___________________指导教师________________用统计软件spss 分析学生成绩摘要:应用统计软件spss ,对某校一、二班学生语文,数学,英语成绩进行分析。
学生成绩分析是考试后老师应做的一项比较麻烦的工作,主要包括:计算平均值和标准差,绘制学生成绩分布直方图等,用统计分析软件spss 来进行这类数据的处理,速度快,直观,全面。
spss 是世界顶尖的统计软件,其功能- 几乎涵盖了数理统计的各个方面,适用于自然科学于社会科学各个领域进行分析统计,给人们进行数据分析爱来很大方便。
关键字:频数分析,描述性分析,均值比较,独立样本均值检验一、数据调查(1)数据调查方法:由于学校的班级比较多,涉及到学生有上千人,如果对于每一个学生的学习成绩进行普查,会加大工作难度,并且不利于从繁杂的数据中获取信息。
因此采用抽样的方法进行数据调查。
(2)数据来源:抽取一班、二班的各十名,共二十名同学,采集语文成绩,数学成绩,英语成绩作为本次统计分析的表1学生成绩表(原始数据)重Untitled - SPSS Data EditorFile Ed ft View 1~ransform Analyze Gr叩辰Utilities V胡回刮團口创京創嚴| c|fe| S J B I E!翌I鱼q:班飯[班Filw Edit DdU IriihifsHm And 餌# £炖谕$ U^I I JK Windcw H#ipB£|B KI1、spss软件应用分析1、频数分析(1)语文成绩的频数分析-r rrequenciesStall sties语文成绩语文成绩66刖7071757E7778S003es@6878E由分析可得,语文成绩为86分的最多,占总人数15% (2)数学成绩频数分析丰FrequenciesStalistks数学成绩N ValidMissing 20 0语文成城0.0FrequencyPercentValid PercentCumulMive PercentValid 401 5.0505,04915.0 5.0 10.060 3 15 0 15.0 250C2 210 010.0 35.0 €6 1 5.&5.0 40.0 69 1 50 50 45J 71 15.05.0 50.073 210.010.0 旳074 1 5.0 5.0 65.0 76 15.05.0 70.078 15,05,0 75,0 S2 15 0 5.0 SD.O£315 0 5.0 85.01 5 0 5.0 90.0 的 1 5.0 5.0 95.0 SO 1 5 0 50 100.0Total20100.0100.0由此得知,数学成绩为60分的人数最多,占总人数的15%『O 5 V _£^2.1 .匚曲ri□(3)英语成绩频数分析* FrequenciesStatistics英语成绩英语成绩Histogrdin2-Nteai-72.35Sid. De¥,^ 10723 忖=20有分析得知,英语成绩为78分的人最多。
SPSS相关分析在学生成绩分析中的应用

SPSS相关分析在学生成绩分析中的应用SPSS相关分析在学生成绩分析中的应用[摘要] 成绩分析是每所学校期中、期末考试之后对教学常规管理的一项基本要求,也是全面提高教学成绩重要的方法和途径。
随着IT 技术的发展,各学校分别采用了不同的应用软件对成绩进行质量分析,从中发现问题并加以改进,以提高教师的教学质量。
本文介绍了SPSS 统计软件的相关分析功能在考试成绩分析中的应用,建立了成绩分析模型,并给出了对学生考试成绩进行分析的SPSS 软件操作方法。
运用此方法,可以直观、高效、科学地对学生的成绩质量进行分析。
[关键词] SPSS;相关分析;成绩;应用1 相关分析概述任何事物的变化都是与其他事物相互联系和相互影响的,用于描述事物数量特征的变量之间自然也存在一定的关系。
变量之间的关系归纳起来可以分为两种类型,即函数关系和统计关系。
当一个变量x取一定值时,另一变量y可以按照确定的函数公式取一个确定的值,记为y = f(x),则称y是x的函数,也就时说y与x两变量之间存在函数关系。
函数关系是一一对应的确定性关系,比较容易分析和测度。
可是在现实中,变量之间的关系往往并不那么简单。
描述变量之间线性相关程度的强弱,并用适当的统计指标表示出来的过程为相关分析。
在实际中,因为研究目的不同,变量的类型不同,采用的相关分析方法也不同。
比较常用的相关分析方法是二元定距变量的相关分析、二元定序变量的相关分析、偏相关分析和距离分析,统称二元变量的相关分析。
二元变量的相关分析是指通过计算变量间两两相关的相关系数,对两个或两个以上变量之间两两相关的程度进行分析。
在二元变量的相关分析过程中比较常用的几个相关系数是Pearson简单相关系数、Spearman和Kendall’s tau-b等级相关系数。
二元定距变量的相关分析是指通过计算定距变量间两两相关的相关系数,对两个或两个以上定距变量之间两两相关的程度进行分析。
定距变量又称为间隔(interval)变量,它的取值之间可以比较大小,可以用加减法计算出差异的大小。
运用SPSS软件因子分析学生综合成绩的管理

关键词 : S P S S 统计学软件;学生综合成绩;因子分析 中图分 类号 :G 6 4 8
要 的公共 因 子,研 究并且挖 掘 出数据 的共性 , 从 而
来 说明火量需要研 究的变 量里面所存在 的内在 联系 。
S P S S因 子分析 的核心 思想 是:通 过对 变量 的矩
阵 内在框 架的的分析 ,得到中间 的核心 变量,从而达
也 就是 说,运用 S P S S软件 因子 分子对 学生 的综合 成 剑研 究所有 变量之 间的内在关系 ,但是就 是这 L 个核 绩进 行充分的分析 ,从里面分 析并且确定所 存在的极 心变量是无法真 正观测 到的 , 过我 们把它称之为 囚子 。
么 样 学 生成 绩 的数 据 中解读 出有利 于教 学 的 内容 它把众 多的指标综合成几 个为数较少 的指标 ,这些指
呢 ?如何从学生 的综 合成绩数据 中挖掘 出学 生的潜在 标 即因子指标 。
能力呢 ? 因子 分析 具体就 是指探 讨 怎么样 用很 小很
因子分析 ( F a c t o r A n a l y s i s )是 S P S S主要部分
山 东 纺 织 经 济
2 0 l 4 年第 2 期( 总第 2 0 4期 )
运 用 SP SS 软 件 因 子 分 析 学 生 综 合 成 绩 的 管 理
荣立 元
( 青岛大学 商学 院公共管理学院 2 6 6 0 7 1 )
[全]SPSS数据分析,基于因子分析学生成绩综合评价
![[全]SPSS数据分析,基于因子分析学生成绩综合评价](https://img.taocdn.com/s3/m/6c7b64ef7375a417876f8f15.png)
SPSS数据分析,基于因子分析学生成绩综合评价因子分析在成绩综合评价中的应用成绩可以是多方面的,包括在校大学生的考试成绩、高考生的入学成绩、公务员考试的笔试(面试)成绩、公司员工或政府官员的测评考核成绩等,本节以学生的考试成绩为例,利用因子分析进行对考核对象的综合评价。
学生成绩能反映学生掌握知识和各种能力的程度,综合得分是评价一个学生学习好坏、评定奖学金和评先评优等工作中最重要的一个指标,也是择优推荐就业很主要的参考因素。
因此,合理的、公平的、科学的对学生成绩做出综合评价显得格外重要。
因子分析概念因子分析是多元统计的重要分析方法之一,其基本思想是根据相关性大小对变量进行分组,使得同组内的变量之间相关性较高,不同组的变量之间相关性较低,每组变量代表了一个基本结构,因子分析中将之称为公共因子。
因子分析在教育学、社会经济学、心理学等领域都有广泛的应用价值。
数据来源SPSS操作依次单击菜单“分析—降维—因子”执行因子分析过程,选取变量。
点击“描述”按钮,依次选系数、显著性水平、KMO 和巴特利特球形度检验,点击继续,返回主菜单。
单击“提取”按钮,勾选“碎石图”,其他选项默认,选择主成份法进行因子提取。
单击“继续”按钮返回主面板。
单击旋转按钮,单击选中最大方差法单选框,表示采用方差最大旋转法进行因子旋转。
单击继续按钮返回主面板。
单击得分按钮,勾选底部的显示因子得分系数矩阵复选框。
单击继续按钮返回主面板。
设置完毕后,点击确定,生成结果。
结果分析KMO检验和Bartlett球形检验。
如图22-11所示,KMO检验研究变量间的偏相关性,计算偏相关时控制了其他因素的影响,所以比简单相关系数要小,一般KMO统计量大于0.9时效果最佳,0.7以上可以接受,0.5以下不宜作因子分析,本例KMO取值0.857进一步印证了作因子分析的必要性。
Bartlett球形检验统计量的Sig值小于0.01,由此否定相关矩阵为单位阵的零假设,即认为各变量之间存在显著的相关性,这与从相关矩阵得出的结论致。
基于某SPSS统计软件对学生成绩地分析报告

基于SPSS统计软件对学生成绩的分析陈利利摘要:应用统计软SPSS,对某校法律专业一、二班76名学生的民法科目的期末成绩进行分析。
学生绩分析是教师应做的一项比较麻烦的工作,主要包括:计算平均值和标准差,绘制学生成绩分布直方图等。
SPSS(Statistics Package for Social Science)社会科学统计软件是全球知名的统计分析软件之一。
运用SPSS 统计软件对学生成绩进行分析处理,速度快、直观、全面,对后续的教学工作和课程评价有着重要意义。
关键字:频数分析,描述统计,独立样本t检验一、数据调查(1)数据调查方法:由于学校的班级和考试科目比较多,如果对于每一个学生的学习成绩进行普查,会加大工作难度,并且不利于从繁杂的数据中获取信息。
因此本文采用抽样的方法进行数据调查。
(2)数据来源:抽取2015级法律专业一班、二班,共七十六名同学,采集民法和英语的期末成绩作为本次统计分析的对象。
二、SPSS软件应用分析统计分析的目的在于研究总体特征。
描述性统计分析是统计分析的第一步,是统计分析的基础,它包括数据的收集、整理、显示,对数据中有用信息的提取和分析。
做好这一步是进行正确统计推断的先决条件。
通过描述性统计分析可以大致了解数据的分布类型和特点、数据分布的集中趋势和离散程度,或对数据进行初步的探索性分析(包括检查数据是否有错误,对数据分布特征和规律进行初步观察)。
1、频数分析(Frequencies)1频数分析多适用于离散变量,其功能是描述离散变量的分布特征。
对把握数据的分布特征是非常有用的。
(1)民法成绩的频数分析输出的结果及解释:系统输出的频数检验结果见表1、表2和图1。
表 1法律专业学生民法成绩统计表1频数分析多适用于离散变量,其功能是描述离散变量的分布特征。
统计量民法N 有效76缺失0均值81.45中值82.50众数83标准差 5.338方差28.491偏度-3.025偏度的标准误.276峰度13.744峰度的标准误.545极小值54极大值90表1为76名法律专业学生的民法科目期末成绩统计表,给出了数据的描述统计量。
基于SPSS统计软件对学生成绩的分析

基于SPSS统计软件对学生成绩的分析基于SPSS统计软件对学生成绩的分析陈利利摘要:应用统计软SPSS,对某校法律专业一、二班76名学生的民法科目的期末成绩进行分析。
学生绩分析是教师应做的一项比较麻烦的工作,主要包括:计算平均值和标准差,绘制学生成绩分布直方图等。
SPSS(Statistics Package for Social Science)社会科学统计软件是全球知名的统计分析软件之一。
运用SPSS 统计软件对学生成绩进行分析处理,速度快、直观、全面,对后续的教学工作和课程评价有着重要意义。
关键字:频数分析,描述统计,独立样本t检验一、数据调查(1)数据调查方法:由于学校的班级和考试科目比较多,如果对于每一个学生的学习成绩进行普查,会加大工作难度,并且不利于从繁杂的数据中获取信息。
因此本文采用抽样的方法进行数据调查。
(2)数据来源:抽取2015级法律专业一班、二班,共七十六名同学,采集民法和英语的期末成绩作为本次统计分析的对象。
二、SPSS软件应用分析统计分析的目的在于研究总体特征。
描述性统计分析是统计分析的第一步,是统计分析的基础,它包括数据的收集、整理、显示,对数据中有用信息的提取和分析。
做好这一步是进行正确统计推断的先决条件。
通过描述性统计分析可以大致了解数据的分布类型和特点、数据分布的集中趋势和离散程度,或对数据进行初步的探索性分析(包括检查数据是否有错误,对数据分布特征和规律进行初步观察)。
1、频数分析(Frequencies)1频数分析多适用于离散变量,其功能是描述离散变量的分布特征。
对把握数据的分布特征是非常有用的。
(1)民法成绩的频数分析输出的结果及解释:系统输出的频数检验结果见表1、表2和图1。
1频数分析多适用于离散变量,其功能是描述离散变量的分布特征。
图1为76名法律专业学生民法科目期末成绩分布的直方图。
从图中可以看出数据分布的频数与标准正太分布存在差异。
分布曲线有一个较长的左,并且比标准正态分布的峰值高出许多,这与偏度系数与峰度系数一致。
用spss对学生成绩进行分析

<<SPSS统计分析软件>> 课程设计报告班级姓名学号指导教师用统计软件spss分析学生成绩摘要:应用统计软件spss,对某校一、二班学生语文,数学,英语成绩进行分析。
学生成绩分析是考试后老师应做的一项比较麻烦的工作,主要包括:计算平均值和标准差,绘制学生成绩分布直方图等,用统计分析软件spss来进行这类数据的处理,速度快,直观,全面。
spss是世界顶尖的统计软件,其功能-几乎涵盖了数理统计的各个方面,适用于自然科学于社会科学各个领域进行分析统计,给人们进行数据分析爱来很大方便。
关键字:频数分析,描述性分析,均值比较,独立样本均值检验一、数据调查(1)数据调查方法:由于学校的班级比较多,涉及到学生有上千人,如果对于每一个学生的学习成绩进行普查,会加大工作难度,并且不利于从繁杂的数据中获取信息。
因此采用抽样的方法进行数据调查。
(2)数据来源:抽取一班、二班的各十名,共二十名同学,采集语文成绩,数学成绩,英语成绩作为本次统计分析的表1 学生成绩表(原始数据)二、spss软件应用分析1、频数分析(1)语文成绩的频数分析由分析可得,语文成绩为86分的最多,占总人数15% (2)数学成绩频数分析由此得知,数学成绩为60分的人数最多,占总人数的15%。
(3)英语成绩频数分析有分析得知,英语成绩为78分的人最多。
占总人数的15%。
2、描述性统计有分析得知:语文成绩的最低分是66分,最大值是88分,标准差是7.725。
数学成绩的最低分是40分,最大值是90分,标准差是13.214 。
英语的最低分是44分,最大值是89分,标准差是10.723可见,英语的标准差最大,水平相差较大。
3、均值比较独立样本均值检验一班和二班的英语成绩分组统计量表独立样本均值检验表由图得知:分组统计量表显示两组数据的样本容量,均值,标准差,和抽样平均误差。
一班的英语平均成绩低于二班。
独立样本均值检验表包含了两组样本的独立检验统计量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017年《SPSS技术应用》----期末考核论文基于SPSS的中学化学例题教学效果研究----以延吉市某中学为例二〇一七年六月摘要课程改革以来,课堂教学备受关注,尤其是如何实现高效课堂,是目前中学师生迫切需要解决的问题。
中学化学是一门自然科学,本身具有微观性和抽象性的特点,使初中生在学习时比较困难,而例题是指导学生如何运用所学知识的范例,例题教学是中学化学课堂常见的教学方法。
本文通过调查统计对一个班级初中生实施案例教学前后的化学成绩,用SPSS统计软件进行对所得数据进行了描述量统计,方差齐性分析,独立单样本T 检验分析和相关分析,得出了在中学化学课堂上实施案例教学,有利于增强学生学习兴趣,提高学习积极性,进而提高化学成绩的结果。
得出中学化学教师应该根据教学内容合理地选择例题并充分利用例题,以促进初中生对化学概念原理的认识和理解,对化学规律和方法的掌握以及化学学习效率的提高。
关键词:中学化学案例教学 SPSS软件统计分析目录摘要II目录III第一章绪论11.1 研究背景11.2 研究目的及意义11.3 国内外研究现状21.3.1 SPSS应用国内外研究现状21.3.2 案例教学国内外发展与研究3 第2章相关概念及理论依据42.1 概念界定42.1.1例题42.1.2例题教学42.1.3 描述性统计分析42.1.4 T检验42.1.5 相关分析5第三章教学实施结果统计分析63.1 数据来源63.2 数据分析63.1.1描述性统计结果73.1.2 独立单样本t-检验结果73.1.2 相关分析结果9第4章结论与建议104.1 研究结论104.2 研究建议10参考文献11第一章绪论1.1 研究背景近年我国一直在进行教育改革,提出要在“以人为本”的基础上培养学生的综合能力和科学素养,鼓励学生积极参与到课堂上,与老师和同学进行讨论学习,学会发现与创新,这和传统的教学方式不同,要求师生的教学观念和教学方法发生转变。
例题作为中学化学教材和教学内容的重要组成部分,重要作用不言而喻,而现阶段对中学化学课堂上例题教学情况及效果的研究不多。
由初中化学教材上对于化学的定义可以知道化学具有科学性;其次,化学所研究的内容是原子和分子水平的,具有微观性、抽象性,有研究表明正确地使用化学课本中的例题,发掘化学例题的潜在价值,有利于对中学生理解并掌握化学概念和原理等抽象(微观)的化学基础知识,也有助于培养学生学习化学的兴趣和能力,这与我国教育改革中提倡的在“以人为本”的基础上培养学生的综合能力和科学素养相吻合。
SPSS是世界上最早采用图形菜单驱动界面的统计软件,也是国际上最有影响的三大统计软件之一[1],具有分析结果清晰、直观、易学易用的特点,已经在我国的社会科学、自然科学的各个领域发挥了巨大作用。
该软件还可以应用于经济学、统计学等方面,今年也有在教育学方面有所应用。
将SPSS统计软件与教育教学相联系,分析学生的学习情况,检测教学方法和策略等实施的效果等非常好。
因此本文调查了延吉市某中学高一一个班级29名学生的化学成绩,并通过SPSS软件分析了例题教学法前后,中学生化学成绩的显著性差异以及物理、数学成绩与化学成绩的相关性,进一步探讨例题教学对中学生化学学习成绩的影响。
1.2 研究目的及意义通过问卷了解中学化学老师对例题教学的认识情况和使用情况。
通过统计分析学生的化学成绩,了解案例教学在中学化学课堂上的效果。
进而探讨学生学习兴趣的激发,学习效率的提高。
为中学化学教师及广大的师范生提供一个具体的数据以及一些建议。
1.3 国内外研究现状1.3.1 SPSS应用国内外研究现状SPSS统计软件在学科中应用的研究涉及到的领域很宽泛,如教育学、心理学等学科。
国外首先国外Danie 在《应用SPSS在教育中做定量研究》按照实验研究的设计与分析思路对SPSS统计软件的功能操作进行了介绍[2],对SPSS在教育中定量研究有很大的借鉴,使用真实数据集来进行教育研究,软件的功能介绍内容全面,但没有讲解具体的数学公式将统计原理与之结合指引。
《在教育和社会研究中应用SPSS定量方法》一书中强调建模中的数据分析的核心概念[3],应用SPSS在教育和社会中做定量研究,以科学研究的思路介绍SPSS统计软件的操作方法,但是操作研究需要一定的基础实践操作能力。
此类书籍主要将SPSS应用于具体学科领域的研究,有一定的针对性,研究分析的案例数据也是与学科相对应,具有很强的操作性和理论指导意义。
总的来看,国外对于SPSS统计软件的研究应用各方面都比较深入,对于SPSS软件的研究结合了具体的数据资料进行分析,将统计原理与具体的操作应用相结合,对于各个学科的专业研究指导性也较强,SPSS软件已经被宽泛的应用到医学、社会科学和心理学等学科,应用研究也具有很强的操作性和针对性。
国内,目前针对教育学SPSS软件应用主要在试卷分析和实验数据处理和成绩痛等方面。
李玲在《基于SPSS软件的《计算机基础》试卷分析》(2016年)一文中提出通过SPSS软件对试卷质量在信度、难度、区分度等方面进行量化分析[4],适当调整或舍弃不符合指标的题目,可以防止教师出题的随意性,有利于试卷的标准化,能更合理、科学、有效的测试出学生的真实水平。
刘飞等人在《利用SPSS和EXCEL实现LSD多重比较的字母标记》一文中提出科技论文中单因素多重比较后样本间经常需要进行多重比较,并用字母进行标记[5]。
当样本较多,要进行字母标记比较费时,大部分统计软件不能够直接将比较结果进行标记。
如果结合SPSS进行方差分析和LSD多重比较,然后利用EXCEL的公式,快捷地实现字母的标记。
总体来看,将SPSS统计软件应用于教育教学方法研究中的较少。
1.3.2 案例教学国内外发展与研究苏格拉底的学生柏拉图将他与老师一问一答式的教学方式编成书,以一个个故事为媒介来教育别人明白故事中的道理。
这也是最早的案例教学法雏形,同时也为后来将案例在课堂中的应用提供了一个方法论的指导。
现代的案例教学首先出现在法学院的教学中,哈佛大学法学院前院长克里斯托弗·哥伦布-兰代尔于1870年创立了案例教学法。
这种教学方法是以法律科学为基础,以案例为素材,以苏格拉底的“问答法”为教学手段,以“像律师一样思考”为目标,能够培养学生科学和理性的思维精神,能够通过个别决策的推广到对法律规则的一般化理解。
1986年美国卡耐基教育与经济论坛成立的教学专业小组发表了教育改革报告书:《准备就绪的国家——21世纪的教师》中提到“应该把案例教学法发展成教学的主要焦点”。
目前,已出现了许多师资培训课程的案例手册,这些都极大的推动了案例教学的发展。
我国出现案例教学法相对较晚,基本从改革开放初期开始,1979年,我国工商行政代表团访问美国,将案例教学法介绍到了国内。
但在开始,案例教学法在中国的发展是比较缓慢的。
近几十年,案例教学法在我国发展迅速,案例教学应用于化学教学,是在国际科学教育和化学课程改革的大趋势下,以提高学生的科学素养为主旨的课程理念的一种积极的探讨,对于培养学生的科学探究能力和终身学习的能力大有益处。
第2章相关概念及理论依据2.1 概念界定2.1.1例题例题是一种用来指导学生如何将所学知识应用于解题过程的范例。
例题一般有下面几个功能:对所学知识的巩固;对解题过程的示范;某一题型思考方法的揭示等。
除此之外,也有学者提出化学例题能帮助中学生正确理解学习的知识;给学生提供科学的解题思路与方法;促使学生规范学习行为的养成;增强学生的应用意识。
例题可以促进学生积极主动地去探索并解决问题,促进学生心智发展水平的不断提高,以及发散思维、严谨态度等科学素养的形成。
2.1.2例题教学例题讲解是课堂中的重要环节,基本每堂课都会涉及到例题教学。
波利亚说:“中学数学教学的首要任务是习题教学[6]。
教师要充分发挥例题教学的示范和引领作用,使之成为促进学生发展的有效途径。
”其实化学教学也一样,通过例题教学可以帮助学生领悟化学思想方法,探寻并掌握化学学习的“捷径”[7],提高教与学的效率。
2.1.3 描述性统计分析所谓描述性统计分析,就是对一组数据的各种特征进行分析,以便于描述测量样本的各种特征及其所代表的总体的特征。
描述性统计分析的项目很多,常用的如平均数、标准差、中位数、频数分布、正态或偏态程度等等[8]。
这些分析是复杂统计分析的基础,是统计分析的第一步,做好这第一步是下面进行正确统计推断的先决条件。
做描述性统计分析要报告以下4个统计量:均值、标准差、最小值和最大值[9]。
之后做直方图,判断数据是否符合正态分布。
2.1.4 T检验T检验,亦称student t检验(Student's t test),主要用于样本含量较小(例如n<30),总体标准差σ未知的正态分布资料[10]。
t检验是用t分布理论来推论差异发生的概率,从而比较两个平均数的差异是否显著。
它与f检验、卡方检验并列。
t检验是戈斯特为了观测酿酒质量而发明的。
2.1.5 相关分析相关性分析是指对两个或多个具备相关性的变量元素进行分析,从而衡量两个变量因素的相关密切程度[11]。
当两个变量的标准差都不为零时,相关性系数才有定义。
当一个或两个变量带有测量误差时,他们的相关性就会受到削弱。
相关系数是变量之间相关程度的指标。
Pearson相关系数[12]用来衡量两个数据集合是否在一条线上面,它用来衡量定距变量间的线性关系。
皮尔逊相关系数大于0 ,表两变量正相关;小于0,表两变量负相关。
第三章教学实施结果统计分析3.1 数据来源本论文数据来自延吉市某中学初三班级月考成绩,笔者去该学校实习,以实习班级为研究对象,统计了该29名同学在接受案例教学前的化学成绩(C1)和实施后的成绩(C2),并统计了他们的的数学成绩和物理成绩,分析数学(第二列)、物理成绩(第三列)对化学成绩(第一列,满分50分)的影响。
数据如下:前30.00 56.00 78.00 前36.00 68.00 75.00 前21.00 56.00 78.00 前40.00 65.00 45.00 前35.00 98.00 85.00 前34.00 65.00 68.00 前35.00 98.00 70.00 前26.00 78.00 53.00 前30.00 58.00 89.00 前31.00 65.00 78.00 前24.00 65.00 56.00 前44.00 34.00 80.00 前28.00 98.00 64.00 前40.00 43.00 67.00 前36.00 46.00 67.00 前38.00 67.00 89.00 前38.00 65.00 96.00 前32.00 89.00 43.00 前45.00 32.00 45.00 前25.00 32.00 56.00 前31.00 34.00 23.00 前37.00 98.00 65.00 前27.00 68.00 67.00 前34.00 65.00 65.00 前35.00 55.00 88.00 前45.00 64.00 85.00 前42.00 98.00 65.00 前19.00 56.00 67.00 前33.00 67.00 88.00 后44.00 76.00 98.00 后40.00 43.00 34.00 后39.00 56.00 65.00 后35.00 64.00 89.00 后31.00 57.00 75.00 后30.00 45.00 86.00 后45.00 56.00 86.00 后49.00 96.00 66.00 后38.00 65.00 87.00 后42.00 87.00 54.00 后35.00 67.00 86.00 后35.00 56.00 74.00 后43.00 45.00 67.00 后45.00 43.00 87.00 后44.00 89.00 74.00 后43.00 75.00 97.00 后42.00 56.00 89.00 后40.00 53.00 56.00 后40.00 54.00 76.00 后39.00 59.00 67.00 后34.00 76.00 87.00 后32.00 98.00 43.00 后43.00 56.00 87.00 后31.00 78.00 87.00 后45.00 89.00 69.00 后28.00 98.00 67.00 后28.00 98.00 73.00 后27.00 79.00 87.00 后34.00 68.00 56.003.2 数据分析3.1.1描述性统计结果描述统计量N 极小值极大值均值标准差C1(前)29 19.00 45.00 33.4828 6.81710C2(后)29 27.00 49.00 37.9655 6.09146有效的 N (列表状态)29图1 实施前化学成绩图2 实施后化学成绩收集到的数据首先做了描述性统计,由描述性统计量的表格数据可知,实施案例教学之前,班级学生的化学最高成绩是45分,最低是19分,平均分是33.5,;实施案例教学之后最高分是49分,最低分数是27分,平均分37.96。
