电路的暂态分析习题解答
暂态分析部分习题答案
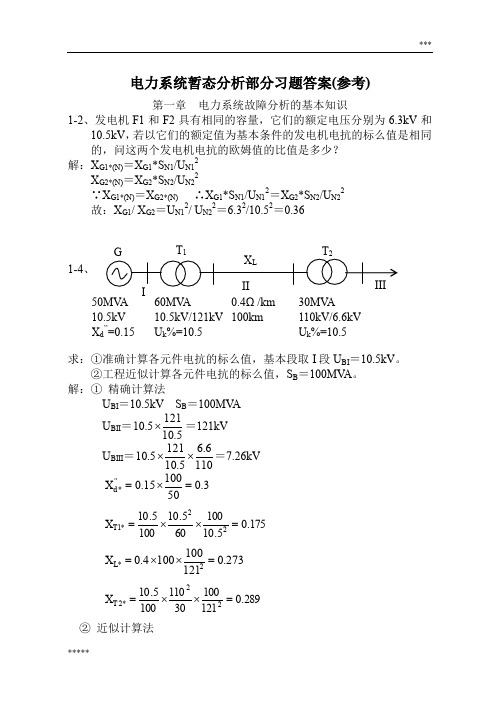
电力系统暂态分析部分习题答案(参考)第一章 电力系统故障分析的基本知识1-2、发电机F1和F2具有相同的容量,它们的额定电压分别为6.3kV 和10.5kV ,若以它们的额定值为基本条件的发电机电抗的标么值是相同的,问这两个发电机电抗的欧姆值的比值是多少? 解:X G1*(N)=X G1*S N1/U N12 X G2*(N)=X G2*S N2/U N22∵X G1*(N)=X G2*(N) ∴X G1*S N1/U N12=X G2*S N2/U N22 故:X G1/ X G2=U N12/ U N22=6.32/10.52=0.361-4、求:①准确计算各元件电抗的标么值,基本段取I 段U BI =10.5kV 。
②工程近似计算各元件电抗的标么值,S B =100MV A 。
解:① 精确计算法U BI =10.5kV S B =100MV AU BII =5.101215.10⨯=121kVU BIII =1106.65.101215.10⨯⨯=7.26kV 3.05010015.0''*=⨯=d X 175.05.10100605.101005.1022*1=⨯⨯=T X 273.01211001004.02*=⨯⨯=L X 289.0121100301101005.1022*2=⨯⨯=T X ② 近似计算法50MV A 10.5kV X d ’’=0.15 60MV A 10.5kV/121kV U k %=10.5 0.4Ω/km 100km 30MV A 110kV/6.6kV U k %=10.5U B =U av S B =100MV A3.05010015.0''*=⨯=d X 175.0601001005.10*1=⨯=T X302.01151001004.02*=⨯⨯=L X 35.0301001005.10*2=⨯=T X1-5、某一线路上安装一台Xk%=5的电抗器,其额定电流为150A ,额定电压为6kV ,若另一台额定电流为300A 、额定电压为10kV 的电抗器来代替它,并要求保持线路的电抗欧姆值不变,问这台电抗器的电抗百分数值应是多少? 解:∵2221113100%3100%N N R N N R R I UX I U X X ⨯=⨯=∴61503001065%%122112=⨯⨯=⨯⨯=N N N N R R I I U U X X1-12、(1) 若短路前空载,计算短路电流的周期分量及短路电流最大有效值; (2) 若A 相非周期分量电流的初值为零及最大时,计算相应的B 、C 相非周期分量电流的初始值;(3) 若短路前变压器满负荷运行,功率因数为0.9(低压侧),计算最大非周期分量电流的初始值,并与空载时短路比较。
电力系统暂态分析习题答案

电力系统暂态分析习题答案电力系统暂态分析习题答案电力系统暂态分析是电力系统工程中的一个重要环节,它涉及到电力系统在短时间内发生的暂态过程,如短路故障、开关操作等。
通过对电力系统暂态分析习题的解答,我们可以更好地理解和掌握电力系统的暂态行为。
一、短路故障分析1. 问题描述:一台发电机在运行过程中发生了短路故障,其短路电流为10kA,短路电压为0.1pu。
求短路电阻和短路电抗的值。
解答:根据短路电流和短路电压的定义,我们可以得到以下公式:短路电流 = 短路电压 / (短路电阻 + j短路电抗)代入已知值,得到:10kA = 0.1pu / (短路电阻 + j短路电抗)通过复数的运算,我们可以将上式转化为实部和虚部相等的两个方程:0.1 / (短路电阻^2 + 短路电抗^2) = 100 = 0.1 / (短路电阻^2 + 短路电抗^2)解方程组,得到短路电阻的值为0.01 pu,短路电抗的值为0。
2. 问题描述:一台发电机在运行过程中发生了短路故障,其短路电流为20kA,短路电压为0.2pu。
已知短路电抗为0.1 pu,求短路电阻的值。
解答:同样地,根据短路电流和短路电压的定义,我们可以得到以下公式:20kA = 0.2pu / (短路电阻 + j0.1pu)通过复数的运算,我们可以将上式转化为实部和虚部相等的两个方程:0.2 / (短路电阻^2 + 0.1^2) = 200 = 0.2 / (短路电阻^2 + 0.1^2)解方程组,得到短路电阻的值为0.01 pu。
二、暂态过程分析1. 问题描述:一台发电机在运行过程中突然断开负荷,导致发电机电压下降。
已知发电机的额定电压为1pu,负荷功率因数为0.8,负荷电流为0.5pu。
求负荷断开后的发电机电压。
解答:根据功率的定义,我们可以得到以下公式:发电机电压 = 负荷电流 * 发电机电压 * 负荷功率因数代入已知值,得到:发电机电压 = 0.5pu * 1pu * 0.8解方程,得到负荷断开后的发电机电压为0.4pu。
第4章 电路的暂态分析-习题解答

4.7 在题 4.7 图所示电路中,开关 S 闭合前电路已处于稳态,试确定 S 闭合后电
4
压 uL 和电流 iL、i1、i2 的初始值和稳态值。 【解】由于 i L (0 ) i L (0 )
uS 6 3A ,则 R1 2
i1 (0 )
R2 4 iL (0 ) 3 2A 24 R1 R2
6
【解】该电容电压的初始值为 20000V,放电的起始瞬间的冲击电流达到最 大值,冲击电流的峰值大小为 流。 这种情况下不会造成触电事故是由于放电时间极短,等效电路的时间常数为
20000 V 200 A ,远远超过了人体允许的致命电 100
RC 100 50 1012 5 109 s 5ns
u c (0 ) u c (0 ) R1i1 (0 ) 6V i1 (0 )
u c (0 ) 1A R1
i2 (0 ) 0 ic (0 ) I S i1 (0 ) 3 1 2A
1
②
) 。
① 立即亮 ③ 由亮逐渐变为不亮
② 逐渐变亮 ④ 由不亮逐渐变亮,再逐渐变为不亮 ① )。
(7)R、C 电路在零状态条件下,时间常数的意义是( ① 响应由零值增长到稳态值的 0.632 倍时所需时间 ② 响应由零值增长到稳态值的 0.368 倍时所需时间 ③ 过渡过程所需的时间 ④ 响应由稳态值下降到零值的 0.632 倍时所需时间 (8)一阶线性电路时间常数的数值取决于( ① 电路的结构形式 ③ )。
因此该电容的初始电压将在 5 25ns 时间内释放完毕,虽然冲击电流很大,但 是作用时间极短,对人体而言最多感觉到颤抖,不会造成致命伤害。
电路的暂态分析习题解答

电路的暂态分析习题解答公司内部档案编码:[OPPTR-OPPT28-OPPTL98-第五章 电路的暂态分析题图所示各电路在换路前都处于稳态,求换路后电流i 的初始值和稳态值。
解:(a )A i i L L 326)0()0(===-+,换路后瞬间 A i i L 5.1)0(21)0(==++稳态时,电感电压为0, A i 326==(b )V u u C C 6)0()0(==-+, 换路后瞬间 02)0(6)0(=-=++C u i 稳态时,电容电流为0, A i 5.1226=+=(c )A i i L L 6)0()0(11==-+,0)0()0(22==-+L L i i 换路后瞬间 A i i i L L 606)0()0()0(21=-=-=+++ 稳态时电感相当于短路,故 0=i(a)(b)(d)(c)CC2Ω2+6V -题5.1图i(d )2(0)(0)6322C C u u V +-==⨯=+ 换路后瞬间 6(0)63(0)0.75224C u i A ++--===+ 稳态时电容相当于开路,故 A i 12226=++=题图所示电路中,S 闭合前电路处于稳态,求u L 、i C 和i R 的初始值。
解:换路后瞬间 (0)6L i A +=,(0)3618C u V +=⨯=(0)6(0)0R L i i ++=-=(0)18(0)(0)6033C C L u i i +++=-=-=(0)(0)(0)0L C R u u Ri ++++==,(0)(0)18L C u u V ++=-=-求题图所示电路换路后u L 和i C 的初始值。
设换路前电路已处于稳态。
解:换路后,(0)(0)4L L i i mA +-==,所以换路后4mA 电流全部流过R 2,即(0)4C i mA +=由于(0)(0)8C C u u V +-==,故2(0)(1)(0)(0)20812L L c u R R i u V +++=-++=-+=-Ω+u L -题5.2图题5.3图C题图所示电路中,换路前电路已处于稳态,求换路后的i 、i L 和 u L 。
一阶线性电路暂态响应基本习题解答

第3章 一阶线性电路暂态响应——基本习题解答3.1题3.1图所示电路中,已知:U S1=20V ,U S2=10V ,R=6Ω,C=5µF ,开关S 合在位置①已久,在t=0时开关合向②,试求电流i 、电压u C 的初始值及稳态值。
解:因为S 合在①已久,在t=0时合向② 所以:u C (0-)= -10V ,根据换路定则 u C (0+)= u C (0-)= -10VA R u U i C S 56)10(20)0()0(1=−−=+−=+当电路重新达到稳态值时, u C (∞)=20V i (∞)=03.2题3.2图所示电路,开关S 在t=0时断开,换路前电路已处于稳态,试求i 1、i 2、i 3及u c 的初始值及稳态值。
解:因为t<0时,电路处于稳态,所以,其初值全为零。
因u C (0+)= u C (0-)=0 画出t=0+时以短路代替电容元件,及t=∞时以开路代替电容元件的等效电路如题3.2图(a )、图(b )所示:于是,求出各量初始值及稳态值如下表:i 1 i 2 i 3 uCt =0- 0 0 0 0R 6Ωc 题3.1图-+u c 题3.2图题3.2图(a )t=0+电路题3.2图(b) t=∞电路Ω(0+) i 3(0+)Ωi (∞)i (∞))t =0+ 1A 1/3A 2/3A 0t=∞ 1A 1A 0 6V3.3题3.3图所示电路,开关S 在t=0时闭合,换路前电路已处于稳态,试求i 1、i 2、i 3及u L 的初始值及稳态值。
解:因为t<0时,电路处于稳态,所以,其初值 全为零。
因为i 3(0+)= i 3(0-)=0画出t=0+时以开路代替电感元件,及t=∞时以短路代替电感元件的等效电路如题3.3图(a )题3.3图(b )所示: 列表求解如下:i 1i 2i 3u Lt =0- 0 0 0 0 t =0+ 1A 1A 0 6Vt=∞ 2.5A 0 2.5A 03.4电路如题3.4.图所示,在t=0开关S 1、S 2闭合,闭合前电路已处于稳态,试求图中各量在t=0+时的值。
(完整版)电力系统暂态分析(第二章习题答案)

(完整版)电⼒系统暂态分析(第⼆章习题答案)第2章作业参考答案2-1 为何要对同步发电机的基本电压⽅程组及磁链⽅程组进⾏派克变换?答:由于同步发电机的定⼦、转⼦之间存在相对运动,定转⼦各个绕组的磁路会发⽣周期性的变化,故其电感系数(⾃感和互感)或为1倍或为2倍转⼦⾓θ的周期函数(θ本⾝是时间的三⾓周期函数),故磁链电压⽅程是⼀组变系数的微分⽅程,求解⾮常困难。
因此,通过对同步发电机基本的电压及磁链⽅程组进⾏派克变换,可把变系数微分⽅程变换为常系数微分⽅程。
2-2 ⽆阻尼绕组同步发电机突然三相短路时,定⼦和转⼦电流中出现了哪些分量?其中哪些部分是衰减的?各按什么时间常数衰减?试⽤磁链守恒原理说明它们是如何产⽣的?答:⽆阻尼绕组同步发电机突然三相短路时,定⼦电流中出现的分量包含:a)基频交流分量(含强制分量和⾃由分量),基频⾃由分量的衰减时间常数为T d’。
b)直流分量(⾃由分量),其衰减时间常数为T a。
c)倍频交流分量(若d、q磁阻相等,⽆此量),其衰减时间常数为T a。
转⼦电流中出现的分量包含:a)直流分量(含强制分量和⾃由分量),⾃由分量的衰减时间常数为T d’。
b)基频分量(⾃由分量),其衰减时间常数为T a。
产⽣原因简要说明:1)三相短路瞬间,由于定⼦回路阻抗减⼩,定⼦电流突然增⼤,电枢反应使得转⼦f绕组中磁链突然增⼤,f绕组为保持磁链守恒,将增加⼀个⾃由直流分量,并在定⼦回路中感应基频交流,最后定⼦基频分量与转⼦直流分量达到相对平衡(其中的⾃由分量要衰减为0).2)同样,定⼦绕组为保持磁链守恒,将产⽣⼀脉动直流分量(脉动是由于d、q不对称),该脉动直流可分解为恒定直流以及倍频交流,并在转⼦中感应出基频交流分量。
这些量均为⾃由分量,最后衰减为0。
2-3 有阻尼绕组同步发电机突然三相短路时,定⼦和转⼦电流中出现了哪些分量?其中哪些部分是衰减的?各按什么时间常数衰减?答:有阻尼绕组同步发电机突然三相短路时,定⼦电流和转⼦电流中出现的分量与⽆阻尼绕组的情况相同。
电力系统暂态分析课后答案(整理版)

第一章1-2-1 对例1-2,取kV 1102=B U ,MVA S B 30=,用准确和近似计算法计算参数标幺值。
解:①准确计算法:选取第二段为基本段,取kV 1102=B U ,MVA S B 30=,则其余两段的电压基准值分别为:9.5kV kV 1101215.10211=⨯==B B U k U kV6.66.6110110223===k U U B B 电流基准值:kA U S I B B B 8.15.9330311=⨯==kA U S I B B B 16.0110330322=⨯==3 2.62B I kA ===各元件的电抗标幺值分别为:发电机:32.05.930305.1026.0221=⨯⨯=*x变压器1T :121.05.3130110121105.02222=⨯⨯=*x输电线路:079.011030804.023=⨯⨯=*x 变压器2T :21.01103015110105.02224=⨯⨯=*x电抗器: 4.03.062.26.6605.05=⨯⨯=*x 电缆线路:14.06.6305.208.026=⨯⨯=*x 电源电动势标幺值: 16.15.911==*E ②近似算法:取MVA S B 30=,各段电压电流基准值分别为:kV U B 5.101=,kA I B 65.15.103301=⨯=kV UB 1152=,20.15B I kA ==kV UB 3.63=,3 2.75B I kA ==各元件电抗标幺值:发电机:26.05.1030305.1026.0221=⨯⨯=*x变压器1T : 2300.1050.131.5x *=⨯= 输电线路: 073.011530804.023=⨯⨯=*x 变压器2T : 4300.1050.2115x *=⨯= 电抗器: 44.03.075.23.6605.05=⨯⨯=*x 电缆线路:151.03.6305.208.026=⨯⨯=*x 电源电动势标幺值: 05.15.1011==*E 习题2 解:(1)准确计算:3(110)115B B U U kV ==322220115209.1121B B U U kV k ==⨯= 312122010.51159.1121242B B U U kV k k ==⨯⨯= 各段的电流基准值为:114.0B I kA ===20.6B I kA ===3 1.1B I kA ===各元件的电抗标幺值分别为:发电机:21210.52200.300.292400.89.1x *=⨯⨯=变压器1T :222210.52200.140.143009.1x *=⨯⨯=输电线路:322200.422300.49209.1x *=⨯⨯= 变压器2T :24222202200.140.12280209.1x *=⨯⨯= (2) 近似算法:kV UB 5.101=,112.10B I kA ==2231B U kV =,20.55B I kA ==3121B U kV =,3 1.05B I kA ==各元件电抗标幺值:发电机:12200.300.22240/0.8x *=⨯=变压器1T : 22200.140.10300x *=⨯= 输电线路:322200.422300.40231x *=⨯⨯=变压器2T : 42200.140.11280x *=⨯= 习题3 要点:以下摘自《国家电网公司电力系统安全稳定计算规定》:暂态稳定是指电力系统受到大扰动后,各同步电机保持同步运行并过渡到新的或恢复到原来稳态运行方式的能力,通常指保持第一、第二摇摆不失步的功角稳定,是电力系统功角稳定的一种形式。
电工学:电路的暂态分析习题与答案

一、单选题1、工程上认为R=25Ω、L=50mH的串联电路中发生暂态过程时将持续()。
A.0~2msB.37.5~62.5msC.6~10msD.30~50ms正确答案:C2、在换路瞬间,下列说法中正确的是()。
A.电感电流不能跃变B.电容电流不能跃变C.电感电压必然跃变D.电容电流必然跃变正确答案:A3、电容元件是()元件。
A.线性元件B.耗能元件C.储能元件D.以上答案都不对正确答案:C4、关于RL电路的时间常数,下面说法正确的是()A.与R成反比,与L成正比B.与R、L成正比C.与R成正比,与L成反比D.与R、L成反比正确答案:A5、动态电路工作的全过程是()。
A.换路—前稳态—过渡过程—后稳态B.换路—前稳态—后稳态—过渡过程C.前稳态—过渡过程—换路—后稳态D.前稳态—换路—过渡过程—后稳态正确答案:D二、判断题1、换路定理指出:电感两端的电压是不能发生跃变的,只能连续变化。
()正确答案:×2、RC串联电路如果在C两端再并联一个电阻,则时间常数会变大。
()正确答案:×3、三要素法只能计算全响应,不能计算零输入响应和零状态响应。
()正确答案:×4、求解时间常数时,一定要使动态电路处于换路之前的状态。
()正确答案:×5、动态电路在换路时一定产生过渡过程。
()正确答案:√6、时间常数越小,电路的变化速度越慢。
()正确答案:×。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章电路的暂态分析
题图所示各电路在换路前都处于稳态,求换路后电流
i
的初始值和稳态值。
题5.1图
解:(a ) i L (0) i L (0 ) 6 3A ,
换路后瞬间
i(o) 1i L (o ) 1.5A
稳态时,电感电压为 0, i — 3A
2
(b)
u C (0 ) u C (0 ) 6V ,
换路后瞬间
i(0 )
6 u C
(0
)o
2
稳态时,电容电流为 0, i 6
1 5A
2 2
(c) i Li (0 ) i Li (0 ) 6A ,心(0 )心(0 ) 0
换路后瞬间
i(0 ) i L1(0 ) i L2(0 ) 6 0 6A
稳态时电感相当于短路,故
i 0
2
(d ) U c (0 )
U C (0 )
6 3V
2 2
L 2
(d
换路后瞬间i(0 ) - 6 3 0.75A
2 2 4
稳态时电容相当于开路,故1A
题图所示电路中,S闭合前电路处于稳态,
解:换路后瞬间i
L(0
)
6A,U C(0 ) 3
i R(O ) i L(0
)
i c(0 ) i L(0
U C(0 )
U L(0 ) U C(0 ) Ri R(0
i c和i R的初始
值。
U L
、
6
3Q
U L (0 ) U C(0 ) 18V
求题图所示电路换路后U L和i c的初始值。
设换路前电路已处于稳态。
解:换路后,i L(0 ) i L(0 ) 4mA,
所以换路后4mA电流全部流过R,即
i C (0 ) 4 mA
由于U C(0 )U C(0 ) W,故
题5.3
图U L(0 ) (R1 R2)i L(0 ) u c(0 ) 20 8 12V
题图所示电路中,换路前电路已处于稳态,求换路后的i、i L和u
L。
解:对RL电路,先求i L(t),再求其它物理量。
L(0 ) L(0 ) 10
20
0.5A
电路换路后的响应为零输入响应
L 2
R 40||(20 20)
L(t) i L(0 )e t/
换路后两支路电阻相等,故
1 i(t) —L(t) O.25e 10t A , 2
10t
u L (t) i(t)(20 20) 10e V
题图所示电路中,换路前电路已处于稳态,求换路后的 u c 和i 。
解:对RC 电路,先求u c (t),再求其它物理量
44
U c (0 ) U c (0 )
24 24V
12 8 24
S 合上后,S 右边部分电路的响应为零输入响应
1
RC (81| 24) — 2S
3
u c (t) u c (0 )e t/
24e 2
i(t) C du e 1
24 1 -
(丄)e 2
t
4e 2
A
dt 3
2
题图所示电路中,已知开关合上前电感中无电流,求 t 0 时的 i L (t)和 U L (t)。
解:由题意知,这是零状态响应,先求
i L
L()
24 3
2A
2 3
6 2||3
L
1
1 s 4
R 2 3||6
故
L(t) L( )(1 e t/
) 2(1 e 4t
)A
u L (t)
di L L - 1 dt
2 4e 4t
8e 4t
V
题图所示电路中, t=0时,开关S 合上。
已知电容电
压的初始值为零,求 U c (t)和i ⑴
解:这也是一个零状态响应问题,先求
u c 再求其它量
100^x s
t=0 25©
+ 20V
300©
0.05F^— U c
t
题5.7图
u c
()
矗
20 15V
RC (25 1001|300) 0.05
5S
U c (t) U c (
)(
1
e t/
) 15(1 e
0.2t
)V
i c (t )
0.05 15 0.2e 0.2t
0.15e 0.2t A
i i c
Uc 25ic
0.15e 0.2t
空
300
0.2t \ CL C <4 L 0.21
e ) 25 0.15e
300
(0.05 0.1125e 0.2t )A
题图所示电路中,已知换路前电路已处于稳态,求换路后的
U c (t
)
解:这是一个全响应问题,用三要素法求解 U c (0 ) u c (0 ) 10V
20 10
U c ()
60 10 16V
40 60
RC
40||60 10 10
6
2.4 10 4
s
U c (t) U c ( ) [U c (0 )
U c ( )]e t/
+
U c
题图所示电路中,换路前电路已处于稳态,求换路后的 解:用三要素求解
L(0 ) L(0 12
) 4A 由叠加定理可求得
12 36 L()
10A
3 6
L
1
1
s
R 3||6 2
(16 6e t/ )V
i(t)。
+ 12V
C)36V
3Q
L(t) L( ) [L(0 ) L( )]e t/ (10 6e 2t
)A
6 Q 1H
t=0 题5.10图。
