2019年山西中考复习——专题一.阴影部分图形面积问题
中考数学专题复习和训练求阴影部分的面积

求阴影部分的面积专题透析:计算平面图形中的面积问题是中考中的常考题型,多以选择题、填空题的形式出现,其中求阴影部分的面积是这类问题的难点.不规则阴影部分常常由三角形、四边形、弓形和圆、圆弧等基本图形组合而成,考查内容涉及平移、旋转、相似、扇形面积等相关知识,还常与函数相结合.在解此类问题时,要注意观察和分析图形,会分析和组合图形,常常借助转化化归思想,将阴影部分不规则图形转化为规则的易求的图形求解.典例精析:例1.如图,菱形ABCD 的对角线BD AC 、分别为223、,以B 为圆心的弧与AD DC 、相切于点E F 、,则阴影部分的面积是A.π-3233 B.π-3433C.π-43D.π-23 分析:本题的阴影部分是不规则的,要直接求出阴影部分的面积不现实,但我们发现阴影部分是菱形ABCD 减去扇形ABC 的面积;菱形ABCD 可根据题中条件直接求出,要求扇形扇形ABC 的面积关键是求出圆心角∠ABC 的度数和半径;连结BD BE 、交于点O ,所有这些问题均可以化归在Rt △AOB 或Rt △BOC 中利用三角函数和勾股定理来解决. 选D 师生互动练习:1. 如图,Rt △ACB 中,C 90AC 15AB 17∠===,,;以点C 为 圆心的⊙C 与AB 相切于D ,与CA CB 、分别交于E F 、两点,则 图中阴影部分的面积为 .2.如图的阴影部分是一商标图案图中阴影部分,它以正方形ABCD的顶点A 为圆心,AB 为半径作BD ,再以B 为圆心,BD 为半径作弧, 交BC 的延长线与E ,BD,DE 和DE 就围成了这个图案,若正方形的边长为4,则这个图案的面积为A.π4B.8C.π3D.π-38 3.如图,Rt △ABC 中,,C 90A 30∠=∠=,点O 在斜边AB 上,半径为2,⊙O 过点B 切AC 于D ,交BC 边于点E E,则由线段CD EC 、及DE 围成的阴影部分的面积为 . 4. 已知直角扇形AOB 的半径OA 2cm =,以OB 为直径在扇形内作半圆⊙M ,过M 引MP ∥AO 交AB 于P ,求AB 与半圆弧及MP 围成的 阴影部分的面积为 .例2.如图,⊙O 的圆心在定角()0180αα∠<<的角平分线上运动,且⊙O 与α∠的两边相切,图中的阴影部分的面积y 关于⊙O 的半径()x x 0>变化的函数图象大致是分析:连结OA OB OC 、、后,本题关键是抓住阴影部分的面积=四边形ACOB 的面积-扇形BOC 的面积.设阴影部分的面积为y ,⊙O 的半径()x x 0>. ∵⊙O 切AM 于点B ,切AN 于点C , ∴OBA OCA 90,OB OC x,AB AC ∠=∠====,∴BOC 3609090180αα∠=---=-;∵AO 平分MAN ∠,xAB AC 1tan 2α==,且图中阴影部分的面积y =四边形ACOB 的面积-扇形BOC 的面积.∴ ()22180x 1x 1180y 2x x 112360360tan tan 22αππαπαα⎛⎫⎪--=⨯⨯⨯-=- ⎪ ⎪⎝⎭∵x 0> ,且()0180αα∠<<是定角∴阴影部分的面积y 关于⊙O 的半径()x x 0>之间是二次函数关系. 故选C .师生互动练习:1.如图,已知正方形ABCD 的边长为1,E F G H 、、、分别为各边上的点,且AE BF CG ==DH =;设小正方形EFGH 的面积为S ,AE 为x ,则S 关于x 的函数图象大致为2.2013.临沂中考如图,正方形ABCD 中,AB 8cm =,对角线AC 与BD 相交于点O ,点E F 、分别从B C 、两点同时出发,以/1cm s 的速度沿BC CD 、运动,到点C D 、停止运动.设运动时间为()t s ,OEF 的面积为()2S cm 与()t s 的函数关系式可用图象表示为3.2014.菏泽中考如图在Rt ABC 中,AC BC 2==,正方形CDEF 的顶点D F 、分别是边AC BC 、的动点,C D 、两点不重合.设CD 的长度为x ,ABC 与正方形CDEF 的重叠部分的面积为y ,则下列图象中能表示y 与x 的函数关系的是 例3.如图,由7个形状、大小完全相同的正六边形组成的网格,正六边形 的顶点称为格点.已知每个正六边形的边长为1,△ABC 的顶点在格点上, 则△ABC 的面积为 . 分析: 延长AB ,然后作出过点C 与格点所在的水平直线,一定交于点E .则图中的阴影部分 = △AEC 的面积 - △BEC 的面积. 由正六边形的边长为1,根据正多边形形的性质,可以得出过正六边 形中心的对角线长为2,间隔一个顶点的对角线长为3,则CE 4=;若△AEC 和△BEC 都以CE 为求其面积的底边,则它们相应的高怎样化归在直角三角形中来求出呢 解:由同学们自我完成解答过程 师生互动练习:1.如图已知网格中每个小正方形的边长为2,图中阴影部分的 每个端点位置情况计算图中的阴影部分的面积之和为 .2.如图,已知下面三个图形中网格中的每个正方形的边长都设为1.结果均保留π⑴.图①中的阴影图案是由两段以格点为圆心,分别以小正方形的边长和对角线长为半径的圆弧和网格的边围成.,图中阴影部分的面积为 ;⑵.图②中的阴影图案是由三段以格点为圆心,半径分别为1和2的圆弧围成.图②中阴影部分的面积是 ;⑶.图③中在AB 的上方,分别以△ABC 的三边为直径作三个半圆围成图中的阴影部分的面积之和为 .3.如图为一张方格纸,纸上有一灰色三角形,其顶点均位于某两网格线的FEBD O A CEC D ABDE OBA C PNMBO A E F D BA C E DB CA F x y 1212O A x y 123412345O C x y 1212O D B αCBAO MNxy OA xy OB xy OC xy ODC E A B ②①③CC交点上,若灰色三角形面积为214,则方格纸的面积为.附专题总结:求含圆图形中不规则阴影部分面积的几个技巧一.旋转、翻折为特殊图形:图①的第一个图是直角扇形OAB和直角扇形OCD搭建的,其中OA=9,OB=4,要求阴影部分的面积,可以将△ODB旋转至△OAC来求扇环BDCA的面积更简便见图①的第二个图.图②的第一个图中是直角扇形OAB和正方形OFED以及矩形OACD,其中OF=1,要求阴影部分的面积,可以将半弓形ODB沿正方形对角线翻折至EFA来求矩形ACEF的面积更简便见图②的第二个图二.图①的第一个图大圆⊙O 的弦并与小圆⊙圆⊙O O图①这样来求圆环的面积更容易;虽三.如图第一个图是以等腰Rt△AOB的直角顶点O为圆心画出的直角扇形OAB和以OA、OB为直径画出的两个半圆组成的图形,要求第一个图形阴影,可以按如图所示路径割补成一个弓形见第二个图中的标示更容易求出阴影图形的面积;如果OA=10,求出第一个图形阴影部分的面积略解:S阴影=2B0A11S S AOB101010255042ππ-=⨯⨯-⨯⨯=-扇形点评:解决.割补法在很多涉及到几何图形的题中都有运用.四.差法求叠合图中形的阴影例1.图①是教材114页的第3题,可以用四个半圆的面积之和减去正方形的面积得到阴影部分的面积;例2.图②自贡市中考题△ABC中,AB=BC=6,AC=10,分别以AB,BC为直径作半圆,则图中阴影部分的面积为.略解:△ABC的底边AC===2ABC1161S2S S21592222ππ⎛⎫⨯⨯-=⨯⨯⨯-⨯=-⎪⎝⎭影点评:本题的图形结构可以看成是三个图形叠合在一起两个半圆和一个等腰三角形端点相接的叠合,具有这种图形结构题其实并不是我们想象那么抽象艰深.比如:本题的阴影部分恰好是两个半圆和一个等腰三角形端点相接的叠合后,两个半圆覆盖等腰三角形后多出来的部分;那么下面的这个题就的计算也就不那么复杂了.举一反三,“难题”不难师生互动练习::见上学期圆单元训练和专题复习的相应部分.迎考精炼:1.如图,AB 是⊙O的直径,弦CD AB,CD⊥=,则S阴影 =A.πB.2π D.23π2. 如图,⊙A、⊙B、⊙C两两不相交,且半径均为,则图中的三个阴影部分的面积之和为A.12πB.8πC.6πD.4π3.如图,⊙O的外切正六边形ABCDEF的边长为2,则图中的阴影部分的面积为2π23πC.2πD.23π4.如图,在Rt△ABC中,C90,AC8BC4∠===, ,分别以AC BC、为直径画半圆,则图中的阴影部分的面积之和为A.2016π- B.1032π- C.1016π- D.20132π-5. 如图,四边形ABCD是正方形, AE垂直于BE于E,且AE3,BE4==,则阴影部分的面积是6. 如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形'''AB C D,图中的阴影部分的面积为A.1 C.1 D.127.如图,ABCD沿对角线AC平移,使A点至AC的中点''''A B C D,新的正方形与原正方形的重叠部分图中的阴影部分的面积是B.12C.148.将n个边长都为4cm的正方形按如图所示的方法摆放,点,,,1nA A风别是正方形对角线的交点,则n个正方形重叠部分的面积的和为A.21cm4B.2n1cm4-C.()24n1cm- D.n21cm4⎛⎫⎪⎝⎭9. 两张宽均为5cm的纸带相交成α角,则这两张带重叠部分图中阴影的面积为A.()225cmsinαB.()225cmcosαC.()250sin cmα D.()225sin cmα10. 如图,△ABC是等边三角形,被一平行于BC的矩形所截,线段AB被截成相等的三部分,则图中的阴影部分的面积是△ABC面积的A.19B.29C.13D.4911.AB是⊙O的直径,以AB为一边作等边△ABC,交⊙O于点E F、,2=,则图中的阴影部分的面积为A.43π- B.23πC.3πD.3π12.如图;三个小正方形的边长都为1,则图中阴影部分面积OC图①CD DB图②BA2A1C'C结果保留π13. 如图①,等边△ABD 和等边△CBD 的边长均为1,将△ABD 沿AC 方向平移得到△'''A B D 的置,得到图 形②,则阴影部分的周长为 .14.如图,△ABC 的边AB 3AC 2==,,Ⅰ、Ⅱ、Ⅲ分别表示以AB AC BC 、、为边的正方形,则图中三个阴影部分的面积之和的最大值为 . 15.若图中正方形F 以上的正方形均是以直角三角形向外作的正方形:①.若正方形A B C D 、、、的边长分别是a b c d 、、、,则正方形F 的面积如何用含a b c d 、、、的式子表示出来为 ;②.如果正方形F 的边长16cm ,那么正方形A B C D 、、、的面积之和是 .16.如图,边长为3的正方形ABCD 绕点按顺时针方向旋转30°后得到的正方形EFCG 交AD 于点H ,S 四边形HFCD = .17.如图, 已知AD DE EF 、、分别是ABC 、ABD 、AED 的中线,若2ABC 24cm S =,则阴影部分DFE 的面积为 .18.如图,在正方形ABCD 内有一折线,其中AE EF EF FC ⊥⊥、,并且AE 6=,EF 8=, AF 10=则正方形与其外接圆之间形成的阴影部分的面积为 . 19.如图把⊙O 向右平移8个单位长度得到⊙O 2,两圆相交于 A 、B,且O 1 A 、O 2 A 分别与⊙O 2、⊙O 1相切,切点均为A 点, 则图中阴影部分的面积为 . 20.如图,矩形ABCD 中,BC 4DC 2==,,以AB 为直径的半圆O 与DC 相切于点E ,则图中的阴影部分的面积是 结果保留π21.在Rt △ABC 中,A 90AB AC 2∠===,,以AB 为直径作圆交BC 于点D ,则图中阴影部分的面积是 .22.如图,在△ABC 中,,AB 5cm AC 2cm ==,将△ABC 绕顶点C 按顺时针方向旋转45°至△11A B C 的位置,则线段AB 扫过的区域图中阴影部分的面积为 2cm .23.如图,半圆A 和半圆B 均与y 轴相切于O ,其直径CD EF 、和x 轴垂直,以O 为顶点的两条抛物线分别经过C E 、和点D F 、,则图中的阴影部分的面积是 .24.如图,抛物线21y x 2=-+向右平移1个单位得到抛物线2y ,则抛物线2y 的顶点坐标为 ;阴影部分的面积S = . 25.如图在边长为2的菱形ABCD ,B 45∠=,AE 为BC 边上的 高,将△ABE 沿AE AE 在直线翻折得△'AB E ,求△'AB E 与四边形 AECD 重叠阴影部分的面积. 26.如图,矩形OBCD 按如右图所示放置在平面直角坐标系中坐标 原点为O ,连结AC 点A C 、的坐标见图示交OB 于点E ;求阴影 部分的四边形OECD 的面积27.如图,在△ABC 中,=90A ∠, O 是BC 边上的一点以O 为圆 心的半圆分别与AB AC 、边相切于点D E 、,连接OD 已知. 求:⑴.tan C ∠.⑵.求图中的阴影部分的面积之和.28.如图,⊙O 的直径AB 为10cm 1,弦AC 为6cm ,ACB ∠的平分线 交⊙O 于点D .⑴.求弦CD 的长; ⑵.求阴影部分的面积;29.如图, 在平面直角坐标系中,以(),10为圆心的⊙P 与y 轴 相切于原点O ,过点(),A 10-的直线AB 于⊙P 相切于点B . ⑴.求AB 的长;⑵.求AB OA 、与OB 围成的阴影部分面积不取近似值; ⑶.求直线AB 上是否存在点M ,使OM PM +的值最小 如果存在,请求出点M 的坐标;如果不存在,请说明理由.FB'EDA BC xy(4,2)(0,-1)E BDC A O BD C A ①B'D 'A'B D C ②FE D A B C 17题H G EF D A B C 16题15题ⅢⅡⅠG F M E B C A 14题18题1086B D C F E A xy –1–2123–1–212O24题A 1C AB 22题DB 21题O DA EBC 20题23题xy 1-1BA O。
题型三 阴影部分面积计算

山西专用
题型二 阴影部分面积计算
阴影部分面积的计算是山西中考近几年的热点题型,常结合的图形有三 角形、四边形、圆,所求图形的面积均为不规则图形.
【例 1】
(2014· 山西)如图,点 E 在正方形 ABCD 的对角线 AC 上,且
EC=2AE, 直角三角形 FEG 的两直角边 EF、 EG 分别交 BC、 DC 于点 M、 N.若正方形 ABCD 的边长为 a,则重叠部分四边形 EMCN 的面积为( D ) 2 2 A. a 3 5 C. a2 9 4 D. a 2 9 1 2 B. a 4
[对应训练] 1.(2016· 淄博)如图,△ABC 的面积为 16,点 D 是 BC 边上一点,且 BD 1 = BC,点 G 是 AB 上一点,点 H 在△ABC 内部,且四边形 BDHG 是 4 平行四边形.则图中阴影部分的面积是( B ) A.3 B.4 C.5 D.6 (导学号 02052=3 cm,BC=4 cm,现将纸片折叠压平,使 A 75 . 与 C 重合,设折痕为 EF,则重叠部分△AEF 的面积等于____ 16 (导学号 02052661)
解析:设 AE=x,由折叠可知,EC=x,BE=4-x,在 Rt△ABE 中,AB2 25 + BE = AE , 即 3 + (4 - x) = x , 解得: x= , 由折叠可知∠AEF = 8
(导学号 02052663)
90π×22 90π×22 解析:S 扇形 EAB+S 扇形 CDF= + =2π,如图,过点 C 作 360 360 CM⊥AE,作 CN⊥BE,垂足分别为 M、N,连接 CE,则四边形 EMCN ︵ 的中点,∴EC 平分∠AEB,∴CM=CN,∴矩形 是矩形,∵点 C 是AB EMCN 是正方形,∵∠MCG+∠FCN=90°,∠NCH+∠FCN=90°, ∠MCG=∠NCH ∴∠MCG=∠NCH,在△CMG 与△CNH 中,CM=CN , ∠CMG=∠CNH=90° ∴△CMG≌△CNH(ASA),∴中间空白区域面积相当于对角线是 2 的正方 1 形面积, ∴S 空白区域= ×2×2=2, ∴S 阴影=S 扇形 EAB+S 扇形 CDF-2S 空白区域=2π 2 -4
中考复习专题:阴影部分的面积计算(共15张ppt)

中考复习专题
阴影部分面积的计算
专题解读
阴影部分面积的计算是中考的必考考点之一,这类问题中 的图形通常比较复杂,涉及的知识点有三角形、四边形、圆、 扇形、正多边形等,具有很强的综合性.阴影部分面积的计算 在选择题和解答题中均有涉及,考查形式也比较灵活,经常在 图形变换背景下进行考查.根据涉及的图形可分为两类:一类 是与扇形有关的阴影部分面积,另一类是与多边形有关的阴影 部分面积.当阴影部分是基本图形时,可直接应用公式进行计 算;当阴影部分为不规则图形时,要灵活运用“割补”“拼凑 ”“等积变形”“去重”等常用方法将不规则图形转化为规则 图形面积的和与差求解,关键是分析清楚阴影部分与背景图形 的关系.
例4 如图,在Rt△ABC中,已知∠C=90°,∠A=60°,AC=3,以斜边 AB的中点P为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′, 则旋转前后两个直角三角形重叠部分的面积为( C )
A. 3 C.9
4
B. 3+1 D.15
4
归纳总结 解答类似问题时,要注意分析已知多边形具备的条件,除了常规“
4
典题精讲
类型一:与扇形有关的阴影部分面积的计算 例1 (2019·重庆)如图,四边形ABCD是矩形,AB=4,AD=2,以点A为 圆心,AB长为半径画弧,交CD于点E,交AD的延长线于点F,则图中阴影部 分的8面积2-是8 8-8 .
【思路分析】 连接 AE,可以求得∠BAE=∠DAE=45°,根据图形可知阴影部分的面积=S 矩形 ABCD-S 扇形 BAE-S△ADE+S 扇形 EAF-S△ADE,而 S 扇形 BAE=S 扇形 EAF,S =S 阴影部分 矩形 ABCD-2S△ ADE 可求解.
2019年山西中考数学专题讲解——专题一.函数与几何动态探究题
第1题图备用图第3题图图①图②备用图第2题图能,请说明理由.第3题图图①图②第1题图第2题图第3题图第1题图第3题图第4题图第1题图备用图第2题图第3题图第2题图第3题图备用图第3题图 第3题解图① 第题解图②解:(1)∵OA =2, ∴A (−2,0).∵点A 与点B 关于直线x =12对称,∴B (3,0),由于A 、B 两点在抛物线上,∴⎪⎩⎪⎨⎧=++-=+--0329022c b c b ,解得⎪⎩⎪⎨⎧==321c b ,∴抛物线的解析式为y =−12x 2+12x +3;如解图①,过点D 作DE ⊥x 轴于点E . ∵∠BOC =90°,OD 平分∠BOC , ∴∠DOB =45°,∠ODE =45°.∴DE =OE ,即x D =y D , ∴x =−12x 2+12x +3,舍去), 第1题图 备用图第1题解图① 第1题解图②解:(1)∵抛物线经过点C (0,4),A (4∴41680c a a c =⎧⎨-+=⎩,解得124a c ⎧=-⎪⎨⎪=⎩,∴抛物线解析式为y =−12x 2+x +4; (2)∵(214212--=++-=x x x y图①图②备用图第2题图第2题解图①题解图③解:(1)将A(−1,0)、B(3、0)≠0),30a b-+=⎧⎨,解得:a BC⎪⎨⎪∠⎩∴△∴∴点设直线∴联立直线第3题图解:(1)由于抛物线y =−x 2+bx +c 经过点B (4,0),∴抛物线的表达式为y =−(x +1)(x −4)=(2)对于抛物线y =−x 2+3x +4, 令x =0,则y =4, ∴C (0,4), ∵B (4,0), ∴OC =OB =4,设P 点的坐标为(t ,−t 2+3t +4),则CF =t ,PF =|−t 2+3t +4−4|=|−t 2+3如果以P ,C ,F 为顶点的三角形与△OBC =PF ,即t =||-t 2+3t ,当t =−t 2+3t 时,解得t 1=0(舍去),t 2=此时,−t 2+3t +4=−22+3×2+4=6, ∴P 的坐标为(2,6);当−t =−t 2+3t 时,解得t 3=0(舍去),t 4此时,−t 2+3t +4=−42+3×4+4=0, ∴P 的坐标为(4,0).∴P 点的坐标为(2,6)或(4,0);(3)设直线BC 的解析式为y =kx +m (k ≠B (4,0)和点C (0,4)得:⎩⎨⎧==+404m m k , 解得⎩⎨⎧=-=41m k , ∴直线BC 的解析式为y =−x +4. 设P 点坐标为(n ,−n 2+3n +4), 图① 图②第1题图第1题解图解:(1)根据题意得425025550a b a b --=+-=⎧⎨⎩, 解得,2321⎪⎪⎩⎪⎪⎨⎧-==b a 则抛物线的解析式是:y =12x 2−32x −5; (2)P (m ,n )在抛物线上,则n = 12 m 2− 32m −5,则l =2m −2( 12 m 2− 3m −5),即l =−m 2+5m +10= −(m −第2题图图解:(1)抛物线与x轴的交点,则令−12x+2,解得x1=−4,x2=2,∴A(2,0),B(−4,0),要求抛物线与y轴的交点,则令,,2−7);,此时方程无解;,使得△ACM是等腰三角形,点M,2+7)或(−1,27).+c与x轴交于点A和点,3).轴下方的动点,过点M作MN,求线段MN的最大值;取得最大值时,在抛物线的使△PBN是等腰三角形?若的坐标;若不存在,请说第3题图第3题解图解:(1)把B(3,0),3)分别代入y=x2+bx+c,第1题图解:(1)把B (3,0),C (0,)代入y =−x ²+bx +c 得9303b c c -++=⎧⎨=⎩,解得23b c ⎧⎨⎩, ∴抛物线的解析式为y =−x ²+2; (2)S 有最大值,理由如下:,把B (3,0),M (1,4)26=-=,32)2+94,有最大值,最大值为94;2,12−62).°; ,即−2m +6=3, 32,3),²,即m ²+(−2m +3)²+3第2题解图 解:(1)∵抛物线y =12(0,2),∴1022b c c ⎧++=⎪⎨⎪=⎩,解得∴抛物线的解析式为y =(2)如解图,过点D 做∵点D 与点C 关于抛物线的对称轴对称轴x =a b 2-=52,∴D (5,2),CD ∥x 轴,∴∠CDA =∠EAD ,在Rt ∆COA 和Rt △AED tan ∠OCA =OA OC =12,tan ∴∠OCA =∠EAD , ∴∠CDA =∠OCA , ∵∠OCA 与∠OAC 互余,∴∠CDA 与∠OAC 互余,第3题图第3题解图解:(1)∵抛物线y=ax经过A(−1,0),B(3 0)两点,∴409340a ba b-+=⎧⎨++=⎩4383ab⎧=-⎪⎪⎨⎪=⎪⎩,∴抛物线的解析式是y+83x+4;(2)设直线BC的解析式为=mx+n,将C(0,4),(3,0)代入,第4题图 第4题第4题解图②解:(1)∵OA =2,OB =4,将△AOB 绕点O 逆时针旋转90°得到△COD ,∴A (0,2),B (4,0),C (−2,0),D (0,4) 将B 、C 、D 三点坐标代入y =ax ²+bx +c 中得:01640424a b c a b c c =++⎧⎪=-+⎨⎪=⎩,解得1214a b c ⎧=-⎪⎪=⎨⎪=⎪⎩, ∴抛物线的解析式为y =12x ²+x +4; 设直线CD 的解析式为y =kx +b , 将C 、D两点的坐标代入得024k bb =-+⎧⎨=⎩24k b =⎧⎨=⎩, ∴直线CD 的解析式为y =2x +4; (2)设点E 坐标为(t ,12t ²+t +4), ∵A 、B 两点的坐标分别为(0,2),(4,0), ∴直线AB 的解析式为y =12x +2, ∵EF ⊥x 轴于点F ,与AB 交于点M ,12t +2). =2,OB =4, 524222=+=,(第1题图备用图第1题解图③解:(1)∵直线y=−34x+3与于点B,∴点B的坐标是(0,3),点∵抛物线y=ax2+34x+c经过B∴3164043a cc+⨯+==⎧⎪⎨⎪⎩,解得∴y=−38x2+34x+3;(2)如解图①,过点E作y于点M,EF交x轴于点F,∵点E是直线BC上方抛物线上的一动点,∴设点E的坐标是(x,−3 8 x第2题图第2题解图①第2题解图②解:(1)∵抛物线y=ax2+bx+3 交x轴于点C(3,0),B(−1,0),∴933030a ba b++=-+=⎧⎨⎩,解得12ab=-=⎧⎨⎩,∴抛物线解析式为y=−x2+2x+3 ;(2)如解图①,设DE与x轴交于点H ∵DE∥y轴,AD=2CD,∴13 DH CDOA AC==,∵∠ACB=45°,A(0,3),∴DH=CH=1 ,∴点D(2,1) ,∴点E的横坐标为2,∵点E在抛物线上,∴y E=−22+2×2+3=3,∴E(2,3) ,∴ED=2,2.第3题图第3题解图解:(1)把A(−1,0(0,2)代入y=ax2+bx−3a(a≠0)得:30132a b aa⎧⎨==---'解得2343ab=-=,23-x2+43x+2,=1,(3,0),C(0,2),,1).D∥y轴,过B1作B1D∥x轴,解:(1)设抛物线的解析式为y =ax 2+把点A (1,0)、B (5,0)、C (0,103)代入解析式得:⎪⎪⎩⎪⎪⎨⎧==++=++3105250c c b a c b a ,解得⎪⎪⎩⎪⎪⎨⎧=-==310432c b a ,∴抛物线的解析式为y =23x 2−4x +103;(2)∵OB 是平行四边形OEBF 的对角线,∴S ▱OEBF =2S △OEB ,∵点E 在x 轴下方,且1<x <5,OB =∴S ▱OEBF =2×12×5×(−y )=2×12×5×(第2题图 解:(1)∵抛物线y =12x 2+bx −1)两点,第3题图备用图第3题解图①第3题解图②第3题解图③解:(1)∵y=ax2−2ax−3a=a(x+1)(x−3),∴A(−1,0),如解图①,过点D作DM⊥x轴于点M,∵CD=4AC,∴14 AO ACOM CD==,∴D(4,5a),将点A、D的坐标代入y=kx+b,得54k ba k b=-+⎧⎨=+⎩,解得k ab a=⎧⎨=⎩,∴y=ax+a;(2)设E(m,a(m+1)(m−3)),直线AE的函数的表达式为则⎧⎨⎩∴∴=∵∴∴(由设(ⅰ)如解图②,若AP则∴∵四边形∴∠∴∴解得∵∴∴(ⅱ)如解图③,若。
中考数学专题复习和训练--求阴影部分的面积

合 .在解此类问题时,要注意观察和分析图形,会分析和组合图形,常常借助
阴影部分(不规则图形)转化为规则的易求的图形求解
.
转化化归 思想,将
典例精析:
例 1.如图 , AB 是⊙ O 的直径,弦 CD AB, C 30 ,CD 2 3 ,则 S 阴影 =
A.
B. 2
2 C. 3
3
分析: 本题的阴影部分是不规则的,要可以转化到规则的阴影部分,比
形中心的对角线长为 2,间隔一个顶点的对角线长为 3 ,则 CE 4 ;若 △AEC 和 △BEC 都以 CE 为求其面积的底边 ,则它们相应的高怎样化归在直角三角形中来求出呢? 解:(由同学们自我完成解答过程)
师生互动练习:
1.如图已知网格中每个小正方形的边长为 2,图中阴影部分的
每个端点位置情况计算图中的阴影部分的面积之和为
小圆⊙ O′向右 平移 至大圆⊙ O 使圆心重合(见 图① 的第二个图) ,这样来求圆环的面积更容易O;
图② 虽然是半圆也可以采用相同的方法求阴影部分半圆环的面积
.
A
B
A
C B
O O'
O
O' O
O
A
B
A
B
C
图① 三 .补转化为一个整体:
图②
如图第一个图是以等腰 Rt△AOB 的直角顶点 O 为圆心画出的直角扇形 OAB 和以 OA 、 OB 为
如转化为扇形 AOD 的面积来求;利用垂径定理和三角函数计算可以得出
C
EC ED,EO EA ,由此可以证明⊿ AEC ≌⊿ DEO ; 所以阴影部分等于
扇形 AOD 的面积,利用扇形面积的计算公式求出结果为
2 . 选D
2019年中考数学:题型(2)阴影部分面积计算(含答案解析)

题型二 阴影部分面积计算针对演练1. 如图,在Rt △ABC 中,∠ACB =90°,AC =BC =2,将Rt △ABC 绕点A 按逆时针方向旋转30°后得到Rt △ADE ,点B 经过的路径为BD ︵,则图中阴影部分的面积是( )A. π6B. π3C. 1+π6D. 1第1题图第2题图2. 如图,在半径为2 cm 的⊙O 中,点C 、点D 是AB ︵的三等分点,点E 是直径AB 的延长线上一点,连接CE 、DE ,则图中阴影部分的面积是( ) A. 3 cm 2 B. 2π3 cm 2 C. 2π3- 3 cm 2 D. 2π3+ 3 cm 2 3. 如图,正方形ABCD 的面积为12,点M 是AB 的中点,连接AC 、DM 、CM ,则图中阴影部分的面积是( )A. 6B. 4.8C. 4D. 3第3题图第4题图4. (2016桂林)如图,在Rt △AOB 中,∠AOB =90°,OA =3,OB =2,将Rt △AOB 绕点O 顺时针旋转90°后得Rt △FOE ,将线段EF 绕点E 逆时针旋转90°后得线段ED ,分别以O ,E 为圆心,OA ,ED 长为半径画AF ︵和DF ︵,连接AD ,则图中阴影部分面积是( )A. πB. 54πC. 3+πD. 8-π5. 如图,四边形ABCD 是菱形,点O 是两条对角线的交点,过点O 的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为10和6时,则阴影部分的面积为________.第5题图第6题图6. (2015赤峰)如图,平行四边形ABCD 中,AB =AC =4,AB ⊥AC ,O 是对角线的交点,若⊙O 过A 、C 两点,则图中阴影部分的面积之和为________.7. (2015武威)如图,半圆O的直径AE=4,点B,C,D均在半圆上,若AB=BC,CD=DE,连接OB,OD,则图中阴影部分的面积为________.第7题图第8题图8. 如图,在△ABC中,已知点D、E、F分别为BC,AD,CE 的中点,且S△ABC=4 cm2,则阴影部分的面积为________.9. 如图,在等腰直角三角形ABC中,∠C=90°,点D为AB的中点,已知扇形EAD和扇形FBD的圆心分别为点A、点B,且AC =2,则图中阴影部分的面积为________(结果保留π).第9题图第10题图10. 如图,在矩形ABCD中,AB=3,AD=1,把该矩形绕点A 顺时针旋转α度得矩形AB′C′D′,点C′落在AB的延长线上,则图中阴影部分的面积是________.11. 如图,在△ABC中,∠C=90°,将△ABC沿直线MN翻折后,顶点C恰好落在AB边上的点D处,已知MN∥AB,MC=6,NC=23,则图中阴影部分的面积为________.第11题图第12题图12. 如图,在矩形ABCD中,点O在BC边上,OB=2OC=2,以O为圆心,OB的长为半径画弧,这条弧恰好经过点D,则图中阴影部分的面积为________.13. 如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形EBF 的半径为2,圆心角为60°,则图中阴影部分的面积是________.第13题图第14题图14. 如图,在▱ABCD中,E、F分别是AB、DC边上的点,AF 与DE相交于点P,BF与CE相交于点Q,若S△APD=16cm2,S△BQC =25 cm2,则图中阴影部分的面积为________cm2.15. 如图,正方形ABCD的边长为1,分别以点A、D为圆心,1为半径画弧BD、AC,两弧相交于点F,则图中阴影部分的面积为________.第15题图第16题图第17题图16. 如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB1E,则△AB1E与四边形AECD重叠部分的面积是________.17. 如图,在矩形ABCD中,AB=6 cm,BC=8 cm,E、F分别是BC、CD的中点,连接BF、DE,则图中阴影部分的面积是________ cm2.【答案】1.B 【解析】在Rt △ABC 中,∵AC =BC =2,∴AB =AC 2+BC 2=2,∴S 阴影=S 扇形DAB =30π×22360= π3.第2题解图2.B 【解析】如解图,连接OC 、OD 、CD ,∵点C 、点D 是AB ︵的三等分点,∴∠DOB =∠COD =60°,又∵CO =OD ,∴CO =OD =CD ,∴∠DOB =∠CDO =60°,∴CD ∥AB ,∴S △CED =S △COD ,∴S阴影=S 扇形COD =60π×22360=2π3cm 2. 3.C 【解析】如解图,设DM 与AC 交于点E ,∵四边形ABCD 是正方形,∴AM ∥CD ,AB =CD ,∴△AME ∽△CDE ,∵点M 是AB的中点,∴AM CD =12,∴AE CE =EM DE =AM CD =12,∵S 正方形ABCD =12,∴S △ABC=12S 正方形ABCD =6,∴S △ACM =12S △ABC =3,∴S △AEM =13S △ACM =1,S △CEM =23S △ACM =2,∴S △AED =2S △AEM =2,∴S 阴影=S △CEM +S △AED =2+2=4,故选C.第3题解图第4题解图4.D 【解析】如解图,过点D 作DH ⊥AE 于点H ,∵∠AOB =90°,OA =3,OB =2,∴AB =OA 2+OB 2=13,由旋转的性质可知,OF =OA =3,OE =OB =2,DE =EF =AB =13,∴AE =OA +OE =5,易证△DHE ≌△BOA ,∴DH =OB =2,∴S 阴影=S △ADE +S △EOF +S 扇形AOF -S 扇形DEF =12AE ·DH +12OE ·OF +90π×OA 2360-90π×DE 2360=12×5×2+12×2×3+90×π×32360-90×π×(13)2360=8-π. 5.15 【解析】∵菱形的两条对角线的长分别为10和6,∴菱形的面积=12×10×6=30,∵点O 是菱形两条对角线的交点,∴阴影部分的面积=12×30=15.第6题解图6.4 【解析】如解图,设BD 与⊙O 交于点E 和F 两点.∵四边形ABCD 是平行四边形,∴OA =OC ,OB =OD ,∵⊙O 过A ,C 两点,∴扇形AOE 与扇形FOC 关于点O 成中心对称,∴S 扇形AOE =S 扇形FOC ,∴S 阴影=S △AOB =12×12AC ·AB =12×12×4×4=4.7.π 【解析】如解图,连接OC ,在半圆O 中,AB =BC ,CD =DE ,∴AB ︵=BC ︵,CD ︵=DE ︵,∴∠AOB =∠BOC ,∠COD =∠DOE ,∴S 阴影=S 扇形OAB +S 扇形ODE =12S 扇形AOC +12S 扇形COE =12S 半圆AOE =12×π×222=π,∴阴影部分的面积为π.第7题解图8.1 cm 2 【解析】∵点E 是AD 的中点,∴S △ABE =12S △ABD ,S △ACE=12S △ADC ,∴S △ABE +S △ACE =12S △ABC =12×4=2 cm 2,∴S △BCE =12S △ABC =12×4=2 cm 2,∵点F 是CE 的中点,∴S △BEF =12S △BCE =12×2=1 cm 2.9.2-π2 【解析】∵BC =AC =2,∠C =90°,∴AB =22,∵点D 为AB 的中点,∴AD =BD =2,∴S 阴影=S △ABC -S 扇形EAD -S 扇形FBD =12×2×2-45π×(2)2360×2=2-π2. 10.32-π4 【解析】根据已知可得∠ABC =90°,∵在Rt △ABC 中,tan ∠CAB =13=33,∠CAB =30°,∴∠BAB ′=30°,∴S 阴影=S △AB ′C ′-S 扇形BAB′=12AB ′·B ′C ′-30π·(3)2360=12×3×1-π4=32-π4.11.183 【解析】∵MC =6,NC =23,∠C =90°,∴S △CMN =63,由折叠性质得△CMN ≌△DMN ,∴△CMN 与△DMN 对应高相等,∵MN ∥AB ,∴△CMN ∽△CAB 且相似比为1∶2,∴两者的面积比为1∶4,从而得S △CMN ∶S 四边形MABN =1∶3,∴S 阴影=S 四边形MABN =18 3.第12题解图12.2π3-3 【解析】设弧与AD 交于点E ,如解图,连接OE ,过点O 作OP ⊥AD 于点P ,由题意得,OB =OE =OD ,∴OD =2OC =2,∴∠ODC =30°,则∠ODE =60°,∴△ODE 为等边三角形,∴S △ODE =12×2×3=3,则S 阴影=S 扇形EOD -S △ODE =60×π×22360-3=2π3- 3.第13题解图13.2π3-3 【解析】如解图,连接BD ,设BE 交 AD 于点G ,BF 交CD 于点H ,∵在菱形ABCD 中,∠A =60°,AB =2,∴BD =BC =2,由题意知扇形圆心角为60°,∴∠DBG =∠CBH ,∠GDB =∠C ,∴△DGB ≌△CHB ,∴S 阴影=S 扇形EBF - S △DBC =60×π×22360-12×2×3=2π3- 3.第14题解图14.41 【解析】如解图,连接EF ,∵四边形ABCD 是平行四边形,∴AB ∥CD ,∴S △EFC =S △BCF ,∴S △EFQ =S △BCQ ,同理,S △EFD =S △ADF ,∴S △EFP =S △ADP ,∵S △APD =16 cm 2,S △BQC =25 cm 2,∴S 阴影=S△EFP+S △EFQ =16+25=41 cm 2.15.32-π6 【解析】如解图,过点F 作FE ⊥AD 于点E ,连接AF 、DF ,∵正方形ABCD 的边长为1,∴AE =12AD =12AF =12, ∴∠AFE =∠BAF =30°,∴∠F AE =60°,EF =32,∴△ADF 为等边三角形,∴∠ADF =60°,∴S 弓形AF =S 扇形ADF -S △ADF =60π×12360-12×1×32=π6-34,∴S 阴影=2(S 扇形BAF -S 弓形AF )=2×(30π×12360-π6+34)=32-π6.第15题解图16.22-2 【解析】如解图,设CD 与AB 1交于点O ,∵在边长为2的菱形ABCD 中,∠B =45°,AE 为BC 边上的高,∴AE =BE =2,由折叠性质易得△ABB 1为等腰直角三角形,∴S △ABB1=12BA ·AB 1=2,S △AB1E =1,CB 1=2BE -BC =22-2,∵AB ∥CD ,∴∠OCB 1=∠B =45°,又∵∠B 1=∠B =45°,∴CO =OB 1=2-2,∴S △COB 1=12CO ·OB 1=3-22,∴S 重叠=S △AB1E -S △COB 1=1-(3-22)=22-2.第16题解图第17题解图17.32 【解析】如解图,连接BD ,EF ,设BF 与ED 相交于点G .∵四边形ABCD 是矩形,∴∠A =∠C =90°,AB =CD =6 cm ,AD =BC =8 cm ,∴S △ABD =S △BCD =12S 矩形ABCD =12×6×8=24 cm 2,∵E 、F 分别是BC 、CD 的中点,∴EF ∥BD ,EF =12BD ,∴△GEF ∽△GDB ,∴DG =2GE ,∵S △BDE =12S △BCD ,∴S △BDG =23S △BDE =13S △BCD =13×24=8 cm 2,∴S 阴影=S △ABD +S △BDG =24+8=32 cm 2.。
中考专题:求平面几何阴影部分的面积

求阴影部分图形面积近年来的中考数学试卷中,围绕图形面积的知识,出现了一批考查应用与创新能力的新题型,归纳起来主要有:一、规律探究型例1宏远广告公司要为某企业的一种产品设计商标图案,给出了如下几种初步方案,供继续设计选用(设图中圆的半径均为r).(1)如图1,分别以线段O1O2的两个端点为圆心,以这条线段的长为半径作出两个互相交错的圆的图案,试求两圆相交部分的面积.(2)如图2,分别以等边△O1O2O3的三个顶点为圆心,以其边长为半径,作出三个两两相交的相同的圆,这时,这三个圆相交部分的面积又是多少呢?(3)如图3,分别以正方形O1O2O3O4的四个顶点为圆心,以其边长为半径作四个相同的圆,则这四个圆的相交部分的面积又是多少呢?(2005年黄冈市中考题)分析(1)利用“S阴=S菱形AO1BO2=4S弓形”即可;(2)利用“S阴=S△O1O2O3+3S弓”即可;(3)•直接求解比较困难,可利用求补法,即“S阴=S正方形O1O2O3O4-S空白”,考虑到四个圆半径相同,若延长O2O1交⊙O1•于A,则S空白=4SO1AB,由(1)根据对称性可求SO1BO4,再由“SO1AB=S扇形AO1O4-SO1BO4”,这样S空白可求.解答(1)设两圆交于A、B两点,连结O1A,O2A,O1B,O2B.则S阴=S菱形AO1BO2+4S弓.∵S菱形=2S△AO1O2,△O1O2A为正△,其边长为r.∴S△AO1O2r2,S弓=-r2=-r2.4260360rπ426rπ4∴S 阴=2×r 2+4(r 2r 2)=r 2r 2.(2)图2阴影部分的面积为S 阴=S △O1O2O3+3S 弓. ∵△O 1O 2O 3为正△,边长为r. ∴S △O1O2O3r 2,S 弓=r 2.∴S 阴r 2+3(r 2)=r 2r 2.(3)延长O 2O 1与⊙O 1交于点A ,设⊙O 1与⊙O 4交于点B ,由(1)知,S O1BO4=(r 2-r 2).∵S O1AB =S 扇形AO1O4-S O1BO4 =-(r 2=r 2)=-r 2+r 2.则S 阴=S 正方形O1O2O3O4-4S O1AB =r 2-4(-r 2r 2)=r 2+r 22=(r 2.46π423π24260360r π4426r π42π21223π2290360r π1223π224r π13π424r π13π413π13π例2 在一块长16m ,宽12m 的矩形荒地上,要建造一个花园,要求花园所占面积为荒地面积的一半.下面分别是小明和小颖的设计方案.小明的设计方案:如图1,其中花园四周小路的宽度相等,经过解方程,•我得到路的宽为2m 或12m .小颖的设计方案:如图2,其中花园中每个角上的扇形都相同. (1)你认为小明的结果对吗?请说明理由. (2)请你帮助小颖求出图中的x (精确到0.1m )(3)你还有其它的设计方案吗?请在右边的矩形中画出你的设计草图,•并加以说明.(2004年新疆建设兵团中考题)分析 (1)由小明的设计知,小路的宽应小于矩形荒地宽的一半,由此判断即可;(2)可由“花园面积为矩形面积一半”列方程求x ;(3)可由图形对称性来设计. 解 (1)小明的结果不对. 设小路宽xm ,则得方程 (16-2x )(12-2x )=×16×12解得:x 1=2,x 2=12.而荒地的宽为12m ,若小路宽为12m ,不符合实际情况,故x 2=12m 不合题意.(2)由题意,4×=×16×12x 2=,x ≈5.5m .(3)方案有多种,下面提供5种供参考:1224x π1296π例3 图中的虚线网格我们称之为正三角形网格,它的每个小三角形都是边长为1个单位长度的正三角形,这样的三角形称为单位正三角形. (1)直接写出单位正三角形的高与面积;(2)图1中的ABCD 含有多少个单位正三角形?ABCD 的面积是多少? (3)求出图1中线段AC 的长(可作辅助线);(4)求出图2中四边形EFGH 的面积.(2005年吉林省中考题)分析 (1)由正三角形边角关系来求;(2)仔细观察图1便可找到答案;(3)考虑到图1中AB=3,BC=4,∠B=60°,可作△ABC 的高AK ,构造直角三角形,•再利用解直角三角形知识即可求得;(4)可利用网格构造特殊格点图形,再由求补法计算四边形EFGH•面积. 解:(1)单位正三角形的角为,面积为,(2)ABCD 含有24个单位正三角形,故其面积为24.(3)如图1,过A 作AK ⊥BC 于K ,在Rt△ACK 中,AK=,KC=.∴.(4)如图3,构造EQSR ,过F 作FT ⊥QG 于T,则S △FQG =FT ·QG=×.同理可求S △GSH S △EHR,S EQSR∴S 四边形EFGH = S EQSR-S △FQG -S △GSH -S△EHR.244325212122四、图形对称型例4 如图,半圆A 和半圆B 均与y 轴相切于点O ,其直径CD 、EF 均和x 轴垂直,以O 为顶点的两条抛物线分别经过C 、E 和D•、•F ,•则图中阴影部分的面积是_________.•(2005年河南省中考题)分析 由题意知,图中两半圆和两抛物线组成的图形关于y 轴对称,故y 轴左侧阴影部分面积等于半圆B 中的空白面积,所以所求阴影部分面积为半圆B 的面积,即S 阴=·12=.解答:.12π12π2π五、图形变换型例5 如图,矩形ABCD 的长与宽分别是2cm 和1cm ,AB 在直线L 上,依次为B 、C ′、•D ″,依次为B 、C ′、D ″为中心将矩形ABCD 按顺时针方向旋转90°.这样点A•走过的曲线依次为、、,其中交CD 于点P .(1)求矩形A ′BC ′D ′的对角线A ′C ′的长;(2)求的长;(3)求图中 部分的面积S ;(4)求图中 部分的面积T .(2005年吉林省中考题)分析 (1)要求A ′C ′,因长宽分别为2和1,利用勾股定理即可;(2)要求,因所对圆心角为∠ABA ′=90°,半径AB=2,利用弧长公式即可;(3)因△A ′C ′D•′≌△A ″C ′D ″,故S=S 扇形A`C``A``;(4)连PB ,则PB=AB=2,又BC=1,故∠PBC=60°,∠ABP=30°,•欲求T ,由“T=S 扇形ABP +S △BCP ”即可.解答 (1)A ′C ′cm ).(2)=×2=(cm ).(3)S=S 扇形A`CA``==(cm )(4)连结BP ,在Rt △BCP 中,BC=1,BP=2, ∴∠BPC=30°,ABP=30°,∴T=S 扇形ABP +S △PBC =×22+=(+)cm 2.'A A '''A A '''''A A'A A'A A'A A'A A'A A 90180ππ290360π54π30360π23π2六、实际应用型例6 在栽植农作物时,一个很重要的问题是“合理密植”.如图是栽植一种蔬菜时的两种方法,A 、B 、C 、D 四珠顺次连结成为一个菱形,且AB=BD ;A ′、B ′、•C ′、D ′四株连结成一个正方形,这两种图形的面积为四株作物所占的面积,•两行作物间的距离为行距;一行中相邻两株作物的距离为株距;设这两种蔬菜充分生长后,每株在地面上的影子近似成一个圆面(相邻两圆如图相切),其中阴影部分的面积表示生长后空隙地面积.在株距都为a ,其他客观因素也相同的条件下,•请从栽植的行距,蔬菜所占的面积,充分生长后空隙地面积三个方面比较两种栽植方法.哪种方法能更充分地利用土地.分析:本题立意很新,要合理密植,充分利用土地,只需分别计算并比较两种方案的行距、阴影面积以及S 和S .对应值小的即为合理密植.解 连结AC 交BD 于点O .在菱形ABCD 中,有AB=AD ,AC ⊥BD ,BO=BD .∵AB=BD=a ,∴BO=OD=a .在Rt △AOD 中,a .∴S 菱形ABCD=2×BD ·AO=a 2, S正方形A`B`C`D`=a 2.设方法(1)中空隙地面积为S 1,方法(2)中空隙地面积为S 2.则S 1=S 菱形ABCD -S ☉A a 2-a 2,S 2=S 正方形A`B`C`D`-S ☉A`=a 2-a 2.∵<1,∴AO<A ′B ′,1212212224π4π2S 菱形ABCD <S 正方形A`B`C`D`,S 1<S 2.∴栽植方法(1)比栽植方法(2)能更充分地利用土地.运用转化思想 巧求阴影面积“转化思想”是中学数学中一种重要的数学思想,将未知转化为已知,将复杂转化为简单,.通过转化,会使问题化繁为简,化难为易,思路清淅,演算简单.而在求与圆有关的阴影部分的面积时,通常是将阴影部分的面积转化为圆、扇形、三角形面积的和或差.现就2008年中考题精选几例解析如下,供同学们参考:例1(2008广西桂林)两同心圆,大圆半径为3,小圆半径为1,则阴影部分面积为分析 本例涉及到同心圆的概念、圆环面积的计算方法.求出圆环的面积,即大圆的面积减去小圆的面积,.将阴影部分的面积转化为圆环面积的一半.解例2(2008湖北孝感)中,,,,两等圆⊙A,⊙B 外切,那么图中两个扇形(即阴影部分)的面积之和为( )A .B .C .D .分析 此例综合考查了圆、扇形面积、勾股定理的知识以及转化的数学思想. 由勾股定理可求得AB=10,则两圆的半径为5,∠A+∠B=900,从而阴影部分的 面积可转化为半径为5, 圆心角为90°的扇形的面积.解Aπππππ8922=-=-=r R S 圆环4πR t ABC △90C ∠=8A C =6B C =254π258π2516π2532π例3(2008四川自贡)如图所示,草地上一根长5米的绳子,一端拴在墙角的木桩上,另一端栓着一只小羊R. 那么,小羊在草地上的最大活动区域的面积是( )A .B .C .D .分析 小羊在草地上的最大活动区域的面积可 转化为1个半径为5米,圆心角为90°的扇形和2个半径为1米,圆心角为90°的扇形的面积之和(即图中)阴影部分的面积).解 B例4(2008广西南宁)如图,Rt △ABC 中,AC=8,BC=6, ∠C=90°,分别以AB 、BC 、AC 为直径作三个半圆,那么 阴影部分的面积为 (平方单位)分析 阴影部分的面积可转化成以AC 、BC 为直径的两个半圆的面积加上Rt △ABC 的面积再减去以AB 为直径的半圆的面积,即 = ===解 24点评 由勾股定理可得2213m π2427m π2213m π2427m π阴影S 22222121221221⎪⎭⎫⎝⎛⋅⋅-⋅⋅+⎪⎭⎫ ⎝⎛⋅⋅+⎪⎭⎫ ⎝⎛⋅⋅AB BC AC BC AC πππ()()()BC AC AB BCAC ⋅⋅+⋅⋅-⋅⋅+⋅⋅21818181222πππBC AC AB BCAC⋅⋅+-+⋅⋅21)(81222πBC AC ⋅⋅210222=-+ABBCAC例5(2008吉林长春)如图,在△ABC 中,BC =4,以点A 为圆心,2为半径的⊙A 与BC 相切于点D ,交AB 于E ,交AC 于F ,点P 是⊙A 上一点,且∠EPF =40°,则图中阴影部分的面积是 ( )A .B .C .D .分析 ∠EPF =40°,则∠EAF =80°,连AD,则AD⊥BC,且AD=2 阴影部分的面积可转化为△ABC 与扇形AEF 的面积之差.解 B例6(2008江西南昌)如图,为⊙O 的直径,于 点,交⊙O 于点,于点. (1)请写出三条与有关的正确结论;(2)当,时,求圆中阴影部分的面积分析 连OC, 圆中阴影部分的面积可转化为扇形OAC 与△OAC 的面积之差.94π-984π-948π-988π-98436028024212ππ-=⋅-⨯⨯=-=∆AEF ABC S S S 扇形阴影A B C D AB ⊥E D O F A C ⊥F B C 30D ∠=1B C= B解(1)答案不唯一,只要正确合理均可.例如:①;②;③;④;⑤;⑥;⑦是直角三角形;⑧是等腰三角形.(2)连,则.,∴∠A=∠D=300,则∠AOC=1200.为⊙O的直径,.∴∠ACB=900.在中,,∴AB=2,.,∴AF=CF.,∴OF是的中位线....B C B D=O F B C∥B C D A∠=∠B C E O A F△∽△BEABBC⋅=2222BC CE BE=+A BC△BC D△O C O C O A O B==30D∠=A B90ACB∴∠=R t ABC△1B C=AC=O F A C⊥O A O B=A B C△1122O F B C∴==1112224AO CS AC O F∴==⨯=△2133A O CS O Aπ=π⨯=扇形34AOCAOCS S Sπ∴=-=-△阴影扇形BA。
2019年山西中考应考策略——中考数学各类问题考查题型及解决办法小结

初中数学各类问题解决办法小结——李伟伟一、小题(选择填空题)考查题型及注意点: 1. 判断轴对称图形/中心对称图形问题(1)判断轴对称图形−−−→−解决办法折叠法(即沿着某条直线折叠,两边能够重合,就是轴对称图形;否则不 是)(2)判断中心对称图形−−−→−解决办法倒看观察法(即将所判断图形倒着看,如果与原图形相同,,就是轴对称 图形;否则不是)2.概率与统计问题(1)概率问题−−−→−考查特点结合实际应用问题考查求概率问题−−→−实质大都可以转化为常见的摸球问题或扔色子问题去解决−−−→−解决办法画树状图法或列表法(2)统计问题−−−→−考查特点结合图形或表格考查求特征数据(平均数,中位数,众数)问题(考众数,中位数情况较多)−−−→−解决关键认真审题,读懂表格中每个数据的含义 −−→−注意求中位数时,一定要先将所给所有数据排序(从小到大或从大到小),后找最中间的一个数据或 求最中间两个数据的平均值3.投影与三视图问题−−−→−考查特点常结合小正方体组合体考查−−−→−考查题型①给正方体组合原图,判断某个三视图−−−→−解决办法直接法(即利用三视图的定义直接判断即可)②给正方体组合的某个视图,判断另一个视图 ③给正方体组合的三视图求小正方体个数④给正方体组着的两个视图判断小正方体个数(最大值/最小 值/可能值等)−−−→−解决办法堆积法(即用小正方体方块堆积,进而做出判断)4.科学计数法问题−−→−知识点将大数表示为a ×10n 的形式(1≤a<10,n 为小数点移动位数).将小数表示为a ×10-n的形式.(1≤a<10,n 为小数点移动位 数).−−−→−考查题型①直接将大数或小数表示成科学计数法形式−−−→−解决办法排除法+定义法(即先利用1≤a<10对 结果作出排除,后利用定义做出选择)−−→−注意与万亿等单位结合考(注意:万=104,亿=108)−−−→−考查题型②先运算(利用物理公式计算或单位换算),后将结果表示成科学计数法形式(这是近几年科学计数法考查的方向)−−→−注意运算时结果单位要统一.5.与反比例函数相关的问题−−−→−考查题型求反比例函数解析式中参数k 的值−−−→−解决办法①几何意义法−−−−−→−常用作辅佐线方法做垂线段(即过双曲线上 的点作坐标轴(一般是x 轴)的垂线段,进 而出现Rt 三角形或矩形,进而利用几何意义 解决)②等面积代换法−−→−注意同底等高的两三角形面积相等 6.找规律型问题−−−→−考查题型常给前几个图形,求第n 个图形的规律问题−−−→−解决办法分别找对应部分的规律−−→−注意(1)检验(即找到第n 项的规律以后,一定要取分别取n=1,n=2,n=3时的值是否符合规律做检验)(2)括号−−−→−加括号原则单加多不加(即若后面有单位,则如果结果是单项式则不加括号,若结果是多项式则必 须加括号)7.实际应用问题−−−→−考查题型(1)借助于古典数学著作中的某个数学问题或实际应用问题考查列方程(组)或解方程问题−−−→−解决关键认真审题,找到等量关系,列方程−−→−注意单位−−−→−加单位原则若题中有单位,则结果不加单位;题中无单位,则结果必须加单位.(2)借助于实际应用问题考查解Rt △应用问题−−−→−考查特点通常将解Rt △应用问题与△相似的应用问题结合考查8.选择题中的求角度/边长(△面积)问题(1)求角度问题−−−→−解决办法测量法(即用量角器测量)(2)求边长(△面积)问题−−−→−解决办法比例尺+测量法(即用直尺测量所求线段和已知线段的实际长度,然后用比例尺解决)9.求阴影面积问题−−−→−考查特点结合圆(弧),等边三角形,正方形,菱形等以及旋转知识考查−−−→−解决办法转化法(即将所求阴影面积通过对称法或直接法转化为几部分面积的和或差)−−−−−→−常用做辅助线方法见弧→连半径→得扇形−−→−注意求扇形面积的关键,确定角度和半径在确定角度时,可以进行适当的猜测❶中考考查此类问题时,所涉及到的角度一般都是特殊角(30°,45°,60°);❷一般你看见的就是出题人想让你看见的,出题人一般不会在 这些地方出陷阱坑人)10.与折叠有关的求线段长问题(1)考查形式:常借助于正方形,矩形等模型考查折叠问题(2)常用解决办法①勾股定理法−−−−→−做辅助线方法做垂线段(即过某个点作垂线段,从而出现 Rt 三角形,进而通过设未知数,利用勾股 定理,从而建立方程解决)②全等相似法−−−−→−做辅助线方法连接对应点连线(利用折叠性质“折痕(对称轴)垂直平分对应点连线”进而出现直角, 进而出现余角,进而出现等角,进而出现相 似,最后用相似解决问题)③等面积代换法−−−→−解决思路利用同一个图形的面积的不同表达形式来求边长.二、基本运算型问题(即16题)考查形式及注意点:考查形式1:数的加减乘除乘方开方运算问题1.考查特点:常将数的加减乘除乘方开方运算与负指数幂,0次幂,特殊角三角函数值结合考查 2.常用公式:①)0(1≠=-a aa n n②)0(10≠=a a③特殊角的常用三角函数值−−−→−解决策略①熟记常用公式及特殊角三角函数值②一步三回头(即计算时在书写每一步步骤时必−−−−解决模板考查形式2注意点:①考查形式31.注意点:2.考查形式4注意点:①②考查形式5考查题型:(−−−−解决模板考查题型:(2)解不等式组+求不等式组的特殊解−−−→−解决模板三、反比例函数与一次函数结合考查问题(17题)1.考查题型:(1)求一次函数或反比例函数解析式 解决办法:待定系数法注意:①专门的求解析式问题,解决步骤(设→列→解→下)四步缺一不可。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
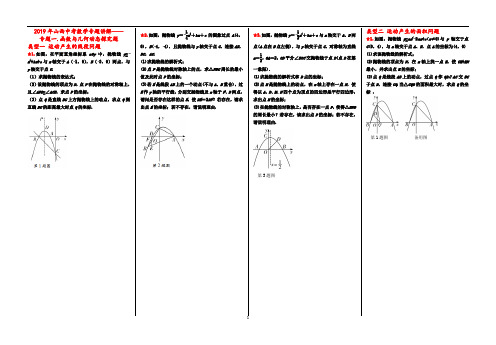
2019年山西中考复习——专题一.阴影部分图形面积问题一.专题解读:阴影部分图形面积计算问题 1.考查题型:选择题/填空题 2.常考类型为:①不涉及扇形问题(即多边形结合球阴影面积问题) ②涉及扇形问题考察形式:❶三角形扇形结合问题❷四边形与扇形结合问题3.考查特点:①所求阴影面积大多为不规则图形的面积;②常与旋转,翻折,对称等结合考查。
4.解决办法: (1)转化法(即将所求阴影面积问题转化为几个规则图形面积的和或差来解决)(2)常用的转化方法:①割补法 ②全等法 ③对称法二.例题讲解:例1.图1是以AB 为直径的半圆形纸片,AB =12 cm ,沿着垂直于AB 的半径OC 剪开,将扇形OAC 沿AB 方向平移至扇形O ′A ′C ′.如图2,其中O ′是OB 的中点,O ′C ′交BC ︵于点F ,则由BF ︵,O ′F ,O ′B 围成的阴影部分周长为 cm ,阴影部分面积为 cm 2.图1 图2例2.如图,小方格都是边长为1的正方形,则以格点为圆心,半径为1和2的两种弧围成的“叶状”阴影图案的面积为 .三.山西8年中考真题命题点1.弧长的计算1.如图,在▱ABCD 中,AB 为⊙O 的直径,⊙O 与DC 相切于点E ,与AD 相交于点F ,已知AB=12, ∠C =60°,则的长为( )A .B .C .ΠD .2π 中考变式:如图,在▱ABCD 中,以点A 为圆心,AB 的长为半径的圆恰好与CD 相切于点C ,交AD 于点E ,若AD=2,BA 的延长线交⊙A 于点F .则的长为( ) A .π22B .π42 C .Π D .2π命题点2.阴影部分图形面积计算2.如图是某公园的一角,∠AOB =90°,弧AB 的半径OA 长是6米,C 是OA 的中点,点D 在弧AB 上,CD ∥OB ,则图中休闲区(阴影部分)的面积是( ) A.(10π﹣)米2B .(π﹣)米2C .(6π﹣)米2D .(6π﹣)米23.如图是某商品的标志图案,AC 与BD 是⊙O的两条直径,首尾顺次连接点A ,B ,C ,D , 得到四边形ABCD .若AC =10cm ,∠BAC = 36°,则图中阴影部分的面积为( ) A .5πcm 2B .10πcm2C .15πcm2D .20πcm 24.如图,正方形ABCD 内接于⊙O ,⊙O 的半 径为2,以点A 为圆心,以AC 长为半径画弧交AB 的延长线于点E ,交AD 的延长线于点F ,则图中阴影部分的面积为( ) A .4π﹣4 B .4π﹣8 C .8π﹣4 D .8π﹣85.如图,四边形ABCD 是菱形,∠A =60°, AB =2,扇形BEF 的半径为2,圆心角为60°,则图中阴影部分的面积是( )A.﹣B .﹣C .π﹣D .π﹣7.如图,△ABC 是等腰直角三角形,∠ACB =90°,BC =AC ,把△ABC 绕点A 按顺时针方向旋转45°后得到△AB ′C ′,若AB =2,则线段BC 在上述旋转过程中所扫过部分(阴影部分)的面积是 (结果保留π).四.课后练习(1)多边形结合求阴影面积问题1.如图,正三角形与正六边形的边长分别为2 和1,正六边形的顶点O 是正三角形的中心, 则阴影部分的面积为( ) A .33B .332C .3D .31(2)三角形扇形结合求阴影面积问题2.如图,A 是半径为3的⊙O 外的一点,OA =6,AB 是⊙O 的切线,B 是切点,弦BC ∥ OA ,连接AC ,则阴影部分的面积为( ) A .π25B .π2C .π23D .π反思:件弧,连半径,得扇形.(3)四边形与扇形结合求阴影面积问题3.如图,在扇形AOB 中∠AOB =90°,正方形 CDEF 的顶点C 是的中点,点D 在OB 上,点E 在OB 的延长线上,当正方形CDEF 的边长为22时,则阴影部分的面积为( )A .4π﹣4B .2π﹣2C .4π﹣2D .2π﹣4 4.如图,菱形ABCD 的边长为2cm ,∠A =60°. 是以点A 为圆心、AB 长为半径的弧,是以点B为圆心、BC 长为半径的弧.则阴影部分的面积为( )A .23B .32C .3D .2335.将直角△ABC 绕顶点B 旋转至如图位置,其中 ∠C =90°,AB =2,BC =1,点C 、B 、A ′在同一 直线上,则阴影部分的面积是( ) A .2334+πB .2334-πC .32316+π D .32316-π8.如图,等边三角形ABC 的边长为2,CD ⊥AB 于D ,若以点C 为圆心,CD 为半径画弧,则图形阴影部分的面积是( )A .﹣πB .2﹣πC .2D .2﹣9.在矩形ABCD 中,AB =,BC =2,以A 为圆心,AD 为半径画弧交线段BC 于E ,连接DE ,则阴影部分的面积为( )A.﹣B .﹣C .π﹣D .π﹣10.如图,以AB 为直径,点O 为圆心的半圆经过点C ,若AC =BC =,则图中阴影部分的面积是( )A .B.C .D .+11.如图,在Rt △ABC 中,∠ACB =90°,AC =2,以点C 为圆心,CB 的长为半径画弧,与AB 边交于点D ,将绕点D 旋转180°后点B 与点A 恰好重合,则图中阴影部分的面积为( )A .B .C .D .12.如图,在△ABC 中,∠C =90°,AC =BC ,斜边AB =4,O 是AB 的中点,以O 为圆心,线段OC 的长为半径画圆心角为90°的扇形OEF ,经过点C ,则图中阴影部分的面积为( )A .2π﹣4B .4﹣πC .π﹣2D .4π﹣814.如图,把半径为2的⊙O 沿弦AB ,AC 折叠,使和都经过圆心O ,则阴影部分的面积为( )A .B .C .2D .4 15.如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE 、CF 交于点G ,半径BE 、CD 交于点H ,且点C 是弧AB 的中点.若扇形的半径是2,则图中阴影部分的面积等于( )A .2π﹣4B .2π﹣2C .π+4D .π﹣1 21.如图,在平行四边形ABCD 中,以AB 中点E 为圆心,EA 为半径画弧交CD 于点F ,点F 恰好为CD 中点,若∠B =60°,BC =6,则图中阴影部分的面积为 .22.如图,A 是半径为2的⊙O 外一点,OA =4,AB 是⊙O 的切线,B 为切点,弦BC ∥OA ,连接AC ,求阴影部分的面积.6.(2017·荆门)已知:如图,△ABC 内接于⊙O ,且半径OC ⊥AB ,点D 在半径OB 的延长线上,且∠A =∠BCD =30°,AC =2,则由劣弧BC ,线段CD 和线段BD 所围成图形(阴影部分)的面积为 .3.(2017·天水)如图所示,AB 是⊙O 的直径,弦CD ⊥AB ,垂足为E ,∠BCD =30°,CD =43,则S 阴影=( ) A .2πB.83πC.43πD.38π3.如图,AB 为半圆O 的直径,C ,D 是弧AB 上的三等分点.若⊙O 的半径为2,E 是直径AB 上任意一点,则图中阴影部分的面积是 .(2)与折叠问题结合考查问题13.如图,半径为2的半圆形纸片,按如图方式折叠,使对折后半圆弧的中点M与圆心O重合,则图中阴影部分的面积是()A.18﹣6πB.4﹣πC.9﹣πD.2﹣π4.如图,已知⊙O的半径为2,弦AB⊥半径OC,沿AB将弓形ACB翻折,使点C与圆心O重合,则月牙形(图中实线围成的部分)的面积是.7.(2017·太原二模)如图,AB是半圆O的直径,且AB=8,点C为半圆上的一点.将此半圆沿BC所在的直线折叠.若圆弧BC恰好过圆心O,则图中阴影部分的面积是.1.(2018•温州)小明发现相机快门打开过程中,光圈大小变化如图1所示,于是他绘制了如图2所示的图形.图2中六个形状大小都相同的四边形围成一个圆的内接正六边形和一个小正六边形,若PQ所在的直线经过点M,5PB cm,小正六边形的面积为2,则该圆的半径为cm.1.小明发现相机快门打开过程中,光圈大小变化如图1所示,于是他绘制了如图2所示的图形.图2中六个形状大小都相同的四边形围成一个圆的内接正六边形和一个小正六边形,若PQ所在的直线经过点M,5PB cm=,小正六边形的面积2,则该圆的半径为8 cm.【考点】M M:正多边形和圆【专题】55B:正多边形与圆【分析】设两个正六边形的中心为O,连接OP,OB,过O作OG PM⊥,OH AB⊥,由正六边形的性质及邻补角性质得到三角形PMN为等边三角形,由小正六边形的面积求出边长,确定出PM的长,进而求出三角形PMN的面积,利用垂径定理求出PG的长,在直角三角形OPG中,利用勾股定理求出OP的长,设OB xcm=,根据勾股定理列出关于x的方程,求出方程的解即可得到结果.【解答】解:设两个正六边形的中心为O,连接OP,OB,过O作OG PM⊥,OH AB⊥,由题意得:60MNP NMP MPN∠=∠=∠=︒,小正六边形的面积为2,∴,即PM=,2MPNS∆∴=,OG PM⊥,且O为正六边形的中心,12PG PM∴=,72OG==,在Rt OPG∆中,根据勾股定理得:7OP cm=,设OB xcm=,OH AB⊥,且O为正六边形的中心,12BH x∴=,OH=,1(5)2PH x cm∴=-,在Rt PHO∆中,根据勾股定理得:2221)(5)492OP x x=+-=,解得:8x=(负值舍去),则该圆的半径为8cm.故答案为:8【点评】此题考查了正多边形与圆,熟练掌握正多边形的性质是解本题的关键.。
