四年级上册数学第三单元《角的度量》知识点归纳
四年级数学上册第三单元 《角的度量》必考点：数角的个数
《角的度量》必考点：数角的个数
方法与线段类似，可以以一条线段为边，再找和它可以组合的角；也可以找到基础角，再数出由基础角组成的组合角。
方法一：
以AB为边，可以和AB构成角的有CB，DB，EB，3个角；以CB为边，可以和CB构成角的有DB，EB，有2个角；以DB为边，可以和DB构成角的有EB，有1个角。
一共有3+2+1=6个角。
方法二：按基本角的方法去数。
上图中的基本角是∠ABC，∠CBD，∠DBE，共3个基本角；其中包含两个基本角的是∠ABD，∠CBE，有2个。
包含三个基本角的是∠ABE，有1个。
一共有3+2+1=6个角。
规律：数角的方法可以采用数线段的方法，大角被分成几个小角，就从1一直加到几。
练习：
1.数一数，下图中一共有多少个角？
5＋4＋3＋2＋1=15（个）
2.数一数，下图中一共有多少个含有“☆”的角？
分类讨论：1个单角：1个
2个单角：2个
3个单角：2个
4个单角：1个
1+2+2+1=6（个）。
四年级数学角的度量知识点
四年级数学角的度量知识点1. 角的定义及分类2. 角的度量单位：度和弧度3. 度数和弧度的换算4. 角的顶点、边和角度符号5. 直角、钝角和锐角6. 角度的比较和排列7. 互补角和补角8. 相邻角和对顶角9. 垂直角和同位角10. 角的相等性质和角平分线角是数学中重要的概念之一，它是由两个射线（或线段）通过一个共同的起点形成的部分。
根据角大小的不同，可将角分为不同的类型：直角、钝角、锐角等。
度数和弧度是角度量的两种单位，其中度数是指将一个圆周分为360份，而弧度是指将一个圆周分为2π份。
换算两种单位的公式为：1°=π/180，1弧度=180/π。
角的度数可以用角度符号来表示，通常用小写字母a、b、c等表示角的顶点。
在角度量中，还需要注意互补角、补角、相邻角、对顶角、垂直角以及同位角等概念。
同时，还需要了解角的相等性质和角平分线的概念，这些都是数学中基础的角度量知识点。
1. 角的定义及分类角的定义是由两条射线或线段共同确定的一对有向角。
根据角度的大小不同，它们可以被分类为直角，锐角和钝角等。
直角是90度的角，它可以用一个封闭的正方形来形象地表示。
锐角是小于90度的角，例如图中的∠BAC，它可以用一个封闭的等腰三角形来表示。
钝角是大于90度而小于180度的角，例如图中的∠BCD，它可以用一个封闭的等腰梯形来表示。
2. 角的度量单位：度和弧度角的度量单位有度和弧度两种，其中度是最常见的单位。
它的定义是将一个圆周分成360份，每份为1度。
弧度是指，圆的长度等于半径的弧所对应的圆心角。
例如，半径为r的圆的圆心角度数为θ，它所对应的弧长为s，则s=rθ。
同时，它也有一个常用的单位π（pi），圆的周长是2πr。
弧度的公式是：θ=弧长/半径，且通常用弧度符号来表示。
3. 度数和弧度的换算度数和弧度可以互相换算。
其换算公式为：1度=π/180弧度，1弧度=180/π度。
例如，若要将60度角转换为弧度，则应将其乘以π/180，即60π/180=π/3弧度。
《角的度量》四年级数学上册复习提纲
角的度量一、角的定义1. 角的基本概念角是由两条射线共同确定的图形部分，射线称为角的边，它们的公共端点称为角的顶点。
2. 角的种类根据其度数的大小，角可以分为以下几种：•零角：度数为0°，两条射线重合，无法看出来的角。
•锐角：度数小于90°，尖角。
•直角：度数为90°的角，两条垂直的直线形成的角。
•钝角：度数大于90°，钝角是大于直角小于180°的角。
•平角：度数为180°，两条直线成一条直线。
二、角的计量1. 角的度量单位角的度量单位是度（°）。
一圆周的角度为360°。
2. 角的测量方法（1）使用量角器测量角度•将量角器其中一条边放在角的边上的顶点上。
•将量角器另一条边与坐标轴或放在图纸上的已知直线对齐。
•观察量角器刻度上所对应的角度值。
（2）使用圆规测量角度•将圆规的一只脚放在角的顶点上，另一只脚转到角的一边上，使圆规的另一只脚指向角的另一边。
•将这种位置转到已知角度的标志物上。
•在转到的角度上读出度数。
3. 角的度数关系（1）互补角两个角的度数之和为90°，则称这两个角为互补角。
（2）补角一个角的补角是与其互补角的角。
（3）对顶角两个相交直线上的两个相邻的角，互为对顶角。
（4）邻补角两个补角互为对顶角，则称这两个角为邻补角。
4. 角的比较大小（1）角的大小比较根据角的度数大小，角可以比较大小：•锐角 < 90°•直角 = 90°•钝角 > 90°（2）角的度数关系及比较根据角的大小关系，可以进行如下比较：•若角A > 角B，则称角A大于角B，记作 A > B。
•若角A < 角B，则称角A小于角B，记作 A < B。
•若角A = 角B，则称角A等于角B，记作 A = B。
三、角的运算1. 角的加法（1）角的和两个角的和是由这两个角的边所在直线作为边的角。
人教版四年级数学上册第三单元 《角的度量》知识点
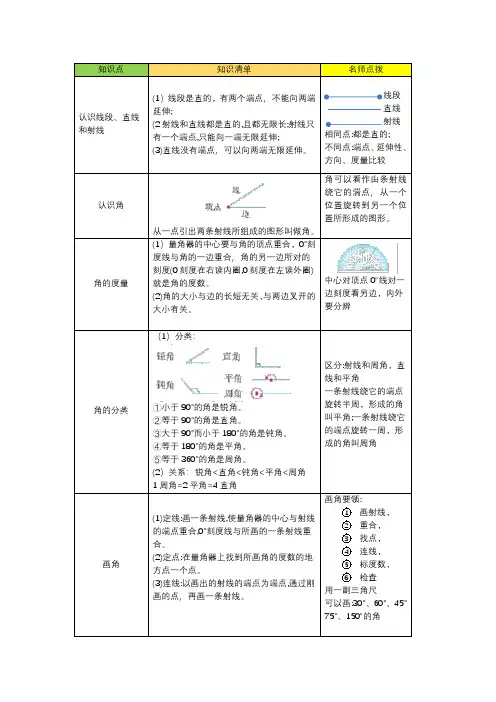
中心对顶点 0o 线对一 边刻度看另边，内外 要分辨
（1）分类：
角的分类 画角
①小于 90°的角是锐角。 ②等于 90°的角是直角。 ③大于 90°而小于 180°的角是钝角。 ④等于 180°的角是平角。 ⑤等于 360°的角是周角。 (2）关系：锐角<直角<钝角<平角<周角 1 周角=2 平角=4 直角
角可以看作由条射线
绕它的湍点﹐从一个
位置旋转到另一个位
置所形成的图形。
从一点引出两条射线所组成的图形叫做角。
(1）量角器的中心要与角的顶点重合，0°刻
度线与角的一边重合﹐角的另一边所对的
刻度(0 刻度在右读内圈,0 刻度在左读外圈) 就是角的度数。 (2)角的大小与边的长短无关，与两边叉开的 大小有关。
知识点
知识清单
名师点拨认识线段、直线 和来自线认识角角的度量
(1）线段是直的，有两个端点﹐不能向两端 延伸; (2 射线和直线都是直的,且都无限长;射线只 有一个端点,只能向一端无限延伸; (3)直线没有端点﹐可以向两端无限延伸。
线段 直线 射线 相同点:都是直的; 不同点:端点、延伸性、 方向、度量比较
(1)定线:画一条射线,使量角器的中心与射线 的端点重合,0°刻度线与所画的一条射线重 合。 (2)定点:在量角器上找到所画角的度数的地 方点一个点。 (3)连线:以画出的射线的端点为端点,通过刚 画的点﹐再画一条射线。
区分:射线和周角，直 线和平角 一条射线绕它的端点 旋转半周，形成的角 叫平角;一条射线绕它 的端点旋转一周，形 成的角叫周角
画角要领: 1 画射线， 2 重合， 3 找点， 4 连线， 5 标度数， 6 检查
用一副三角尺 可以画:30°、60°、45° 75°、150o.的角
四年级数学《角的度量》知识点梳理
四年级数学《角的度量》知识点梳理角是数学中的重要概念之一，它在几何图形和实际生活中都有广泛应用。
本篇文章将对四年级学生学习的《角的度量》这一知识点进行梳理和总结，以便帮助学生更好地理解和掌握。
一、角的定义角是由两条线段或线段和射线的公共端点以及其余部分组成的图形。
我们可以用大写字母来表示角的名称，例如∠ABC表示以点B为顶点的角。
二、角的度量单位1. 角度角的度量单位是角度，用符号°表示。
一个圆共分为360度，这被称为一个圆周角。
当我们需要度量小于或大于一个圆周角的角时，可以使用角度进行表示。
2. 直角直角是一个特殊的角度，它的度量为90度，用符号∠ABC = 90°来表示。
直角的两条边相互垂直。
3. 角度的比较我们可以通过比较两个角的度量来判断它们的大小关系。
例如，∠ABC的度量大于∠DEF的度量，可以表示为∠ABC > ∠DEF；相反，∠ABC的度量小于∠DEF的度量，可以表示为∠ABC < ∠DEF。
三、角的分类根据角的度量，我们可以将角分为以下几类：1. 锐角一个角的度量小于90度时，称为锐角。
例如，∠ABC = 60°。
2. 直角一个角的度量等于90度时，称为直角。
例如，∠DEF = 90°。
3. 钝角一个角的度量大于90度但小于180度时，称为钝角。
例如，∠GHI = 120°。
4. 对顶角当两个角的顶点和边成一条直线时，它们被称为对顶角。
对顶角的度量是相等的。
例如，∠ABC和∠CBD是对顶角，可以表示为∠ABC = ∠CBD。
四、角的度量方法在测量角的度量时，我们可以使用以下几种方法：1. 用量角器测量量角器是用来测量角度的工具，它通常呈半圆形，分为180度。
我们将量角器的中心点对齐于角的顶点，然后读取量角器上的刻度，就可以知道角的度量。
2. 用直尺测量当我们遇到较大的角度时，可以使用直尺来近似测量其度量。
我们将直尺的一条边与角的一条边对齐，然后观察直尺上的刻度，就可以得到角的近似度量。
四年级上册角的度量知识点
四年级上册角的度量知识点小伙伴，今天咱们来唠唠四年级上册角的度量这个知识点哈。
一、角的概念。
1. 角啊，就像是从一个点伸出来的两条胳膊，这个点呢就叫做角的顶点，那两条胳膊就是角的两条边。
你可以想象一下，就像你伸开双臂做个“大”字，你的身体中间那个点就是顶点，两条胳膊就是边啦。
2. 角有大有小哦。
比如说，你把胳膊张得大大的，这个角就大；要是胳膊靠得近近的，角就小。
二、角的度量单位。
1. 角的度量单位是度，用那个小圆圈“°”来表示。
就像我们量身高用厘米一样，量角就用度。
2. 把一个圆平均分成360份，每一份所对的角的大小就是1度。
你可以想象一个大披萨，切成360小块，每一块的边和圆心组成的角就是1度的角呢。
三、量角器。
1. 量角器可是量角的神器啊。
它长得像个半圆形的大饼干，上面还有好多刻度线。
2. 量角器的中心要和角的顶点重合，就像把量角器稳稳地放在角的头顶上一样。
3. 量角器的0刻度线要和角的一条边重合。
这里要注意哦，如果角的一条边对着的是内圈的0刻度线，那读度数的时候就要读内圈的刻度；要是对着外圈的0刻度线，就得读外圈的刻度啦。
就像坐公交车，你从哪个门上车，就从哪个门下车一样，可不能乱哦。
四、角的分类。
1. 锐角，锐角是那种小小的角，比直角小。
锐角就像小朋友刚长出来的小牙齿，小小的，尖尖的。
锐角的度数是大于0°小于90°的。
2. 直角，这个就好认啦，直角就像墙角一样，方方正正的，它的度数正好是90°。
3. 钝角，钝角比直角大，但是比平角小。
钝角就像一个大嘴巴，想要一口吞下好多东西的感觉。
它的度数是大于90°小于180°的。
4. 平角，平角就像一条直直的线，不过它可不是直线哦，它中间有个顶点的。
平角的度数是180°，就像把一个圆切成两半，其中一半的边和圆心组成的角就是平角。
5. 周角，周角就更厉害了，它转了一圈，度数是360°，就像一个完整的圆。
四年级数学上册第三单元 《角的度量》必考知识点
《角的度量》必考知识点
角的定义：自一点引两条射线所成的图形叫角
角的符号：∠
角的分类：锐角、直角、钝角、平角、周角
锐角：大于0°小于90°的角叫做锐角
直角：等于90°的角叫做直角
钝角：大于90°小于180°的角叫做钝角
平角：等于180°的角叫做平角
周角：等于360°的角叫做周角
角的大小：角的大小与边的长短没关系，角的大小决定于角的两条边张开的程度。
三角形定义：由三条边首尾相接组成的封闭图形叫三角形
三角形内角和：三角形的内角和为180度
三角形外角：三角形的一个外角等于另外两个内角和
三角形的分类：
按角分：锐角三角形的三个角都小于90度
直角三角形有一个角等于90度
钝角三角形有一个角大于90度
按边分：不等腰三角形，等腰三角形（含等边三角形）注：锐角三角形和钝角三角形可统称为斜三角形。
四年级上册数学《角的度量》知识点整理
角的度量一、本节学习指导本节学习角的相关知识，同学们可以先回忆一下直线、斜线相关知识。
本节中我们要掌握角的表示、量角器的使用。
本节有配套免费学习视频。
二、知识要点1、直线、射线、角直线：向两端无限延伸的线，直线无端点。
射线：能像一个方向延伸的线，射线有一个端点。
线段：不能延伸的线，线段有两个端点。
角：具有公共端点的两条射线组成的图形叫做角。
这个公共端点叫做角的顶点，这两条射线叫做角的两条边。
2、直线、射线与线段的联系和区别（1）、直线和射线都可以无限延伸，因此无法量出长短。
（2）、线段可以量出长度。
（3）、线段有两个端点，直线没有端点，射线只有一个端点。
3、角的特征角有一个顶点，两条边，如下图角通常用符号“∠”来表示上图中的两个角表示为：∠1 ，∠2；读作：角 1 ，角24、角的大小比较：角的计量单位是“度”，符号“°”，把半圆平分成180 等份，每一份所对的角的大小是l 度。
记做1°。
角大小的测量借助量角器，如下图。
测量方法：量角注意两对齐：量角器的中心和角的顶点对齐；量角器的0刻度线和角的一条边对齐。
做到两对齐后看角的另一条边对着刻度线几，这个角就是几度。
看刻度要分清内外圈。
这里我教大家一个小窍门：分清内外圈，紧跟0刻度；0刻度在外圈就看外圈的刻度。
0刻度在内圈就看内圈的刻度。
牢牢记住不忘记。
注意：角的大小与角的两边画出的长短没关系。
角的大小要看两条边叉开的大小，叉开得越大，角越大。
5、角的分类：锐角＜90°，直角=90°，90°＜钝角＜180°，平角=180°=2个直角，周角=360°=2个平角=4个平角6、画角步骤：以画65°的角为例（1）画一条射线，使量角器的中心和封线的端点重合，0 刻度线和射线重合。
（2）在量角器65°刻度线的地方点一个点。
（3）以画出的射线的端点为端点，通过刚画的点，再画一条射线。
人教版四年级数学上册 角的度量 知识点归纳
角的度量知识点归纳知识点一、线1、线包括三种：直线、射线、线段。
①直线：没有端点，向两端无限延长，长度无法测量。
②射线：从1个端点出发，向一端无限延长，长度无法测量。
③线段: 包括2个端点及它们之间的有限部分，长度可以测量。
知识点二、直线、射线、线段的区别和性质1、直线、射线、线段的区别：端点长度字母表示方法图形表示方法直线0个无法测量直线AB，直线l射线1个无法测量射线AB、射线l线段2个可测量线段AB、线段l2、直线、射线、线段的性质：①直线AB和直线BA是同一条直线；射线AB和射线BA不是同一条直线；线段AB和线段BA是同一条线段。
②经过任意一点，可以画无数条直线、无数条射线、无数条线段。
③经过任意两点，可以画1条直线、无数条射线、无数条线段。
④两点之间线段最短。
知识点三、角1、由两条有公共端点的射线构成的图形叫做角，符号是“∠”。
这个公共端点叫做顶点，两条射线叫做这个角的边。
2、角的计量单位是“度”，符号为“°”。
3、把一个圆分成360份，每一份所占的角就是1度。
知识点四、角的度量1、度量角的工具叫做量角器。
2、量角器的使用步骤：①把量角器的中心点和角的顶点重合，角的一边与量角器的零刻度线重合。
②角的另一边所对的量角器上的刻度，就是这个角的度数。
温馨提示：量角器上有里、外两排角度，如果测量的角小于90°，则读取较小的度数；如果测量的角大于90°，则读取较大的度数。
3、角的大小与两边的长短无关，与两边的张开程度有关。
张开得越大，角越大；张开得越小，角越小。
知识点五、角的分类1、如果0°<角度<90°，那么这个角是锐角。
2、如果90°<角度<180°，那么这个角是钝角。
3、1个直角=90°1平角=180°1周角=360°知识点六、角的画法1、画角的步骤：①画一条射线。
②把量角器的中心点和角的顶点重合，角的一边与量角器的零刻度线重合。
四年级上册《角的度量》单元知识点整理
角的度量知识点整理1、线段：是直线的一部分，有2个端点，可以度量长度，不可延长。
2、射线：是直线的一部分，只有1个端点，可以向一端无限延长，不可度量长度。
3、直线：没有端点（或者说“有0个端点”），可以向两端无限延长，不可度量长度。
4、角：从一点引出两条射线所组成的图形叫做角。
这一点叫做角的“顶点”，两条射线叫做角的两条“边”。
角要用弧线表示大小。
5、角的标注：角的标注方法有两种：（1）用数字代表角，并在旁边标出角的度数（如果有的话）（2）直接将角的度数标注在弧线旁6、过点画直线的数量：过一点可以画无数条射线、无数条直线。
过两点只能画出一条直线，也就是“两点可以确定一条直线”。
7、角的度量方法：量角的大小，要用量角器。
角的计量单位是“度”，用符号“°”表示。
把半圆分成180等份，每一份所对的角的大小是1度，记作1°。
步骤：（1）（量角器的）中心点与（待测角的）顶点重合（2）（量角器的其中一条）0刻度线与（待测角的）一条边重合（3）角的另一条边所对应的（与0刻度线同圈的）刻度就是这个角的度数8、角的大小比较：角的大小与角的两边画出的长短没有关系。
角的大小要看两条边叉开的大小，叉开得越大，角越大。
用放大镜看角，角的大小不变。
9、一副（两个）三角板的度数：一副三角板有2个直角，4个锐角一个三角板有1个直角，2个锐角，且这两个锐角互为余角。
10、角的分类：（1）锐角：大于0°且小于90°的角是锐角（2）直角：等于90°的角是直角（3）钝角：大于90°且小于180°的角是钝角2：00或14：00，时针和分针夹角为2个整点，即30°×2=60°4：00或16：00，时针和分针夹角为4个整点，即30°×4=120°（4） 平角：等于180°的角是平角（5） 周角：等于360°的角是周角1周角=2平角=4直角=360°钟面时间问题（求时针与分针的夹角）：因为周角是360°，而钟面上有12个整点刻度，所以每两个整点刻度间的夹角是360°÷12=30°11、 角的画法： A 、用量角器画角（如画65°的角）（1）画一条射线，作为角的顶点和一条边 （2）使量角器的中心和射线的端点重合，0刻度线和射线重合（3）在量角器（与0刻度线同圈的）65°刻度线的地方点一个点 （4）以画出的射线的端点为端点，通过刚画的点，再画一条射线（因为“两点确定一条直线”，用端点和刚画的点来确定另外一条边的位置）（5）画小弧线，标注13、 拼角而用“一副（两个）三角板”可以“拼．出”75°、105°、120°、135°、150°这几个角 14、求度数常见规律：三角形的内角和是180度四边形内角和是360度两条直线相交，相对的角相等，相邻的角和是180度图形计数：数线段：数射线：数角：。
人教版小学四年级数学上册第三单元《角的度量》知识点总结
四年级数学上册第三单元【角的度量】知识点总结-人教版学生姓名学校班级1．直线、射线、角小结：没有端点，可以向两端无限延伸，这种线叫直角。
只有一个端点，向一端无限延伸，这种线叫射线。
直线、射线与线段有什么联系和区别？①、直线和射线都可以无限延伸，因此无法量出长短。
②、线段可以量出长度。
③、线段有两个端点，直线没有端点，射线只有一个端，点。
2．角大小的比较：角的计量单位是“度”，用符号“°”表示。
把半圆平分成180 等份，每一份所对的角的大小是l 度。
记做1°角的大小与角的两边画出的长短没关系。
角的大小要看两条边叉开的大小，叉开得越大，角越大。
3．角的分类：锐角＜90°，直角=90°，90°＜钝角＜180°，平角=180°=2个直角，周角=360°=2个平角=4个平角4．画角步骤：①画一条射线，使量角器的中心和封线的端点重合，0 刻度线和射线重合。
②在量角器65°刻度线的地方点一个点。
③以画出的射线的端点为端点，通过刚画的点，再画一条射线。
人教版小学四年级数学上册第三单元《角的度量》测试卷学生姓名学校班级一、填空1．5时整，时针与分针所组成的角是（）度。
（）时整, 时针与分针成平角。
2．120°的角比平角小（）度。
比直角大（）度。
3．写出下面各角的度数。
(1)(2) (3)4．1周角= （）平角= （）直角= （）度。
5．如果∠1 + ∠2 = ∠2 + ∠3，∠1 = 40°，那么∠3 = （）。
二、选择1．一个锐角和一个直角可以组成一个（）。
A、锐角B、钝角C、平角2．经过两点，可以画（）条线段。
经过一点可以画（）多少条射线。
A、1B、2C、3D、无数条3．角的两条边是（）A、直角。
B、线段。
C、射线。
4．下面说法错误的是（）A、一条直线长6厘米。
B、角的两边张开得越大，角越大。
C、钟面上2时整，分针和时针成锐角。
四年级数学上册《角的度量》重点、难点梳理
四年级数学上册《角的度量》重点、难点梳理
类别
锐角
钝角
直角
平角
周角
图形
特点
小于90°
大于90°
小于180°
等于90°
等于180°
等于360°
1.线段有(2)个端点，(可以)测量出长度，射线有(1)个端点，直线没有端点，射线和直线(不能)测出长度；过一点可以画(无数条)直线也可以画(无数条)射线。
7.用一个10倍的放大镜看一个10°的角，角的大小(不变)，还是数学·暑假预习
四年级数学上册《角的度量》重点、难点梳理
9.周角(360°)>平角(180°)>钝角(大于90°小于180°)>直角(90°)>锐角(大于0°小于90°)
1周角=2平角=4直角=360°
2.从一点引出两条(射线)所组成的图形叫做(角)，符号“(∠)”表示。
3.把一条线段向一端无限延伸，就得到一条(射线)；把一条线段向两端无限延伸，就得到一条(直线)。
4.角的度量单位是(度)，用符号(°)表示。
5.把半圆平均分成180份，每1份所对的角是1度，记作(1°)
6.用量角器测量角的方法：把量角器的中心与(顶点)重合，0°刻度线与角的一条边(重合)，角的另一边所对的量角器上的刻度，就是这个角的(度数)。
10.把平角分成两个角，如果一个是锐角，另一个角一定是(钝角)。
11.3点钟和9点钟形成的是(直角)，6点钟和12点钟形成(平角)。
12.能用一副三角尺子画出的角是(15°，75°、105°、135°、150°、180°)。
13.画角时注意：量角器的中心与射线的端点重合，0°刻度线与射线(重合)。
14.画角的方法：先画一条射线，确定角度，确定角的另外一边后，最后标好角的度数和符号。画角一要用铅笔来画。
四年级上册数学 《角的度量》知识点总结
四年级上册数学
《角的度量》知识点总结
一、线段、直线、射线
1.线段的特点
（1）是直的
（2）有两个端点
（3）不能延伸，可以量出它的长度
（4）表示：用两个大写字母表示它的两个端点，记作：线段AB 或线段BA。
2.直线的特点
（1）是直的
（2）没有端点（有0个端点）
（3）可以向两端无限延伸，无法测量出它的长度
（4）表示：在直线上取两个点，并用两个大写字母表示，记作：直线AB或直线BA。
也可以用小写字l表示。
3.射线的特点
（1）是直的
（2）只有一个端点
（3）可以向一端无限延伸，无法测量出它的长度
（4）表示：用射线的端点和射线上的一个点来表示，并用两个
大写字母表示，记作：射线AB。
四年级数学《角的度量》知识点
四年级数学《角的度量》知识点
四年级数学《角的度量》知识点
以下是店铺精心为大家分享的人教版四年级数学《角的度量》知识点欢迎大家参考学习。
1、认识度。
将圆平均分成360份，把其中的.1份所对的角叫做1度，记作1°，通常用1°作为度量角的单位。
2、认识量角器。
量角器是把半圆平均分成180份，一份表示1度。
量角器上有中心点、0刻度线、内刻度线、外刻度线。
3、量角器的使用方法。
“两合一看”,“两合”是指中心点与角的顶点重合;0刻度线与角的一边重合。
“一看”就是要看角的另一边所对的量角器的刻度。
4、看角的度数时要注意是看外刻度还是内刻度。
交的开口向左看外刻度线，角的开口向右看内刻度线。
通过店铺为大家分享的人教版四年级数学《角的度量》知识点希望对大家有所帮助。
下载全文。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第三单元角的度量
一、线段、直线、射线
1、
2、经过一点可以画无数条直线（图一）。
经过两点只可以画一条直线（两点确定一条直线）（图二）。
3、把线段的一端无限延长，就得到一条射线。
把线段的两端都无限延长，就得到一条直线。
线段和射线都是直线的一部分。
4、像手电筒、汽车灯和太阳等射出来的光线，都可以看成是射线。
二、角
1、从一点引出的两条射线所组成的图形叫做角。
这一点叫做角的“顶点”，两条射线叫做角的两条“边”。
角有一个顶点，两条边。
2、角通常用符号“∠”表示，如图：记作：∠1；读作：角1。
3、角的大小与两条边的长短无关，与两条边张开的大小有关。
两条边张开的越开，角越大；张开
名称图形命名相同点不同点
线段
线段AB；
线段BA
直的有两个端点不能延伸可以测量其长度射线
射线AB（只
有一种读法，
从端点读起）
直的有一个端点
只向一端
无限延伸
不能测量其长度直线
直线AB；
直线BA；
直线l
直的没有端点
向两端无
限延伸
不能测量其长度
得越小，角就越小。
（放大镜不能把角放大。
）
4、量角器就是度量角的工具。
角的计量单位是“度”，用“°”表示；如1度记做1°
5、人们将圆平均分成360份，其中1份所对的角的大小就是1°；
把半圆分成180等份，每一份所对的角的大小就是1°。
三、用量角器量角的方法：
（1）把量角器的中心点与角的顶点重合，0°刻度线与角的一条边重合。
（2）角的另一边所对的量角器上的刻度，就是这个角的度数。
（量角时，角的一条边与内圈的0°刻度线重合，读内圈的度数；与外圈的0°刻度线重合，读外圈的度数。
）
四、用量角器画角的方法：（如画65°的角）
（1）画一条射线，作为角的顶点和一条边
（2）使量角器的中心和射线的端点重合，0°刻度线和射线重合
（3）在量角器（与0刻度线同圈的）65°刻度线的地方点一个点
（4）以画出的射线的端点为端点，通过刚画的点，再画一条射线
（5）画小弧线，标注
五、角的分类：
（1）平角：一条射线绕它的端点旋转半周，形成的角叫做平角。
（2）周角：一条射线绕它的端点旋转一周，形成的角叫做周角。
（3）0°＜锐角＜90°；直角=90°； 90°＜钝角＜180°；平角=180°；周角=360°
（4） 1个平角=2个直角；1个周角=2个平角=4个直角
（5）锐角<直角<钝角<平角<周角
六、三角板
（1）三角板上的度数有：30°、60°、90°、45°
（2)用一副三角板可以拼出75°、105°、120°、135°、150°、180°的角。
七、钟面时间问题（求时针与分针的夹角）：
（1）因为周角是360°，而钟面上有12个整点刻度，所以每两个整点刻度间的夹角是
360°÷12=30°
（2）3时整或9时整，时针和分针成直角；6时整，时针和分针成平角；12时整，时针和分针成周角。
（3）1小时，时针转一大格，所对的角是30°；分针转一圈，所对的角是360°。
八、会求一个已知角的余角、补角和对顶角：
如右图，若∠3=25°，
（1)那么∠4=90°－25°=65°（∠3和∠4互为余角）
（2) ∠2=180°－25°=155°（∠3和∠2互为补角）
（3）∠1=∠3=25°（∠3和∠1是对顶角，对顶角相等）。