七年级下册几何题精编版
七年级数学(下册)几何典型题
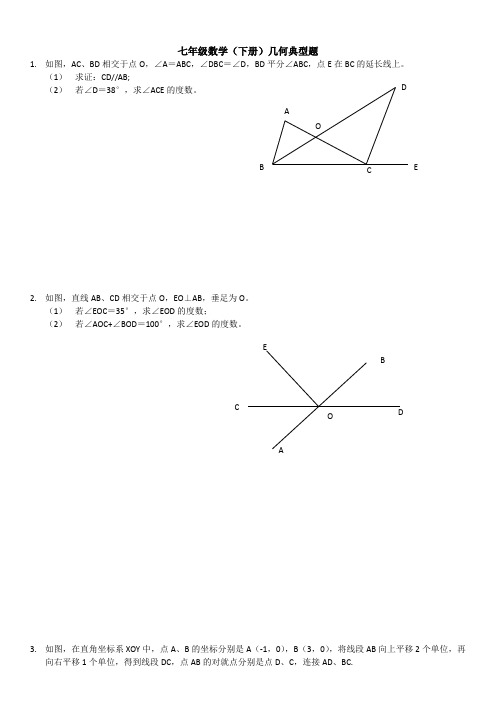
七年级数学(下册)几何典型题1. 如图,AC 、BD 相交于点O ,∠A =ABC ,∠DBC =∠D ,BD 平分∠ABC ,点E 在BC 的延长线上。
(1) 求证:CD//AB;(2) 若∠D =38°,求∠ACE 的度数。
2. 如图,直线AB 、CD 相交于点O ,EO ⊥AB ,垂足为O 。
(1) 若∠EOC =35°,求∠EOD 的度数;(2) 若∠AOC+∠BOD =100°,求∠EOD 的度数。
3. 如图,在直角坐标系XOY 中,点A 、B 的坐标分别是A (-1,0),B (3,0),将线段AB 向上平移2个单位,再向右平移1个单位,得到线段DC ,点AB 的对就点分别是点D 、C ,连接AD 、BC.(1) 直接写出点C 、D 的坐标; (2) 求四边形ABCD 的面积;(3) 点P 为线段BC 上任意一点(与点B 、C 不重合),连接PD 、PO.求证:∠CDP+∠BOP=∠OPD.4. 如图,直接EF 分别与直线AB ,CD 相交于点P 和点Q ,PG 平分∠APQ, QH 平分∠DQP ,并且∠1=∠2,说出图中哪些直线平行。
5. 平面内的两条直线有相交和平行两种位置关系。
(1) 如图1,若AB//CD ,点P 在AB 、CD 内部,∠B =50°,∠D =30°,求∠BPD 的度数。
(2) 如图2,将点P 移到AB 、CD 外部,则∠BPD 、∠B 、∠D 之间有何数量关系?请写出你的结论并加以证6. 如图,方格纸中每个小方格都是长为1个单位的正方形,若学校位置坐标为A (1,2),解答以下问题。
(1) 请在图中建立适当的直角坐标系,并写出图书馆(B )的位置坐标。
(2) 若体育馆位置坐标为C (-3,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC ,求△ABC 的面积。
7. 如圖,CE ⊥AB 于E ,DF ⊥AB 于F ,AC ∥A CE FB8. 如图,在平面直角坐标系中,已知点A (-3,3),B (-5,1),C (-2,0),P (a,b )是△ABC 的边AC 上任意一点,△ABC 经过平移后得到△A ’B ’C ’,点P 的对应点为P ’(a+6,b-2). (1) 直接写出点C ’的坐标; (2) 在图中画出△A ’B ’C ’; (3) △AOA ’的面积。
七下数学证明必考题精选(经典)

图①DA EC B Fl图②ABEF C lD 七年级下册数学期末考试几何大题证明必考题精选类型一、正方形中三角形全等与线段长度之间的关系例1、如图①,直线l 过正方形ABCD 的顶点B ,A 、C 两顶点在直线l 同侧,过点A 、C 分别作AE ⊥直线l 、CF ⊥直线l . (1)试说明:EF =AE +CF ;(2)如图②,当A 、C 两顶点在直线l 两侧时,其它条件不变,猜想EF 、AE 、CF 满足什么数量关系(直接写出答案,不必说明理由).练习: 如图,△ABC 中,AB=AC ,∠BAC =90°.(1)过点A 任意一条直线l (l 不与BC 相交),并作B D ⊥l ,C E ⊥l ,垂足分别为D 、E .度量BD 、CE 、DE ,你发现它们之间有什么关系?试对这种关系说明理由; (2)过点A 任意作一条直线l (l 与BC 相交),并作B D ⊥l ,C E ⊥l ,垂足分别为D 、E .度量BD 、CE 、DE ,你发现经们之间有什么关系?试对这种关系说明理由.例2、已知正方形的四条边都相等,四个角都是90º。
如图,正方形ABCD 和正方形AEFG 有一个公共点A ,点G 、E 分别在线段AD 、AB 上。
(1)如图1, 连结DF 、BF ,说明:DF =BF ; (2)若将正方形AEFG 绕点A 按顺时针方向旋转,连结DG ,在旋转的过程中,你能否找到一条长度与线A E B图1D CG FA BD CGFE图2段DG 的长始终相等的线段?并以图2为例说明理由。
练习:如图,正方形ABCD 的边CD 在正方形ECGF 的边CE 上,B 、C 、G 三点在一条直线上,且边长分别为2和3,在BG 上截取GP =2,连结AP 、PF. (1)观察猜想AP 与PF 之间的大小关系,并说明理由.(2)图中是否存在通过旋转、平移、反射等变换能够互相重合的两个三角形?若存在,请说明变换过程;若不存在,请说明理由.(3)若把这个图形沿着PA 、PF 剪成三块,请你把它们拼成一个大正方形,在原图上(1)BD 与CE 相等吗?请说明理由.(2)你能求出BD与CE 的夹角∠BFC 的度数吗?(3)若将已知条件改为:四边形ABCD 与四边形AEFG 都是正方形,例3、正方形四边条边都相等,四个角都是90.如图,已知正方形ABCD 在直线MN 的上方,BC 在直线MN 上,点E 是直线MN 上一点,以AE 为边在直线MN 的上方作正方形AEFG .(1)如图1,当点E 在线段BC 上(不与点B 、C 重合)时: ①判断△ADG 与△ABE 是否全等,并说明理由;②过点F 作FH ⊥MN ,垂足为点H ,观察并猜测线段BE 与线段CH 的数量关系,并说明理由;FB(2)如图2,当点E 在射线CN 上(不与点C 重合)时: ①判断△ADG 与△ABE 是否全等,不需说明理由;②过点F 作FH ⊥MN ,垂足为点H ,已知GD =4,求△CFH 的面积.练习:如图1,四边形ABCD 是正方形,G 是CD 边上的一个点(点G 与C 、D 不重合),以CG 为一边作正方形CEFG ,连结BG ,DE .(1)如图1,说明BG= DE 的理由(2)将图1中的正方形CEFG 绕着点C 按顺时针方向旋转任意角度 ,得到如图2.请你猜想①BG= DE 是否仍然成立?②BG 与DE 位置关系?并选取图2验证你的猜想.类型二、探究题例1、如图,已知等边△A B C 和点P ,设点P 到△A B C 三边A B 、A C 、B C (或其延长线)的距离分别为h 1、h 2、h 3,△A B C 的高为h .图 2FG D A 图 1F G D A在图(1)中,点P 是边B C 的中点,此时h 3=0,可得结论:h h h h =++321. 在图(2)--(5)中,点P 分别在线段M C 上、M C 延长线上、△A B C 内、△A B C 外.(1)请探究:图(2)--(5)中, h 1、h 2、h 3、h 之间的关系;(直接写出结论)(2)证明图(2)所得结论; (3)证明图(4)所得结论. (4)(附加题2分)在图(6)中,若四边形R B C S 是等腰梯形,∠B =∠C =60o , R S =n ,B C =m ,点P 在梯形内,且点P 到四边B R 、R S 、S C 、C B 的距离分别是h 1、h 2、h 3、h 4,桥形的高为h ,则h 1、h 2、h 3、h 4、h 之间的关系为: ;图(4)与图(6)中的等式有何关系?练习:1、如图,在△ABC 中,AB=AC ,P 为底边上任意一点,PE ⊥AB ,PF ⊥AC ,BD ⊥AC.(1)求证:PE+PF=BD ;(2)若点P 是底边BC 的延长线上一点,其余条件不变,(1)中的结论还成立吗?如果成立,请说明理由;如果不成立,请画出图形,并探究它们的关系.2、如图,已知△ABC 三边长相等,和点P ,设点P 到△ABC 三边AB 、AC 、BC (或其A B C D EP A B C DE P M(3) A B C D EP M(2) A B C D EM (P )(1) A B C D E P M (5)C B APDEFC B E 延长线)的距离分别为h 1、h 2、h 3,△ABC 的高为h .在图(1)中, 点P 是边BC 的中点,由S △ABP+S △ACP=S △ABC 得,h BC h AC h AB ⋅=⋅+⋅21212121可得h h h =+21又因为h 3=0,所以:h h h h =++321.图(2)~(5)中,点P 分别在线段MC 上、MC 延长线上、△ABC 内、△ABC 外.(1)请探究:图(2)~(5)中,h 1、h 2、h 3、h 之间的关系;⑵ ⑶ ⑷ ⑸ (2)说明图(2)所得结论为什么是正确的;例2、已知△ABC 是等边三角形,将一块含30角的直角三角板DEF 如图1放置,当点E 与点B 重合时,点A 恰好落在三角板的斜边DF 上. (1)AC=CF 吗? 为什么?(2)让三角板在BC 上向右平行移动,在三角板平行移动的过程中,(如图2)是否存在与线段EB 始终相等的线段(设AB ,AC 与三角板斜边的交点分别为G ,H )?如果存在,请指出这条线段,并证明;如果不存在,请说明理由.(B)CE F图1ABC DEP ABCDEPM(3)ABCDE P M (2)ABCDEM (P )(1)练习:1、如图1,一等腰直角三角尺GEF (∠EGF=90°,∠GEF=∠GFE=45°,GE=GF )的两条直角边与正方形ABCD 的两条边分别重合在一起.现正方形ABCD 保持不动,将三角尺GEF 绕斜边EF 的中点O (点O 也是BD 中点)按顺时针方向旋转.(1)如图2,当EF 与AB 相交于点M ,GF 与BD 相交于点N 时,通过观察或测量BM ,FN 的长度,猜想BM ,FN 相等吗?并说明理由;(2)若三角尺GEF 旋转到如图3所示的位置时,线段FE 的延长线与AB 的延长线相交于点M ,线段BD 的延长线与GF 的延长线相交于点N ,此时,(1)中的猜想还成立吗?请说明理由.2、已知:△ABC 为等边三角形,M 是BC 延长线上一点,直角三角尺的一条直角边经过点A ,且60º角的顶点E 在BC 上滑动,(点E 不与点B 、C 重合),斜边∠ACM 的平分线CF 交于点F(1)如图(1)当点B 在BC 边得中点位置时(6分) ○1猜想AE 与BF 满足的数量关系是 。
初一几何题

初一几何题第一篇:初一几何题初一几何试题一、选择题(每题2分,共52分)1.下列说法中,正确的是()A、棱柱的侧面可以是三角形BC、正方体的各条棱都相等D、棱柱的各条棱都相等2.用一个平面去截一个正方体,截面不可能是()A、梯形B、五边形C、六边形D、圆3.下列立体图形中,有五个面的是()A、四棱锥B、五棱锥C、四棱柱D、五棱柱4.一个正方体,六个面上分别写着六个连续的整数的一个数字,且每个相对面上的两个数之和相等,如图所示,你能看到的数为7、10、11,则六个整数的和为()A、51B、52C、57D、585.如图中是正方体的展开图的有()个A、2个B、3个C、4个D、5个6、下列说法中,正确的个数为()①两点确定一条直线②两条直线相交,只有一个交点③将一条线段分成两条相等线段的点叫线段的中点④用5倍放大镜看一个20º的角,看到的是100º的角A、4B、3C、2D、17、下列命题正确的是()A、射线是直线的一半;B、若线段AB=BC,则B是线段AC的中点;C、两点之间,只有线段最短;D、把角平分的直线是这角的平分线.8、已知BD为∠ABC的平分线,则∠ABD=A、∠ACB,B、∠BCD,C、∠DBC,D、以上都不对9、∠a的四等分线的条数为()A、2条B、3条C、4条D、无数条10、线段AB=9cm,C、D为AB的三等分点,则CD=()A、6cm2B、3cmC、92cm D、以上都不对 11.下列说法正确的是()A、若AP=AB,则P是AB的中点;B、若AB=2PB,则P是AB的中点;2ABC、若AP=PB,则P是AB的中点;D、若AP=PB=,则P是AB的中点;12、如果在一条直线上得到10条不同的线段,那么在这条直线上至少要选用()个不同的点A、20B、10C、7D、513.平面内两两相交的6条直线,其交点个数最少为m个,最多为n个,则m+n=()A、12B、16C、20D、以上都不对14.已知x,y都是钝角的度数,甲、乙、丙、丁计算(x+y)的结果依次为500,260,720,900,其中只有61一个正确的结果,那么算得结果正确的是()A、甲B、乙C、丙D、丁 15.如图,已知A、B、C、D、E五点A D C E 在同一直线上,D点是线段AB的中点,点E是线段BC的中点,若线段AC=12,则线段DE等于()BA、10B、8C、6D、416.如右图所示,C是线段AD上任意两点,M是AB的中点,N是CD中点,若MN=a,BC=b,则线段AD的长是()DA2(a-b)B2a-bCa+bDa-b17.如图,∠1=15︒,∠AOC=90︒,点B、O、D在同一直线上,CB则∠2的度数为()A. 75︒B.15︒C.105︒D.165︒ D2OA18.在海上,灯塔位于一艘船的北偏东40度方向,那么这艘船位于这个灯塔的()A 南偏西50度方向B南偏西40度方向C 北偏东50度方向D北偏东40度方向19、一个角的余角是它的补角的,则这个角为()31(A)22.5°(B)45°(C)50°(D)135°20、如果一个角的补角是150°,那么这个角的余角的度数是()A30° B60°C90°D120°21、已知∠1和∠2互补,且∠1>∠2,那么∠2与012(∠1—∠2)的关系是()A、互余B、互补C、和为45D、差为22.5022、五位老朋友a、b、c、d、e在公园聚会,见面时候握手致意问候,已知a握了4次,b握了1次,c 握了3次,d握了2次,到目前为止,e握了()次。
初一下册几何证明题(完整版)

初一下册几何证明题初一下册几何证明题第一篇:初一下册几何证明题初一下册几何证明题1.已知在三角形ab中,be,f分别是角平分线,d是ef中点,若d到三角形三边b,ab,a的距离分别为x,,z,求证:x=+z证明;过e点分别作ab,b上的高交ab,b于m,n点.过f点分别作a,b上的高交于p,q点.根据角平分线上的点到角的2边距离相等可以知道fq=fp,em=en.过d点做b上的高交b于o点.过d点作ab上的高交ab于h点,过d点作ab上的高交a于j点.则x=do,=h,z=dj.因为d是中点,角ane=角ahd=90度.所以hd平行me,me=2hd同理可证fp=2dj。
又因为fq=fp,em=en.fq=2dj,en=2hd。
又因为角fq,do,en都是90度,所以四边形fqne是直角梯形,而d是中点,所以2do=fq+en又因为fq=2dj,en=2hd。
所以do=hd+jd。
因为x=do,=h,z=dj.所以x=+z。
在正五边形abde中,m、n分别是de、ea上的点,bm与n相交于点o,若∠bon=108°,请问结论bm=n是否成立?若成立,请给予证明;若不成立,请说明理由。
当∠bon=108°时。
bm=n还成立证明;如图5连结bd、e.在△bi)和△de中∵b=d,∠bd=∠de=108°,d=de∴δbd≌δde∴bd=e,∠bd=∠ed,∠db=∠en∵∠de=∠de=108°,∴∠bdm=∠en∵∠ob+∠ed=108°,∠ob+∠od=108°∴∠mb=∠nd又∵∠db=∠ed=36°,∴∠dbm=∠en∴δbdm≌δne∴bm=n3.三角形ab中,ab=a,角a=58°,ab的垂直平分线交a与n,则角nb=3°因为ab=a,∠a=58°,所以∠b=61°,∠=61°。
七年级下几何证明题

第4题H2DC 几何说理题1、填空完成推理过程: 如图,∵AB ∥EF (已知)∴∠A+=1800() ∵DE ∥BC (已知) ∴∠DEF=() ∠ADE=()2.如图,EF ∥AD ,∠1=∠2,∠BAC=70°.将求∠AGD 的过程填写完整.因为EF ∥AD ,所以∠2=. 又因为∠1=∠2,所以∠1=∠3. 所以AB ∥. 所以∠BAC+=180°. 又因为∠BAC=70°, 所以∠AGD=.3.已知:如图,∠ADE =∠B ,∠DEC =115°.求∠C 的度数.4.已知:如图,AD ∥BC ,∠D =100°,AC 平分∠BCD ,求∠DAC 的度数.5.已知:如图,AB ∥CD ,直线EF 分别交AB 、CD 于点E 、F ,∠BEF 的平分线与∠DEF 的平分线相交于点P .求∠P 的度数 6、直线AB 、CD 相交于O ,OE 平分∠AOC ,∠EOA :∠AOD=1:4,求∠EOB 的度数.49、如图,AB ∥CD ,AE 交CD 于点C ,DE ⊥AE ,垂足为E ,∠A =37o ,求∠D 的度数.50、如图,已知:21∠∠=,50=D ∠,求B ∠的度数。
51、如图所示,∠1=72°,∠2=72°,∠3=60°,求∠4的度数.52、AB//CD,EF ⊥AB 于点E ,EF 交CD 于点F ,已知∠1=600.求∠2的度数.53、如图,AB∥CD,BF∥CE,则∠B 与∠C 有什么关系?请说明理由.54.如图,已知:DE∥BC,CD 是∠ACB 的平分线,∠B=70°,∠ACB =50°,求∠EDC 和∠BDC 的度数.55.如图AB∥CD,∠NCM=90°,∠NCB=30°,CM 平分∠BCE,求∠B 的大小.56、如图,AB ⊥BD ,CD ⊥MN ,垂足分别是B 、D 点,∠FDC =∠EBA . (1)判断CD 与AB 的位置关系;(2)BE 与DE 平行吗?为什么?DEB CAENMCD BANMFDCBA57、如图,∠1+∠2=180°,∠DAE =∠BCF ,DA 平分∠BDF . (1)AE 与FC 会平行吗?说明理由. (2)AD 与BC 的位置关系如何?为什么?(3)BC 平分∠DBE 吗?为什么.58、如图,已知:E 、F 分别是AB 和CD 上的点,DE 、AF 分别交BC 于G 、H ,∠A =∠D ,∠1=∠2,求证:∠B =∠C .59、如图所示,求∠A +∠B +∠C +∠D +∠E +∠F 的度数.60、如图,在△ABC 中,∠ABC =80°,∠ACB =50°,BP 平分∠ABC ,CP 平分∠ACB ,求∠BPC 的度数.61、如图,点D 是△ABC 内一点,∠A =65°,∠1=20°,∠2=25°,求∠BDC 的度数。
七年级下册数学几何专题(一)

七年级下册数学几何专题(一)一、三角形三边关系及内角和问题1、(1)一个三角形的三边长分别为2,x-1,3,则x的取值范围是_____________(2)一个三角形两边的长分别是2cm和7cm,第三边的长是偶数,则这个三角形的周长为____________2、一个三角形三个内角度数的比是2∶3∶4,那么这个三角形是 __________三角形3、在△ABC中,∠A-∠B=36,∠C=2∠B,则∠C=___________4、如图,∠A+∠B+∠C+∠D+∠E+∠F=_______________5、(1)如图,在△ABC中,P是∠ABC和∠ACB的平分线的交点,试探索∠A 与∠P的数量关系,并说出你的理由。
(2)如图,在△ABC中,P是∠ABC与∠ACE的平分线的交点,试探索∠A 与∠P的数量关系,并说出你的理由。
(3)如图,PB、PC别是△ABC的∠ABC、∠ACB的外角角平分线,BP、CP相交于P,试探索∠BPC 与∠A之间的数量关系,并说出你的理由、6、如图,在中,D是BC上任意一点,E是AD上任意一点。
求证:(1)∠BEC>∠BAC;(2)AB+AC>BE+EC。
二、线段的垂直平分线与角平分线转化问题1、如图,AB=AC,DE垂直平分AB交AB于D,交AC于E,若△ABC的周长为28,BC=8,求△BCE的周长。
变式:如图,如图,△ABC中边AB的垂直平分线分别交BC,AB于点D,E,AE=3cm,△ADC的周长为9cm,则△ABC的周长是____________2、如图,已知在△ABC中,AD垂直平分BC,AC=EC,点B、D、E在同一直线上,那么AB+DB=DE会成立么?为什么?3、如图,∠ABC,∠ACB的平分线交于0,过0作MN∥BC,交AB于M,交AC于N。
求证:BM+NC=MN。
4如图,∠B=∠C=90,M 是BC的中点,DM平分∠ADC,求证:AM平分∠DAB5如图,己知,AD平分∠BAC,EF垂直平分AD,交BC延长线于F,连结AF,试说明∠B=∠CAF、三、等腰三角形中的分类讨论:1、已知等腰三角形的一个内角为75则其顶角为_________________、2、等腰三角形中,一个角是另一个角的两倍,求它各角的度数___________________、3、(1)若等腰三角形的一个外角为70,则它的底角为________________、(2)等腰三角形的一个外角等于110,则顶角的度数为___________________4、等腰三角形中,两个内角的比为4:1,则顶角的度数为______________5、已知等腰三角形的一边等于5,另一边等于6,则它的周长等于_________________6、已知一等腰三角形两边为2,4,则它的周长为__________________7、有一个等腰三角形,三边分别是3x-2,4x-3,6-2x,等腰三角形的周长为 ___________8、(1)等腰三角形的周长为13,其中一边长为3,则该等腰三角形的底边长为________________(2)等腰三角形的周长是30,其中两边的差是3,则这个三角形的三边分别为________________________9、一等腰三角形一腰上的中线把这个三角形的周长分成15cm 和18cm两部分,则这个等腰三角形的底边长是_________________10、等腰三角形底边长为5cm,一腰上的中线把周长分成的两部分之差为2cm,则腰长为_____________11、等腰三角形一腰上的高与另一腰所成的夹角为30,这个等腰三角形的顶角的度数 ___12、等腰三角形的一个角是50,它的一腰上的高与底边的夹角为____________13、己知在△ABC中,AB=AC,AC边的垂直平分线与AB边所在的直线相交所得的锐角为38,则∠C=___________14、如图,CA=CB,DF=DB,AE=AD,求∠A的度数、15、如图,在△ABC中,AB=AC,BC=BD,AD=DE=EB,求∠A的度数16、如图,∠A=16,AB=BC=CD=DE=EF,求∠FEM的度数。
(完整版)初一下册数学角度几何解析题以及练习题(附答案).doc

七年级下册数学几何解析题以及练习题(附答案)9.(2011 ·扬州 ) 如图,C岛在A岛的北偏东60°方向,在B岛的北偏西 45°方向,则从C岛看 A、 B 两岛的视角∠ ACB=________.答案105°解析如图,∵ (60 °+∠CAB)+(45 °+∠ABC)=180°,∴∠CAB+∠ABC=75°,在△ ABC中,得∠ C=105°.12.如图所示,在△ABC中,∠ A=80°,∠ B=30°, CD平分∠ ACB, DE∥AC.(1)求∠ DEB的度数;(2)求∠ EDC的度数.解(1) 在△ABC中,∠A=80°,∠B=30°,∴∠ ACB=180°-∠ A-∠ B=70°.∵ DE∥AC,∴∠ DEB=∠ ACB=70°.(2)∵ CD平分∠ ACB,1∴∠ DCE=2∠ ACB=35°.∵∠ DEB=∠ DCE+∠ EDC,∴∠ EDC=70°-35°=35°.13.已知,如图,∠1=∠ 2,CF⊥AB于F,DE⊥AB于E,求证:FG∥BC.( 请将证明补充完整 )证明∵ CF⊥ AB, DE⊥ AB(已知),∴ ED∥FC() .∴∠ 1=∠BCF() .又∵∠ 1=∠ 2( 已知 ) ,1∴ FG ∥BC () .解 在同一平面内, 垂直于同一直线的两条直线互相平行;两直线平行, 同位角相等;内错角相等,两直线平行.14.如图,已知三角形ABC ,求证:∠ A +∠ B +∠ C =180°.分析:通过画平行线,将∠A 、∠B 、∠C 作等角代换,使各角之和恰为一平角,依辅助线不同而得多种证法,如下:证法 1:如图甲,延长 BC 到 D ,过 C 画 CE ∥ BA .∵BA ∥ CE ( 作图所知 ) ,∴∠ B =∠ 1,∠ A =∠ 2( 两直线平行,同位角、内错角相等) .又∵∠ BCD =∠ BCA +∠ 2+∠ 1=180°( 平角的定义 ) ,∴∠ A +∠ B +∠ ACB =180°( 等量代换 ) .如图乙,过 BC 上任一点 F ,画 FH ∥AC , FG ∥ AB ,这种添加辅助线的方法能证明∠A +∠B +∠C =180°吗?请你试一试.解 ∵ FH ∥AC ,∴∠ BHF =∠ A ,∠ 1=∠ C .∵ FG ∥AB ,∴∠ BHF =∠ 2,∠ 3=∠ B ,∴∠ 2=∠ A .∵∠ BFC =180°,∴∠ 1+∠ 2+∠ 3=180°,即∠ A +∠ B +∠ C =180°.15.(2010 ·玉溪 ) 平面内的两条直线有相交和平行两种位置关系.(1) 如图 a ,若 AB ∥ CD ,点 P 在 AB 、 CD 外部,则有∠ B =∠ BOD .又因∠ BOD 是△ POD的外角,故∠ BOD =∠ BPD +∠ D ,得∠ BPD =∠ B -∠ D . 将点 P 移到 AB 、CD 内部,如图 b ,以上结论是否成立?若成立,说明理由;若不成立,则∠、∠ 、∠ D 之BPD B间有何数量关系?请证明你的结论;(2) 在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点 Q,如图 c,则∠ BPD、∠ B、∠ D、∠ BQD之间有何数量关系?( 不需证明 )(3)根据 (2) 的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.解(1) 不成立,结论是∠BPD=∠B+∠D.延长 BP交 CD于点 E,∵ AB∥CD,∴∠ B=∠ BED.又∠ BPD=∠ BED+∠ D,∴∠ BPD=∠ B+∠ D.(2)结论:∠ BPD=∠ BQD+∠ B+∠ D.(3)设 AC与 BF交于点 G.由 (2) 的结论得:∠AGB=∠ A+∠ B+∠ E.又∵∠ AGB=∠ CGF,∠ CGF+∠ C+∠ D+∠ F=360°,∴∠ A+∠ B+∠ C+∠D+∠ E+∠ F=360°.A 14.把一副常用的三角板如图所示拼在一起,那么图中∠ADE是度. DEBC第 14 题2.如图,在△ ABC和△ ABD中,现给出如下三个论断:①AD=BC;②∠C=∠D;③∠1=∠2。
七年级下几何练习题

七年级下几何练习题--------------------------------------------------------------------------作者: _____________--------------------------------------------------------------------------日期: _____________七年级下第九、第十章练习题1.如图(1),共有三角形的个数是 。
如图(2),共有三角形的个数是 。
2如图,在△ABC 中,AB=AC ,∠A=36°,∠ABC 和∠ACB 的平分线分别交AC 、AB 于D 、E ,则图中一共有 个等腰三角形。
3.如图所示,若∠A=32°,∠B=45°,∠C=38°,则∠DFE 等于 。
4.如果等腰三角形的两边长分别为3和5,那么这个三角形的周长是 。
5.三角形中,最大角α的取值范围是( ) A 、0°<α<90°B 、60°<α<180°C 、60°≤α<90 D 、60°≤α<180° 6.下列正多边形的组合中,能够铺满地面不留缝隙的是( ) A 、正八边形和正三角形 B 、正五边形和正八边形 C 、正六边形和正三角形; D 、正六边形和正五边形 7.下面的说法正确的个数是( )①三条线段首位顺次连结所组成的的图形叫三角形 ②直角三角形的高只有一条③三角形的高至少有一条在三角形内 ④三角形的高、内角平分线、中线不一定是线段⑤三角形具有稳定性⑥各内角相等的多边形是正多边形⑦等边三角形不是等腰三角形⑧同种的任意三角形和四边形都能铺满地面⑨只要围绕一点拼在一起的几种正多边形的内角之和为一个周角,就一定能拓展下去并铺满地面.正确的有( ) A 、3个 B 、4个 C 、5个 D 、6个 8.AD 是△ABC 的中线,△AB D 面积是5,则△ABC 面积为_______. 9.一个多边形最多有_____个内角是锐角.10. 若过m 边形的一个顶点有7条对角线,n 边形没有对角线,k 边形有k 条对角线,正h 边形的内角和与外角和相等,则代数式(m -k)(h-n)=_______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
02
a)AD是ΔABC的高;
b)AD是ΔABC中BC边上的高;
c)AD垂直于BC。垂足为D;
d)∠ADB=∠ADC=90°。
大家一起来看看下面着一条题:
2. 求证: 三角形的一个外角等于和它不相邻的两个内角 的和. 已知: 如图27.1.4,∠CBD是△ABC的一个外角. 求证: ∠CBD=∠A+∠C.
图 27.2.3
05
大家一起来看看下面着一条题:
5.已知:如图27.2.4,QD⊥OA,QE⊥OB,点D、E为垂足,QD=QE.求证: 点Q在∠AOB的平分线上.
图 27.2.4
06
大家一起来看看下面着一条题:
6.已知: MN⊥AB,垂足为点C, AC=BC,点P 是直线 MN上任意一点. 求证: PA=PB.
图 27.3.1
08
07
大家一起来看看下面着一条题:
平行四边形判定定理1 一组对边平行且相等的四边形是平行四边形. 7.已知:四边形ABCD中,AB∥CD,AB=CD. 求证:四边形ABCD是平行四边形. 分析 要证明四边形ABCD是平行四边形,只要证明另一组对边平行,因此,可 以连结其中一条对角线,然后证明内错角相等.
图 27.1.4
03
03
大家一起来看看下面着一条题:
3.已知: 如图27.2.2,在△ABC和△AˊBˊCˊ中, ∠ACB=∠AˊCˊBˊ=90°, AB=AˊBˊ,AC=AˊCˊ. 求证: △ABC≌△AˊBˊCˊ.
图 27.2.2
04
按照角分类:
大家一起来看看下面着一条题:
4.已知: 如图27.2.3,OC是∠AOB平分线,点P是OC上任意一点,PD⊥OA, PE⊥OB,点D、E为垂足. 求证: PD=PE. 分析 图中有两个直角三角形△PDO与△PEO,容易看出满足(A.A.S.)定理 的条件.
七下几何题
--潘老师
01
大家一起来看看下面着一条题:1.已知:△ABC源自 求证:∠A+∠B+∠C=180°
图 27.1.3
02
a)AD是三角形ABC的平分线; b)AD平分∠BAC交BC于D; c)∠BAD=∠DAC= 1∠2 BAC。 d)∠BAC=2∠BAD=2∠DAC。
02
a)AM是ΔABC的中线; b)AM是ΔABC中BC边上的中线; c)点M是BC边的中点; d)BM=MC。
