2008年考研真题数学二
考研数学二真题(2008年)

2008年全国硕士研究生入学统一考试
数学二试题
一、选择题:1~10小题,每小题4分,共40分. 在每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.
1.
2.
3.
4.
6.
7.
8.
二、填空题:9~14小题,每小题4分,共24分. 把答案填在题中横线上.
9.
11.
12.
13.
14.
三、解答题:15~22小题,共86分. 解答应写出文字说明、证明过程或演算步骤.
15.
17.
19.
21.
2008年全国硕士研究生入学统一考试
数学二试题答案
一、选择题:1~10小题,每小题4分,共40分. 在每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.
1. D
2. C
3. D
4. A
5. B
6. A
7. C
8. D
二、填空题:9~14小题,每小题4分,共24分. 把答案填在题中横线上.
9. 2
10. y=-xe-x+Cx
11. y=x+1
12. (-1,-6)
14. λ=-1
三、解答题:15~22小题,共86分. 解答应写出文字说明、证明过程或演算步骤.
16.
17.
18.
19.
20.
21.
22.
23.。
2008考研数学二真题及参考答案

2008年研究生入学统一考试数学二试题与答案一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内. (1)设2()(1)(2)f x x x x,则'()f x 的零点个数为()A 0BCD 3(2)曲线方程为()y f x 函数在区间[0,]a 上有连续导数,则定积分()a taf x dx ()A 曲边梯形ABCD 面积.B 梯形ABCD 面积.C 曲边三角形ACD 面积. D 三角形ACD 面积. (3)在下列微分方程中,以123cos2sin 2xy C eC x C x (123,,C C C 为任意常数)为通解的是()(5)设函数()f x 在(,)内单调有界,n x 为数列,下列命题正确的是()A 若n x 收敛,则()n f x 收敛. B 若n x 单调,则()n f x 收敛.C 若()n f x 收敛,则n x 收敛.D 若()n f x 单调,则n x 收敛.(6)设函数f 连续,若2222()(,)uvD f x y F u v dxdy xy,其中区域uv D 为图中阴影部分,则F u(7)设A 为n 阶非零矩阵,E 为n 阶单位矩阵.若30A ,则()A E A 不可逆,E A 不可逆.B EA 不可逆,EA 可逆.C EA 可逆,EA 可逆.D EA 可逆,EA 不可逆.(8)设1221A,则在实数域上与A 合同的矩阵为()A2112. B2112.C 2112.D 1221.二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.(9)已知函数()f x 连续,且201cos[()]lim1(1)()x x xf x ef x ,则(0)____f .(10)微分方程2()0xy x e dxxdy的通解是____y .(11)曲线sin ln xy yx x 在点0,1处的切线方程为.(12)曲线23(5)y xx 的拐点坐标为______.(13)设xyy zx,则(1,2)____z x.(14)设3阶矩阵A 的特征值为2,3,.若行列式248A ,则___.三、解答题:15-23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. (15)(本题满分9分)求极限4sin sin sin sin limx x xxx.(16)(本题满分10分)设函数()y y x 由参数方程2()ln(1)t xx t yu du确定,其中()x t 是初值问题200xt dx tedt x的解.求22yx.(17)(本题满分9分)求积分12arcsin 1x x dx x.(18)(本题满分11分)求二重积分max(,1),Dxy dxdy 其中{(,)02,02}Dx y x y (19)(本题满分11分)设()f x 是区间0,上具有连续导数的单调增加函数,且(0)1f .对任意的0,t,直线0,xxt ,曲线()yf x 以及x 轴所围成的曲边梯形绕x 轴旋转一周生成一旋转体.若该旋转体的侧面积在数值上等于其体积的2倍,求函数()f x 的表达式.(20)(本题满分11分)(1)证明积分中值定理:若函数()f x 在闭区间[,]a b 上连续,则至少存在一点[,]a b ,使得()()()baf x dx f ba (2)若函数()x 具有二阶导数,且满足32(2)(1),(2)()x dx ,证明至少存在一点(1,3),()使得(21)(本题满分11分)求函数222uxyz 在约束条件22zxy 和4xy z 下的最大值与最小值.(22)(本题满分12分)设矩阵2221212n naaa AaaO OO ,现矩阵A 满足方程AX B ,其中1,,TnXx x L ,1,0,,0B L ,(1)求证1nA n a ;(2)a 为何值,方程组有唯一解,并求1x ;(3)a 为何值,方程组有无穷多解,并求通解.(23)(本题满分10分)设A 为3阶矩阵,12,为A 的分别属于特征值1,1特征向量,向量3满足323A,(1)证明123,,线性无关;(2)令123,,P,求1P AP.2008年全国硕士研究生入学统一考试数学二试题解析一、选择题(1)【答案】D 【详解】因为(0)(1)(2)0f f f ,由罗尔定理知至少有1(0,1),2(1,2)使12()()0f f ,所以()f x 至少有两个零点.又()f x 中含有因子x ,故0x 也是()f x 的零点,D 正确.本题的难度值为. (2)【答案】C 【详解】()()()()()()a a a a a xf x dxxdf x xf x f x dx af a f x dx其中()af a 是矩形ABOC 面积,0()a f x dx 为曲边梯形ABOD 的面积,所以()a xf x dx为曲边三角形的面积.本题的难度值为. (3)【答案】D【详解】由微分方程的通解中含有xe 、cos2x 、sin 2x 知齐次线性方程所对应的特征方程有根1,2rri ,所以特征方程为(1)(2)(2)0r ri r i ,即32440rrr .故以已知函数为通解的微分方程是4yyy本题的难度值为. (4)【答案】A 【详解】0,1xx时()f x 无定义,故0,1x x是函数的间断点因为000ln 11lim ()limlimlimcsc |1|csc cot xxxxx x f x xx x x同理0lim ()xf x 又1111ln 1lim ()limlim sin limsin1sin11xxx xx f x xx x所以0x 是可去间断点,1x 是跳跃间断点. 本题的难度值为. (5)【答案】B 【详解】因为()f x 在(,)内单调有界,且{}n x 单调.所以{()}n f x 单调且有界.故{()}n f x 一定存在极限.本题的难度值为. (6)【答案】A【详解】用极坐标得222()22211,()v u u f r r Df u v F u vdudvdvrdr vf r druv所以2F vf uu本题的难度值为.(7)【答案】C 【详解】23()()E A EAA E AE ,23()()E A E A A E AE故,EA EA 均可逆.本题的难度值为. (8)【答案】D【详解】记1221D,则2121421E D ,又2121421E A 所以A 和D 有相同的特征多项式,所以A 和D 有相同的特征值.又A 和D 为同阶实对称矩阵,所以A 和D 相似.由于实对称矩阵相似必合同,故D 正确.本题的难度值为. 二、填空题(9)【答案】2 【详解】2222201cos[()]2sin [()2]2sin [()2]()limlim lim ()[()2]4(1)()xxx x xf x xf x xf x f x x f x xf x ef x 所以(0)2f 本题的难度值为. (10)【答案】()xx e C 【详解】微分方程20xyx edx xdy可变形为xdy y xedxx所以111()dxdxxxxxxyexe e dx Cxxedx C x e C x本题的难度值为. (11)【答案】1yx【详解】设(,)sin()ln()F x y xy y x x ,则1cos()11cos()x yy xy F dy y x dxF x xy y x,将(0)1y 代入得1xdydx ,所以切线方程为10y x ,即1y x 本题的难度值为. (12)【答案】(1,6)【详解】53235y xx23131351010(2)333x yxxx1x 时,0y;0x 时,y 不存在在1x左右近旁y 异号,在0x左右近旁0y,且(1)6y 故曲线的拐点为(1,6)本题的难度值为. (13)【答案】2(ln 21)2【详解】设,y x uvx y ,则vzu所以121()ln v vz z u z v y vuu uxuxvxxy所以(1,2)2(ln 21)2z x 本题的难度值为. (14)【答案】-1 【详解】||236A Q 3|2|2||A A 本题的难度值为. 三、解答题(15)【详解】方法一:43[sin sin(sin )]sin sin sin(sin )limlimxxx x x x x x x方法二:331sin ()6xx x o x Q 331sin(sin )sin sin (sin )6x xxo x本题的难度值为. (16)【详解】方法一:由20xdx tedt得2xe dxtdt ,积分并由条件0t x 得21xet ,即2ln(1)xt 所以2222ln(1)2(1)ln(1)21dydy t tdt t t dx t dxdtt方法二:由20xdx tedt得2x e dxtdt ,积分并由条件0t x 得21xet ,即2ln(1)xt 所以2222ln(1)2(1)ln(1)21xdydy t tdt t t e xdx t dxdt t所以22(1)xd ye x dx本题的难度值为. (17)【详解】方法一:由于221arcsin lim1x x x x,故212arcsin 1x x dx x是反常积分.令arcsinx t ,有sin x t ,[0,2)t 方法二:212arcsin 1x x dxx1221(arcsin )2x d x 令arcsinxt ,有sin x t ,[0,2)t故,原式21164本题的难度值为.(18)【详解】曲线1xy 将区域分成两个区域1D 和23D D ,为了便于计算继续对区域分割,最后为max ,1Dxy dxdy本题的难度值为.D 1D 3D 2(19)【详解】旋转体的体积2()tV f x dx ,侧面积22()1()tSf x fx dx ,由题设条件知上式两端对t 求导得22()()1()f t f t f t ,即21y y 由分离变量法解得21ln(1)y yt C ,即21ty yCe将(0)1y 代入知1C,故21tyye ,1()2ttyee 于是所求函数为1()()2xxy f x e e 本题的难度值为.(20)【详解】(I)设M 与m 是连续函数()f x 在[,]a b 上的最大值与最小值,即由定积分性质,有()()()b am b a f x dx M b a ,即()baf x dx mMba 由连续函数介值定理,至少存在一点[,]ab ,使得()()b af x dx f b a即()()()b af x dx f b a (II)由(I)的结论可知至少存在一点[2,3],使32()()(32)()x dx 又由32(2)()()x dx,知23对()x 在[1,2][2,]上分别应用拉格朗日中值定理,并注意到(1)(2),()(2)得在12[,]上对导函数()x 应用拉格朗日中值定理,有本题的难度值为. (21)【详解】方法一:作拉格朗日函数22222(,,,,)()(4)F x y z xyzxyz x y z 令2222022020040x yzF x x F y y F z F x y zFxyz 解方程组得111222(,,)(1,1,2),(,,)(2,2,8)x y z x y z故所求的最大值为72,最小值为 6. 方法二:问题可转化为求2242242u xyxx yy 在224x y x y条件下的最值设44222222(,,)2(4)F x y u xyx y x y xyxy令323222442(12)0442(12)040xyF x xyx x F y x y y y Fxy xy解得1122(,)(1,1),(,)(2,2)x y x y ,代入22z xy ,得122,8z z 故所求的最大值为72,最小值为 6. 本题的难度值为.(22)【详解】(I)证法一:证法二:记||nD A ,下面用数学归纳法证明(1)nnD n a .当1n 时,12D a ,结论成立.当2n时,2222132a D a aa,结论成立.假设结论对小于n 的情况成立.将n D 按第1行展开得故||(1)nA n a证法三:记||n D A ,将其按第一列展开得2122n nnD aD a D ,所以211212()n nnn n n D aD aD a D a D aD 即12122()2nnn nnnn nD aaD aa aaD aa D (II)因为方程组有唯一解,所以由AxB 知0A,又(1)nAn a ,故0a.由克莱姆法则,将n D 的第1列换成b ,得行列式为所以11(1)n nD n x D n a(III)方程组有无穷多解,由0A ,有0a ,则方程组为此时方程组系数矩阵的秩和增广矩阵的秩均为1n ,所以方程组有无穷多解,其通解为10000100,TTk k LL 为任意常数.本题的难度值为. (23)【详解】(I) 证法一:假设123,,线性相关.因为12,分别属于不同特征值的特征向量,故12,线性无关,则3可由12,线性表出,不妨设31122l l ,其中12,l l 不全为零(若12,l l 同时为0,则3为0,由323A可知20,而特征向量都是非0向量,矛盾)32321122A l l ,又311221122()AA l l l l 112221122l l l l ,整理得:11220l 则12,线性相关,矛盾.所以,123,,线性无关.证法二:设存在数123,,k k k ,使得1122330k k k (1)用A 左乘(1)的两边并由11,A22A得1123233()0k k k k (2)(1)—(2)得113220k k (3)因为12,是A 的属于不同特征值的特征向量,所以12,线性无关,从而130k k ,代入(1)得220k ,又由于20,所以20k ,故123,,线性无关.(II)记123(,,)P ,则P 可逆,所以110001101P AP. 本题的难度值为.。
考研数学二真题及参考答案

2008年研究生入学统一考试数学二试题与答案一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.(1)设2()(1)(2)f x x x x =--,则'()f x 的零点个数为( )()A 0()B 1. ()C 2 ()D 3(2)曲线方程为()y f x =函数在区间[0,]a 上有连续导数,则定积分()at af x dx ⎰( )()A 曲边梯形ABCD 面积. ()B 梯形ABCD 面积. ()C 曲边三角形ACD 面积. ()D 三角形ACD 面积.(3)在下列微分方程中,以123cos 2sin 2xy C e C x C x =++(123,,C C C 为任意常数)为通解的是( ) (5)设函数()f x 在(,)-∞+∞内单调有界,{}n x 为数列,下列命题正确的是( ) ()A 若{}n x 收敛,则{}()n f x 收敛. ()B 若{}n x 单调,则{}()n f x 收敛. ()C 若{}()n f x 收敛,则{}n x 收敛.()D 若{}()n f x 单调,则{}n x 收敛.(6)设函数f 连续,若2222()(,)uvD f x y F u v dxdy x y +=+⎰⎰,其中区域uv D 为图中阴影部分,则Fu∂=∂ (7)设A 为n 阶非零矩阵,E 为n 阶单位矩阵. 若30A =,则( )()A E A -不可逆,E A +不可逆.()B E A -不可逆,E A +可逆.()C E A -可逆,E A +可逆.()D E A -可逆,E A +不可逆.(8)设1221A ⎛⎫=⎪⎝⎭,则在实数域上与A 合同的矩阵为( )()A 2112-⎛⎫⎪-⎝⎭.()B 2112-⎛⎫⎪-⎝⎭.()C 2112⎛⎫⎪⎝⎭.()D 1221-⎛⎫ ⎪-⎝⎭.二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上. (9) 已知函数()f x 连续,且21cos[()]lim1(1)()x x xf x e f x →-=-,则(0)____f =.(10)微分方程2()0xy x e dx xdy -+-=的通解是____y =.(11)曲线()()sinln xy y x x +-=在点()0,1处的切线方程为 .(12)曲线23(5)y x x =-的拐点坐标为______. (13)设xyy z x ⎛⎫=⎪⎝⎭,则(1,2)____z x ∂=∂.(14)设3阶矩阵A 的特征值为2,3,λ.若行列式248A =-,则___λ=.三、解答题:15-23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. (15)(本题满分9分)求极限()40sin sin sin sin lim x x x x x →-⎡⎤⎣⎦. (16)(本题满分10分)设函数()y y x =由参数方程20()ln(1)t x x t y u du =⎧⎪⎨=+⎪⎩⎰确定,其中()x t 是初值问题0200x t dx te dt x --⎧-=⎪⎨⎪=⎩的解.求22yx∂∂. (17)(本题满分9分)求积分 12arcsin 1x x dx x-⎰.(18)(本题满分11分)求二重积分max(,1),Dxy dxdy ⎰⎰其中{(,)02,02}D x y x y =≤≤≤≤(19)(本题满分11分)设()f x 是区间[)0,+∞上具有连续导数的单调增加函数,且(0)1f =.对任意的[)0,t ∈+∞,直线0,x x t ==,曲线()y f x =以及x 轴所围成的曲边梯形绕x 轴旋转一周生成一旋转体.若该旋转体的侧面积在数值上等于其体积的2倍,求函数()f x 的表达式. (20)(本题满分11分)(1) 证明积分中值定理:若函数()f x 在闭区间[,]a b 上连续,则至少存在一点[,]a b η∈,使得()()()baf x dx f b a η=-⎰(2)若函数()x ϕ具有二阶导数,且满足32(2)(1),(2)()x dx ϕϕϕϕ>>⎰,证明至少存在一点(1,3),()0ξϕξ''∈<使得(21)(本题满分11分)求函数222u x y z =++在约束条件22z x y =+和4x y z ++=下的最大值与最小值. (22)(本题满分12分)设矩阵2221212n na a aA a a ⨯⎛⎫⎪⎪= ⎪⎪⎝⎭,现矩阵A 满足方程AX B =,其中()1,,Tn X x x =,()1,0,,0B =,(1)求证()1n A n a =+;(2)a 为何值,方程组有唯一解,并求1x ; (3)a 为何值,方程组有无穷多解,并求通解. (23)(本题满分10分)设A 为3阶矩阵,12,αα为A 的分别属于特征值1,1-特征向量,向量3α满足323A ααα=+, (1)证明123,,ααα线性无关; (2)令()123,,P ααα=,求1P AP -.2008年全国硕士研究生入学统一考试数学二试题解析一、选择题 (1)【答案】D【详解】因为(0)(1)(2)f f f===,由罗尔定理知至少有1(0,1)ξ∈,2(1,2)ξ∈使12()()0f f ξξ''==,所以()f x '至少有两个零点. 又()f x '中含有因子x ,故0x =也是()f x '的零点, D 正确.本题的难度值为0.719. (2)【答案】C 【详解】00()()()()()()aaaaaxf x dx xdf x xf x f x dx af a f x dx '==-=-⎰⎰⎰⎰其中()af a 是矩形ABOC 面积,0()af x dx ⎰为曲边梯形ABOD 的面积,所以0()axf x dx '⎰为曲边三角形的面积.本题的难度值为0.829. (3)【答案】D【详解】由微分方程的通解中含有xe 、cos2x 、sin 2x 知齐次线性方程所对应的特征方程有根1,2r r i ==±,所以特征方程为(1)(2)(2)0r r i r i --+=,即32440r r r -+-=. 故以已知函数为通解的微分方程是40y y y ''''''-+-= 本题的难度值为0.832. (4) 【答案】A【详解】0,1x x ==时()f x 无定义,故0,1x x ==是函数的间断点因为 0000l n 11l i m ()l i m l i m l i m c s c |1|c s c c o tx x xx xxf x xx x x ++++→→→→=⋅=-- 同理0l i m ()0x f x -→= 又 1111ln 1lim ()lim lim sin lim sin1sin11x x x x x f x x x x ++++→→→→⎛⎫=⋅== ⎪-⎝⎭ 所以0x =是可去间断点,1x =是跳跃间断点.本题的难度值为0.486. (5)【答案】B【详解】因为()f x 在(,)-∞+∞内单调有界,且{}n x 单调. 所以{()}n f x 单调且有界. 故{()}n f x 一定存在极限.本题的难度值为0.537. (6)【答案】A【详解】用极坐标得()()222()22211,()vu uf r r Df u v F u v dudv dv rdr v f r dr u v +===+⎰⎰⎰⎰⎰所以()2F v f u u∂=∂ 本题的难度值为0.638. (7) 【答案】C【详解】23()()E A E A A E A E -++=-=,23()()E A E A A E A E +-+=+= 故,E A E A -+均可逆. 本题的难度值为0.663. (8) 【答案】D【详解】记1221D -⎛⎫= ⎪-⎝⎭,则()2121421E D λλλλ--==---,又()2121421E A λλλλ---==----所以A 和D 有相同的特征多项式,所以A 和D 有相同的特征值.又A 和D 为同阶实对称矩阵,所以A 和D 相似.由于实对称矩阵相似必合同,故D 正确.本题的难度值为0.759. 二、填空题 (9)【答案】2【详解】222220001cos[()]2sin [()2]2sin [()2]()lim lim lim ()[()2]4(1)()x x x x xf x xf x xf x f x x f x xf x e f x →→→-⋅==⋅- 所以 (0)2f = 本题的难度值为0.828. (10)【答案】()xx e C --+【详解】微分方程()20xy x e dx xdy -+-=可变形为xdy yxe dx x--=所以 111()dx dx x x xx x y e xe e dx C x xe dx C x e C x ----⎡⎤⎛⎫⎰⎰=+=⋅+=-+⎢⎥ ⎪⎝⎭⎣⎦⎰⎰本题的难度值为0.617. (11)【答案】1y x =+【详解】设(,)sin()ln()F x y xy y x x =+--,则1cos()11cos()x yy xy F dy y x dx F x xy y x--'-=-=-'+-,将(0)1y =代入得1x dydx ==,所以切线方程为10y x -=-,即1y x =+本题的难度值为0.759.(12)【答案】(1,6)-- 【详解】53235y xx =-⇒23131351010(2)333x y x x x -+'=-=1x =-时,0y ''=;0x =时,y ''不存在在1x =-左右近旁y ''异号,在0x =左右近旁0y ''>,且(1)6y -=- 故曲线的拐点为(1,6)-- 本题的难度值为0.501. (13)【答案】2(ln 21)2- 【详解】设,y xu v x y==,则v z u = 所以121()l n v v z z u z v y vu u u x u x v x x y-∂∂∂∂∂=⋅+⋅=-+⋅∂∂∂∂∂ 所以(1,2)2(l n 21)2z x ∂=-∂ 本题的难度值为0.575. (14)【答案】-1【详解】||236A λλ =⨯⨯= 3|2|2||A A = 本题的难度值为0.839. 三、解答题 (15)【详解】方法一:4300[sin sin(sin )]sin sin sin(sin )lim limx x x x x x x x x →→--= 方法二:331sin ()6x x x o x =-+ 331sin(sin )sin sin (sin )6x x x o x =-+本题的难度值为0.823. (16)【详解】方法一:由20x dxte dt--=得2x e dx tdt =,积分并由条件0t x =得21x e t =+,即2ln(1)x t =+ 所以 2222ln(1)2(1)ln(1)21dydy t tdt t t dxt dx dt t +⋅===+++方法二:由20x dxte dt--=得2x e dx tdt =,积分并由条件0t x =得21x e t =+,即2ln(1)x t =+所以 2222ln(1)2(1)ln(1)21x dydy t tdt t t e x dxt dx dt t +⋅===++=+所以 22(1)x d ye x dx=+ 本题的难度值为0.742. (17)【详解】 方法一:由于221arcsin lim 1x x x x-→=+∞-,故212arcsin 1x x dx x-⎰是反常积分.令arcsin x t =,有sin x t =,[0,2)t π∈方法二:212arcsin 1x x dx x -⎰12201(arcsin )2x d x =⎰令arcsin x t =,有sin x t =,[0,2)t π∈故,原式21164π=+ 本题的难度值为0.631.(18)【详解】 曲线1xy =将区域分成两个区域1D 和23D D +,为了便于计算继续对 区域分割,最后为()max ,1Dxy dxdy ⎰⎰本题的难度值为0.524.(19)【详解】旋转体的体积2()tV f x dx π=⎰,侧面积202()1()tS f x f x dx π'=+⎰,由题设条件知 上式两端对t 求导得 22()()1()f t f t f t '=+, 即 21y y '=-由分离变量法解得 21l n (1)y y t C+-=+, 即 21t y y C e+-= 将(0)1y =代入知1C=,故21t y y e +-=,1()2t t y e e -=+于是所求函数为 1()()2x xy f x e e -==+ 本题的难度值为0.497.(20)【详解】(I) 设M 与m 是连续函数()f x 在[,]a b 上的最大值与最小值,即O 0.5 2 x D 1D 3 D 2由定积分性质,有 ()()()bam b a f x dx M b a -≤≤-⎰,即 ()baf x dx m M b a≤≤-⎰由连续函数介值定理,至少存在一点[,]a b η∈,使得 ()()b af x dx f b aη=-⎰即()()()baf x dx f b a η=-⎰(II) 由(I)的结论可知至少存在一点[2,3]η∈,使 32()()(32)()x dx ϕϕηϕη=-=⎰又由32(2)()()x d x ϕϕϕη>=⎰,知 23η<≤对()x ϕ在[1,2][2,]η上分别应用拉格朗日中值定理,并注意到(1)(2)ϕϕ<,()(2)ϕηϕ<得 在12[,]ξξ上对导函数()x ϕ'应用拉格朗日中值定理,有 本题的难度值为0.719. (21)【详解】方法一:作拉格朗日函数22222(,,,,)()(4)F x y z x y z x y z x y z λμλμ=++++-+++-令 2222022020040x y z F x x F y y F z F x y z F x y z λμλμλμλμ'=++=⎧⎪'=++=⎪⎪'=-+=⎨⎪'=+-=⎪'=++-=⎪⎩解方程组得111222(,,)(1,1,2),(,,)(2,2,8)x y z x y z ==-- 故所求的最大值为72,最小值为6.方法二:问题可转化为求2242242u x y x x y y =++++在224x y x y +++=条件下的最值 设44222222(,,)2(4)F x y u x y x y x y x y x y λλ==++++++++-令 323222442(12)0442(12)040x y F x xy x x F y x y y y F x y x y λλλ'⎧=++++=⎪'=++++=⎨⎪'=+++-=⎩解得1122(,)(1,1),(,)(2,2)x y x y ==--,代入22z x y =+,得122,8z z == 故所求的最大值为72,最小值为6. 本题的难度值为0.486. (22)【详解】(I)证法一:证法二:记||n D A =,下面用数学归纳法证明(1)nn D n a =+. 当1n =时,12D a =,结论成立.当2n =时,2222132a D a aa==,结论成立.假设结论对小于n 的情况成立.将n D 按第1行展开得故 ||(1)nA n a =+ 证法三:记||n D A =,将其按第一列展开得 2122n n n D aD a D --=-, 所以 211212()n n n n n n D aD aD a D a D aD ------=-=- 即 12122()2nnn n n n n n D a aD a a aaD a a D ----=+=++=++(II)因为方程组有唯一解,所以由Ax B =知0A ≠,又(1)n A n a =+,故0a ≠.由克莱姆法则,将n D 的第1列换成b ,得行列式为 所以 11(1)n n D nx D n a-==+ (III)方程组有无穷多解,由0A =,有0a =,则方程组为此时方程组系数矩阵的秩和增广矩阵的秩均为1n -,所以方程组有无穷多解,其通解为()()10000100,TTk k +为任意常数.本题的难度值为0.270.(23)【详解】(I)证法一:假设123,,ααα线性相关.因为12,αα分别属于不同特征值的特征向量,故12,αα线性无关,则3α可由12,αα线性表出,不妨设31122l l ααα=+,其中12,l l 不全为零(若12,l l 同时为0,则3α为0,由323A ααα=+可知20α=,而特征向量都是非0向量,矛盾)∴32321122A l l αααααα=+=++,又311221122()A A l l l l ααααα=+=-+ ∴112221122l l l l ααααα-+=++,整理得:11220l αα+=则12,αα线性相关,矛盾. 所以,123,,ααα线性无关.证法二:设存在数123,,k k k ,使得1122330k k k ααα++= (1)用A 左乘(1)的两边并由11,A αα=-22A αα=得1123233()0k k k k ααα-+++= (2)(1)—(2)得 113220k k αα-= (3) 因为12,αα是A 的属于不同特征值的特征向量,所以12,αα线性无关,从而130k k ==,代入(1)得220k α=,又由于20α≠,所以20k =,故123,,ααα线性无关.(II) 记123(,,)P ααα=,则P 可逆,所以 1100011001P A P --⎛⎫ ⎪=⎪ ⎪⎝⎭. 本题的难度值为0.272.。
2008考研数二真题及解析
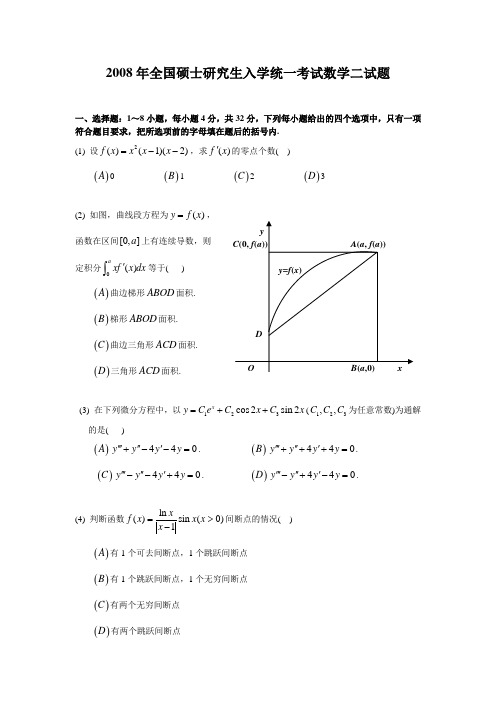
2008年全国硕士研究生入学统一考试数学二试题一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内. (1) 设2()(1)(2)f x x x x =--,求()f x '的零点个数( )()A 0()B 1 ()C 2()D 3(2) 如图,曲线段方程为()y f x =, 函数在区间[0,]a 上有连续导数,则 定积分()axf x dx '⎰等于( )()A 曲边梯形ABOD 面积.()B 梯形ABOD 面积. ()C 曲边三角形ACD 面积.()D 三角形ACD 面积.(3) 在下列微分方程中,以123cos 2sin 2xy C e C x C x =++(123,,C C C 为任意常数)为通解的是( )()A 440y y y y ''''''+--=. ()B 440y y y y ''''''+++=. ()C 440y y y y ''''''--+=.()D 440y y y y ''''''-+-=.(4) 判断函数ln ()sin (0)1xf x x x x =>-间断点的情况( ) ()A 有1个可去间断点,1个跳跃间断点 ()B 有1个跳跃间断点,1个无穷间断点 ()C 有两个无穷间断点 ()D 有两个跳跃间断点yC (0, f (a )) A (a , f (a ))y =f (x )O B (a ,0) xD(5) 设函数()f x 在(,)-∞+∞内单调有界,{}n x 为数列,下列命题正确的是( )()A 若{}n x 收敛,则{}()n f x 收敛. ()B 若{}n x 单调,则{}()n f x 收敛. ()C 若{}()n f x 收敛,则{}n x 收敛.()D 若{}()n f x 单调,则{}n x 收敛.(6) 设函数f 连续. 若()()2222,uvD f x y F u v dxdy x y+=+⎰⎰,其中区域uv D 为图中阴影部分,则Fu∂=∂( ) ()A ()2vf u()B ()2vf u u()C ()vf u()D ()vf u u(7) 设A 为n 阶非零矩阵,E 为n 阶单位矩阵. 若3A O =,则( )()A E A -不可逆,E A +不可逆.()B E A -不可逆,E A +可逆. ()C E A -可逆,E A +可逆.()D E A -可逆,E A +不可逆.(8) 设1221A ⎛⎫=⎪⎝⎭,则在实数域上与A 合同的矩阵为( ) ()A 2112-⎛⎫⎪-⎝⎭.()B 2112-⎛⎫⎪-⎝⎭.()C 2112⎛⎫ ⎪⎝⎭.()D 1221-⎛⎫⎪-⎝⎭.二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上. (9) ()f x 连续,21cos(sin )lim1(1)()x x x e f x →-=-,则(0)f =(10) 微分方程2()0xy x e dx xdy -+-=的通解是y =O xvx 2+y 2=u 2 x 2+y 2=1 D uvy(11) 曲线()()sin ln xy y x x +-=在点()0,1处的切线方程为 . (12) 求函数23()(5)f x x x =-的拐点______________. (13) 已知xyy z x ⎛⎫=⎪⎝⎭,则(1,2)_______z x ∂=∂. (14) 矩阵A 的特征值是,2,3λ,其中λ未知,且248A =-,则λ=_______.三、解答题:15-23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. (15)(本题满分9分)求极限()40sin sin sin sin limx x x x x →-⎡⎤⎣⎦.(16) (本题满分10分)设函数()y y x =由参数方程20()ln(1)t x x t y u du =⎧⎪⎨=+⎪⎩⎰确定,其中()x t 是初值问题 020|0xt dx te dtx -=⎧-=⎪⎨⎪=⎩的解. 求22d y dx .(17)(本题满分9分)计算212arcsin 1x x dx x-⎰(18)(本题满分11分)计算{}max ,1,Dxy dxdy ⎰⎰其中{(,)02,02}D x y x y =≤≤≤≤(19)(本题满分11分)设()f x 是区间[0,)+∞上具有连续导数的单调增加函数,且(0)1f =. 对于任意的[0,)t ∈+∞,直线0,x x t ==,曲线()y f x =以及x 轴所围成曲边梯形绕x 轴旋转一周生成一旋转体. 若该旋转体的侧面面积在数值上等于其体积的2倍,求函数()f x 的表达式.(20)(本题满分11分)(I) 证明积分中值定理:若函数()f x 在闭区间[,]a b 上连续,则至少存在一点[,]a b η∈,使得()()()baf x dx f b a η=-⎰;(II) 若函数()x ϕ具有二阶导数,且满足,32(2)(1),(2)()x dx ϕϕϕϕ>>⎰,则至少存在一点(1,3)ξ∈,()0ϕξ''<使得.(21)(本题满分11分)求函数222u x y z =++在约束条件22z x y =+和4x y z ++=下的最大和最小值.(22)(本题满分12分)设n 元线性方程组Ax b =,其中2221212n n a a a A a a ⨯⎛⎫ ⎪ ⎪= ⎪⎪⎝⎭,12n x x x x ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭,100b ⎛⎫⎪ ⎪= ⎪ ⎪⎝⎭(I) 证明行列式()1nA n a =+(II) 当a 为何值时,该方程组有唯一解,并求1x (III) 当a 为何值时,该方程组有无穷多解,并求通解(23)(本题满分10分)设A 为3阶矩阵,12,αα为A 的分别属于特征值1,1-的特征向量,向量3α满足323A ααα=+,(I) 证明123,,ααα线性无关; (II) 令()123,,P ααα=,求1P AP -2008年全国硕士研究生入学统一考试数学二试题解析一、选择题 (1)【答案】D【详解】因为(0)(1)(2)0f f f ===,由罗尔定理知至少有1(0,1)ξ∈,2(1,2)ξ∈使12()()0f f ξξ''==,所以()f x '至少有两个零点. 由于()f x '是三次多项式,三次方程()0f x '=的实根不是三个就是一个,故D 正确.(2)【答案】C 【详解】00()()()()()()aa a aaxf x dx xdf x xf x f x dx af a f x dx '==-=-⎰⎰⎰⎰其中()af a 是矩形ABOC 面积,0()af x dx ⎰为曲边梯形ABOD 的面积,所以0()axf x dx '⎰为曲边三角形的面积.(3)【答案】D【详解】由微分方程的通解中含有xe 、cos2x 、sin 2x 知齐次线性方程所对应的特征方程有根1,2r r i ==±,所以特征方程为(1)(2)(2)0r r i r i --+=,即32440r r r -+-=. 故以已知函数为通解的微分方程是440y y y ''''''-+-=(4) 【答案】A【详解】0,1x x ==时()f x 无定义,故0,1x x ==是函数的间断点因为 000ln 11lim ()lim lim lim csc |1|csc cot x x x x x xf x x x x x++++→→→→=⋅=-- 200sin lim lim 0cos cos x x x xx x x++→→=-=-=同理 0lim ()0x f x -→= 又 1111ln 1lim ()lim lim sin lim sin1sin11x x x x x f x x x x ++++→→→→⎛⎫=⋅== ⎪-⎝⎭ 111ln lim ()lim lim sin sin11x x x xf x x x --+→→→=⋅=--所以 0x =是可去间断点,1x =是跳跃间断点.(5)【答案】B【详解】因为()f x 在(,)-∞+∞内单调有界,且{}n x 单调. 所以{()}n f x 单调且有界. 故{()}n f x 一定存在极限.(6)【答案】A【详解】用极坐标得 ()()222()22211,()vu uf r r Df u v F u v dudv dv rdr v f r dr u v +===+⎰⎰⎰⎰⎰所以()2Fvf u u∂=∂(7) 【答案】C【详解】23()()E A E A A E A E -++=-=,23()()E A E A A E A E +-+=+= 故,E A E A -+均可逆.(8) 【答案】D 【详解】记1221D -⎛⎫=⎪-⎝⎭,则()2121421E D λλλλ--==---,又()2121421E A λλλλ---==----所以A 和D 有相同的特征多项式,所以A 和D 有相同的特征值.又A 和D 为同阶实对称矩阵,所以A 和D 相似.由于实对称矩阵相似必合同,故D 正确.二、填空题 (9)【答案】2【详解】222220001cos[()]2sin [()2]2sin [()2]()lim lim lim ()[()2]4(1)()x x x x xf x xf x xf x f x x f x xf x e f x →→→-⋅==⋅- 011lim ()(0)122x f x f →=== 所以 (0)2f =(10)【答案】()xx eC --+【详解】微分方程()20xy x edx xdy -+-=可变形为x dy yxe dx x--= 所以 111()dx dx x x xx x y e xe e dx C x xe dx C x e C x ----⎡⎤⎛⎫⎰⎰=+=⋅+=-+⎢⎥ ⎪⎝⎭⎣⎦⎰⎰(11)【答案】1y x =+【详解】设(,)sin()ln()F x y xy y x x =+--,则1cos()11cos()x y y xy F dy y x dx F x xy y x--'-=-=-'+-,将(0)1y =代入得01x dy dx==,所以切线方程为10y x -=-,即1y x =+(12)【答案】(1,6)-- 【详解】53235y xx =-⇒23131351010(2)333x y x x x -+'=-=⇒134343101010(1)999x y x x x--+''=+= 1x =-时,0y ''=;0x =时,y ''不存在在1x =-左右近旁y ''异号,在0x =左右近旁0y ''>,且(1)6y -=- 故曲线的拐点为(1,6)--(13)【答案】2(ln 21)2- 【详解】设,y xu v x y==,则v z u = 所以121()ln v v z z u z v y vu u u x u x v x x y-∂∂∂∂∂=⋅+⋅=-+⋅∂∂∂∂∂ 2ln 11ln x yv vy u y y u ux y x y x ⎛⎫⎛⎫⎛⎫=-+=⋅-+ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭ 所以(1,2)2(ln 21)2z x ∂=-∂(14)【答案】-1【详解】||236A λλ =⨯⨯= 3|2|2||A A =32648λ∴ ⨯=- 1λ⇒=-三、解答题 (15)【详解】 方法一:4300[sin sin(sin )]sin sin sin(sin )limlim x x x x x x x x x→→--= 22220001sin cos cos(sin )cos 1cos(sin )12lim lim lim 3336x x x xx x x x x x x →→→--==== 方法二:331sin ()6x x x o x =-+ 331sin(sin )sin sin (sin )6x x x o x =-+4444400[sin sin(sin )]sin sin (sin )1lim lim 66x x x x xx o x x x x →→⎡⎤-∴ =+=⎢⎥⎣⎦(16)【详解】方法一:由20x dx te dt--=得2x e dx tdt =,积分并由条件0t x =得21x e t =+,即2l n (1)x t =+所以 2222ln(1)2(1)ln(1)21dydy t tdt t t dxt dx dt t +⋅===+++222222[(1)ln(1)]2ln(1)221dt t d y d dy t t tdt dx t dx dx dx dt t ++++⎛⎫=== ⎪⎝⎭+ 22(1)[ln(1)1]t t =+++方法二:由20x dx te dt--=得2x e dx tdt =,积分并由条件0t x =得21x e t =+,即2l n (1)x t =+所以 2222ln(1)2(1)ln(1)21x dydy t tdt t t e x dxt dx dt t +⋅===++=+所以 22(1)x d ye x dx=+(17)【详解】 方法一:由于221arcsin lim 1x x x x-→=+∞-,故212arcsin 1x x dx x-⎰是反常积分.令arcsin x t =,有sin x t =,[0,2)t π∈22122222000arcsin sin cos 2cos sin ()cos 221x x t t t t t dx tdt t tdt dt t x πππ===--⎰⎰⎰⎰2222220001sin 21sin 2sin 2441644tt t td t tdt πππππ=-=-+⎰⎰ 222011cos 2168164t πππ=-=+ 方法二:212arcsin 1x x dx x -⎰12201(arcsin )2x d x =⎰ 121122220001(arcsin )(arcsin )(arcsin )28x x x x dx x x dx π=-=-⎰⎰令arcsin x t =,有sin x t =,[0,2)t π∈12222200011(arcsin )sin 2cos 224x x dx t tdt t d t ππ==-⎰⎰⎰ 222200111(cos 2)cos 242164t t t tdt πππ=-+=-⎰故,原式21164π=+(18)【详解】 曲线1xy =将区域分成两 个区域1D 和23D D +,为了便于计算继续对 区域分割,最后为()max ,1Dxy dxdy ⎰⎰123D D D xydxdy dxdy dxdy =++⎰⎰⎰⎰⎰⎰112222211102211x xdx dy dx dy dx xydy =++⎰⎰⎰⎰⎰⎰1512ln 2ln 24=++-19ln 24=+(19)【详解】旋转体的体积20()tV f x dx π=⎰,侧面积22()1()tS f x f x dx π'=+⎰,由题O 0.5 2 xD 1D 3 D 2设条件知220()()1()ttf x dx f x f x dx '=+⎰⎰上式两端对t 求导得 22()()1()f t f t f t '=+, 即 21y y '=-由分离变量法解得 21l n (1)y y t C+-=+, 即 21t y y C e+-= 将(0)1y =代入知1C =,故21t y y e +-=,1()2t t y e e -=+于是所求函数为 1()()2t ty f x e e -==+(20)【详解】(I) 设M 与m 是连续函数()f x 在[,]a b 上的最大值与最小值,即()m f x M ≤≤ [,]x a b ∈由定积分性质,有 ()()()bam b a f x dx M b a -≤≤-⎰,即 ()baf x dx m M b a≤≤-⎰由连续函数介值定理,至少存在一点[,]a b η∈,使得 ()()b af x dx f b aη=-⎰即()()()baf x dx f b a η=-⎰(II) 由(I)的结论可知至少存在一点[2,3]η∈,使32()()(32)()x dx ϕϕηϕη=-=⎰又由 32(2)()()x d x ϕϕϕη>=⎰,知 23η<≤对()x ϕ在[1,2][2,]η上分别应用拉格朗日中值定理,并注意到(1)(2)ϕϕ<,()(2)ϕηϕ<得 1(2)(1)()021ϕϕϕξ-'=>- 112ξ<<2()(2)()02ϕηϕϕξη-'=<- 123ξη<<≤在12[,]ξξ上对导函数()x ϕ'应用拉格朗日中值定理,有2121()()()0ϕξϕξϕξξξ''-''=<- 12(,)(1,3)ξξξ∈⊂(21)【详解】方法一:作拉格朗日函数22222(,,,,)()(4)F x y z x y z x y z x y z λμλμ=++++-+++-令 2222022020040x y z F x x F y y F z F x y z F x y z λμλμλμλμ'=++=⎧⎪'=++=⎪⎪'=-+=⎨⎪'=+-=⎪'=++-=⎪⎩解方程组得111222(,,)(1,1,2),(,,)(2,2,8)x y z x y z ==-- 故所求的最大值为72,最小值为6.方法二:问题可转化为求2242242u x y x x y y =++++在224x y x y +++=条件下的最值 设44222222(,,)2(4)F x y u x y x y x y x y x y λλ==++++++++-令 323222442(12)0442(12)040x y F x xy x x F y x y y y F x y x y λλλ'⎧=++++=⎪'=++++=⎨⎪'=+++-=⎩解得1122(,)(1,1),(,)(2,2)x y x y ==--,代入22z x y =+,得122,8z z == 故所求的最大值为72,最小值为6.(22)【详解】(I)证法一:2222122212132101221221122a a a a a a aa aA r ar aaa a =-=121301240134(1)2(1)3231(1)0n n n a a a n a a n ar ar a n a nnn a n--+-=⋅⋅⋅=++ 证法二:记||n D A =,下面用数学归纳法证明(1)nn D n a =+.当1n =时,12D a =,结论成立.当2n =时,2222132a D a a a==,结论成立.假设结论对小于n 的情况成立.将n D 按第1行展开得2212102121212n n a a a aD aD a a-=-21221222(1)(1)n n n n n aD a D ana a n a n a ---- =-=--=+故 ||(1)nA n a =+证法三:记||n D A =,将其按第一列展开得 2122n n n D aD a D --=-, 所以 211212()n n n n n n D aD aD a D a D aD ------=-=-222321()()n n n n a D aD a D aD a ---=-==-=即 12122()2n n n n n n n n D a aD a a a aD a a D ----=+=++=++2121(2)(1)n n n n n a a D n a a D --==-+=-+1(1)2(1)n n n n a a a n a -=-+⋅=+(II)因为方程组有唯一解,所以由Ax B =知0A ≠,又(1)nA n a =+,故0a ≠. 由克莱姆法则,将n D 的第1列换成b ,得行列式为2221122(1)(1)112102*********n n n nn n a a a aa aa aD na a a a a --⨯-⨯-===所以 11(1)n n D nx D n a-==+(III)方程组有无穷多解,由0A =,有0a =,则方程组为12101101001000n n x x x x -⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪⎪ ⎪ ⎪⎪ ⎪ ⎪=⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 此时方程组系数矩阵的秩和增广矩阵的秩均为1n -,所以方程组有无穷多解,其通解为()()10000100,TTk k +为任意常数.(23)【详解】(I)证法一:假设123,,ααα线性相关.因为12,αα分别属于不同特征值的特征向量,故12,αα线性无关,则3α可由12,αα线性表出,不妨设31122l l ααα=+,其中12,l l 不全为零(若12,l l 同时为0,则3α为0,由323A ααα=+可知20α=,而特征向量都是非0向量,矛盾)11,A αα=-22A αα=∴32321122A l l αααααα=+=++,又311221122()A A l l l l ααααα=+=-+ ∴112221122l l l l ααααα-+=++,整理得:11220l αα+=则12,αα线性相关,矛盾. 所以,123,,ααα线性无关.证法二:设存在数123,,k k k ,使得1122330k k k ααα++= (1)用A 左乘(1)的两边并由11,A αα=-22A αα=得1123233()0k k k k ααα-+++= (2)(1)—(2)得 113220k k αα-= (3) 因为12,αα是A 的属于不同特征值的特征向量,所以12,αα线性无关,从而130k k ==,代入(1)得220k α=,又由于20α≠,所以20k =,故123,,ααα线性无关.(II) 记123(,,)P ααα=,则P 可逆,123123(,,)(,,)AP A A A A αααααα==1223(,,)αααα=-+123100(,,)011001ααα-⎛⎫ ⎪= ⎪ ⎪⎝⎭100011001P -⎛⎫ ⎪= ⎪ ⎪⎝⎭所以 1100011001P AP --⎛⎫ ⎪= ⎪ ⎪⎝⎭.。
2008年考研数学二真题答案解析

2008年全国硕士研究生入学统一考试数学二试题解析一、选择题 (1)【答案】D【详解】因为(0)(1)(2)0f f f ===,由罗尔定理知至少有1(0,1)ξ∈,2(1,2)ξ∈使12()()0f f ξξ''==,所以()f x '至少有两个零点. 又()f x '中含有因子x ,故0x =也是()f x '的零点, D 正确.本题的难度值为0.719. (2)【答案】C 【详解】00()()()()()()aa a aaxf x dx xdf x xf x f x dx af a f x dx '==-=-⎰⎰⎰⎰其中()af a 是矩形ABOC 面积,0()af x dx ⎰为曲边梯形ABOD 的面积,所以0()axf x dx '⎰为曲边三角形的面积.本题的难度值为0.829.(3)【答案】D【详解】由微分方程的通解中含有xe 、cos 2x 、sin 2x 知齐次线性方程所对应的特征方程有根1,2r r i ==±,所以特征方程为(1)(2)(2)0r r i r i --+=,即32440r r r -+-=. 故以已知函数为通解的微分方程是40y y y ''''''-+-= 本题的难度值为0.832. (4) 【答案】A【详解】0,1x x ==时()f x 无定义,故0,1x x ==是函数的间断点因为 000ln 11lim ()lim lim lim csc |1|csc cot x x x x x xf x x x x x++++→→→→=⋅=-- 200sin lim lim 0cos cos x x x xx x x++→→=-=-=同理 0lim ()0x f x -→= 又 1111ln 1lim ()lim lim sin lim sin1sin11x x x x x f x x x x ++++→→→→⎛⎫=⋅== ⎪-⎝⎭ 所以 0x =是可去间断点,1x =是跳跃间断点.本题的难度值为0.486.(5)【答案】B【详解】因为()f x 在(,)-∞+∞内单调有界,且{}n x 单调. 所以{()}n f x 单调且有界. 故{()}n f x 一定存在极限.本题的难度值为0.537. (6)【答案】A【详解】用极坐标得 ()222()2011,()vu uf r r Df u v F u v dv rdr v f r dr +===⎰⎰⎰所以()2Fvf u u∂=∂ 本题的难度值为0.638. (7) 【答案】C【详解】23()()E A E A A E A E -++=-=,23()()E A E A A E A E +-+=+= 故,E A E A -+均可逆. 本题的难度值为0.663. (8) 【答案】D【详解】记1221D -⎛⎫= ⎪-⎝⎭,则()2121421E D λλλλ--==---,又()2121421E A λλλλ---==---- 所以A 和D 有相同的特征多项式,所以A 和D 有相同的特征值.又A 和D 为同阶实对称矩阵,所以A 和D 相似.由于实对称矩阵相似必合同,故D 正确. 本题的难度值为0.759. 二、填空题 (9)【答案】2【详解】222220001cos[()]2sin [()2]2sin [()2]()lim lim lim ()[()2]4(1)()x x x x xf x xf x xf x f x x f x xf x e f x →→→-⋅==⋅- 011lim ()(0)122x f x f →=== 所以 (0)2f = 本题的难度值为0.828. (10)【答案】()xx eC --+【详解】微分方程()20xy x e dx xdy -+-=可变形为x dy yxe dx x--= 所以 111()dx dx xx x x x y e xe e dx C x xe dx C x e C x ----⎡⎤⎛⎫⎰⎰=+=⋅+=-+⎢⎥ ⎪⎝⎭⎣⎦⎰⎰本题的难度值为0.617. (11)【答案】1y x =+【详解】设(,)sin()ln()F x y xy y x x =+--,则1cos()11cos()x y y xy F dy y x dx F x xy y x--'-=-=-'+-,将(0)1y =代入得1x dy dx==,所以切线方程为10y x -=-,即1y x =+本题的难度值为0.759. (12)【答案】(1,6)-- 【详解】5325y xx =-⇒23131351010(2)333x y x x x -+'=-= ⇒134343101010(1)999x y x x x--+''=+= 1x =-时,0y ''=;0x =时,y ''不存在在1x =-左右近旁y ''异号,在0x =左右近旁0y ''>,且(1)6y -=- 故曲线的拐点为(1,6)-- 本题的难度值为0.501. (13)【答案】21)2- 【详解】设,y xu v x y==,则v z u = 所以121()ln v v z z u z v y vu u u x u x v x x y-∂∂∂∂∂=⋅+⋅=-+⋅∂∂∂∂∂ 2ln 11ln x yv vy u y y u ux y x y x ⎛⎫⎛⎫⎛⎫=-+=⋅-+ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭ 所以(1,2)21)2z x ∂=-∂本题的难度值为0.575.(14)【答案】-1【详解】||236A λλ =⨯⨯= 3|2|2||A A =32648λ∴⨯=- 1λ⇒=- 本题的难度值为0.839.三、解答题 (15)【详解】 方法一:4300[sin sin(sin )]sin sin sin(sin )limlim x x x x x x x x x →→--=22220001sin cos cos(sin )cos 1cos(sin )12lim lim lim 3336x x x xx x x x x x x →→→--==== 方法二:331sin ()6x x x o x =-+ 331sin(sin )sin sin (sin )6x x x o x =-+4444400[sin sin(sin )]sin sin (sin )1lim lim 66x x x x xx o x x x x →→⎡⎤-∴ =+=⎢⎥⎣⎦ 本题的难度值为0.823. (16)【详解】方法一:由20x dx te dt--=得2x e dx tdt =,积分并由条件0t x =得21x e t =+,即2l n (1)x t =+所以 2222ln(1)2(1)ln(1)1dydy t tdt t t dx dt t +⋅===+++222222[(1)ln(1)]2ln(1)221dt t d y d dy t t tdt dx t dx dx dx dt t ++++⎛⎫===⎪⎝⎭+ 22(1)[ln(1)1]t t =+++方法二:由20x dx te dt--=得2x e dx tdt =,积分并由条件0t x =得21x e t =+,即2l n (1)x t =+所以 2222ln(1)2(1)ln(1)21x dydy t tdt t t e x dxt dx dt t +⋅===++=+所以 22(1)x d ye x dx=+ 本题的难度值为0.742. (17)【详解】 方法一:由于21x -→=+∞,故21⎰是反常积分.令arcsin x t =,有sin x t =,[0,2)t π∈2212222000sin cos 2cos sin ()cos 22t t t t t tdt t tdt dt t πππ===-⎰⎰⎰⎰2222220001sin 21sin 2sin 2441644tt t td t tdt πππππ=-=-+⎰⎰ 222011cos 2168164t πππ=-=+方法二:21⎰12201(arcsin )2x d x =⎰121122220001(arcsin )(arcsin )(arcsin )28x x x x dx x x dx π=-=-⎰⎰令arcsin x t =,有sin x t =,[0,2)t π∈1222200011(arcsin )sin 2cos 224x x dx tdt t d t ππ==-⎰⎰⎰ 222200111(cos 2)cos 242164t t t tdt πππ=-+=-⎰故,原式21164π=+ 本题的难度值为0.631.(18)【详解】 曲线1xy =将区域分成两个区域1D 和23D D +,为了便于计算继续对 区域分割,最后为()max ,1Dxy dxdy ⎰⎰123D D D xydxdy dxdy dxdy =++⎰⎰⎰⎰⎰⎰112222211102211x xdx dy dx dy dx xydy =++⎰⎰⎰⎰⎰⎰1512ln 2ln 24=++-19ln 24=+ 本题的难度值为0.524.(19)【详解】旋转体的体积2()tV f x dx π=⎰,侧面积02(tS f x π=⎰,由题设条件知20()(ttf x dx f x =⎰⎰上式两端对t 求导得2()(f t f t = 即y '=由分离变量法解得1l n ()y t C +=+, 即t y C e =将(0)1y =代入知1C =,故t y e +=,1()2tt y e e -=+ 于是所求函数为 1()()2x xy f x e e -==+ 本题的难度值为0.497.(20)【详解】(I) 设M 与m 是连续函数()f x 在[,]a b 上的最大值与最小值,即()m f x M ≤≤ [,]x a b ∈由定积分性质,有 ()()()bam b a f x dx M b a -≤≤-⎰,即 ()baf x dx m M b a≤≤-⎰由连续函数介值定理,至少存在一点[,]a b η∈,使得 ()()b af x dx f b aη=-⎰即()()()baf x dx f b a η=-⎰(II) 由(I)的结论可知至少存在一点[2,3]η∈,使 32()()(32)()x dx ϕϕηϕη=-=⎰又由32(2)()()x d x ϕϕϕη>=⎰,知 23η<≤对()x ϕ在[1,2][2,]η上分别应用拉格朗日中值定理,并注意到(1)(2)ϕϕ<,()(2)ϕηϕ<得 1(2)(1)()021ϕϕϕξ-'=>- 112ξ<<2()(2)()02ϕηϕϕξη-'=<- 123ξη<<≤在12[,]ξξ上对导函数()x ϕ'应用拉格朗日中值定理,有2121()()()0ϕξϕξϕξξξ''-''=<- 12(,)(1,3)ξξξ∈⊂本题的难度值为0.719. (21)【详解】方法一:作拉格朗日函数22222(,,,,)()(4)F x y z x y z x y z x y z λμλμ=++++-+++-令 2222022020040x y z F x x F y y F z F x y z F x y z λμλμλμλμ'=++=⎧⎪'=++=⎪⎪'=-+=⎨⎪'=+-=⎪'=++-=⎪⎩解方程组得111222(,,)(1,1,2),(,,)(2,2,8)x y z x y z ==-- 故所求的最大值为72,最小值为6.方法二:问题可转化为求2242242u x y x x y y =++++在224x y x y +++=条件下的最值 设44222222(,,)2(4)F x y u x y x y x y x y x y λλ==++++++++-令 323222442(12)0442(12)040x y F x xy x x F y x y y y F x y x y λλλ'⎧=++++=⎪'=++++=⎨⎪'=+++-=⎩解得1122(,)(1,1),(,)(2,2)x y x y ==--,代入22z x y =+,得122,8z z == 故所求的最大值为72,最小值为6. 本题的难度值为0.486. (22)【详解】(I)证法一:2222122212132101221221122aa a a a a aa aA r ar aaa a =-=121301240134(1)2(1)3231(1)0n n n a a a n a a n ar ar a n a nnn a n--+-=⋅⋅⋅=++ 证法二:记||n D A =,下面用数学归纳法证明(1)nn D n a =+.当1n =时,12D a =,结论成立. 当2n =时,2222132a D a a a==,结论成立. 假设结论对小于n 的情况成立.将n D 按第1行展开得2212102121212n n a a a aD aD a a-=-21221222(1)(1)n n n n n aD a D ana a n a n a ---- =-=--=+故 ||(1)n A n a =+证法三:记||n D A =,将其按第一列展开得 2122n n n D aD a D --=-, 所以 211212()n n n n n n D aD aD a D a D aD ------=-=-222321()()n n n n a D aD a D aD a ---=-==-=即 12122()2n n n n n n n n D a aD a a a aD a a D ----=+=++=++2121(2)(1)n n n n n a a D n a a D --==-+=-+1(1)2(1)n n n n a a a n a -=-+⋅=+(II)因为方程组有唯一解,所以由Ax B =知0A ≠,又(1)nA n a =+,故0a ≠.由克莱姆法则,将n D 的第1列换成b ,得行列式为2221122(1)(1)112102121221122n n n nn n a aa a a aa aD na a a a a --⨯-⨯-===所以 11(1)n n D nx D n a-==+ (III)方程组有无穷多解,由0A =,有0a =,则方程组为12101101001000n n x x x x -⎛⎫⎛⎫⎛⎫⎪⎪ ⎪⎪ ⎪ ⎪⎪ ⎪ ⎪=⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 此时方程组系数矩阵的秩和增广矩阵的秩均为1n -,所以方程组有无穷多解,其通解为()()10000100,TTk k +为任意常数.本题的难度值为0.270. (23)【详解】(I)证法一:假设123,,ααα线性相关.因为12,αα分别属于不同特征值的特征向量,故12,αα线性无关,则3α可由12,αα线性表出,不妨设31122l l ααα=+,其中12,l l 不全为零(若12,l l 同时为0,则3α为0,由323A ααα=+可知20α=,而特征向量都是非0向量,矛盾)11,A αα=-22A αα=∴32321122A l l αααααα=+=++,又311221122()A A l l l l ααααα=+=-+ ∴112221122l l l l ααααα-+=++,整理得:11220l αα+=则12,αα线性相关,矛盾. 所以,123,,ααα线性无关.证法二:设存在数123,,k k k ,使得1122330k k k ααα++= (1)用A 左乘(1)的两边并由11,A αα=-22A αα=得1123233()0k k k k ααα-+++= (2)(1)—(2)得 113220k k αα-= (3) 因为12,αα是A 的属于不同特征值的特征向量,所以12,αα线性无关,从而130k k ==,代入(1)得220k α=,又由于20α≠,所以20k =,故123,,ααα线性无关.(II) 记123(,,)P ααα=,则P 可逆,123123(,,)(,,)AP A A A A αααααα==1223(,,)αααα=-+123100(,,)011001ααα-⎛⎫ ⎪= ⎪ ⎪⎝⎭100011001P -⎛⎫ ⎪= ⎪ ⎪⎝⎭所以 1100011001P AP --⎛⎫ ⎪= ⎪ ⎪⎝⎭.本题的难度值为0.272.。
2008年全国硕士研究生入学统一考试数学二真题答案

全国硕士研究生入学统一考试数学二试题答案速查: 一、选择题二、填空题三、解答题 (15)16(16)2222(1)[ln(1)1]d y t t dx =+++(17)21416π+(18)19ln 24+ (19)1()()2x xf x e e -=+(20)略(21)最大值为72,最小值为6 (22)(Ⅰ)略;(Ⅱ)10,(1)n a x n a≠=+;(Ⅲ)0,(0,1,0,,0)(1,0,,0)T Ta x k ==+L L ,其中k 为任意常数(23)(Ⅰ)略;(Ⅱ)1100011001P AP --⎛⎫ ⎪= ⎪ ⎪⎝⎭一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内. (1)【答案】()D【解析】()()()()()()22221212494f x x x x xx x x x x x '=--+-+-=-+令()0f x '=,则可得()f x '零点的个数为3. (2)【答案】()C【解析】()()()()aa a xf x dx xdf x af a f x dx '==-⎰⎰⎰,其中()af a 是矩形面积,0()af x dx⎰为曲边梯形的面积,所以0()axf x dx '⎰为曲边三角形的面积。
(3)【答案】()D【解析】由123cos 2sin 2xy C e C x C x =++可知其特征根为12,31,2i λλ==±.故对应的特征方程为 2(1)(2)(2)(1)(4)i i λλλλλ-+-=-+,即32440λλλ-+-=所以所求微分方程为440y y y y ''''''-+-=, 选()D . (4)【答案】()A【解析】()f x 的间断点为1,0x =,而0lim ()0x f x →+=,故0x =是可去间断点;1lim ()sin1x f x →+=,1lim ()sin1x f x →+=-,故1x =是跳跃间断点故选()A 。
2008年全国硕士研究生入学统一考试数学二真题及答案

(Ⅱ)记 则 可逆,
即 .
【难易度】★★
【详解】
解析:
则 。记 ,则
则 ,正、负惯性指数相同,故选
二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.
(9)已知函数 连续,且 ,则
【答案】2
【考点】等价无穷小
【难易度】★★
【详解】
解析:利用等价无穷小因子替换有
.
(10)微分方程 的通解是 .
【答案】y=Cx-xe-x,其中C为任意常数
2个无穷间断点
2个跳跃间断点
【答案】
【考点】函数间断点的类型
【难易度】★★
Hale Waihona Puke 【详解】解析: 的间断点为 ,而 ,故 是可去间断点;
, ,故 是跳跃间断点
故选 .
(5)设函数 在 内单调有界, 为数列,下列命题正确的是( )
若 收敛,则 收敛. 若 单调,则 收敛.
若 收敛,则 收敛. 若 单调,则 收敛.
【详解】
解析:令
得方程组 即 ,解得 或
得 .
.
(22)(本题满分11分)
设 元线性方程组 ,其中 , , .
(Ⅰ)证明行列式 ;
(Ⅱ)当 为何值时,该方程组有唯一解,求 ;
(Ⅲ)当 为何值时,该方程组有无穷多解,求通解.
【考点】行列式的基本性质,非齐次线性方程组解的判定
【难易度】★★★
【详解】
解析:(Ⅰ)证明:消元法.记
.
(Ⅱ)由克莱姆法则, 时方程组有唯一解,故 时方程组有唯一解.
由克莱姆法则,将 得第一列换成 ,得行列式为
所以, .
(Ⅲ)当 时,方程组为
此时方程组系数矩阵的秩和增广矩阵的秩均为 ,所以方程组有无穷多组解,其通解为 ,其中 为任意常数.
考研数学二真题及参考答案

考研数学二真题及参考答案Last updated on the afternoon of January 3, 20212008年研究生入学统一考试数学二试题与答案一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内. (1)设2()(1)(2)f x x x x =--,则'()f x 的零点个数为()()A 0 ()B ()C ()D 3(2)曲线方程为()y f x =函数在区间[0,]a 上有连续导数,则定积分0()a t af x dx ⎰()()A 曲边梯形ABCD 面积.()B 梯形ABCD 面积.()C 曲边三角形ACD 面积. ()D 三角形ACD 面积.(3)在下列微分方程中,以123cos 2sin 2x y C e C x C x =++(123,,C C C 为任意常数)为通解的是()(5)设函数()f x 在(,)-∞+∞内单调有界,{}n x 为数列,下列命题正确的是()()A 若{}n x 收敛,则{}()n f x 收敛. ()B 若{}n x 单调,则{}()n f x 收敛. ()C 若{}()n f x 收敛,则{}n x 收敛.()D 若{}()n f x 单调,则{}n x 收敛.(6)设函数f连续,若22(,)uvD F u v =⎰⎰,其中区域uv D 为图中阴影部分,则Fu∂=∂ (7)设A 为n 阶非零矩阵,E 为n 阶单位矩阵.若30A =()A E A -不可逆,E A +不可逆. ()B E A -()C E A -可逆,E A +可逆.()D E A -可逆,E A +不可逆.(8)设1221A ⎛⎫= ⎪⎝⎭,则在实数域上与A 合同的矩阵为()()A 2112-⎛⎫⎪-⎝⎭.()B 2112-⎛⎫ ⎪-⎝⎭. ()C 2112⎛⎫⎪⎝⎭.()D 1221-⎛⎫⎪-⎝⎭.二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上. (9)已知函数()f x 连续,且21cos[()]lim1(1)()x x xf x e f x →-=-,则(0)____f =.(10)微分方程2()0x y x e dx xdy -+-=的通解是____y =.(11)曲线()()sin ln xy y x x +-=在点()0,1处的切线方程为 . (12)曲线23(5)y x x =-的拐点坐标为______.(13)设xyy z x ⎛⎫= ⎪⎝⎭,则(1,2)____z x ∂=∂.(14)设3阶矩阵A 的特征值为2,3,λ.若行列式248A =-,则___λ=.三、解答题:15-23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. (15)(本题满分9分)求极限()40sin sin sin sin lim x x x x x →-⎡⎤⎣⎦. (16)(本题满分10分)设函数()y y x =由参数方程20()ln(1)t x x t y u du =⎧⎪⎨=+⎪⎩⎰确定,其中()x t 是初值问题020xt dx te dtx --⎧-=⎪⎨⎪=⎩的解.求22y x ∂∂.(17)(本题满分9分)求积分1⎰.(18)(本题满分11分)求二重积分max(,1),Dxy dxdy ⎰⎰其中{(,)02,02}D x y x y =≤≤≤≤(19)(本题满分11分)设()f x 是区间[)0,+∞上具有连续导数的单调增加函数,且(0)1f =.对任意的[)0,t ∈+∞,直线0,x x t ==,曲线()y f x =以及x 轴所围成的曲边梯形绕x 轴旋转一周生成一旋转体.若该旋转体的侧面积在数值上等于其体积的2倍,求函数()f x 的表达式.(20)(本题满分11分)(1)证明积分中值定理:若函数()f x 在闭区间[,]a b 上连续,则至少存在一点[,]a b η∈,使得()()()ba f x dx fb a η=-⎰(2)若函数()x ϕ具有二阶导数,且满足32(2)(1),(2)()x dx ϕϕϕϕ>>⎰,证明至少存在一点(1,3),()0ξϕξ''∈<使得 (21)(本题满分11分)求函数222u x y z =++在约束条件22z x y =+和4x y z ++=下的最大值与最小值. (22)(本题满分12分)设矩阵2221212n na a aA a a ⨯⎛⎫⎪⎪= ⎪⎪⎝⎭,现矩阵A 满足方程AX B =,其中()1,,Tn X x x =,()1,0,,0B =,(1)求证()1n A n a =+;(2)a 为何值,方程组有唯一解,并求1x ;(3)a 为何值,方程组有无穷多解,并求通解. (23)(本题满分10分)设A 为3阶矩阵,12,αα为A 的分别属于特征值1,1-特征向量,向量3α满足323A ααα=+,(1)证明123,,ααα线性无关; (2)令()123,,P ααα=,求1P AP -.2008年全国硕士研究生入学统一考试数学二试题解析一、选择题 (1)【答案】D【详解】因为(0)(1)(2)0f f f ===,由罗尔定理知至少有1(0,1)ξ∈,2(1,2)ξ∈使12()()0f f ξξ''==,所以()f x '至少有两个零点.又()f x '中含有因子x ,故0x =也是()f x '的零点,D 正确.本题的难度值为. (2)【答案】C 【详解】00()()()()()()a a a aaxf x dx xdf x xf x f x dx af a f x dx '==-=-⎰⎰⎰⎰其中()af a 是矩形ABOC 面积,0()af x dx ⎰为曲边梯形ABOD 的面积,所以()axf x dx '⎰为曲边三角形的面积.本题的难度值为. (3)【答案】D【详解】由微分方程的通解中含有x e 、cos2x 、sin 2x 知齐次线性方程所对应的特征方程有根1,2r r i ==±,所以特征方程为(1)(2)(2)0r r i r i --+=,即32440r r r -+-=.故以已知函数为通解的微分方程是40y y y ''''''-+-= 本题的难度值为. (4)【答案】A【详解】0,1x x ==时()f x 无定义,故0,1x x ==是函数的间断点因为000ln 11lim ()lim lim lim csc |1|csc cot x x x x x xf x x x x x++++→→→→=⋅=-- 同理0lim ()0x f x -→=又1111ln 1lim ()lim lim sin lim sin1sin11x x x x x f x x x x ++++→→→→⎛⎫=⋅== ⎪-⎝⎭ 所以0x =是可去间断点,1x =是跳跃间断点. 本题的难度值为. (5)【答案】B【详解】因为()f x 在(,)-∞+∞内单调有界,且{}n x 单调.所以{()}n f x 单调且有界.故{()}n f x 一定存在极限.本题的难度值为. (6)【答案】A【详解】用极坐标得()222()2011,()vu uf r r Df u v F u v dv rdr v f r dr +===⎰⎰⎰所以()2Fvf u u∂=∂ 本题的难度值为. (7)【答案】C【详解】23()()E A E A A E A E -++=-=,23()()E A E A A E A E +-+=+= 故,E A E A -+均可逆. 本题的难度值为. (8)【答案】D【详解】记1221D -⎛⎫= ⎪-⎝⎭,则()2121421E D λλλλ--==---,又()2121421E A λλλλ---==----所以A 和D 有相同的特征多项式,所以A 和D 有相同的特征值.又A 和D 为同阶实对称矩阵,所以A 和D 相似.由于实对称矩阵相似必合同,故D 正确.本题的难度值为. 二、填空题 (9)【答案】2【详解】222220001cos[()]2sin [()2]2sin [()2]()lim lim lim ()[()2]4(1)()x x x x xf x xf x xf x f x x f x xf x e f x →→→-⋅==⋅- 所以(0)2f = 本题的难度值为. (10)【答案】()x x e C --+【详解】微分方程()20x y x e dx xdy -+-=可变形为x dy yxe dx x--= 所以111()dx dx x x x x xy e xe e dx C x xe dx C x e C x ----⎡⎤⎛⎫⎰⎰=+=⋅+=-+⎢⎥ ⎪⎝⎭⎣⎦⎰⎰本题的难度值为. (11)【答案】1y x =+【详解】设(,)sin()ln()F x y xy y x x =+--,则1cos()11cos()x y y xy F dy y x dx F x xy y x--'-=-=-'+-,将(0)1y =代入得01x dydx ==,所以切线方程为10y x -=-,即1y x =+ 本题的难度值为.(12)【答案】(1,6)-- 【详解】53235y x x =-⇒2131351010(2)333x y x x x -+'=-=1x =-时,0y ''=;0x =时,y ''不存在在1x =-左右近旁y ''异号,在0x =左右近旁0y ''>,且(1)6y -=- 故曲线的拐点为(1,6)-- 本题的难度值为. (13)【答案】21)2- 【详解】设,y xu v x y==,则v z u = 所以121()ln v v z z u z v y vu u u x u x v x x y-∂∂∂∂∂=⋅+⋅=-+⋅∂∂∂∂∂所以(1,2)21)2z x ∂=-∂ 本题的难度值为. (14)【答案】-1【详解】||236A λλ =⨯⨯=3|2|2||A A = 本题的难度值为. 三、解答题 (15)【详解】方法一:4300[sin sin(sin )]sin sin sin(sin )limlim x x x x x x x x x→→--= 方法二:331sin ()6x x x o x =-+331sin(sin )sin sin (sin )6x x x o x =-+本题的难度值为. (16)【详解】 方法一:由20x dxte dt--=得2x e dx tdt =,积分并由条件0t x =得21x e t =+,即2ln(1)x t =+所以2222ln(1)2(1)ln(1)21dydy t t dt t t dxt dx dt t +⋅===+++方法二:由20x dxte dt--=得2x e dx tdt =,积分并由条件0t x =得21x e t =+,即2ln(1)x t =+所以2222ln(1)2(1)ln(1)21x dydy t t dt t t e x dxt dx dt t +⋅===++=+所以22(1)x d ye x dx=+本题的难度值为. (17)【详解】 方法一:由于21x -→=+∞,故21⎰是反常积分.令arcsin x t =,有sin x t =,[0,2)t π∈方法二:21⎰12201(arcsin )2x d x =⎰ 令arcsin x t =,有sin x t =,[0,2)t π∈故,原式21164π=+ 本题的难度值为.(18)【详解】曲线1xy =将区域分成两 个区域1D 和23D D +,为了便于计算继续对 区域分割,最后为()max ,1Dxy dxdy ⎰⎰本题的难度值为.(19)【详解】旋转体的体积20()t V f x dx π=⎰,侧面积02(tS f x π=⎰,由题设条件知上式两端对t求导得2()(f t f t =y '=由分离变量法解得1ln(y t C =+,即t y Ce =将(0)1y =代入知1C =,故t y e =,1()2t t y e e -=+于是所求函数为1()()2x x y f x e e -==+本题的难度值为.(20)【详解】(I)设M 与m 是连续函数()f x 在[,]a b 上的最大值与最小值,即 由定积分性质,有()()()bam b a f x dx M b a -≤≤-⎰,即()baf x dx m M b a≤≤-⎰由连续函数介值定理,至少存在一点[,]a b η∈,使得()()b af x dx f b aη=-⎰即()()()ba f x dx fb a η=-⎰(II)由(I)的结论可知至少存在一点[2,3]η∈,使32()()(32)()x dx ϕϕηϕη=-=⎰又由32(2)()()x dx ϕϕϕη>=⎰,知23η<≤对()x ϕ在[1,2][2,]η上分别应用拉格朗日中值定理,并注意到(1)(2)ϕϕ<,()(2)ϕηϕ<得在12[,]ξξ上对导函数()x ϕ'应用拉格朗日中值定理,有 本题的难度值为. (21)【详解】方法一:作拉格朗日函数22222(,,,,)()(4)F x y z x y z x y z x y z λμλμ=++++-+++-令2222022020040x y z F x x F y y F z F x y z F x y z λμλμλμλμ'=++=⎧⎪'=++=⎪⎪'=-+=⎨⎪'=+-=⎪'=++-=⎪⎩ 解方程组得111222(,,)(1,1,2),(,,)(2,2,8)x y z x y z ==-- 故所求的最大值为72,最小值为6.方法二:问题可转化为求2242242u x y x x y y =++++在224x y x y +++=条件下的最值设44222222(,,)2(4)F x y u x y x y x y x y x y λλ==++++++++-令323222442(12)0442(12)040x y F x xy x x F y x y y y F x y x y λλλ'⎧=++++=⎪'=++++=⎨⎪'=+++-=⎩ 解得1122(,)(1,1),(,)(2,2)x y x y ==--,代入22z x y =+,得122,8z z == 故所求的最大值为72,最小值为6. 本题的难度值为. (22)【详解】(I)证法一:证法二:记||n D A =,下面用数学归纳法证明(1)n n D n a =+. 当1n =时,12D a =,结论成立. 当2n =时,2222132a D a aa==,结论成立.假设结论对小于n 的情况成立.将n D 按第1行展开得 故||(1)n A n a =+证法三:记||n D A =,将其按第一列展开得2122n n n D aD a D --=-, 所以211212()n n n n n n D aD aD a D a D aD ------=-=-即12122()2n n n n n n n n D a aD a a a aD a a D ----=+=++=++(II)因为方程组有唯一解,所以由Ax B =知0A ≠,又(1)n A n a =+,故0a ≠. 由克莱姆法则,将n D 的第1列换成b ,得行列式为 所以11(1)n n D nx D n a-==+ (III)方程组有无穷多解,由0A =,有0a =,则方程组为此时方程组系数矩阵的秩和增广矩阵的秩均为1n -,所以方程组有无穷多解,其通解为()()10000100,TTk k +为任意常数.本题的难度值为. (23)【详解】(I)证法一:假设123,,ααα线性相关.因为12,αα分别属于不同特征值的特征向量,故12,αα线性无关,则3α可由12,αα线性表出,不妨设31122l l ααα=+,其中12,l l 不全为零(若12,l l 同时为0,则3α为0,由323A ααα=+可知20α=,而特征向量都是非0向量,矛盾)∴32321122A l l αααααα=+=++,又311221122()A A l l l l ααααα=+=-+ ∴112221122l l l l ααααα-+=++,整理得:11220l αα+=则12,αα线性相关,矛盾.所以,123,,ααα线性无关.证法二:设存在数123,,k k k ,使得1122330k k k ααα++=(1)用A 左乘(1)的两边并由11,A αα=-22A αα=得1123233()0k k k k ααα-+++=(2)(1)—(2)得113220k k αα-=(3)因为12,αα是A 的属于不同特征值的特征向量,所以12,αα线性无关,从而130k k ==,代入(1)得220k α=,又由于20α≠,所以20k =,故123,,ααα线性无关.(II)记123(,,)P ααα=,则P 可逆,所以1100011001P AP --⎛⎫ ⎪= ⎪ ⎪⎝⎭.本题的难度值为.。
