数据分析(梅长林)习题
第三章数据分析(梅长林)习题答案
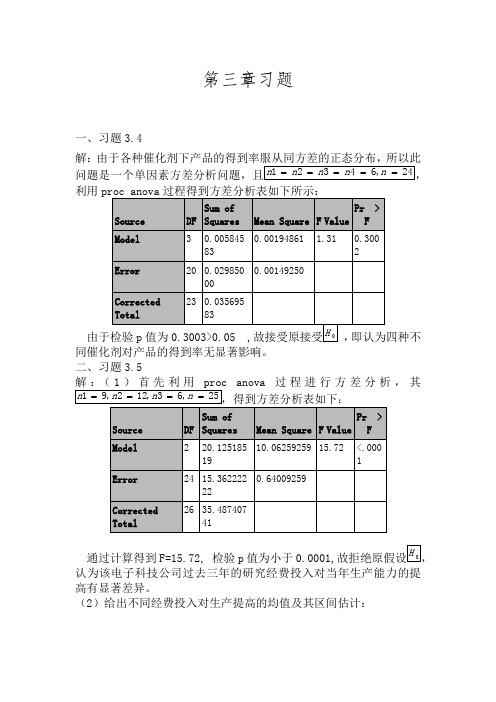
第三章习题一、习题3.4解:由于各种催化剂下产品的得到率服从同方差的正态分布,所以此利用proc anova过程得到方差分析表如下所示:同催化剂对产品的得到率无显著影响。
二、习题3.5anova过程进行方差分析,其通过计算得到F=15.72, 检验p值为小于0.0001,认为该电子科技公司过去三年的研究经费投入对当年生产能力的提高有显著差异。
(2)给出不同经费投入对生产提高的均值及其区间估计:为95%的置信区间为:95%的Bonferroni 同时置信区间为:Bonferroni 同时置信区间都位于负值区间可知随着三年科研经费的投入越高,当年生产能力的改善越显著。
三、习题3.6解:(1)首先利用SAS 的proc anova 过程的means 语句,求出各水平的均值和标准差:如下所示:由上表可知,(a1,b1)组合和(a1,b3)组合的标准差分别为2.030875、2.8067751与其他组合的标准差相差较大,所以我认为假定误差的等方差性不太合理。
故不能直接进行方差分析。
(2)由(1)可知直接进行方差分析是不合理的,所以对观测数据做对数变换,首先来分析个水平组合是否是方差齐性的。
由以上结果可以看出各组合水平上的标准差趋于一致,各组之间的标准差差异比较小。
说明各组合的离散程度比较接近。
故可以利用变换之后的数据在进行方差分析。
(3)由SAS系统的proc anova过程对进行自然对数变换后的数据进行方差分析,得到如下的误差分析表:x1*x2的影响是不显著的,检验P=0.3143>0.05,即两种铁离子残留量的百分比差异在不同剂量水平下可认为是相同的。
而由因素A和因素B对残留量的百分比的影响均显著,检验P值分别为0.0161和<.0001,所以两种铁离子残留量的百分比是有显著差异的,不同剂量水平下残留量的百分比也是有显著差异的。
(4)求出各因素在不同水平下的均值以及估计区间:SAS系统的proc anova过程对数据进行方差分析,得到各因素两两的Bonferroni同时置信区间为:均值之差的置信度为95%(注:可编辑下载,若有不当之处,请指正,谢谢!)。
数据分析方法实验(范金城梅长林)习题报告

习题4.5实验报告一、实验目的问题描述:在习题1.5表1.9中,列出了历年人口出生率、死亡率和自然增长率(单位:%)。
设对应于人口出生率、人口死亡率、自然增长率的数据变量分别为x1,x2,x3。
(1)分别从样本协方差矩阵S及样本相关矩阵R出发,求x1,x2,x3的样本主成分y1,y2,计算各样本主成分的贡献率。
(2)分别从样本协方差矩阵S及样本相关矩阵R出发,将第一样本主成分y1从小到大排序,并给与分析。
二、所用方法及工具(1)主成分分析法与贡献率:主成分分析法即构造原变量的一系列线性组合,使各线性组合在彼此不相关的前提下尽可能多地反映原变量的信息,即使其方差最大。
求的各主成分,等价于求它的协方差矩阵的各特征值及相应的正交单位化特征向量.按特征值由大到小所对应的正交单位化特征向量为组合系数的X,Xz ,…,X,的线性组合分别为X的第一,第二、直至第p个主成分,而各主成分的方差等于相应的特征值。
(2)SAS编程:SAS语言是一种专用的数据管理与分析语言,它提供了一种完善的编程语言。
类似于计算机的高级语言,SAS用户只需要熟悉其命令、语句及简单的语法规则就可以做数据管理和分析处理工作。
因此,掌握SAS编程技术是学习SAS的关键环节。
在SAS中,把大部分常用的复杂数据计算的算法作为标准过程调用,用户仅需要指出过程名及其必要的参数。
这一特点使得SAS编程十分简单。
三、实验内容本次实验采用SAS编程实现,代码如下:data a;set sjfx.rk1;run;proc princomp n=2 cov out=out1;var x1 x2 x3;run;proc sort data=out1 out=a1;by prin1;run;proc print data=a1;run;proc princomp n=2 out=out2;var x1 x2 x3;run;proc sort data=out2 out=a2;by prin1;run;proc print data=a2;run;实验结果:PRINCOMP 过程。
第2章 数据分析(梅长林)习题题答案
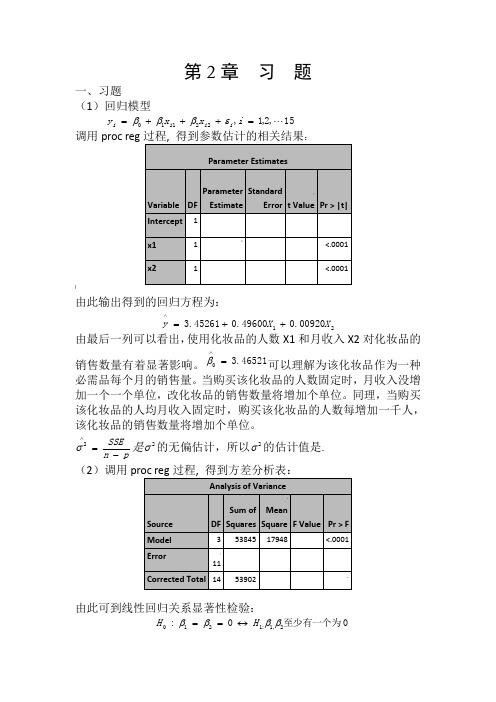
第2章 习 题一、习题(1)回归模型15,2,1,22110 =+++=i x x y i i i i εβββ调用proc reg:]由此输出得到的回归方程为:2100920.049600.045261.3X X y ++=∧由最后一列可以看出,使用化妆品的人数X1和月收入X2对化妆品的销售数量有着显著影响。
46521.30=∧β可以理解为该化妆品作为一种必需品每个月的销售量。
当购买该化妆品的人数固定时,月收入没增加一个一个单位,改化妆品的销售数量将增加个单位。
同理,当购买该化妆品的人均月收入固定时,购买该化妆品的人数每增加一千人,该化妆品的销售数量将增加个单位。
pn SSE-=∧2σ是2σ的无偏估计,所以2σ的估计值是. (2)调用由此可到线性回归关系显著性检验:0至少有一个为0:2,1:1210ββββH H ↔==的统计量/(1)/()SSR p MSRF SSE n p MSE-==-的观测值47.56790=F ,检验的p 值0001.0)(000<>==F F p p H另外9989.053902538452===SST SSR R ,2R 描述了由自由变量的线性关系函数值所能反映的Y 的总变化量的比例。
2R 越大,表明线性关系越明显。
这些结果均表明Y 与X1,X2之间的回归关系高度显著。
(3)若置信水平05.0=α,由17881.2)12(975.0=t ,利用参数估计值得到21,0,βββ的置信区间分别为:对,0β2942.54516.343065.21781.245216.3±=⨯±,即)7458.8,8426.1(-) 对1β:01318.049600.000605.01781.249600.0±=⨯±,即)50198.0,48282.0( )2β:0021.000920.00009681.01781.200920.0±=⨯±,即)00113.0,0071.0(-(4)首先检验X1对Y 是否有显著性影:假设其约简模型为:15,2,1,220 =++=i x y i i i εββ 由观测数据并利用proc reg 过程拟合此模型求得:88137.484)(=R SSE 13215=-=R f 88357.56)(=F SSE 12315=-=R f由[()()]()()/R F FSSE R SSE F f f F SSE F f --=求得检验统计量的值为:3.9012/88357.5688357.5688137.4840=-=F05.0))13,1(()(0000<>==>==F F P F F p p H由此拒绝原假设,所以x2对Y 有显著影响。
数据分析方法课后答案

数据分析方法课后答案【篇一:数据的分析练习题及答案】、选择题:(每题3分,共15分)1.小明家要买台电脑,下面是甲、乙、丙三种电脑近几年来的销量,如果小明想买一台近期比较流行的电脑,他应买()a.甲b.乙c.丙2.小李是个彩票迷,为了能得奖,他特意询问了前15天的中奖号码分别是:519、、706、328、556、768、215、435、741、624、307、821、696、741、471、285. 你认为这样的观点是否合理()a.不合理b.合理3.小靖想买双好的运动鞋,于是她上网查找有关资料,得到下表:她想买一双价格在300-600元之间,且她喜欢白色、红白相间、浅绿或淡黄色, 并且防水性能很好,那么她应选()a.甲b.乙c.丙d.丁4.为了计算植树节时本班同学所种植的30棵树苗的平均高度, 三位同学先将所有树苗的然后,他们分别这样计算这30棵树苗的平均高度:130130列式正确的是()a.(1)b.(1)和(2);c.(1)和(3)d.(2)和(3)5.某班在一次物理测试中的成绩为:100分7人,90分14人,80分17人,70分8人, 60分2人,50分2人.则该班此次测试的平均成绩为() a.82分b.62分c.64分d.75分二、填空题:(每题4分,共20分)6.一次知识竞赛中,36名参赛选手的得分情况为:5人得75分,8人得80分,6 人得85分,8人得90分,7人得95 分, 2 人得100 分, 要计算他们的平均得分, 可列算式:_____________.(1)7.某校九年级6个班级的学生的人数和平均体重如下表:要计算全校学生的平均体重,可列算式________,平均体重约为__________.8.某家庭搬进新居后,又添置了新的家用电器,为了了解用电量的大小, 该家庭在6月初连续几天观察电表的度数,如下表所示:9.为了解我国14岁男孩的平均身高,从北方抽取了300个男孩,平均身高1.60m; 从南方抽取了200个男孩,平均身高为1.50m;若北方14岁男孩数与南方14岁男孩数的比为3:2,由此可推断我国14岁男孩的平均身高约为______m.10.小明先用5千米/时的速度行驶3小时后,又用4千米/时的速度行驶5小时到达目的地,则小明的平均速度为________. 三、解答题:(每题9分,共54分)11.某同学对他在本学期的自我检测成绩进行了统计:95分的有12次,90 分的有10次,85分的有15次,80分的有3次,75分的有1次,65分的有3次.试计算该同学本学期自我检测的平均成绩..12.超市里要举行转盘摇奖活动,转盘如图所示,买满100元可摇奖一次,有人说:如果大家都摇到自行车,那么超市岂不是亏本了?如果你是超市决策者,会不会因此而改变有奖销售的方案呢?说说你的理由?自行车300元洗洁精2.80元酱油5.0元西红柿2.00元墨水3.50元13.请你根据上表比较这两个国家的数据,你能得出什么结论?14.由于水资源贫乏,节约用水非常重要,请你调查一下,本班每位学生所在家庭的月人均用水量,并据此制作频数分布图,同时估计一下当地家庭的月人均用水量.15.爸爸给小明一串钥匙,共有4把,小明决定先试试哪把是防盗门的钥匙. 请你用模拟实验方法估计一下,他第1次试开就成功的机会有多大?16.转动如图所示的转盘两次,每次指针都指向一个数字. 如果两次所指的数字之积是质数,游戏者a得10分;乘积不是质数,游戏者b得10分.你认为这个游戏公平吗?如果你认为这个游戏不公平,你愿意做游戏者a还是游戏者b?为什么?31246517.有人对记忆和遗忘的规律进行研究,人在记忆过某些知识后, 在不同时间段对其进行测试,结果如下表:分析测试结果,在图中绘制曲线图,并回答遗忘在数量上的变化规律.记忆效果1%记忆的保持曲线图答案:一、1.b 2.a 3.d 4.d 5.a148?50?49.8?46?50.2?55?49.5?48?51?52?50.3?547., 49.8kg50?46?55?48?52?54358.387.75 9.1.56 10.千米/时8三、144所以,美国的吸烟总人数和每天吸烟的总数都大于日本,但吸烟人口占总人口的比例小于日本.14.列出调查表,对本班学生实事求是地进行调查以获得真实的信息.15.可用4个相同的球,1个白的,3个黑的,每次抽1个,则第1次抽到白球的概率为所求概率,1为. 41516.不公平,愿做b 解:乘积是质数的概率是,乘积不是质数的概率是, 游戏不公平,故66愿做b.17.遗忘曲线表明了遗忘在数量上的变化规律,遗忘的数量随时间的前进而递增;这种递增先快后慢,在识记后的短时间内特别迅速,然后逐渐缓慢下来.二、6.记忆效果1%/d记忆的保持曲线图【篇二:定性数据分析第三章课后答案】9、对72个可疑患者用两种不同的方法进行检测,检测结果如下:问:检测方法1阳性和阴性的比例是否与检测方法2阳性和阴性的比例相同?解:(1)提出原假设根据题意,我们假设检测方法1阳性和阴性的比例与检测方法2阳性和阴性的比例是相同。
数据分析答案梅长林

数据分析答案梅长林【篇一:1.1一维数据数字特征】013学年第一学期主讲教师李晓燕课程名称数据分析课程类别专业限选课学时及学分 68;4授课班级信息101 102使用教材《数据分析方法》系(院.部) 数理系教研室(实验室) 信息和计算科学教研室数据分析总学时:68 理论38.上机28 适用专业:信息和计算科学内容:? sas软件介绍 3学时 ? 数据的描述性分析10学时 ? 线性回归分析 13学时 ? 方差分析 10学时 ? 主成分分析和典型相关分析8学时? 判别分析 8学时 ? 聚类分析 8学时 ? 学生报告 8学时教材:《数据分析方法》,梅长林、范金城编,高等教育出版社.2006. 参考资料:《实用统计方法》,梅长林编,科学出版社;《使用多元统计分析》,高惠璇编,北京大学出版社,2005;《使用统计方法和sas系统》,高惠璇编,北京大学出版社,2001;《多元统计分析》(二版),何晓群编,中国人民大学出版社,2008;《使用回归分析》(二版),何晓群编,中国人民大学出版社,2007;《统计建模和r软件》,薛毅编著,清华大学出版社,2007. 考核:期末成绩(闭卷测试+上机测试):70%。
平时成绩(平时作业+考勤+大报告):30%。
课程作业(1)作业题目在网络教学平台公布,按格式要求,以电子版方式通过平台提交。
(2)大报告:2-3人一组,每组一个选题,成员按相同的成绩计分。
收集数据,撰写小论文,做ppt讲解。
每组讲10-20分钟,提问环节。
同学打分。
课时授课计划课次序号: 01一、课题:1.1 一维数据的数字特征及相关系数二、课型:新授课三、目的要求:1.掌握数据的数字特征(均值、方差等);2.掌握几种描述性分析的sas过程和作图过程计算这些数字特征及进行描述性分析.四、教学重点:均值、方差等数字特征.教学难点:基本概念的理解.五、教学方法及手段:传统教学和上机实验相结合.六、参考资料:1.《实用统计方法》,梅长林,周家良编,科学出版社;2.《sas统计分析使用》,董大钧主编,电子工业出版社.七、作业:1.1八、授课记录:九、授课效果分析:0 绪论0.1 课程内涵数据分析(即多元统计学statistics):是以数据为依据,以统计方法为理论、计算机及软为工具,研究多变量问题、挖掘数据的统计规律的学科. 通过收集数据、整理数据、分析数据和由数据得出结论的一组概念、原则和方法。
数据分析软件应用练习题

数据分析软件应用练习题在当今数字化的时代,数据分析已经成为了企业决策、科学研究以及日常生活中不可或缺的一部分。
而熟练掌握数据分析软件的应用,则是进行有效数据分析的关键。
为了帮助大家更好地掌握数据分析软件的使用,下面为大家准备了一系列的练习题。
一、基础操作练习1、数据导入与导出从本地文件夹中导入一个包含销售数据的 Excel 文件,文件中包含产品名称、销售数量、销售单价等字段。
将处理好的数据导出为 CSV 格式,保存到指定的文件夹中。
2、数据清理数据中存在一些缺失值,使用合适的方法对缺失值进行处理。
去除数据中的重复行。
3、数据筛选与排序筛选出销售数量大于 100 的记录。
按照销售单价从高到低对数据进行排序。
二、数据分析练习1、描述性统计分析计算销售数据的均值、中位数、众数、标准差等统计指标。
绘制销售数量和销售单价的直方图。
2、相关性分析分析销售数量与销售单价之间的相关性。
3、分组统计分析按照产品类别对销售数据进行分组,计算每组的销售总额和平均销售单价。
三、数据可视化练习1、绘制柱状图以产品类别为横轴,销售总额为纵轴,绘制柱状图。
2、绘制折线图绘制销售数量随时间变化的折线图。
3、绘制饼图展示不同产品类别在总销售额中所占的比例,绘制饼图。
四、高级应用练习1、假设检验假设某种产品的平均销售单价为 50 元,通过样本数据进行假设检验,判断该假设是否成立。
2、回归分析建立销售数量与销售单价、促销活动等因素之间的线性回归模型。
在进行这些练习题的过程中,大家需要注意以下几点:首先,要仔细阅读数据分析软件的操作手册和帮助文档,了解每个功能的具体用法和参数设置。
其次,要善于运用软件提供的快捷键和快捷操作,提高工作效率。
再次,对于分析结果要进行合理的解读和判断,避免得出错误的结论。
最后,要多做练习,不断积累经验,提高自己的数据分析能力。
希望通过这些练习题,大家能够熟练掌握数据分析软件的应用,为今后的工作和学习打下坚实的基础。
最新第2章 数据分析(梅长林)习题题答案
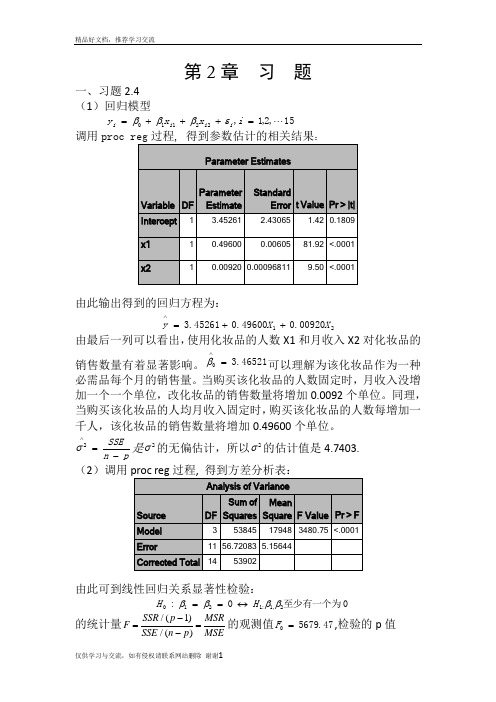
第2章 习 题一、习题2.4 (1)回归模型15,2,1,22110 =+++=i x x y i i i i εβββ调用:由此输出得到的回归方程为:2100920.049600.045261.3X X y ++=∧由最后一列可以看出,使用化妆品的人数X1和月收入X2对化妆品的销售数量有着显著影响。
46521.30=∧β可以理解为该化妆品作为一种必需品每个月的销售量。
当购买该化妆品的人数固定时,月收入没增加一个一个单位,改化妆品的销售数量将增加0.0092个单位。
同理,当购买该化妆品的人均月收入固定时,购买该化妆品的人数每增加一千人,该化妆品的销售数量将增加0.49600个单位。
pn SSE-=∧2σ是2σ的无偏估计,所以2σ的估计值是4.7403. (2)调用由此可到线性回归关系显著性检验:0至少有一个为0:2,1:1210ββββH H ↔== 的统计量/(1)/()SSR p MSRF SSE n p MSE-==-的观测值47.56790=F ,检验的p 值0001.0)(000<>==F F p p H另外9989.053902538452===SST SSR R ,2R 描述了由自由变量的线性关系函数值所能反映的Y 的总变化量的比例。
2R 越大,表明线性关系越明显。
这些结果均表明Y 与X1,X2之间的回归关系高度显著。
(3)若置信水平05.0=α,由17881.2)12(975.0=t ,利用参数估计值得到21,0,βββ的置信区间分别为:对,0β2942.54516.343065.21781.245216.3±=⨯±,即)7458.8,8426.1(-) 对1β:01318.049600.000605.01781.249600.0±=⨯±,即)50198.0,48282.0( 2β:0021.000920.00009681.01781.200920.0±=⨯±,即)00113.0,0071.0(-(4)首先检验X1对Y 是否有显著性影:假设其约简模型为:15,2,1,220 =++=i x y i i i εββ 由观测数据并利用proc reg 过程拟合此模型求得:88137.484)(=R SSE 13215=-=R f 88357.56)(=F SSE 12315=-=R f由[()()]()()/R F FSSE R SSE F f f F SSE F f --=求得检验统计量的值为:3.9012/88357.5688357.5688137.4840=-=F05.0))13,1(()(0000<>==>==F F P F F p p H由此拒绝原假设,所以x2对Y 有显著影响。
八年级数学下册第二十章《数据的分析》习题(2)

一、选择题1.某中学足球队的18名队员的年龄情况如下表:则这些队员年龄的众数和中位数分别是()A.15,15 B.15,15.5 C.15,16 D.16,15B解析:B【分析】根据众数和中位数的定义求解即可.【详解】解:这组数据按从小到大顺序排列为:14,14,14,15,15,15,15,15,15,16,16,16,16,17,17,17,17,18,则众数为:15,中位数为:(15+16)÷2=15.5.故答案为B.【点睛】本题考查了众数和中位数的知识,属于基础题,解答本题的关键是掌握众数和中位数的定义.2.八年级某班五个合作学习小组人数如下:5,7,6,x,7.已知这组数据的平均数是6,则x的值为()A.7 B.6 C.5 D.4C解析:C【分析】根据平均数的计算公式列出算式,再进行计算即可得出x的值.【详解】解:∵5,7,6,x,7的平均数是6,∴15(5+7+6+x+7)=6,解得:x=5;故选:C.【点睛】本题考查了算术平均数的知识,解题的关键是根据算术平均数求出数据总和.3.某次数学趣味竞赛共有10道题目,每道题答对得10分,答错或不答得0分.全班40名同学的成绩的中位数和众数分别是()A.75,70 B.70,70 C.80,80 D.75,80A解析:A【分析】根据中位数和众数的定义解答即可.【详解】共40个数据中第20和第21个数分别是70、80,∴这组数据的中位数是75,这组数据中出现次数最多的是70,所以众数是70,故选:A.【点睛】此题考查了中位数和众数的定义,一组数据最中间的一个数或两个数的平均数是这组数据的中位数,出现次数最多的数是这组数据的众数,正确掌握定义是解题的关键.4.下列说法正确的是()A.为了解我国中学生课外阅读的情况,应采取全面调查的方式B.一组数据1、2、5、5、5、3、3的中位数和众数都是5C.若甲组数据的方差是003,乙组数据的方差是0.1,则甲组数据比乙组数据稳定D.抛掷一枚硬币100次,一定有50次“正面朝上”C解析:C【分析】可根据调查的选择、中位数和众数的求法、方差及随机事件的意义,逐个判断得结论.【详解】解:因为我国中学生人数众多,其课外阅读的情况也不需要特别精确,所以对我国中学生课外阅读情况的调查,宜采用抽样调查,故选项A不正确;因为B中数据按从小到大排列为1、2、3、3、5、5、5,位于中间的数是3,故该组数据的中位数为3,所以选项B说法不正确;因为0.003<0.1,方差越小,波动越小,数据越稳定,所以甲组数据比乙组数据稳定,故选项C说法正确;因为抛掷硬币属于随机事件,抛掷一枚硬币100次,不一定有50次“正面朝上”故选项D说法不正确.故选:C.【点睛】本题的关键在于掌握调查的选择、中位数和众数的求法、方差及随机事件的意义.5.一组数据3,4,6,8,8,9的中位数和众数分别是()A.7,8 B.7,8,5 C.5,8 D.7,5,7A解析:A【分析】中位数是一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数);众数是一组数据中出现次数最多的数据,据此可得答案.【详解】解:将数据从小到大排列为3、4、6、8、8、9,则这组数据的中位数为(6+8)÷2=7,众数为8.故选:A.【点睛】本题考查众数与中位数的意义.将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数)叫做这组数据的中位数;如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.6.某校10名学生参加某项比赛成绩统计如图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章习题
1.习题
解:假定两总体服从正态分布,且协方差矩阵21∑=∑,误判损失相同又先验概
即:0.4285711=P 0.5714292=P 又计算可得:
(1)(2)25.31622.025,2.416 1.187x x ⎡⎤⎡⎤==--⎢⎥⎢⎥⎣⎦⎣⎦
并且:-2.38145ln =S 计算广义平方距离函数:
2()1
()()()()ln 2ln j T j j j j j d p -=--+-x x x
S x x S 并计算后验概率:
2
2
2
ˆˆ0.5()0.5()1
ˆ(|)e e j k d d j
k P G --==∑x x x 1,2j =
回代判别结果如下:
由此可见误判的回代估计:
0.07141/14*
==r P
若按照交叉确认法,定义广义平方距离如下:
2()1()
()()()()()()()ln 2ln j j j T j j x x x x j d p -=--+-x x x S x x S
逐个剔除, 交叉判别,后验概率按下式计算:
2
2
2
ˆˆ0.5()0.5()1
ˆ(|)e e j k d d j
k P G --==∑x x x 1,2j =
通过SAS 计算得到表所示结果。
发现同样也是属于G1的4号被误判为G2,因此误判率的交
叉确认估计为*
ˆ1/140.0714c p
==
*121p p p ΦΦ⎛⎫
=+- ⎪⎝
⎭
其中(1)
(2)1(1)(2)ˆ()()T λ
-=--x x S x x =,
2
1(1|2)ln
(2|1)c p d c p =,又因为(1|2)(2|1)c c c ==,所以288.0ln 1
2==P P d ,
最后可得后验概率p 为:
习题
解:(1)在21∑≠∑并且先验概率相同的的假设前提下,建立矩离判别的线性判别函数。
利用SAS 的proc discrim 过程首先计算得到总体的协方差矩阵,如表:
各个总体的马氏平方距离见表:
8
765
432118
765
43211909.0465.13054.1581.400.263-702.03.0698.269-176.33030916.1578.9046.0670.5818.1389.0179.2006.71995.121x x x x x x x x W x x x x x x x x W ++++-++=++++--++-=
得到训练样本回判法判别结果如表:
(2)假设两总体服从正态分布,先验概率按比例分配且误判损失相同,在两总体协方差矩阵相同,即21∑=∑的条件下进行Bayes 判别分析,通过SAS discrim 过程得到结果:
在21∑≠∑,并且先验概率按比例分配的假设前提下利用SAS 的proc discrim 过程进行Bays 判别分析,这时以个总体的训练样本单独估计各总体的协方差矩阵,可到的训练样本的回判和交叉确认结果: 回判结果:
交叉确认判别结果:
(3)在不同的假设前提,采用不同判别方法得到待判样本的判别结果:
3在协方差不同矩阵相同的前提下,Bayes对西藏、上海、广东的判别结果:
3.习题
解:(1)假设两总体服从正态分布且在两总体协方差矩阵相同,即21∑=∑,先验概率按相同的条件下进行Bayes 判别分析,通过SAS discrim 过程得到结果:
首先得到线性判别函数:
7
65
432117
65
43211259.0337.85065.01.395227.00.152-29.878-95.000312.0102.108589.0952.1789.0152.0351.308475.98x x x x x x x W x x x x x x x W --++-+=--+---+-=
回代误判结果:
交叉确认判别结果:由计算发现总共有四个样本被判错,分别是9、28、29、35号样品。
累计误判率为%
(1)假设两总体服从正态分布且在两总体协方差矩阵相同,即21∑=∑,先验概率按比例分配且误判损失相同的条件下进行Bayes 判别分析,通过SAS discrim 过程得到结果: 首先得到线性判别函数:
回代误判结果。
