典型环节的Bode图资料
典型环节的Bode图

控制系统的开环频率特性目的:掌握开环Bode 图的绘制根据Bode 图确定最小相位系统的传递函数 重点:开环Bode 图的绘制、根据Bode 图确定最小相位系统的传递函数1 开环伯德图手工作图的一般步骤:1)将开环传递函数表示为时间常数表达形式,计算各个典型环节的交接频率2)求20lgK 的值,并明确积分环节的个数ν 3)通过(1,20lgK )绘制斜率为-20vdB/dec 低频段 4)随着频率增加,每遇到一个典型环节的交接频率,就改变一次斜率最小相位系统定义: 递函数的零点、极点全部位于S 左半平面,同时又无纯滞后环节的系统称为最小相位系统。
否则就是非最小相位系统。
对数幅频特性与相频特性之间存在确定的对应关系。
对于一个最小相位系统,我们若知道了其幅频特性,它的相频特性也就唯一地确定了。
也就是说:只要知道其幅频特性,就能写出此最小相位系统所对应的传递函数,而无需再画出相频特性。
非最小相位系统高频时相角迟后大,起动性能差,响应缓慢。
对响应要求快的系统,不宜采用非最小相位元件。
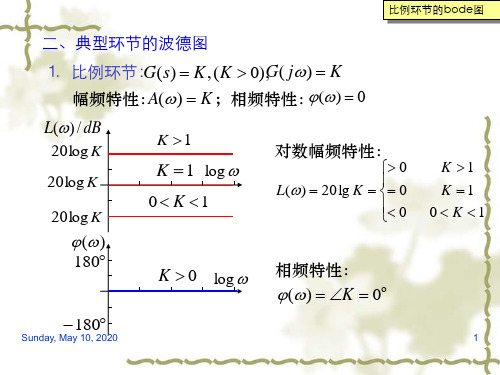
2 典型环节的伯德图绘制曲线在MA TLAB 中实现,利用下述的程序段:num=[b2 b1 b0]; den=[1 a2 a1 a0]; H=tf(num,den); bode(H) margin(H) hold on2.1 比例环节传递函数:()G s K = 频率特性:()G j K ω=对数幅频特性:()20lg L j K ω= 对数相频特性:()0ϕω=程序段:num=[0 10]; den=[0 1]; H=tf(num,den); bode(H)margin(H) holdon结论:放大环节的对数幅频特性是一条幅值为20lgK 分贝,且平行于横轴的直线,相频特性是一条和横轴重合的直线。
K>1时,20lgK>0dB ;K<1时,20lgK<0dB 。
2.2 惯性环节(低通滤波特性)传递函数:1()1G s sτ=+频率特性:()()()j G j A e ϕωωω=对数幅频特性:21()20lg 1()L ωτω=+对数相频特性:()arctan ϕωτω=-绘制1()10.1G s s=+的Bode 图程序段:num=[0 1]; den=[0.1 1];H=tf(num,den); bode(H) margin(H) holdon结论:惯性环节的对数幅频特性可以用在1ωτ= 处相交于0分贝的两条渐近直线来近似表示:当1ωτ时,是一条0分贝的直线; 当1ωτ时,是一条斜率为-20dB/dec 的直线。
典型环节伯德图ppt课件

当有n个积分环节串联时,即: 其对数幅频特性为: 相频特性是一条与ω无关, 值为-n×900 且与ω轴平行 的直线。两个积分环节串联 的Bode图如图5-13所示。
是一条斜率为-n×20dB/dec, 且在ω=1(弧度/秒)处过零 分贝线(ω轴)的直线。
图5-13 两个积分环节串联的Bode图
7
2
一放大环节(比例环节)
放大环节的频率特性为:
其幅频特性是:
对数幅频特性为:
3
放大环节的对数幅频特性如图5-11所示,它是一条与角 频率ω无关且平行于横轴的直线,其纵坐标为20lgK。 当有n个放大环节串联时,即:
(5-62)
幅值的总分贝数为:
(5-63)
放大环节的相频特性是:
(5-64)
如图5-11所示,它是一条与角频率ω无 关且与ω轴重合的直线。
六二阶微分环节
二阶微分环节的频率特性是: 其对数幅频特性是:
相频特性是:
二阶微分环节与振荡节 的Bode图关于ω轴对称 ,如图5-21。渐近线的 转折频率为,相角变化 范围是00至+1800。 二阶微分环节的Bode图
19
七不稳定环节
不稳定环节的频率特性是:
其对数幅频特性和相频特性分别为:
不稳定惯性环节的Bode图
当 时, ,它是阻尼比 ξ的函数;当ξ=1时为-6(dB); 当ξ=0.5时为0(dB); 当ξ=0.25时为+6(dB);误差曲线如图5-18所示。
图5-17 振荡环节渐进线对数幅频特性
图5-18 振荡环节对数幅频特性误差修正曲线 15
由图知,振荡环节的误差可正可负,它们是阻尼比 ξ的函数,且以 的转折频率为对称,距离转折频率 愈远误差愈小。通常大于(或小于)十倍转折频率时, 误差可忽略不计。经过修正后的对数幅频特性曲线如图 5-19所示。
典型环节伯德图

其对数幅频特性与惯性环节相同;相频特性与惯性环 节相比是以 为对称,相角的变化范围是 至 。Bode如图5-22所示
八滞后环节
滞后环节的频率特性是: 其对数幅频特性和相频特性分别为:
滞后环节伯德图如图5-23 所示。其对数幅频特性与 ω无关,是一条与ω轴重 合的零分贝线。滞后相角 由式(5-92)计算,分别 与滞后时间常数τ和角频 率ω成正比。
当 时, ,它是阻尼比 ξ的函数;当ξ=1时为-6(dB); 当ξ=0.5时为0(dB); 当ξ=0.25时为+6(dB);误差曲线如图5-18所示。
图5-17 振荡环节渐进线பைடு நூலகம்数幅频特性
图5-18 振荡环节对数幅频特性误差修正曲线
由图知,振荡环节的误差可正可负,它们是阻尼比 ξ的函数,且以 的转折频率为对称,距离转折频率 愈远误差愈小。通常大于(或小于)十倍转折频率时, 误差可忽略不计。经过修正后的对数幅频特性曲线如图 5-19所示。
一阶微分环节的相频特性 如图5-16 所示,相角变化 范围是00至900,转折频率 1/T处的相角为450。
图5-16 一阶微分环节的Bode图
比较图5-16和5-14,可知 ,一阶微分环节与惯性环 节的对数幅频特性和相频 特性是以横轴(ω轴)为 对称的。
五振荡环节 振荡环节的频率特性是: 其对数幅频特性为:
惯性环节的相频特性为:
对应的相频特性曲线如图5-14所 示。它是一条由 至 范围内变 化的反正切函数曲线,且以 和 的交点为斜对称.
四一阶微分环节
一阶微分环节频率特性为:
其对数幅频特性是:
一阶微分环节的对数幅频特性如图5-16所示, 渐近线的转折频率为 ,转折频率处渐近特性与精 确特性的误差为 ,其误差均为正分贝数 ,误差范围与惯性环节类似。 相频特性是: 当 时,
绘制伯德图
幅频和相频特性为:
A( ) (1 T 2 2 )2 (2 T )2, ( ) tg 1
1 T 1 ,o ,称为转折频率或交换频率。 T
Monday, March 09, 2015
可以用这两段渐近线近似的表示惯性环节的对数幅频特性。
3
惯性环节的Bode图
10 渐近线 0 -10 -20 0° -45° -90° 1 20T
20dB / Dec
图中,红、绿线分别是低频、高频渐近线,蓝线是实际曲线。
T
( )
2.0
-63.4
3.0
-71.5
4.0
-76
5.0
-78.7
7.0
-81.9
10
-84.3
20
-87.1
50
-88.9
100
-89.4
1 1 当 0时, (0) 0;当 时, ( ) ;当 时, () 。 T T 4 2 由图不难看出相频特性曲线在半对数坐标系中对于(0, -45°) 点是斜对称的,这是对数相频特性的一个特点。
当时间常数T 变化时,对数幅频特性和对数相频特性的形状 都不变,仅仅是根据转折频率1/T 的大小整条曲线向左或向 右平移即可。而当增益改变时,相频特性不变,幅频特性上 下平移。
Monday, March 09, 2015 6
振荡环节的频率特性
K Kn 2 ⒋ 振荡环节的频率特性: G( s) 2 2 T s 2Ts 1 s 2 n s n 2
0 L( ) 20 lg K 0 0
K 1 K 1 0 K 1
( )
180
K 0
log
典型环节传递函数及伯德图
1 T
10 T
L( )(dB)
0 0.01
( ) G( j ) 90
0.1 1 10
20
20dB / dec
j
40
( )()
0 90 60 30 0 0.01 0.1 1 10
4.惯性环节 (一阶积分环节,是一个相位滞后环节)
惯性环节的特点:当输入量突变时,输出量不会突变,只能按指数 规律逐渐变化,即具有惯性。 惯性环节的微分方程:
比例环节功能框图
1.比例环节(放大环节)
G( j ) K , L( ) 20lg G( j ) 20lg K G( s) K G( j ) K G( j ) K 0 ( ) G( j ) 0
L( )(dB)
20lgK j 0 K 0 0.1 1 10
1
转折频率
1 T
渐近线 1
10 T
0
0 -20
实际幅相曲线
( )()
0 .1 1 T
20dB / dec
0.707
1 T
0 -45
1 T
10
1 T
5 一阶微分环节
特点:此环节的输出量不仅与输入量本身有关,而且与输 入量的变化率有关。
方块图为:
R( s )
τs + 1
C (s)
6.振荡环节
G jω 1 2 2 L ω 20lg 1 T ω 2 2 T jω 2ζ T jω 1
2ζ Tω
2
2
ω t g1
2ζ Tω 2 2 1 T ω
控制工程-典型环节的对数坐标图(Bode图)

(
j
)
arctan
1
2T T 2
2
南华大学
第四章 系统的频率响应分析
特点:
转折频率:
TT
=1,T
=1
T
=
n
。
低频段T<<1,→ 0dB线;
高频段T>>1,→-40dB/dec 线。
L() 20 0 -20 -40 () 0
-90
-180
-40dB/dec
T
T
100 ω(rad/s)
南华大学
典型环节的对数坐标图
(1) 比例环节
对数幅频特性为:
G( j) K
L() 20lg G( j) 20lg K
L(ω)为常数是平行于横轴的一条直线。
对数相频特性为(ω)=0 ,与横轴重合。
L(ω )
20lgK
0 ω
(ω)
0 ω
第四章 系统的频率响应分析
南华大学
第四章 系统的频率响应分析
(3) 积分环节
对数幅频特性:
G( j ) 1 j
dB 20lg G( j)
40
L( ) 20 lg G( j ) 20 lg 1 20 lg 20
-20dB/dec
对数相频特性:
0.1 1 10
( ) 90
180 G
南华大学
(2) 惯性环节
对数幅频特性为:
G( j) 1 jT 1
L( ) 20lg G( j ) 20lg
1
20lg 1 T 2 2
1 T 2 2
对数相频特性: ( ) G( j ) arctan T
《典型环节伯德图》课件

稳定性分析
稳定性定义:系统 在受到扰动后能够 恢复到其原始状态 的能力
稳定性分类:稳定、 不稳定、临界稳定
稳定性分析方法: 伯德图分析、奈奎 斯特图分析、根轨 迹分析等
伯德图分析:通过绘制 伯德图,观察系统在不 同频率下的增益和相位 变化,判断系统的稳定 性。
动态性能分析
伯德图:描述系统动态性能的图形工具 频率响应:系统对不同频率信号的响应 相位裕度:系统稳定性的指标 增益裕度:系统放大能力的指标 动态性能分析方法:如根轨迹法、频率响应法等
MATLAB还提供了丰富的函数库,可以方便地进行各种数学计算和仿真。
Simulink软件介绍
软件名称: Simulink
开发商: MathWorks
公司
软件功能:用 于建模、仿真 和分析动态系
统
应用领域:广 泛应用于控制 工程、信号处 理、通信等领
域
软件特点:图 形化界面,易 于操作,支持 多种编程语言
软件版本:最 新版本为 Simulink 2022a
其他绘制软件介绍
AutoCAD:一款专业的CAD软件,可以绘制 各种类型的伯德图
SolidWorks:一款三维设计软件,可以绘制 伯德图
Inventor:一款三维设计软件,可以绘制伯 德图
SketchUp:一款三维设计软件,可以绘制伯 德图
Blender:一款三维设计软件,可以绘制伯德 图
幅频特性的分析
幅频特性的定义:描述信号在频率域上的分布特性 幅频特性的表示方法:通常采用伯德图或奈奎斯特图 幅频特性的应用:用于分析信号的频率响应、滤波器设计等 幅频特性的测量方法:通过频谱分析仪或示波器等仪器进行测量
相频特性的分析
相频特性的定义:描述信号频率与相位之间的关系 相频特性的表示方法:通常用相频特性曲线表示 相频特性的应用:在信号处理、通信等领域有广泛应用 相频特性的测量方法:通过实验或仿真进行测量
考研复习题典型环节伯德图

相频特性是:
二阶微分环节与振荡节 的Bode图关于ω轴对称 ,如图5-21。渐近线的 转折频率为,相角变化 范围是00至+1800。 二阶微分环节的Bode图
七不稳定环节
不稳定环节的频率特性是:
其对数幅频特性和相频特性分别为:
不稳定惯性环节的Bode图
二积分环节
积分环节的频率特性是: 其幅频特性为: 对数幅频特性是:
设
,则有: (5-68)
可见,其对数幅频特性是一条 在ω=1(弧度/秒)处穿过零分贝 线(ω轴),且以每增加十倍频率 降低20分贝的速度(-20dB/dec) 变化的直线。 积分环节的相频特性是:
(5-69)
是一条与ω无关,值为-900 且平行于ω轴的直线。积分环 节的对数幅频特性和相频特性 如图5-12所示。
振荡环节的相频特性是:
除上面三种特殊情况外,振荡环节相频特性还是 阻尼比ξ的函数,随阻尼比ξ变化,相频特性在转折 频率 附近的变化速率也发生变化,阻尼比ξ越小, 变化速率越大,反之愈小。但这种变化不影响整个相 频特性的大致形状。不同阻尼比ξ的相频特性如图520 所示。
振荡环节对数相频特性图
六二阶微分环节
一放大环节(比例环节)
放大环节的频率特性为:
其幅频特性是:
对数幅频特性为:
放大环节的对数幅频特性如图5-11所示,它是一条与角 频率ω无关且平行于横轴的直线,其纵坐标为20lgK。 当有n个放大环节串联时,即:
(5-62)
幅值的总分贝数为:
(5-63)
放大环节的相频特性是:
(5-64)
如图5-11所示,它是一条与角频率ω无 关且与ω轴重合的直线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
典型环节的B o d e图控制系统的开环频率特性目的:掌握开环Bode图的绘制根据Bode图确定最小相位系统的传递函数重点:开环Bode图的绘制、根据Bode图确定最小相位系统的传递函数1 开环伯德图手工作图的一般步骤:1)将开环传递函数表示为时间常数表达形式,计算各个典型环节的交接频率2)求20lgK的值,并明确积分环节的个数ν3)通过(1,20lgK)绘制斜率为-20vdB/dec 低频段4)随着频率增加,每遇到一个典型环节的交接频率,就改变一次斜率最小相位系统定义:递函数的零点、极点全部位于S 左半平面,同时又无纯滞后环节的系统称为最小相位系统。
否则就是非最小相位系统。
对数幅频特性与相频特性之间存在确定的对应关系。
对于一个最小相位系统,我们若知道了其幅频特性,它的相频特性也就唯一地确定了。
也就是说:只要知道其幅频特性,就能写出此最小相位系统所对应的传递函数,而无需再画出相频特性。
非最小相位系统高频时相角迟后大,起动性能差,响应缓慢。
对响应要求快的系统,不宜采用非最小相位元件。
Tf函数用来建立实部或复数传递函数模型或将状态方程、或零级增益模型转化成传递函数形式。
sys = tf(num,den)命令可以建立一个传递函数,其中分子和分母分别为num和den。
输出sys是储存传递函数数据的传递函数目标。
单输入单输出情况下,num和den是s的递减幂级数构成的实数或复数行向量。
这两个向量并不要求维数相同。
如h = tf([1 0],1)就明确定义了纯导数形式h(s)=s。
若要构建多输入多输出传递函数,要分别定义每一个单输入单输出系统的端口的分子与分母。
2 典型环节的伯德图绘制曲线在MATLAB中实现,利用下述的程序段:num=[b2 b1 b0];den=[1 a2 a1 a0];H=tf(num,den);bode(H)margin(H)hold on2.1 比例环节传递函数:()G s K=频率特性:()G j Kω=对数幅频特性:()20lgL j Kω=对数相频特性:()0ϕω=程序段:num=[0 10]; den=[0 1]; H=tf(num,den);bode(H)margin(H) hold on结论:放大环节的对数幅频特性是一条幅值为20lgK分贝,且平行于横轴的直线,相频特性是一条和横轴重合的直线。
K>1时,20lgK>0dB;K<1时,20lgK<0dB。
2.2 惯性环节(低通滤波特性)传递函数:1()1G ssτ=+频率特性:()()()jG j A eϕωωω=对数幅频特性:2()1()Lωτω=+对数相频特性:()arctanϕωτω=-绘制1()10.1G ss=+的Bode图程序段:num=[0 1]; den=[0.1 1];H=tf(num,den);bode(H)margin(H)hold on结论:惯性环节的对数幅频特性可以用在1ωτ= 处相交于0分贝的两条渐近直线来近似表示:当1ωτ=时,是一条0分贝的直线; 当1ωτ?时,是一条斜率为-20dB/dec 的直线。
惯性环节具有低通特性,对低频输入能精确地复现,而对高频输入要衰减,且产生相位迟后。
因此,它只能复现定常或缓慢变化的信号。
2.3 积分环节传递函数:1()G s sτ=频率特性:()()()j G j A e ϕωωω=对数幅频特性:1()20lg L j ωτω=对数相频特性:()2πϕω=-在同一坐标中绘制1()G s s =、1()0.1G s s=和1()0.01G s s=的Bode 图 num1=[0 1];den1=[1 1];H1=tf(num1,den1); bode(H1)margin(H1)hold on num1=[0 1];den1=[0.11];H1=tf(num1,den1);bode(H1)margin(H1) hold onnum1=[0 1];den1=[0.01 1];H1=tf(num1,den1);bode(H1)margin(H1) hold on蓝色的线为:1()G s s=,红色的线为:1()0.1G s s=紫色的线为:1()0.01G s s=结论:积分环节的对数幅频曲线是一条经过横轴上ω=1这一点,且斜率为-20的直线;相频与ω无关,值为-90°且平行于横轴的直线, 2.4 微分环节传递函数:()G s s τ=频率特性:()()()j G j A e ϕωωω= 对数幅频特性:()20lg L j ωτω= 对数相频特性:()2πϕω=在同一坐标中绘制()G s s =、()0.01G s s =和()0.001G s s =的Bode 图num1=[1 0];den1=[0 1];H1=tf(num1,den1); bode(H1) margin(H1) hold onnum1=[0.1 0];den1=[0 1]; H1=tf(num1,den1); bode(H1) margin(H1) hold onnum1=[0.01 0];den1=[0 1]; H1=tf(num1,den1); bode(H1) margin(H1) hold on蓝色的线为:()G s s =,红色的线为:()0.01G s s =,紫色的线为:()0.001G s s =结论:微分环节是积分环节的倒数,它们的曲线斜率和相位移也正好相差一个负号。
2.5 一阶比例微分环节 传递函数:()1G s s τ=+频率特性:()()()j G j A e ϕωωω=对数幅频特性:2()20lg 1()L j ωτω=+ 对数相频特性:()arctan ϕωτω=在同一坐标系中,绘制()1G s s =+,()10.1G s s =+和()10.01G s s =+的Bode 图。
num1=[1 1];den1=[0 1];H1=tf(num1,den1); bode(H1) margin(H1) hold onnum1=[0.1 1];den1=[0 1]; H1=tf(num1,den1); bode(H1) margin(H1) hold onnum1=[0.01 1];den1=[0 1]; H1=tf(num1,den1); bode(H1) margin(H1) hold on2.6 二阶比例微分环节传递函数:22()12G s s s ξττ=++ 频率特性:()()()j G j A e ϕωωω= 对数幅频特性:2222()20lg (2)(1)L j ωξτωτω=+-对数相频特性:222()arctan1ξτωϕωτω=-绘制22()12G s s s ξττ=++的Bode 图。
1)取0.707ξ=,1τ=则2()12G s s s =++2)取1ξ=,1τ=则2()12G s s s =++3)取0.2ξ=,1τ=则2()10.4G s s s =++4)取0.5ξ=,1τ=则2()11G s s s=++5)取0.1ξ=,1τ=则2()10.2G s s s=++在同一个标系中绘制以上曲线num1=[1 1.414 1];den1=[0 1]; H1=tf(num1,den1);bode(H1)margin(H1)hold onnum1=[1 2 1];den1=[0 1];H1=tf(num1,den1);bode(H1) margin(H1)hold onnum1=[1 0.4 1];den1=[0 1];H1=tf(num1,den1);bode(H1)margin(H1)hold onnum1=[1 1 1];den1=[0 1];H1=tf(num1,den1);bode(H1)margin(H1)hold onnum1=[1 0.2 1];den1=[0 1];H1=tf(num1,den1);bode(H1)margin(H1)hold on二阶微分环节Bode2.7 振荡环节传递函数:222()2nn nG ss sωωξω=++令1nτω=则:221()12G ss sξττ=++频率特性:()221()()12jG j A ejϕωωωξτωτω==+-对数幅频特性:2222()(2)(1)L jωξτωτω=+-对数相频特性:22222arctan11()2arctan11ξτωτωτωϕωξτωπτωτω⎧-≤⎪⎪-=⎨⎪-->⎪-⎩绘制221()12G ss sξττ=++的Bode图。
1)1)取0.707ξ=,1τ=则2()12G ss s++2)取1ξ=,1τ=则21()12G s s s =++3)取0.2ξ=,1τ=则21()10.4G s s s =++4)取0.5ξ=,1τ=则21()11G s s s =++5)取0.1ξ=,1τ=则21()10.2G s s s=++ 在同一个标系中绘制以上曲线num1=[0 1];den1=[1 1.414 1]; H1=tf(num1,den1); bode(H1) margin(H1) hold onnum1=[0 1];den1=[1 2 1]; H1=tf(num1,den1); bode(H1) margin(H1) hold onnum1=[0 1];den1=[1 0.4 1]; H1=tf(num1,den1); bode(H1) margin(H1) hold onnum1=[0 1];den1=[1 1 1]; H1=tf(num1,den1); bode(H1) margin(H1) hold onnum1=[0 1];den1=[1 0.2 1]; H1=tf(num1,den1); bode(H1) margin(H1) hold on3 对控制系统的一般要求开环对数频率特性的一般要求或者说怎样的Bode 图才算是比较理想的频率特性?(1)中频段以-20dB/dec 的斜率穿越零分贝 线,而且这一斜率占有足够的频带宽度,则系统的稳定性好。
(2)截止频率c ω越高,则系统的快速性越好。
(3)低频段的斜率陡,增益高,表示系统的稳态精度好(即稳态误差小)。
(4)高频段衰减得越快,即高频特性负分贝值低,说明系统抗高频噪声干扰的能力越强。
