解一元一次方程复习课讲解学习
一元一次方程(复习课教案)

一元一次方程(单元复习课)【复习目标】1.系统了解一元一次方程的知识框架;2.知道解一元一次方程的步骤,熟练掌握一元一次方程的解法;3.知道列一元一次方程解应用题的步骤,会列方程解应用题;4.在小组合作交流的过程中培养学生学习数学的习惯和复习的方法.【复习重点】形成一元一次方程章节知识框架图.【活动设计】活动一、一元一次方程知识复习1.(1)已知关于x 的方程150k x -+=是一元一次方程,则k = .(2)已知关于x 的方程()250k x -+=是一元一次方程,则k .(3)已知关于x 的方程()1250k k x --+=是一元一次方程,则k = .说明:本题引导学生回忆一元一次方程的概念.2.已知3x =是关于x 的方程8203x a -=的解,则a = . 说明:本题引导学生回忆方程的解的概念.3.下列运用等式的性质进行的变形,不正确...的是( ) A.如果a b =,那么55a b +=+ B.如果a b =,那么ma mb =C.如果a b =,那么a b c c = D.如果a b c c=,那么a b = 说明:本题引导学生回忆等式的性质. 4.若2260x y --=,则2635y x --的值为 .说明:本题引导学生回忆方程的解的概念.5.解方程:211135x x ++-=. 说明:本题引导学生回忆解一元一次方程的步骤,及每一步骤的注意点. 6.如果方程()()322212x x ---=-也是关于x 的方程203m x --=的解,求m 的值. 说明:本题引导学生回忆方程的解的概念.【课堂小结】(1)一元一次方程、方程的解的概念?等式的基本性质?(2)解一元一次方程的步骤有哪些?每一步骤变形的依据是什么?活动二、利用一元一次方程知识解决实际问题思考:我们在这一章中重点学习了哪几种类型的应用题?(1)引导学生回忆类型:调配问题、行程问题、工程问题、数字问题、方案问题、盈亏问题; (2)引导学生回忆典型问题中的数量关系:如行程问题中:速度、时间、路程的关系;工程问题中:工作效率、工作时间、工作总量的关系;工作效率、工作时间、工作人数、工作总量之间的关系.盈亏问题中:利润=售价—进价=进价×利润率折数售价=标价×10……解决下列问题:1.某种长方体包装盒的表面展开图如图所示,如果该长方体包装盒的长比宽多4cm,求这种长方体包装盒的体积.2.小王逛超市看到如下两个超市的促销信息:(1)当一次性购物标价总额是300元时,甲乙超市实际付款分别是多少?(2)当标价总额是多少时,甲、乙超市实付款一样?(3)小王两次到乙超市分别购物付款198元和466元,若他只去一次该超市购买同样多的商品,可以节省多少元?【课堂小结】列方程解应用题的步骤?教师总结:审.题,设.未知数,列.方程,解.方程,检验.,写出答.案.“审”是关键,“验”是保证,“设、列、解、答”是过程.附:板书设计:。
4.2解一元一次方程(6)(复习课)

把原方程化为ax=b(a≠0)的形式.其解法可分为两大步:一步是化为ax=b 的形式,再一步是解方程ax=b.在计算或变形时,要养成良好的学习习惯,注意书写格式的规范性,避免在去分母,去括号、移项时易犯的错误.解下列方程:1.17(2-3y)-5(12-y)=8(1-7y);2.5(z-4)-7(7-z)-9=12-3(9-z);3.3(x-7)-2[9-4(2-x)]=22;4.3{2x-1-[3(2x-1)+3]}=5;解方程2(x-2)-3(4x-1)=9(1-x).解:(怎样才能将所给方程转化为例1所示方程的形式呢?请学生回答) 去括号,得2x-4-12x+3=9-9x,移项,得2x-12x+9x=9+4-3,合并同类项,得-x=10,系数化1,得x=-10.2、解方程:(1)2x+5=25-8x;(2)8x-2=7x-2;(3)2x+3=11-6x;(4)3x-4+2x=4x-3;(5)10y+7=12-5-3y;(6)2.4x-9.8=1.4x-9.(7)3(y+4)12;(8)2-(1-z)=-2;(9)2(3y-4)+7(4-y)=4y;(10)4x-3(20-x)=6x-7(9-x);(11)3(2y+1)=2(1+y)+3(y+3).号)让学生把自己的做题过程到黑板上讲给同学听,注意纠正他的不规范表达和不严谨的地方,给全体学生做示范,加强推理能力的训练板书设计情境创设1、2、例1:………………例2:………………习题………………作业布置P102课后随笔在小结里提出解一元一次方程分为两大步,目的是进一步强调解一元一次方程的指导思想是化归思想.从而使学生明确最简方程是解一元一次方程的化归目标,而解一元一次方程的过程是,首先寻求所给方程与目标的差异,然后设法消除差异,直至达到化归目标,即化为最简方程,求出方程的解.这里化归的具体方法是去分母、去括号、移项、合并同类项等.这样处理,可使学生在解题时思路明确,有章可循。
一元一次方程(复习)

小结与复习
要点梳理
考点讲练
课堂小结
课后作业
目标导学1
1.解一元一次方程的一般步骤:
(1) 去分母:方程两边都乘各分母的最小公倍数, 别漏乘.
(2) 去括号:注意括号前的系数与符号. (3) 移项:把含有未知数的项移到方程的左边,常 . 数项移到方程右边,移项注意要改变符号 (4) 合并同类项:把方程化成 ax = b (a≠0)的形式.
(5) 系数化为1:方程两边同除以 x 的系数,得 x=m 的形式.
2. 列方程解决实际问题的一般步骤: 审:审清题意,分清题中的已知量、未知量. 设:设未知数,设其中某个未知量为x. 列:根据题意寻找等量关系列方程. 解:解方程. 验:检验方程的解是否符合题意. 答:写出答案 (包括单位).
审题是基础,找 等量关系是关键.
(2) 工程问题中基本量之间的关系:
① 工作量 = 工作效率×工作时间; ② 合作的工作效率 = 工作效率之和; ③ 工作总量 = 各部分工作量之和 = 合作的工作效
率×工作时间; ④ 在没有具体数值的情况下,通常把工作总量看
做1.
例2 一项工作,甲单独做8天完成,乙单独做12天完 成,丙单独做24天完成.现甲、乙合作3天后,甲 因有事离去,由乙、丙合作,则乙、丙还要几天才 能完成这项工作?
10
解:设最多可以打 x 折,根据题意得
5001 40% x 500112%.
10 解得 x = 8.
答:广告上可写出最多打 8 折.
针对训练
7. 一家商店将某种商品按进价提高40%后标价,节假 日期间又以标价打八折销售,结果这种商品每件 仍可获利24元,问这件商品的进价是多少元?
解:设这件商品的进价是 x 元,根据题意得
北师大版七年级上册数学《求解一元一次方程》一元一次方程说课教学复习课件

知2-练
1 已知关于x的方程3a-x= x +3的解为2,则式子a2 2
-2a+1的值是_____1___.
2 方程3x-4=3-2x的解答过程的正确顺序是( C )
①合并同类项,得5x=7;②移项,得3x+2x=3+4;
③系数化为1,得x= 7 . 5
A.①②③
B.③②①
C.②①③
总结
知1-讲
移项与交换律的根本区别是移项时移动的 项要跨越等号,并且一定要记住移项要变号.
(来自《点拨》)
知1-练
1 把方程3y-6=y+8变形为3y-y=8+6,这种变形 叫做___移__项___,依据是__等__式__的__性__质__1__.
2 解方程时,移项法则的依据是( C )
A.加法交换律
数的系数.
解:(1)系数化为1,得x=-3.
(2)系数化为1,得x=-2.
(3)系数化为1,得x=-6.
(来自《点拨》)
总结
知1-讲
将系数化为1是解一元一次方程的最后一步, 解答时注意两点:一是未知数的系数是1而不是 “-1”;二是未知数的系数是分数时,可以将方 程两边同时乘以未知数系数的倒数.
(来自《点拨》)
C)
A.x=20
B.x=40
C.x=60
D.x=80
知3-练
(来自《典中点》)
2 下面解方程的结果正确的是( D )
A.方程4=3x-4x的解为x=4
B.方程 3 x= 1 的解为x=2 23
CD..方方程程312-=48=x的1解x的为x解=为x14=-9 3
知3-练
(来自《典中点》)
知3-讲
第五章 一元一次方程
5.2 求解一元一次方程
一元一次方程复习课教案

一元一次方程复习课教案一、教学目标1. 知识与技能:(1)掌握一元一次方程的定义及解法。
(2)能够运用一元一次方程解决实际问题。
(3)熟练运用解方程的方法求解方程。
2. 过程与方法:(1)通过复习,巩固一元一次方程的基本概念和解法。
(2)培养学生的逻辑思维能力和解决问题的能力。
(3)学会检验解的方法,确保解的正确性。
3. 情感态度与价值观:(1)培养学生对数学的兴趣和自信心。
(2)培养学生积极主动探索问题的习惯。
二、教学重点与难点1. 教学重点:(1)一元一次方程的定义及解法。
(2)运用一元一次方程解决实际问题。
2. 教学难点:(1)解一元一次方程的步骤和技巧。
(2)检验解的方法。
三、教学准备1. 教师准备:(1)复习相关的一元一次方程资料。
(2)设计具有代表性的练习题和实际问题。
2. 学生准备:(1)回顾一元一次方程的基本概念和解法。
(2)准备笔记本,记录复习内容。
四、教学过程1. 导入新课(1)回顾一元一次方程的基本概念:未知数、系数、常数、方程等。
(2)引导学生回顾解一元一次方程的步骤:去分母、去括号、移项、合并同类项、化系数为1。
2. 知识梳理(1)讲解一元一次方程的定义及解法。
(2)通过例题,展示解一元一次方程的步骤和技巧。
3. 课堂练习(1)让学生独立完成练习题,检验解的方法。
(2)引导学生运用一元一次方程解决实际问题。
4. 课堂讨论(1)让学生分享解题心得和经验。
(2)讨论解一元一次方程时可能遇到的问题和解决方法。
5. 总结与反思(1)总结一元一次方程的基本概念和解法。
(2)强调检验解的方法和重要性。
五、课后作业1. 巩固练习:(1)完成课后练习题,巩固一元一次方程的解法。
(2)挑选几道实际问题,运用一元一次方程解决。
2. 拓展提高:(1)研究一元一次方程在实际生活中的应用。
(2)探索解一元一次方程的其它方法。
六、教学评价1. 课堂表现评价:观察学生在课堂上的参与程度、提问回答情况以及合作交流的表现,评价学生的学习态度和合作精神。
一元一次方程复习课教案

一元一次方程复习课教案一、教学目标1. 知识与技能:(1)理解一元一次方程的概念及其基本性质。
(2)掌握一元一次方程的解法,包括代入法、加减法、乘除法等。
(3)能够应用一元一次方程解决实际问题。
2. 过程与方法:(1)通过复习,加深对一元一次方程的理解,提高解题能力。
(2)培养学生运用一元一次方程解决实际问题的能力。
3. 情感态度与价值观:(2)培养学生勇于探索、积极思考的精神。
二、教学内容1. 一元一次方程的概念及基本性质。
2. 一元一次方程的解法:代入法、加减法、乘除法。
3. 应用一元一次方程解决实际问题。
三、教学重点与难点1. 教学重点:(1)一元一次方程的概念及其基本性质。
(2)一元一次方程的解法。
(3)应用一元一次方程解决实际问题。
2. 教学难点:(1)一元一次方程的解法。
(2)运用一元一次方程解决实际问题。
四、教学过程1. 复习导入:(1)回顾一元一次方程的概念及其基本性质。
(2)引导学生回忆一元一次方程的解法。
2. 课堂讲解:(1)讲解一元一次方程的解法,包括代入法、加减法、乘除法。
(2)举例演示解题过程,引导学生跟随步骤进行解题。
3. 课堂练习:(1)布置练习题,让学生独立完成。
(2)选取部分学生的作业进行点评,纠正错误,解答疑问。
4. 应用拓展:(1)给出实际问题,引导学生运用一元一次方程进行解决。
(2)分小组讨论,分享解题思路和方法。
五、课后作业1. 复习一元一次方程的概念及其基本性质。
2. 巩固一元一次方程的解法,包括代入法、加减法、乘除法。
3. 运用一元一次方程解决实际问题。
4. 总结本节课的学习内容,思考还有什么问题需要进一步解决。
六、教学评估1. 课堂讲解评估:观察学生对一元一次方程解法的理解和掌握程度,以及能否熟练运用解法解决实际问题。
2. 课堂练习评估:检查学生的作业完成情况,评估其对一元一次方程解法的应用能力。
3. 应用拓展评估:通过小组讨论和分享,评估学生运用一元一次方程解决实际问题的能力和团队合作精神。
人教版七年级上册第三章一元一次方程全章小结复习说课稿

(二)新知讲授
在新知讲授阶段,我将逐步呈现知识点,引导学生深入理解:
1.理论讲解:以简明扼要的语言讲解一元一次方程的定义、一般形式,让学生明确学习目标。
2.案例分析:通过具体实例,演示一元一次方程的解法,让学生在实际操作中理解并掌握解法步骤。
2.生生互动:通过小组合作学习,学生之间将进行讨论、交流和分工合作,共同解决实际问题。在小组活动中,我会设置明确的任务和评价标准,确保每个学生都能参与到互动中来。
3.课堂讨论:组织全班范围的讨论,让学生分享各自小组的解题过程和答案,鼓励他们相互提问、质疑和补充,以提高课堂氛围和学生思维的深度。
四、教学过程设计
2.情境教学法:将一元一次方程的知识点融入到生活情境中,让学生在具体情境中感受数学的应用价值。这种方法的理论依据是情境学习理论,认为知识需要在真实情境中通过活动和实践来获得。
3.分组合作学习法:将学生分成小组,鼓励他们在小组内进行讨论、交流和合作解决问题。这种教学方法基于社会建构主义理论,强调学习是一个社会互动的过程。
3.教师评价:针对学生的表现,给予积极的评价和鼓励,同时指出需要改进的地方,并提供具体的建议。
(五)作业布置
课后作业布置如下:
1.基础作业:布置一些基础的一元一次方程题目,目的是巩固课堂所学知识,提高解题技能。
2.提高作业:设计一些综合性的题目,让学生运用所学知识解决实际问题,培养他们的应用能力和创新思维。
4.游戏化学习:设计一些与一元一次方程相关的数学游戏,让学生在轻松愉快的氛围中学习,提高他们的学习积极性。
三、教学方法与手段
(一)教学策略
在本节课中,我将采用问题驱动法、情境教学法和分组合作学习法为主要教学方法。
解一元一次方程(复习课)
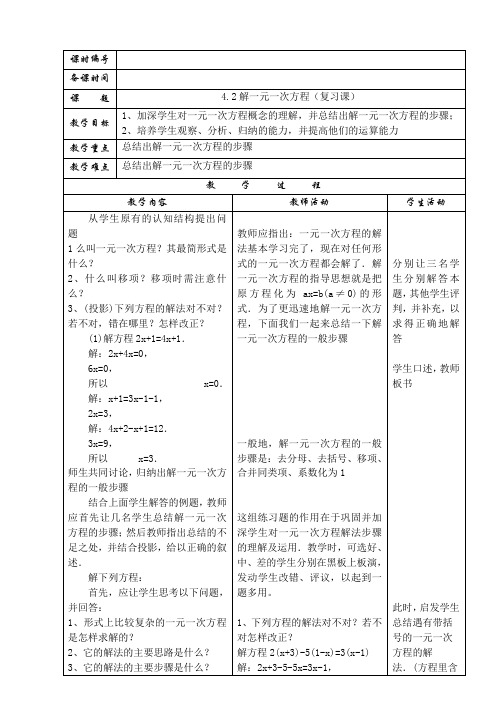
例 7 解方程
x 1 4 x 1 2 3
例 8 解方程
1 1 1 (2x-5)= (x-3)3 4 12
去分母时须注意: 1、 确定各分母的最小公倍数; 2、不要漏乘没有分母的项;
解:两边都乘以 6,得 3(x+1)=8x+6 去括号,得
3、分数线有括号作用,去掉分母后, 若分子是多项式,要加括号,视多项式 为一整体.建议进行专项训练,如源自教学目标 教学重点 教学难点
分别让三名学 生分别解答本 题, 其他学生评 判,并补充,以 求得正确地解 答 学生口述, 教师 板书
一般地,解一元一次方程的一般 步骤是:去分母、去括号、移项、 合并同类项、系数化为 1
这组练习题的作用在于巩固并加 深学生对一元一次方程解法步骤 的理解及运用.教学时,可选好、 中、差的学生分别在黑板上板演, 发动学生改错、评议,以起到一 题多用。 1、下列方程的解法对不对?若不 对怎样改正? 解方程 2(x+3)-5(1-x)=3(x-1) 解:2x+3-5-5x=3x-1, 此时, 启发学生 总结遇有带括 号的一元一次 方程的解 法.(方程里含
课时编号 备课时间 课 题 4.2 解一元一次方程(复习课) 1、加深学生对一元一次方程概念的理解,并总结出解一元一次方程的步骤; 2、培养学生观察、分析、归纳的能力,并提高他们的运算能力 总结出解一元一次方程的步骤 总结出解一元一次方程的步骤 教 教学内容 从学生原有的认知结构提出问 题 1 么叫一元一次方程?其最简形式是 什么? 2、什么叫移项?移项时需注意什 么? 3、(投影)下列方程的解法对不对? 若不对,错在哪里?怎样改正? (1)解方程 2x+1=4x+1. 解:2x+4x=0, 6x=0, 所以 x=0. 解:x+1=3x-1-1, 2x=3, 解:4x+2-x+1=12. 3x=9, 所以 x=3. 师生共同讨论, 归纳出解一元一次方 程的一般步骤 结合上面学生解答的例题, 教师 应首先让几名学生总结解一元一次 方程的步骤; 然后教师指出总结的不 足之处,并结合投影,给以正确的叙 述. 解下列方程: 首先,应让学生思考以下问题, 并回答: 1、形式上比较复杂的一元一次方程 是怎样求解的? 2、它的解法的主要思路是什么? 3、它的解法的主要步骤是什么? 教师应指出:一元一次方程的解 法基本学习完了,现在对任何形 式的一元一次方程都会解了.解 一元一次方程的指导思想就是把 原 方 程 化 为 ax=b(a ≠ 0) 的 形 式.为了更迅速地解一元一次方 程,下面我们一起来总结一下解 一元一次方程的一般步骤 学 过 程 教师活动 学生活动
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(5).等式的性质:等式的两边同时乘以或除以 一个不等于0的数,结果仍是 等式.
(6).分数的性质:分数的分子、分母同 时 乘以或除以同一个不,等分于数0的的值数不变.
(7). q ( mq 用“>”、“<”或“=”填空).
p = mp m 0,
2.解一元一次方程的一般步骤: 一.去分母 二.去括号 三.移项 四.合并同类项 五.系数化为1
3.将方程 x2 的2x两3边同时乘以:
46
可得到: 3(x2)2 .(x3)
, 12
4.(1)将方程 512去x 分0母,
2
得: 1 0(12x)0
.
(2)将方程 2x1去x分1母1,
10 4
得: 2 (2 x 1 ) 5 (x 1 )20
5.将方程 0.3x10.2x的系0.1数化1为整
0.02 0.5
数,有
30x1002x11
2
5
6.解下列一元一次方程:
(1) 2x53x21
6
8
(2) 0.2x0.10.0x30.02 2
0.3
0.02
7.应用:
当x等于什么数时,代数式3(3x-2)的值 比 4 x 1 的值的2倍小6?
2
解一元一次方程复习课
一 方程
1.方程的概念
方程是含有未知数的等式.
2.方程的解 方程的解是使方程的左右两边相等的未知 数的取值.
3.一元一次方程的概念 一元一次方程是只含有一个未知数,且未 知数的次数是1,各项均为整式的方程.
4.下列方程中,哪些是一元一次方程?不 是的说明理由.
(1) x2y32x1×
课堂作业
课本:P115 第1题 :(6) 、(8) 第4题
(2) 5x32x10√
(3) 3x 1 x1 ×
x6 关m 于x的一元一次方程,
(1)求m的值; (2)求
的(值m. 3)2009
解: (1) 由题意得: 2m31
m 2
(2) (m 3)2009(23)2009 (1)20091
练习:1.关于x的方程(k+2)x2+4kx-5k=0是
