ch3-3 循环
ch3-3 函数极限存在的条件

设数列{xn } U ( x0 ; )且 lim xn x0 . n 则由定义知,对上述 0, 存在N 0, 使得当n, m N时有xn , xm U ( x0 ; ),
从而有 f ( xn ) f ( xm ) .
于是, 按数列的柯西收敛准则, 数列{ f ( xn )}的极限存在, 记为A, 即 lim f ( xn ) A.
n
' '' ' 或找到两个都以x0为极限的数列{xn }{xn }, 使 lim f ( xn )与 n '' lim f ( xn )都存在而不相等,则 lim f ( x)不存在. n x x0
归结原则可用来证明函数极限不存在和利用 已知函数的极限求数列极限.
例1
证 明 极 限 i msi n l
对于任给 0, 存在正数 ( ' ), 使得对任何x' , x '' U 0 ( x0 ; ) 都有 | f ( x ' ) f ( x '' ) | .
证 必 要 性 设 l i m f ( x ) A, 则 对 任 给 的 0, 存 在
x x0
正 数( ), 使 得 对 任 何 U ( x0 ; )有 f ( x ) A x
相应于数列极限的单调有界定理,单侧极限也有相应
的定理,以x x0 为例叙述并证明如下:
0 定理3.10(修改) 设f 为定义在U ( x0 )上的递增(减)有下(上)界
函数, 则右极限 lim f ( x)存在.
x x0
证 设f 在U ( x0 )上递增有下界,
xU ( x0 )
三羧酸

,而且会引起硫酯键水解的天门冬氨酸残基,只有在形成柠檬酰CoA后才会
接近活性中心。
柠檬酸合成酶是一个调控酶。酶活性在体外受ATP, NADH,
琥珀酰CoA和长链脂肪酸的抑制。它催化的反应是可调控的限
速步骤。
氟乙酰CoA可与柠檬酸合成酶反应形成氟柠檬酸,因它可抑制 酶的下一步反应,所以称这步反应为致死合成。
GDP+Pi
氧化脱羧
CO2, [2H]
丁二酸 琥珀酸
GTP CO2, [2H]
2H
α- 酮戊二酸 α-酮戊二酸 琥珀酰辅酶A 琥珀酰辅酶A 氧化脱羧 氧化脱羧
底物水平磷酸化
底物水平磷酸化
图3-3. 三羧酸循环的反应
丙酮酸到乙酰辅酶A的总反应
0’
总反应是高度放能的,在细胞中是不可逆的。 丙酮酸氧化脱羧形成乙酰CoA的反应是在真核细胞的线粒体基质中进行的, 这是一个连接酵解和三羧酸循环的中心环节。 这个反应由丙酮酸脱氢酶复合体催化。丙酮酸脱氢酶复合体包括3个不同的 酶和5种不同的辅酶,包括焦磷酸硫胺素(TPP),硫辛酸,FAD,NAD+ 和 CoA。
三种不同的酶。
dihydrolipoyl transacetylase(E2) dihydrolipoyl dehydrogenase(E3)
丙酮酸脱氢酶的作用方式:
1.丙酮酸脱羧形成羟乙基-TPP 丙酮酸与 丙酮酸脱羧酶(E1) 上的TPP连接,TPP的噻唑环中氮 和硫原子之间的碳原子的氢比大多数有=CH-基的氢更容易解 离,使该碳原子形成反应性很强的负碳离子,因而可亲核攻 击丙酮酸的羰基碳原子形成加成物。TPP的噻唑环上的N带有
释是丙酮酸氧化需消耗草酰乙酸,合成柠檬酸,若加入丙二 酸,由于不能再生成草酰乙酸,所以丙酮酸氧化被抑制。
ch3-3自旋和轨道相互作用以及能级精细结构

一、自旋-轨道耦合能
原子内部由于带电粒子的运动,会产生磁场即原子的内磁场。 电子处在这内磁场中,其自旋磁距与磁场要发生相互作用,由 此引起能级的分裂。
自旋-轨道相互作用是磁相互作用,这种作用较弱,只使原子能 级发生细微的改变,而产生精细结构。
具有自旋磁距的电子处在由于轨道运动而感受的磁场中(电磁 理论,一个磁性物体在磁场中的能量是cos),附加自旋的 能量为:
1
电子的自旋量子数s ,单电子S只能有两个取向。
2
S L可以有两个值,对应能级分裂为两层结构。对于
轨道角动量量子数l 0的原子态E 0,能级不分裂
二、总角动量和原子磁距
1. 总角动量
原子中的电子具有轨道角动量L和自旋角动量 S,
如不考虑自旋-轨道相互作用,它们都是守恒的,
L、S 的大小和 z 轴分量都有确定实值。
2me
2mN
总磁矩:只需要考虑轨道磁矩和自旋磁矩
l
gl
B
L
s
gs
B
S
单电子原子的有效总磁矩
磁矩的方向与角动量的方向相反
J
轨道和自旋角动量分别绕总角动量旋进,
相应的磁矩也绕总角动量旋进
L
轨道磁矩和自旋磁矩合成为一个总磁矩
e
=l
s =
2me
L 2S
S
与j不平行
//
其变化与L有关,这样S
不再具有确定值了
z
自旋-轨道相互作用是原子内部的作用力,的反作用力矩
dL
则作用L上: (r)S L
dt
同理:L变化与S有关。总之:由于自旋-轨道相互作用
使L和S耦合起来,以至每个取向都与另一个相关
ch3-3焊缝例题

翼缘焊缝的最大应力: 翼缘焊缝的最大应力:
σ f1
M = Iw h 127 .8 × 10 6 ⋅ = × 205 .6 = 138 N / mm 2 ≤ β f f fw = 1.22 × 160 = 195 kN 2 19029 × 10 4
腹板焊缝中由于弯矩M引起的最大应力为 腹板焊缝中由于弯矩 引起的最大应力为
剪力V在 点产生的应力为 点产生的应力为: 剪力 在A点产生的应力为:
τ Vy
V 217 × 10 3 = = = 38.8 N / mm 2 ∑ he lW 0.7 × 8 × (2 × 300 + 400)
因此: 因此:
σ f = τ Ty + τ Vy = 106 + 38.8 = 144.8 N / mm 2
角焊缝计算问题归纳 (2)设计型问题
①特点:已知荷载情况和连接节点构造情况,要求完成连 特点:已知荷载情况和连接节点构造情况, 接节点设计。 接节点设计。 ②求解方法 a.确定连接方式和焊缝布置方式。 .确定连接方式和焊缝布置方式。 b.确定焊缝受力特征,可能的危险点位置。 .确定焊缝受力特征,可能的危险点位置。 c.依据构造条件初选 f,由相应计算公式反求焊缝长度 w。 .依据构造条件初选h 由相应计算公式反求焊缝长度l 或者根据问题已定出的焊缝长度,由相应公式反求h 或者根据问题已定出的焊缝长度,由相应公式反求 f。 d. 根据求出的 w或hf.确定设计采用的 w或hf值。 根据求出的l 确定设计采用的l e.验算所用lw或hf是否满足构造条件。若不满足,重选 f或 .验算所用 是否满足构造条件。若不满足,重选h lw , 重复上述过程直至满足。 重复上述过程直至满足。
三面围焊
宽度b=240mm,则 , 宽度
热质交换pptch3第3章 固液相变原理和应用

1.1沸腾换热现象及分析 沸腾换热现象及分析 液界面上发生的蒸发, 固-液界面上发生的蒸发,称为沸腾,当表面 s超过对应 液界面上发生的蒸发 称为沸腾,当表面T 液体压力下的饱和温度t 发生沸腾, 液体压力下的饱和温度 s时,发生沸腾, s = h(t w − t s ) = h∆t q 热量由固体表面传向液体。 热量由固体表面传向液体。 1.沸腾过程的特点:有蒸汽泡形成,长大后脱离表面。 沸腾过程的特点: 沸腾过程的特点 有蒸汽泡形成,长大后脱离表面。 2.分类: 分类: 分类 (1)按沸腾空间分为池内沸腾 大容器沸腾 和强迫对流沸 按沸腾空间分为池内沸腾(or大容器沸腾 按沸腾空间分为池内沸腾 大容器沸腾)和强迫对流沸 腾; 池内沸腾(or大容器沸腾 大容器沸腾)指加热面沉浸在具有自由表面的 池内沸腾 大容器沸腾 指加热面沉浸在具有自由表面的 液体中发生的沸腾, 液体中发生的沸腾,液体的运动仅由自然对流或气泡的搅 动而引起的。 动而引起的。
18
3.3 一维凝固和融解问题及其分析方法 自学 一维凝固和融解问题及其分析方法(自学 自学) 3.3.1 常见一维相变传热问题 3.3.2 求解方法及举例 3.3.3多维相变传热问题 多维相变传热问题 3.3.4考虑固、液密度差的简单区域中的相变传热 考虑固、 考虑固 3.3.5相变潜热贮能系统的贮、传热模型和热性能 相变潜热贮能系统的贮、 相变潜热贮能系统的贮 分析
Rmin = pv − pl
式中: 汽泡内压力, 气泡外压力, 式中:Pv:汽泡内压力,Pl:气泡外压力,pl≈ps; γ:单位长度汽液界面的表面张力。 :单位长度汽液界面的表面张力。 汽泡最小半径R≥Rmin,否则汽泡瓦解。 汽泡最小半径 ,否则汽泡瓦解。
CH3-插值法与最小二乘法—3
待定函数
(x x0 )(x x1)(x xn )
Rn (x) f (x) Pn (x) K (x)n1(x)
5
f (x) Pn (x) K (x)n1(x) 0
(3)
引入辅助函数(为了确定K (x))
(t) f (t) Pn (t) K (x)n1(t)
(4)
若x为(a,b)上的一个固定的点,且x xi (i 0,1,..., n). 那么x和xi (i 0,1,..., n)代入上式有:
例
设函数
f
(
x)
1
1 x
2(x
[5,5]),
将[5,5]n等分,
取n 1个节点:
xi
5 ih(h
10 n
,i
0,1,, n)
试就n 2,4,6,8,10作f (x)的n次Lagrange插值多项
式,并作图比较.
解:
yi
f (xi )
1 1 xi2
作n次Lagrange插值多项式:
Ln(x)
3
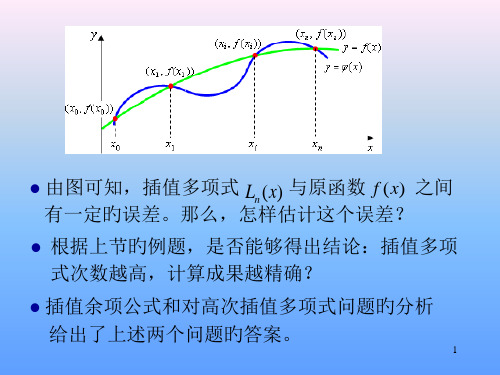
这就意味着插值多项式存在着截断误差,而一般情况 下f(x)旳精确值都是未知旳,那么我们该怎样估计这 个截断误差呢?
定理:设 f (x)在含节点 xi (i 0,1,..., n) 旳区间[a,b]上n+1
次可微,Pn (x) 是有关给定旳n+1个节点旳n次插值多项
式,则对于 x [a,b],存在与x有关旳 (a,b),使得
n 1阶导数为零,即 :
(n1) ( ) 0
(t) f (t) Pn (t) K (x)n1(t)
因为 所以
(n1) (t)
f
(
n1)
(t
)
三磷酸循环
下面是我演示文稿的大纲部分,希望能帮到你。
抱歉,文字有限,只有三羧酸循环部分,如果还需要光合作用的请Hi我。
第三章柠檬酸循环EMP途径并不是高等生物获能的主要途径。
首先,EMP途径只净产生了2个ATP,只释放出了葡萄糖分子5%左右的能量;而且,EMP途径的产物丙酮酸任然具有很高的自由能,可以继续氧化继而释放出来。
柠檬酸循环是存在于线粒体(原核生物细胞质)中的一种有机物循环途径,其主要功能是将丙酮酸的三个碳原子逐步裂解掉,最终生成CO2和H2O,生成ATP,并将NAD+或FAD还原,以完成能量的释放和转换。
在了解柠檬酸循环之前,有必要知道这几点。
1.柠檬酸循环可以简单的概括为C4+C2-C2=C4,柠檬酸循环的起始是四碳单位的草酰乙酸,经过一轮循环,草酰乙酸每次循环接受一个二碳单位,释放两次CO2。
2.柠檬酸循环是糖类、脂肪酸、氨基酸等燃料分子氧化的共同途径,因为它们大都是以二碳单位进入柠檬酸循环的。
3.柠檬酸循环虽然将丙酮酸彻底氧化成了CO2和H2O,但是,释放的全部能量只有一部分转化为了ATP,更多的能量将在氧化磷酸化中转化为ATP。
章节概要第一节柠檬酸循环概述第二节柠檬酸循环的准备阶段第三节柠檬酸循环的循环阶段第四节柠檬酸循环的综合评价第五节柠檬酸循环中产物的讨论第六节柠檬酸循环的调控第一节柠檬酸循环概述柠檬酸循环(Citric acid cycle),也称为三羧酸循环(TriCarboxylic Acid cycle,TCA),Krebs循环。
草酰乙酸接受一个二碳单位(通常是二碳烃基)并将从二碳单位的C-C键处裂解,释放出二氧化碳和水,期间释放出的能量一部分转移给ADP,一部分转移给辅酶。
这个过程,就是柠檬酸循环。
柠檬酸循环是生物体内最重要的物质循环,理解柠檬酸循环需要结合脂肪酸、氨基酸的代谢,这里不做详述。
只是要再强调一点,柠檬酸循环得以实现的驱动力是二碳单位的不断进入以及酶、辅酶的不断供给。
环烯烃教学
3
2、多环烯烃
桥环烃
编号原则:从较大环中的桥头碳原子开始,从大环到小环编号, 以双键碳原子编号最小为基本原则。
命名:根据成环碳原子的总数称为“二环[n1.n2.n3]某烯”,
在方括号中标出各碳环中除桥头碳原子以外的碳原子数目(大的 在先,小的排后,最后是桥上的),其它同普通烯烃的命名。
3
2 19 8
主
次
CH3
HCl
CH3
Cl
Cl (主)1,4-加成
1,2-加成
6
2、环烯烃的加成反应
中等和大环烯烃能发生与烯类似的加成反 应,可发生加H2,加HX,加H2SO4等反应。
Br
+ Br2 CCl4
环戊烷 CH3
Br 反-1,2-二溴环戊烷
H CH3 HI
(符合马氏规则)
7
3、环烯烃的氧化Biblioteka 应环烯烃易被KMnO4和O2等氧化剂氧化,双键 断裂生成开链的氧化产物。
6 54 1
7
2
83
螺[3.4]-1-辛烯
6
5 4
1
7
2
83
8-甲基螺[3.4]-5-辛烯
5
二、环烯烃的化学性质
1、普通环烯烃的通性
环烯烃具有烯烃的通性。
CH3 CH3
CH3
Br Br2/CCl4
Br
O3
H2O/Zn
O
CH3-C-CH2CH2CH2CHO
500℃ 1mol Cl2
CH3 Cl
Cl
CH3
KMnO4 CH3 CHCH2COOH
CH2CH2COOH
4-甲基环己烯
3-甲基- 1,6-己二酸
O3
Suzuki反应-药明康德
经典化学合成反应标准操作Suzuki 反应编者:刘德军、武伟药明康德新药开发有限公司化学合成部目录1 前言 (3)1.1 Suzuki反应的通式 (3)1.2 Suzuki反应的机理 (3)1.3 Suzuki反应的特点及研究方向 (4)2 有机硼试剂的合成 (4)2.1 通过金属有机试剂制备单取代芳基硼酸 (4)2.1.1 通过Grinard试剂制备单取代芳基硼酸示例 (4)2.1.2 通过有机锂试剂制备单取代芳基硼酸示例 (5)2.2 通过二硼烷频哪酯制备芳基硼酸酯 (6)2.2.1 通过二硼烷频哪酯制备芳基硼酸酯示例(一) (9)2.2.2 通过二硼烷频哪酯制备芳基硼酸酯示例(二) (10)2.2.3 通过芳基硼酸转化为芳基硼酸酯 (10)2.3 烯基硼酸酯的制备 (10)2.4 烷基硼酸酯的制备 (10)3 催化剂的制备 (11)3.1 Pd(PPh3)4的制备 (11)3.2 Pd(PPh3)2Cl2的制备 (12)3.3 Pd(dppf)Cl2的制备 (12)4Suzuki偶联的应用 (12)4.1 普通的芳卤和芳基硼酸的Suzuki偶联 (13)4.1.1 Pd(PPh3)4-Na2CO3-DME-H2O 体系Suzuki偶联反应示例 (14)4.2 大位阻芳基硼酸参与Suzuki偶联反应 (14)4.3 含敏感功能团的芳基硼酸(酯)参与Suzuki偶联反应 (15)4.3.1 芳基硼酸频哪酯和芳基卤代物的Suzuki偶联 (16)4.3.2 带着酯基底物的Suzuki偶联反应示例(一) (16)4.3.3 带着酯基底物的Suzuki偶联反应示例(二) (17)4.4 杂环芳基硼酸参与Suzuki偶联反应 (17)4.5烷基硼酸参与Suzuki偶联反应 (18)4.6烯基硼酸参与Suzuki偶联反应 (19)4.7 Triflate参与Suzuki偶联反应 (19)4.7.1芳基的三氟甲基磺酸酯与芳基硼酸偶联示例 (20)4.7.2 芳基的Triflate与芳基硼酸偶联示例 (20)4.8 芳基氯参与Suzuki偶联反应 (21)4.8.1钯催化下芳基氯参与Suzuki偶联反应示例(一) (21)4.8.2钯催化下芳基氯参与Suzuki偶联反应示例(二) (22)4.9 镍催化体系用于Suzuki偶联反应 (22)4.9.1 NiCl2(dppf)和n-BuLi催化下芳基氯参与Suzuki偶联反应示例 (22)4.10 其他方法 (23)4.10.1 直接Pd/C用于Suzuki偶联反应示例 (23)4.10.2 直接Pd(OAc)2用于Suzuki偶联反应示例 (23)1 前言1.1 Suzuki 反应的通式在钯催化下,有机硼化合物与有机卤素化合物进行偶联反应,这就提供了一类常用和有效的合成碳-碳键化合物的方法,我们称之为Suzuki 偶联反应,或Suzuki-Miyaura 偶联反应。
3-3 醛、酮 (教学课件)——高中化学人教版(2019)选择性必修三
【想一想】 1. 如何配置银氨溶液?写出此过程中涉及到的化学方程式
取1 mLቤተ መጻሕፍቲ ባይዱ2%的AgNO3溶液于洁净试管中,一边振荡试管,一边逐滴滴入 2%的稀氨水,至生成的沉淀恰好完全溶解,制得银氨溶液。
AgNO3+NH3·H2O=AgOH↓+NH4NO3 AgOH+2NH3·H2O=Ag(NH3)2OH+2H2O
【学习任务一】认识常见的醛、酮
甲醛:无色有强烈刺激性气味的气体,易溶于水 防腐杀菌剂(消毒、浸制标本)(水溶液称福尔马林);制药,香料,染料。 注意:儿童房甲醛超标易诱发儿童白血病
苯甲醛:最简单的芳香醛,是一种有苦杏仁味的无色液体,制造染料、香料及药物 的重要原料
乙醛:无色有强烈刺激性气味的液体,密度比水小,易挥发,容易燃烧,能与水、乙醇 等互溶。
【想一想】 2. 实验过程中有些同学没有得到光亮的银镜,可能的原因有哪些?
①试管内壁必须光滑、洁净; ②实验的银氨溶液应现配现用; ③必须用水浴加热,不可用酒精灯直接加热; ④加热时不能振荡和摇动试管。 3. 试管内部光亮的银镜,如何除去?
可用稀硝酸浸泡,再用水洗除去。
(2)与新制Cu(OH)2悬浊液反应
②与银氨溶液反应的化学方程式
CH3CHO+2Ag(NH3)2OH 水浴加热 CH3COONH4+2Ag↓+3NH3+H2O 1. 该反应可以用来检验分子中是否存在醛基 2. 工业上可用银镜反应对玻璃涂银制镜和制保温瓶瓶胆。 【想一想】能发生银镜反应的一定是醛类物质吗? 还原性糖(葡萄糖)、甲酸、甲酸某酯
丙酮的物理性质:无色透明液体,沸点56.2℃,易挥发,能与水、乙醇等互溶
【学习任务二】认识醛、酮的化学性质
1.请分析醛的结构特点,①分析含有何种官能团,是否含有不饱和键? ②找出极性键的位置,根据基团的相互影响,思考哪些极性键容易断裂?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
"time="<<time<<endl; }
【例】求100以内的奇数、偶数之和 分析: 设:●偶数和放在even变量中 #include <iostream.h> void main( ) even=2+4+6+…+100 {int n=1,odd=0,even=0 ; ●奇数和放在odd变量中 while (n<100) odd=1+3+5+…+99 {odd+=n; ●计数器n初值为1 even+=n+1; n+=2; ●循环体中:每次n=n+2 } 故 odd=odd+n even=even+(n+1) cout<< "odd和="<<odd<<",even和
t=n!
【例】编程序.有一足够大的纸厚0.15mm,问对折多少次后其厚度超 过珠穆朗玛峰 h=0.15,time=0 #include <iostream.h> 分析: h<=8848000 void main( ) 珠峰高8848m h=2*h {int time=0 ; 纸厚:h0=0.15mm float h=0.15; time++ 对折:h1=2* h0 while (h<=8848000) h2=2*h1=2*(2*h0) 输出h,time …… { h*=2; hn=2*hn-1 time++; } 对折一次计数器time cout<< "hight="<<h<<" " 加1,直到h>8848000为止
3. y是相邻两次迭代的差,可用 |y|<(用户提供)作迭代终止条件。
用do-while语句编写的程序如下: #include<cmath> #include<cmath> using namespace std; using namespace std; N-S图如下: main( ) main( ) 输入eps(即) { float x=1.5,y,y1,eps; { float x=1.5,y,y1,eps; cout<<"输入 :"; 用while做,程 cout<<"输入 :"; x=1.5 序如何改? cin>>eps; cin>>eps; y =((2*x-4)*x+3)*x-6 do y=((2*x-4)*x+3)*x-6; y1=(6*x-8)*x+3 { y=((2*x-4)*x+3)*x-6; y1=(6*x-8)*x+3; y=-y/y1; y=-y/y1 y1=(6*x-8)*x+3; y=-y/y1; while (fabs(y)>=eps) x=x+y x=x+y; { x=x+y; } y=((2*x-4)*x+3)*x-6; |y|>=eps while (fabs(y)>=eps); y1=(6*x-8)*x+3; y=-y/y1; 输出x cout<<"方程的根="<<x<<endl; } } cout<<"方程的根="<<x<<endl; }
§3.11.3
for 循环
for 循环的一般形式: for(表达式1 ; 表达式2 ; 表达式3) 语句
求解表达式1 表达式2 语句 求解表达式3 求解表达式1 假 表达式2 真 语 句 N-S图
•表达式1在进入循环之前求解
求解表达式3
(循环变量赋初值)
•表达式3是循环体的一部分
下一语句
例:t=n!
显示结果s的值: s=6
这个语句有什么作用? 答:①求和项增值 ②修改循环变量
【例】读程序
#include <iostream.h> void main( ) {int k,s,n; cout<<"enter n"; cin>>n; s=0; k=1; while (k<=n) { s+=k; k++; } cout<< "" <<n"=" <<s<<endl; }
#include <iostream> using namespace std; void main ( ) { int k, s ; s = 0; k = 1; do 先做后判 { s = s + k; k++; } while ( k <= 3); cout<< "s "<< s<<endl; }
输出n1 及 m*n/n1
§3.11.2
do-while循环
do-while语句用来实现"直到型"循环, 它的一般形式为:
do 语句 while(表达式);
真
语句
表达式 假 下一语句
不可省略! 切记切记 !!!
(注意点与while循环同) N-S图
语句 表达式
do-while至少执行一次
【例】计算 s =【例源自计算s kk 1
3
分析:这是一个累加求和问题 s = 1+2+3 s=0 s=s+1 s=s+2 s=s+3 s = s + k
和的 新值 和的 当前值 求和项 当前值
N-S图如下:
s=0,k=1 k<=3 s=s+k k++
输出s
根据N-S图用while语句的程序如下: #include <iostream.h>
(用for语句做)
#include <iostream> using namespace std; void main( ) {int k,t,n ; cout<<"enter n"; cin>>n; t=1; k=1; while (k<=n) { t*=k; k++; } cout<<n<<"!="<<t<<endl; }
【例 】用Newton迭代法求下面方程在1.5附近的近似根。
2 x 3 4 x 2 3x 6 0
分析: 1. 设方程为f(x)=0,则Newton迭代 公式为: f ( xn ) xn1 xn ' f ( xn ) 1.5 附近意为取初值 x0 1.5
2. 把 xn 存于变量x中,x 存于y中,
#include <iostream.h> void main( ) {int k,t,n ; cout<<"enter n"; cin>>n; t=1; k=1; while (k<=n) { t*=k; k++; } cout<< n<<"!="<<t<<endl; }
s=n
t=n!
#include <iostream.h> void main( ) {int k,t,n , s=0 ; cout<<"enter n"; cin>>n; t=1; k=1; while (k<=n) { t*=k; s+=t; k++; } cout<< "s="<<s<<endl; }
3
0
注意 保留m、n的原始值, 以便求最小公倍数
用while语句编写的程序如下:
#include <iostream> using namespace std; void main( ) { int m,n,m1,n1,a; cout<<"输入两个正整数:\n"; cin>>m>>n; N-S图如下:
输入 m,n
m1=m,n1=n,a=m1%n1 a≠0 m1=n1
改变循环变量的值
m1=m;n1=n;
a=m1 % n1; while(a!=0)
循环变量置初值
n1=a a=m1%n1
{ m1=n1; n1=a; a=m1 % n1; } cout<<"最大公约数是"<<n1<<endl; cout<<"最小公倍数是"<<m*n/n1<<endl; }
循环控制 表达式 循环控制 变量 循环体
注意: ★若循环体包含一条以上的语句,应以复合语句形式出现 ★循环前,必须给循环控制变量赋初值 ★循环体中,必须有改变循环控制变量值的语句 (使循环趋向结束的语句)
符,直到输入A为止
★循环体可以为空
如:while((c=getche())!=‘A’);从键盘输入字 等价: c=getche(); while(c!=‘A’)c=getche();
n=1,even=odd=0 n<100 odd=odd+n even=even+(n+1) n=n+2 ="<<even<<endl); } /***************************/ while(n<=100) { if (n%2==0) even+=n; else odd+=n; n++; }
