逻辑电路图、真值表
第六讲 真值表与基本逻辑运算

1 10
11
灌电流
IOL
IIL …
1
低电平扇出数:
N OL
I OL ( 驱 动 门) I IL (负 载 门)
IIL n个 IOL(max) ≥ IIL(total)
0 拉电流
11
IOH
10
IIH
…
1
IIH n个 IOH(max) ≥IIH(total)
高电平扇出数:
N OH
IOH ( 驱 动 门) IIH (负 载 门)
3 基本逻辑门电路
1 逻辑门:实现基本逻辑运算和复合逻辑运算的单元电路。
2 逻辑门电路的分类 分立门电路
逻辑门电路 集成门电路
二极管门电路
三极管门电路 MOS门电路
TTL门电路
NMOS门 PMOS门 CMOS门
1.CMOS门电路和TTL门电路
(1)CMOS集成电路:
广泛应用于超大规模、甚大规模集成电路
00000011 数字输出
保持、量化、 编码
(4)数字信号的描述方法
二值数字逻辑 0、1数码 ---表示数量时称二进制数
表示方式
---表示事物状态时称二值逻辑
逻辑电平与电压值的关系(正逻辑)
电压(V) 二值逻辑 +5(3.3~5) 1 0(0~1.5) 0
电平 H(高电平) L(低电平)
2 二值逻辑变量与基本逻辑运算
最大数目。驱动器件必须对负载器件提供足够大的拉电流和灌 电流。
负载器件所要求的输入电压
1 vO
驱动门
vI 1
负载门
vO
VOH (min)
vI
VIH (min)
VOH(min)
≥ VIH(min)
组合逻辑电路——血型匹配电路 3

电子课程设计血型匹配电路学院:班级:姓名:学号:指导教师:每个人都拥有各自不同的血型,但并不是谁都清楚自己能接受哪些血型的人献血,能给哪些人献血。
在献血、受血的时候,如果不清楚而搞错了,就会出很大问题。
例如:如果B型血输给O型血,可引起凝集反应,也就是说血液凝结在一起,堵塞小血管,发生血液循环障碍,从而破坏肾功能,严重时甚至可致人死亡。
血型匹配指示器能够在操作人按下自己血型的对应按钮后,通过指示灯告诉操作人他的血能为哪些血型的人群服务;同时,操作人也能够知道按下某个按钮时,若自己血型对应的指示灯亮了,意味着自己可以接受这个血型的人群的献血。
有了这个血型匹配指示器后,在受血时,就不会出现那些不必要的错误而造成不必要的严重后果。
我们这次制作的血型匹配指示器,每一个开关都代表一个受血者或献血者的血型,按下相应的开关后,亮绿灯代表是可以的,亮红灯代表不可以。
下面就是我这次制作的详细过程。
组合逻辑电路——血型匹配电路一、题目:人的血型由A、B、AB、O四种。
输血时输血者的血型与受血者血型必须符合图1中用箭头指示的授受关系。
判断输血者与受血者的血型是否符合上述规定,要求用八选一数据选择器(74LS151)及与非门(74LS00)实现。
(提示:用两个逻辑变量的4种取值表示输血者的血型,例如00代表A、01代表B、10代表AB、11代表O。
)如图1-1.图1-1 血型匹配图二、分析:人的血型由A、B、AB、O四种刚好可以用两个逻辑变量表示,在这里我们不妨设00代表血型A、01代表血型B、10代表血型AB、11代表血型O。
由于我们是要来判断两个血型是否匹配,则我们需要用四个逻辑变量,通过对四个逻辑变量进行逻辑设计,从而得到所需要求电路。
题目要求用八选一数据选择器(74LS151)及与非门(74LS00)实现。
74LS151只有8个数据输入端要来实现四个逻辑变量(16个数据最小项)的数据逻辑组合。
这是必须有一个逻辑变量接到74LS151的数据输入端。
5逻辑电路图、真值表和逻辑函数式转换

周测5逻辑电路图、真值表和逻辑函数式转换
一、综合分析题(每题10分,共100分)
1.将逻辑电路转换为用与非门表示的电路图。
2.将逻辑电路图转换为用与非门表示的电路图。
3.分析如图所示逻辑电路,写出表达式并化简,画出最简逻辑电路图。
4.如图所示真值表和逻辑电路图,按要求回答问题:
(1)由真值表列写逻辑表达式Y1。
(不化简)
(2)由正辑图列写逻辑表达式Y2。
(不化简)
(3)判断真值和逻辑所表示的逻辑功能是否一致,并写明分析过程。
5. 根据所示逻辑电路图。
(1)写出逻辑表达式并化简。
(2)列出其简化后表达式的真值表。
(3)总结器逻辑功能。
6.根据所示逻辑电路图:(1)写出输出函数逻辑表达式。
(2)列出真值表。
(3)进行逻辑功能分析,
7.如图所示逻辑电路,求:
(1)写出其逻辑表达式并化简。
(2)列出简化后表达式的真值表。
(3)总结逻辑功能。
8.根据给出的逻辑函数式进行化简,并化成与非门的形式。
BCD B B A Y ++=。
9.已知逻辑函数Y=A+B+C,写出它的最小项表达式。
10.变换函数式D A AC B A Y ++=为与非—与非表达式,并画出对应的逻辑电路图。
数字逻辑基础卡诺图化简

例5:已知 YA BA C D A B C D ,画卡诺图。
Y1 AB AB(CC)(DD)
ABCDABCDABCDABCD
m(12,13,14,15)
Y2 AC D A(B B )C D
例3: 已知Y的真值表,要求画Y的卡诺图。
表1-19 逻辑函数Y的真值表
图1-12 例3的卡诺图
ABC
Y
000
0
001
1
010
1
011
0
100
1
101
0
110
0
1 2020/7/26 1 1
1
.
14
练习:三变量表决逻辑真值表填入卡诺图
ABC
Y
000
0
001
0
010
0
011
1
100
0
101
1
110
1
或:Y(A,B,C)m3m6m7
m(3,6,7)
2020/7/26
.
8
例2: 写出三变量函数的最小项表达式。
解 利用摩根定律将函数变换为与或表达式, 然后展开成最小项之和形式。
Y ( A, B, C ) AB AB C AB
AB ABCAB
(A BA B )CA B (CC )
A B C A B C A B C A B C
2020/7/26
.
2
2.4 逻辑函数的卡诺图化简法
公式化简法评价: 优点:变量个数不受限制。 缺点:目前尚无一套完整的方法,结果是否最简 有时不易判断。
第4章 组合逻辑电路课后答案
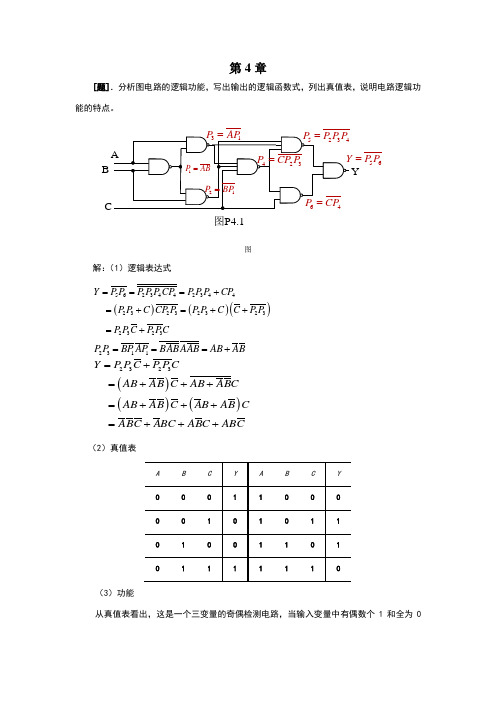
第4章[题].分析图电路的逻辑功能,写出输出的逻辑函数式,列出真值表,说明电路逻辑功能的特点。
图P4.1B YAP 56P P =图解:(1)逻辑表达式()()()5623442344232323232323Y P P P P P CP P P P CP P P C CP P P P C C P P P P C P PC ===+=+=++=+ 2311P P BP AP BABAAB AB AB ===+()()()2323Y P P C P P CAB AB C AB ABC AB AB C AB AB CABC ABC ABC ABC=+=+++=+++=+++(2)真值表(3)功能从真值表看出,这是一个三变量的奇偶检测电路,当输入变量中有偶数个1和全为0时,Y =1,否则Y=0。
[题] 分析图电路的逻辑功能,写出Y 1、、Y 2的逻辑函数式,列出真值表,指出电路完成什么逻辑功能。
图P4.3B1Y 2[解]解: 2Y AB BC AC =++12Y ABC A B C Y ABC A B C AB BC AC ABC ABC ABC ABC =+++=+++++=+++()())真值表:由真值表可知:、C 为加数、被加数和低位的进位,Y 1为“和”,Y 2为“进位”。
[题] 图是对十进制数9求补的集成电路CC14561的逻辑图,写出当COMP=1、Z=0、和COMP=0、Z=0时,Y 1~Y 4的逻辑式,列出真值表。
图P4.4[解](1)COMP=1、Z=0时,TG 1、TG 3、TG 5导通,TG 2、TG 4、TG 6关断。
3232211 , ,A A Y A Y A Y ⊕===, 4324A A A Y ++=(2)COMP=0、Z=0时,Y 1=A 1, Y 2=A 2, Y 3=A 3, Y 4=A 4。
、COMP=1、Z=0时的真值表COMP=0、Z=0的真值表从略。
[题]用与非门设1,输入为其他状态时输出为0。
74ls00与74ls10三人表决电路真值表

74LS00与74LS10三人表决电路真值表1. 引言本文将介绍74LS00与74LS10三人表决电路的真值表。
首先,我们将简要介绍74LS00和74LS10芯片的基本功能,然后详细描述三人表决电路的工作原理,并给出相应的真值表。
2. 74LS00芯片74LS00是一种集成逻辑门芯片,具有四个二输入与门。
每个输入引脚都有一个对应的输出引脚。
当且仅当所有输入引脚同时为逻辑高电平(1)时,对应的输出引脚才会输出逻辑高电平(1)。
否则,输出引脚将输出逻辑低电平(0)。
3. 74LS10芯片74LS10是一种集成逻辑门芯片,具有三个三输入与非门。
每个输入引脚都有一个对应的输出引脚。
当且仅当所有输入引脚同时为逻辑低电平(0)时,对应的输出引脚才会输出逻辑高电平(1)。
否则,输出引脚将输出逻辑低电平(0)。
4. 三人表决电路三人表决电路利用了74LS00和74LS10芯片的逻辑门功能,实现了一种简单的表决机制。
该电路由三个输入信号A、B和C组成,以及一个输出信号Y。
三人表决电路的工作原理如下:•当输入信号A、B和C中有两个或三个为逻辑高电平(1)时,74LS00芯片将输出逻辑低电平(0),此时74LS10芯片不会发挥作用。
因此,输出信号Y为逻辑低电平(0)。
•当输入信号A、B和C中只有一个为逻辑高电平(1)时,74LS00芯片将输出逻辑高电平(1),此时74LS10芯片开始工作。
根据74LS10的功能,当且仅当所有输入引脚都为逻辑低电平(0)时,对应的输出引脚才会输出逻辑高电平(1)。
因此,在这种情况下,输出信号Y为逻辑低电平(0)。
•综上所述,在三人表决电路中,只有当输入信号A、B和C中恰好有一个为逻辑高电平(1)时,输出信号Y才会为逻辑高电平(1),否则输出信号Y 为逻辑低电平(0)。
5. 真值表根据上述描述的工作原理,我们可以得到74LS00与74LS10三人表决电路的真值表如下:A B C Y0 0 0 00 0 1 00 1 0 00 1 1 11 0 0 01 0 1 11 1 0 11110其中,输入信号A、B和C的取值为逻辑低电平(0)或逻辑高电平(1),输出信号Y的取值也为逻辑低电平(0)或逻辑高电平(1)。
常用数字电子技术芯片电路图&真值表
0
0
1
1
K
0
1
0
1
C
0
1
0
0
异或门
A
0
0
1
1
B
0
1
0
1
C
0
1
1
0
与非门
A
0
0
1
1
B
0
1
0
1
C
1
1
1
0
与门
A
0
0
1
1
B
0
1
0
1
C
0
0
0
1
半加器
输入
输出
A
B
X1
X2
0
0
0
0
0
1
1
0
1
0
1
0
1
1
0
1
加法运算:0010+1001=?实验结果。
加法运算:1011+1001=?实验结果.
输入
输出
A
B
C
X1
X2
占空比可调范围:0~0.5
0
1
0
11011111
1
0
0
1
1
11111101
1
0
1
0
0
10111111
1
0
1
0
1
11111011
1
0
1
1
0
11101111
1
0
1
1
1
11111110
D触发器
D
CP
电工学组合逻辑电路习题
AB C
7、试用8选1数据选择器74151实现逻辑函数: LA BB CAC
解:将逻辑函数转换成最 小项表达式:
LAB CABCAC BABC
=m3+m5+m6+m7
画出连线图。
8、试用4选1数据选 择器实现逻辑函数:
LAB BC AC 解:将A、B接到地址输入端,C加到适当的数据输入端。 作出逻辑函数L的真值表,根据真值表画出连线图。
G A B C A B C A B C AC B m 0 m 2 m 4 m 6 m 0m 2m 4m 6
用一片74138加三个与非门就可实现该组合逻辑电路。
G
F
L
&
&
&
Y7 Y 6 Y5 Y 4 Y 3 Y 2 Y 1 Y0
74 13 8
G 1 G 2 AG 2 B
A 2 A 1 A0
1 00
根据真值表,写出化简后的逻辑表达式为:
画逻辑图:
2、某单位举办文艺晚会,男同志持红票入场,女同志持
黄票入场,持绿票的不分男女均可以入场,试设计一控制
入场放行的逻辑电路,并分别用分立门电路、数据选择器、 译码器来实现。
解:用A为1、0分别表示持票者为男、女同志,用B、C、 D为1分别表示持票者有红、黄、绿票,规定每人最多只 能持有1张票,有2张或2张以上者为约束项。F=1表示放行。 根据要求,列真值表如下:
AA3A2A1A0 、 BB3B2B1B0 相比较的大小比较器。
解:利用全加器和补码运算的规则,设计一个全减器。利 用2个数之差和借位判断其大小关系,即
A 3 A 2 A 1 A 0 B 3 B 2 B 1 B 0 S 3 S 2 S 1 S 0 S
第3章 组合逻辑电路
F
&
&
&
&
A
B
C
本例采用的是“真值表法”,真值表法的优点是规整、清晰; 缺点是不方便,尤其当变量较多时十分麻烦。
例 设计一个组合逻辑电路,用于判别以余3码表示的1 位十进制数是否为合数(一个数,如果除了一和他本身还有 别的因数,这样的数叫做合数,与之相对的是质数)。 解 设输入变量为ABCD,输出函数为 F,当ABCD表示 的十进制数为合数 (4 、 6 、 8、 9) 时,输出 F 为 1,否则 F为 0。
毛刺
使用卡诺图判断一个组合逻辑电路是否存在着 竞争冒险的一般步骤是: • 先画出该电路逻辑函数的卡诺图; • 然后在函数卡诺图上画出与表达式中所有乘积项 相对应的卡诺圈; • 如果图中有相切的卡诺圈,则该逻辑电路存在着 竞争冒险。(“0”冒险是1构成的圈,“1”冒险是 0构成的圈。
所谓卡诺圈相切即两个卡诺圈之间存在不被同一卡 诺圈包含的相邻最小项。
产生冒险的原因
A
1
≥1
F=A+A=1 理想情况
以例说明
A A
F 实际情况
造成冒险的原因是由于A和 A到达或门的时间不同。
再举一例 A C B
1 & BC & AC ≥1
A B F=AC+BC C C AC BC F
(分析中略去与门和或门的延时)
产生冒险的原因 : 电路存在由非门产生的互补信 号,且互补信号的状态发生变化 时有可能出现冒险现
有公用项
经变换后,组成电路时可令其共享同一个异或门,从而 使整体得到进一步简化,其逻辑电路图如下图所示。
多数出组合电路达到最简的关键是在函数化简时找出各输 出函数的公用项,使之在逻辑电路中实现对逻辑门的“共享”, 从而达到电路整体结构最简。
逻辑电路图、真值表与逻辑函数间的关系
总结
1、逻辑运算 2、逻辑函数及其描述 3、逻辑代数的运算法则 4、逻辑函数的表达式及相互转换 5、逻辑函数的标准形式(最小项) 6、代数化简法 7、卡诺图化简法
1状态组合按二进制数填写 到真值表的左边一栏; 然后将每一行的变量值代
A BY
00 0 01 1
入逻辑表达式,算出输出逻 1 0 1
辑值,记入右边一栏中。
11 0
2.3 逻辑函数及其表示方法
2.由真值表写出逻辑表达式 三变量真值表
(1) 在真值表上找出输出为1的行; A B C Y (2) 将这一行中所有自变量写成 0 0 0 0
逻辑函数, 真值表与逻辑电路 之间的关系
2020年1月30日
2.3 逻辑函数及其表示方法
逻辑函数及其表示方法
一. 逻辑函数(Logic Functions) 普通代数中的函数: Y=A×B+C
因变量
自变量
逻辑代数中的函数: Y=AB+C
输出变量
输入变量
2.3 逻辑函数及其表示方法
逻辑函数的特点: 1.输入和输出之间是逻辑运算关系; 2.基本运算:与、或、非; 3.逻辑变量取值只能为0和1。
2.3 逻辑函数及其表示方法
4. 时序波形图
定义 :由输入变量的所有可能取值组合的 高、低电平及其对应的输出函数值的高、低 电平所构成的图形。
A
A
& YB
B
Y
2.3 逻辑函数及其表示方法
三、 逻辑函数各种表示方法间的相互转换
1. 由逻辑表达式列出真值表
首先将n个变量的2n种0、 Y AB AB
4.由逻辑表达式画出逻辑电路图
P=ABC+BC
P
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、画出空卡诺图;
2、填写输出为1的小方格;
3、画圈:
①数量――2n(为自然数1、2、3);
②最大原则;
③相邻原则和滚圈相邻原则;
④每个圈中至少有1个小方格没有出现在别的圈中。
4、提取每个圈组成的项――n个圈就有n个乘积项;
圈中的各小方格代表的输入变量组合中的不变量提出组成一个乘积项。
简单介绍,说Байду номын сангаас楚就行
重点讲解
精心搜集整理,只为你的需要
4、真值表转换成逻辑表达式
复习真值表
(对学生作引导性提问)
讲解
由学生根据真值转换成逻辑表达式的方法来推导
教学过程
教学方法
真值表列写方法:将函数化成与或表达式。各个与项中的原变量为1,反变量为0,表示出完整输入状态,从真值表中找出并确定输出为1,其余输出为0。
5、逻辑图和波形图
6、卡诺图
根据逻辑函数可以画出卡诺图,用卡诺图对逻辑函数化简。
2、逻辑表达式
逻辑表达式:是由逻辑变量和与、或、非3种运算符连接起来所构成的式子。
3、真值表转换成逻辑表达式
表达式列写方法:将那些使函数值为1的各个状态表示成全部变量(值为1的表示成原变量,值为0的表示成反变量)的与项(例如A=0、B=1时函数F的值为1,则对应的与项为AB)以后相加,即得到函数的与或表达式。
课题
逻辑电路图、真值表与逻辑函数间的关系(一、真值表与逻辑函数的互换)
课时
教学目的和要求
掌握真值表与逻辑函数的互换方法
教 具
教学过程
教学方法
1、真值表
真值表:是由变量的所有可能取值组合及其对应的函数值所构成的表格。
真值表列写方法:每一个变量均有0、1两种取值,个变量共有2n种不同的取值,将这2n种不同的取值按顺序(一般按二进制递增规律)排列起来,同时在相应位置上填入函数的值,便可得到逻辑函数的真值表。
