北邮《数字信号处理》Matlab实验——实现重叠相加和重叠保留算法完成线性卷积的分段计算
北邮《数字信号处理》Matlab实验——实现重叠相加和重叠保留算法完成线性卷积的分段计算
实验目的:
实现重叠相加和重叠保留算法,完成线性卷积的分段计算(可任意指定 x(n)及 h(n)) 。
试验内容:
1、对算法的概括性说明
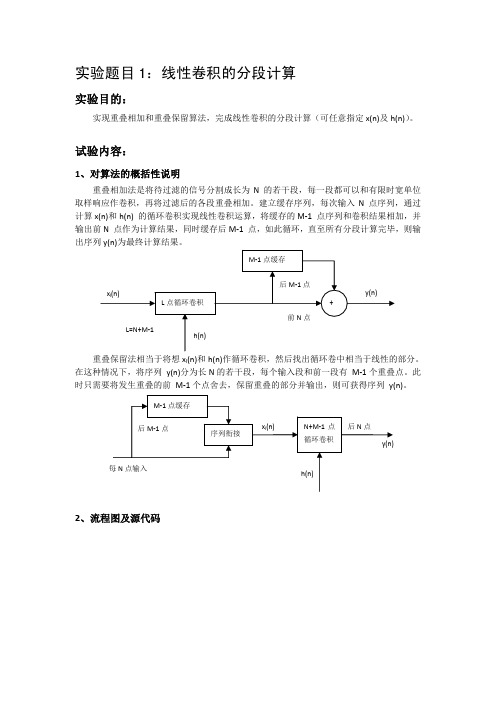
重叠相加法是将待过滤的信号分割成长为 N 的若干段,每一段都可以和有限时宽单位 取样响应作卷积,再将过滤后的各段重叠相加。建立缓存序列,每次输入 N 点序列,通过 计算 x(n)和 h(n) 的循环卷积实现线性卷积运算,将缓存的 M‐1 点序列和卷积结果相加,并 输出前 N 点作为计算结果,同时缓存后 M‐1 点,如此循环,直至所有分段计算完毕,则输 出序列 y(n)为最终计算结果。
5、总结实验过程中出现的问题以及解决问题的具体措施
1.利用自定义函数解决代码重复使用的问题,避免多次输入同样代码。 2.构造分段补零不会实现,通过上网查资料后获得实现相关功能的代码。
可见, 用重叠相加法和重叠保留发分别计算的卷积结果与直接利用线性卷积计算的结果 一致。算法正确性得以验证。
4、结合教材 3.5.1 节作运算量分析
若有限长因果序列 x(n)和 h(n)的长度分别为 N 和 M,计算其线性卷积 y(n),需 MN 次乘 法运算,(M‐1)(N‐1)次加法运算。如果利用循环卷积方法,按基 2 时域抽选法实现 L 点 FFT 和 IFFT,需
3、实验结果
输入(参考教材例 3.4、3.5) :
n = 0:9; xn = n+1; hn = [1,0,-1]; N = 6;
y1 = conv(hn, xn) y2 = overlap_add(xn, hn, N) y3 = overlap_save(xn, hn, N)
输出:
y1 = 1 y2 = Columns 1 through 10 1.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2 2 2 2 2 2 2 2 2 -9 -10
重叠相加法和重叠保留法的原理与实现

重叠相加法与重叠保存法的原理实现侯凯(吉林大学 通信工程学院 吉林 长春 130012)0概述线性卷积是求离散系统响应的主要方法之一,许多重要应用都建立在这一理论基础上,如卷积滤波等。
用圆周卷积计算线性卷积的方法归纳如下:将长为N 2的序列x(n)延长到L,补L -N 2个零,将长为N 1的序列h(n)延长到L,补L -N 1个零。
如果L ≥N1+N2-1,则圆周卷积与线性卷积相等,此时,可有FFT 计算线性卷积,方法如下:a.计算X(k)=FFT[x(n)]b.求H(k)=FFT[h(n)]c.求Y(k)=H(k)Y(k) k=0~L -1d.求y(n)=IFFT[Y(k)] n=0~L -1可见,只要进行二次FFT,一次IFFT 就可完成线性卷积计算。
上述结论适用于x(n)、h(n)两序列长度比较接近或相等的情况,如果x(n)、h(n)长度相差较多。
例如,h(n)为某滤波器的单位脉冲响应,长度有限,用来处理一个很长的输入信号x(n),或者处理一个连续不断的信号,按上述方法,h(n)要补许多零再进行计算,计算量有很大的浪费,或者根本不能实现。
为了保持快速卷积法的优越性,可将x(n)分为许多段后处理,每小段的长与h(n)接近,其处理方法有两种:重叠相加法和重叠保留法。
1重叠相加法——由分段卷积的各段相加构成总的卷积输出假定x i (n)表示图中第i 段x(n)序列如下图:22()(1)1()0i x n iN n i N x n ≤≤+-⎧=⎨⎩则输入序列可表为:()()i i x n x n ∞=-∞=∑图1 长序列分段滤波于是输出可分解为: ()()*()()*()()i i i i i y n x n h n x n h n y n ∞∞=-∞=-∞===∑∑其中 ()()*()i i y n x n h n =由此表明,只要将x(n)的每一段分别与h(n)卷积,然后再将这些卷积结果相加起来就可得到输出序列,这样,每一段的卷积都可用上面讨论的快速卷积来计算。
【含源代码】北邮dsp-MATLAB实验一重叠相加和重叠保留

Dsp-matlab实验实验一:重叠相加法和重叠保留法的实现设计报告课题名称:学生姓名:班级:班内序号:学号:日期:2015/06/15目录一、实验原理·········································二、Matlab源代码·································三、Matlab运行结果····························四、Matlab结果分析····································五、遇到的难题与解决方法····························参考文献·························································一、实验原理1、算法来源DFT 是连续傅里叶变换在时域和频域上都离散的形式,将时域信号的采样变换为在离散时间傅里叶变换频域的采样。
【含源代码】北邮dsp-MATLAB试验一重叠相加和重叠保留

Dsp-matlab实验实验一:重叠相加法和重叠保留法的实现设计报告课题名称:学生姓名:级:班班内序号:学号:2015/06/15 日期:目录一、实验原理·········································二、Matlab源代码·································运行结果Matlab三、····························结果分析Matlab四、····································五、遇到的难题与解决方法····························参考文献·························································一、实验原理1、算法来源DFT 是连续傅里叶变换在时域和频域上都离散的形式,将时域信号的采样变换为在离散时间傅里叶变换频域的采样。
MATLAB实验报告北京邮电大学

Matlab实验报告学院:信息与通信工程学院班级:201321113学号:2013210381班内序号:18姓名:石雪原实验题目1.实现重叠相加和重叠保留算法一.实验原理重叠相加法和重叠保留法的实质都是以逐段地方式通过循环卷积来完成线性卷积的计算。
将输入序列x (n)进行分段,每段长为N,且N>M(M为有限长因果序列h (n)的长度),x (n) 逐段与h (n)进行循环卷积,在重叠保留法中需在x (n)序列首部加入长度为M-1的0序列。
在算法中,在获得N个点的输入后,进行N+M-1点循环卷积计算,之后输出N个点。
通过for循环逐段进行循环卷积,使用FFT和IFFT 计算两个有限长序列的N点循环卷积结果。
二.源代码和流程图重叠相加法代码function [Y]=overpl(x,h,N)Lx=length(x); % 序列长度M=length(h); %h (n )长度x=[x,zeros(1,N-1)];t=zeros(1,M-1);Y=zeros(1,Lx+M-1);a=floor(Lx/N);for k=0:aA=x(k*N+1:k*N+N);y1=fft(A,Lx+M-1); % 利用fft 进行运算y2=fft(h,Lx+M-1);y3=y1.*y2;q=ifft(y3,Lx+M-1);Y(k*N+1:k*N+M-1)=q(1:M-1)+t(1:M-1);Y(k*N+M:k*N+N)=q(M:N);t(1:M-1)=q(N+1:N+M-1);endY(1:Lx+M-1);对应流程图图一:每段利用fft和ifft实现循环卷积图二:对X (n)逐段进行循环卷积然后相加得输出线性卷积结果y (n)重叠保留法代码fun cti on [Y]二overlpsav(x,h,N)Lx=le ngth(x);M=le ngth(h);M仁M -1;L=N-M1;h=[h,zeros(1,N-M)];图x=[zeros(1,M1),x,zeros(1,N-1)];a 二floor ((Lx+M1-1)/(L))+1; Y=zeros(1,N); for k=0:a-1 xk=x(k*L+1:k*L+N); b=fft(xk,N); C=fft(h,N); Z=b.*C;Y (k+1,:)=ifft(Z,N); end Y=Y (:,M:N): Y=( Y(:))'对应流程图装成单列向量再转置成行向量 输出输入数据 x I 各段搭接长 长度及脉冲 —\度M1,有效 响应长度k数据长度L将h 延长 至循环 长度N㈡把x 前面 加上(M- 1)个零各段进 行卷积把 K+1X N 阶输出矩 阵Y 初始 化Y 中各行均去 掉前M-1个样 Z 本,转置后构V成新的Y三.实验结果重叠相加法x=[1,2,3] h二[1,2,3] N=41 5]? 3X] 1 K 12 9 0緒=1 1 10 12 9 0重叠保留法x=[1,2,3,4,5,6,7,8,9,10] h=[1,0,-1] N=4四.结果分析(有关运算量的定量分析结果)有限长因果序列x (n)h (n)的长度分别为N和M直接计算线性卷积y (n),y(n)可视为N个序列的叠加结果,序列长度为M 所以每生成一个序列需完成M次乘法,共需完成MN次乘法运算。
数字信号处理MATLAB实验

出该信号,并讨论信号的混叠情况。
(3) 令
,其中 f/fs=1/16,即每个周期有 16 个
点。试利用 MATLAB 编程实现:
○1 作 M=4 倍的抽取,使每个周期变成 4 点。
○2 作 L=3 倍的插值,使每个周期变成 48 点。
(4)输入信号 x(n)为归一化频率分别为 f1=0.04,f2=0.3 的正 弦信号相加而成,N=50,插因子为 5,抽取因子为 3,给出 按有理因子 5/3 做采样率变换的输入输出波形。
(8) 用 FFT 分别计算 xa (n)( p 8, q 2) 和 xb(n) (a=0.1,f=0.0625)的自 相关函数。
三、思考题
(1)实验中的信号序列 xc(n)和 xd(n),在单位圆上的 z 变换频谱
和 一些,为什么?
会相同吗?如果不同,说明哪一个低频分量更多
(2)对一个有限长序列进行 DFT 等价于将该序列周期延拓后进行
0≤n≤15
c)x(n)=3cos(0.125πn+0.2π)+2sin(0.25πn+0.1π) 0≤n≤15 d)将c)中的x(n)扩展为以16为周期的函数x16(n)=x(n+16),绘出四个周 期。 e)将c)中的x(n)扩展为以10为周期的函数x10(n)=x(n+10),绘出四个周 期。 (3)x(n)=[1,-1,3,5],产生并绘出下列序列的样本。
(6)产生一 512 点的随机序列 xe(n),并用 xc(n)和 xe(n)做线性卷积, 观察卷积前后 xe(n)频谱的变化。要求将 xe(n)分成 8 段,分别采用重 叠相加法和重叠保留法。
(7) 用 FFT 分别计算 xa (n)( p 8, q 2) 和 xb(n) (a=0.1,f=0.0625)的 16 点循环相关和线性相关,问一共有多少种结果,他们之间有何异同点。
基于MATLAB的线性圆周卷积(DFT)及重叠相加法代码

基于MATLAB的线性圆周卷积(DFT)及重叠相加法代码主程序:x1=[1,2,3,4,5,5,4,3,2,1];x2=[1,0,1];L=8;y=chongdie(x1,x2,L);s=1:10;subplot(2,2,1);stem(s,x1)r=1:3;subplot(2,2,2);stem(r,x2)u=1:13;subplot(2,2,3);stem(u,y)函数juanji()function y=juanji(x1,x2,L)if length(x1)>L %如果x1长度大于L则产生错误error('L must not be less than length of x1');endif length(x2)>N %如果x2长度大于L则产生错误error('L must not be less than length of x2');endX1k=fft(x1,L); %对x1进行L点FFT计算X2k=fft(x2,L); %对x2进行L点FFT计算Yk=X1k.*X2k; %频域相乘y=ifft(Yk); %反变换得卷积结果if (all(imag(x1)==0))&(all(imag(x2)==0))y=real(y);end函数chongdie()方案1:function[y]=chongdie(x,h,N)Lenx=length(x); %取x(n)的长度M=length(h); %取h(n)的长度L=N+M-1; %计算圆周卷积的周期L使其不发生混叠x=(x,zero(1,N-1)); %填充序列使得循环中对序列的索引不会超出围K=floor(Lenx/N);y=zeros(1,Lenx+L-1); %确定分段数Kfor i=0:1:Kix=i*N;x_seg=x(ix+1:ix+N); %将x(n)分段y_seg=juanji(x_seg,h,L); %调用函数juanji()计算圆周卷积y(ix+1:ix+L)=y(ix+1:ix+L)+y_seg(1:L); %各段重叠相加endy=y(1:Lenx+M-1); %取出实际的输出序列方案2:function[y]=chongdie(x,h,L)Lenx=length(x); %取x(n)的长度M=length(h); %取h(n)的长度N=L-M+1; %计算分段大小Nx=[x,zeros(1,N-1)]; %填充序列使得循环中对序列的索引不会超出围K=floor(Lenx/N); %确定分段数Ky=zeros(1,Lenx+L-1);for i=0:1:Kix=i*N;x_seg=x(ix+1:ix+N); %将x(n)分段y_seg=juanji(x_seg,h,L); %调用函数juanji()计算圆周卷积y(ix+1:ix+L)=y(ix+1:ix+L)+y_seg(1:L); %各段重叠相加endy=y(1:Lenx+M); %取出实际的输出序列。
北邮《数字信号处理》Matlab实验——梳状滤波器的应用

实验题目3:梳状滤波器的应用实验目的:录制一段自己的话音,时间长度及取样频率自定;对该段声音加入一次反射、三次反射和无穷多次反射。
试验内容:1、对试验原理的说明回声可以认为是由原始声音衰减后的多个延迟叠加组成的,因此回声可以用延迟单元来生成。
x(n)表示原始声音信号,a为衰减系数,T为延迟周期,回声信号Y(n)=X(n)+a*x(n‐T)+a^2*x(n‐2T)+……+a^k*x(n‐kT)。
Z变换后的系统函数H(z)可由梳状滤波器实现。
本实验用MATLAB中的filter(b,a,x)函数可用来仿真差分方程a(1)*y(n)=b(1)*x(n)+b(2)*x(n‐1)+...+b(nb+1)*x(n‐nb)‐a(2)*y(n‐1)‐...‐a(na+1)*y(n‐na)。
2、在同一张图上,绘制原声音序列x(n)、加入一次反射后的声音序列x1(n)、加入三次反射后的声音序列x3(n)和加入无穷多次反射后的声音序列x I(n)。
[x, fs] = wavread('a.wav');% sound(x, fs);a = 0.6; T = 0.2;y1 = filter([1, zeros(1,T*fs-1), a], 1, x);% sound(y1, fs); wavwrite(y1, fs, 'echo1.wav');y2 = filter([1, zeros(1,T*fs-1), a, zeros(1,T*fs-1), a^2, zeros(1,T*fs-1), a^3], 1, x);% sound(y2, fs); wavwrite(y2, fs, 'echo2.wav');y3 = filter(1, [1, zeros(1,T*fs-1), a], x);% sound(y3, fs); wavwrite(y3, fs, 'echo3.wav');plot(y3, 'm');hold on; plot(y2, 'r');hold on; plot(y1, 'g');hold on; plot(x, 'b');其中蓝色为原声音序列x(n),粉红色为加入一次反射后的声音序列x1(n),绿色为加入三次反射后的声音序列x3(n),红色为加入无穷多次反射后的声音序列x I(n)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5、总结实验过程中出现的问题以及解决问题的具体措施
1.利用自定义函数解决代码重复使用的问题,避免多次输入同样代码。 2.构造分段补零不会实现,通过上网查资料后获得实现相关功能的代码。
M‐1 点缓存 后 M‐1 点 xl(n) N+M‐1 点 循环卷积 后 N 点 y(n)
序列衔接
每 N 点输入
h(n)
2、流程图及源代码
重叠相加法
开始
重叠保留法
开始
输入序列 X(n),h(n)
输入序列 X(n),h(n)
计算各序列长度、 分 段数、 生成临时序列
实验题目 1:线性卷积的分段计算
实验目的:
实现重叠相加和重叠保留算法,完成线性卷积的分段计算(可任意指定 x(n)及 h(n)) 。
试验内容:
1、对算法的概括性说明
重叠相加法是将待过滤的信号分割成长为 N 的若干段,每一段都可以和有限时宽单位 取样响应作卷积,再将过滤后的各段重叠相加。建立缓存序列,每次输入 N 点序列,通过 计算 x(n)和 h(n) 的循环卷积实现线性卷积运算,将缓存的 M‐1 点序列和卷积结果相加,并 输出前 N 点作为计算结果,同时缓存后 M‐1 点,如此循环,直至所有分段计算完毕,则输 出序列 y(n)为最终计算结果。
3L log 2 L L 次乘法运算, 3L log 2 L 次加法运算。可以看出: (1)当 M、N 2
取值较大且相近时,可实现对线性卷积的快速计算; (2)当 M、N 有较大差异时,线性卷积 和循环卷积运算量相当, 此时若希望降低线性卷积计算开销, 需采用重叠相加法或重叠保留 法。 重叠保留法和相加运行效率与分段长度关性较强。 分段数和卷积运算的序列长度为非线 性关系,在实际应用中,重叠保留和相加主要用于实施信号处理,在保证实时性的要求下, 输入序列的分段不能太长。
3、实验结果
输入(参考教材例 3.4、3.5) :
n = 0:9; xn = n+1; hn = [1,0,-1]; N = 6;
Hale Waihona Puke y1 = conv(hn, xn) y2 = overlap_add(xn, hn, N) y3 = overlap_save(xn, hn, N)
输出:
y1 = 1 y2 = Columns 1 through 10 1.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2 2 2 2 2 2 2 2 2 -9 -10
可见, 用重叠相加法和重叠保留发分别计算的卷积结果与直接利用线性卷积计算的结果 一致。算法正确性得以验证。
4、结合教材 3.5.1 节作运算量分析
若有限长因果序列 x(n)和 h(n)的长度分别为 N 和 M,计算其线性卷积 y(n),需 MN 次乘 法运算,(M‐1)(N‐1)次加法运算。如果利用循环卷积方法,按基 2 时域抽选法实现 L 点 FFT 和 IFFT,需
M‐1 点缓存 后 M‐1 点 xl(n) L 点循环卷积 前 N 点 L=N+M‐1 h(n) + y(n)
重叠保留法相当于将想 xl(n)和 h(n)作循环卷积,然后找出循环卷中相当于线性的部分。 在这种情况下,将序列 y(n)分为长 N 的若干段,每个输入段和前一段有 M‐1 个重叠点。此 时只需要将发生重叠的前 M‐1 个点舍去,保留重叠的部分并输出,则可获得序列 y(n)。
2.0000
Columns 11 through 12 -9.0000 -10.0000 y3 = Columns 1 through 10 1.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000 2.0000
2.0000
Columns 11 through 12 -9.0000 -10.0000
结束
Lx = length(x); %获得 x(n)的长度 T = ceil(Lx/N); %确定分段数 T t = zeros(1,M-1); %初始化序列 t(n) x = [x,zeros(1, (T+1)*N-Lx)]; %不足的分段补零 y = zeros(1, (T+1)*N); %生成输出序列 y(n),长度足够长 for i = 0:1:T xi = i*N+1; x_seg = x(xi:xi+N-1); %选择低点数计算时的分段 x(n) y_seg = circular_conv(x_seg, h, L); %调用循环卷积计算线性卷积 y_seg(1:M-1) = y_seg(1:M-1)+t(1:M-1);%完成重叠相加 t(1:M-1) = y_seg(N+1:L); %重新对 t(n)赋值为保留的后 M-1 点 y(xi:xi+N-1) = y_seg(1:N); %直接输出前 N 个点 end y=y(1:Lx+M-1); %取出最终的输出序列 end function [ y ] = overlap_save( x, h, N ) %重叠保留法实现 %核心为将高点数 DFT 转化为低点数 DFT,且用循环卷积计算线性卷积 Lx = length(x); %获得 x(n)的长度 M = length(h); %获得 h(n)的长度 if N < M %为 N 选择合适的值保证运算正确 N = M+1; end L = N+M-1; %为降低点数,取 M+N-1 点循环卷积即可 t = zeros(1,M-1); %初始化序列 t(n) T = ceil(Lx/N); %确定分段数 x = [x,zeros(1, (T+1)*N-Lx)]; %为不足的分段补零 y = zeros(1, (T+1)*N); for i = 0:1:T xi = i*N+1; x_seg = [t,x(xi:xi+N-1)]; %确定每个低点数卷积的分段 x(n) t = x_seg(N+1:N+M-1); %为 t(n)重新赋值为后 M-1 个点的值 y_seg = circular_conv(x_seg,h,L); %循环卷积计算线性卷积 y(xi:xi+N-1) = y_seg(M:N+M-1);%直接取出后 N 个点作为一次计算的输出 end y=y(1:Lx+M-1); %取出实际的输出序 end
计算各序列长度、 分 段数、 生成临时序列
分段循环卷积
填入保留之后 分段循环卷积
重叠相加后输 出前 N 点 否 完成所有分段 计算?
输出前 N 个点 并为 t(n)重新赋 为保留值 否
完成所有分段 计算?
是 是 输出序列 y(n) 输出序列 y(n)
结束 function [ y ] = circular_conv( x1, x2, L ) % 利用循环卷积计算线性卷积 % 循环卷积采用频域计算方法,已 FFT 代替 DFT,降低运算量 X1k = fft(x1,L); %x1 做 L 点 FFT X2k = fft(x2,L); %x1 做 L 点 FFT Yk = X1k.*X2k; %频域相乘 y = ifft(Yk); %FFT 反变换得循环卷积结果 end function [ y ] = overlap_add( x, h, N ) %重叠相加法实现 %核心为将高点数 DFT 转化为低点数 DFT,且用循环卷积计算线性卷积 M = length(h); %获得 h(n)的长度 if N < M %为 N 选择合适的值保证运算正确 N = M+1; end L = M+N-1; %循环卷积与线性卷积结果相同时需要进行运算的最少点数
