2009年考研数学三真题
2009年考研数学三真题及完整解析

2009年全国硕士研究生入学统一考试数学三试题一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内. (1)函数3()sin x xf x xπ-=的可去间断点的个数为:( )()A .1()B . 2 ()C .3()D .无穷多个(2)当0x →时,()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小,则( )()A .1a=,16b =-()B . 1a =,16b = ()C .1a =-,16b =-()D .1a =-,16b =(3)使不等式1sin ln xt dt x t>⎰成立的x 的范围是( )()A .(0,1)()B .(1,)2π ()C .(,)2ππ()D .(,)π+∞(4)设函数()y f x =在区间[]1,3-上的图形为:则函数()()0xF x f t dt =⎰的图形为( )()A .()B .()f x 02 3x1 -2-11()f x 0 2 3x1 -2 -11 1()f x -2 0 2 3x-1O()C .()D .(5)设,A B 均为2阶矩阵,*,A B *分别为,A B 的伴随矩阵,若||2,||3A B ==则分块矩阵 00A B⎛⎫⎪⎝⎭的伴随矩阵为( ) ()A .**0320B A ⎛⎫⎪⎝⎭()B . **230B A⎛⎫⎪⎝⎭ ()C .**0320A B⎛⎫⎪⎝⎭()D .**0230A B⎛⎫⎪⎝⎭(6)设,A P 均为3阶矩阵,TP 为P 的转置矩阵,且100010002TP AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭,若123122(,,),(,,)P Q ααααααα==+,则TQ A Q 为( ) ()A .210110002⎛⎫ ⎪ ⎪ ⎪⎝⎭()B . 110120002⎛⎫⎪⎪ ⎪⎝⎭ ()C .200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭()D .100020002⎛⎫⎪ ⎪ ⎪⎝⎭(7)设事件A 与事件B 互不相容,则( )()A .()0P A B =()B . ()()()P AB P A P B = ()C .()1()P A P B =-()D .()1P A B ⋃=(8)设随机变量X 与Y 相互独立,且X 服从标准正态分布(0,1)N ,Y 的概率分布为1{0}{1}2P Y P Y ====,记()z F Z 为随机变量Z XY =的分布函数,则函数()z F Z 的间断点个数为( )()A .()B . 1 ()C .2()D . 3二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.()f x 0 2 3x1 -2-11()f x 02 3x1 -1 1(9)cos 320lim11x x e ex →-=+- .(10)设()y x z x e =+,则(1,0)z x∂=∂(11)幂级数21(1)n nnn e x n∞=--∑的收敛半径为(12)设某产品的需求函数为()Q Q P =,其对应价格P 的弹性0.2p ξ=,则当需求量为10000件时,价格增加1元会使产品收益增加 元(13)设(1,1,1)T α=,(1,0,)T k β=,若矩阵T αβ相似于300000000⎛⎫⎪⎪ ⎪⎝⎭,则k = (14)设1X ,2X ,…n X 是来自二项分布总体(,)B n p 的简单随机样本,X 和2S 分别为样本均值和样本方差,记统计量2T X S =-,则E T =三、解答题:15-23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.(15)(本题满分9分)求二元函数()22(,)2ln f x y x y y y =++的极值。
大学历年考研真题-2009年全国硕士研究生入学统一考试(数三)试题及答案

2009年全国硕士研究生入学统一考试数学三试题一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一个选项是符合题目要求的,请把所选项前的字母填在答题纸指定位置上.(1)函数3()sin x x f x xπ-=的可去间断点的个数为(A)1. (B)2.(C)3.(D)无穷多个.(2)当0x →时,()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小,则(A)1a =,16b =-. (B )1a =,16b =. (C)1a =-,16b =-. (D )1a =-,16b =.(3)使不等式1sin ln x tdt x t>⎰成立的x 的范围是(A)(0,1).(B)(1,)2π. (C)(,)2ππ.(D)(,)π+∞.(4)设函数()y f x =在区间[]1,3-上的图形为则函数()()0xF x f t dt =⎰的图形为(A)(B)(C)(D)(5)设,A B 均为2阶矩阵,*,A B *分别为,A B 的伴随矩阵,若||2,||3A B ==,则分块矩阵O A B O ⎛⎫ ⎪⎝⎭的伴随矩阵为(A)**32O B A O ⎛⎫ ⎪⎝⎭.(B)**23OB AO ⎛⎫⎪⎝⎭. (C)**32O A B O ⎛⎫⎪⎝⎭.(D)**23OA BO ⎛⎫⎪⎝⎭. (6)设,A P 均为3阶矩阵,TP 为P 的转置矩阵,且100010002T P AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭,若1231223(,,),(,,)P Q ααααααα==+,则TQ AQ 为(A)210110002⎛⎫⎪ ⎪ ⎪⎝⎭.(B)110120002⎛⎫⎪⎪ ⎪⎝⎭.(C)200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭.(D)100020002⎛⎫ ⎪⎪ ⎪⎝⎭.(7)设事件A 与事件B 互不相容,则 (A)()0P AB =.(B)()()()P AB P A P B =.(C)()1()P A P B =-.(D)()1P A B ⋃=.(8)设随机变量X 与Y 相互独立,且X 服从标准正态分布(0,1)N ,Y 的概率分布为1{0}{1}2P Y P Y ====,记()z F Z 为随机变量Z XY =的分布函数,则函数()Z F z 的间断点个数为(A) 0.(B)1. (C)2. (D)3.二、填空题:9~14小题,每小题4分,共24分,请将答案写在答题纸指定位置上. (9)cos x x →= .(10)设()y xz x e =+,则(1,0)zx ∂=∂ .(11)幂级数21(1)n n nn e x n ∞=--∑的收敛半径为 . (12)设某产品的需求函数为()Q Q P =,其对应价格P 的弹性0.2p ξ=,则当需求量为10000件时,价格增加1元会使产品收益增加 元.(13)设(1,1,1)T α=,(1,0,)Tk β=,若矩阵T αβ相似于300000000⎛⎫⎪ ⎪ ⎪⎝⎭,则k = .(14) 设1X ,2X ,…,m X 为来自二项分布总体(,)B n p 的简单随机样本,X 和2S 分别为样本均值和样本方差,记统计量2T X S =-,则ET = .三、解答题:15~23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.(15)(本题满分9分)求二元函数()22(,)2ln f x y x y y y =++的极值. (16)(本题满分10 分)计算不定积分ln(1dx +⎰(0)x >. (17)(本题满分10 分) 计算二重积分()Dx y dxdy -⎰⎰,其中22{(,)(1)(1)2,}D x y x y y x =-+-≤≥.(18)(本题满分11 分)(Ⅰ)证明拉格朗日中值定理,若函数()f x 在[],a b 上连续,在(),a b 上可导,则(),a b ξ∈,得证()'()()()f b f a f b a ξ-=-.(Ⅱ)证明:若函数()f x 在0x =处连续,在()0,,(0)σσ>内可导,且'0lim ()x f x A +→=,则'(0)f +存在,且'(0)f A +=. (19)(本题满分10 分)设曲线()y f x =,其中()f x 是可导函数,且()0f x >.已知曲线()y f x =与直线0,1y x ==及(1)x t t =>所围成的曲边梯形绕x 轴旋转一周所得的立体体积值是该曲边梯形面积值的t π倍,求该曲线的方程.(20)(本题满分11 分) 设111A=111042--⎛⎫ ⎪- ⎪ ⎪--⎝⎭,1112ξ-⎛⎫⎪= ⎪ ⎪-⎝⎭.(Ⅰ)求满足21A ξξ=,231A ξξ=的所有向量2ξ,3ξ.(Ⅱ)对(Ⅰ)中的任意向量2ξ,3ξ,证明1ξ,2ξ,3ξ线性无关. (21)(本题满分11 分) 设二次型2221231231323(,,)(1)22f x x x ax ax a x x x x x =++-+-.(Ⅰ)求二次型f 的矩阵的所有特征值.(Ⅱ)若二次型f 的规范形为2212y y +,求a 的值.(22)(本题满分11 分)设二维随机变量(,)X Y 的概率密度为0(,)0xe y xf x y -⎧<<=⎨⎩其他(Ⅰ)求条件概率密度()Y X f y x ; (Ⅱ)求条件概率{}11P X Y ≤≤. (23)(本题满分11分)袋中有一个红球,两个黑球,三个白球,现在放回的从袋中取两次,每次取一个,求以X 、Y 、Z 分别表示两次取球所取得的红、黑与白球的个数.(Ⅰ)求{}10P X Z ==;(Ⅱ)求二维随机变量(,)X Y 的概率分布.2009年全国硕士研究生入学统一考试数学三试题及答案解析一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.(1)函数3()sin x x f x xπ-=的可去间断点的个数为()A .1()B . 2 ()C .3()D .无穷多个【答案】C 【解析】()3sin x x f x xπ-=则当x 取任何整数时,()f x 均无意义故()f x 的间断点有无穷多个,但可去间断点为极限存在的点,故应是30x x -=的解1,2,30,1x =±320032113211131lim lim sin cos 132lim lim sin cos 132lim lim sin cos x x x x x x x x x x x x x x x x x x x x x ππππππππππππ→→→→→-→---==--==--== 故可去间断点为3个,即0,1±(2)当0x →时,()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小,则()A .1a =,16b =-()B . 1a =,16b = ()C .1a =-,16b =- ()D .1a =-,16b =【答案】 A【解析】2()sin ,()(1)f x x ax g x x ln bx =-=-为等价无穷小,则222200000()sin sin 1cos sin lim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a ax g x x bx x bx bx bx→→→→→---==-⋅---洛洛230sin lim 166x a ax a b b axa→==-=-⋅ 36a b ∴=- 故排除,B C 。
2009—数三真题、标准答案及解析

2009年全国硕士研究生入学统一考试数学三试题一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一个选项是符合题目要求的,请把所选项前的字母填在答题纸指定位置上.(1)函数3()sin x x f x xπ-=的可去间断点的个数为(A)1.(B)2. (C)3.(D)无穷多个.(2)当0x →时,()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小,则(A)1a =,16b =-. (B )1a =,16b =. (C)1a =-,16b =-. (D )1a =-,16b =.(3)使不等式1sin ln x tdt x t>⎰成立的x 的范围是(A)(0,1).(B)(1,)2π. (C)(,)2ππ.(D)(,)π+∞.(4)设函数()y f x =在区间[]1,3-上的图形为则函数()()0xF x f t dt =⎰的图形为(A)(B)(C)(D)(5)设,A B 均为2阶矩阵,*,A B *分别为,A B 的伴随矩阵,若||2,||3A B ==,则分块矩阵O A B O ⎛⎫⎪⎝⎭的伴随矩阵为(A)**32O B A O ⎛⎫⎪⎝⎭.(B)**23OB A O ⎛⎫⎪⎝⎭.(C)**32O A BO ⎛⎫⎪⎝⎭.(D)**23O A BO ⎛⎫⎪⎝⎭. (6)设,A P 均为3阶矩阵,T P 为P 的转置矩阵,且100010002TP AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭,若1231223(,,),(,,)P Q ααααααα==+,则TQ AQ 为(A)210110002⎛⎫⎪ ⎪ ⎪⎝⎭.(B)110120002⎛⎫⎪⎪ ⎪⎝⎭.(C)200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭.(D)100020002⎛⎫ ⎪ ⎪ ⎪⎝⎭.(7)设事件A 与事件B 互不相容,则(A)()0P AB =.(B)()()()P AB P A P B =. (C)()1()P A P B =-.(D)()1P A B ⋃=.(8)设随机变量X 与Y 相互独立,且X 服从标准正态分布(0,1)N ,Y 的概率分布为1{0}{1}2P Y P Y ====,记()z F Z 为随机变量Z XY =的分布函数,则函数()z F Z 的间断点个数为(A) 0. (B)1. (C)2 . (D)3.二、填空题:9~14小题,每小题4分,共24分,请将答案写在答题纸指定位置上. (9)cos 0x x →= .(10)设()y xz x e =+,则(1,0)zx ∂=∂ .(11)幂级数21(1)n n nn e x n ∞=--∑的收敛半径为 . (12)设某产品的需求函数为()Q Q P =,其对应价格P 的弹性0.2p ξ=,则当需求量为10000件时,价格增加1元会使产品收益增加 元.(13)设(1,1,1)T α=,(1,0,)T k β=,若矩阵Tαβ相似于300000000⎛⎫⎪ ⎪ ⎪⎝⎭,则k = .(14)设1X ,2X ,…,n X 为来自二项分布总体(,)B n p 的简单随机样本,X 和2S 分别为样本均值和样本方差,记统计量2T X S =-,则ET = .三、解答题:15~23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. (15)(本题满分9分) 求二元函数()22(,)2ln f x y x y y y =++的极值. (16)(本题满分10 分)计算不定积分ln(1dx +⎰(0)x >. (17)(本题满分10 分) 计算二重积分()Dx y dxdy -⎰⎰,其中22{(,)(1)(1)2,}D x y x y y x =-+-≤≥. (18)(本题满分11 分)(Ⅰ)证明拉格朗日中值定理,若函数()f x 在[],a b 上连续,在(),a b 上可导,则(),a b ξ∈,得证()'()()()f b f a f b a ξ-=-.(Ⅱ)证明:若函数()f x 在0x =处连续,在()0,,(0)σσ>内可导,且'0lim ()x f x A +→=,则'(0)f +存在,且'(0)f A +=.(19)(本题满分10 分)设曲线()y f x =,其中()f x 是可导函数,且()0f x >.已知曲线()y f x =与直线0,1y x ==及(1)x t t =>所围成的曲边梯形绕x 轴旋转一周所得的立体体积值是该曲边梯形面积值的t π倍,求该曲线的方程.(20)(本题满分11 分)设111A=111042--⎛⎫ ⎪- ⎪ ⎪--⎝⎭,1112ξ-⎛⎫⎪= ⎪ ⎪-⎝⎭.(Ⅰ)求满足21A ξξ=,231A ξξ=的所有向量2ξ,3ξ.(Ⅱ)对(Ⅰ)中的任意向量2ξ,3ξ,证明1ξ,2ξ,3ξ线性无关. (21)(本题满分11 分)设二次型2221231231323(,,)(1)22f x x x ax ax a x x x x x =++-+-.(Ⅰ)求二次型f 的矩阵的所有特征值.(Ⅱ)若二次型f 的规范形为2211y y +,求a 的值.(22)(本题满分11 分)设二维随机变量(,)X Y 的概率密度为0(,)0x e y xf x y -⎧<<=⎨⎩其他(Ⅰ)求条件概率密度()Y X f y x ; (Ⅱ)求条件概率11P X Y =⎡≤≤⎤⎣⎦. (23)(本题满分11分)袋中有一个红球,两个黑球,三个白球,现在放回的从袋中取两次,每次取一个,求以X 、Y 、Z 分别表示两次取球所取得的红、黑与白球的个数. (Ⅰ)求10P X Z ⎡==⎤⎣⎦;(Ⅱ)求二维随机变量(,)X Y 的概率分布.2009年全国硕士研究生入学统一考试数学三试题解析一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一个选项是符合题目要求的,请把所选项前的字母填在答题纸指定位置上.(1)函数3()sin x x f x xπ-=的可去间断点的个数为(A)1. (B)2. (C)3.(D)无穷多个.【答案】C. 【解析】()3sin x x f x xπ-=则当x 取任何整数时,()f x 均无意义故()f x 的间断点有无穷多个,但可去间断点为极限存在的点,故应是30x x -=的解1,2,30,1x =±320032113211131lim lim sin cos 132lim lim sin cos 132lim lim sin cos x x x x x x x x x x x x x x x x x x x x x ππππππππππππ→→→→→-→---==--==--== 故可去间断点为3个,即0,1±(2)当0x →时,()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小,则(A)1a =,16b =-. (B )1a =,16b =. (C)1a =-,16b =-. (D )1a =-,16b =.【答案】A.【解析】2()sin ,()(1)f x x ax g x x ln bx =-=-为等价无穷小,则222200000()sin sin 1cos sin lim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a axg x x bx x bx bx bx→→→→→---==-⋅---洛洛230sin lim 166x a ax a b b axa→==-=-⋅ 36a b ∴=- 故排除(B)、(C). 另外201cos lim3x a axbx →--存在,蕴含了1cos 0a ax -→()0x →故 1.a =排除(D).所以本题选(A).(3)使不等式1sin ln xtdt x t>⎰成立的x 的范围是 (A)(0,1).(B)(1,)2π. (C)(,)2ππ. (D)(,)π+∞.【答案】A.【解析】原问题可转化为求111sin sin 1()ln xx x tt f x dt x dt dt t t t =-=-⎰⎰⎰11sin 11sin 0x x t t dt dt t t --==>⎰⎰成立时x 的取值范围,由1sin 0tt->,()0,1t ∈时,知当()0,1x ∈时,()0f x >.故应选(A).(4)设函数()y f x =在区间[]1,3-上的图形为则函数()()0xF x f t dt =⎰的图形为(A)(B)(C)(D)【答案】D.【解析】此题为定积分的应用知识考核,由()y f x =的图形可见,其图像与x 轴及y 轴、0x x =所围的图形的代数面积为所求函数()F x ,从而可得出几个方面的特征: ①[]0,1x ∈时,()0F x ≤,且单调递减. ②[]1,2x ∈时,()F x 单调递增. ③[]2,3x ∈时,()F x 为常函数.④[]1,0x ∈-时,()0F x ≤为线性函数,单调递增. ⑤由于F(x)为连续函数结合这些特点,可见正确选项为(D).(5)设,A B 均为2阶矩阵,*,A B *分别为,A B 的伴随矩阵,若||2,||3A B ==,则分块矩阵O A B O ⎛⎫⎪⎝⎭的伴随矩阵为(A)**32O B A O ⎛⎫⎪⎝⎭.(B)**23OB A O ⎛⎫⎪⎝⎭.(C)**32O A BO ⎛⎫⎪⎝⎭.(D)**23O A BO ⎛⎫⎪⎝⎭. 【答案】B.【解析】根据CC C E *=,若111,C C C CC C*--*==分块矩阵O A B O ⎛⎫⎪⎝⎭的行列式221236O A A B B O ⨯=-=⨯=(),即分块矩阵可逆 1111661O B BO A O A O A O B B O B O B O AO A O A **---*⎛⎫ ⎪⎛⎫⎛⎫⎛⎫⎪=== ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎪⎝⎭1236132O BOB AO A O ****⎛⎫ ⎪⎛⎫== ⎪ ⎪ ⎪⎝⎭⎪⎝⎭故答案为(B).(6)设,A P 均为3阶矩阵,T P 为P 的转置矩阵,且100010002TP AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭,若1231223(,,),(,,)P Q ααααααα==+,则TQ AQ 为(A)210110002⎛⎫⎪ ⎪ ⎪⎝⎭.(B)110120002⎛⎫⎪⎪ ⎪⎝⎭.(C)200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭.(D)100020002⎛⎫ ⎪ ⎪ ⎪⎝⎭.【答案】A.【解析】122312312312100(,,)(,,)110(,,)(1)001Q E αααααααααα⎡⎤⎢⎥=+==⎢⎥⎢⎥⎣⎦,即: 12121212122112(1)[(1)][(1)](1)[](1)100(1)010(1)002110100100210010010110110001002001002T T TT Q PE Q AQ PE A PE E P AP E E E ===⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦(7)设事件A 与事件B 互不相容,则(A)()0P AB =.(B)()()()P AB P A P B =. (C)()1()P A P B =-.(D)()1P A B ⋃=.【答案】D.【解析】因为,A B 互不相容,所以()0P AB =(A)()()1()P AB P A B P A B ==-U U ,因为()P A B U 不一定等于1,所以(A)不正确. (B)当(),()P A P B 不为0时,(B)不成立,故排除. (C)只有当,A B 互为对立事件的时候才成立,故排除.(D)()()1()1P A B P AB P AB ==-=U ,故(D)正确.(8)设随机变量X 与Y 相互独立,且X 服从标准正态分布(0,1)N ,Y 的概率分布为1{0}{1}2P Y P Y ====,记()z F Z 为随机变量Z XY =的分布函数,则函数()z F Z 的间断点个数为( ) (A) 0. (B)1. (C)2 .(D)3.【答案】 B.【解析】()()(0)(0)(1)(1)Z F z P XY z P XY z Y P Y P XY z Y P Y =≤=≤==+≤==1[(0)(1)]21[(00)(1)]2P XY z Y P XY z Y P X z Y P X z Y =≤=+≤==⋅≤=+≤=,X Y Q 独立1()[(0)()]2Z F z P x z P x z ∴=⋅≤+≤(1)若0z <,则1()()2Z F z z =Φ(2)当0z ≥,则1()(1())2Z F z z =+Φ0z ∴=为间断点,故选(B).二、填空题:9~14小题,每小题4分,共24分,请将答案写在答题纸指定位置上. (9)cos 0x x →= .【答案】32e .【解析】cos cos 10xx x x -→→=02(1cos )lim 13x e x x→-=20212lim 13x e x x →⋅=32e =. (10)设()y xz x e =+,则(1,0)zx ∂=∂ .【答案】2ln 21+. 【解析】由()xy z x e=+,故()(),01xz x x =+()''ln(1)ln(1)1ln(1)1x x x x x dz x x e e x dx x ++⎡⎤⎡⎤⎡⎤=+==++⎣⎦⎢⎥⎣⎦+⎣⎦ 代入1x =得,()ln 21,01ln 22ln 212ze x∂⎛⎫=+=+ ⎪∂⎝⎭.(11)幂级数21(1)n n nn e x n ∞=--∑的收敛半径为 . 【答案】1e. 【解析】由题意知,()210nn n e a n --=>()()()()111122122111()11111n n n n n nn n nn e e ea n n e n a n e n e e +++++⎡⎤⎛⎫--⎢⎥ ⎪⎝⎭--⎢⎥⎣⎦=⋅=⋅→→∞⎡⎤+--+⎛⎫--⎢⎥⎪⎝⎭⎢⎥⎣⎦所以,该幂级数的收敛半径为1e(12)设某产品的需求函数为()Q Q P =,其对应价格P 的弹性0.2p ξ=,则当需求量为10000件时,价格增加1元会使产品收益增加 元. 【答案】8000.【解析】所求即为()QP Q P Q ''=+ 因为0.2p Q PQξ'==-,所以0.2Q P Q '=- 所以()0.20.8QP Q Q Q '=-+= 将10000Q =代入有()8000QP '=.(13)设(1,1,1)T α=,(1,0,)T k β=,若矩阵Tαβ相似于300000000⎛⎫ ⎪ ⎪ ⎪⎝⎭,则k = .【答案】2.【解析】T αβ相似于300000000⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦,根据相似矩阵有相同的特征值,得到Tαβ的特征值为3,0,0.而T αβ为矩阵Tαβ的对角元素之和,1300k ∴+=++,2k ∴=.(14)设1X ,2X ,…,n X 为来自二项分布总体(,)B n p 的简单随机样本,X 和2S 分别为样本均值和样本方差,记统计量2T X S =-,则ET = . 【答案】2np【解析】由222()(1)ET E X S E X ES np np p np =-=-=--=.三、解答题:15~23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. (15)(本题满分9分) 求二元函数()22(,)2ln f x y x y y y =++的极值.【解析】2(,)2(2)0x f x y x y '=+=,2(,)2ln 10y f x y x y y '=++=,故10,x y e= =. 2212(2),2,4xxyy xyf y f x f xy y''''''=+ =+ =. 则12(0,)12(2)xxef e ''=+,1(0,)0xyef ''=,1(0,)yy ef e ''=.0xxf ''>Q 而2()0xy xx yy f f f ''''''-< ∴二元函数存在极小值11(0,)f e e=-.(16)(本题满分10 分)计算不定积分ln(1dx +⎰(0)x >.t =得22212,1(1)tdtx dx t t -= =--2221ln(1ln(1)1ln(1)11111dx t d t t dt t t t =+-+=---+⎰⎰⎰而22111112()11411(1)111ln(1)ln(1)2441dt dtt t t t t t t C t =---+-++--++++⎰⎰所以2ln(1)111ln(1ln 1412(1)1ln(1.2t t dx C t t t x C ++=+-+--+=+-⎰(17)(本题满分10 分) 计算二重积分()Dx y dxdy -⎰⎰,其中22{(,)(1)(1)2,}D x y x y y x =-+-≤≥. 【解析】由22(1)(1)2x y -+-≤得2(sin cos )r θθ≤+,32(sin cos )4()(cos sin )04Dx y dxdy d r r rdr πθθθθθπ+∴-=-⎰⎰⎰⎰332(sin cos )14(cos sin )034r d πθθθθθπ⎡+⎤=-⋅⎢⎥⎣⎦⎰ 2384(cos sin )(sin cos )(sin cos )34d πθθθθθθθπ=-⋅+⋅+⎰3384(cos sin )(sin cos )34d πθθθθθπ=-⋅+⎰3344438814(sin cos )(sin cos )(sin cos )3344d πππθθθθθθπ=++=⨯+⎰83=-.(18)(本题满分11 分)(Ⅰ)证明拉格朗日中值定理,若函数()f x 在[],a b 上连续,在(),a b 上可导,则(),a b ξ∈,得证()'()()()f b f a f b a ξ-=-.(Ⅱ)证明:若函数()f x 在0x =处连续,在()0,,(0)σσ>内可导,且'0lim ()x f x A +→=,则'(0)f +存在,且'(0)f A +=.【解析】(Ⅰ)作辅助函数()()()()()()f b f a x f x f a x a b aϕ-=----,易验证()x ϕ满足:()()a b ϕϕ=;()x ϕ在闭区间[],a b 上连续,在开区间(),a b 内可导,且''()()()()f b f a x f x b aϕ-=--. 根据罗尔定理,可得在(),a b 内至少有一点ξ,使'()0ϕξ=,即'()f ξ'()()0,()()()()f b f a f b f a f b a b aξ--=∴-=--(Ⅱ)任取0(0,)x δ∈,则函数()f x 满足:在闭区间[]00,x 上连续,开区间()00,x 内可导,从而有拉格朗日中值定理可得:存在()()000,0,x x ξδ∈⊂,使得()0'00()(0)x f x f f x ξ-=-……()*又由于()'lim x f x A +→=,对上式(*式)两边取00x +→时的极限可得:()()000000'''0000()00lim lim ()lim ()0x x x x x f x f f f f A x ξξξ++++→→→-====-故'(0)f +存在,且'(0)f A +=.(19)(本题满分10 分)设曲线()y f x =,其中()f x 是可导函数,且()0f x >.已知曲线()y f x =与直线0,1y x ==及(1)x t t =>所围成的曲边梯形绕x 轴旋转一周所得的立体体积值是该曲边梯形面积值的t π倍,求该曲线的方程.【解析】旋转体的体积为22()()11x x t t V f dx f dx ππ==⎰⎰曲边梯形的面积为:()1x ts f dx =⎰,则由题可知22()()()()1111x x x x t t t tV ts f dx t f dx f dx t f dx πππ=⇒=⇒=⎰⎰⎰⎰两边对t 求导可得22()()()()()()11t x t t t x t t f f dx tf f tf f dx =+⇒-=⎰⎰ V继续求导可得''2()()()()()f t f t f t tf t f t --=,化简可得'1(2())()2()12dt f t t f t f t t dy y -=⇒+=,解之得1223t c y y -=⋅+在V 式中令1t =,则2(1)(1)0,()0,(1)1f f f t f -=>∴=Q ,代入1223t cyy -=+得11,2)33c t y =∴=+.所以该曲线方程为:230y x +=.(20)(本题满分11 分)设111A=111042--⎛⎫ ⎪- ⎪ ⎪--⎝⎭,1112ξ-⎛⎫ ⎪= ⎪ ⎪-⎝⎭. (Ⅰ)求满足21A ξξ=,231A ξξ=的所有向量2ξ,3ξ.(Ⅱ)对(Ⅰ)中的任意向量2ξ,3ξ,证明1ξ,2ξ,3ξ线性无关. 【解析】(Ⅰ)解方程21A ξξ=()1111111111111,111100000211042202110000A ξ---------⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=-→→ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭()2r A =故有一个自由变量,令32x =,由0Ax =解得,211,1x x =-=求特解,令120x x ==,得31x =故21101021k ξ⎛⎫⎛⎫ ⎪ ⎪=-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,其中1k 为任意常数解方程231A ξξ=2220220440A ⎛⎫ ⎪=-- ⎪ ⎪⎝⎭()21111022012,2201000044020000A ξ-⎛⎫ ⎪-⎛⎫ ⎪ ⎪=--→⎪ ⎪ ⎪ ⎪-⎝⎭ ⎪⎝⎭故有两个自由变量,令231,0x x =-=,由20A x =得11x = 令230,1x x ==-,由20A x =得10x =求得特解21200η⎛⎫- ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭故 3231102100010k k ξ⎛⎫-⎪⎛⎫⎛⎫ ⎪ ⎪ ⎪=-++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭ ⎪⎝⎭,其中23,k k 为任意常数(Ⅱ)证明:由于12121212122111121112(21)()2()(21)22221k k k k k k k k k k k k k -+--=+++-+-+-+102=≠故123,,ξξξ 线性无关.(21)(本题满分11 分)设二次型2221231231323(,,)(1)22f x x x ax ax a x x x x x =++-+-.(Ⅰ)求二次型f 的矩阵的所有特征值.(Ⅱ)若二次型f 的规范形为2211y y +,求a 的值.【解析】(Ⅰ) 0101111a A a a ⎛⎫ ⎪=- ⎪ ⎪--⎝⎭0110||01()1111111aaaE A aa a a λλλλλλλλ-----=-=---+---+222()[()(1)1][0()]()[()(1)2]()[22]19(){[(12)]}24()(2)(1)a a a a a a a a a a a a a a a a a λλλλλλλλλλλλλλλλ=---+--+-=---+-=--++--=-+--=--+--123,2,1a a a λλλ∴==-=+.(Ⅱ) 若规范形为2212y y +,说明有两个特征值为正,一个为0.则1) 若10a λ==,则 220λ=-< ,31λ= ,不符题意 2) 若20λ= ,即2a =,则120λ=>,330λ=>,符合3) 若30λ= ,即1a =-,则110λ=-< ,230λ=-<,不符题意 综上所述,故2a =(22)(本题满分11 分)设二维随机变量(,)X Y 的概率密度为0(,)0x e y xf x y -⎧<<=⎨⎩其他(Ⅰ)求条件概率密度()Y X f y x (Ⅱ)求条件概率11P X Y =⎡≤≤⎤⎣⎦ 【解析】(Ⅰ)由0(,)0x y xe f x y -<<⎧= ⎨⎩其它得其边缘密度函数()0xx x x f x e dy xe x --== >⎰故 |(,)1(|)0()y x x f x y f y x y x f x x== << 即 |1(|)0y x y xf y x x ⎧ 0<<⎪=⎨⎪ ⎩其它(Ⅱ)[1,1][1|1][1]P X Y P X Y P Y ≤≤≤≤=≤而111011[1,1](,)12xx x x y P X Y f x y dxdy dx e dy xe dx e ---≤≤≤≤====-⎰⎰⎰⎰⎰()|,0xxyY yf y e dx e e y y+∞---+∞==-= >⎰11101[1]|110y y P Y e dy e e e ----∴ ≤==-=-+=-⎰11122[1|1]11e e P X Y e e ----∴ ≤≤==--.(23)(本题满分11分)袋中有一个红球,两个黑球,三个白球,现在放回的从袋中取两次,每次取一个,求以X 、Y 、Z 分别表示两次取球所取得的红、黑与白球的个数. ①求10P X Z ⎡==⎤⎣⎦.②求二维随机变量(,)X Y 的概率分布.【解析】(Ⅰ)在没有取白球的情况下取了一次红球,利用压缩样本空间则相当于只有1个红球,2个黑球放回摸两次,其中摸了一个红球12113324(10)9C P X Z C C ⨯∴====⋅.(Ⅱ)X ,Y 取值范围为0,1,2,故()()()()()()()()()1111332311116666111223111166661122116611221166110,0,1,0461112,0,0,136311,1,2,10910,291,20,2,20C C C C P X Y P X Y C C C C C C C P X Y P X Y C C C C C C P X Y P X Y C C C C P X Y C C P X Y P X Y ⋅⋅========⋅⋅⋅⋅========⋅⋅⋅=======⋅⋅====⋅======。
2009~2012考研数学三试题(卷)与解析
2009年全国硕士研究生入学统一考试数学三试题一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一个选项是符合题目要求的,请把所选项前的字母填在答题纸指定位置上.(1)函数3()sin x x f x xπ-=的可去间断点的个数为(A)1. (B)2.(C)3.(D)无穷多个.(2)当0x →时,()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小,则(A)1a =,16b =-. (B )1a =,16b =. (C)1a =-,16b =-. (D )1a =-,16b =.(3)使不等式1sin ln x tdt x t>⎰成立的x 的X 围是(A)(0,1).(B)(1,)2π. (C)(,)2ππ.(D)(,)π+∞.(4)设函数()y f x =在区间[]1,3-上的图形为则函数()()0xF x f t dt =⎰的图形为(A)(B)(C)(D)(5)设,A B 均为2阶矩阵,*,A B *分别为,A B 的伴随矩阵,若||2,||3A B ==,则分块矩阵O A B O ⎛⎫ ⎪⎝⎭的伴随矩阵为(A)**32O B A O ⎛⎫ ⎪⎝⎭.(B)**23OB AO ⎛⎫⎪⎝⎭. (C)**32O A B O ⎛⎫⎪⎝⎭.(D)**23OA BO ⎛⎫⎪⎝⎭. (6)设,A P 均为3阶矩阵,T P 为P 的转置矩阵,且100010002TP AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭,若1231223(,,),(,,)P Q ααααααα==+,则TQ AQ 为(A)210110002⎛⎫⎪ ⎪ ⎪⎝⎭.(B)110120002⎛⎫⎪⎪ ⎪⎝⎭.(C)200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭.(D)100020002⎛⎫ ⎪⎪ ⎪⎝⎭.(7)设事件A 与事件B 互不相容,则 (A)()0P AB =.(B)()()()P AB P A P B =.(C)()1()P A P B =-.(D)()1P A B ⋃=.(8)设随机变量X 与Y 相互独立,且X 服从标准正态分布(0,1)N ,Y 的概率分布为1{0}{1}2P Y P Y ====,记()z F Z 为随机变量Z XY =的分布函数,则函数()Z F z 的间断点个数为(A) 0.(B)1. (C)2. (D)3.二、填空题:9~14小题,每小题4分,共24分,请将答案写在答题纸指定位置上. (9)cos x x →= .(10)设()y xz x e =+,则(1,0)zx ∂=∂ . (11)幂级数21(1)n n nn e x n ∞=--∑的收敛半径为 . (12)设某产品的需求函数为()Q Q P =,其对应价格P 的弹性0.2p ξ=,则当需求量为10000件时,价格增加1元会使产品收益增加 元.(13)设(1,1,1)T α=,(1,0,)Tk β=,若矩阵T αβ相似于300000000⎛⎫⎪ ⎪ ⎪⎝⎭,则k = .(14) 设1X ,2X ,…,m X 为来自二项分布总体(,)B n p 的简单随机样本,X 和2S 分别为样本均值和样本方差,记统计量2T X S =-,则ET = .三、解答题:15~23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.(15)(本题满分9分)求二元函数()22(,)2ln f x y x y y y =++的极值. (16)(本题满分10 分)计算不定积分ln(1dx +⎰(0)x >. (17)(本题满分10 分) 计算二重积分()Dx y dxdy -⎰⎰,其中22{(,)(1)(1)2,}D x y x y y x =-+-≤≥.(18)(本题满分11 分)(Ⅰ)证明拉格朗日中值定理,若函数()f x 在[],a b 上连续,在(),a b 上可导,则(),a b ξ∈,得证()'()()()f b f a f b a ξ-=-.(Ⅱ)证明:若函数()f x 在0x =处连续,在()0,,(0)σσ>内可导,且'0lim ()x f x A +→=,则'(0)f +存在,且'(0)f A +=. (19)(本题满分10 分)设曲线()y f x =,其中()f x 是可导函数,且()0f x >.已知曲线()y f x =与直线0,1y x ==及(1)x t t =>所围成的曲边梯形绕x 轴旋转一周所得的立体体积值是该曲边梯形面积值的t π倍,求该曲线的方程.(20)(本题满分11 分) 设111A=111042--⎛⎫ ⎪- ⎪ ⎪--⎝⎭,1112ξ-⎛⎫⎪= ⎪ ⎪-⎝⎭.(Ⅰ)求满足21A ξξ=,231A ξξ=的所有向量2ξ,3ξ.(Ⅱ)对(Ⅰ)中的任意向量2ξ,3ξ,证明1ξ,2ξ,3ξ线性无关. (21)(本题满分11 分) 设二次型2221231231323(,,)(1)22f x x x ax ax a x x x x x =++-+-.(Ⅰ)求二次型f 的矩阵的所有特征值.(Ⅱ)若二次型f 的规X 形为2212y y +,求a 的值.(22)(本题满分11 分)设二维随机变量(,)X Y 的概率密度为0(,)0xe y xf x y -⎧<<=⎨⎩其他(Ⅰ)求条件概率密度()Y X f y x ; (Ⅱ)求条件概率{}11P X Y ≤≤. (23)(本题满分11分)袋中有一个红球,两个黑球,三个白球,现在放回的从袋中取两次,每次取一个,求以X 、Y 、Z 分别表示两次取球所取得的红、黑与白球的个数.(Ⅰ)求{}10P X Z ==;2009年全国硕士研究生入学统一考试数学三试题和解析一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.(1)函数3()sin x x f x xπ-=的可去间断点的个数为:( )()A .1()B . 2 ()C .3()D .无穷多个【答案】C 【解析】()3sin x x f x xπ-=则当x 取任何整数时,()f x 均无意义故()f x 的间断点有无穷多个,但可去间断点为极限存在的点,故应是30x x -=的解1,2,30,1x =±320032113211131lim lim sin cos 132lim lim sin cos 132lim lim sin cos x x x x x x x x x x x x x x x x x x x x x ππππππππππππ→→→→→-→---==--==--== 故可去间断点为3个,即0,1±(2)当0x →时,()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小,则( )()A .1a =,16b =-()B . 1a =,16b = ()C .1a =-,16b =- ()D .1a =-,16b =【答案】 A【解析】2()sin ,()(1)f x x ax g x x ln bx =-=-为等价无穷小,则222200000()sin sin 1cos sin lim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a ax g x x bx x bx bx bx→→→→→---==-⋅---洛洛230sin lim 166x a ax a b b axa→==-=-⋅ 36a b ∴=- 故排除,B C 。
2009-2012考研数学三试题及解析

2009年全国硕士研究生入学统一考试数学三试题一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一个选项是符合题目要求的,请把所选项前的字母填在答题纸指定位置上.(1)函数3()sin x x f x xπ-=的可去间断点的个数为(A)1. (B)2.(C)3.(D)无穷多个.(2)当0x →时,()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小,则(A)1a =,16b =-. (B )1a =,16b =. (C)1a =-,16b =-. (D )1a =-,16b =.(3)使不等式1sin ln x tdt x t>⎰成立的x 的范围是(A)(0,1).(B)(1,)2π. (C)(,)2ππ.(D)(,)π+∞.(4)设函数()y f x =在区间[]1,3-上的图形为则函数()()0xF x f t dt =⎰的图形为(A)(B)()f xO 23x1-2-11()f xO 2 3x1 -2 -11 1()f x -2O 2 3x-11(C)(D)(5)设,A B 均为2阶矩阵,*,A B *分别为,A B 的伴随矩阵,若||2,||3A B ==,则分块矩阵O A B O ⎛⎫ ⎪⎝⎭的伴随矩阵为(A)**32O B A O ⎛⎫⎪⎝⎭. (B)**23OB AO ⎛⎫⎪⎝⎭. (C)**32O A BO ⎛⎫⎪⎝⎭.(D)**23OA BO ⎛⎫⎪⎝⎭. (6)设,A P 均为3阶矩阵,T P 为P 的转置矩阵,且100010002TP AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭,若1231223(,,),(,,)P Q ααααααα==+,则TQ AQ 为(A)210110002⎛⎫⎪ ⎪ ⎪⎝⎭.(B)110120002⎛⎫⎪⎪ ⎪⎝⎭.(C)200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭.(D)100020002⎛⎫ ⎪⎪ ⎪⎝⎭.(7)设事件A 与事件B 互不相容,则 (A)()0P AB =.(B)()()()P AB P A P B =.(C)()1()P A P B =-.(D)()1P A B ⋃=.(8)设随机变量X 与Y 相互独立,且X 服从标准正态分布(0,1)N ,Y 的概率分布为1{0}{1}2P Y P Y ====,记()z F Z 为随机变量Z XY =的分布函数,则函数()Z F z 的间断()f x O2 3x1 -2-11()f x O23x1-11点个数为(A) 0.(B)1. (C)2. (D)3.二、填空题:9~14小题,每小题4分,共24分,请将答案写在答题纸指定位置上. (9)cos 320lim11x x e e x →-=+- .(10)设()y xz x e =+,则(1,0)zx ∂=∂ . (11)幂级数21(1)n n nn e x n ∞=--∑的收敛半径为 . (12)设某产品的需求函数为()Q Q P =,其对应价格P 的弹性0.2p ξ=,则当需求量为10000件时,价格增加1元会使产品收益增加 元.(13)设(1,1,1)T α=,(1,0,)Tk β=,若矩阵T αβ相似于300000000⎛⎫⎪ ⎪ ⎪⎝⎭,则k = .(14) 设1X ,2X ,…,m X 为来自二项分布总体(,)B n p 的简单随机样本,X 和2S 分别为样本均值和样本方差,记统计量2T X S =-,则ET = .三、解答题:15~23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.(15)(本题满分9分)求二元函数()22(,)2ln f x y x y y y =++的极值. (16)(本题满分10 分) 计算不定积分1ln(1)xdx x++⎰(0)x >. (17)(本题满分10 分) 计算二重积分()Dx y dxdy -⎰⎰,其中22{(,)(1)(1)2,}D x y x y y x =-+-≤≥.(18)(本题满分11 分)(Ⅰ)证明拉格朗日中值定理,若函数()f x 在[],a b 上连续,在(),a b 上可导,则(),a b ξ∈,得证()'()()()f b f a f b a ξ-=-.(Ⅱ)证明:若函数()f x 在0x =处连续,在()0,,(0)σσ>内可导,且'0lim ()x f x A +→=,则'(0)f +存在,且'(0)f A +=.(19)(本题满分10 分)设曲线()y f x =,其中()f x 是可导函数,且()0f x >.已知曲线()y f x =与直线0,1y x ==及(1)x t t =>所围成的曲边梯形绕x 轴旋转一周所得的立体体积值是该曲边梯形面积值的t π倍,求该曲线的方程.(20)(本题满分11 分) 设111A=111042--⎛⎫ ⎪- ⎪ ⎪--⎝⎭,1112ξ-⎛⎫⎪= ⎪ ⎪-⎝⎭.(Ⅰ)求满足21A ξξ=,231A ξξ=的所有向量2ξ,3ξ. (Ⅱ)对(Ⅰ)中的任意向量2ξ,3ξ,证明1ξ,2ξ,3ξ线性无关. (21)(本题满分11 分) 设二次型2221231231323(,,)(1)22f x x x ax ax a x x x x x =++-+-.(Ⅰ)求二次型f 的矩阵的所有特征值.(Ⅱ)若二次型f 的规范形为2212y y +,求a 的值. (22)(本题满分11 分)设二维随机变量(,)X Y 的概率密度为0(,)0x e y x f x y -⎧<<=⎨⎩其他(Ⅰ)求条件概率密度()Y X f y x ; (Ⅱ)求条件概率{}11P X Y ≤≤. (23)(本题满分11分)袋中有一个红球,两个黑球,三个白球,现在放回的从袋中取两次,每次取一个,求以X 、Y 、Z 分别表示两次取球所取得的红、黑与白球的个数.(Ⅰ)求{}10P X Z ==;2009年全国硕士研究生入学统一考试数学三试题和解析一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.(1)函数3()sin x x f x xπ-=的可去间断点的个数为:( )()A .1()B . 2 ()C .3()D .无穷多个【答案】C 【解析】()3s i n x x f x xπ-=则当x 取任何整数时,()f x 均无意义故()f x 的间断点有无穷多个,但可去间断点为极限存在的点,故应是30x x -=的解1,2,30,1x =±320032113211131lim lim sin cos 132lim lim sin cos 132lim lim sin cos x x x x x x x x x x x x x x x x x x x x x ππππππππππππ→→→→→-→---==--==--== 故可去间断点为3个,即0,1±(2)当0x →时,()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小,则( )()A .1a =,16b =-()B . 1a =,16b = ()C .1a =-,16b =- ()D .1a =-,16b =【答案】 A【解析】2()sin ,()(1)f x x ax g x x ln bx =-=-为等价无穷小,则222200000()sin sin 1cos sin lim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a ax g x x bx x bx bx bx→→→→→---==-⋅---洛洛230sin lim 166x a ax a b b axa→==-=-⋅ 36a b ∴=- 故排除,B C 。
2009年数学三真题答案解析

lim e(1 cos x)
x0
1 x2
e 1 x2
lim x0
2 1 x2
3e. 2
3
3
(10)设 z (x e y )x ,则 z
.
x (1,0)
【答案】 2 ln 2 1 .
【解析】由 z x e y x ,故 z x, 0 x 1x
dz dx
x
1x
'
e xln(1x)
O
6
O 1 A A
1 B
B
O
O
6
1 2
A
1 B 3 O
O 3 A
2B
O
故答案为(B).
1 0 0
(6)设
A,
P
均为
3
阶矩阵,
PT
为
P
的转置矩阵,且
PT
AP
0
1
0
,
0 0 2
若 P (1,2,3),Q (1 2,2,3) ,则 QT AQ 为
2 1 0
(A)
1
1
0
(C)
2
B*
. O
O 2A*
(D)
3B*
. O
【答案】B.
【解析】根据 CC C E ,若 C C C 1,C 1 1 C C
O
分块矩阵
B
A
O
O
的行列式
B
A (1)22 A B 2 3 6 ,即分块矩阵可逆 O
-3-
O
B
A
O
O B
A O
O
B
A1
O
6
O A1
B
1
lim x0
09真题考研数学真题解析--数三修订版

2009年全国硕士研究生入学统一考试数学三试题一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.1. (09年,4分)函数()3sin x x f x xπ-=的可去间断点的个数为 ( )(A ) 1. (B ) 2. (C ) 3. (D ) 无穷多个.【考查分析】本题考查间断点的定义和分类,属于间断点计算与判别的基本题型 【详解】由于()3sin x x f x xπ-=,则当x 取任何整数时,()f x 均无意义,故()f x 的间断点有无穷多个,但可去间断点为极限存在的点,故应是30x x -=的解1,2,30,1x =±.320032113211131lim lim ,sin cos 132lim lim ,sin cos 132lim lim .sin cos x x x x x x x x x x x x x x x x x x x x x ππππππππππππ→→→→→-→---==--==--== 故可去间断点为3个,即1,2,30,1x =±.选C【评注】此题有相当多的考生选择(D ),认为使sin 0x π=成立的点有无穷多个,同时审题不细,没有利用()f x 的极限值以确定可去间断点的个数,故错误率较高。
2.(09年,4分)当0x →时,()sin f x x ax =-与()()2ln 1g x x bx =-是等价无穷小,则 ( )(A ) 11,6a b ==-. (B ) 11,6a b ==. (C ) 11,6a b =-=-. (D ) 11,6a b =-=.【考查分析】本题考查等价无穷小替换,洛比达法则的计算极限,属于极限计算基本题型 【详解】方法1:()sin f x x ax =-与()()2ln 1g x x bx =-是0x →时的等价无穷小,则2200232000330()sin sin limlim lim ()ln(1)()sin 1cos sin lim lim lim36sin lim 1,66x x x x x x x f x x ax x axg x x bx x bx x ax a ax a axbx bx bx a ax a b ax b →→→→→→→--=-⋅---=---⎛⎫=-=-= ⎪⎝⎭等洛洛 即36a b =-,故排除(B ),(C ).另外,201cos lim3x a axbx→--存在,蕴含了1cos 0a ax -→()0x →,故1,a =排除D. 所以本题选(A ).方法2:由泰勒公式3331sin () (0)6ax ax a x x x ο=-+→ 3333001(1)()()6lim lim 1()111, 1 1, .66x x a x a x x f x g x bx a a b b ο→→-++⇒==-⇒=-=⇒==-因此选(A ).【评注】求极限的问题是考试的热点和重点,洛比达法则和等价无穷小替换是常用的计算和简化的方法。
2009年考研数学三答案解析

2009年全国硕士研究生入学统一考试数学三试题及解析一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.(1)函数3()sin x x f x xπ-=的可去间断点的个数为:( )()A .1()B . 2 ()C .3()D .无穷多个【答案】C 【解析】()3s i n x x f x xπ-=则当x 取任何整数时,()f x 均无意义故()f x 的间断点有无穷多个,但可去间断点为极限存在的点,故应是30x x -=的解1,2,30,1x =±320032113211131lim lim sin cos 132lim lim sin cos 132lim lim sin cos x x x x x x x x x x x x x x x x x x x x x ππππππππππππ→→→→→-→---==--==--== 故可去间断点为3个,即0,1±(2)当0x →时,()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小,则( )()A .1a =,16b =-()B . 1a =,16b = ()C .1a =-,16b =- ()D .1a =-,16b =【答案】 A【解析】2()sin ,()(1)f x x ax g x x ln bx =-=-为等价无穷小,则222200000()sin sin 1cos sin lim lim lim lim lim ()ln(1)()36x x x x x f x x ax x ax a ax a ax g x x bx x bx bx bx→→→→→---==-⋅---洛洛230sin lim 166x a ax a b b axa→==-=-⋅ 36a b ∴=- 故排除,B C 。
另外201cos lim3x a axbx→--存在,蕴含了1cos 0a ax -→()0x →故 1.a =排D 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2009年全国硕士研究生入学统一考试
数学三试题
一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一个选项是符合题目要求的,请把所选项前的字母填在答题纸指定位置上.
(1)函数3
()sin x x f x x
π-=的可去间断点的个数为
(A)1. (B)2. (C)3. (D)无穷多个.
(2)当0x →时,()sin f x x ax =-与2
()ln(1)g x x bx =-是等价无穷小,则
(A)1a =,16b =-. (B )1a =,16b =. (C)1a =-,16b =-. (D )1a =-,1
6
b =.
(3)使不等式
1
sin ln x
t
dt x t
>⎰
成立的x 的范围是 (A)(0,1).
(B)(1,
)2π
. (C)(,)2
π
π. (D)(,)π+∞.
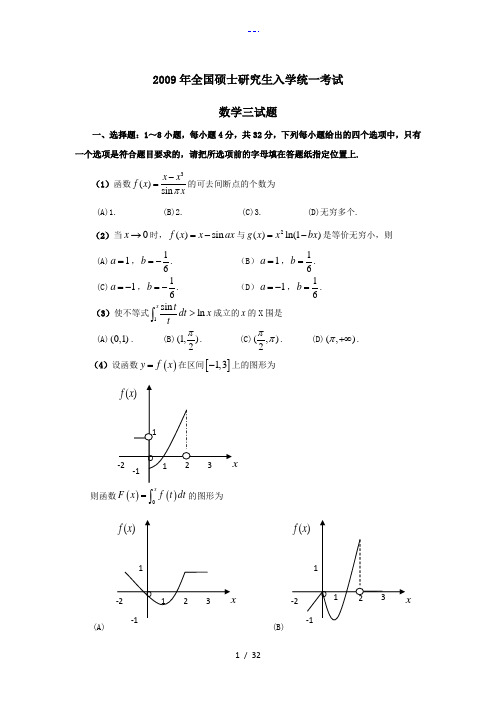
(4)设函数()y f x =在区间[]1,3-上的图形为:
则函数()()0x
F x f t dt =⎰的图形为( ).
(A ) (B )
(C ) (D )
(5)设,A B 均为2阶矩阵,*
,A B *
分别为,A B 的伴随矩阵,若||2,||3A B ==,则分块矩
阵O A B O ⎛⎫
⎪⎝⎭
的伴随矩阵为
(A)**32O B A O ⎛⎫ ⎪⎝⎭.
(B)**
23O
B A
O ⎛⎫
⎪⎝⎭.
(C)**32O A B O ⎛⎫
⎪⎝⎭
.
(D)**
23O A B
O ⎛⎫
⎪⎝⎭
.
(6)设,A P 均为3阶矩阵,T P 为P 的转置矩阵,且100010002T
P AP ⎛⎫ ⎪= ⎪ ⎪⎝⎭
,
若1231223(,,),(,,)P Q ααααααα==+,则T
Q AQ 为
(A)210110002⎛⎫ ⎪ ⎪ ⎪⎝⎭. (B)110120002⎛⎫
⎪
⎪ ⎪⎝⎭.
(C)200010002⎛⎫ ⎪ ⎪ ⎪⎝⎭. (D)100020002⎛⎫ ⎪ ⎪ ⎪⎝⎭
.
(7)设事件A 与事件B 互不相容,则
(A)()0P AB =.
(B)()()()P AB P A P B =. (C)()1()P A P B =-.
(D)()1P A B ⋃=.
(8)设随机变量X 与Y 相互独立,且X 服从标准正态分布(0,1)N ,Y 的概率分布为
1
{0}{1}2
P Y P Y ====
,记()z F Z 为随机变量Z XY =的分布函数,则函数()z F Z 的间断点个数为 (A) 0. (B)1. (C)2 .
(D)3.
二、填空题:9~14小题,每小题4分,共24分,请将答案写在答题纸指定位置上. (9
)cos 0x x →= .
(10)设()y x
z x e =+,则
(1,0)
z
x ∂=∂ .
(11)幂级数2
1
(1)n n n
n e x n ∞
=--∑的收敛半径为 . (12)设某产品的需求函数为()Q Q P =,其对应价格P 的弹性0.2p ξ=,则当需求量为10000件时,价格增加1元会使产品收益增加 元.
(13)设(1,1,1)T α=,(1,0,)T k β=,若矩阵T
αβ相似于300000000⎛⎫
⎪ ⎪ ⎪⎝⎭
,则k = .
(14)设1X ,2X ,…,n X 为来自二项分布总体(,)B n p 的简单随机样本,X 和2
S 分别为样本均值和样本方差,记统计量2
T X S =-,则ET = .
三、解答题:15~23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤. (15)(本题满分9分) 求二元函数()
22(,)2ln f x y x y y y =++的极值.
(16)(本题满分10 分)
计算不定积分ln(1dx +
⎰
(0)x >.
(17)(本题满分10 分) 计算二重积分
()D
x y dxdy -⎰⎰
,其中22
{(,)(1)(1)2,}D x y x y y x =-+-≤≥.
(18)(本题满分11 分)
(Ⅰ)证明拉格朗日中值定理,若函数()f x 在[],
a b 上连续,在(),a b 上可导,则
(),a b ξ∈,得证()'()()()f b f a f b a ξ-=-.
(Ⅱ)证明:若函数()f x 在0x =处连续,在()0,
,(0)σσ>内可导,且'0lim ()x f x A +
→=,
则'(0)f +存在,且'
(0)f A +=.
(19)(本题满分10 分)
设曲线()y f x =,其中()f x 是可导函数,且()0f x >.已知曲线()y f x =与直线
0,1y x ==及(1)x t t =>所围成的曲边梯形绕x 轴旋转一周所得的立体体积值是该曲边梯
形面积值的t π倍,求该曲线的方程.
(20)(本题满分11 分)
设 111A=111042--⎛⎫ ⎪- ⎪ ⎪--⎝⎭,1112ξ-⎛⎫
⎪
= ⎪ ⎪-⎝⎭
.
(Ⅰ)求满足21A ξξ=,2
31A ξξ=的所有向量2ξ,3ξ.
(Ⅱ)对(Ⅰ)中的任意向量2ξ,3ξ,证明1ξ,2ξ,3ξ线性无关.
(21)(本题满分11 分)
设二次型222
1231231323(,,)(1)22f x x x ax ax a x x x x x =++-+-.
(Ⅰ)求二次型f 的矩阵的所有特征值.
(Ⅱ)若二次型f 的规范形为22
11y y +,求a 的值.
(22)(本题满分11 分)
设二维随机变量(,)X Y 的概率密度为0(,)0
x e y x f x y -⎧<<=⎨
⎩其他
(Ⅰ)求条件概率密度()Y X f y x ; (Ⅱ)求条件概率11P X Y =⎡≤≤⎤⎣⎦.
(23)(本题满分11分)
袋中有一个红球,两个黑球,三个白球,现在放回的从袋中取两次,每次取一个,求以X 、Y 、Z 分别表示两次取球所取得的红、黑与白球的个数. (Ⅰ)求10P X Z ⎡==⎤⎣⎦;
(Ⅱ)求二维随机变量(,)X Y 的概率分布.。
