类比探究—直角结构(含答案)1

合集下载

类比探究(习题及答案)

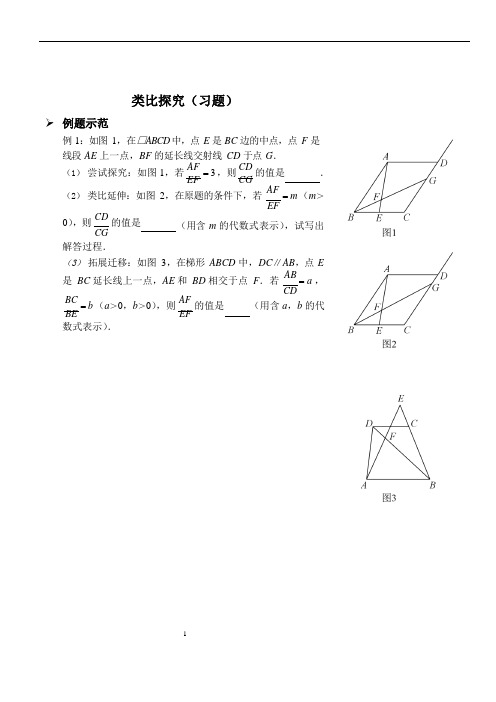
➢例题示范类比探究（习题）例1：如图1，在□ABCD 中，点E 是BC 边的中点，点F 是线段AE 上一点，BF 的延长线交射线CD 于点G．（1）尝试探究：如图1，若AF= 3 ，则CD的值是．EF CG（2）类比延伸：如图2，在原题的条件下，若AF=m （m＞EF0），则CD的值是CG解答过程．（用含m 的代数式表示），试写出（3）拓展迁移：如图3，在梯形ABCD 中，DC∥AB，点E是BC 延长线上一点，AE 和BD 相交于点F．若AB=a ，CDBC=b（a＞0，b＞0），则AF的值是（用含a，b 的代BE EF 数式表示）．1【思路分析】根据特征确定问题结构，设计方案解决第一问．问题背景是平行四边形，且已知线段比例关系，考虑通过相似传递比例关系，进而求 CD的值．CG构造相似利用作平行线的方法，即过中点 E 作 EH ∥AB 交 BG于点 H ，可得“A ”字型相似△BEH ∽△BCG ，“X ”型相似△EFH ∽△AFB ，结合 AF= 3 ，可得 CG =2EH ，AB =3EH ，故EFCD = 3 ．CG 2类比第一问思路，解决第二问．分析不变特征，此时平行四边形、中点特征均不变，变化的是 AF ，EF 的比例，照搬第一问思路，过点 E 作 EH ∥AB 交BG 于点 H ，同样可得△BEH ∽△BCG ，△EFH ∽△AFB ，此时 CG =2EH ，AB =mEH ，故 CD = m．CG 2照搬思路解决第三问．虽然此问中图形、中点 E 、比例关系均发生变化，但 DC ∥AB 不变，依然可利用相似来整合条件，可照搬前面思路处理，依然构造平行．过点 E 作 EH ∥AB 交 BD 的延长线于点 H ，可得△BCD ∽△BEH ，△AFB ∽△EFH ，可得 BC = CD，BE EHAF = AB ，结合 AB = a ， BC = b ，可知 EF EH CD BE AF = AB = a ⋅CD = ab ． EF EH EH212 3➢巩固练习1.如图1，一副直角三角板满足AB=BC，AC=DE，∠ABC=∠DEF=90°，∠EDF=30°．【操作】将三角板DEF 的直角顶点E 放置于三角板ABC 的斜边AC 上，再将三角板DEF 绕点E 旋转，并使边DE 与边AB 交于点P，边EF 与边BC 交于点Q．【探究】在旋转过程中，（1）如图2，当CE=1时，EP 与EQ 满足怎样的数量关系？EA并给出证明．（2）如图3，当CE= 2 时，EP 与EQ 满足怎样的数量关系？EA并给出证明．（3）根据你对（1），（2）的探究结果，试写出当CE=m时，EAEP 与EQ 满足的数量关系式为．3，=2.如图1，在等边三角形ABC 中，线段AD 为其内角角平分线，过点D 的直线B1C1⊥AC 于C1，交AB 的延长线于B1．（1）请你探究：AC =CD AC1 C1D 是否都成立？AB BD AB1DB1（2）请你继续探究：如图2，若△ABC 为任意三角形，线段AD 为其内角角平分线，请问AC=CD一定成立吗？并证明AB BD你的判断．（3）如图3，在Rt△ABC 中，∠ACB=90°，AC=8，AB=40，3E 为AB 上一点且AE=5，CE 交其内角角平分线AD 于F．试求DF的值．FA43.如图1，将两个完全相同的三角形纸片ABC 和DEC 重合放置，其中∠C =90°，∠B =∠E =30°．（1）操作发现如图 2，固定△ABC ，使△DEC 绕点 C 旋转，当点 D 恰好落在 AB 边上时，填空：①线段 DE 与 AC 的位置关系是；②设△BDC 的面积为 S 1，△AEC 的面积为 S 2，则 S 1 与 S 2 的数量关系是．图 1图 2（2）猜想论证当△DEC 绕点 C 旋转到图 3 所示的位置时，小明猜想（1）中 S 1 与 S 2 的数量关系仍然成立，并尝试分别作出了△BDC 和△AEC 中 BC ，CE 边上的高，请你证明小明的猜想．（3）拓展探究如图 4 ，已知∠ ABC =60°，点 D 是其角平分线上一点， BD =CD =4，DE ∥AB 交 BC 于点 E ．若在射线 BA 上存在点 F ，使 S △DCF =S △BDE ，请直．接．写．出．相应的 BF 的长．5➢思考小结总结类比探究问题中的常见结构①旋转结构始终含有等腰结构（正方形、等腰直角三角形等），并且经过旋转后，能将各条件重新组合应用．②中点结构平行夹中点（类）倍长中线中位线始终含有中点，常考虑利用中点结构补全图形，然后将所证目标放在一个较大的背景下（等腰三角形、直角三角形、等腰直角三角形等）研究．③直角结构始终含有直角，常构造直角与斜直角配合，得到同角的余角相等；再配合构造的其他直角证明相似，所求目标往往和比例关系相关．6④平行结构所求目标为线段间的比例关系，题目中没有相似三角形，往往考虑利用平行线构造相似求解．78 3 3 【参考答案】 ➢ 巩固练习1. （1）EP =EQ ，证明略；（2） EP = 1EQ ，证明略；2 （3） EP = 1EQ ．m2. （1）都成立，证明略；（2）一定成立，证明略；（3） DF = 5 ．FA 83. （1）①DE ∥AC ；②S 1=S 2．（2）证明略；（3） BF 的长为4 3或．38。

几何类比探究题型-2024年中考数学答题技巧与模板构建(解析版)

几何类比探究题型题型解读|模型构建|通关试练几何的类比探究题型是近年中招解答题的必考题型，该题型往往以压轴题的形式出现，有一定的难度。

探究型问题是指命题中缺少一定的条件或无明确的结论，需要经过推断，补充并加以证明的一类问题．根据其特征大致可分为：条件探究型、结论探究型、规律探究型和存在性探究型等四类。

由于探究型试题的知识覆盖面较大，综合性较强，灵活选择方法的要求较高，再加上题意新颖，构思精巧，具有相当的深度和难度，所以要求同学们在复习时，首先对于基础知识一定要复习全面，并力求扎实牢靠；其次是要加强对解答这类试题的练习，注意各知识点之间的因果联系，选择合适的解题途径完成最后的解答．模型01图形旋转模型模型一、A字形(手拉手)及其旋转模型二、K字型及其旋转手拉手模型是有两个等腰的三角形或者两个等边的三角形，他们有一个共同的顶点，且两个等腰三角形的顶角是相等的，那么就可以用角的和差求得共顶点的另外两个角相等等，然后利用等腰的边对应相等，可证明两个三角形全等(边角边)组成这样的图形模样的我们就说他是手拉手模型。

在类比探究题型中，往往会对等腰三角形或者等边三角形进行演变，变成一般三角形进行旋转，通常全等三角形变为相似三角形。

模型特征：双等腰；共顶点；顶点相等；绕着顶点作旋转解题依据：等腰共顶手拉手，旋转全等马上有；左手拉左手，右手拉右手，两根拉线抖一抖，它们相等不用愁；拉线夹角与顶角，相等互补答案有。

模型02图形平移模型探究1.四边形平移变换四边形的平移变换题型中主要考查了全等三角形的判定和性质，相似三角形的判定和性质，平移几何性质、三角形内角和定理的应用，勾股定理，解题的关键是熟练掌握三角形全等或相似的判定方法，画出相应的图形，注意分类讨论．2.三角形平移变换三角形平移变换主要利用三角形全等和三角形相似的判定和性质，勾股定理，矩形的判定和性质，平移性质、平行线的判定和性质，解题的关键是作出辅助线，熟练掌握三角形相似的判定方法.3.其它图形平移类比探究问题综合考查了全等三角形的判定和性质，相似三角形的判定和性质，三角形内角和定理的应用，勾股定理，解题的关键是熟练掌握三角形相似的判定方法，画出相应的图形，注意分类讨论.模型03动点引起的题型探究动点型问题是指题设中的图形中存在一个或多个动点，它们在线段、射线、直线、抛物线、双曲线、弧线等上运动的一类非常具有开放性的题目。

类比探究(人教版)(含答案)

类比探究（人教版）一、单选题(共9道，每道11分)1.如图1，△ABC的边BC在直线l上，AC⊥BC，且AC=BC；△EFP的边FP也在直线l上，边EF与边AC重合，且EF=FP．如图1，易证AB=AP，且AB⊥AP.（1）将△EFP沿直线l向左平移到图2的位置时，EP交AC于点O，连接AP，BO．则BO与AP所满足的数量及位置关系是( )A.相等但不垂直B.不相等但垂直C.相等且垂直D.不相等也不垂直答案：C解题思路：试题难度：三颗星知识点：类比探究2.（上接第1题）（2）将△EFP沿直线l继续向左平移到图3的位置时，EP的延长线交AC 的延长线于点O，连接AP，BO．此时，BO与AP的数量关系和位置关系是( )A.相等但不垂直B.不相等但垂直C.相等且垂直D.不相等也不垂直答案：C解题思路：试题难度：三颗星知识点：类比探究3.已知：如图，在Rt△ABC中，AB＝BC，∠ABC＝90°．一块等腰直角三角板的直角顶点放在斜边AC的中点O处，将三角板绕点O旋转，三角板的两直角边分别交AB，BC或其延长线于点E，F，图1，图2是旋转三角板所得图形的两种情况．（1）如图1，当点E和点F分别在AB和BC边上时，OE和OF的大小关系是( )A.OE＞OFB.OE=OFC.OE<OFD.无法确定答案：B解题思路：试题难度：三颗星知识点：类比探究4.（上接第3题）（2）如图2，当点E和点F分别在AB和BC边的延长线上时，OE和OF的大小关系是( )A.OE＞OFB.OE=OFC.OE<OFD.无法确定答案：B解题思路：试题难度：三颗星知识点：类比探究5.如图1，在正方形ABCD和正方形CGEF（CG＞BC）中，点B，C，G在同一直线上，点M是AE的中点。

（1）探究线段MD，MF的位置关系，并证明。

解题思路：（1）小明猜测MD⊥MF，看到图1中M是AE的中点，并且AD∥EF，考虑延长DM交EF于点H，如下图，先利用全等三角形的判定定理_____，证明_____，由全等的性质可以得到_____，所以CD＝EH，进而可以得到FD＝FH，在等腰△DFH中，由等腰三角形三线合一可以得到_____，从而证明结论。

类比探究之结构类比((类)倍长中线)(北师版)(含答案)

学生做题前请先回答以下问题问题1：类比探究属于几何综合题，解决此问题的主要方法是什么？问题2：目前我们所学的结构类比中有两种结构，分别是什么？问题3：如图1，△ABC和△BDE均为等腰直角三角形，BA⊥AC，ED⊥BD，点D在AB边上．连接EC，取EC的中点F，连接AF，DF．为了证明FA⊥FD，FA=FD，我们只需要延长DF交线段AC于点G，说明AF是等腰直角三角形ADG的中线即可．将△BDE旋转至如图2所示的位置，使点E在AB的延长线上，点D在CB的延长线上，其他条件不变，类比上面的做法，为了证明FA⊥FD，FA=FD，我们需要作的辅助线是( )A．连接ADB．过点C作CG⊥DF，交DF的延长线于点GC．延长DF到G，使FG=DF，连接CG，AD，AGD．延长DF交AC的延长线于点G，连接AD分析题目中的不变特征，画出其线路图.类比探究之结构类比（（类）倍长中线）（北师版）一、单选题(共5道，每道20分)1.如图1，△ABC和△BDE均为等腰直角三角形，BA⊥AC，ED⊥BD，点D在AB边上．连接EC，取EC的中点F，连接AF，DF．为了证明FA⊥FD，FA=FD，我们只需要延长DF交线段AC于点G，说明AF是等腰直角三角形ADG的中线即可．将△BDE旋转至如图2所示的位置，使点E在AB的延长线上，点D在CB的延长线上，其他条件不变，类比上面的做法，为了证明FA⊥FD，FA=FD，我们需要作的辅助线是( )A.连接ADB.过点C作CG⊥DF，交DF的延长线于点GC.延长DF到G，使FG=DF，连接CG，AD，AGD.延长DF交AC的延长线于点G，连接AD答案：C解题思路：试题难度：三颗星知识点：类比探究问题2.在试题1图2的证明中，说明△ADG是等腰直角三角形之前，证明AD=AG需要直接使用到某对三角形全等，则判定这对三角形全等的条件是( )A.AASB.ASAC.SSSD.SAS答案：D解题思路：试题难度：三颗星知识点：类比探究问题3.已知等腰直角三角形ABC中，D为斜边BC上一点，过D点作DE⊥BC交AB于E，连接CE，F为CE中点，连接AF、DF，易证AF=DF；（1）若将图①中△BDE绕点B顺时针旋转45°，如图②所示，取CE的中点F，连接AF、DF，则下列结论中错误的是( )．A.AF=DFB.C. D.AF⊥DF答案：B解题思路：故选B．试题难度：三颗星知识点：类比探究问题4.（上接试题3）（2）将图①中△BDE绕B点旋转任意角度，如图③所示，再连接相应的线段，则（1）中的结论中，AF=DF以及AF⊥DF仍然成立，我们需要作的辅助线是( )A.连接ADB.过点C作CM⊥DF，交DF的延长线于点MC.延长AF到M，使FM=AF，连接DM，AD，EMD.延长DF交AC的于点M，连接AD答案：C解题思路：试题难度：三颗星知识点：类比探究问题5.（上接试题3,4）（3）如图③，说明△ADM是等腰直角三角形之前，证明AD=DM需要直接使用到某对三角形全等，则判定这对三角形全等的条件是( )A.AASB.ASAC.SSSD.SAS答案：D解题思路：试题难度：三颗星知识点：类比探究问题。

三角形全等之类比探究-经典题型过关(含答案)

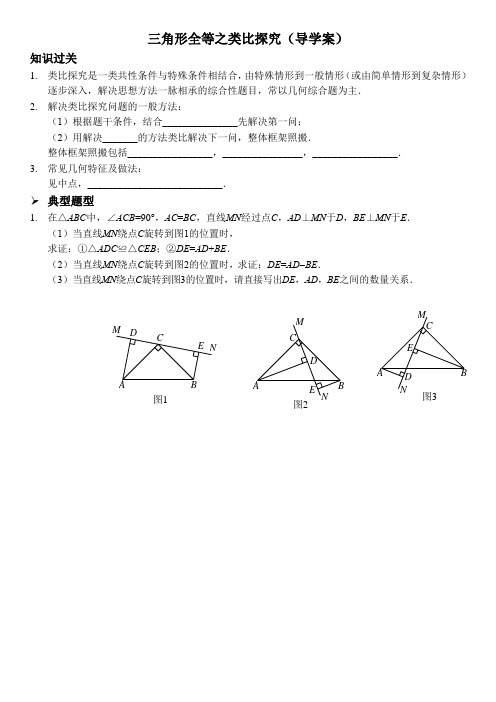
三角形全等之类比探究（导学案）知识过关1. 类比探究是一类共性条件与特殊条件相结合，由特殊情形到一般情形（或由简单情形到复杂情形）逐步深入，解决思想方法一脉相承的综合性题目，常以几何综合题为主． 2. 解决类比探究问题的一般方法：（1）根据题干条件，结合_______________先解决第一问；（2）用解决_______的方法类比解决下一问，整体框架照搬．整体框架照搬包括_________________，________________，_________________． 3. 常见几何特征及做法：见中点，___________________________．➢ 典型题型1. 在△ABC 中，∠ACB =90°，AC =BC ，直线MN 经过点C ，AD ⊥MN 于D ，BE ⊥MN 于E ．（1）当直线MN 绕点C 旋转到图1的位置时，求证：①△ADC ≌△CEB ；②DE =AD +BE ．（2）当直线MN 绕点C 旋转到图2的位置时，求证：DE =AD BE ．（3）当直线MN 绕点C 旋转到图3的位置时，请直接写出DE ，AD ，BE 之间的数量关系．图1B NE CDM A图2ACDEMNB 图3ABC D EM N2. 如图1，四边形ABCD 是正方形，AB =BC ，∠B =∠BCD =90°，点E 是边BC 的中点，∠AEF =90°，EF 交正方形外角∠DCG 的平分线CF 于点F ．（1）求证：AE =EF （提示：在AB 上截取BH =BE ，连接HE ，构造全等三角形，经过推理使问题得到解决）．（2）如图2，如果把“点E 是边BC 的中点”改为“点E 是边BC 上（除B ，C 外）的任意一点”，其他条件不变，那么结论“AE =EF ”仍然成立吗？说明理由．（3）如图3，点E 是BC 的延长线上（除C 点外）的任意一点，其他条件不变，结论“AE =EF ”是否成立？说明理由．GABCDFE 图1E FDC BA G图2FDC A G图3图1M ADC E3. 以△ABC 的边AB ，AC 为直角边向外作等腰直角三角形ABE 和等腰直角三角形ACD ，∠BAE =∠CAD =90°，AB =AE ，AC =AD ，M 是边BC 的中点，连接AM ，DE ．（1）如图1，在△ABC 中，当∠BAC =90°时，求AM 与DE 的数量关系和位置关系．（2）如图2，当△ABC 为一般三角形时，（1）中的结论是否成立？并说明理由．（3）如图3，若以△ABC 的边AB ，AC 为直角边向内作等腰直角三角形ABE 和等腰直角三角形ACD ，其他条件不变，（1）中的结论是否成立，并说明理由．4. （1）如图1，已知∠MAN =120°，AC 平分∠MAN ，∠ABC =∠ADC =90°，则能得到如下两个结论： ①DC =BC ；②AD +AB =AC ．请你证明结论②．（2）如图2，把（1）中的条件“∠ABC =∠ADC =90°”改为“∠ABC +∠ADC =180°”，其他条件不变，则（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．（3）如图3，如果D 在AM 的反向延长线上，把（1）中的条件“∠ABC =∠ADC =90°”改为“∠ABC =∠ADC ”，其他条件不变，（1）中的结论是否仍然成立？若成立，请直接回答；若不成立，请直接写出你的结论．E D A M 图2B MCEA D图3A B CDMN图3图1NMDCBA B CDMN图2【参考答案】➢ 知识过关：解决类比探究问题的一般方法：（1）根据题干条件，结合分支条件先解决第一问；（2）用解决第（1）问的方法类比解决下一问，整体框架照搬．整体框架照搬包括照搬字母，照搬辅助线，照搬思路．常见几何特征及做法：见中点，考虑倍长中线． ➢ 典型题型1. 证明：（1）如图，∵∠ACB =90° ∴∠1+∠2=90° ∵AD ⊥MN ，BE ⊥MN ∴∠ADC =∠CEB =90° ∴∠3+∠2=90° ∴∠1=∠3在△ADC 和△CEB 中∴△ADC ≌△CEB (AAS) ∴AD =CE ，DC =EB ∴DE =CE +DC=AD +BE （2）如图，∵∠ACB =90° ∴∠1+∠2=90° ∵AD ⊥MN ，BE ⊥MN ∴∠ADC =∠CEB =90° ∴∠CBE +∠2=90° ∴∠1=∠CBE 在△ADC 和△CEB 中∴△ADC ≌△CEB (AAS) ∴AD =CE ，DC =EB ∴DE =CE -DC=AD -BE13ADC CEB AC CB ∠=∠⎧⎪∠=∠⎨⎪=⎩1ADC CEB CBEAC CB ∠=∠⎧⎪∠=∠⎨⎪=⎩321AM DC E NB321NM ED C BA（3）DE =BE -AD ，理由如下：如图，∵∠ACB =90° ∴∠1+∠2=90° ∵AD ⊥MN ，BE ⊥MN ∴∠ADC =∠CEB =90° ∴∠3+∠2=90° ∴∠1=∠3在△ADC 和△CEB 中∴△ADC ≌△CEB (AAS) ∴AD =CE ，DC =EB ∴DE =DC -CE=BE -AD2. 解：（1）AE =EF ，理由如下：如图，在AB 上截取BH =BE ，连接HE ．∵AB =BC ∴AH =EC ∵∠B =90° ∴∠1=∠2=45° ∴∠AHE =135° ∵∠BCD =90° ∴∠DCG =90° ∵CF 平分∠DCG ∴∠GCF =45° ∴∠ECF =135° ∴∠AHE =∠ECF ∵∠AEF =90°，∠B =90°∴∠AEB +∠3=90°，∠AEB +∠4=90° ∴∠3=∠4在△AHE 和△ECF 中∴△AHE ≌△ECF (ASA) ∴AE =EF（2）AE =EF 仍成立，理由如下：13ADC CEB AC CB ∠=∠⎧⎪∠=∠⎨⎪=⎩43AH ECAHE ECF ∠=∠⎧⎪=⎨⎪∠=∠⎩21B NM EDC A4321H GA B CDFE如图，在AB 上截取BH =BE ，连接HE ．∵AB =BC ∴AH =EC ∵∠B =90° ∴∠1=∠2=45° ∴∠AHE =135° ∵∠BCD =90° ∴∠DCG =90° ∵CF 平分∠DCG ∴∠GCF =45° ∴∠ECF =135° ∴∠AHE =∠ECF ∵∠AEF =90°，∠B =90°∴∠AEB +∠3=90°，∠AEB +∠4=90° ∴∠3=∠4在△AHE 和△ECF 中∴△AHE ≌△ECF (ASA) ∴AE =EF（3）AE =EF 仍成立，理由如下：如图，延长BA 到H ，使BH =BE ，连接HE ．∵AB =BC ∴AH =EC ∵∠B =90° ∴∠H =45° ∵∠BCD =90° ∴∠DCG =90° ∵CF 平分∠DCG ∴∠1=45° ∴∠H =∠1∵∠AEF =90°，∠B =90°∴∠AEB +∠3=90°，∠AEB +∠2=90° ∴∠2=∠3∵∠HAE +∠2=180°，∠CEF +∠3=180° ∴∠HAE =∠CEF 在△AHE 和△ECF 中43AH ECAHE ECF ∠=∠⎧⎪=⎨⎪∠=∠⎩H 4123E FDC BA G∴△AHE ≌△ECF (ASA) ∴AE =EF3. 解：（1）DE =2AM ，AM ⊥DE ，理由如下：如图，延长AM 到F ，使MF =AM ，连接BF ，延长MA 交DE 于G ．∴AF =2AM ∵M 是BC 中点 ∴BM =CM在△BMF 和△CMA 中∴△BMF ≌△CMA (SAS) ∴FB =AC ，∠3=∠4 ∴BF ∥AC∴∠FBA +∠BAC =180° ∵∠BAE =∠CAD =90° ∴∠DAE +∠BAC =180° ∴∠FBA =∠DAE ∵AC =AD ∴BF =AD在△FBA 和△DAE 中∴△FBA ≌△DAE (SAS) ∴AF =ED ，∠5=∠6 ∴DE =2AM ∵∠BAE =90° ∴∠5+∠7=90° ∴∠6+∠7=90° ∴∠EGA =90° 即AM ⊥DE（2）（1）中的结论成立，理由如下：如图，延长AM 到F ，使MF =AM ，连接BF ，延长MA 交DE 于G ．∴AF =2AM ∵M 是BC 中点1H AH ECHAE CEF ∠=∠⎧⎪=⎨⎪∠=∠⎩12BM CM MF MA =⎧⎪∠=∠⎨⎪=⎩BF AD FBA DAE AB EA =⎧⎪∠=∠⎨⎪=⎩H123FDB AG∴BM =CM在△BMF 和△CMA 中∴△BMF ≌△CMA (SAS) ∴FB =AC ，∠3=∠4 ∴BF ∥AC∴∠FBA +∠BAC =180° ∵∠BAE =∠CAD =90° ∴∠DAE +∠BAC =180° ∴∠FBA =∠DAE ∵AC =AD ∴BF =AD在△FBA 和△DAE 中∴△FBA ≌△DAE (SAS) ∴AF =ED ，∠5=∠6 ∴DE =2AM ∵∠BAE =90° ∴∠5+∠7=90° ∴∠6+∠7=90° ∴∠EGA =90° 即AM ⊥DE（3）（1）中的结论成立，理由如下：如图，延长AM 到F ，使MF =AM ，交DE 于G ，连接BF ．∴AF =2AM ∵M 是BC 中点 ∴BM =CM在△BMF 和△CMA 中∴△BMF ≌△CMA (SAS) ∴FB =AC ，∠FBM =∠ACM ∴BF ∥AC∴∠FBA +∠BAC =180°12BM CM MF MA =⎧⎪∠=∠⎨⎪=⎩BF AD FBA DAE AB EA =⎧⎪∠=∠⎨⎪=⎩BM CM BMF CMA MF MA =⎧⎪∠=∠⎨⎪=⎩FGD A EC MB∵∠BAE =∠CAD =90°∠BAC =∠BAE +∠CAD -∠DAE ∴∠DAE +∠BAC =180° ∴∠FBA =∠DAE ∵AC =AD ∴BF =AD在△FBA 和△DAE 中∴△FBA ≌△DAE (SAS) ∴AF =ED ，∠BAF =∠AED ∴DE =2AM ∵∠BAE =90° ∴∠BAF +∠EAF =90° ∴∠AED +∠EAF =90° ∴∠EGA =90° 即AM ⊥DE4. （1）证明：如图，在BN 上截取BE=AD ．∵AC 平分∠DAB ，∠MAN =120° ∴∠1=∠2=60° 在△CDA 和△CBA 中∴△CDA ≌△CBA (AAS) ∴DC =BC ，AD =AB 在△CDA 和△CBE 中∴△CDA ≌△CBE (SAS) ∴AC =EC ∵∠2=60°∴AC=AE =BE+AB =AD+AB（2）成立，证明如下：如图，过C 作CG ⊥AM 于G ，CF ⊥AN 于F ，在BN 上截取BE=AD ．BF AD FBA DAE AB EA =⎧⎪∠=∠⎨⎪=⎩12CDA CBA CA CA ∠=∠⎧⎪∠=∠⎨⎪=⎩DC BC CDA CBE AD EB =⎧⎪∠=∠⎨⎪=⎩21E图1NM DCB A∵CG ⊥AM ，CF ⊥AN ∴∵AC 平分∠DAB ，∠MAN =120° ∴∠1=∠2=60°，CG=CF ∵∠ABC +∠ADC =180° ∠CDG +∠ADC =180° ∠ABC +∠EBC =180°∴∠CDG =∠CBF ，∠ADC =∠EBC 在△CGD 和△CFB 中∴△CGD ≌△CFB （AAS ） ∴CD =CB在△CDA 和△CBE 中三角形全等之类比探究（实战演练）1. 在四边形ABCD 中，AB =AD ，∠BAD =90°，P 是直线CD 上一点，连接PA ，过点B ，D 作BE ⊥PA ，DF ⊥PA ，垂足分别为点E ，F ．（1）如图1，请探究BE ，DF ，EF 这三条线段的数量关系．（2）若点P 在DC 的延长线上，如图2，则这三条线段又具有怎样的数量关系？（3）若点P 在CD 的延长线上，如图3，直接写出BE ，DF ，EF 这三条线段的数量关系．【参考答案】CGD CFB ∠=∠CDG CBF CGD CFB CG CF ∠=∠⎧⎪∠=∠⎨⎪=⎩CD CB ADC AD EB =⎧⎪∠=⎨⎪=⎩G FE A B C DMN图3图3图2图1PABCDEFP FED CBA PF EDCBA1. （1）EF=BE -DF ，证明略（2）EF= DF -BE ，证明略（3）EF=BE +DF 路线图：(AAS) 123ABE DAF AE DF BE AF EF AF AEBE DFEF AE AFDF BEEF AF AEDF BE↓==↓=-=-=-=-=+=+△≌△（）（）（）三角形全等之类比探究（作业）➢ 例题示范例1：已知，在△ABC 中，∠BAC =90°，AB =AC ，点D 为直线BC 上一动点（点D 不与点B ，C 重合）．以AD 为边作正方形ADEF ，AD =AF ，∠DAF =90°，连接CF ．（1）如图1，当点D 在线段BC 上时，求证：CF +CD =BC ；（2）如图2，当点D 在线段BC 的延长线上时，其他条件不变，请直接写出CF ，BC ，CD 三条线段之间的关系；（3）如图3，当点D 在线段BC 的反向延长线上时，且点A ，F 分别在直线BC 的两侧，其他条件不变，求CF ，BC ，CD 三条线段之间的关系．【思路分析】结合题目特征，本题为类比探究问题．解决方法：（1）根据题目条件及（1）问中D 在线段BC 上，证明△ABD ≌△ACF ，就可以得出BD =CF ，结论可证．图2图1ABCDEFFED CBA图3AB CDF 图1FED CBA（2）用解决第（1）问的方法解决后续问题，方法上完全照搬．如图2，通过证明△ABD ≌△ACF ，就可以得出BD =CF ，进而得到BC +CD =CF ；如图3，通过证明△ABD ≌△ACF ，就可以得出BD =CF ，进而得到BC +CF =CD ．【过程书写】证明：如图，∵∠DAF =90°，∠BAC =90° ∴∠BAD =∠CAF 在△BAD 和△CAF 中，AB AC BAD CAF AD AF =⎧⎪∠=∠⎨⎪=⎩∴△BAD ≌△CAF （SAS ） ∴BD =CF ∵BD +CD =BC ∴CF +CD =BC （2）BC +CD =CF（3）BC +CF =CD ，理由如下： ∵∠DAF =90°，∠BAC =90° ∴∠BAD =∠CAF 在△BAD 和△CAF 中，∴△BAD ≌△CAF （SAS ） ∴BD =CF ∵BC +BD =CD ∴BC +CF =CD➢ 巩固练习1. 已知AB ⊥BD ，ED ⊥BD ，AC ⊥CE ，BC =DE ，如图1．（1）求证：AC =CE ．（2）若将△ECD 沿CB 方向平移至如图2的位置（C 1，C 2不重合），其余条件不变，结论AC 1=C 2E 还成立吗？请说明理由．（3）若将△ECD 沿CB 方向平移至如图3的位置（B ，C 2重合），其余条件不变，结论AC 1=C 2E 还成立吗？请说明理由．AB AC BAD CAF AD AF =⎧⎪∠=∠⎨⎪=⎩图3图2图1A C DEEDAEDB (C 2)AC 2C 1C 1图3AB CDEF图2图1CE MN NM D C BA2. （1）【问题发现】小明学习中遇到这样一个问题：如图1，△ABC 是等边三角形，点D 为BC 的中点，且满足∠ADE =60°，DE 交等边三角形外角平分线CE 所在直线于点E ，试探究AD 与DE 的数量关系．小明发现，过点D 作DF ∥AC ，交AB 于点F ，通过构造全等三角形，经过推理论证，能够使问题得到解决，请直接写出AD 与DE 的数量关系：_______________；（2）【类比探究】如图2，当点D 是线段BC 上（除B ，C 外）任意一点时（其他条件不变），试猜想AD 与DE 之间的数量关系，并证明你的结论；（3）【拓展应用】如图3，当点D 在线段BC 的延长线上（其他条件不变），试猜想AD 与DE 之间的数量关系，并证明你的结论．3. 如图1所示，在△ABC 和△ADE 中，AB =AC ，AD =AE ，∠BAC =∠DAE ，且点B ，A ，D 在一条直线上，连接BE ，CD ，M ，N 分别为BE ，CD 的中点，连接AM ，AN ，MN ．（1）求证：①BE =CD ；②△AMN 是等腰三角形．（2）在图1的基础上，将△ADE 绕点A 按顺时针方向旋转180°，其他条件不变，得到如图2所示的图形．（1）中的两个结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由．图3EDC BA图2E DCBA【参考答案】1. 证明略路线图：(AAS) A DCE ABC CDE AC CE∠=∠↓↓=△≌△ 提示：（1）AC=CE ，由垂直转互余可以得到∠A =∠DCE ，结合BC=DE 证明△ABC ≌△CDE ，得到对应边相等，可以得到AC=CE ．（2）成立，照搬第一问的字母、思路和过程可以得到AC 1=C 2E ．（3）成立，照搬第一问的字母、思路和过程可以得到AC 1=C 2E ． 2. 证明略D DF AC AB F 过点作∥，交于点路线图(AAS) BDF BF BD AF CD ADF DEC AD DE↓==↓↓=△为等边三角形，△≌△ 提示：（1）AD =DE（2）AD =DE 成立，根据△ABC 以及△BDF 是等边三角形，得到AF =DC ，再结合∠ADE =60°，倒角，得到∠DAF =∠EDC ，结合外角平分线，知∠DCE =∠AFD =120°，得到△ADF ≌ △DEC ，得到对应边相等，可得AD =DE ．（3）成立，照搬第二问的字母、思路和过程可以得到AD =DE ．图1F E DC B A3. 证明略路线图(SAS) (SAS) BAE CAD BE CD ABE ACD ABM ACN AM AN AMN ↓=∠=∠↓↓=↓△≌△，△≌△△是等腰三角形提示：（1）由已知条件先证明△BAE ≌△CAD (SAS)，得到BE=CD ，结合第一次全等提供的条件证明△ABM ≌△ACN (SAS)得到AM=AN ，因而△AMN 是等腰三角形．（2）成立，照搬第一问的字母、思路和过程可以得到BE=CD ，△AMN 是等腰三角形．。

中招考试几何类比探究题集锦一参考答案

中招考试几何类比探究题集锦（附参考答案）参考答案与试题解析一．解答题（共11小题）1．在△ABC中，AB=AC，∠BAC=2∠DAE=2α．（1）如图1，若点D关于直线AE的对称点为F，求证：△ABD≌△ACF；（2）如图2，在（1）的条件下，若α=45°，求证：DE2=BD2+CE2；（3）如图3，若α=45°，点E在BC的延长线上，请直接写出DE2，BD2，CE2三者之间的等量关系．【解答】解：（1）∵点D关于直线AE的对称点为F，∴EF=DE，AF=AD，∠DAE=∠EAF=α∴∠CAE+∠CAF=α∵∠BAC=2∠DAE=2α．∴∠BAD+∠CAE=∠BAC﹣∠DAE=α，∴∠BAD=∠CAF，在△ABD和△ACF中，第1页（共33页）第2页（共33页）∴△ABD ≌△ACF （SAS ），（2）由（1）知，△ABD ≌△ACF （SAS ），∴CF=BD ，∠ACF=∠B ，∵AB=AC ，∠BAC=2α，α=45°，∴△ABC 是等腰直角三角形，∴∠B=∠ACB=45°，∴∠ECF=∠ACB +∠ACF=45°+45°=90°，在Rt △CEF 中，由勾股定理得，EF 2=CF 2+CE 2，∴DE 2=BD 2+CE 2，（3）DE 2=BD 2+CE 2；理由：如图，∵∠BAC=2∠DAE=2α．∴∠DAE=α，∵点D 关于直线AE 的对称点为F ，∴EF=DE ，AF=AD ，∠DAE=∠EAF=α∴∠CAF=∠EAF +∠CAE=α+∠CAE∴∠BAD=∠BAC ﹣∠DAC=2α﹣∠DAC=2α﹣（∠DAE ﹣∠CAE ）=2α﹣（α﹣∠CAE）=α+∠CAE∴∠BAD=∠CAF，在△ABD和△ACF中，∴△ABD≌△ACF（SAS），∴CF=BD，∠ACF=∠B，∵AB=AC，∠BAC=2α，α=45°，∴△ABC是等腰直角三角形，∴∠B=∠ACB=45°，∴∠ECF=∠ACB+∠ACF=45°+45°=90°，在Rt△CEF中，由勾股定理得，EF2=CF2+CE2，∴DE2=BD2+CE2，2．（1）如图（1），已知：在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E．猜测DE、BD、CE三条线段之间的数量关系（直接写出结果即可）．（2）如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问第（1）题中DE、BD、CE之间的关系是否仍然成立？如成立，请你给出证明；若不成立，请说明理由．（3）拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF 均为等第3页（共33页）边三角形，连接BD、CE，若∠BDA=∠AEC=∠BAC，试判断线段DF、EF的数量关系，并说明理由．【解答】解：（1）DE=BD+CE．理由如下：如图1，∵BD⊥l，CE⊥l，∴∠BDA=∠AEC=90°又∵∠BAC=90°，∴∠BAD+∠CAE=90°，∠BAD+∠ABD=90°，∴∠CAE=∠ABD在△ABD和△CAE中，，∴△ABD≌△CAE（AAS）∴BD=AE，AD=CE，∵DE=AD+AE，∴DE=CE+BD；（2）如图2，∵∠BDA=∠AEC=∠BAC=α，∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α，第4页（共33页）∴∠CAE=∠ABD，在△ADB和△CEA中，，∴△ADB≌△CEA（AAS），∴AE=BD，AD=CE，∴BD+CE=AE+AD=DE；（3）DF=EF．理由如下：由（2）知，△ADB≌△CAE，BD=EA，∠DBA=∠CAE，∵△ABF和△ACF均为等边三角形，∴∠ABF=∠CAF=60°，∴∠DBA+∠ABF=∠CAE+∠CAF，∴∠DBF=∠FAE，∵BF=AF在△DBF和△EAF中，，∴△DBF≌△EAF（SAS），∴DF=EF，∠BFD=∠AFE，第5页（共33页）∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°，∴△DEF为等边三角形．∴DF=EF．3．（1）问题发现如图1，△ABC和△ADE均为等边三角形，点D在边BC上，连接CE．请填空：①∠ACE的度数为60°；②线段AC、CD、CE之间的数量关系为AC=CD+CE．（2）拓展探究如图2，△ABC和△ADE均为等腰直角三角形，∠BAC=∠DAE=90°，点D在边BC 上，连接CE．请判断∠ACE的度数及线段AC、CD、CE之间的数量关系，并说明理由．（3）解决问题如图3，在四边形ABCD中，∠BAD=∠BCD=90°，AB=AD=2，CD=1，AC与BD交于点E，请直接写出线段AC的长度．第6页（共33页）【解答】解：（1）①∵△ABC和△ADE均为等边三角形，∴AB=AC，AD=AE，∠BAC=∠DAE=∠B=60°，∴∠BAC﹣∠DAC=∠DAE﹣∠DAC，即∠BAD=∠CAE，∴△BAD≌△CAE（SAS），∴∠ACE=∠B=60°，故答案为：60°；②线段AC、CD、CE之间的数量关系为：AC=CD+CE；理由是：由①得：△BAD≌△CAE，∴BD=CE，∵AC=BC=BD+CD，∴AC=CD+CE；故答案为：AC=CD+CE；（2）∠ACE=45°，AC=CD+CE，理由是：如图2，∵△ABC和△ADE均为等腰直角三角形，且∠BAC=∠DAE=90°，∴AB=AC，AD=AE，∠BAC﹣∠DAC=∠DAE﹣∠DAC，即∠BAD=∠CAE，第7页（共33页）∴△ABD≌△ACE，∴BD=CE，∠ACE=∠B=45°，∵BC=CD+BD，∴BC=CD+CE，∵在等腰直角三角形ABC中，BC=AC，∴AC=CD+CE；（3）如图3，过A作AC的垂线，交CB的延长线于点F，∵∠BAD=∠BCD=90°，AB=AD=2，CD=1，∴BD=2，BC=，∵∠BAD=∠BCD=90°，∴∠BAD+∠BCD=180°，∴A、B、C、D四点共圆，∴∠ADB=∠ACB=45°，∴△ACF是等腰直角三角形，由（2）得：AC=BC+CD，∴AC===．第8页（共33页）4．【探究发现】如图1，△ABC是等边三角形，∠AEF=60°，EF交等边三角形外角平分线CF所在的直线于点F，当点E是BC的中点时，有AE=EF成立；【数学思考】某数学兴趣小组在探究AE、EF的关系时，运用“从特殊到一般”的数学思想，通过验证得出如下结论：当点E是直线BC上（B，C除外）任意一点时（其它条件不变），结论AE=EF仍然成立．假如你是该兴趣小组中的一员，请你从“点E是线段BC上的任意一点”；“点E是线段BC延长线上的任意一点”；“点E是线段BC反向延长线上的任意一点”三种情况中，任选一种情况，在备用图1中画出图形，并证明AE=EF．【拓展应用】当点E在线段BC的延长线上时，若CE=BC，在备用图2中画出图形，并运用上述结论求出S△ABC ：S△AEF的值．【解答】证明：第一种情况：点E是线段BC上的任意一点，可作三种辅助线：方法一：如图1，在AB上截取AG，使AG=EC，连接EG，第9页（共33页）∵△ABC是等边三角形，∴AB=BC，∠B=∠ACB=60°．∵AG=EC，∴BG=BE，∴△BEG是等边三角形，∠BGE=60°，∴∠AGE=120°．∵FC是外角的平分线，∠ECF=120°=∠AGE．∵∠AEC是△ABE的外角，∴∠AEC=∠B+∠GAE=60°+∠GAE．∵∠AEC=∠AEF+∠FEC=60°+∠FEC，∴∠GAE=∠FEC．在△AGE和△ECF中，∴△AGE≌△ECF（ASA），∴AE=EF；方法二：在CA上截取CG=CE，连结GE，证明类似方法一；方法三：延长FC到G，使CG=CE，连结EG，易证△CEG是等边三角形，第10页（共33页）∴CE=EG，∠G=∠ACB=60°，∠CEG=∠AEF=60°，∴∠CEG+∠CEF=∠AEF+∠CEF，即∠GEF=∠AEC，∴△GEF≌△CEA，∴AE=EF．第二种情况：点E是线段BC延长线上的任意一点如图2，可作三种辅助线：①在CF上截取CG=CE，连接GE②延长AC到G，使CG=CE，连结EG；③或延长BA到G，使BG=BE，连结EG．第②种添加辅助线的方法证明如下：证明：延长AC到G，使CG=CE，连结EG，易证△CEG为等边三角形，∴∠G=∠ECF=60°，EG=CE，又∠AEG=∠CEG+∠AEC=60°+∠AEC，∠CEF=∠AEF+∠AEC=60°+∠AEC，第11页（共33页）∴∠AEG=∠CEF，∴△AEG≌△FEC，∴AE=EF．第三种情况：点E是线段BC反向延长线上的任意一点如图3，可作三种辅助线：①延长AB到G，使BG=BE，连结EG；②延长CF到G，使CG=CE，连结EG；③在CE上截取CG=CF，连结GF现就第①种添加辅助线的方法证明如下：证明：延长AB到G，使BG=BE，连结EG，易证△BEG为等边三角形，∴∠G=∠ECF=60°，第12页（共33页）∵∠AEB+∠BAE=∠ABC=60°，∠AEB+∠CEF=∠AEF=60°，∴∠BAE=∠CEF，∵AB=BC，BG=BE，∴AB+BG=BC+BE，即AG=CE，∴△AEG≌△EFC，∴AE=EF．拓展应用：如图4：作CH⊥AE于H点，∴∠AHC=90°．由数学思考得AE=EF，又∵∠AEF=60°，∴△AEF是等边三角形，∴△ABC∽△AEF．第13页（共33页）∵CE=BC=AC，△ABC是等边三角形，∴∠CAH=30°，AH=EH．∴CH=AC，AH=AC，AE=AC，∴．∴==．5．问题情境：在Rt△ABC中，AB=BC，∠B=90°，将一块等腰直角三角板的直角顶点O放在斜边AC上，将三角板绕点O旋转．（1）操作发现：当点O为AC中点时：①如图1，三角板的两直角边分别交AB，BC于E、F两点，连接EF，猜想线段AE、CF与EF之间存在的等量关系：AE2+CF2=EF2（无需证明）；②如图2，三角板的两直角边分别交AB，BC延长线于E、F两点，连接EF，判断①中的结论是否成立．若成立，请证明；若不成立，请说明理由；第14页（共33页）（2）类比延伸：当点O不是AC中点时，如图3，三角板的两直角边分别交AB，BC于E、F两点，若=，请直接写出=．【解答】解：（1）①猜想：AE2+CF2=EF2，连接OB，如图1，∵AB=BC，∠ABC=90°，O点为AC的中点，∴OB=AC=OC，∠BOC=90°，∠ABO=∠BCO=45°．∵∠EOF=90°，∴∠EOB+∠BOF=∠FOC+∠BOF．∴∠EOB=∠FOC，在△OEB和△OFC中，，∴△OEB≌△OFC（ASA）．∴BE=CF，又∵BA=BC，∴AE=BF．在Rt△EBF中，∵∠EBF=90°，∴BF2+BE2=EF2，∴AE2+CF2=EF2；故答案为：AE2+CF2=EF2；第15页（共33页）②成立．证明：连结OB．如图2，∵AB=BC，∠ABC=90°，O点为AC的中点，∴OB=AC=OC，∠BOC=90°，∠ABO=∠BCO=45°．∵∠EOF=90°，∴∠EOB=∠FOC．在△OEB和△OFC中，，∴△OEB≌△OFC（ASA）．∴BE=CF，又∵BA=BC，∴AE=BF．在Rt△EBF中，∵∠EBF=90°，∴BF2+BE2=EF2，∴AE2+CF2=EF2；（2）=，如图3，过点O作OM⊥AB于M，ON⊥BC于N．∵∠B=90°，第16页（共33页）∴∠MON=90°，∵∠EOF=90°，∴∠EOM=∠FON．∵∠EMO=∠FNO=90°，∴△OME∽△ONF，∴=，∵△AOM和△OCN为等腰直角三角形，∴△AOM∽△OCN，∴=，∵=，∴=，故答案为．第17页（共33页）第18页（共33页）6．阅读发现：（1）如图①，在Rt △ABC 和Rt △DBE 中，∠ABC=∠DBE=90°，AB=BC=3，BD=BE=1，连结CD ，AE ．易证：△BCD ≌△BAE ．（不需要证明）提出问题：（2）在（1）的条件下，当BD ∥AE 时，延长CD 交AE 于点F ，如图②，求AF 的长．解决问题：（3）如图③，在Rt △ABC 和Rt △DBE 中，∠ABC=∠DBE=90°，∠BAC=∠DEB=30°，连结CD ，AE ．当∠BAE=45°时，点E 到AB 的距离EF 的长为2，求线段CD的长为．【解答】（2）解：如图②中，AB与CF交于点O．由（1）可知：△BCD≌△BAE，∴∠OAF=∠OCB，CD=AE，∵∠AOF=∠COB，∴∠AFO=∠CBO=90°，∴CF⊥AE，∵BD∥AE，∴BD⊥CF，在RT△CDB中，∵∠CDB=90°，BC=3，BD=1，∴CD=AE==2，∵∠BDF=∠DFE=∠DBE=90°，∴四边形EFDB是矩形，∴EF=BD=1，∴AF=AE﹣EF=2﹣1．（3）解：在RT△ABC，RT△EBD中，∵∠ABC=∠DBE=90°，∠BAC=∠DEB=30°，∴AB=BC，BE=BD，∴==，∵∠ABC=∠EBD=90°，∴∠ABE=∠DBC，∴△ABE∽△CBD，∴==，第19页（共33页）第20页（共33页）在RT △AEF 中，∵∠AFE=90°，∠EAF=45°，EF=2，∴AF=EF=2，AE=2，∴=，∴CD=．故答案为．7．如图1，两个完全相同的三角形纸片ABC 和DEC 重合放置，其中∠C=90°，∠B=∠E=30°．（1）操作发现：如图2，固定△ABC，使△DEC绕点C旋转，当点D恰好落在AB边上时，填空：①线段DE与AC的位置关系是DE∥AC；②设△BDC的面积为S1，△AEC的面积为S2，则S1与S2的数量关系是S1=S2．（2）猜想论证当△DEC绕点C旋转到如图3所示的位置时，请猜想（1）中S1与S2的数量关系是否仍然成立？若成立，请证明；若不成立，请说明理由．（3）拓展探究已知∠ABC=60°，BD平分∠ABC，BD=CD，BC=9，DE∥AB交BC于点E（如图4）．若在射线BA上存在点F，使S△DCF=S△BDE，请求相应的BF的长．【解答】解：（1）①∵△DEC绕点C旋转点D恰好落在AB边上，∴AC=CD，∵∠BAC=90°﹣∠B=90°﹣30°=60°，第21页（共33页）∴△ACD是等边三角形，∴∠ACD=60°，又∵∠CDE=∠BAC=60°，∴∠ACD=∠CDE，∴DE∥AC；故答案为：DE∥AC；②∵∠B=30°，∠C=90°，∴CD=AC=AB，∴BD=AD=AC，根据等边三角形的性质，△ACD的边AC、AD上的高相等，∴△BDC的面积和△AEC的面积相等（等底等高的三角形的面积相等），即S1=S2=×2×2=2；故答案为：S1=S2；（2）如图，∵△DEC是由△ABC绕点C旋转得到，∴BC=CE，AC=CD，∵∠ACN+∠BCN=90°，∠DCM+∠BCN=180°﹣90°=90°，∴∠ACN=∠DCM，∵在△ACN和△DCM中，，第22页（共33页）∴△ACN≌△DCM（AAS），∴AN=DM，∴△BDC的面积和△AEC的面积相等（等底等高的三角形的面积相等），即S1=S2；（3）如图，过点D作DF1∥BE，易求四边形BEDF1是菱形，所以BE=DF1，且BE、DF1上的高相等，此时S△DCF1=S△BDE；过点D作DF2⊥BD，∵∠ABC=60°，F1D∥BE，∴∠F2F1D=∠ABC=60°，∵BF1=DF1，∠F1BD=∠ABC=30°，∠F2DB=90°，∴∠F1DF2=∠ABC=60°，∴△DF1F2是等边三角形，∴DF1=DF2，∵BD=CD，∠ABC=60°，点D是角平分线上一点，∴∠DBC=∠DCB=×60°=30°，∴∠CDF1=180°﹣∠BCD=180°﹣30°=150°，∠CDF2=360°﹣150°﹣60°=150°，∴∠CDF1=∠CDF2，第23页（共33页）∵在△CDF1和△CDF2中，，∴△CDF1≌△CDF2（SAS），∴点F2也是所求的点，∵∠ABC=60°，点D是角平分线上一点，DE∥AB，∴∠DBC=∠BDE=∠ABD=×60°=30°，又∵BD=4，∴BE=×6÷cos30°=3÷=2，∴BF1=2，BF2=BF1+F1F2=2+2=4，故BF的长为2或4．8．问题解决：如图（1），将正方形纸片ABCD折叠，使点B落在CD边上一点E（不与点C，D 重合），压平后得到折痕MN．当时，求的值．类比归纳：第24页（共33页）在图（1）中，若，则的值等于；若，则的值等于；若（n 为整数），则的值等于．（用含n的式子表示）联系拓广：如图（2），将矩形纸片ABCD折叠，使点B落在CD边上一点E（不与点C，D 重合），压平后得到折痕MN，设，则的值等于．（用含m，n的式子表示）【解答】解：（1）方法一：如图（1﹣1），连接BM，EM，BE．由题设，得四边形ABNM和四边形FENM关于直线MN对称．∴MN垂直平分BE，∴BM=EM，BN=EN．∵四边形ABCD是正方形，∴∠A=∠D=∠C=90°，设AB=BC=CD=DA=2．∵，∴CE=DE=1．第25页（共33页）设BN=x，则NE=x，NC=2﹣x．在Rt△CNE中，NE2=CN2+CE2．∴x2=（2﹣x）2+12，解得x=，即BN=．在Rt△ABM和在Rt△DEM中，AM2+AB2=BM2，DM2+DE2=EM2，∴AM2+AB2=DM2+DE2．设AM=y，则DM=2﹣y，∴y2+22=（2﹣y）2+12，解得y=，即AM=（6分）∴．方法二：同方法一，BN=．如图（1﹣2），过点N做NG∥CD，交AD于点G，连接BE．∵AD∥BC，∴四边形GDCN是平行四边形．∴NG=CD=BC．同理，四边形ABNG也是平行四边形．∴AG=BN=∵MN⊥BE，∴∠EBC+∠BNM=90度．∵NG⊥BC，∴∠MNG+∠BNM=90°，第26页（共33页）∴∠EBC=∠MNG．在△BCE与△NGM中，∴△BCE≌△NGM，EC=MG．∵AM=AG﹣MG，AM=﹣1=．∴．（2）如图1，当四边形ABCD为正方形时，连接BE，=，不妨令CD=CB=n，则CE=1，设BN=x，则EN=x，EN2=NC2+CE2，x2=（n﹣x）2+12，x=；作MH⊥BC于H，则MH=BC，又点B，E关于MN对称，则MN⊥BE，∠EBC+∠BNM=90°；而∠NMH+∠BNM=90°，故∠EBC=∠NMH，则△EBC≌△NMH，∴NH=EC=1，AM=BH=BN﹣NH=﹣1=则：==．故当=，则的值等于；若=，则的值等于；第27页（共33页）（3）若四边形ABCD为矩形，连接BE，=，不妨令CD=n，则CE=1；又==，则BC=mn，同样的方法可求得：BN=，BE⊥MN，易证得：△MHN∽△BCE．故=，=，HN=，故AM=BH=BN﹣HN=，故==．故答案为：；；；．第28页（共33页）第29页（共33页）9．阅读理解：如图1，在直角梯形ABCD 中，AB ∥CD ，∠B=90°，点P 在BC 边上，当∠APD=90°时，易证△ABP ∽△PCD ，从而得到BP•PC=AB•CD ，解答下列问题．（1）模型探究：如图2，在四边形ABCD 中，点P 在BC 边上，当∠B=∠C=∠APD 时，结论BP•PC=AB•CD 仍成立吗？试说明理由；（2）拓展应用：如图3，M 为AB 的中点，AE 与BD 交于点C ，∠DME=∠A=∠B=45°且DM 交AC 于F ，ME 交BC 于G ．AB=，AF=3，求FG 的长．【解答】解：（1）∵∠APC=∠APD +∠CPD ，∠APC=∠BAP +∠B （三角形外角定理），∠B=∠APD （已知），∴∠BAP=∠CPD，又∵∠B=∠C，∴△ABP∽△PCD∴=，∴BP•PC=AB•CD；（2）∵∠AFM=∠DME+∠E（三角形外角定理），∠DME=∠A（已知），∴∠AFM=∠A+∠E（等量代换），又∠BMG=∠A+∠E（三角形外角定理），∴∠AFM=∠BMG．∵∠A=∠B，∴△AMF∽△BGM．当∠A=∠B=45°时，∠ACB=180°﹣∠A﹣∠B=90°，即AC⊥BC且AC=BC．∵M为AB的中点，∴AM=BM=，AC=BC=4．又∵△AMF∽△BGM，∴，∴BG===，又∵，CF=4﹣3=1，∴．第30页（共33页）10．基本模型如下图，点B、P、C在同一直线上，若∠B=∠1=∠C=90°，则△ABP∽△PCD成立，（1）模型拓展如图1，点B、P、C在同一直线上，若∠B=∠1=∠C，则△ABP∽△PCD成立吗？为什么？（2）模型应用①如图2，在等腰梯形ABCD中，AD∥BC，AD=1，AB=2，BC=4，在BC上截取BP=AD，作∠APQ=∠B，PQ交CD于点Q，求CQ的长；②如图3，正方形ABCD的边长为1，点P是线段BC上的动点，作∠APQ=90°，PQ交CD于Q，当P在何处时，线段CQ最长？最长是多少？【解答】解：（1）成立，∵∠A=180°﹣（∠B+∠APB），第31页（共33页）∠CPD=180°﹣（∠1+∠APB），∠B=∠1，∴∠A=∠CPD，∵∠B=∠C，∴△ABP∽△PCD；（2）①∵四边形ABCD是等腰梯形，∴∠B=∠C，∵∠B=∠APQ，∴∠B=∠APQ=∠C，由（1）知，△ABP∽△PCD，∴=，∴=，∴CQ=；②设BP=x，CQ=y．∵∠B=∠APQ=90°，∴△ABP∽△PCQ，∴=，即=，∴y=﹣x2+x=﹣（x﹣）2+，第32页（共33页）∴当x=时，y=，最大即当P是BC的中点时，CQ最长，最长为．第33页（共33页）。

几何难点突破之类比探究讲义及答案

几何难点突破之类比探究（讲义）一、知识点睛识别类比探究题型特征：1.题目中一般有三问或者更多，每小问的条件和图形相似度很高，因此可以“照搬”第一问的方法；2.每一问的图形或点的位置会有所变化（通常条件从特殊走向一般），但可以在这些变化过程中按照第一问的思路和对应关系找角、找边、找全等．二、精讲精练1. 如图1所示，在△ABC 和△ADE 中，AB =AC ，AD =AE ，∠BAC =∠DAE ，且点B 、A 、D 在一条直线上，连接BE 、CD ，M 、N 分别为BE 、CD 的中点．（1）求证：①BE =CD ；②△AMN 是等腰三角形．（2）在图1的基础上，将△ADE 绕点A 按顺时针方向旋转180°，其他条件不变，得到图2所示的图形．（1）中的两个结论是否仍然成立，若成立，请给予证明；若不成立，请说明理由．图2ME CBNDA图1CBMN ED A2. 已知△ABC 为等边三角形，点D 为直线BC 上一动点（点D 不与B ，C 重合），以AD 为边作菱形ADEF （A 、D 、E 、F 按逆时针排列），使∠DAF ＝60°，连接CF ．（1）如图1，当点D 在边BC 上时，求证：①BD ＝CF ；②AC ＝CF ＋CD ；（2）如图2，当点D 在边BC 的延长线上且其他条件不变时，结论AC ＝CF ＋CD 是否成立？若不成立，请写出AC 、CF 、CD 之间存在的数量关系，并说明理由；（3）如图3，当点D 在边CB 的延长线上且其他条件不变时，探究AC 、CF 、CD 之间存在的数量关系．图1AFECDB图2ABC DFEABCD F3. 如图1，四边形ABCD 是正方形，点E 是边BC 的中点．且90AEF ∠=，且EF 交正方形外角DCG ∠的平分线CF 于点F ．（1）求证：AE =EF ；（2）如图2，如果把“点E 是边BC 的中点”改为“点E 是边BC 上（除B ，C 外）的任意一点”，其它条件不变，那么结论“AE =EF ”仍然成立吗？如果成立，写出证明过程；如果不成立，请说明理由；（3）如图3，点E 是BC 的延长线上（除C 点外）的任意一点，其他条件不变，结论“AE =EF ”是否成立？如果成立，写出证明过程；如果不成立，请说明理由．图1GFE DC B A图2A B CDE FG图3GFE DCBA4.如图1，在△ABC 中，点P 为BC 边的中点，直线a 绕顶点A 旋转，若B 、P 在直线a 的异侧，BM ⊥直线a 于点M ，CN ⊥直线a 于点N ，连接PM 、PN ；（1）求证：PM =PN ；（2）若直线a 绕点A 旋转到图2的位置时，点B 、P 在直线a 的同侧，其它条件不变．此时PM =PN 还成立吗？若成立，请给予证明；若不成立，请说明理由；（3）如图3，若直线a 绕点A 旋转到与BC 边平行的位置时，其它条件不变．请判断四边形MBCN 的形状及此时PM =PN 还成立吗？图1ABCP aMN图2ABCP aM N图3NMaP CBA5.如图1所示,已知A、B为直线l上两点，点C为直线l上方一动点，连接AC、BC，分别以AC 、BC为边向△ABC外作正方形CADF和正方形CBEG，过点D作DD1⊥l于点D1，过点E作EE1⊥l于点E1.(1)如图2，当点E恰好在直线l上时(此时E1与E重合)，试说明DD1=AB；(2)在图1中，当D、E两点都在直线l的上方时，试探求三条线段DD1、EE1、AB之间的数量关系，并说明理由；(3)如图3，当点E在直线l的下方时，请探究三条线段DD1、EE1、AB之间的数量关系.DA BGEFCl D1E1图1GEBACFD1DE1()l图2图3lFGEBACD1DE16. 如图，点P 是正方形ABCD 对角线AC 上一动点，点E 在射线BC 上，且PE ＝PB ，连接PD ，O 为AC 中点．（1）如图1，当点P 在线段AO 上时，试猜想PE 与PD 的数量关系和位置关系，不用说明理由；（2）如图2，当点P 在线段OC 上时，（1）中的猜想还成立吗？请说明理由；（3）如图3，当点P 在AC 的延长线上时，判断（1）中的猜想是否成立？若成立，请直接写出结论；若不成立，请说明理由．图1BB图2三、课后作业1．已知：如图所示，直线MA∥NB，∠MAB与∠NBA的平分线交于点C，过点C作一条直线l与两条直线MA、NB分别相交于点D、E．（1）如图1所示，当直线l与直线MA垂直时，猜想线段AD、BE、AB之间的数量关系，请直接写出结论，不用证明；（2）如图2所示，当直线l与直线MA不垂直且交点D、E都在AB的同侧时，（1）中的结论是否成立？如果成立，请证明：如果不成立，请说明理由；（3）如图3所示，当直线l与直线MA不垂直且交点D、E在AB的异侧时，（1）中的结论是否仍然成立？如果成立，请说明理由；如果不成立，那么线段AD、BE、AB之间还存在某种数量关系吗？如果存在，请写出它们之间的数量关系．【几何难点突破之类比探究参考答案】二、精讲精练图1A lCEBDNM图2M NDBElACMNDBEClA图3(1)lCENM1.提示：（1）①证△CAD≌△BAE（SAS）；②证△ACN≌△ABM（SAS）；或证△MEA≌△NDA（SAS）；（2）成立，同（1）可证．2.证明：（1）如图1，在等边△ABC中，AB=AC=BC，∠BAC=60°∴ ∠BAD+∠DAC=60°∵ 在菱形ADEF中，∠DAF=60°∴ AD=AF，∠DAC+∠CAF=60°∴ ∠BAD=∠CAF∴ △ABD≌△ACF（SAS）∴ BD=CF∵ BC=BD+DC∴ BC=CF+CD即AC= CF+CD（2）此时AC=CF+CD不成立，CF = AC +CD.理由如下：如图2，在等边△ABC中，AB=AC=BC，∠BAC=60°∵ 在菱形ADEF中，∠DAF=60°∴ AD=AF∴ ∠BAC+∠CAD=∠DAF+∠CAD∴ ∠BAD=∠CAF∴ △ABD≌△ACF（SAS）∴ BD=CF∵ BD=BC+CD∴ CF= BC+CD即CF = AC +CD（3）CF = CD-AC.理由如下：如图3，在等边△ABC中，AB=AC=BC，∠BAC=60°∴ ∠CAF+∠BAF=60°∵ 在菱形ADEF中，∠DAF=60°∴ AD=AF，∠DAB+∠BAF=60°∴ ∠DAB+∠BAF =∠CAF+∠BAF∴ ∠DAB=∠F AC∴△ABD≌△ACF（SAS）∴ BD=CF图1AFECDB图2AB C DFE图3AB CDEF∵ BD=CD-CB∴ CF= CD-CB即CF = CD-AC3.提示：（1）在AB上取点M，使得AM=CE，证△AME≌△ECF（ASA）；（2）成立，同（1）可证；（3）成立，在BA的延长线上取点M，使得AM=CE，证△AME≌△ECF（ASA）．4.提示：（1）延长MP交CN于点E，证△BPM≌△CPE（ASA），直角三角形斜边中线等于斜边一半；（2）延长MP交NC的延长线于点E，同（1）可证；（3）四边形MBCN为矩形；成立，同（1）可证．5.提示：（1）△ADD1≌△CAB；（2）AB＝DD1＋EE1，过点C作CM⊥AB于点M，证△ADD1≌△CAM，△EBE1≌△BCM；（3）DD1=AB＋EE1，同（2）可证．6.提示：（1）过P作PM⊥BC于点M，PN⊥DC于点N．证△APB≌△APD（SAS），△PME≌△PND（HL）即可；（2）成立，同（1）可证；（3）作图略；成立，过P分别作BC，DC的垂线，交BE于点M，DC的延长线于点N，同（1）可证．四、课后作业1．解：（1）AD+BE＝AB（2）成立．证明：（方法一）：在AB上截取AG=AD，连接CG．∵ ∠1＝∠2，AC＝AC∴△ADC≌△AGC（SAS）∴∠5＝∠6∵ AM∥BN∴ ∠1+∠2+∠3+∠4=180°图1A lCEBDNM876541C lEDNM∵∠1＝∠2，∠3＝∠4∴ ∠2+∠3=90°∴ ∠ACB＝90°即∠6＋∠7＝90°∵ ∠5+∠6+∠7+∠8=180°∴ ∠5＋∠8＝90°∴∠7＝∠8∵∠3＝∠4，BC＝BC∴△BGC≌△BEC（ASA）∴BG＝BE∴AG+BG＝AD+BE∴AD+BE＝AB（方法二）：过点C作直线FG⊥AM，垂足为点F，交BN于点G．作CH⊥AB，垂足为点H．由（1）得AF+BG=AB∵AM∥BN，∠AFG＝90°∴ ∠BGF＝∠FGE＝90°∵∠1＝∠2，∠3＝∠4∴ CF＝CH，CH＝CG∴ CF＝CG∵ ∠FCD＝∠GCE∴△CFD≌△CGE（ASA）∴DF＝EG∴ AD+BE=AF-DF+GE+BG=AF+BG=AH+BH=AB （方法三）：延长BC，交AM于点F．∵AM∥BN∴∠5＝∠4∵ ∠3＝∠4∴∠5＝∠3HFG1234CAlEBDNM图2方法二51234FCAlEBDNM∴ AF =AB∵ ∠1＝∠2，∴ CF ＝CB∵∠FCD ＝∠BCE∴ △FCD ≌△BCE （ASA ）∴ DF ＝BE∴ AD +BE =AD +DF =AF =AB（3）不成立．存在．当点D 在射线AM 上，点E 在射线BN 的反向延长线上时（如图3（1）），AD -BE =AB当点D 在射线AM 的反向延长线上，点E 在射线BN 上时（如图3（2）），BE -AD =AB图3(2)图3(1)A l C E B D N M MN DBEClA。

八年级数学勾股定理的应用——类比探究(专题)(含答案)

勾股定理的应用——类比探究（专题）一、单选题(共7道，每道14分)1.如图，△ABC和△DBE都是等腰直角三角形，点D在AC上，其中∠ABC=∠DBE=90°，则∠DCE 的度数( )A.60°B.70°C.90°D.100°答案：C解题思路：∵△ABC和△DBE都是等腰直角三角形，∠ABC=∠DBE=90°∴AB=BC，BD=BE，∠A=∠ACB=45°，∴∠ABD=∠CBE，∴△ABD≌△CBE（SAS），∴∠A=∠BCE=45°，∴∠DCE=∠ACB+∠BCE=90°，故选C．试题难度：三颗星知识点：略2.（上接第1题）（2）若AD=5，CD=12，则CE的长为_______，DE的长为_______．( )A.5，12B.3，17C.5，17D.5，13答案：D解题思路：∵△ABC和△DBE都是等腰直角三角形，∠ABC=∠DBE=90°∴AB=BC，BD=BE，∠A=∠ACB=45°，∴∠ABD=∠CBE，∴△ABD≌△CBE（SAS），∴∠A=∠BCE=45°，AD=CE，∴∠DCE=∠ACB+∠BCE=90°，∵AD=5，∴CE=5，在Rt△CDE中，∠DCE=90°，CD=12，CE=5，由勾股定理得，，∴∴DE=13，故选D．试题难度：三颗星知识点：略3.（上接第1，2题）（3）当点D在线段AC上运动时（D不与A重合），则AD，CD，DE之间的数量关系为( )A. B.C. D.答案：A解题思路：∵△ABC和△DBE都是等腰直角三角形，∠ABC=∠DBE=90°∴AB=BC，BD=BE，∠A=∠ACB=45°，∴∠ABD=∠CBE，∴△ABD≌△CBE（SAS），∴∠A=∠BCE=45°，AD=CE，∴∠DCE=∠ACB+∠BCE=90°，在Rt△CDE中，∠DCE=90°，由勾股定理得，，∵AD=CE，∴，故选A．试题难度：三颗星知识点：略4.如图1，点Q是等边△ABC的边AB上的一点，以CQ为边作等边△CPQ，连接AP，则∠PAQ 的度数为_______，线段AP，BQ之间的数量关系为_______．( )A.60°，AP=BQB.120°，AP=BQC.90°，AP=BQD.140°，AP=BQ答案：B解题思路：∵△ABC和△CPQ都是等边三角形，∴AC=BC，CP=CQ，∠CAB=∠B=60°，∠PCQ=∠ACB=60°，∴∠ACP=∠BCQ，∴△ACP≌△BCQ（SAS），∴∠PAC=∠B=60°，AP=BQ，∴∠PAQ=∠PAC+∠CAB=120°，故选B．试题难度：三颗星知识点：略5.（上接第4题）（2）如图2，△ABC是等腰直角三角形，点Q在斜边AB上，以CQ为直角边作等腰直角△PCQ，其中∠PCQ=∠ACB=90°．则AQ，BQ，PQ之间的数量关系为( )A. B.C. D.答案：B解题思路：如图，连接AP，∵△ABC和△CPQ都是等腰直角三角形，∠PCQ=∠ACB=90°，∴AC=BC，CP=CQ，∠CAB=∠B=45°，∴∠ACP=∠BCQ，∴△ACP≌△BCQ（SAS），∴∠PAC=∠B=45°，AP=BQ，∴∠PAQ=∠PAC+∠CAB=90°，在Rt△APQ中，∠PAQ=90°，由勾股定理得，，∵AP=BQ，∴，故选B．试题难度：三颗星知识点：略6.（上接第4，5题）在（2）的条件下，则CQ，AQ，BQ三者之间的数量关系为( )A. B.C. D.答案：D解题思路：如图，连接AP，∵△ABC和△CPQ都是等腰直角三角形，∠PCQ=∠ACB=90°∴AC=BC，CP=CQ，∠CAB=∠B=45°，∴∠ACP=∠BCQ，∴△ACP≌△BCQ（SAS），∴∠PAC=∠B=45°，AP=BQ，∴∠PAQ=∠PAC+∠CAB=90°，在Rt△APQ中，∠PAQ=90°，由勾股定理得，，∵AP=BQ，∴，∵△CPQ是等腰直角三角形，PQ为斜边∴故选D．试题难度：三颗星知识点：略7.如图，在Rt△ABC中，AB=AC，∠BAC=90°，D，E为BC上两点，∠DAE=45°，F为△ABC 外一点，且FB⊥BC，FA⊥AE，则下列结论：①CE=BF；②；③，其中正确的是( )A.①②③B.①②C.②③D.①③答案：A解题思路：①由题意可得，∠BAC=∠EAF=90°，∴∠CAE+∠BAE=∠BAF+∠BAE=90°∴∠CAE=∠BAF在△ABC中，AB=AC，∠BAC=90°∴∠C=∠ABC=45°∵FB⊥BC∴∠FBE=90°∴∠ABF=45°=∠C∴△ABF≌△ACE（ASA）∴CE=BF，故①正确②如图，连接DF，由①可知，AF=AE，∵∠EAF=90°，∠DAE=45°，∴∠DAF=45°=∠DAE又AD=AD∴△ADF≌△ADE（SAS）∴DF=DE在Rt△BDF中，∠DBF=90°根据勾股定理得，，∴，故②正确；③在Rt△BEF中，∠EBF=90°由勾股定理可得，，在等腰直角△AEF中，，∴，故③正确；综上，①②③均正确，故选A试题难度：三颗星知识点：略。

中考数学类比探究实战演练(一)(含答案)

学生做题前请先回答以下问题问题1：类比探究的处理思路是什么？问题2：类比迁移的具体操作是什么？问题3：想一想类比探究问题常见的不变结构有哪些，处理方式是什么？以下是问题及答案，请对比参考:问题1：类比探究的处理思路是什么？答：①类比上一问，迁移解决下一问；②依据不变结构，分析特征解决问题．问题2：类比迁移的具体操作是什么？答：类比字母、类比辅助线、类比思路、类比结构．问题3：想一想类比探究问题常见的不变结构有哪些，处理方式是什么？答：类比探究中常见不变结构及处理方式分别为：①旋转结构，找等腰结构，借助全等整合条件；②中点结构，作倍长，通过全等转移边和角；③平行结构，找相似，转比例；④直角结构，作横平竖直的线，找全等或相似．中考数学类比探究实战演练（一）一、单选题(共6道，每道4分)1.阅读下面材料：小腾遇到这样一个问题：如图1，在△ABC中，点D在BC边上，∠BAD=75°，∠CAD=30°，AD=2，BD=2CD，求AC的长．（1）小腾发现，过点C作CE∥AB，交AD的延长线于点E，通过构造△ACE，经过推理和计算能够使问题得到解决（如图2）．请回答：∠ACE的度数为_____，AC的长为_____．( )A. B.C. D.答案：C解题思路：见第2题中解析试题难度：三颗星知识点：探究应用2.（上接第1题）（2）参考小腾思考问题的方法，解决问题：如图3，在四边形ABCD中，∠BAC=90°，∠CAD=30°，∠ADC=75°，AC与BD交于点E，AE=2，BE=2DE，则BC的长为( )A.6B.C. D.答案：C解题思路：试题难度：三颗星知识点：探究应用3.已知正方形ABCD中，O是对角线AC的中点，P是对角线AC上一动点，过点P作PF⊥CD 于点F，连接PB．（1）如图1，当点P在线段AO上时（不与点A，O重合），过点P作PE⊥PB，交CD于点E，则DF，EF之间有怎样的数量关系？线段PA，PC，CE之间有怎样的一个等量关系？请给出证明过程．（2）如图2，当点P在线段OC上时（不与点O，C重合），过点P作PE⊥PB，交直线CD 于点E，（1）中的两个结论是否仍成立？若不成立，写出相应的结论．（所写结论均不必证明）（建议学生打印做题，并在做完之后对比解题思路中的过程，推敲里面是如何踩点得分的）（1）中DF，EF之间的数量关系是( )A. B.C.DF=EFD.答案：C解题思路：见第6题中解析试题难度：三颗星知识点：中考数学几何中的类比探究4.（上接第3题）（1）中线段PA，PC，CE之间的一个等量关系为( )A. B.C. D.答案：D解题思路：见第6题中解析试题难度：三颗星知识点：中考数学几何中的类比探究5.（上接第3，4题）（2）中DF，EF之间的数量关系是( )A. B.C.DF=EFD.答案：C解题思路：见第6题中解析试题难度：三颗星知识点：中考数学几何中的类比探究6.（上接第3，4，5题）（2）中线段PA，PC，CE之间的一个等量关系为( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：中考数学几何中的类比探究。

类比探究专题(一)——平行结构(含答案)

学生做题前请先回答以下问题问题1：类比探究问题的处理思路是什么？以下是问题及答案，请对比参考:问题1：类比探究问题的处理思路是什么？答：类比探究问题的处理思路为：（1）类比探究往往会围绕一个不变结构进行考查．类比探究中常见的不变结构有：中点结构、直角结构、旋转结构、平行结构．（2）若不属于常见结构类型，则需要我们尝试着去寻找不变结构解决问题．①根据题干条件，结合支干条件先解决第一问．②类比解决下一问．如果不能，分析条件变化，寻找不变特征．③结合所求目标，依据不变特征尝试找不变结构，大胆猜测、尝试、验证．若属于类比探究常见的结构类型，调用结构类比解决．类比探究专题（一）——平行结构一、单选题(共6道，每道16分)1.如图1，D是△ABC的边BC上一点，过点D的一条直线交AC于点F，交BA的延长线于点E．（1）若BD=CD，CF=2AF，则的值为( )A.2B.C. D.答案：B解题思路：试题难度：三颗星知识点：平行结构2.（上接第1题）（2）如图2，若BD=CD，CF=mAF，则的值为( ) （用含m的代数式表示）A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：平行结构3.（上接第1，2题）（3）如图3，将原题改为“过点D的一条直线交AC的延长线于点F，交AB于点E”，若BD=nCD，CF=mAF，则的值为( )（用含m，n的代数式表示）A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：平行结构4.已知AD是△ABC的中线，将BC边所在直线绕点D顺时针旋转角，交AB边于点M，交射线AC于点N，设．（1）如图1，满足的函数关系式为( ) A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：平行结构5.（上接第4题）（2）如图2，当G是AD上任意一点时（点G不与点A重合），过点G的直线交AB边于点，交AC边于点，设，则满足的函数关系式为( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：平行结构6.（上接第4，5题）（3）如图3，当G是AD上任意一点时（点G不与点A重合），过点G 的直线交AB边于点，交AC的延长线于点，设，则满足的函数关系式为( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：平行结构。

中考类比探究专项

第六讲几何类比探究（一）几何类比探究是河南中考数学的重点、难点，虽是考试难点，但依然有法可破！【知识点睛】1. 类比探究一般会围绕一个不变结构进行考查．常见结构有：平行结构、直角结构、旋转结构、中点结构．2. 类比是解决类比探究问题的主要方法．往往会类比字母、类比辅助线、类比结构、类比思路来解决类比探究问题．3. 常见结构：【例题精讲】例1.（2015•潜江24．）已知∠MAN=135°，正方形ABCD绕点A旋转．（1）当正方形ABCD旋转到∠MAN的外部（顶点A除外）时，AM，AN分别与正方形ABCD的边CB，CD的延长线交于点M，N，连接MN．①如图1，若BM=DN，则线段MN与BM+DN之间的数量关系是；②如图2，若BM≠DN，请判断①中的数量关系是否仍成立？若成立，请给予证明；若不成立，请说明理由；（2）如图3，当正方形ABCD旋转到∠MAN的内部（顶点A除外）时，AM，AN 分别与直线BD交于点M，N，探究：以线段BM，MN，DN的长度为三边长的三角形是何种三角形，并说明理由．例2.（2015•贵港26．）已知：△ABC是等腰三角形，动点P在斜边AB所在的直线上，以PC为直角边作等腰三角形PCQ，其中∠PCQ=90°，探究并解决下列问题：（1）如图①，若点P在线段AB上，且AC=1+，PA=，则：①线段PB= ，PC= ；②猜想：PA2，PB2，PQ2三者之间的数量关系为；（2）如图②，若点P在AB的延长线上，在（1）中所猜想的结论仍然成立，请你利用图②给出证明过程；（3）若动点P满足=，求的值．（提示：请利用备用图进行探求）图1AD NPECBM 图2M BCE PNDA图3A D NPECBM例3.在等腰直角三角形ABC 中，∠BAC =90°，AB =AC ，直线MN 过点A 且MN ∥BC ．以点B 为一锐角顶点作Rt △BDE ，∠BDE =90°，且点D 在直线MN 上（不与点A 重合）．如图1，DE 与AC 交于点P ，易证：BD =DP ．（1）在图2中，DE 与CA 的延长线交于点P ，则BD =DP 是否成立？如果成立，请给予证明；如果不成立，请说明理由．（2）在图3中，DE 与AC 的延长线交于点P ，BD 与DP 是否相等？请直接写出你的结论，无需证明．例4.在正方形ABCD中，对角线AC与BD交于点O；在Rt△PMN中，∠MPN=90°．（1）如图1，若点P 与点O 重合且PM ⊥AD ，PN ⊥AB ，分别交AD ，AB 于点E ，F ，请直接写出PE 与PF 的数量关系．（2）将图1中的Rt △PMN 绕点O 顺时针旋转角度α（0°<α<45°）．①如图2，在旋转过程中（1）中的结论依然成立吗？若成立，请证明；若不成立，请说明理由．②如图3，旋转后，若Rt △PMN 的顶点P 在线段OB 上移动（不与点O ，B 重合），当BD =3BP 时，猜想此时PE 与PF 的数量关系，并给出证明． ③当BD =m ·BP 时，请直接写出PE 与PF 的数量关系．（3）在（2）②的条件下，当∠DPM =15°时，连接EF，若正方形的边长为，请直接写出线段EF 的长．图1MN F E O (P )DCBA 图2A BD O (P )E FN图3PABCDO E F NM【练习】1、（2015•齐齐哈尔26．（8分））如图1所示，在正方形ABCD和正方形CGEF中，点B、C、G在同一条直线上，M是线段AE的中点，DM的延长线交EF于点N，连接FM，易证：DM=FM，DM⊥FM（无需写证明过程）（1）如图2，当点B、C、F在同一条直线上，DM的延长线交EG于点N，其余条件不变，试探究线段DM与FM有怎样的关系？请写出猜想，并给予证明；（2）如图3，当点E、B、C在同一条直线上，DM的延长线交CE的延长线于点N，其余条件不变，探究线段DM与FM有怎样的关系？请直接写出猜想．2.如图，在Rt△ABC中，∠ACB=90°，∠A=30°，点O为AB的中点，点P为直线BC上的动点（不与点B、点C重合），连接OC，OP，将线段OP绕点P 顺时针旋转60°，得到线段PQ，连接BQ．（1）如图1，当点P在线段BC上时，请直接写出线段BQ与CP的数量关系：________________；（2）如图2，当点P在CB延长线上时，（1）中结论是否成立？若成立，请加以证明；若不成立，请说明理由；（3）如图3，当点P 在BC 延长线上时，若∠BPO =15°，BP =4，请求出BQ 的长．图1 图2 图3ABC OP ABCO PQQPOCBA3如图，△ABC 中，点E ，P 在边AB 上，且AE =BP ，过点E ，P 作BC 的平行线，分别交AC 于点F ，Q ，记△AEF 的面积为S 1，四边形EFQP 的面积为S 2，四边形PQCB 的面积为S 3．（1）①若EP =2AE ，则EF :PQ :BC =__________；②求证：EF +PQ =BC ．（2）若S 1+S 3=S 2，求PEAE的值．（3）若S 3-S 1=S 2，直接写出PEAE的值．QPFE CB A4、在△ABC 中，AD 为BC 边上的中线，E 为AD 上一动点，设DE =nEA ，连接CE 并延长交AB 于点F ．（1）如图1，当∠BAC =90°，∠B =30°，DE =EA 时，求FBFA的值；（2）如图2，当△ABC 为锐角三角形，DE =EA 时，求FBFA的值；（3）如图3，当△ABC 为锐角三角形，DE =nEA 时，求FBFA的值．图3图2图1FAE B D CCD B EA FEAD CF第六讲几何类比探究（二）例1.如图1，∠QPN的顶点P在正方形ABCD两条对角线的交点处，∠QPN=α，将∠QPN绕点P旋转，旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD 交于点E和点F（点F与点C，D不重合）．（1）如图1，当α=90°时，DE，DF，AD之间满足的数量关系是____________；（2）如图2，将图1中的正方形ABCD改为∠ADC=120°的菱形，其他条件不变，当α=60°时，（1）中的结论变为DE+DF=12AD，请给出证明；（3）在（2）的条件下，若旋转过程中∠QPN的边PQ与射线AD交于点E，其他条件不变，探究在整个运动变化过程中，DE，DF，AD之间满足的数量关系，直接写出结论，不用加以证明．图2NQFEPDC BA图1N QPFE DC BA例2.已知直线m ∥n ，点C 是直线m 上一点，点D 是直线n 上一点，CD 与直线m ，n 不垂直，点P 为线段CD 的中点．（1）操作发现：直线l ⊥m ，l ⊥n ，垂足分别为A ，B ，当点A与点C 重合时（如图1所示），连接PB ，请直接写出线段PA 与PB 的数量关系：____________．（2）猜想证明：在图1的情况下，把直线l 向上平移到如图2的位置，试问（1）中的PA 与PB 的关系式是否仍然成立？若成立，请证明；若不成立，请说明理由．（3）延伸探究：在图2的情况下，把直线l 绕点A 旋转，使得∠APB =90°（如图3所示），已知两平行线m ，n 之间的距离为2k ．求证：PA PB k AB ⋅=⋅．图3ABCD图1lmn A (C )BD P图2PDBCAn m ll m n A CBDP图3例3在Rt △ACB 和Rt △AEF 中，∠ACB =∠AEF =90°，若点P 是BF 的中点，连接PC ，PE ．特殊发现：如图1，若点E ，F 分别落在边AB ，AC 上，则结论：PC =PE 成立（不要求证明）．问题探究：把图1中的△AEF 绕着点A 顺时针旋转．（1）如图2，若点E 落在边CA 的延长线上，则上述结论是否成立？若成立，请给予证明；若不成立，请说明理由．（2）如图3，若点F 落在边AB 上，则上述结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由．（3）记ACk BC，当k 为何值时，△CPE 总是等边三角形（请直接写出k 的值，不必说明理由）？图1PFEC BAPABCEF图2图3PCBAF例4．（2017洛阳一模）（10分）如图①，C为线段BE上的一点，分别以BC和CE为边在BE的同侧作正方形ABCD和正方形CEFG，M、N分别是线段AF和GD的中点，连接MN（1）线段MN和GD的数量关系是，位置关系是；（2）将图①中的正方形CEFG绕点C逆时针旋转90°，其他条件不变，如图②，（1）的结论是否成立？说明理由；（3）已知BC=7，CE=3，将图①中的正方形CEFG绕点C旋转一周，其他条件不变，直接写出MN的最大值和最小值．例5（2017开封）如图所示，平行四边形ABCD中，∠B=60°，将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转，且60°角的顶点始终与点C重合，角的两边所在的两直线分别交线段AB、AD于点E、F（不包括线段的端点）．（1）问题发现：如图1，若平行四边形ABCD为菱形，试猜想线段AE、AF、AC之间的数量关系，请证明你的猜想．（2）类比探究：如图2，若AB：AD=1：2，过点C作CH⊥AD于点H，求AE：FH的比值；（3）拓展延伸：如图3，若AB：AD=1：4，请直接写出（AE+4AF）：AC的比值为．例6（2017新乡）如图1，过等边三角形ABC边AB上一点D作DE∥BC交边AC于点E，分别取BC，DE的中点M，N，连接MN．（1）发现：在图1中，= ；（2）应用：如图2，将△ADE绕点A旋转，请求出的值；（3）拓展：如图3，△ABC和△ADE是等腰三角形，且∠BAC=∠DAE，M，N 分别是底边BC，DE的中点，若BD⊥CE，请直接写出的值．例7．已知：△ACB和△DCE都是等腰直角三角形，∠ACB=∠DCE=90°，连接AE、BD交于点O．AE与DC交于点M，BD与AC交于点N．（1）如图1，求证：AE=BD；（2）如图2，若AC=DC，在不添加任何辅助线的情况下，请直接写出图2中四对全等的直角三角形．。

类比探究(教师用)

类比探究(教师用)类比探究一）直角结构问题1：类比探究是几何综合题，类比（相似、全等、等腰）是解决此问题的主要方法，做好类比需要把握变化过程中的不变量。

若属于类比探究常见的结构类型，可以调用结构类比解决。

若不属于常见结构类型，可以先根据题干条件，结合已知条件先解决第一问，然后类比解决下一问。

如果不能，可以分析条件变化，寻找不变量。

结合所求目标，依据猜想、尝试、验证的思路大胆猜测，尝试，验证。

问题2：类比探究问题常见的不变结构有：勾股定理、直角三角形两锐角互余、直角边看成高（等面积结构）、直角+中点、直角+特殊角、直角+角平分线、斜直角放正、弦图结构、三等角模型、母子型相似、射影定理、函数背景下考虑、圆背景下考虑等。

处理方式是根据所求目标和已知条件，结合不变结构进行类比，寻找解题思路。

问题3：直角结构的思考角度有：1.边：勾股定理；2.角：直角三角形两锐角互余；3.面积：直角边看成高（等面积结构）；4.固定模型和用法：直角+中点、直角+特殊角、直角+角平分线、斜直角放正、弦图结构、三等角模型、母子型相似、射影定理；5.函数背景下考虑；6.圆背景下考虑：直径所对的圆周角是直角，垂径定理。

在类比探究之直角结构中，常用的结构有勾股定理、直角三角形两锐角互余、直角边看成高（等面积结构）、直角+中点、直角+特殊角、直角+角平分线、斜直角放正等。

例如，对于Rt△ABC中，∠B=90°，∠A=30°，将一块三角板的直角顶点放在△ABC斜边AC的中点P处，将三角板绕点P旋转，可以利用不变结构进行类比解题。

为折痕EF上的任一点P，作PG⊥BE，PH⊥BC，垂足分别为G，H。

已知AD=8，CF=3，求PG+PH的值。

解题思路：根据垂足定理，PG=PE-EG，PH=PF-FH。

由于EF是折痕，所以PE=PF，EG=FC，FH=AD。

因此，PG+PH=PE+FC-AD=PE+CF-AD=PE-ED+CF。

类比探究(一)——平行、直角(习题)

类比探究（一）——平行、直角（习题）1. 如图1，在□ABCD 中，点E 是BC 边的中点，点F 是线段AE 上一点，BF的延长线交射线CD 于点G ，若3AFEF=，求CD CG 的值．（1）尝试探究在图1中，过点E 作EH ∥AB 交BG 于点H ，则AB 和EH 的数量关系是________________，CG 和EH 的数量关系是_________________，CDCG的值是___________．图1ABCDE FG图2ABCDE F G图1 图2（2）类比延伸如图2，在原题的条件下，若AFm EF=（m >0），则CD CG 的值是________（用含m 的代数式表示），试写出解答过程．（3）拓展迁移如图3，在梯形ABCD 中，DC ∥AB ，点E 是BC 延长线上一点，AE 和BD 相交于点F ．若AB BC a b CD BE ==，（a >0，b >0），则AF EF 的值是________（用含a ，b 的代数式表示）．图32. 如图1，在Rt △ABC 中，∠ACB =90°，CD ⊥AB ，垂足为D ，点E 在AC 上，BE 交CD 于点G ，EF ⊥BE 交AB 于点F ，AC =mBC ，CE =nEA （m ，n 为实数）.试探究线段EF 与EG 的数量关系．图3F EC D A（1）如图2，当m =1，n =1时，求EF 与EG 的数量关系．（2）如图3，当m =1，n 为任意实数时，求EF 与EG 的数量关系．（3）如图1，当m ，n 均为任意实数时，求EF 与EG 的数量关系．C EFD A BG图1CEFD A G 图2EFD A BGC 图33.已知两条平行线l1，l2之间的距离为6，截线CD分别交l1，l2于点C，D，一直角的顶点P在线段CD上运动（不与点C，D重合），两边分别交l1，l2于点A，B．（1）操作发现如图1，过点P作直线l3∥l1，作PE⊥l1于点E，过点B作BF⊥l3于点F．此时，小明认为△PEA∽△PFB，你同意吗？为什么？（2）猜想论证将直角∠APB从图1的位置开始，绕点P顺时针旋转，在这一过程中，试观察、猜想：当AE满足什么条件时，以P，A，B为顶点的三角形是等腰三角形？请在图2中画出图形，并证明你的猜想．（3）延伸探究在（2）的条件下，当截线CD与直线l1所夹的钝角为150°时，设CP=x，试探究：是否存在实数x，使△PAB的边AB的长为l2l1l3BFE CD PA图1l2l1DC图2【参考答案】1.（1）AB=3EH；CG=2EH；3 2（2）2m（3）ab 2.（1）EF=EG（2）1 EF EGn=（3）1EF EGmn=3.（1）同意，证明略；（2）AE BF=时，为等腰三角形；（3）不存在，理由略．。

类比探究之探究(一)(北师版)(含答案) (1)

学生做题前请先回答以下问题问题1：类比探究属于几何综合题，解决此问题的主要方法是什么？问题2：目前我们所学的结构类比中有两种结构，分别是什么？问题3：什么特征我们会考虑旋转结构？类比探究之探究（一）（北师版）一、单选题(共5道，每道20分)1.在△ABC中，AB=AC=a，BC=b，且2a b，BG⊥AC于G，DE⊥AB于E，DF⊥AC于F．在图1中，D是BC边上的中点，请判断DE+DF与BG的关系．( )A. B.C. D.无法判断答案：B解题思路：试题难度：三颗星知识点：类比探究2.（上接第1题）在图2中，D是线段BC上的任意一点，DE+DF与BG的关系仍然成立．下列3种思路中你认为可行的是( )思路①：连接AD，借助S△ABD+S△ACD=S△ABC思路②：过点D作DM⊥BG于点M，然后证明△BMD≌△DEB思路③：连接EF，证明EF=BGA.①②③B.①③C.②③D.①②答案：D解题思路：试题难度：三颗星知识点：类比探究3.（上接第1，2题）在图3中，D是线段BC延长线上的点，探究DE，DF与BG的关系，你认为正确的是( )A. B.C. D.无法判断答案：B解题思路：试题难度：三颗星知识点：类比探究4.在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且CE=DE．为判断AE和BD 之间的关系，小明准备分情况进行讨论．当E是AB中点时，如图1，小明发现，由于E是AB边的中点，利用三线合一可以得到AE=BE，∠ECB=30°，再由CE=DE 可以得到∠D=30°，进而得到∠BED=30°，就可以得到BD=BE=AE．但是当E不是AB中点时，就不能照搬上述方式进行证明，此时小明想到了另外一种方式：过点E作EF∥BC，交AC于点F，也能证明AE=BD．（1）当E是线段AB上除端点和中点外的任一点时，如图2，按照上述辅助线证明AE=BD，证明过程中需要使用一对三角形全等，则证明此对三角形全等不能使用的条件是( )A.AASB.ASAC.SASD.SSS答案：D解题思路：试题难度：三颗星知识点：类比探究5.（上接第4题）（2）当点E在BA的延长线上时，如图3，点D在BC边上，且CE=DE，按照下面的操作，能够证明AE=BD的是( )A.直接证明△EAC≌△BDEB.①过点A作AF∥BC，交EC于点F；②△AEF是等边三角形；③△AFC≌△BDEC.①过点E作EF∥BC，交CA的延长线于点F；②△AEF是等边三角形；③△EFC≌△DBED.①过点A作AF∥BC，交EC于点F，连接DF；②四边形FDBE是等腰梯形答案：C解题思路：试题难度：三颗星知识点：类比探究学生做题后建议通过以下问题总结反思问题1：类比探究属于几何综合题，解决此问题的主要方法是什么？问题2：目前我们所学的结构类比中有两种结构，分别是什么？问题3：什么特征我们会考虑旋转结构？问题4：在△ABC中，AB=AC=a，BC=b，且2a b，BG⊥AC于G，DE⊥AB于E，DF⊥AC于F．在图1中，D是BC边上的中点，请判断DE+DF与BG的关系．( )A.B.C.D. 无法判断根据不同的特征，本题可以有不同的思路，你能想出几种？。

三角形全等之类比探究(照搬字母、辅助线一)(北师版)(含答案)

学生做题前请先回答以下问题问题1：解决类比探究问题的一般方法：（1）根据题干条件，结合____________先解决第一问；（2）用解决_______的方法类比解决下一问，整体框架照搬．问题2：整体框架照搬包括____________，____________，____________．问题3：“三角形全等”的辅助线：见中线，要________，________之后___________．问题4：当见到线段的______________考虑截长补短，构造全等或等腰转移____、转移____，然后和_________重新组合解决问题．问题5：当见到线段的______________考虑截长补短，截长补短的作用是把_________________________转化成_____________________．以下是问题及答案，请对比参考:问题1：解决类比探究问题的一般方法：（1）根据题干条件，结合先解决第一问；（2）用解决的方法类比解决下一问，整体框架照搬．答：分支条件；第一问．问题2：整体框架照搬包括，，．答：字母照搬，辅助线照搬，思路照搬．问题3：“三角形全等”的辅助线：见中线，要，之后．答：倍长，倍长，证全等．问题4：当见到线段的考虑截长补短，构造全等或等腰转移、转移，然后和重新组合解决问题．答：和差倍分，边，角，已知条件．问题5：当见到线段的考虑截长补短，截长补短的作用是把转化成．答：和差倍分，多条线段间的数量关系，两条线段间的等量关系．三角形全等之类比探究（照搬字母、辅助线一）（北师版）一、单选题(共5道，每道20分)1.在四边形ABCD中，BA=BC，．（1）如图1，当点M，N分别在AD，CD上时，若∠BAD+∠BCD=180°，求证：MN=AM+CN．先在图上走通思路后再填写空格内容：（1）如图，延长NC到E，使CE=AM，连接BE．由∠BAD+∠BCD=180°，∠BCE+∠BCD=180°，利用同角的补角相等，得∠BAD=∠BCE；因为BA=BC，AM=CE，因此根据三角形全等的判定___________，可以得到△BAM≌△BCE，由全等的性质得到______________________；又因为，可得_____________，因此根据三角形全等的判定SAS，可以得到___________，由全等的性质得MN=EN；所以MN=EN=CE+CN=AM+CN．请你仔细观察下列序号所代表的内容：①ASA；②SAS；③SSA；④AM=CE，BM=BE；⑤∠1=∠2，BM=BE；⑥∠1=∠2；⑦∠MBN=∠EBN；⑧△MBN≌△EBN；⑨△BAM≌△MDN．以上空缺处依次所填最恰当的是( )A.③⑤⑦⑨B.①④⑥⑧C.②⑤⑥⑨D.②⑤⑦⑧答案：D解题思路：试题难度：三颗星知识点：三角形全等之类比探究2.（上接第1题）（2）如图2，当点M，N分别在DA，CD的延长线上时，若∠BAD与∠BCD互补，求证：MN=CN-AM．如图，下面给出了证明的路线图：请你仔细观察下列序号所代表的内容：①△BAM≌△BCE（SAS）；②△BMN≌△BEN（SAS）；③∠1=∠2，BM=BE；④BM=BE，BA=BC；⑤∠1=∠2．以上横线处，依次所填最恰当的是( )A.①③②B.②④①C.②⑤①D.①④②答案：A解题思路：试题难度：三颗星知识点：三角形全等之类比探究3.△ABC和△CDE均为等腰直角三角形，∠ABC=∠CDE=90°，AB=BC，DC=DE，CD＞BC，M是AE的中点．（1）如图1，当点C，B，D在同一直线上，求证：DM⊥BM．如图，下面给出了证明的路线图：请你仔细观察下列序号所代表的内容：①延长BM，交DE于点F，使MF=MB；②延长BM，交DE于点F；③AB=EF，BM=FM；④AM=EM，∠ABM=∠EFM．以上横线处，依次所填最恰当的是( )A.①④B.②③C.②④D.①③答案：B解题思路：试题难度：三颗星知识点：三角形全等之类比探究4.（上接第3题）（2）如图2，当BC⊥CE时，求证：DM⊥BM．需要添加的辅助线正确的是( )A.延长BM，交CE于点F，使MF=BM，连接BD，DFB.延长BM，交CE于点F，连接BD，DFC.延长BM，DE交于点F，连接BDD.连接BD答案：B解题思路：试题难度：三颗星知识点：三角形全等之类比探究5.（上接第4题）（3）题干中的其他条件不变，当BC⊥CE时，要证明MD⊥MB，在4第题添加的辅助线的基础上，要证明△BCD≌△FED，理由是( )A.SASB.AASC.ASAD.HL答案：A解题思路：试题难度：三颗星知识点：全等三角形的判定和性质。

类比探究专项训练(二)(含答案) (1)

类比探究专项训练（二）试卷简介:类比探究是一类共性条件与特殊条件相结合，由特殊情形到一般情形（或由简单到复杂情形）逐步深入，解决思想方法一脉相承的综合性题目。

本套主要训练学生对于类比探究题目的认识（问与问之间有共性条件），在旋转，中点结构下训练学生能够照搬字母，照搬辅助线，照搬思路来解决问题。

一、单选题(共6道，每道16分)1.探究问题：（1）方法感悟：如图1，在正方形ABCD中，E，F分别为边CD，BC上的点，且满足∠EAF=45°，连接EF，求证：DE+BF=EF．关于证明上述结论的辅助线的作法，下列说法不合适的是( )A.延长CB到G，使BG=DE，连接AGB.过点A作AG⊥AE，交CB的延长线于点GC.将△ADE绕点A顺时针旋转90°得到△ABG（之后证明点G，B，F在同一条直线上）D.过点A作AG⊥EF于点G答案：D1．解题要点①分析题目特征，属于类比探究中对旋转结构的考查．最终的目标是将DE和BF拼接起来，有下列几种实现方式：A选项：延长CB到G，使BG=DE，连接AG，可以得到△ADE≌△ABG（SAS），之后利用△AGF≌△AEF（SAS）可以证明结论；B选项：过点A作AG⊥AE，交CB的延长线于点G，可以得到△ADE≌△ABG（ASA），之后利用△AGF≌△AEF（SAS）可以证明结论；C选项：将△ADE绕点A顺时针旋转90°得到△ABG，利用∠ABG+∠ABC=180°说明点G，B，F在同一条直线上，进而证明△AGF≌△AEF（SAS），之后可以证明结论；所以答案选D．②利用选项A中的辅助线分析上述证明过程，可分为以下几步：辅助线描述；△ADE≌△ABG；∠GAF=∠EAF；△AGF≌△AEF．2．解题过程利用选项A中的辅助线来证明DE+BF=EF．如图，延长CB到G，使GB=DE，连接AG．在正方形ABCD中，AB=AD，∠ABG=∠ADE=90°，∵BG=DE，∴△ADE≌△ABG，∴AG=AE，∠GAB=∠EAD．∵∠EAF=45°，∴∠BAF+∠EAD=45°，∴∠BAF+∠GAB=45°，∴∠GAF=∠EAF，∴△AGF≌△AEF，∴GF=EF，即BG+BF=EF，∴DE+BF=EF．试题难度：三颗星知识点：中考数学几何中的类比探究2.（上接第1题）（2）方法迁移：如图2，将Rt△ABC沿斜边翻折得到△ADC，E，F分别为边CD，BC上的点，且满足．则DE，BF，EF之间的数量关系为( )A. B.DE+BF=EFC.2DE+BF=EFD.DE+2BF=EF答案：B1．解题要点①照搬（1）中的思路：辅助线描述；△ADE≌△ABG；∠GAF=∠EAF；△AGF≌△AEF．②辅助线同样是：延长CB到G，使得BG=DE，连接AG．③能够按照①中的框架操作的关键特征在于：AB=AD，∠ABC+∠ADC=180°，能够实现旋转，即能够得到△ADE≌△ABG；，能够保证△AGF≌△AEF．不变特征是：AB=AD，∠ABC+∠ADC=180°，．2．解题过程如图，延长CB到G，使得BG=DE，连接AG．∵△ADC是由Rt△ABC沿斜边AC翻折得到的，∴AB=AD，∠ABC=∠ADC=90°．∵BG=DE，∴△ADE≌△ABG，∴AG=AE，∠GAB=∠EAD．∵，∴∠BAF+∠EAD=∠EAF，∴∠BAF+∠GAB=∠EAF，∴∠GAF=∠EAF，∴△AGF≌△AEF，∴EF=GF=BG+BF，∴DE+BF=EF．试题难度：三颗星知识点：中考数学几何中的类比探究3.（上接第1，2题）（3）问题拓展：如图3，在四边形ABCD中，AB=AD，E，F分别为边CD，BC上的点，且满足，则当∠B和∠D满足( )时，DE+BF=EF成立．A.∠B=∠DB.∠B+∠D=180°C.∠B=2∠DD.∠B+∠D=120°答案：B1．解题要点照搬（1），（2）中的思路：辅助线描述；△ADE≌△ABG；∠GAF=∠EAF；△AGF≌△AEF．发现在作出辅助线之后，要证明△ADE≌△ABG，缺少角度条件．与前面的不变特征相比较，若要结论仍成立，需要让∠ABC+∠D=180°．2．解题过程当“∠B+∠D=180°”时，完整的证明过程如下：如图，延长CB到G，使得BG=DE，连接AG．∵∠ABC+∠D=180°，∴∠ABG=∠D．∵AB=AD，BG=DE，∴△ADE≌△ABG，∴AG=AE，∠GAB=∠EAD．∵，∴∠BAF+∠EAD=∠EAF，∴∠BAF+∠GAB=∠EAF，∴∠GAF=∠EAF，∴△AGF≌△AEF，∴EF=GF=BG+BF，∴DE+BF=EF．试题难度：三颗星知识点：中考数学几何中的类比探究4.（1）如图1，在正方形ABCD的边AB上任取一点E，过点E作EF⊥AB，交BD于点F，取DF的中点G，连接EG，CG．为了研究线段EG和CG之间的数量和位置关系，可通过作辅助线：延长EG，交AD的延长线于点H，连接EC，HC，来进行分析．则得到的结论是( )A.EG=CG且EG⊥CGB.EG=CG但EG与CG不垂直C.EG⊥CG但EG≠CGD.答案：A1．解题要点利用题干中给出的辅助线信息继续研究，寻找进一步的结论来说明EG和CG之间的关系．由“平行＋中点”可以得到DH=EF=BE，则△CBE≌△CDH（SAS），进而得到△ECH是等腰直角三角形，所以EG=CG且EG⊥CG．2．解题过程如图，延长EG，交AD的延长线于点H，连接EC，HC．由题意得，EF∥AD，△BEF是等腰直角三角形．∵G是DF的中点，∴FG=DG．∵DH∥EF，∴∠DHG=∠FEG，∠EFG=∠HDG，∴△EFG≌△HDG，∴DH=EF=BE，EG=HG．∵BC=DC，∠EBC=∠HDC=90°，∴△CBE≌△CDH，∴EC=HC，∠BCE=∠DCH，∴∠ECH=∠ECD+∠DCH=∠ECD+∠BCE=90°，∴△ECH是等腰直角三角形．∵EG=HG，∴EG=CG且EG⊥CG．试题难度：三颗星知识点：中考数学几何中的类比探究5.（上接第4题）（2）在图1的基础上，将△BEF绕点B逆时针旋转90°，其他条件不变，如图2，为了证明EG和CG之间的数量和位置关系仍成立，类比（1）中的辅助线和证明思路，需要作出的辅助线是( )A.延长EG，交AD于点H，连接HCB.延长BG，交AD于点H，连接HCC.延长EG，交CD的延长线于点HD.延长EF，交DA的延长线于点H，连接HC答案：C1．解题要点①要类比（1）中的辅助线和证明思路，需要明白（1）中的辅助线和思路带给我们什么．首先能够得到全等，利用的是“平行＋中点”，也即是“EF∥CD，FG=DG”．那么此题中也应该利用“平行+中点”，所以需要延长EG，交CD的延长线于点H．其次是△CBE≌△CDH，进而得到△ECH是等腰直角三角形．而在此题中△CBE和△CDH是不存在的，但是可以直接利用EC=HC判断△ECH是等腰直角三角形．②比较两问的特点，都是观察到G是DF的中点，从“平行+中点”入手判断结论，证明框架是：辅助线（平行+中点）；△CBE≌△CDH（EC=HC，∠ECH=90°）；△ECH是等腰直角三角形．2．解题过程完整地证明结论的过程如下：如图，延长EG，交CD的延长线于点H．由题意得，EF∥CD，FG=DG，∴∠H=∠GEF，∠EFG=∠HDG，∴△EFG≌△HDG，∴HD=EF=BE，EG=HG．∵CB=CD，∴EC=HC，∴△ECH是等腰直角三角形．∵EG=HG，∴EG=CG且EG⊥CG．试题难度：三颗星知识点：中考数学几何中的类比探究6.（上接第4，5题）（2）在图1的基础上，将△BEF绕点B逆时针旋转180°，其他条件不变，如图3，为了证明EG和CG之间的数量和位置关系仍成立，类比（1），（2）中的辅助线和证明思路，需要证明两个直角三角形全等，则判断该三角形全等时使用的条件是( )A.AASB.ASAC.HLD.SAS答案：D1．解题要点照搬（1），（2）中的证明思路：辅助线（平行+中点）；△CBE≌△CDH（EC=HC，∠ECH=90°）；△ECH是等腰直角三角形．2．解题过程如图，延长EG，交AD于点H，连接EC，HC．由题意得，F，B，D三点共线，EF∥AD，∴∠DHG=∠FEG，∠F=∠HDG．∵FG=DG，∴△FEG≌△DHG，∴DH=EF=BE，EG=HG．∵BC=DC，∠HDC=∠EBC=90°，∴Rt△BEC≌Rt△DHC，∴EC=HC，∠ECB=∠HCD，∴∠ECH=∠ECB+∠BCH=∠HCD+∠BCH=90°，∴△ECH是等腰直角三角形．∵EG=HG，∴EG=CG且EG⊥CG，故证明过程中，判断两个直角三角形全等时使用的条件是SAS．试题难度：三颗星知识点：中考数学几何中的类比探究。

类比探究之结构类比(旋转)(北师版)(含答案) (1)

学生做题前请先回答以下问题问题1：类比探究属于几何综合题，解决此问题的主要方法是什么？问题2：目前我们所学的结构类比中有两种结构，分别是什么？问题3：什么特征我们会考虑旋转结构？问题4：如图1，在正方形ABCD中，点M，N分别在AD，CD上，若∠MBN=45°，易证MN=AM+CN．（1）如图2，在梯形ABCD中，BC∥AD，AB=BC，∠A＝∠D，点M，N分别在AD，CD上，若，则线段MN，AM，CN之间的数量关系为( )A．B．C．D．分析题目中的不变特征，画出其路线图.类比探究之结构类比（旋转）（北师版）一、单选题(共8道，每道12分)1.如图1，在正方形ABCD中，点M，N分别在AD，CD上，若∠MBN=45°，易证MN=AM+CN．（1）如图2，在梯形ABCD中，BC∥AD，AB=BC，∠A＝∠D，点M，N分别在AD，CD上，若，则线段MN，AM，CN之间的数量关系为( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：类比探究问题2.（上接第1题）（2）如图3，在四边形ABCD中，AB=BC，∠ABC+∠ADC=180°，点M，N分别在DA，CD的延长线上，若，则线段MN，AM，CN之间的数量关系为( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：类比探究问题3.如图1，在正方形ABCD中，点E，F分别为DC，BC边上的点，且满足∠EAF=45°，连接EF．利用旋转的思想很容易证明DE+BF=EF．如图2，将Rt△ABC沿斜边翻折得到△ADC，点E，F分别为DC，BC边上的点，且．则DE，BF，EF之间的数量关系为( )A. B.C.DE+2BF=EFD.DE+BF=EF答案：D解题思路：试题难度：三颗星知识点：类比探究问题4.（上接第3题）如图3，在四边形ABCD中，AB=AD，E，F分别为DC，BC边上的点，且满足，当∠ABC与∠ADC满足( )时，可使得上问结论依然成立．A.∠ABC=∠ADCB.∠ABC+∠ADC=180°C.∠ABC=2∠ADC-180°D.∠ABC+2∠ADC=270°答案：B解题思路：试题难度：三颗星知识点：类比探究问题5.如图1所示，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，且点B，A，D在一条直线上．连接BE，CD，M，N分别为BE，CD的中点，容易证明△AMN是等腰三角形．在图1的基础上，将△ADE绕点A按顺时针方向旋转180°，其他条件不变，得到图2所示的图形，则在图2中下列说法不正确的是( )A.△ADC≌△AEBB.△CAN≌△BAMC.∠CAM=∠NAED.AM=AN可以通过全等三角形对应边上的对应中线相等来说明答案：C解题思路：试题难度：三颗星知识点：类比探究问题6.已知△ABC为等边三角形，点D为直线BC上一动点（不与点B，C重合），以AD为边作等边三角形ADF（A，D，F按顺时针排列），连接CF．（1）如图，当点D在边BC上时，容易证明AC＝CF＋CD，在证明过程中需要用到某对三角形全等，则证明全等时用到的条件是( )A.AASB.ASAC.SASD.SSS答案：C解题思路：试题难度：三颗星知识点：类比探究问题7.（上接第6题）（2）如图，当点D在边BC的延长线上时，其他条件不变，则AC，CF，CD 之间的数量关系为( )A.AC=CF+CDB.AC=CF-CDC.AC=CF-2CDD.AC=CF+2CD答案：B解题思路：试题难度：三颗星知识点：类比探究问题8.（上接第6，7题）（3）如图，当点D在边CB的延长线上时，其他条件不变，则AC，CF，CD之间的数量关系为( )A.AC=CF+CDB.AC=CF-CDC.AC=CF-2CDD.AC=CD-CF答案：D解题思路：试题难度：三颗星知识点：类比探究问题第11页共11页。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

学生做题前请先回答以下问题
问题1：类比探究属于几何综合题，类比（__________，___________，___________）是解决此问题的主要方法，做好类比需要把握变化过程中的____________．
若属于类比探究常见的结构类型，调用结构类比解决．
若不属于常见结构类型
①根据题干条件，结合___________________先解决第一问．
②类比解决下一问．
如果不能，分析条件变化，寻找______________．
结合所求目标，依据_____________，大胆猜测、尝试、验证
问题2：想一想类比探究问题常见的不变结构有哪些，处理方式是什么？
以下是问题及答案，请对比参考:
问题1：解决路径长问题的思路为：
①分析、，寻找；
②确定运动路径；
通过“、、”猜测运动路径，并结
合进行验证，在做的过程中要大胆猜测，小心验证．
③设计方案，求出路径长．
答：
类比探究—直角结构
一、单选题(共6道，每道16分)
1.在Rt△ABC中，∠B=90°，∠A=30°，将一块三角板的直角顶点放在△ABC斜边AC的中点P 处，将三角板绕点P旋转．
（1）如图1，三角板的两直角边分别交AB，BC于点M，N，此时PN和PM的数量关系是( )
A. B.
C. D.
答案：B
解题思路：
试题难度：三颗星知识点：中考数学几何中的类比探究
2.（上接第1题）（2）如图2，三角板的两直角边分别交AB，BC的延长线于点M，N，此时PN和PM的数量关系是( )
A. B. C. D.
答案：C
解题思路：
试题难度：三颗星知识点：中考数学几何中的类比探究
3.（上接第1，2题）（3）如图3，若将三角板的直角顶点放在斜边上的点P处，三角板的两直角边分别交AB，BC的延长线于点M，N，当时，PN和PM的数量关系是( )
A. B.
C. D.
答案：B
解题思路：
试题难度：三颗星知识点：中考数学几何中的类比探究
4.正方形ABCD中，O是对角线AC的中点，P是对角线AC上一动点，连接PB．
（1）过点P作PF⊥CD于点F，PE⊥PB，交CD（或CD的延长线）于点E，则DF和EF之间的数量关系是( )
A. B.
C.DF=EF
D.
答案：C
解题思路：
试题难度：三颗星知识点：直角结构
5.（上接第4题）（2）在（1）中，当点P在线段OA上时，如图所示，则线段PA，PC，CE 之间的数量关系为( )
A. B.
C. D.
答案：D
解题思路：
试题难度：三颗星知识点：直角结构
6.（上接第4，5题）（3）在（1）中，当点P在线段OC上时（不与点O，C重合），类比（2）中的做法，可以判断线段PA，PC，CE之间的数量关系为( )
A. B.
C. D.
答案：C
解题思路：
试题难度：三颗星知识点：直角结构。