【免费下载】误差理论作业参考答案
误差理论 作业及参考答案

第一章1、熟悉误差、精度、有效数字的基本概念和相关计算方法。
答案:略2、用两种方法分别测量L1=50mm,L2=80mm。
测得值各为50.004mm,80.006mm。
试评定两种方法测量精度的高低。
解:两种测量方法进行的测量绝对误差分别为:δ1=50.004-50=0.004(mm);δ2=80.006-80=0.006(mm);两种测量方法的相对误差分别为:δ1/L1=0.004/50=0.008%;和δ2/L2=0.006/80=0.0075 %;显然,测量L2尺寸的方法测量精度高些。
3、若某一量值Q用乘积ab表示,而a与b是各自具有相对误差f a和f b的被测量,试求量值Q的相对误差。
解:∵相对误差=绝对误差/真值=(测得值-真值)/真值∴ a = a0(1+f a);b = b0(1+f b);式中a0、b0分别为a、b的真值。
则Q =ab = a0(1+f a) b0(1+f b)≈a0 b0(1+f a+ f b)因此,Q的相对误差约为(f a+ f b)第二章1、在立式测长仪上测量某校对量具,重复测量5次,测得数据(单位为mm)为20.0015,20.0016,20.0018,20.0015,20.0011。
若测量值服从正态分布,试以99%的置信概率确定测量结果。
解:①求算术平均值②求残余误差:各次测量的残余误差依次为 0,0.0001,0.0003,0,-0.0004。
③求测量列单次测量的标准差用贝塞尔公式计算:用别捷尔斯公式计算:④求算术平均值的标准差⑤求单次测量的极限误差和算术平均值的极限误差因假设测量值服从正态分布,并且置信概率P=2Φ(t)=99%,则Φ(t)=0.495,查附录表1 正态分布积分表,得置信系数t=2.6。
故:单次测量的极限误差:算术平均值的极限误差:⑥求得测量结果为:2、甲、乙两测试者用正弦尺对一锥体的锥角α个各重复测量 5 次,测得值如下:α甲:7°2’20”,7°3’0”,7°2’35”,7°2’20”,7°2’15”,α乙:7°2’25”,7°2’25”,7°2’20”,7°2’50”,7°2’45”;试求其测量结果。
误差理论第二章习题答案

2-4测量某电路电流共5次,测得数据(单位为mA )为168.41,168.54,168.59,168.40,168.50。
试求算术平均值及其标准差、或然误差和平均误差。
168.41168.54168.59168.40168.505x ++++=168.488()mA =)(082.015512mA vi i=-=∑=σ0.037()x mA σ=== 或然误差:0.67450.67450.0370.025()x R mA σ==⨯= 平均误差:0.79790.79790.0370.030()x T mA σ==⨯=2-5在立式测长仪上测量某校对量具,重量测量5次,测得数据(单位为mm )为20.0015,20.0016,20.0018,20.0015,20.0011。
若测量值服从正态分布,试以99%的置信概率确定测量结果。
20.001520.001620.001820.001520.00115x ++++=20.0015()mm =0.00025σ==正态分布 p=99%时,t 2.58= lim x x t δσ=±2.58=± 0.0003()mm =±测量结果:lim (20.00150.0003)x X x mm δ=+=±2-7用某仪器测量工件尺寸,在排除系统误差的条件下,其标准差mm 004.0=σ,若要求测量结果的置信限为mm 005.0±,当置信概率为99%时,试求必要的测量次数。
正态分布 p=99%时,t 2.58=lim x tδ=±2.580.0042.0640.0054.265n n ⨯====取2-10某时某地由气压表得到的读数(单位为Pa )为102523.85,102391.30,102257.97,102124.65,101991.33,101858.01,101724.69,101591.36,其权各为1,3,5,7,8,6,4,2,试求加权算术平均值及其标准差。
大物实验《误差理论》作业参考答案1

《误差理论》作业参考答案1、(1)74.63±0.05cm 或 746.3±0.5mm (2) 7.25±0.01cm 或 72.5±0.1mm (3)42.6 ±0.2s (4)27.6 ±0.2℃(5)2.734±0.001v2、(1)2位 (2)7位(3)5位(4)6位(5)5位(6)2位3、(1) 299300=2.99300510⨯;983±4=()21004.083.9⨯±;0.00400=4.00310-⨯0.004521±0.000001=()310001.0521.4-⨯±;32476510⨯=3.2476910⨯; (2) 15.48g =1.548mg 410⨯=1.548Kg 210-⨯(3) m =312.670±0.002Kg =(3.1267±0.00002)510⨯g =(3.12670±0.00002)mg 810⨯ (4) =t 17.9±0.1S =0.298±0.002min =(2.98±0.02)×10-1 min 4、(1)N=10.8±0.2cm(2)首位数码“0”不是有效数字,未位数码“0”是有效数字,正确答案是四位有效数字。
(3)28cm =2.8mm 210⨯ 280mm =28.0cm (4)L=(3.8±0.2)mm 410⨯(5)0.0221⨯0.0221=“0.00048841”≈0.000488(6)31010.460.1160.121500400⨯≈⨯⨯ 5、(1)X =81(4.113+4.198+4.152+4.147+4.166+4.154+4.132+4.170)=81⨯33.232=4.154cm X ∆={()1881-⨯ [(4.154-4.113)2+ (4.154-4.198)2+ (4.154-4.152)2+(4.154-4.147)2+ (4.154-4.166)2+ (4.154-4.154)2 +(4.154-4.132)2+ (4.154-4.170)2]}21 ≈0.00904~0.009cmX =X ±x σ=4.154±0.009cm 或 X =X ±x σ=4.15±0.01cm E =154.4009.0⨯100%=0.22% 或 E =15.401.0⨯100% =0.23%注:使用计算器时计算过程中有效数字的位数可以不考虑,最后结果应按照教材P7的“不确定度取位规则”和“测量有效数字取位规则”。
《误差理论与数据处理》部分课后作业参考答案精品文档18页

《误差理论与数据处理》部分课后作业参考答案1-18根据数据运算规则,分别计算下式结果: (1)3151.0+65.8+7.326+0.4162+152.28=? (2)28.13X0.037X1.473=? 【解】(1) 原式≈3151.0+65.8+7.33+0.42+152.28=3376.83 ≈3376.8(2) 原式≈28.1X0.037X1.47 =1.528359 ≈1.52-12某时某地由气压表得到的读数(单位为Pa )为102523.85,102391.30,102257.97,102124.65,101991.33,101858.01,101726.69,101591.36,其权各为1,3,5,7,8,6,4,2,试求加权算术平均值及其标准差。
【解】(1) 加权算术平均值: ∑∑==-+=m i imi ii px xp x x 1100)(=100000+1×2523.85+3×2391.30+5×2257.97+7×2124.65+8×1991.33+∙∙∙=102028.3425Pa(2) 标准差:∑∑==-=mi imi x i x p m vp i112)1(σ=√1×(102523.85−102028.3425)+3×(102391.30−102028.3425)+∙∙∙(1+3+5+7+8+6+4+2)∗(8−1)=86.95Pa2-17对某量进行10次测量,测得数据为14.7,1.0,15.2,14.8,15.5,14.6,14.9,14.8,15.1,15.0,试判断该测量列中是否存在系统误差。
【解】对数据进行列表分析,如下:作出残差与次数的关系图:(1) 线性系统误差:根据关系图利用残余误差观察法可知,不存在线性系统误差。
根据不同公式计算标准差比较法可得:按贝塞尔公式:2633.01121=-=∑=n vni iσ按别捷尔斯公式:2642.0)1(253.112=-=∑=n n vni iσ|u |=|σ2σ1−1|=|0.26420.2633−1|=0.0032<2√n −1=23故不存在线性系统误差。
(整理)误差理论作业-年总结--有答案

1. 若用两种测量方法测量某零件的长度110m m L 1=,其测量误差分别为m 11μ±和m 9μ±,而用第三种测量方法测量另一零件的长度为150m m L 2=,其测量误差为m 12μ±,试比较三种测量方法精度的高低。
解:对于1110L mm =:第一种方法的相对误差为:3111100.00010.01%110r -⨯=±=±=± 第二种方法的相对误差为:329100.0000820.0082%110r -⨯=±=±=± 对于2150L mm =:第三种方法的相对误差为:3312100.000080.008%150r -⨯=±=±=± 因为123r r r <<,故第三种方法的测量精度高。
2. 用两种方法测量1L 50mm =,2L 80mm =。
分别测得50.004mm ;80.006mm 。
试评定两种方法测量精度的高低。
解:因被测量不同,故用相对误差的大小来评定其两种测量方法之精度高低。
相对误差小者,其测量精度高。
第一种方法的相对误差为:150.004500.000080.008%50r -===第二种方法的相对误差为:280.006800.0000750.0075%80r -===因为12r r <,故第二种方法的测量精度高。
3. 若某一被测件和标准器进行比对的结果为008mm .20D =,现要求测量的正确度、精密度及准确度均高,下述哪一种方法测量结果符合要求? A. 0.004m m 012.20D 1±= B. 0.003m m 015.20D 2±= C. 0.002m m 015.20D 3±= D. 0.002m m 005.20D 4±= 解:D1. 测量某电路电流共5次,测得数据(单位mA )为168.41,168.54,168.59,168.40,168.50。
误差理论和测量平差习题5(含答案)
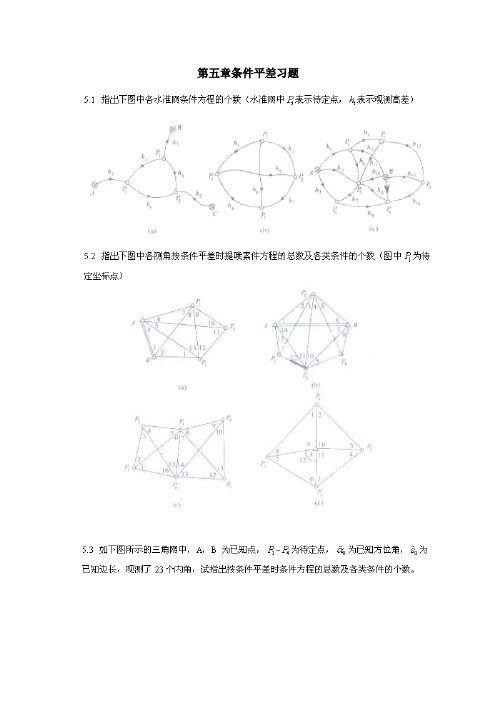
第五章条件平差习题第五章思考题参考答案5.1(a)n=6,t=3,r=3(b)n=6,t=3,r=3(c)n=14,t=5,r=95.2(a)n=13,t=6,r=7共有7个条件方程,其中有5个图形条件,2个极条件。
(b)n=14,t=8,r=6共有6个条件方程,其中有3个图形条件,3个极条件。
(c)n=16,t=8,r=8共有8个条件方程,其中有6个图形条件,2个极条件。
(d)n=12,t=6,r=6共有6个条件方程,其中有4个图形条件,1个圆周条件,1个极条件。
5.3n=23,t=6,r=17共有17个条件方程,其中有9个图形条件,1个圆周条件,1个固定角条件,1个固定边条件,5个极条件。
5.4 (1)n=22,t=9,r=13:7个图形条件,1个圆周条件,2个极条件,2个边长条件,一个基线条件。
(2)12837941314121520111718195610166101119910111213510ˆˆˆ1800ˆˆˆ1800ˆˆˆ1800ˆˆˆ1800ˆˆˆˆ1800ˆˆˆˆ1800ˆˆˆˆ1800ˆˆˆˆˆ1800ˆˆˆsin sin sin L L L L L L L L L L L L L L L L L L L L L L L L L L L L L L L L ++-=++-=++-=++-=+++-=+++-=+++-=++++-=171961116203614184715192211151217121318124ˆsin 1()ˆˆˆˆsin sin sin sin ˆˆˆˆsin sin sin sin 1()ˆˆˆˆsin sin sin sin ˆˆ()ˆˆˆˆsin sin sin sin ˆˆ(ˆˆˆˆsin sin sin sin FG FG L L L L L L L L L L L L L S S S S L L L L S S L L L L ===→=以大地四边形中心为极以中点四边形D 点为极的边长条件1213611891719ˆˆ)ˆˆˆˆsin sin sin sin ˆˆˆˆsin sin sin sin FG AB S S L L L L S S L L L L →=的边长条件(基线条件)5.5 n=8,t=4,r=4;有多种条件方程的列法,其中之一为:1001000100110000120001001104000011014V ⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥-=⎢⎥⎢⎥--⎢⎥⎢⎥---⎣⎦⎣⎦(注意常数项单位为mm ) 5.6 (1)P=3/2,(2)P=15.7 (1)P B =1.6,P C =2.1,P D =2.1,P E =1.6(2)P hCD =1.85.8 []ˆ 2.4998 1.9998 1.3518 1.8515h=2P σ=0.32(mm)5.9 1234561110009100110900101016V V V V V V ⎡⎤⎢⎥⎢⎥-⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥+=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎢⎥⎢⎥⎢⎥⎣⎦ []045452TV mm =---[]ˆ 1.576 2.219 3.7950.867 2.443 1.352T h m =--- 5.10 (1)1ˆ10.3556h m = 2ˆ15.0028h m = 3ˆ20.3556h m = 4ˆ14.5008h m =5ˆ 4.6472h m = 6ˆ 5.8548h m = 7ˆ10.5020h m =(2)±2.2mm。
误差理论和测量平差习题集(含答案)

误差理论和测量平差习题集(含答案)1.1 观测条件是由那些因素构成的?它与观测结果的质量有什么联系?1.2 观测误差分为哪⼏类?它们各⾃是怎样定义的?对观测结果有什么影响?试举例说明。
1.3⽤钢尺丈量距离,有下列⼏种情况使得结果产⽣误差,试分别判定误差的性质及符号:(1)尺长不准确;(2)尺不⽔平;(3)估读⼩数不准确;(4)尺垂曲;(5)尺端偏离直线⽅向。
1.4 在⽔准了中,有下列⼏种情况使⽔准尺读书有误差,试判断误差的性质及符号:(1)视准轴与⽔准轴不平⾏;(2)仪器下沉;(3)读数不准确;(4)⽔准尺下沉。
1.5 何谓多余观测?测量中为什么要进⾏多余观测?答案:1.3 (1)系统误差。
当尺长⼤于标准尺长时,观测值⼩,符号为“+”;当尺长⼩于标准尺长时,观测值⼤,符号为“-”。
(2)系统误差,符号为“-”(3)偶然误差,符号为“+”或“-”(4)系统误差,符号为“-”(5)系统误差,符号为“-”1.4 (1)系统误差,当i⾓为正时,符号为“-”;当i⾓为负时,符号为“+”(2)系统误差,符号为“+”(3)偶然误差,符号为“+”或“-”(4)系统误差,符号为“-”2.1 为了鉴定经纬仪的精度,对已知精确测定的⽔平⾓'"450000α=作12次同精度观测,结果为:'"450006 '"455955'"455958'"450004'"450003455958'"455959 '"455959 '"450006 '"450003设a 没有误差,试求观测值的中误差。
2.2 已知两段距离的长度及中误差分别为300.465m ±4.5cm 及660.894m ±4.5cm ,试说明这两段距离的真误差是否相等?他们的精度是否相等?2.3 设对某量进⾏了两组观测,他们的真误差分别为:第⼀组:3,-3,2,4,-2,-1,0,-4,3,-2 第⼆组:0,-1,-7,2,1,-1,8,0,-3,1试求两组观测值的平均误差1?θ、2θ和中误差1?σ、2?σ,并⽐较两组观测值的精度。
误差理论与测量平差基础习题集5(参考答案)

参考答案第一章1.1.04 (1)系统误差。
当尺寸大于标准尺长时,观测值小,符号为“+”;当尺长小于标准尺长时,观测值大,符号为“-”。
(2)系统误差,符号为“-”。
(3)偶然误差,符号为“+”或“-”。
(4)系统误差,符号为“-”。
(5)系统误差,符号为“-”。
1.1.05 (1)系统误差。
当i角为正值时,符号为“-”;当i角为负值时,符号为“+”。
(2)系统误差,符号为“+”。
(3)偶然误差,符号为“+”或“-”。
(4)系统误差,符号为“-”。
第二章2.3.08 σ=3.62″2.3.09 真误差可能出现的范围是|△|45mm,或写为-45mm,1/23045.2.3.10 他们的真误差不一定相等,相对精度不相等,后者高于前者。
2.6.17 θ1 =2.4,θ2 =2.4,σ 1 =2.7,σ 2 =3.6。
两组观测值的平均误差相同,而中误差不同。
由于中误差对大的误差反应灵敏,故通常采用中误差作为衡量精度的指标。
本题中,σ1σ2,因此,第一组观测值的精度高。
2.6.18 Dxx22=4229(秒2)2.6.19 σL1 =2 σL2 =3 σL3 =4 σL1L2 =-2 σL1L3 =0 σL2L3 =-3第三章3.2.07 (1)σX = 32σ (2)σx =L 12L 22 L 12L 32 L 22L 32L 32σ3.2.08 σx=2σ σy = 5σ σz = L 12L 22σ σt = 13σ3.2.09 (1)σx = σ124σ22(2)σy = (L1 L2)2σ12L 12σ22(3)σx = sin²L2σ12sin²L1 cos²(L1 L2)σ22sin²(L1 L2)3.2.10 (1)DF1 =22 (2)DF2 =18L 2227L 323.2.12 (2)DXL =ADLLDYL = BADLL 或DYL =ADLXBT DXY =ADLLATBT 或DXY =ADLXBT 3.2.13 D φ1 =4L 12+ 3L 22D φ2 =18 D φ1φ2 =7L2 – L13.2.14 DWW = XXXY XZ YX YY YZ ZX ZYZZ D D D D D D DD D ⎛⎫ ⎪ ⎪ ⎪⎝⎭= TT T 111213T T 212223TTT 313233AD A AD B AD C BD ABD B BD CD A CD A CD A ⎛⎫⎪ ⎪ ⎪⎝⎭TC3.2.15 X σy σ3.2.16 122222AB y 113''223S =cos L +sin L cot L sin L σρ⋅()22y2=1σ(秒)y1y2=0σ3.2.17 c =185.346(m )C σ=0.154(m )3.2.18 S σ=123.2.19 令p 点坐标X 、Y 的协方差阵为22x xy yz y σσσσ⎛⎫ ⎪ ⎪⎝⎭式中:2222222022()AP xS AP AP X Y Y S βσσσσρρ∆=+∆-+∆222222222()+X X oAP yS AP AP X S βσσσσρρ∆=∆+∆222222o AP AP xy S AP AP AP AP X Y X Y X Y S βσσσσρρ∆∆=-∆∆-∆∆yz xyσσ=3.2.20 (1)22111121()3112LLD ∧∧-⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦秒(2) 1321()3L L D ∧∧=-秒 3.3.24 (1)2hσ=1.73(mm) (2)1H ρσ=1.29(mm)3.3.25 最多可设25站 3.3.26 16km 3.3.27ρσ=0.097(m)3.3.28 在增加5个测回 3.3.29 S =4 635.563(m2) S σ=2.88(m)3.3.30ασ=βσ=3.34(秒)3.4.35 P1 P2 P3 σ0 =2.0’’ 1.0 0.25 4.0 σ0 =4.0’’ 4.0 1.0 16.0 σ0 =1.0’’ 0.25 0.0625 1.0 按各组权分别计算得X ∧= 3041’17.2’’ σS =0.87’’3.4.36 P1 =4.0 P2 =5.0 P3 =10.0 σ0 = 40σ(km) 3.4.37 P =np 3.4.38 PD =dD3.4.39 PC(平差前) =140PC (平差后)=1203.4.40 σ0 =5.66’’ σA =11.31’’3.4.41 (1)观测∠A 两次的算术平均值 (2)σ0 =1.70’’ (3)N =12(次)3.4.42 不对。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《误差理论》作业参考答案1、(1)74.63±0.05cm 或 746.3±0.5mm (2) 7.25±0.01cm 或 72.5±0.1mm (3)42.6 ±0.2s (4)27.6 ±0.2℃(5)2.734±0.001v2、(1)2位 (2)7位(3)5位(4)6位(5)5位(6)2位3、(1) 299300=2.99300;983±4=;0.00400=4.00510⨯()21004.083.9⨯±310-⨯0.0045210.000001=;32476=3.2476;±()310001.0521.4-⨯±510⨯910⨯(2) 15.48=1.548=1.548g mg 410⨯Kg210-⨯(3) =312.670±0.002=(3.1267±0.00002)=(3.12670±0.00002)m Kg 510⨯g mg 810⨯(4) 17.9±0.1=0.298±0.002=(2.98±0.02)×10-1 min=t S min 4、(1)N=10.8±0.2cm (2)首位数码“0”不是有效数字,未位数码“0”是有效数字,正确答案是四位有效数字。
(3)28=2.8 280=28.0cm mm 210⨯mm cm (4)L=(3.8±0.2)mm410⨯(5)0.02210.0221=“0.00048841”0.000488 ⨯≈000005.00001.00221.02=⨯⨯=∆(6)31010.460.1160.121500400⨯≈⨯⨯5、(1)=(4.113+4.198+4.152+4.147+4.166+4.154+4.132+4.170)=33.232X 8181⨯ =4.154cm ={ [(4.154-4.113)+ (4.154-4.198)+ (4.154-4.152)X ∆()1881-⨯222+(4.154-4.147)+ (4.154-4.166)+ (4.154-4.154)222+(4.154-4.132)+ (4.154-4.170)]}0.00904~0.009cm2221≈=±=4.154±0.009cm 或 =±=4.15±0.01cm X X X ∆X X X ∆=100%=0.22% 或 =100% =0.23%E 154.4009.0⨯E 15.401.0⨯注:使用计算器时计算过程中有效数字的位数可以不考虑,最后结果应按照教材P7的“不确定度取位规则”和“测量有效数字取位规则”。
(2)、=(2.904+2.902+2.900+2.903+2.900+2.904)==2.902167cm X 616413.17={(0.002+ 0.000+ 0.002+0.001+ 0.002+ 0.002)}X ∆()1661-⨯22222221=0.0008cm 30000017.0≈ ±=2.9022±0.0008cm =100%=0.028%X X ∆E 9022.20008.0⨯(3)=(2.010+2.010+2.011+2.012+2.009+1.980)= 2.0053cm X 616032.12≈=[(0.0047+ 0.0047+ 0.0057+0.0067+ 0.0037+ 0.0253)]x ∆()1661-⨯22222221 =0.005cm3000077534.0≈±=2.005±0.005cm =100%=0.25% X x ∆E 005.2005.0⨯6、(1)=∆N N 222⎪⎭⎫⎝⎛∆+⎪⎭⎫ ⎝⎛∆+⎪⎭⎫ ⎝⎛∆C B A C B A (2)222⎪⎭⎫⎝⎛∆+⎪⎭⎫ ⎝⎛∆=∆R U P R U P (3)㏑=㏑ +㏑ - ㏑(-)f U V U V=+()V U V U d V dV U dU f df ---+=⎪⎭⎫ ⎝⎛--V U U 11dU dV VU V ⎪⎭⎫⎝⎛-+11=-()()dVV U V UdU V U U V -+-()()22⎪⎪⎭⎫ ⎝⎛∆-+⎪⎪⎭⎫ ⎝⎛∆-=∆V U V U V UV U U V f f (4)㏑=㏑+㏑ + ㏑+㏑ +2㏑-2㏑- ㏑N m g r R T π4lm m 1㏑N =∂∂0g N ㏑ =∂∂r 1r N ㏑ =∂∂R 1R N ㏑=∂∂T T N 2ln =∂∂0ln =∂∂πN ll N 1ln -=∂∂21222222⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛∆+⎪⎭⎫ ⎝⎛∆+⎪⎭⎫ ⎝⎛∆+⎪⎭⎫ ⎝⎛∆+⎪⎭⎫ ⎝⎛∆=∆l T R r m N l T R r m N 7、3222084.1112.404.2142.318.1494441cm g h d m h d m V m =⨯⨯⨯====ππρ hd m g ln ln 24lnln ln ---==πρ 全微分 hdhd dd m dm d dg --==2ρρ相对不确定度 2222⎪⎭⎫⎝⎛∆+⎪⎭⎫ ⎝⎛∆+⎪⎭⎫ ⎝⎛∆=∆=h d m E h d m ρρ010.012.401.004.202.018.14905.0222=⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛= 2.0084.11010.0=⨯=⋅=∆ρρE 3cm g 3/)2.01.11(cm g ±=ρ8. 解:()()cm a a a a a a 00.297.198.104.200.201.2515154321=++++⨯=++++=22200.400.2cm a s ===cma L 00.800.244=⨯==;()cm A 02.003.002.004.000.001.0)15(512122222≈⎥⎦⎤⎢⎣⎡++++-=∆cm B 03.0305.0==∆cmB A a 04.0036.003.002.022≈=+=∆+∆=∆ 222.016.004.000.222cm cm a a s ≈≈⨯⨯=∆=∆cma L 2.004.044≈⨯=∆=∆∴ ±=4.0±0.2100%=5%S s ∆2cm ⨯=∆0.42.0S s ± =2.5%L cm L 2.00.8±=∆%1000.82.0:⨯=∆L L 9、四则运算法(1) 478.2 (2) 49.27+ 3.462 - 3.4————— —————481.662 45.87∴ 478.2+3.462=481.7 ∴ 49.27-3.4=45.9(3) 8 3 4. 5× 2 3. 9 ——————— 7 5 1 0 52 5 03 5 1 6 6 9——————— 1 9 9 4 4.5 5∴ 834.5×23.9=1.994410⨯ (4)∴ 2569.4÷19.5=132 (5) (6) ()66.53325.72=73.58.32=(7) =0.8667 0.86670 (8) 2.0+2345=2345357.7lg 510-⨯(9)(10) 2.00+2345=2.0200.20.38000.760.200.40000.76==-510⨯510⨯(11)+110= +110.0=4.76 + 110.0=114.8()()000.100.7700.98412.46.50.100⨯-+⨯000.100.210.100.100⨯⨯ (12)==3()398.10811.304678.89-⨯310.104678.89⨯10⨯10.由不确定度传递公式计算下列函数。
3.14(1) 3.14,?"23.10386685",ln ln ,0.010.0123.10386685~0.323.1x x y xxxx y x e y e e y e y e x yE y y =====∆====∆∆≈∆=⋅=⨯∴=解:计算 计算不确定度如下 设则相对不确定度为 取计算, 553105555(2)310,10?:1010"1.00006908"10,ln ln10ln10,ln10110,ln10ln10110 1.000069082.310~3101.00007x x x x y xx y x x y y y x yy y --⨯----=⨯=======∆=⨯∆∆≈⨯∆=⨯∆⨯=⨯⨯⨯=⨯⨯∴=解计算 设则 相对不确定度为 取 计算(3).?:0.01,"2.340939982"10.01ln ln ,0.00092222 5.480.0032.341y x y x x y y y x E y x y E y ==∆≈===∆∆======⨯∆=⋅=∴=解设则(4)..9.80,ln ?:0.01,..ln ,..ln 9.80"2.282382386"10.010.0019.802.282'x y x x x y x y x y ==∆≈===∆=∆=≈∴=解设则112121(5).0.5376,sin ?,?:0.0001,..sin ,...sin 0.5376"0.512076108",0.5376"0.596172097"cos cos 0.53760.0001~0.000090.51208x y x x x tgx y x y tgxy y tg x y ===∆≈======∆=∆=⨯∴=解设则P741.设电阻箱的额定功率,问当取值时允许通过的电流等于多少?w P 5.0=Ω=6.4321R 解:取A R P I 02236.010005.0===mA 3.221.电阻箱的准确度等级为0.2级,当取值为56.3Ω时,其误差等于多少?R ∆ 解:Ω≈=⨯==∆=⨯+=+=∆2.01246.03.56002213.0%2213.0%2213.0)%3.5662.02.0((R R m b R R R εP811.设负载电阻,要求控制电流范围,试设计一个制流电路。
Ω=500R mA 0.8~4.1解:VA R I E 45000080.0max =Ω⨯=∙= ΩΩ=-=-=-=+=2500235750028575000014.040min00min 取得据R AVR I E R R R EI 2.本实验用的量程3V 的直流电压表,准确度等级为0.1级,当读数为2.624V 时,其误差等于多少?如果是一次测量,那么应该怎样表达?解: 一次测量表达式V A m V 03.03%1%=⨯==∆εVV 03.064.2±=3.准确度等级为0.1级,额定功率为0.25W 的电阻箱,若电源为6V ,电阻箱分别取值43.7Ω和12.5Ω。
