第三章 单位线分析计算
第三章量纲分析和相似理论知识讲解

对于第一现象 Fma 对于第二现象 Fma
若此两现象各物理量之间存在下列关系:
导出量纲由基本量纲组合表示,如: 加速度的量纲 [a]=LT-2 力的量纲 [F]=[ma]=MLT-2 任何物理量B的量纲可写成 [B]=MLT。
无量纲量: 指该物理量的量纲为1,用L0M0T0表示,实际是一个数,但与单
纯的数不一样,它是几个物理量组合而成的综合物理量。例如角度, 可以用弧长和半径的值来度量,其单位可用弧度表示。但由于与基 本量纲无关,故角度是无量纲的。
2020/7/3
第二节 量纲分析
量纲和谐性原理:量纲和谐性原理又被称为量纲一 致性原理,也叫量纲齐次性原理。指一个物理现 象或一个物理过程用一个物理方程表示时,方程 中每项的量纲应该是和谐的、一致的、齐次的。
• 物理方程量纲的均匀性:一个正确的物理方程, 式中的每项的量纲应该相同,并应采用同一度量 单位。
2020/7/3
物理现象相似 是指除了几何相似之外,在进行物理过程的系
统中,在相应的地点(位置)和对应的时刻,模型 与原型的各相应物理量之间的比例应保持常数。
在两个系统中,所有向量在对应点和 对应时刻方向相同、大小成比例,所 有标量也在对应点和对应时刻成比例
2020/7/3
模型试验的优点: ➢ 经济性好-模型尺寸小 ➢ 针对性强-突出主要因素,略去次要因素 ➢ 数据准确-室内试验 模型试验的应用: ➢ 代替大型结构试验或作为大型结构试验的辅助试验。 ➢ 作为结构分析计算的辅助手段。 ➢ 验证和发展结构计算理论。
1960年第十一届国际大会通过了国际单位制(SI) ,在国际制单位 中202,0/7国/3 际制单位分为三类:⑴基本单位;⑵导出单位;⑶辅助单位。
1)基本单位 第十一届国际计量大会(1954年)和第十四届计量大会,决定
第三章 单位线分析计算

第三章 单位线分析计算本章着重介绍如何由净雨量过程预报流域出口的流量过程。
净雨量经过流域汇流形成出口的流量过程线,流域汇流历时是降雨径流预报预见期的来源,流域汇流物理过程是编制预报方案的理论依据。
3.1 舍尔曼时段单位线 3.1.1 基本原理舍尔曼(L. K. Sherman)于1932年提出了单位线的概念。
其定义为:流域上分布均匀的1个单位净雨直接径流产流量,所形成的直接径流过程线,即为单位线,记为UH 。
1个单位净雨是指单位时段内单位净雨深。
单位时段长可以任取,例如2h 、3h 、6h ,等。
而单位净雨深通常取为10mm 。
而实际发生的净雨,常常不是1个时段,也不是1个单位,应用于分析单位线时,有一些假定。
这些假定可归纳为以下两点:(1) 如果单位时段内净雨深不是一个单位,而是n 个,它所形成的出流过程线,总历时与UH 相同,流量则是UH 的n 倍。
(2) 如果净雨历时不是一个时段,而是m 个,则各个时段净雨所形成的出流过程之间互不干扰,出流过程的流量过程等于m 个流量过程之和。
由以上假定,净雨d r 、出流d Q 与UH 的纵坐标q 之间的关系如下:∑=+-=mi i t i d t d q r Q 11,, (2-1)式中:m i ,3,2,1Λ=,为净雨时段数。
d Q 和q 的单位为s /m 3,d r 则用单位净雨深的n 倍来表示。
如果UH 已知,根据上式,可由净雨转换为出流,计算十分简便。
关键是如何求得UH 。
可以根据流域的实测水文资料,分析出净雨及直接径流过程后,依据上式推求出UH ,为式(2-1)的逆过程。
3.1.2 单位线的推求推求UH 是使用次洪时段净雨深及相隔为计算时段长的直接径流时序过程。
前者由次洪降雨量经过扣损后得到,后者由径流过程线分割地下水后得到。
这里需要补充说明一下具体问题:(1) 由扣损方案求得的次洪净雨深,常不等于过程线分割得到的实测值,为了不把扣损的误差带入汇流计算,需要将计算值改正,或谓平差。
单位线法ppt课件

由6h单位线转换成12h单位线
时 间 (h) 0 6 12 6h单位 S(t) 线纵标 (m3/s) 3 (m /s) 0 18 140 0 18 158 0
S(t-12) (m3/s)
12h单位线纵标 S(t-12)- S(t) (m3/s) (m3/s) 0 18 158 0 9 79
18
24 30 36 42 48
径流量计算
地面径流
表层流径流
本次洪水形成
一次洪水流量过程
地下径流
前期洪水未退完的部分水量 割除 非本次降雨补给的深层地下径流
Q(m3/s) B
本次降雨形成的径流过程
H
前期 洪水 未退 完的 部分
C
I
A
E
F G
深层地下径流(基流)
D t(h)
基流的分割: 取历年最枯流量的平均值或本年汛前最枯流量用水平 线分割(ED线)。 流量过程线的分割及不同水源的划分(AF线和CD线):
地面径流
直接径流 本次洪水的径流过程 表层流径流
地下径流
Q(m3/s) B
N
0 . 2 N 0 . 84 F
本次降雨形成的径流过程
H
C
直接径流
I B’
A
C’ D D’ t(h)
E
G
地下径流
F
3、单位线分析
方法: 直接代数解法(分析法) 试错法 最小二乘法 矩法
倍比假定
叠加假定
• 四、单位线时段转换
•
6.某流域根据三场雨强相同,但暴雨中心分别在 上、中、下游的洪水分析的三条6h10mm 单位 线,它们的洪峰流量分别为q上、q中、q下 ,则 b [__ _] 它们之间一般应该 a、 q上>q中>q下 b、q上<q中<q下 c、 q上=q中=q下 d、q上>=q中>=q 下 7.某流域根据暴雨中心都在中游,但三场净雨 强度分别为5、10、20mm/h的洪水分析出三条 6h10mm单位线,它们的单位线洪峰流量分别为 b q5,q10,q20,则它们之间一般应[_ ___] a、 q5>q10>q20 b、 q5<q10<q20
单位线法计算例题
1.49
3.0
1.49
1.49
3.0
1.49
1.49
3.0
0.87
0.87
1.7
0.87
0.87
1.7
0.87
0.87
1.7
1.29
h24净
350.11
91 92 93 94 95 96 97 98 99 100 101 102 103
hm1净
#NUM!
毛雨
净雨 1.63 1.63 2.67 2.67 2.67 2.67 2.67 2.67 6.95 6.95
净雨计算
表
序号
时段
毛雨
净雨 时段雨量 序号
时段
毛雨
净雨
21
6.55
6.95
62
1.22
1.29
22
6.55
6.95
13.9
63
1.22
1.29
23
6.55
6.95
64
1.22
1.29
24
6.55
1.13 0.75 0.38 0.00 0.38 0.75 1.13 1.50 1.88 2.26 2.63 3.01 3.39 3.76 4.14 4.51 4.89 5.27
单位线计
算表
3
4
5
ui
qi=uiw/tp qi’=k’qi
0
0.0975
0.365
0.905
0.525 0.3 0.174 0.115 0.081 0.057 0.041 0.031 0.023 0.017 0.011 0.005 0.001
浙教版八年级下册数学第三章《数据分析初步》复习课件(共32张)

2. 求下面一组数据的中位数和平均数:
17,12,5,9,5,14;
解 把这组数据从小到大排列:
5,5,9,12,14,17 位于中间的数是9和12,这两个数的平均数是10.5,因此 这组数据的中位数是10.5; 这组数据的平均数是:(17+12+5+9+5+14)÷6=10.3
众数的定义:在一组数据中,把出现次数最多的数叫做这
老师对同学们每学期总评成绩是这样做的: 平时练习占
30%, 期中考试占30%, 期末考试占40%. 某同学平时练习93
分, 期中考试87分, 期末考试95分, 那么如何来评定该同学的
学期总评成绩呢?
加权平均数
解: 该同学的学期总评成绩是:
93×30% + 87×30% + 95×40% =92(分)
(1)3,4,4,5,3,5,6,5,6;
解 根据题意可知,5出现的次数最多,
因此,5是这组数据的众数.
(2)1.0,1.1,1.0,0.9,0.8,0.9,1.1,0.9
解 根据题意可知,0.9出现的次数最多,因此, 0.9是这组数据的众数.
2. 某班30人所穿运动服尺码的情况为:穿75号码的有5 人,穿80号码的有6人,穿85号码的有15人,穿90号 码的有3人,穿95号码的有1人. 穿哪一种尺码衣服的 人最多?这个数据称为什么数?
解 先把这组数据从小到大排列:
10,11,13,14,16,17,28 中位数
位于中间的数是14,因此这组数据的中位数 是14.
(2)453,442,450,445,446,457,448,449, 451,450.
解 把这组数据从小到大排列:
442,445,446,448,449,450,450,451,453,457
第三章陆地表面水的组成与运动课件

20
• 壤中径流的产生与降雨强度没有直接关系, 它只取决于上层的下渗率。
• 只要上层下渗率大于下层下渗率,形成临 时饱和带,即可产生壤中径流。
21
3.地下径流的产流机制
• 指包气带较薄、地下水位较高时的地下水 产流机制。产流条件与壤中径流相同。
fc—稳定下渗率 rg—地下径流产流率
22
• 地下径流的产流条件:
– 界面:包气带下界面 – 上层有下渗水 – 存在比上层下渗能力小的界面 – 供水强度大于下渗强度 – 产生临时饱和水带并具有产生侧向流动的动力
条件
23
4.饱和地面径流产流机制
• 在表层土壤具有较强透水性情况下的地面 产流机制。
– 随着壤中流积水的增加,继续下雨终将达到地 面,即包气带全部变成临时饱和水带,此后继 续降雨所形成的就不是壤中流,而是以地面径 流的形式出现,这种地面径流就成为饱和地面 径流。
产流 机制
• 壤中径流 的产流机制
• 饱和地面径流 的产流机制
11
1.超渗地面径流的产流机制
• 干旱地区的地下水埋藏很深,包气带可达 几十米甚至上百米,降水不易使包气带蓄 满,下渗的水量一般不会产生地下径流。 只有降水强度超过下渗率时才有地面径流 产生。这种产流方式,称为超渗产流。
12
• Horton产流理论
等流时线汇流计算示意图
若取 =1,则
f ( )
,即为汇流曲线
46
等流时面积分配线
47
3)出口流量过程的计算
假定把分成5块等流时面积等 1, 2 , 3, 4 , (5 图3
-21),现有 h1, h2 , h33 个时段的均匀净雨量,根据
水文学-洪水计算 单位线

一.河流与流域 二.正常径流量的计算 三.径流量的年际变化 四.径流的年内分配 五.小流域设计洪水计算 六.枯水径流 七.河流泥沙
2021/8/4
第一节 河流与流域
一、基本概念
河流:在重力的作用下,沿着陆地表面上的线形凹地流动,并 汇集于各级河槽上的水流。
河流的两个因素:经常或间歇性的水流及河槽(河床)。 水系:大小河流构成脉络相通的水流系统。 干流:直接入海或内陆湖泊的河流。
横断面分单式及复式两种. 单式断面水面宽度随水深的变化没有突变点,是 连续变化的,而复式断面水面宽度随水深的变化有突 变点,是不连续的。 枯水期水流通过的部分称基本河槽。在洪水期淹 没的部分称河漫滩。
2021/8/4
2021/8/4
3.河流的比降
(1)河道纵比降:
河槽纵断面特征用落差、比降和河槽平均坡度表示。 落差:河段两端的河底高程差。 河道的总落差:河源至河口的高程差。 比降:河段落差与相应河段长度之比。 河底比降=河段上、下游两点的高程差 / 河段长度
中游比降与流速减小、流量加大、冲刷淤积都不严重、河槽多为粗沙。 长江从宜昌到江西的湖口,黄河从河口镇到河南孟津为中游。
下游位于河流的最下一段。比降与流量更小、流量更大、淤积占优势、 多浅滩沙洲、河槽多细沙或淤泥。长江从湖口以下,黄河从孟津以下为下游 。
河口是河流的出口处。河流注入海洋或湖泊处,有大量的泥沙淤积形成 三角洲。一条河流直接注入另一河流的叫支流河口,汛期易受相互洪水顶托 的影2响021,/8/产4 生回水现象。
ai——相邻两等高线间的面积,km2 hi——相邻两等高线的平均高度,m A——流域总面积,km2
2021/8/4
(2)流域平均坡度:
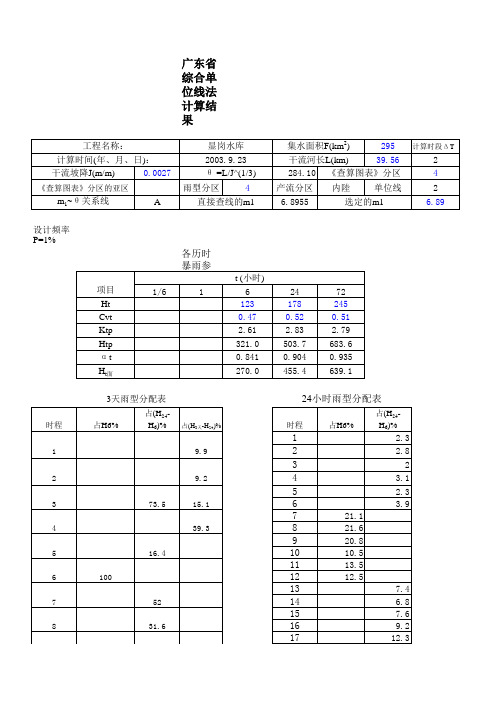
单位线

用 Excel 自带公式计算,对比后发现差别不大,故之后试算皆采用公式进行计算,对比
如表 4所示。
表 4 对比表
查表数据 0.000 0.181 0.259 0.393 0.503 0.551 0.632 0.699 0.727 0.777 0.817 0.835 公式计算 0.00 0.15 0.28 0.39 0.49 0.57 0.63 0.69 0.74 0.78 0.81 0.83
图 2 分析单位线
图 3 修正单位线 从图中可以清晰的看到锯齿已经消失,后半部分近似可认为光滑。同时,在与地 面净雨进行推流检验后发现结果差别不大,该单位线的纵标值可以采用。
3
三、 S 曲线法推求时段单位线
3 . 1 时段转换
时段转换的过程中,本文选择了 S 形曲线法,由于 S 形曲线的纵坐标就是单位线 沿时程累积曲线的对应值,即:
10mm
表 3 10mm 单位线
分析 0 39 127 157 89 96 73 56 47 35 28 19 19 13 10 3 5 1 2 0 0 修正 0 39 127 157 102 88 69 59 45 36 26 23 18 13 7 4 3 2 1 0 0
调整使得单位时间径流深为 10mm 后,发现该单位线存在锯齿的情况,所以根据 水量平衡的原理对该时段单位线进行修匀,单位线结果如表 3 所示,修匀结果如图 2、 图 3所示:
652.6562874 , 从而可以利用公式(10)与(11)求得初步的 n,K 值。
K
=
M2(Q) M1(Q)
− −
M2(h) M1(h)
− [M1(h)
+
M1(Q)]
(10)
5
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章 单位线分析计算本章着重介绍如何由净雨量过程预报流域出口的流量过程。
净雨量经过流域汇流形成出口的流量过程线,流域汇流历时是降雨径流预报预见期的来源,流域汇流物理过程是编制预报方案的理论依据。
舍尔曼时段单位线 3.1.1 基本原理舍尔曼(L. K. Sherman)于1932年提出了单位线的概念。
其定义为:流域上分布均匀的1个单位净雨直接径流产流量,所形成的直接径流过程线,即为单位线,记为UH 。
1个单位净雨是指单位时段内单位净雨深。
单位时段长可以任取,例如2h 、3h 、6h ,等。
而单位净雨深通常取为10mm 。
而实际发生的净雨,常常不是1个时段,也不是1个单位,应用于分析单位线时,有一些假定。
这些假定可归纳为以下两点:(1) 如果单位时段内净雨深不是一个单位,而是n 个,它所形成的出流过程线,总历时与UH 相同,流量则是UH 的n 倍。
(2) 如果净雨历时不是一个时段,而是m 个,则各个时段净雨所形成的出流过程之间互不干扰,出流过程的流量过程等于m 个流量过程之和。
由以上假定,净雨d r 、出流d Q 与UH 的纵坐标q 之间的关系如下:(∑=+-=mi i t i d t d q r Q 11,, (2-1)式中:m i ,3,2,1 =,为净雨时段数。
d Q 和q 的单位为s /m 3,d r 则用单位净雨深的n 倍来表示。
如果UH 已知,根据上式,可由净雨转换为出流,计算十分简便。
关键是如何求得UH 。
可以根据流域的实测水文资料,分析出净雨及直接径流过程后,依据上式推求出UH ,为式(2-1)的逆过程。
3.1.2 单位线的推求推求UH 是使用次洪时段净雨深及相隔为计算时段长的直接径流时序过程。
前者由次洪降雨量经过扣损后得到,后者由径流过程线分割地下水后得到。
这里需要补充说明一下具体问题:(1) 由扣损方案求得的次洪净雨深,常不等于过程线分割得到的实测值,为了不把扣损的误差带入汇流计算,需要将计算值改正,或谓平差。
在平差前应分析误差的来源,作出较为合理的修正,以不改变原来的雨型为原则。
(2) 计算时段长t ∆的确定,主要考虑峰形的控制,一般取涨洪历时的1/3~1/4,常与流域大小成正比对于多时段净雨而言,传统的单位线分析方法有以下一些: (1) 分析法由 ∑=+-=mi i t i d t d q r Q 11,,,得到《4)-(3 3)-(3 2)-(3 13,22,31,3,12,21,2,11,1,q r q r q r Q q r q r Q q r Q d d d d d d d d d ++=+==因此,上式组成的方程组为一个多元线性代数方程组,求解该代数方程组可以得到1q 、2q 的数值。
最简单的解法是逐一消去法。
由上面的方程组可以看出,由式(3-2),已知1,d Q 和1,d r ,解出1q :1,1,1d d r Q q =(3-5)1q 已知,将其带入式(3-3),可得到1,12,2,2d d d r q r Q q -=(3-6)如此递推下去,得到1,21,,d mi i t i d t d t r q r Q q ∑=+--=(3-7)计算结果见表3-1和图3-1所示。
直接代数法对于降雨与径流实测资料没有误差,流域汇流符合线性时不变系统时,能得出正确的唯一解。
但实际情况是:提供分析UH 的实测资料存在着观测与分析误差,流域汇流为非线性系统,因此直接分析解法不但不能得出唯一解,由于误差累积,其解常很不合理。
如分析得到的tq~呈锯齿形,如表3-1和图3-1的退水段,有的甚至出现负值,无法继续计算下去。
所以很少有人使用。
图3-1 分析法得到的单位线/表3-1 单位线分析法结果(2) 试错法这个方法是假设单位线,目估对比推流的与实测的tQ~。
当两者最接近时,d所假设的UH即为所求。
初始的UH,可用其它洪水已分析得来的成果,或用斜线分割法的结果,也可任意假定。
试错法应用比较广泛,有的用科林法试错,有的凭经验试错。
但主要确定是单位线过程的初始假定比较困难,试错过程有时也会出现不合理现象,对其过程进行修正也不易做得完好。
(3) 系统识别方法—UH既然是线性系统的单位响应,进一步可以应用线性系统鉴别的方法推求UH的最优解,如有约束的最小二乘法和回归法等。
(4) 各种方法的特点如上所述,推求单位线的方法主要有分析法、试错法和系统识别法。
试错法又可分为目估试错法和科伦试错法,后者是一种迭代性质的试错法。
分析法当降雨为1个时段时能取得很好的效果,但当降雨时段数大于1个时段,分析法推求的结果可能出现锯齿型,甚至出现负值,主要原因是误差的累积。
目估试错法是通过人工目估,逐步试错,使计算的流量过程与实测的流量过程吻合,避免了误差的累积,但任意性大,吻合程度缺乏客观标准,并且要求调试者具有相当的经验,费时费力。
科伦试错法是首先拟定初始单位线,然后按初始单位线计算出除最大降雨时段外的其它时段降雨产生的流量过程,并从实测流量过程中将其减去,差值即当成最大降雨时段产生的流量过程,据此推求新的单位线,将新单位线作为初始单位线,重复上述步骤,直至新旧单位线之间的差值达到给定的误差要求。
优点是当初始单位线拟定后,不必目估试错,能自动逐步修正,适合计算机编程。
缺点是计算结果及迭代的收敛性与初始单位线的拟定有关,推求的结果不一定是最佳结果。
另外当降雨时段较多时,迭代难以继续下去。
因此,科伦试错法仅当降雨较集中在最大时段或降雨时段数较小时,效果才较好。
3.1.3 单位线的综合为求得流域的单位线预报方案,需分析多次洪水。
多数流域,各次洪水所得到的UH 会有差别。
这时,首先要检查原始资料的观测误差,及根据原始资料计算用于分析UH 的t r d ~和t Q d ~过程中的操作误差,作出可能的改正,然后对UH 的变化根据UH 原理上存在的问题进行分析及处理。
如果各次洪水的UH 变化不大,可求出平均UH 。
平均UH 的绘制须注意,平均纵标值不宜取同时流量的平均值。
应先根据各个UH ,计算出平均峰值及峰现时间,确定峰点位置。
然后根据各个UH 的外形,初绘光滑的平均UH ,最后修正并校核总量为单位雨深。
3.1.4 单位线时段转换UH 是有一定长度的,同一次洪水,如单位时段长度不同,实际雨强不等,UH 不相同。
如原来UH 时段长为T ,现推求T 2的UH ,根据线性假定,可将UH 滞后T h ,与原UH 相加,将该过程线的纵坐标除以2即得T 2的UH 。
该UH 的峰值应等于上述两个UH 的交点,比原来UH 峰值低并滞后,这是由于历时增长,雨强降低所致。
因此,对一个给定的流域综合UH 方案,或将不同地区的UH 方案综合,需将不同时段的UH 换算为同一时段。
UH 是作为一个经验方法提出来的,但方法简易,使用精度不错,生产上一直沿用至今。
系统概念引入后,建立了UH 的理论,明确了方法的物理实质,这对于推求UH 及正确的应用都有益。
UH 是个黑箱模型,并和流域上实际的水力状态没有关系,使用时必须有实测水文资料,这是它的应用受到限制的主要原因。
—纳须单位线(Nash)纳须模型是现行概念性流域汇流模型中得到比较广泛应用的一种,该模型结构简单,包含的参数较少,且具有较好的适应性。
本文介绍纳须模型的结构及其参数率定方法。
3.2.1 纳须瞬时单位线1945年克拉克(C. O. Clark)首先提出瞬时单位线的概念。
所谓瞬时单位线,就是流域上均匀分布的、历时趋于无限小、强度趋于无穷大、但净雨总量为1个单位的净雨所形成的流域出口断面过程线。
通常用)(t u 表示。
1957年,纳须(Nash)把流域看作是一连串的n 个相同的“线性水库”,如图3-2所示。
可以推导出一个单位的瞬时入流进入水库系统后,其对应的出流即瞬时单位线的数学方程式为ktn kt n k t u --Γ=e )()(1)(1 (3-8)式中:Γ为伽马函数,当n 为整数时,其值为)!1(-n ;n 为相当于水库个数;k 为一个线性水库的蓄泄系数。
图3-2 纳须模型示意图3.2.2 纳须时段单位线在实际应用中,需要将瞬时单位线转换成时段单位线,一般用)(t S 曲线。
按照)(t S 曲线的定义,)(t S 等于瞬时单位线的积分,即 ⎰=tt t u t S 0d )( )(,对该式进行积分,可以很方便地导出)(t S 曲线,再利用线性叠加原理,)()(),(t t S t S t t u ∆--=∆,从而得到时段单位线。
即为∑∑=-=-∆---∆--=∆n i i n n i i n kt k tkti n k t t i n t t u 11])()!(1)()!(1e [e ),( (3-9)'式(3-9)为当n 为自然数时,计算步长为t ∆时的纳须时段单位线的计算公式。
3.2.3 纳须单位线参数n 、k 的确定如何确定参数n 和k 是纳须模型应用中的重要问题之一。
纵观目前所有的确定该模型的方法,按依据的资料分,则可归纳为3类:一是依据降雨和径流一一对应资料的方法,如矩法、累积量法、最优化方法等;二是依据流域地形和地貌资料的方法,如经验公式法等;三是依据流域出口断面流量资料的方法。
本文着重介绍应用较为广泛的矩法。
根据矩法,可以求出参数:)2()2(2)1()1(][IQI Q NNM M n --=(3-10))1()1()2()2(I Q I Q M M N N K --=(3-11)式中:)1(I M 、)1(Q M 分别为入流量(净雨量)及出流量的一阶原点矩;)2(I N 、)2(Q N 分别为入流量和出流量的二阶中心矩。
入流量和出流量的一阶原点矩的计算公式分别为2)()()()(d )( d )( 111100)1(tt I mt I t I t t I t t I t t t I Mni i ni ii ni i ni ii I∆⋅===∑∑∑∑⎰⎰====∞∞ (3-12) 2)()()()(d )( d )( 111100)1(tt Q mt Q t Q t t Q t t Q t t t Q Mni ini iini ini ii Q∆⋅===∑∑∑∑⎰⎰====∞∞(3-13) 式中:)(t I 、)(t I i 分别为t 时刻的净雨量和净雨量的时段平均值;)(t Q 、)(t Q i 分别为t 时刻的出流量和出流量的时段平均值。
12 ,32 ,,7 ,5 ,3 ,1--=n n m i 。
!同理,可以计算出净雨量和出流量的二阶原点矩为2112)2()2()()(t t I mt I M ni i ni ii I ∆⋅=∑∑== (3-14) 2112)2()2()()(t t Q mt Q Mni ini iiQ∆⋅=∑∑== (3-15) 由于入流量和出流量的二阶中心矩可用原点矩来表示,即2)1()2()2(][I I I M M N -= (3-16)2)1()2()2(][Q Q Q M M N -= (3-17)在推求某一流域纳须时段单位线时,首先选择几场有代表性的洪水资料,根据每场次洪水的相应入流和出流过程,分别求出它们的单位线参数n和k,然后把n和k平均(如果相差较大,可以分成几组)概化出流域的单位线参数,便可用纳须时段单位线计算公式计算出流域时段单位线。
