小学奥数知识讲解第十五讲 最短路线问题
最短路径问题PPT课件

A
·
C′ C
B
·
l
B′
问题1 归纳
B A
l
解决实 际问题
B
A
C
l
B′
抽象为数学问题 用旧知解决新知
B
A
C
l
联想旧知
A
C
l
B
尝试应用:
1.如图,直线l是一条河,P、Q是两个村庄.欲在l上的某处修建
一个水泵站,向P、Q两地供水,现有如下四种铺设方案,图中
实线表示铺设的管道,则所需要管道最短的是( D )
A
·
l C
B′
问题3 你能用所学的知识证明AC +BC最短吗? 证明:如图,在直线l 上任取一点C′(与点C 不
重合),连接AC′,BC′,B′C′.
由轴对称的性质知,
BC =B′C,BC′=B′C′. ∴ AC +BC
= AC +B′C = AB′, AC′+BC′
= AC′+B′C′. 在△AB′C′中,
从图中的A 地出发,到一条笔直的河边l 饮马,然 后到B 地.到河边什么地方饮马可使他所走的路线全程 最短?
B A
l
将A,B 两地抽象为两个点,将河流l 抽象为一条直 线.
·B A·
l
你能用自己的语言说明这个问题的意思, 并把它抽象为数学问题吗?
(1)从A 地出发,到河流l边 饮马,然后到B 地;
AM+NB+MN.
问题3:还有其他的方法选两点M,N,使得 AM+MN+NB的和最小吗?试一试。
a
b
A
M
N
B
问题2 归纳
解决实 际问题
《最短路径问题》PPT课件教学

你能要自己的语言重新描述一下问题吗? C是l上一个动点, 当点C在l的什么位置时,AC+BC最小?
探究 如图,点A,B 在直线l 的同侧,点C 是直线上的一个动点,当点C 在l 的什么位置时,AC 与CB 的和最小?
一开始的时候我们就讨论过点A,B在直线异侧的情况, 你还记得是怎么做的吗? 连接两点,交点就是所求 同侧的情况也能直连接两点吗?不行
拓广探索
在纸上画五个点,使任意三个点组成的三角形都 是等腰三角形 . 这五个点应该怎样画?
拓广探索
如图,△ABC 是等边三角形,BD 是中线,延长BC 至 E,使CE =CD . 求证DB =DE .
拓广探索
如图,△ABC 是等腰三角形,AC =BC,△BDC 和△ACE 分别为等边三角形,AE 与BD 相较于F,连接CF 并延长 ,交AB 于点G . 求证:G 为AB 的中点 .
复习巩固
如图,在△ABC 中,∠ABC =50°,∠ACB =80°,延长 CB至D,使DB =BA,延长BC 至E,使CE =CA,连接 AD,AE .求∠D,∠E,∠DAE 的度数 .
复习巩固 如图,AD =BC,AC=BD,求证:△EAB 是等腰三角形 .
复习巩固
综合应用
试确定如图所示的正多边形的对称轴的条数,一般地 ,一个正n边形有多少条对称轴?
综合应用
如图,从图形Ι 到图形Ⅱ是进行了平移还是轴对称?如果 是轴对称,找出对称轴;如果是平移,是怎样平移?
综合应用
如图,AD是△ABC 的角平分线,DE,DF 分别是△ABD 和△ACD的高 . 求证:AD 垂直平分EF .
综合应用
如图,在等边三角形 ABC 的三边上,分别取点D,E,F ,使AD =BE =CF . 求证△DEF 是等边三角形 .
《最短路径问题》PPT课件

A
a 3、连接PA,PB,由对称轴 的性质知,PA= P1A,
P1
PB=P2B
∴先到点A处吃草,再到点B
处饮水,最后回到营地,
这时的放牧路线总路程最
短,即 (PB+BA+AP)min
• 证明:
P2
b ∵ PA1+A1B1+B1P
B1 B
.P
河
= P1A1+A1B1+B1P2 > P1A+AB+BP2
前面和右面
D D1
③
A 1 A1
C1
2
4
B1
AC1 =√52+22 =√29
左面和上面
• 1、如图是一个长方体木块,已知 AB=5,BC=3,CD=4,假设一只蚂蚁 在点A处,它要沿着木块侧面爬到点D 处,则蚂蚁爬行的最短路径是 7 4 。
D
4
C
A
5
B3
• 2、现要在如图所示的圆柱体侧面A点 与B点之间缠一条金丝带(金丝带的宽 度忽略不计),圆柱体高为6cm,底面 圆周长为16cm,则所缠金丝带长度的 最小值为 10cm 。
在河上建一座桥MN,桥造在何处才能使从A到B
的路径最短?(假设河的两岸是平行的直线,桥
要与河垂直)
.A M
作法: 1、将点B沿垂直与河岸的方
向平移一个河宽到E
N
2、. E连接AE交河对岸与点M,则
.点BM为建桥的位置,MN为 所建的桥。
A C
M ND E
B
• 证明: ∵ AC+CD+DB = AC+CD+CE = AC+CE+CD > AE+CD = AM+ME+CD = AM+NB+MN ∴ AC+CD+DB > AM+NB+MN
四年级下册数学讲义-奥数讲练: 最短路线问题
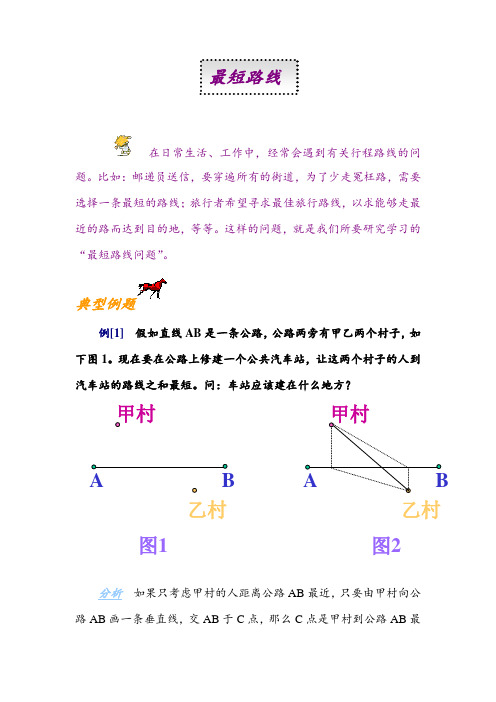
在日常生活、工作中,经常会遇到有关行程路线的问题。
比如:邮递员送信,要穿遍所有的街道,为了少走冤枉路,需要选择一条最短的路线;旅行者希望寻求最佳旅行路线,以求能够走最近的路而达到目的地,等等。
这样的问题,就是我们所要研究学习的“最短路线问题”。
典型例题例[1] 假如直线AB 是一条公路,公路两旁有甲乙两个村子,如下图1。
现在要在公路上修建一个公共汽车站,让这两个村子的人到汽车站的路线之和最短。
问:车站应该建在什么地方?分析 如果只考虑甲村的人距离公路AB 最近,只要由甲村向公路AB 画一条垂直线,交AB 于C 点,那么C 点是甲村到公路AB 最甲村 乙村AB 甲村乙村 图1图2最短路线近的点,但是乙村到C点就较远了。
反过来,由乙村向公路AB画垂线,交AB于D点,那么D点是乙村到公路AB最近的点。
但是这时甲村到公路AB的D点又远了。
因为本题要求我们在公路AB上取的建站点,能够兼顾甲村和乙村的人到这个车站来不走冤枉路(既路程之和最短),根据我们的经验:两个地点之间走直线最近,所以,只要在甲村乙村间连一条直线,这条直线与公路AB交点P,就是所求的公共汽车站的建站点了(图2)。
解用直线把甲村、乙村连起来。
因为甲村乙村在公路的两侧,所以这条连线必与公路AB有一个交点,设这个交点为P,那么在P 点建立汽车站,就能使甲村乙村的人到汽车站所走的路程之和最短。
例[2] 一个邮递员投送信件的街道如图3所示,图上数字表示各段街道的千米数。
他从邮局出发,要走遍各街道,最后回到邮局。
问:走什么样的路线最合理?全程要走多少千米?3分析选择最短的路线最合理。
那么,什么路线最短呢?一笔画路线应该是最短的。
邮递员从邮局出发,还要回到邮局,按一笔画问题,就是从偶点出发,回到偶点。
因此,要能一笔把路线画出来,必须途径的各点全是偶点。
但是图中有8个奇点,显然邮递员要走遍所有街道而又不走重复的路是不可能的。
要使邮递员从邮局出发,仍回到邮局,必须使8个奇点都变成偶点,就是要考虑应在哪些街道上重复走,也就是相当于在图上添哪些线段,能使奇点变成偶点。
六年级奥数最短路线

最短路线一、学习目标:通过最短路线的学习,体会转化的数学思想。
二、基础知识:最短路线通常的最短路线问题是以“平面内连结两点的线中,直线段最短”为原则引伸出来的。
在求最短路线时,常常先用“对称”的方法化成两点之间的最短距离问题。
利用对称性把折线化成易求的直线段,所以这种方法也叫做化直法,其他还有旋转法、翻折法等。
有时所求最短路线位于凸多面体的不同平面上,需将它们展开在同一平面上。
三、例题解析:例1:如图,A、B两个学校在公路的两侧.想在这两校的附近的公路上建一个汽车站,要求车站到两个学校的距离之和最小,应该把车站建在哪里?解:例2:如图,A、B两个学校都在公路的同侧.想在这两校的附近的公路上建一个汽车站,要求车站到两个学校的距离之和最小,应该把车站建在哪里?解:练一练:如下图,侦察员骑马从A地出发,去B地取情报.在去B地之前需要先饮一次马,如果途中没有重要障碍物,那么侦察员选择怎样的路线最节省时间,请你在图中标出来。
并说明做法。
解:例3:少先队一小队组织一次有趣的赛跑比赛,规则是从A点出发(见下图),跑到墙边,用手触摸墙壁,然后跑到B点.接着,离B点再次跑到墙边手触摸墙壁后,跑到C点.问选择怎样的路线最节省时间,请你在图中标出来。
分析:实际上是两个最短路线问题。
解:例4:在河中有A、B两岛(如下图),六年级一班组织一次划船比赛,规则要求船从A岛出发,必须先划到甲岸,又到乙岸,再到B岛,最后回到A岛,试问应选择怎样的路线才能使路程最短?解:例5:如图13—6,河流EF与公路FD所夹的角是一个锐角,某公司A在锐角EFD内.现在要在河边建一个码头,在公路边修建一个仓库,工人们从公司出发,先到河边的码头卸货,再把货物转运到公路边的仓库里去,然后返回到A处,问仓库、码头各应建在何处,使工人们所行的路程最短。
解:例6:A、B两个村子,中间隔了一条小河,现在要在小河上架一座桥,使它垂直于河岸。
请你在河两岸选择合适的架桥地点。
奥数 最短距离

最短路线例1.下图是从学校到邮局经过的所有马路,问从学校到邮局共有几条最短路线?思路分析:为了便于叙述,在各交叉点上标出字母.要想从家到学校走的路程最短,就不能走回头路,这道题中,最短也要走长方形ACGI的一个长和一个宽.为保证走得路线最短,只能向下和向右走.如果我们一条一条地数,可以发现共有以下六条路线最短:A→B→C→F→I;A→D→G→H→I;A→B→E→F→I;A→D→E→F→I;A→B→E→H→I;A→D→E→H→I;但如果按上述方法找,难免发生重复遗漏的路线.下面我们观察一下,看看是否有规律可循.①从A点出发向下或向右走只能到达B、D两点,到B点有一种走法,到D点同样只有一种走法,所以在B点、D点处各标角码1,表示从A点到此点的最近走法只有1种.②从B点可以向右走到达C点,因为从A到C的最短路线也仅有1条,所以角码为1.从B点向下可到E点,另外从D点到达E点的距离也最短,所以E点角标角码2.如图所示.继续做下去,我们会发现,每一个小格右下角的数正好是这个小格右上角与左下角的数的和,这个和就是从出发点A到I点所有最短路线的条数.例2.一个邮递员投送信件,街道如图所示,图上的数字表示各段街道的公里数.他从邮局出发,走遍各街道,最后回到邮局,怎样走路线最合理?思路分析:由于街道是含8个奇点的图形,所以,不可能不重复地走遍所有街道,为了保证邮递员从邮局出发再回到邮局,图形中8个奇点都应变为偶点.即将奇点两两相配对用线连结,有很多连法,下图仅列出了三种情形:添加的路线的里程分别是:(1)3×4=12(公里)(2)3×2+2×2=10(公里)(3)2×4=8(公里)由此可见邮递员按图(3)的路线走,重复的路最少,最合理.全程共走:3×6+1×4+2×8+2×4=46(公里)例3.小刚家和小明家之间各条道路的示意图,请问要从小刚家到小明家,最近路线有几条?思路分析:要求从小刚家到小明家的最近路线有几条,就是要求从小刚家到小明家的最短路线.把各交点标上字母,如下图.这道题和前面例1有所不同,要格外注意由哪两点的和来确定另一点的.①由A→B,A→C各有1种走法,可以确定A→D有1+1=2(种)走法.②由A→I有1种走法,A→D有2种走法,可以确定A→J有1+2=3(种)走法.③由A→M有1种走法,A→J有3种走法,可以确定A→N有1+3=4(种)走法.④A→E有2种走法,A→J有3种走法,A→K有2+3=5(种)走法.⑤A→E有2种走法,A→G有2种走法,A→H与2+2=4(种)走法.⑥A→K有5种走法,A→H有4种走法,A→L有5+4=9(种)走法.⑦A→N有4种走法,A→K有5种走法,A→O有4+5=9(种)走法.⑧A→O有9种走法,A→L有9种走法,A→L上有9种走法,A→P有9+9=18(种)走法.。
小学奥数-最短路线

最短路线
1、请你画出从小明家去图书馆的最短路线,并说出理由。
2、一只小蚂蚁想从下图中的点A爬到对边BC。
沿怎样的路线爬行需要的时间最少?在图中画一画。
3、如图,三角形ABC的三条边AB,AC,BC分别表示三条公路。
在D点处有一名士兵接到一个紧急任务,需要他先到达BC公路,然后再到达AB公路。
他怎样走才能以最短的时间完成任务呢?在图中画出路线。
(假设士兵的速度一定)
4、如图,三角形ABC的三条边AB,AC,BC分别表示三条公路。
在D处有一个村庄,现准备修一条通往公路的小路,在图中画出最短的小路。
5、一只小蚂蚁想从下图中的点A爬到对边CD。
你能帮它开辟一条最短的路线,使它尽快到达吗?在图中画一画。
6、一个邮递员投送信件的街道如下图所示,你能帮他设计一条最短路线,使自己从邮局出发,走遍每一条街道并回到邮局吗?
7、如右图,每个小方格的边长是1厘米,一条贪吃的蛇从左下角出发,沿着格线爬行,如果它想吃掉图中的3个“”,最少要爬多远?请你画出路线。
8、下图是一个公园的平面图,A点是出入口,B,C,D,E,F,G,H,I,J是各个景点,你能帮游客设计一条最短路线,使他从出入口出发,走遍每一条路后,最终回到出入口吗?。
最短路线问题 技巧解析

最短路线问题技巧解析最值问题遵循一个原则:“平面内连结两点的线中,直线段最短”如果研究问题的限制条件允许已知的两点在同一平面内,那么所求的最短路线是线段;如果它们位于凸多面体的不同平面上,而允许走的路程限于凸多面体表面,那么所求的最短路线是折线段;如果它们位于圆柱和圆锥面上,那么所求的最短路线是曲线段;但允许上述哪种情况,它们都有一个共同点:当研究曲面仅限于可展开为平面的曲面时,例如圆柱面、圆锥面和棱柱面等,将它们展开在一个平面上,两点间的最短路线则是连结两点的直线段.在求最短路线时,一般先用“对称”的方法化成两点之间的最短距离问题,而两点之间直线段最短,从而找到所需的最短路线.其中也体现了数学中的转化思想。
1、A、B两个村子,中间隔了一条小河(如下图),现在要在小河上架一座小木桥,使它垂直于河岸.请你在河的两岸选择合适的架桥地点,使A、B两个村子之间路程最短.分析因为桥垂直于河岸,所以最短路线必然是条折线,直接找出这条折线很困难,于是想到要把折线化为直线.由于桥的长度相当于河宽,而河宽是定值,所以桥长是定值.因此,从A点作河岸的垂线,并在垂线上取AC等于河宽,就相当于把河宽预先扣除,找出B、C两点之间的最短路线,问题就可以解决.解:如上图,过A点作河岸的垂线,在垂线上截取AC的长为河宽,连结BC交河岸于D 点,作DE垂直于河岸,交对岸于E点,D、E两点就是使两村行程最短的架桥地点.即两村的最短路程是AE+ED+DB.2、如下图,侦察员骑马从A地出发,去B地取情报.在去B地之前需要先饮一次马,如果途中没有重要障碍物,那么侦察员选择怎样的路线最节省时间,请你在图中标出来.解:要选择最节省时间的路线就是要选择最短路线.作点A关于河岸的对称点 A′,即作 AA′垂直于河岸,与河岸交于点C,且使AC=A′C,连接A′B交河岸于一点P,这时 P点就是饮马的最好位置,连接 PA,此时 PA+PB就是侦察员应选择的最短路线.证明:设河岸上还有异于P点的另一点P′,连接P′A,P′B, P′A′.∵P′A+P′B=P′A′+P′B>A′B=PA′+PB=PA+PB,而这里不等式 P′A′+P′B>A′B成立的理由是连接两点的折线段大于直线段,所以PA+PB是最短路线.此例利用对称性把折线APB化成了易求的另一条最短路线即直线段A′B,所以这种方法也叫做化直法,其他还有旋转法、翻折法等.看下面例题.3、长方体ABCD—A′B′C′D′中,AB=4,A′A=2′,AD=1,有一只小虫从顶点D′出发,沿长方体表面爬到B点,问这只小虫怎样爬距离最短?(见图(1))解:因为小虫是在长方体的表面上爬行的,所以必需把含D′、B两点的两个相邻的面“展开”在同一平面上,在这个“展开”后的平面上 D′B间的最短路线就是连结这两点的直线段,这样,从D′点出发,到B点共有六条路线供选择.①从D′点出发,经过上底面然后进入前侧面到达B点,将这两个面摊开在一个平面上(上页图(2)),这时在这个平面上D′、B间的最短路线距离就是连接D′、B两点的直线段,它是直角三角形ABD′的斜边,根据勾股定理,D′B2=D′A2+AB2=(1+2)2+42=25,∴D′B=5.②容易知道,从D′出发经过后侧面再进入下底面到达B点的最短距离也是5.③从D′点出发,经过左侧面,然后进入前侧面到达B点.将这两个面摊开在同一平面上,同理求得在这个平面上D′、B两点间的最短路线(上页图(3)),有:D′B2=22+(1+4)2=29.④容易知道,从D′出发经过后侧面再进入右侧面到达B点的最短距离的平方也是29.⑤从D′点出发,经过左侧面,然后进入下底面到达B点,将这两个平面摊开在同一平面上,同理可求得在这个平面上D′、B两点间的最短路线(见图),D′B2=(2+4)2+12=37.⑥容易知道,从D′出发经过上侧面再进入右侧面到达B点的最短距离的平方也是37.比较六条路线,显然情形①、②中的路线最短,所以小虫从D′点出发,经过上底面然后进入前侧面到达B点(上页图(2)),或者经过后侧面然后进入下底面到达B点的路线是最短路线,它的长度是5个单位长度.利用例2、例3中求相邻两个平面上两点间最短距离的旋转、翻折的方法,可以解决一些类似的问题,例如求六棱柱两个不相邻的侧面上A和B两点之间的最短路线问题(下左图),同样可以把A、B两点所在平面及与这两个平面都相邻的平面展开成同一个平面(下右图),连接A、B成线段AP1P2B,P1、P2是线段AB与两条侧棱线的交点,则折线AP1P2B就是AB 间的最短路线.圆柱表面的最短路线是一条曲线,“展开”后也是直线,这条曲线称为螺旋线.因为它具有最短的性质,所以在生产和生活中有着很广泛的应用.如:螺钉上的螺纹,螺旋输粉机的螺旋道,旋风除尘器的导灰槽,枪膛里的螺纹等都是螺旋线,看下面例题.4、景泰蓝厂的工人师傅要给一个圆柱型的制品嵌金线,如下左图,如果将金线的起点固定在A点,绕一周之后终点为B点,问沿什么线路嵌金线才能使金线的用量最少?解:将上左图中圆柱面沿母线AB剪开,展开成平面图形如上页右图(把图中的长方形卷成上页左图中的圆柱面时,A′、B′分别与A、B重合),连接AB′,再将上页右图还原成上页左图的形状,则AB′在圆柱面上形成的曲线就是连接AB且绕一周的最短线路.圆锥表面的最短路线也是一条曲线,展开后也是直线.请看下面例题.5、有一圆锥如下图,A、B在同一母线上,B为AO的中点,试求以A为起点,以B为终点且绕圆锥侧面一周的最短路线.解:将圆锥面沿母线AO剪开,展开如上右图(把右图中的扇形卷成上图中的圆锥面时,A′、B′分别与A、B重合),在扇形中连AB′,则将扇形还原成圆锥之后,AB′所成的曲线为所求.6、如下图,在圆柱形的桶外,有一只蚂蚁要从桶外的A点爬到桶内的B点去寻找食物,已知A点沿母线到桶口C点的距离是12厘米, B点沿母线到桶口 D点的距离是8厘米,而C、D两点之间的(桶口)弧长是15厘米.如果蚂蚁爬行的是最短路线,应该怎么走?路程总长是多少?分析我们首先想到将桶的圆柱面展开成矩形平面图(下图),由于B点在里面,不便于作图,设想将BD延长到F,使DF=BD,即以直线CD为对称轴,作出点B的对称点F,用F代替B,即可找出最短路线了.解:将圆柱面展成平面图形(上图),延长BD到F,使DF=BD,即作点B关于直线CD 的对称点F,连结AF,交桶口沿线CD于O.因为桶口沿线CD是 B、F的对称轴,所以OB=OF,而A、F之间的最短线路是直线段AF,又AF=AO+OF,那么A、B之间的最短距离就是AO+OB,故蚂蚁应该在桶外爬到O点后,转向桶内B点爬去.延长AC到E,使CE=DF,易知△AEF是直角三角形,AF是斜边,EF=CD,根据勾股定理,AF2=(AC+CE)2+EF2 =(12+8)2+152=625=252,解得AF=25.即蚂蚁爬行的最短路程是25厘米.7、如图一只壁虎要从一面墙壁α上A点,爬到邻近的另一面墙壁β上的B点捕蛾,它可以沿许多路径到达,但哪一条是最近的路线呢?解:我们假想把含B点的墙β顺时针旋转90°(如下页右图),使它和含A点的墙α处在同一平面上,此时β转过来的位置记为β′,B点的位置记为B′,则A、B′之间最短路线应该是线段AB′,设这条线段与墙棱线交于一点P,那么,折线4PB就是从A点沿着两扇墙面走到B点的最短路线.证明:在墙棱上任取异于P点的P′点,若沿折线AP′B走,也就是沿在墙转90°后的路线AP′B′走都比直线段APB′长,所以折线APB是壁虎捕蛾的最短路线.由此例可以推广到一般性的结论:想求相邻两个平面上的两点之间的最短路线时,可以把不同平面转成同一平面,此时,把处在同一平面上的两点连起来,所得到的线段还原到原始的两相邻平面上,这条线段所构成的折线,就是所求的最短路线.8、在河中有A、B两岛(如下图),六年级一班组织一次划船比赛,规则要求船从A 岛出发,必须先划到甲岸,又到乙岸,再到B岛,最后回到A岛,试问应选择怎样的路线才能使路程最短?解:如上图,分别作A、B关于甲岸线、乙岸线的对称点A′和B′,连结A′、B′分别交甲岸线、乙岸线于E、F两点,则A→E→F→B→A是最短路线,即最短路程为:AE+EF+FB+BA.证明:由对称性可知路线A→E→F→B的长度恰等于线段A′B′的长度.而从A岛到甲岸,又到乙岸,再到B岛的任意的另一条路线,利用对称方法都可以化成一条连接A′、B′之间的折线,它们的长度都大于线段 A′B′,例如上图中用“·—·—·”表示的路线A→E′→F′→B的长度等于折线AE′F′B的长度,它大于A′B′的长度,所以A→E→F→B→A 是最短路线.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在日常生活、工作中,经常会遇到有关行程路线的问
题。
比如:邮递员送信,要穿遍所有的街道,为了少走冤枉路,需要选择一条最短的路线;旅行者希望寻求最佳旅行路线,以求能够走最近的路而达到目的地,等等。
这样的问题,就是我们所要研究学习的“最短路线问题”。
典型例题
例[1] 假如直线AB 是一条公路,公路两旁有甲乙两个村子,如下图1。
现在要在公路上修建一个公共汽车站,让这两个村子的人到汽车站的路线之和最短。
问:车站应该建在什么地方?
分析 如果只考虑甲村的人距离公路AB 最近,只要由甲村向公
路AB 画一条垂直线,交AB 于C 点,那么C 点是甲村到公路AB 最
甲乙
乙图1
图
2
近的点,但是乙村到C点就较远了。
反过来,由乙村向公路AB画垂线,交AB于D点,那么D点是乙村到公路AB最近的点。
但是这时甲村到公路AB的D点又远了。
因为本题要求我们在公路AB上取的建站点,能够兼顾甲村和乙村的人到这个车站来不走冤枉路(既路程之和最短),根据我们的经验:两个地点之间走直线最近,所以,只要在甲村乙村间连一条直线,这条直线与公路AB交点P,就是所求的公共汽车站的建站点了(图2)。
解用直线把甲村、乙村连起来。
因为甲村乙村在公路的两侧,所以这条连线必与公路AB有一个交点,设这个交点为P,那么在P 点建立汽车站,就能使甲村乙村的人到汽车站所走的路程之和最短。
例[2] 一个邮递员投送信件的街道如图3所示,图上数字表示各段街道的千米数。
他从邮局出发,要走遍各街道,最后回到邮局。
问:走什么样的路线最合理?全程要走多少千米?
3
分析选择最短的路线最合理。
那么,什么路线最短呢?一笔画路线应该是最短的。
邮递员从邮局出发,还要回到邮局,按一笔画问
题,就是从偶点出发,回到偶点。
因此,要能一笔把路线画出来,必须途径的各点全是偶点。
但是图中有8个奇点,显然邮递员要走遍所有街道而又不走重复的路是不可能的。
要使邮递员从邮局出发,仍回到邮局,必须使8个奇点都变成偶点,就是要考虑应在哪些街道上重复走,也就是相当于在图上添哪些线段,能使奇点变成偶点。
如果有不同的添法,就还要考虑哪一种添法能使总路程最短。
为使8个奇点变成偶点,我们可以用图4的4种方法走重复的路
图4中添虚线的地方,就是重复走的路线。
重复走的路程分别为: (a )
3×4=12(千米) (b ) 3×2+2×2=10(千米) (c ) 2×4=8(千米) (d ) 3×2+4×2=14(千米)
3
3
3
3
( a )
( b )
( c )
( d )
图4
当然,重复走的路程最短,总路程就最短。
从上面的计算不难找出最合理的路线了。
解 邮递员应按图4(c )所示的路线走,这条路重复的路程最短,所以最合理。
全程为: (1+2+4+2+1)×2+3×6+2×4 =20+18+8 =46(千米)
例[3] 图5中的线段表示的是小明从家到学校所能经过的所有街道。
小明上学走路的方向都是向东或向南,因为他不想偏离学校的方向而走冤枉路。
那么小明从家到学校可以有多少条不同的路线?
分析 为了叙述的方便,我们在各交叉点标上字母(见图6)。
学校
小明家
A B F E
F D E
F
我们从小明家出发,顺序往前推。
由于从小明家到A 、B 、C 、D 各处都是沿直线行走,所以都只有一种走法。
我们分别在交叉点处标上“1”。
而从小明家到E 处,就有先到A 或先到D 的两种走法,正好是两个对角上标的数1+1的和。
从小明家到F 点,则有3条路线,又正好是两个对角上标的数1+2的和。
标在各交叉点的数,就是依次顺序推出的到各交叉点能有多少种不同的路线的数。
从中我们可以看出,每个格内上右角与下左角两个对角上的数的和,正好等于下右角上的数。
解 从小明家到学校有13条不同的路线。
如图7所示。
图7
学校
H M
N
K。
