第4章 静定拱
合集下载
01-静定拱和悬梁结构知识点小结
K
截面的弯矩、剪力；
K 值为 K 截面法线的倾角（如图 4-1(a)所示的坐标系中），在拱顶铰以左取正，以右
取负。
K 可根据其与拱轴方程 y = f (x) 之间的关系式确定，即：
3、受力特征总结
cosK =
1
1+ ( y)2
, sinK = ycosK
x = xK
（1）支座反力与拱轴线形式无关，只与三个铰的位置有关； （2）两个竖向支座反力与相应简支梁竖向支反力对应相等，这说明竖向支反力与拱高 无关；
以上公式均适用于带拉杆的三铰平拱（承受竖向荷载作用），拉杆拉力即为水平推力 FH ，
其支座反力和内力和的计算公式不变。 5、一般荷载（含水平力）作用下，支座反力和内力不能套用上述公式，而应直接采用截面 法求内力，此时两个支座的水平反力也不相同。
二、三铰斜拱的计算
三铰斜拱在竖向荷载作用下，可根据三个整体平衡条件，以及半拱对拱顶铰 C 的平衡
y = M 0(x) FH
式中， M 0 为相应简支梁的弯矩图表达式， FH 为拱的水平推力。这表明，在竖向荷载 作用下三铰平拱合理轴线的纵坐标 y 与相应简支梁弯矩图的竖标 M 0 成比例。
三铰平拱在满跨竖向均布荷载 q 作用下的合理轴线为二次抛物线（图 4-3），即：
y
=
4f l2
x(l − x)
F 'AV = FA0V ,
F 'BV
=
FB0V ， FA' H
= FB'H
= FH'
=
M
0 C
h
式中，h
为斜拱中拱顶铰
C
至拱趾连线的垂直距离，M
0 C
为相应水平简支梁中相应
第四章-静定拱
§4-1 基本概念 2.常见形式
铰 静 拱 三 拱—— 定 拱两 拱 铰 静 结 无 拱 超 定 构 铰
三铰拱
两铰拱
无铰拱
第四章 静定拱式结构（Arch） 静定拱式结构（Arch）
§4-1 基本概念 3. 几何特性：
拱 顶 拱轴线 (拱轴 )拱高 起拱线来自拱趾 、 ) ( 跨度
内力不仅与三铰拱位置有关， 内力不仅与三铰拱位置有关，且与拱轴线形 状有关。
谢
谢 ！
第四章 静定拱式结构（Arch） 静定拱式结构（Arch）
§4-4 三铰拱的合理拱轴线
3.方法： 方法： 先作出压力线， ⑴ 先作出压力线，然后以压力线代 替拱轴。 替拱轴。 ° M 利用弯矩方程： ⑵ 利用弯矩方程： = M − Hy ° M∗ 令 M = M − Hy = 0 ⇒ y = H 即为合理拱轴线的纵坐标。 y即为合理拱轴线的纵坐标。
第四章 静定拱式结构（Arch） 静定拱式结构（Arch）
§4-4 三铰拱的合理拱轴线（Optimal centre line of arch） 三铰拱的合理拱轴线（ arch）
1.定义： 定义： 在已知荷载作用下， 在已知荷载作用下，能选择三铰拱的 轴线， 轴线，使得拱的所有横截面上的弯矩 为零。该拱的轴线就称为三铰拱的合 为零。该拱的轴线就称为三铰拱的合 理拱轴线。 理拱轴线。 条件： 2.条件： 拱轴线与压力线重合时， 拱轴线与压力线重合时，满足横截面 上的弯矩M Q=0 而仅有轴力N 上的弯矩M＝0、Q=0，而仅有轴力N。
l 9
dy 2 tgϕ = = (6 − x) dx 9
截面1 截面1：x1 = 1.56m
y1 = 1.75m tgϕ1 = 1 ϕ1 = 450
铰 静 拱 三 拱—— 定 拱两 拱 铰 静 结 无 拱 超 定 构 铰
三铰拱
两铰拱
无铰拱
第四章 静定拱式结构（Arch） 静定拱式结构（Arch）
§4-1 基本概念 3. 几何特性：
拱 顶 拱轴线 (拱轴 )拱高 起拱线来自拱趾 、 ) ( 跨度
内力不仅与三铰拱位置有关， 内力不仅与三铰拱位置有关，且与拱轴线形 状有关。
谢
谢 ！
第四章 静定拱式结构（Arch） 静定拱式结构（Arch）
§4-4 三铰拱的合理拱轴线
3.方法： 方法： 先作出压力线， ⑴ 先作出压力线，然后以压力线代 替拱轴。 替拱轴。 ° M 利用弯矩方程： ⑵ 利用弯矩方程： = M − Hy ° M∗ 令 M = M − Hy = 0 ⇒ y = H 即为合理拱轴线的纵坐标。 y即为合理拱轴线的纵坐标。
第四章 静定拱式结构（Arch） 静定拱式结构（Arch）
§4-4 三铰拱的合理拱轴线（Optimal centre line of arch） 三铰拱的合理拱轴线（ arch）
1.定义： 定义： 在已知荷载作用下， 在已知荷载作用下，能选择三铰拱的 轴线， 轴线，使得拱的所有横截面上的弯矩 为零。该拱的轴线就称为三铰拱的合 为零。该拱的轴线就称为三铰拱的合 理拱轴线。 理拱轴线。 条件： 2.条件： 拱轴线与压力线重合时， 拱轴线与压力线重合时，满足横截面 上的弯矩M Q=0 而仅有轴力N 上的弯矩M＝0、Q=0，而仅有轴力N。
l 9
dy 2 tgϕ = = (6 − x) dx 9
截面1 截面1：x1 = 1.56m
y1 = 1.75m tgϕ1 = 1 ϕ1 = 450
结构力学-静定拱
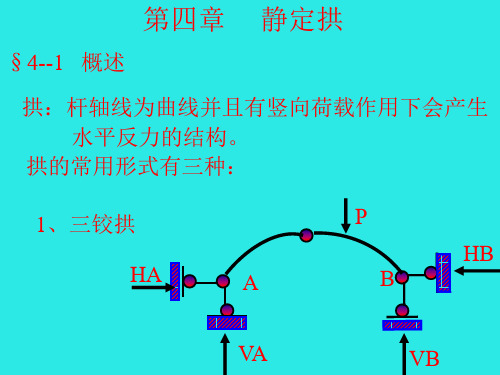
H=M’C/f 2 内力计算：
截面Ｋ的弯矩： M=[Vax－P1(x－a1)]－Hy
即 M=M’－Hy
A
P1
P2
B
ＫC
剪力：
Ｑ=VA cos --P1 cos--H sin V’A
V’B
＝Ｑ’ cos --H sin
轴力：
HA
P1 Ｋ
A
P2
B
HB
N=(VA--P1) sin+
Hcos
第四章 静定拱
§4--1 概述
拱：杆轴线为曲线并且有竖向荷载作用下会产生 水平反力的结构。
拱的常用形式有三种：
1、三铰拱
HA
A
P
HB B
VA
VB
2 两铰拱
3 无铰拱
拱的各部分名称如右图：拱 趾
起拱线
A
拱轴线
拱
拱高f
趾
B
跨度l
§4--2 三铰拱的数解法
1 支座反力计算
如右图： 由MB=0
a1
b1
VA
VB
=Q’sin +Hsin
综上所述，三铰平拱的内力计算公
式可写为：
M=M’--Hy
Q=Q’ cos --H sin
N=Q’ sin --H cos
§4--3 三铰拱的合理拱轴线
当拱上所有截面的弯矩都为零而只有轴力时，这
时的拱轴线为合理拱轴线。其方程为： y=M’/H
q
例４－２
y
a2
b2
P1
P2
MA=0
HA
A
HB B
HA=HB=H
l1
MC=0
VA
l2 VB
VAl1－P1(l1－a1)－Hf=0 l
第四章静定拱
第四章 静定拱
§4–1概述 拱——曲线杆件， 竖向荷载作用下有水平反力。 常用形式： 三铰拱、两铰拱、无铰拱
重要特点：
竖向荷载产生水平推力（与梁相比）
优点：
M减小，FN为主 ——便于使用抗压材料：砖、石、混凝土 缺点：
水平反力要求
——地基、支承结构、（墙、柱、墩等） 更坚固。
——可称拱式结构或推力结构
∑m0 = 0 FNρ-(FN+dFN)ρ=0 dFN=0 FN=常数
∑s = 0（投影方程）
2FNsin(dφ/2)-qρdφ=0
dφ极小，sin(dφ/2)=dφ/2
FN-qρ=0 ρ=FN/q ＝常数 合理拱轴——圆弧线
【例4－3】 q = qc+ γy 解：坐标系如图，
M=M0－FH（f－y）=0
带拉杆的拱 ——消除推力
（消除对支承结构的影响） 拱的各部名称（参数）
基本参数
拱高f 跨度l 高跨比f/l
平拱/斜拱： 拱趾是 / 否 在同一水平线
§4 – 2 三铰拱的计算
1．支座反力计算 （与相应代梁比较）
FVA=F0VA FVB=F0VB
FH
M
0 c
f
M0C—— 代梁
相应截面 C的弯矩
①推力FH∝1/f， 与曲线形式无关， 与铰位置有关，
（a）竖向荷载——计算公式 （b）非竖向荷载——截面法 3、特点(与梁比较） ——水平推力，使M减少 4、代拉杆的三铰拱 5、合理拱轴线：满跨均布荷载
静水压力
f y M0 FH
求导二次： y"
1 FH
d2M 0 dx2
1 FH
(q)
微分方程 解－双曲线函数
y q FH
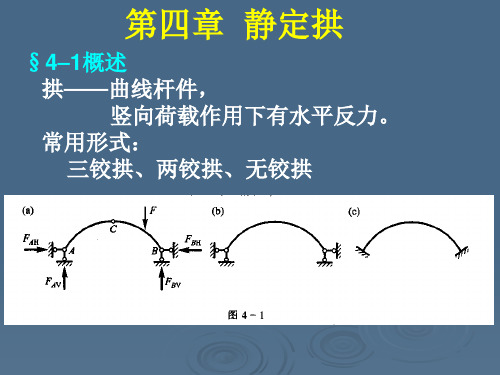
§4–1概述 拱——曲线杆件， 竖向荷载作用下有水平反力。 常用形式： 三铰拱、两铰拱、无铰拱
重要特点：
竖向荷载产生水平推力（与梁相比）
优点：
M减小，FN为主 ——便于使用抗压材料：砖、石、混凝土 缺点：
水平反力要求
——地基、支承结构、（墙、柱、墩等） 更坚固。
——可称拱式结构或推力结构
∑m0 = 0 FNρ-(FN+dFN)ρ=0 dFN=0 FN=常数
∑s = 0（投影方程）
2FNsin(dφ/2)-qρdφ=0
dφ极小，sin(dφ/2)=dφ/2
FN-qρ=0 ρ=FN/q ＝常数 合理拱轴——圆弧线
【例4－3】 q = qc+ γy 解：坐标系如图，
M=M0－FH（f－y）=0
带拉杆的拱 ——消除推力
（消除对支承结构的影响） 拱的各部名称（参数）
基本参数
拱高f 跨度l 高跨比f/l
平拱/斜拱： 拱趾是 / 否 在同一水平线
§4 – 2 三铰拱的计算
1．支座反力计算 （与相应代梁比较）
FVA=F0VA FVB=F0VB
FH
M
0 c
f
M0C—— 代梁
相应截面 C的弯矩
①推力FH∝1/f， 与曲线形式无关， 与铰位置有关，
（a）竖向荷载——计算公式 （b）非竖向荷载——截面法 3、特点(与梁比较） ——水平推力，使M减少 4、代拉杆的三铰拱 5、合理拱轴线：满跨均布荷载
静水压力
f y M0 FH
求导二次： y"
1 FH
d2M 0 dx2
1 FH
(q)
微分方程 解－双曲线函数
y q FH
结构力学第4章静定拱(f)
FH
FH
由边界条件
x 0, y 0 : x 0, y 0 :
A qc
B0
合理拱轴线的方程为
y qc (cosh x 1)
FH
§4-3 三铰拱的合理拱轴线
例4-3 试求三铰拱在垂直于拱轴线的均布荷载作用下的合理 拱轴线。
解：由图a，荷载为非竖向荷载。
思路：假定拱处于无弯矩状态，根据平衡 条件推求合理拱轴线方程。
Fi ai l
Fx 0 FAH FBH FH
相应简支梁
取左半拱为隔离体
MC 0
FH
FAV l1 F1(l1 a1) f
可 得
FAV FBV
FA0V FB0V
FH
M
0 C
f
三铰拱的反力只与 荷载及三个铰的位置有 关，与拱轴线形状无关；
推力FH 与拱高 f 成反比。
§4-2 三铰拱的计算
§4-2 三铰拱的计算
2、内力的计算
压力为正
任一截面的轴力等于该截面一 侧所有外力在该截面法线方向 上的投影代数和。
FN FAV sin FH cos F1 sin (FAV F1) sin FH cos FS0 sin FH cos
相应简支梁
§4-2 三铰拱的计算
2、内力的计算
区别拱与梁的主要标志：推力的存在与否。
§4-1 概述
拉杆拱： 拱两支座间的拉杆代替支座承受水平推力
拉杆做成折线形可获得较大空间
高跨比：f/l
平拱： 两拱趾在同一水平线上 斜拱： 两拱趾不在同一水平线上
§4-2 三铰拱的计算
1、支座反力的计算
由拱的整体平衡
M B 0 FAV
Fibi l
M A 0 FBV
第四章结构力学静定拱
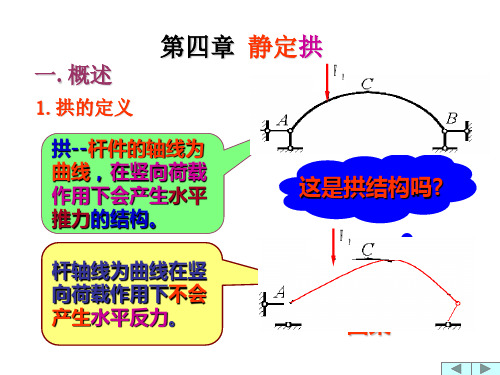
15kN
A
K左
A
K右
12.5kN
12.5kN
FºSK左＝12.5kN
FºSK右＝－2.5kN
( F H 1 0 k N ,F S 0 K 左 1 2 . 5 k N ,F S 0 K 右 2 . 5 k N )
( s i n 0 .4 4 7 ,c o s 0 .8 9 4 )
FSK左FS0K左cosFHsin12.50.894100.447
r FP1 90。 D D
C
FQD A
FP2 B
FRA
FRB
M D FRD rD
FQD FRD sin D FND FRD cos D
r D ——截面D形心到FRD作用线之距离。
D ——FRD作用线与截面D轴线切线的夹角。
由此看出，确定截面内力的问题归结为确定 截面一边所有外力的合力之大小、方向及作用线 的问题。
tgy'4l2f
(l2x)a b
F
V
0 A
FP1
D
F
0 SD
代梁
a2+b2 a
b
2) FºSD是代梁截面D的剪力，设为正方向。 故FºSD可能大于零、等于零或小于零。
下面用上述公式求FSK、FNK。
xK＝4m y'41 624(1624)1 2 FºSK左＝12.5kN
5
1 2
FºSK右＝－2.5kN
FP2 E FP1
D
FRA A
o
C FP1 FP2
FRA
FRB
FP3
FP3 F
B
FRB
在上图所示力多边形中，射线1－2代表FRA与 FP1合力的大小和方向；射线2－3代表FRA与FP1、 FP2合力的大小和方向。
第四章：静定拱(李廉锟第五版配套)
第4章 静定拱
4.1 概述
4.2 静定拱的计算
4.3 静定拱的合理拱轴线
4.1 概述
静定拱的特点
静定拱的特点
拱的特点： 在竖向荷载作用下有水 平反力或称推力，如图(a)。 推力是拱式结构的主要标志 优点：弯矩小得多，主要承受压力。应力分布均匀。 缺点：地基或者支撑结构要坚固 图(b)为有拉杆的三铰拱， 推力就是拉杆内的拉力。
ql 2
ql 2
先列出简支梁的弯矩方程
q M x x l x 2
拱的推力为：
MC ql 2 H f 8f
注意
*合理轴线对应的是
一组固定荷载； *合理轴线是一组。
所以拱的合理轴线方程为：
q 8f 4f y x x l x 2 2 x l x 2 ql l
f=4m
8 B
பைடு நூலகம்
1 x
y1
A
50.25kN
H 50.25kN
VB 58.5kN
4f y 2 x l x l 制内力图。
计算反力并绘
3m VA 75.5kN
3m 6m 6m
（1）计算支座反力
（2）内力计算
y1
以截面1为例
4f 4 4 x l x 312 1.5 1.75m 2 2 l 12
dy dx
x 3
14 6 9 50 3 75.5kN 12 14 6 3 50 9 VB VB 58.5kN 12 MC 75.5 6 14 6 3 H 50.25kN f 4
VA VA
M1 M1 Hy2 75.5 1.5 141.5 1.5 / 2 50.251.75 9.6kN m
4.1 概述
4.2 静定拱的计算
4.3 静定拱的合理拱轴线
4.1 概述
静定拱的特点
静定拱的特点
拱的特点： 在竖向荷载作用下有水 平反力或称推力，如图(a)。 推力是拱式结构的主要标志 优点：弯矩小得多，主要承受压力。应力分布均匀。 缺点：地基或者支撑结构要坚固 图(b)为有拉杆的三铰拱， 推力就是拉杆内的拉力。
ql 2
ql 2
先列出简支梁的弯矩方程
q M x x l x 2
拱的推力为：
MC ql 2 H f 8f
注意
*合理轴线对应的是
一组固定荷载； *合理轴线是一组。
所以拱的合理轴线方程为：
q 8f 4f y x x l x 2 2 x l x 2 ql l
f=4m
8 B
பைடு நூலகம்
1 x
y1
A
50.25kN
H 50.25kN
VB 58.5kN
4f y 2 x l x l 制内力图。
计算反力并绘
3m VA 75.5kN
3m 6m 6m
（1）计算支座反力
（2）内力计算
y1
以截面1为例
4f 4 4 x l x 312 1.5 1.75m 2 2 l 12
dy dx
x 3
14 6 9 50 3 75.5kN 12 14 6 3 50 9 VB VB 58.5kN 12 MC 75.5 6 14 6 3 H 50.25kN f 4
VA VA
M1 M1 Hy2 75.5 1.5 141.5 1.5 / 2 50.251.75 9.6kN m
结构力学第4章 静定拱结构
一、工程中的拱结构轴线为曲线、仅在竖向荷载下能产生水平反力(推力)的结构称为拱。
图4-1所示为拱结构的工程实例。
图4-1工程中的拱结构二、拱式结构的特征及其应用1、定义：通常杆轴线为曲线，在竖向荷载作用下，支座产生水平反力的结构。
2、特点：（1）弯矩比相应简支梁小，水平推力存在的原因。
（2）用料省、自重轻、跨度大。
（3）可用抗压性能强的砖石材料。
（4）构造复杂，施工费用高。
3、拱的种类：图4-2拱的种类4、拱各部分的名称：一、支座反力的计算C拱顶铰BA拱肋跨度拱趾铰(a) 等高三铰拱C高差hAB(b) 不等高三铰拱严格的来说，实体三铰拱支座反力的计算与一般三铰刚架结构反力计算相同。
本书介绍的是等代梁解法。
图4-4实体三铰拱第二节实体三铰拱的数解法图4-5等代粱ll 1l 2a 3b 3b 2b 1a 2a 1F P1F P2F P3F P1F P2F P3F A yF B yF A yF B yF B xF A x 00A CBAB C(b)(a )f0CH M F =HB A F F F ==x x 0Ay Ay F F =0ByBy FF =二、拱内截面内力的计算图4-6拱内截面内力1、拱的内力计算原理仍然是截面法。
2、拱通常受压力，所以计算拱时，规定轴力以受压为正。
对于竖向荷载作用三铰拱，其内力计算有简捷公式。
(c)CB A00F B yF A yF P3F P2F P1B F B xAF A x F A yF B y(a )C F P3F P2F P1a 1a 2b 1b 2b 3a 3lϕK F A y F A xF P1KM K F NKF QKx KK ϕy KxyK K(b)yF MM H 0-=ϕϕsin cos H 0Q Q F F F -=ϕϕcos sin H 0Q N F F F --=A0AyFQ F 0M (b) 代梁受力F Ax =F H F Ayx A y k F y FxyϕM(a) 截面k 坐标方向力图4-7拱内截面内力需要指出的是，非竖向荷载作用不等高三铰拱等情形，上述公式是不适用的。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第四章 静定拱
§4—1概述 拱——曲线杆件， 竖向荷载作用下有水平反力。 常用形式： 三铰拱、两铰拱、无铰拱
重要特点： 竖向荷载产生水平推力（与梁相比）
优点： M减小，N为主 ——便于使用抗压材料：砖、石、混凝土
缺点： 水平反力要求 ——地基、支承结构、（墙、柱、墩等）
更坚固。 ——可称拱式结构或推力结构
y(x) x1=1.5,y1=1.75 tanφ=y’ sinφ,cosφ
3.M1=M10-FHy1 S1=S10*c-FH*s N1=S10*s+FH*c
4.表4－1，作图。
3．特点： （1）竖向荷载作用下，
有水平推力H （2）推力使拱M减小，
M = M0 － Hy （3）拱截面内轴力较大，
（梁N=0） 4．斜拱与一般荷载作用 ①斜拱
【例4—2】 均布荷载满跨 【解】
M 0 ql x qx2 qx (l x) 2 22
H
M
0 c
1
ql 2
f f8
y M 0 qx (l x) 8 f 4 f x(l x)
H2
ql 2 l 2
具有不同髙跨比的一组抛物线——合理拱轴线
[例4—3]q = qc+ γy 解：坐标系如图，
M=M0－H（f－y）=0
f y M0 H
求导二次：
y"
1 H
d2M 0 dx2
1 H
(q)
y q H
q=qc+γy
y " x y qc HH
微分方程解 边界条件
——二阶常系数线性非齐次方程 ——确定合理拱轴线方程
[例4-4] 静水压力 解：非竖向荷载，设M＝0状态，
用微元平衡求合理拱轴线 微段：N 平衡：
带拉杆的拱 ——消除推力
（消除对支承结构的影响） 拱的各部名称（参数）
基本参数 拱高f 跨度l 高跨比f/l
平拱/斜拱： 拱趾是 / 否 在同一水平线
§4 – 2 三铰拱的计算
1．支座反力计算 （与相应代梁比较）
VA=VA0 VB=VB0
H
M
0 c
f
M0C—— 代梁
相应截面 C的弯矩
①推力H∝1/f， 与曲线形式无关，
（a）竖向荷载——计算公式 （b）非竖向荷载——截面法 3、特点(与梁比较） ——水平推力，使M减少 4、代拉杆的三铰拱 5、合理拱轴线：满跨均布荷载
静水压力
【思考题－3】 试绘制合理拱轴线形状：y＝M0/H
习题
与铰位置有关，
②若f→0， 则H→∞
（瞬变体系）
2．内力计算 M=M0-Hy
c sQ0
N
s
c
H
c－cosφ s－sinφ
φ—为截面轴线切向的锐角。
注意： ①M0，Q0 —— 对应代梁相应截面 的弯矩、剪力 ②M—拱内受拉为正 ③φ—拱左部“+”，
右部“-”
【例4－1】 1.支座反力 2.截面水平8等分：
∑m0 = 0 FNρ-(FN+dFN)ρ=0 dFN=0 FN=常数
∑s = 0（投影方程）
2FNsind(φ/2)-qρdφ=0
dφ极小，sin(dφ/2)=dφ/2
FN-qρ=0 ρ=FN/q ＝常数 合理拱轴——圆弧线
小结： 1、三铰拱——三铰刚架：几何组成、反力计算 2、内力计算——截面法
②一般荷载作用
——与三铰刚架计算相同， 求反力，截面法求内力
合理拱§轴4线—3 三铰拱的合理拱轴线
——在固定荷载作用下， 拱上各截面M＝0（则Q=0），只有N≠0的轴线 ——截面上正应力分布均为，材料得以充分利用 合理轴线方程：M0－Hy = 0
y M0 H
——竖向荷载作用下， 三铰拱合理拱轴线的纵坐标y 与相应代梁弯矩图竖标成正比
§4—1概述 拱——曲线杆件， 竖向荷载作用下有水平反力。 常用形式： 三铰拱、两铰拱、无铰拱
重要特点： 竖向荷载产生水平推力（与梁相比）
优点： M减小，N为主 ——便于使用抗压材料：砖、石、混凝土
缺点： 水平反力要求 ——地基、支承结构、（墙、柱、墩等）
更坚固。 ——可称拱式结构或推力结构
y(x) x1=1.5,y1=1.75 tanφ=y’ sinφ,cosφ
3.M1=M10-FHy1 S1=S10*c-FH*s N1=S10*s+FH*c
4.表4－1，作图。
3．特点： （1）竖向荷载作用下，
有水平推力H （2）推力使拱M减小，
M = M0 － Hy （3）拱截面内轴力较大，
（梁N=0） 4．斜拱与一般荷载作用 ①斜拱
【例4—2】 均布荷载满跨 【解】
M 0 ql x qx2 qx (l x) 2 22
H
M
0 c
1
ql 2
f f8
y M 0 qx (l x) 8 f 4 f x(l x)
H2
ql 2 l 2
具有不同髙跨比的一组抛物线——合理拱轴线
[例4—3]q = qc+ γy 解：坐标系如图，
M=M0－H（f－y）=0
f y M0 H
求导二次：
y"
1 H
d2M 0 dx2
1 H
(q)
y q H
q=qc+γy
y " x y qc HH
微分方程解 边界条件
——二阶常系数线性非齐次方程 ——确定合理拱轴线方程
[例4-4] 静水压力 解：非竖向荷载，设M＝0状态，
用微元平衡求合理拱轴线 微段：N 平衡：
带拉杆的拱 ——消除推力
（消除对支承结构的影响） 拱的各部名称（参数）
基本参数 拱高f 跨度l 高跨比f/l
平拱/斜拱： 拱趾是 / 否 在同一水平线
§4 – 2 三铰拱的计算
1．支座反力计算 （与相应代梁比较）
VA=VA0 VB=VB0
H
M
0 c
f
M0C—— 代梁
相应截面 C的弯矩
①推力H∝1/f， 与曲线形式无关，
（a）竖向荷载——计算公式 （b）非竖向荷载——截面法 3、特点(与梁比较） ——水平推力，使M减少 4、代拉杆的三铰拱 5、合理拱轴线：满跨均布荷载
静水压力
【思考题－3】 试绘制合理拱轴线形状：y＝M0/H
习题
与铰位置有关，
②若f→0， 则H→∞
（瞬变体系）
2．内力计算 M=M0-Hy
c sQ0
N
s
c
H
c－cosφ s－sinφ
φ—为截面轴线切向的锐角。
注意： ①M0，Q0 —— 对应代梁相应截面 的弯矩、剪力 ②M—拱内受拉为正 ③φ—拱左部“+”，
右部“-”
【例4－1】 1.支座反力 2.截面水平8等分：
∑m0 = 0 FNρ-(FN+dFN)ρ=0 dFN=0 FN=常数
∑s = 0（投影方程）
2FNsind(φ/2)-qρdφ=0
dφ极小，sin(dφ/2)=dφ/2
FN-qρ=0 ρ=FN/q ＝常数 合理拱轴——圆弧线
小结： 1、三铰拱——三铰刚架：几何组成、反力计算 2、内力计算——截面法
②一般荷载作用
——与三铰刚架计算相同， 求反力，截面法求内力
合理拱§轴4线—3 三铰拱的合理拱轴线
——在固定荷载作用下， 拱上各截面M＝0（则Q=0），只有N≠0的轴线 ——截面上正应力分布均为，材料得以充分利用 合理轴线方程：M0－Hy = 0
y M0 H
——竖向荷载作用下， 三铰拱合理拱轴线的纵坐标y 与相应代梁弯矩图竖标成正比