二次函数的应用题
(完整版)二次函数应用题(含答案)整理版

(完整版)二次函数应用题(含答案)整理版题目1:某公司的销售额可以用二次函数$y=-2x^2+20x$来表示,其中$x$表示月份(从1开始),$y$表示对应月份的销售额。
求解下列问题:问题1:请计算公司第6个月的销售额。
解答:将$x=6$代入二次函数中,可得:$y=-2\times6^2+20\times6=-72+120=48$所以公司第6个月的销售额为48。
问题2:请问公司销售额最高的月份是哪个月?解答:二次函数$y=-2x^2+20x$是一个开口朝下的抛物线,最高点即为销售额最高的月份。
通过求导数,我们可以找到函数的最高点。
首先,求导得到一次函数$y'=-4x+20$,令$y'=0$,解方程可得$x=5$。
因此,公司销售额最高的月份是第5个月。
题目2:一架火箭从地面起飞后,高度$h$(以米为单位)随时间$t$(以秒为单位)变化的规律可以用二次函数$h=-5t^2+100t$表示。
求解下列问题:问题1:请问火箭多少秒后达到最大高度?解答:同样地,通过求导数,我们可以找到火箭高度的最高点。
将二次函数$h=-5t^2+100t$求导得到一次函数$h'=-10t+100$,令$h'=0$,解方程可得$t=10$。
因此,火箭在10秒后达到最大高度。
问题2:请计算火箭达到最大高度时的高度。
解答:将$t=10$代入二次函数中,可得:$h=-5\times10^2+100\times10=-500+1000=500$所以火箭达到最大高度时的高度为500米。
以上是对二次函数应用题的解答,希望能帮助到您。
二次函数的应用题及解答

二次函数的应用题及解答在数学中,二次函数是一类常见的函数类型,由形如y=ax²+bx+c的方程所定义,其中a、b和c是实数且a不等于零。
二次函数在现实生活中有着广泛的应用,例如在物理学、经济学和工程学等领域。
本文将探讨二次函数的应用题及解答,帮助读者更好地理解和应用这一概念。
1. 弹射问题假设有一个小球从地面上以初速度v0竖直上抛,忽略空气阻力的影响。
则小球的高度可用二次函数模型y=-gt²+v0t+h来描述,其中g是重力加速度,t为时间,h为抛射的起始高度。
问题:一个小球从地面上以10 m/s的速度竖直上抛,起始高度为1.5m。
求小球的高度和时间的关系,并计算小球落地时的时间。
解答:根据模型y=-gt²+v0t+h,将已知数据代入,得到二次函数模型为y=-5t²+10t+1.5。
我们需要求解该函数的根,即令y=0,解得t=0和t=2。
因此,小球的高度和时间的关系可用二次函数y=-5t²+10t+1.5表示。
落地时的时间为t=2秒。
2. 投射问题假设有一枚炮弹以一定角度a和初速度v0被抛射出去,并忽略空气阻力的影响。
则炮弹的水平位移可用二次函数模型x=v0cos(a)t来表示,垂直位移可用二次函数模型y=-gt²+v0sin(a)t来表示。
问题:一枚炮弹以60°的角度和100 m/s的速度被抛射,求炮弹的轨迹和最远射程。
解答:根据模型x=v0cos(a)t和y=-gt²+v0sin(a)t,将已知数据代入,得到二次函数模型x=50t和y=-5t²+86.6t。
炮弹的轨迹由这两个函数表示。
为了求解最远射程,我们需要找到函数y=-5t²+86.6t的顶点坐标。
通过求导可得到顶点坐标为(8.66, 346.4)。
因此,最远射程为346.4米,对应的水平位移为8.66米。
3. 经济问题假设某个公司的固定成本为C0,每单位产品的生产成本为C,每单位产品的售价为P。
二次函数应用题专题(带答案)

二次函数应用题专题(带答案)0)时,可用交点式y=a(x-x1x-x2求其解析式。
4)根据问题要求,利用解析式求出所需的未知量。
三、练1、一枚炮弹在发射点上空爆炸,爆炸点离发射点水平距离1800米,爆炸高度为400米,求炮弹的初速度和仰角。
2、一架飞机以900km/h的速度飞行,飞行高度为2km,发现前方有一座山峰,山顶离飞机水平距离为10km,求飞机的爬升率和俯冲率。
3、一个人从距离地面20米的悬崖上抛出一个物体,物体抛出初速度为20m/s,抛出角度为60度,求物体落地点到悬崖的水平距离。
XXX:1、设炮弹飞行时间为t,初速度为v,仰角为θ,则可列出方程组:x=vtcosθy=vtsinθ-1/2gtx2y21800)2400)=xxxxxxx解得v600m/s,θ≈48.6°。
2、设飞机的爬升率和俯冲率分别为a和b,则可列出方程组:tan(θ-a)=4000/tan(θ+b)=2000/解得a≈2.5°,b≈1.4°。
3、设物体落地点到悬崖的水平距离为d,则可列出方程:d=vcosθtt=2vsinθ/g代入可得d≈40.8m。
评析:二次函数应用题需要学生熟练掌握建立坐标系、求解析式、利用解析式求未知量的方法,同时也需要学生对物理知识有一定的掌握,如抛物线运动、平抛运动等。
练中的例题和练题都体现了这些要点,可以帮助学生加深对二次函数应用的理解和掌握。
在教学过程中,可以引导学生多思考实际问题中的数学应用,提高他们的应用能力和解决问题的能力。
例2、某商场购进一批单价为16元的日用品,经试验发现,若按每件20元的价格销售时,每月能卖360件,若按每件25元的价格销售时,每月能卖210件,假定每月销售件数y(件)是价格x(元/件)的一次函数.1)求y与x之间的关系式;2)在商品不积压,且不考虑其他因素的条件下,问销售价格定为多少时,才能使每月获得最大利润?每月的最大利润是多少?解:(1)依题意设y=kx+b,则有 y= -30x+960 (16≤x≤32).2)每月获得利润P=(-30x+960)(x-16)=30(-x+32)(x-16)=-30+48x-512+1920.所以当x=24时,P有最大值,最大值为1920.答:当价格为24元时,才能使每月获得最大利润,最大利润为1920元.注意:数学应用题来源于实践,用于实践,在当今社会市场经济的环境下,应掌握一些有关商品价格和利润的知识,总利润等于总收入减去总成本,然后再利用一次函数求最值.例3、在体育测试时,初三的一名高个子男同学推铅球,已知铅球所经过的路线是某个二次函数图像的一部分,如图所示,如果这个男同学的出手处A点的坐标为(0,2),铅球路线的最高处B点的坐标为(6,5)1)求这个二次函数的解析式;2)该男同学把铅球推出去多远?(精确到0.01米)解:(1)设二次函数的解析式为 y=ax^2+bx+c。
二次函数应用题

二次函数应用题1、某食品零售店为食品厂代销一种面包,未售出的面包可退回厂家,经统计销售情况发现,当这种面包单价定为7角时,每天卖出160个,在此基础上,这种面包单价每提高1角,该零售店每天就会少卖出20个,该零售店每个面包的成本是5角.(1)如果每天卖出面包100个,那么这种面包的单价定为多少?这天卖面包的利润是多少?(2)如果每天销售这种面包获得的利润是48元,那么这种面包的单价是多少?2、某工厂生产的某种产品按质量分为10个档次,第一档次(最低档次)的产品一天可生产80件,每件产品的利润为10元,每提高一个档次,每件产品的利润增加2元.(1)当每件产品的利润为16元时,此产品质量在第几档次?(2)由于生产工序不同,此产品每提高一个档次,一天的产量减少4件.若生产某档次产品一天的总利润为1200元,问该工厂生产的是第几档次的产品?3、某宾馆有30间房间要出租,经过一段时间的经营发展,当每间房的租金为每日200元时,恰好全部租出.在此基础上,当每间房的租金每日提高10元时,就少租出一间,已知该宾馆每日平均每间房需支出各种费用150元,设每间房每日租金为x元,该宾馆出租房间的日收益为y元.(1)用含x的代数式表示每日未租出的房间数;(2)求y与x之间的函数关系式;(3)当x为何值时,该宾馆日收益最大,最大的日收益是多少?4.某商场购进一种单价为40元的篮球,如果以单价50元出售,那么每月可售出500个,根据销售经验,售价每提高1元,销售量相应减少10个.(1)假设销售单价提高x元,那么销售300个篮球所获得的利润是_______ 元;这种篮球每月的销售量是_______ 个.(用含x的代数式表示)(2)若每月销售这种篮球的最大利润是8000元,要使顾客得到实惠,则商场需要涨价多少?5.国家发改委公布的《商品房销售明码标价规定》,从2011年5月1日起商品房销售实行一套一标价.商品房销售价格明码标价后,可以自行降价、打折销售,但涨价必须重新申报.某市某楼盘准备以每平方米5000元的均价对外销售,由于新政策的出台,购房者持币观望.为了加快资金周转,房地产开发商对价格两次下调后,决定以每平方米4050元的均价开盘销售.(1)求平均每次下调的百分率;(2)某人准备以开盘均价购买一套100平方米的房子,开发商还给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,送两年物业管理费,物业管理费是每平方米每月1.5元.请问哪种方案更优惠?6. 某商场在销售旺季临近时,某品牌的童装销售价格呈上升趋势,假如这种童装第1周的售价为50元/件,并且每周涨价2元/件,从第6周开始,保持60元/件的稳定价格销售,直到第11周结束,该童装不再销售.(1)求销售价格y(元)与周次x之间的函数关系式;(2)若该品牌的童装每周进货一次,并于进货当周售完,且这种童装每件进价z(元)与周次x之间的关系为z=-1/8 (x-8)2+12,(1≤x≤11,x为整数),那么该品牌童装在第几周售出后,每件获得的利润最大?并求每件的最大利润.答案及提示1、解:(1)设这种面包单价为x角,得 160-( x-7)×20=100,解得x=10,利润为100×(10-5)=500角=50元,答:这种面包的单价定为10角,这天卖面包的利润是50元.…(5分)(2)设这种面包单价为y角,由题意得,[160-20(y-7)](y-5)=480,化简得,y2-20y+99=0,解得 y1=9,y2=11,答:这种面包的单价定为9角或11角(0.9元或1.1元).2、解:(1)当每件利润是16元时,提高了(16-10)÷2=3个档次,∵提高3个档次,∴此产品的质量档次是第4档次.(2)设生产产品的质量档次是在第x档次时,一天的利润是y,由题意可得y=[10+2(x-1)][80-4(x-1)],整理得y=-8x2+136x+672,当利润是1200元时,即=-8x2+136x+672=1200,解得:x1=6,x2=11(11>10,不符合题意,舍去),答:当生产产品的质量档次是在第6档次时,一天的总利润为1200元.3、解:由题意得(1)x-200/10(2)y=x(30-x-200/10)-150×30=-1/10x2+50x-4500;(3)y=1/10x2+50x-4500=-1/10(x-250)2+1750∴当x=250时,y最大=1750(12分).4、解:(1)销售一个篮球的利润为50-40+x=10+x(元),∴销售300个篮球所获得的利润是300×(10+x)元,这种篮球每月的销售量是500-10x,故答案为300×(10+x);(500-10x);(2)(10+x)(500-10x)=8000,(10+x)(50-x)=800,-x2+40x-300=0,x2-40x+300=0,(x-10)(x-30)=0,解得x1=10,x2=30,要使顾客得到实惠,∴x=10.答:要使顾客得到实惠,应涨价10元.5、解:(1)设平均每次下调的百分率为x.5000×(1-x)2=4050.(1-x)2=0.81,∴1-x=±0.9,∴x1=0.1=10%,x2=1.9(不合题意,舍去).答:平均每次下调的百分率为10%;(2)方案一的总费用为:100×4050×9.8/10=396900元;方案二的总费用为:100×4050-2×12×1.5×100=401400元;∴方案一优惠.6、解:(1)由题意得,童装销售价格呈上升趋势,且第一周的售价为每件50元,并且从第二周开始每周涨价2元,直到第6周结束,当1≤x≤6时,y=50+2(x-1)=2x+48;当6≤x≤11时,y=60;(2)设每件获得利润为w元,则当1≤x≤6时,w=y-z,=2x+48+1/8(x-8)2-12=1/8x2+44,∵1/8>0,∴当x>0时,w随x的增大而增大,∴当x=6时,w最大=48.5.当6≤x≤11时,w=y-z,=60+1/8(x-8)2-12=1/8(x-8)2+48∵1/8>0,∴当x>8时,w随x的增大而增大,∴当x=11时,w最大=49 *1/8.答:该品牌童装在第11周售出后,每件获得的利润最大,每件的最大利润为49*1/8元.。
二次函数的应用题及解析

二次函数的应用题及解析二次函数是数学中重要的函数之一,广泛应用于各个领域。
本文将探讨几个常见的二次函数应用题,并进行详细解析。
问题一:某天气预报显示,一天内温度的变化服从二次函数关系。
已知该地点上午8时的温度为15摄氏度,下午2时的温度为25摄氏度,晚上8时的温度为18摄氏度。
问该地点第二天早上6时的温度是多少摄氏度?解析:根据已知条件构建二次函数的关系式。
假设时间为x,温度为y,则可以得出二次函数表达式为:y = ax^2 + bx + c。
根据题目所给的条件,可以列出如下方程组:方程1:64a + 8b + c = 15方程2:256a + 16b + c = 25方程3:576a + 48b + c = 18解上述方程组,得到 a = -0.005, b = 0.16, c = 15.16。
带入x = 22(第二天早上6时的时间),计算二次函数的值,即可得到第二天早上6时的温度为20.62摄氏度。
问题二:某公司销售某款产品,预测未来几个月的销售情况。
已知该产品销售量符合二次函数模型。
已知该产品2月份的销售量为2000件,5月份的销售量为3000件,8月份的销售量为4000件。
预测11月份的销售量是多少件?解析:同样地,假设时间为x,销售量为y,构建二次函数关系式:y = ax^2 + bx + c。
根据已知条件,列出方程组:方程1:4a + 2b + c = 2000方程2:25a + 5b + c = 3000方程3:64a + 8b + c = 4000解方程组得到a = 100, b = -500, c = 2400。
带入x = 14(11月份的时间),计算二次函数的值,可得到预测11月份的销售量为3400件。
通过以上两个实例,我们可以看到二次函数在温度预测和销售预测中的应用。
根据给定的条件,构建二次函数关系式,并解方程组可以得到问题所求的结果。
通过这种方法,我们可以更加准确地评估和预测未来的发展趋势。
二次函数的应用题

二次函数综合应用1.某宾馆有50个房间供游客住宿,当每个房间的房价为每天180元时,房间会全部住满。
当每个房间每天的房价每增加10元时,就会有一个房间空闲。
宾馆需对游客居住的每一个房间每天支出20元的各种费用,根据规定,每个房间每天的房价不得高于340元。
设每个房间的房价每天增加x元。
(1)设一天定住的房间数为y间,写出y与x的函数解析式及自变量x的取值范围(2)设宾馆一天的利润为w元,求w与x的函数解析式(3)一天定住房价多少个时,宾馆的利润最大?最大利润为多少元?2.某商场经营某种品牌的童装,购进时的单价是60元.根据市场调查,在一段时间内,销售单价是80元时,销售量是200件,而销售单价每降低1元,就可多售出20件.(1)写出销售量y件与销售单价x元之间的函数关系式;(2)写出销售该品牌童装获得的利润w元与销售单价x元之间的函数关系式;(3)若童装厂规定该品牌童装销售单价不低于76元,且商场要完成不少于240件的销售任务,则商场销售该品牌童装获得的最大利润是多少?3.某商厦将进货价30元的书包以40元售出,平均每月能售出600个。
调查表明:这种书包的售价每上涨1元,其销售量就减少10个。
(1)求出销售量y个与销售单价x元之间的函数解析式(2)求出销售这种书包获得利润z元与销售单价x元之间的函数关系式(3)若商厦规定销售这种书包的单价不高于62元,且商厦的进货成本不高于12000元,当销售单价定为多少元时,可获得最大利润?最大利润是多少?26.某商店经销一种销售成本为每千克40元的水产品,根据市场分析,若按每千克50元销售,一个月能售出500千克,销售单价每涨1元,月销量就减少10千克.针对这种水产品的销售情况,请解决下列问题:(1)当销售单价为每千克55元时,计算月销售量和月销售利润;(2)设销售单价为每千克x元,月销售利润为y元,求y与x间的函数关系式;(3)商店想在月销售成本不超过10000元的情况下,使得月利润达到8000元,销售单价应为多少?4. 一座拱桥的轮廓是抛物线型(如图1所示),拱高6m,跨度20m,相邻两支柱间的距离均为5m.(1)将抛物线放在所给的直角坐标系中(如图2所示),求抛物线的解析式;(2)求支柱EF的长度;(3)拱桥下地平面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道能否并排行驶宽2m、高3m的三辆汽车(汽车间的间隔忽略不计)?请说明你的理由.x图15. 我市某工艺厂为配合北京奥运,设计了一款成本为20元∕件的工艺品投放市场(1)把上表中x 、y 的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想y 与x 的函数关系,并求出函数关系式;(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价-成本总价)(3)当地物价部门规定,该工艺品销售单价最高不能..超过45元/件,那么销售单6. 随着开发区近几年城市建设的快速发展,对花木的需求量逐年提高。
二次函数实际应用题

二次函数实际应用题1.端午节前夕,某超市从厂家分两次购进A、B两种品牌的粽子,两次进货时,两种品牌粽子的进价不变.第一次购进A品牌粽子 100袋和B品牌粽子 150袋,总费用为 7000元;第二次购进A品牌粽子 180袋和B品牌粽子120袋,总费用为 8100元。
(1)求A、B两种品牌粽子每袋的进价各是多少元;(2)当B品牌粽子销售价为每袋54元时,每天可售出20袋,为了促销,该超市决定对B品牌粽子进行降价销售,经市场调研,若每袋的销售价每降低1元,则每天的销售量将增加5袋,当B品牌粽子每袋的销售价降低多少元时,每天售出B品牌粽子所获得的利润最大?最大利润是多少元?2.某商店购进了一种消毒用品,进价为每件8元,在销售过程中发现,每天的销售量y(件)与每件售价x(元)之间存在一次函数关系(其中8≤x≤15,且x为整数).当每件消毒用品售价为9元时,每天的销售量为105件;当每件消毒用品售价为11元时,每天的销售量为95件.(1)求y与x之间的函数关系式。
(2)若该商店销售这种消毒用品每天获得425元的利润,则每件消毒用品的售价为多少元?(3)设该商店销售这种消毒用品每天获利w(元),当每件消毒用品的售价为多少元时,每天的销售利润最大?最大利润是多少元?3.某超市购进一批水果,成本为8元/kg,根据市场调研发现,这种水果在未来10天的售价m(元/kg)与时间第x天之间满足函数关系式m=12x+18(1≤x≤10)x为整数),又通过分析销售情况,发现每天销售量y(kg)与时间第x天之间满足一次函数关系,下表是其中的三组对应值.(1)求y与x的函数解析式;(2)在这10天中,哪一天销售这种水果的利润最大,最大销售利润为多少元?4.丹东是我国的边境城市,拥有丰富的旅游资源. 某景区研发一款纪念品,每件成本为30元,投放景区内进行销售,规定销售单价不低于成本且不高于 54元,销售一段时间调研发现,每天的销售数量y(件)与销售单价x(元/件)满足一次函数关系,部分数据如下表所示:5.某超市采购了两批同样的冰墩墩挂件,第一批花了6600元,第二批花了8000元,第一批每个挂件的进价是第二批的1.1倍,且第二批比第一批多购进50个。
二次函数的应用题(含答案)
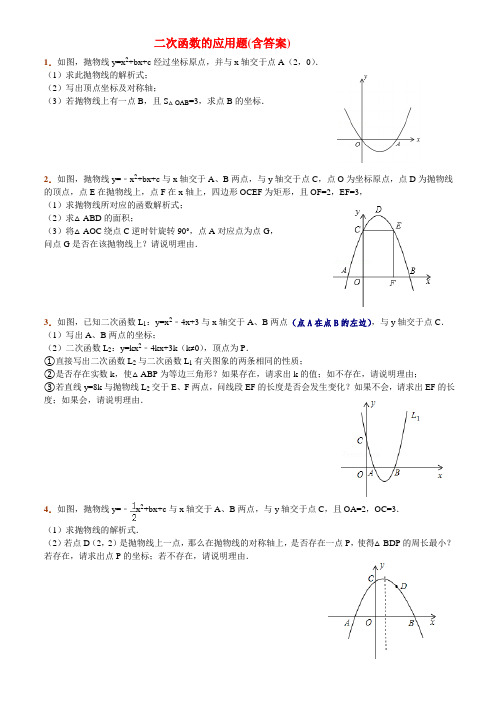
二次函数的应用题(含答案)1.如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0).(1)求此抛物线的解析式;(2)写出顶点坐标及对称轴;(3)若抛物线上有一点B,且S△OAB=3,求点B的坐标.2.如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C,点O为坐标原点,点D为抛物线的顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3,(1)求抛物线所对应的函数解析式;(2)求△ABD的面积;(3)将△AOC绕点C逆时针旋转90°,点A对应点为点G,问点G是否在该抛物线上?请说明理由.3.如图,已知二次函数L1:y=x2﹣4x+3与x轴交于A、B两点(点A在点B的左边),与y轴交于点C.(1)写出A、B两点的坐标;(2)二次函数L2:y=kx2﹣4kx+3k(k≠0),顶点为P.①直接写出二次函数L2与二次函数L1有关图象的两条相同的性质;②是否存在实数k,使△ABP为等边三角形?如果存在,请求出k的值;如不存在,请说明理由;③若直线y=8k与抛物线L2交于E、F两点,问线段EF的长度是否会发生变化?如果不会,请求出EF的长度;如果会,请说明理由.4.如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.(1)求抛物线的解析式.(2)若点D(2,2)是抛物线上一点,那么在抛物线的对称轴上,是否存在一点P,使得△BDP的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.5.如图,抛物线y=﹣x 2+bx+c 经过坐标原点,并与x 轴交于点A (2,0). (1)求此抛物线的解析式; (2)写出顶点坐标及对称轴;(3)若抛物线上有一点B ,且S △OAB =8,求点B 的坐标.6.如图,在平面直角坐标系中放置一直角三角板,其顶点为A (0,1),B (2,0),O (0,0),将此三角板绕原点O 逆时针旋转90°,得到△A ′B ′O .(1)一抛物线经过点A ′、B ′、B ,求该抛物线的解析式;(2)设点P 是在第一象限内抛物线上的一动点,是否存在点P ,使四边形PB ′A ′B 的面积是△A ′B ′O 面积的4倍?若存在,请求出P 的坐标;若不存在,请说明理由.(3)在(2)的条件下,试指出四边形PB ′A ′B 是哪种形状的四边形?并写出四边形PB ′A ′B 的两条性质.7.某汽车租赁公司拥有20辆汽车.据统计,当每辆车的日租金为400元时,可全部租出;当每 辆车的日租金每增加50元,未租出的车将增加1辆;公司平均每日的各项支出共4800元.设公司每日租出工辆车时,日收益为y元.(日收益=日租金收入一平均每日各项支出) (1)公司每日租出x 辆车时,每辆车的日租金为 _________ 元(用含x 的代数式表示); (2)当每日租出多少辆时,租赁公司日收益最大?最大是多少元? (3)当每日租出多少辆时,租赁公司的日收益不盈也不亏?8.某工厂生产一种合金薄板(其厚度忽略不计),这写薄板的形状均为正方向,边长在(单位:cm)在5~50之间.每张薄板的成本价(单位:元)与它的面积(单位:cm2)成正比例,每张薄板的出厂价(单位:元)有基础价和浮动价两部分组成,其中基础价与薄板的大小无关,是固定不变的.浮动价与薄板的边长成(2)已知出厂一张边长为40cm的薄板,获得的利润为26元(利润=出厂价﹣成本价),①求一张薄板的利润与边长之间满足的函数关系式.②当边长为多少时,出厂一张薄板所获得的利润最大?最大利润是多少?9.牡丹花会前夕,我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销.经过调查,得到如下数据:(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(3)菏泽市物价部门规定,该工艺品销售单价最高不能超过35元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?答案得×,解得±;x得,﹣,﹣+解得,y=﹣时,×+1=,故,5.(2012•黑龙江)解:(1)把(0,0),(2,0)代入y=﹣x2+bx+c,得,解得b=2,c=0,所以解析式为y=﹣x2+2x;(2)∵a=﹣1,b=2,c=0,∴﹣=﹣=1,==1,∴顶点为(1,1),对称轴为直线x=1;(3)设点B的坐标为(a,b),则×2|b|=8,∴b=8或b=﹣8,∵顶点纵坐标为1,8>1(或﹣x2+2x=8中,x无解),∴b=﹣8,∴﹣x2+2x=﹣8,解得x解:(1)△A′B′O是由△ABO绕原点O逆时针旋转90°得到的,又A(0,1),B(2,0),O(0,0),∴A′(﹣1,0),B′(0,2).设抛物线的解析式为:y=ax2+bx+c(a≠0),∵抛物线经过点A′、B′、B,∴,解得:,∴满足条件的抛物线的解析式为y=﹣x2+x+2.(2)∵P为第一象限内抛物线上的一动点,设P(x,y),则x>0,y>0,P点坐标满足y=﹣x2+x+2.连接PB,PO,PB′,∴S四边形PB′A′B=S△B′OA′+S△PB′O+S△POB,=×1×2+×2×x+×2×y,=x+(﹣x2+x+2)+1,=﹣x2+2x+3.假设四边形PB′A′B的面积是△A′B′O面积的4倍,则4=﹣x2+2x+3,即x2﹣2x+1=0,解得:x1=x2=1,此时y=﹣12+1+2=2,即P(1,2).∴存在点P(1,2),使四边形PB′A′B的面积是△A′B′O面积的4倍.(3)四边形PB′A′B为等腰梯形,答案不唯一.①等腰梯形同一底上的两个内角相等;②等腰梯形对角线相等;③等腰梯形上底与下底平行;④等腰梯形两腰相等.或用符号表示:①∠B′A′B=∠PBA′或∠A′B′P=∠BPB′;②PA′=B′B;③B′P∥A′B;④B′A′=PB.由表格中的数据,得,解得﹣<==35解:(1)画图如图:由图可猜想y与x是一次函数关系,设这个一次函数为y=kx+b(k≠0),∵这个一次函数的图象经过(20,500)、(30,400)这两点,∴,解得:,∴函数关系式是y=﹣10x+700.(2)设工艺厂试销该工艺品每天获得的利润是W元,依题意得:W=(x﹣10)(﹣10x+700),=﹣10x2+800x﹣7000,=﹣10((x﹣40)2+9000,∴当x=40时,W有最大值9000.(3)对于函数W=﹣10((x﹣40)2+9000,当x≤35时,W的值随着x值的增大而增大,故销售单价定为35元∕件时,工艺厂试销该工艺品每天获得的利润最大.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数的应用知识点:二次函数图象的画法 (五点绘图法):利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.一般我们选取的五点为:顶点、与y 轴的交点()0c ,、以及()0c ,关于对称轴对称的点()2h c ,、与x 轴的交点()10x ,,()20x ,(若与x 轴没有交点,则取两组关于对称轴对称的点).画草图时应抓住以下几点:开口方向,对称轴,顶点,与x 轴的交点,与y 轴的交点.二次函数的图象及性质1. 二次函数2y ax =0a ≠()的性质:⑴抛物线2y ax =的顶点是坐标原点(0,0),对称轴是0x =(y 轴). ⑵函数2y ax =的图像与a 的符号关系.①当0a >时⇔抛物线开口向上⇔顶点为其最低点; ②当0a <时⇔抛物线开口向下⇔顶点为其最高点;2.二次函数2(0)y ax c a =+≠的性质3. 二次函数2y ax bx c =++0a ≠()或2()y a x h k =-+(0a ≠)的性质⑴开口方向:00a a >⇔⎧⎨<⇔⎩向上向下⑵对称轴:2bx a=-(或x h =)⑶顶点坐标:24(,)24b ac b a a--(或(,)h k )⑷最值:0a >时有最小值244ac b a -(或k )(如图1); 0a <时有最大值244ac b a-(或k )(如图2); ⑸单调性:二次函数2y ax bx c =++(0a ≠)的变化情况(增减性)①如图1所示,当0a >时,对称轴左侧2b x a <-,y 随着x 的增大而减小,在对称轴的右侧2bx a<- ,y 随x 的增大而增大;②如图2所示,当0a >时,对称轴左侧2b x a <-, y 随着x 的增大而增大,在对称轴的右侧2bx a<-,y 随x 的增大而减小; ⑹与坐标轴的交点:①与y 轴的交点:(0,C );②与x 轴的交点:使方程20ax bx c ++=(或2()0a x h k -+=) 成立的x 值.一、图象信息题【例1】 如图1,在矩形矩形ABCD 中,动点P 从点B 出发,沿BC ,CD ,DA 运动至点A 停止.设点P 运动的路程为x ,ABP ∆的面积为y ,如果y 关于x 的函数图象如图2所示,则ABC ∆的面积是 ( ) A .10 B .16 C .18 D .20C DBAP【解析】由图象知矩形ABCD 中,5AB CD ==,宽4BC AD ==,所以ABC ∆的面积为145102⨯⨯=.【答案】A2.如图,点G 、D 、C 在直线a 上,点E 、F 、A 、B 在直线b 上,若a b ∥,Rt GEF ∆从如图所示 的位置出发,沿直线b 向右匀速运动,直到EG 与BC 重合.运动过程中GEF ∆与矩形ABCD 重合部分....的面积()S 随时间()t 变化的图象大致是FE GA BCDABCD【答案】B3.正方形边长为3,若边长增加x ,则面积增加y .求y 与x 之间的函数关系式.【答案】26y x x =+4.有一边长为5米的正方形场地,现在要在里面建一矩形游泳池,如图所示,要求一边距场地边缘为x米,一边为2x 米,求矩形的面积y 与x 的关系表达式.【答案】221525y x x =-+(0 2.5)x <<二、 利润问题1.已知某种水果的批发单价与批发量的函数关系如图所示.(1)请说明图中①、②两段函数图象的实际意义.(2)写出批发该种水果的资金金额w (元)与批发量m (kg )之间的函数关系式;在下图的坐标系中画出该函数图象;指出金额在什么范围内,以同样的资金可以批发到较多数量的该种水果. (3)经调查,某经销商销售该种水果的日最高销量与零售价之间的函数关系如图所示,该经销商拟每日售出60kg 以上该种水果,且当日零售价不变,请你帮助该经销商设计进货和销售的方案,使得当日获得的利润最大。
kg )【答案】(1)图①表示批发量不少于20kg 且不多于60kg 的该种水果,可按5元/kg 批发;图②表示批发量高于60kg 的该种水果,可按4元/kg 批发.(2) 2060 6054m m w m m ⎧=⎨⎩≤≤()(>),由图可知资金金额满足240<w ≤300时,以同样的资金可批发到较多数量的该种水果.(3)即经销商应批发80kg 该种水果,日零售价定为6元/kg ,当日可获得最大利润160元.2.某商场试销一种成本为每件60元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量y (件)与销售单价x (元)符合一次函数y kx b =+,且65x =时,55y =;75x =时,45y =. (1)求一次函数y kx b =+的表达式;(2)若该商场获得利润为W 元,试写出利润W 与销售单价x 之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?(3) 若该商场获得利润不低于500元,试确定销售单价x 的范围.【答案】(1)120y x =-+;(2)W2(90)900x =--+,∴当销售单价定为87元时,商场可获得最大利润,最大利润是891元.(3)销售单价x 的范围是7087x ≤≤.3.某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.(1)假设每台冰箱降价x 元,商场每天销售这种冰箱的利润是y 元,请写出y 与x 之间的函数表达式;(不要求写自变量的取值范围)(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?(3) 每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少? 【答案】(1)2224320025y x x =-++;(2)每台冰箱应降价200元.(3)每台冰箱的售价降价150元时,商场的利润最大,最大利润是5000元.三、 增长率问题1某电视机生产厂家去年销往农村的某品牌电视机每台的售价y (元)与月份x 之间满足函数关系502600y x =-+,去年的月销售量p (万台)与月份x 之间成一次函数关系,其中两(1(2)由于受国际金融危机的影响,今年1、2月份该品牌电视机销往农村的售价都比去年12月份下降了%m ,且每月的销售量都比去年12月份下降了1.5m%.国家实施“家电下乡”政策,即对农村家庭购买新的家电产品,国家按该产品售价的13%给予财政补贴.受此政策的影响,今年3至5月份,该厂家销往农村的这种电视机在保持今年2月份的售价不变的情况下,平均每月的销售量比今年2月份增加了1.5万台.若今年3至5月份国家对这种电视机的销售共给予了财政补贴936万元,求m 的值(保留一位小数).5.831 5.9166.083 6.164)【答案】(1)7月销售金额最大,最大值是10125万元;(2)m=52.78≈52.82.已知某种商品去年售价为每件a 元,可售出b 件.今年涨价x 成(1成=10%),则售出的数量减少x成(m 是正常数).试问: ⑴ 如果涨价1.25成价格,营业额将达到()214ab m m+,求m ;⑵ 如果适当的涨价,能使营业额增加,求m 应在什么范围内?【答案】(1)89m =;(2)10m >>四、 拱形图问题1某工厂要赶制一批抗震救灾用的大型活动板房.如图,板房一面的形状是由矩形和抛物线的一部分组成,矩形长为12m ,抛物线拱高为5.6m . (1)在如图所示的平面直角坐标系中,求抛物线的表达式.(2)现需在抛物线AOB 的区域内安装几扇窗户,窗户的底边在AB 上,每扇窗户宽1.5m ,高1.6m ,相邻窗户之间的间距均为0.8m ,左右两边窗户的窗角所在的点到抛物线的水平距离至少为0.8m .请计算最多可安装几扇这样的窗户?【解析】(1)设抛物线的表达式为2y ax = 点(6 5.6)B -,在抛物线的图象上.∴ 5.636a -=,745a =-∴抛物线的表达式为2745y x =- (2)设窗户上边所在直线交抛物线于C 、D 两点,D 点坐标为(k ,t )已知窗户高1.6m ,∴ 5.6( 1.6)4t =---=-27445k --=125.07 5.07k k -≈,≈(舍去)∴ 5.07210.14CD =⨯≈(m ) 又设最多可安装n 扇窗户 ∴1.50.8(1)10.14n n ++≤4.06n ≤.答:最多可安装4扇窗户.(本题不要求学生画出4个表示窗户的小矩形)2.如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度OM 为12米. 现 以O 点为原点,OM 所在直线为x 轴建立直角坐标系. (1)直接写出点M 及抛物线顶点P 的坐标; (2)求这条抛物线的解析式;(3)若要搭建一个矩形“支撑架”AD - DC- CB ,使C 、D 点在抛物线上,A 、B 点在地面OM 上,则这个“支撑架”总长的最大值是多少?【解析】 (1) M (12,0),P (6,6).(2) 设抛物线解析式为:2(6)6y a x =-+. ∵抛物线2(6)6y a x =-+经过点(0,0),∴20(06)6a =-+,即16a =-∴抛物线解析式为:2211(6)6,266y x y x x =--+=-+即 .(3) 设A (m ,0),则B (12-m ,0),21(12,2)6C m m m --+,21(,2)6D m m m -+.∴“支撑架”总长AD+DC+CB =2211(2)(122)(2)66m m m m m -++-+-+=2211212(3)1533m m m -++=--+. ∵ 此二次函数的图象开口向下.∴ 当m = 3米时,AD+DC+CB 有最大值为15米.3.王强在一次高尔夫球的练习中,在某处击球,其飞行路线、满足抛物线21855y x x =-+,其中y (m)是球的飞行高度, x (m )是球飞出的水平距离,结果球离球洞的水平距离还有2m .⑴ 请写出抛物线的开口方向、顶点坐标、对称轴. ⑵ 请求出球飞行的最大水平距离. ⑶ 若王强再一次从此处击球,要想让球飞行的最大高度不变且球刚好进洞,则球飞行路线应满足怎样的抛物线,求出其解析式.【解析】⑴ 21855y x x =-+2116(4)55x =--+∴抛物线21855y x x =-+开口向下,顶点为1645⎛⎫ ⎪⎝⎭,,对称轴为4x =.⑵ 令0y =,得:218055x x -+=,解得:10x =,28x =,∴球飞行的最大水平距离是8m .⑶ 要让球刚好进洞而飞行最大高度不变,则球飞行的最大水平距离为10m ∴抛物线的对称轴为5x =,顶点为1655⎛⎫⎪⎝⎭,设此时对应的抛物线解析式为216(5)5y a x =-+,又∵点(00),在此抛物线上,∴162505a +=, 16125a =-.五、 面积问题1.张大爷要围成一个矩形花圃.花圃的一边利用足够长的墙另三边用总长为32米的篱笆恰好围成.围成的花圃是如图所示的矩形ABCD .设AB 边的长为x 米.矩形ABCD 的面积为S 平方米.(1)求S 与x 之间的函数关系式(不要求写出自变量x 的取值范围). (2)当x 为何值时,S 有最大值?并求出最大值.(参考公式:二次函数2y ax bx c =++(0a ≠),当2bx a=-时)【解析】由题意得()322S AB BC x x =⋅=-∴223S x x =-+由20a =-<∴()328222b x a =-=-=⨯-241284ac b S a-==最大值∴8x =时,S 有最大值是1282.某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD 是矩形,其中AB=2米,BC=1米;上部CDG 是等边三角形,固定点E 为AB 的中点.△EMN 是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN 是可以沿设施边框上下滑动且始终保持和AB 平行的伸缩横杆.(1)当MN 和AB 之间的距离为0.5米时,求此时△EMN 的面积;(2)设MN 与AB 之间的距离为x 米,试将△EMN 的面积S (平方米)表示成关于x 的函数; (3)请你探究△EMN 的面积S (平方米)有无最大值,若有,请求出这个最大值;若没有,请说明理由.E CD【解析】(1)由题意,当MN 和AB 之间的距离为0.5米时,MN 应位于DC 下方,且此时△EMN 中 MN 边上的高为0.5米.所以,S △EMN =120.52⨯⨯=0.5(平方米).即△EMN 的面积为0.5平方米.(2)①如图1所示,当MN 在矩形区域滑动,即0<x ≤1时, △EMN 的面积S =122x ⨯⨯=x ;②如图2所示,当MN 在三角形区域滑动,即1<x<1 如图,连接EG ,交CD 于点F ,交MN 于点H , ∵ E 为AB 中点,∴ F 为CD 中点,GF ⊥CD ,且FG又∵ MN ∥CD , ∴ △MNG ∽△DCG .∴MN GHDC GF =,即MN = 故△EMN 的面积S=12x=2(1x +;综合可得:()(201111x x S x x x ≤⎧⎪=⎛⎨++ ⎪ ⎝⎭⎩,<.<< (3)①当MN 在矩形区域滑动时,S x =,所以有01S <≤ ②当MN 在三角形区域滑动时,S=2(1x +.因而,当2b x a =-=(米)时, S 得到最大值,最大值S =244ac b a -21-(12(平方米).∵112>,∴ S有最大值,最大值为12平方米.综合练习1. 进入夏季后,某电器商场为减少库存,对电热取暖器连续进行两次降价.若设平均每次降价的百分率是x ,降价后的价格为y 元,原价为a 元,则y 与x 之间的函数关系式为( )A. 2(1)y a x =-B. 2(1y a x =- 2C. (1)ya x =- 2D. (1)y a x =- 【答案】D2. 某公司生产一种产品,每件成本为2元,售价为3元,年销售量为100万件.为获 取更好的效益,公司准备拿出一定资金做广告.通过市场调查发现:每年投入的广告费用为x (十 万元)时,产品的年销售量将是原销售量的y 倍;同时y 又是x 的二次函数,相互关系如下表:⑵ 如果把利润看作是销售总额减去成本费和广告费,试写出年利润S (十万元)与广告费x (十万元)的函数关系式;⑶ 如果一年投入的广告费为10~30万元,问广告费在什么范围内时,公司获得的年利润随广告费的增大而增大? 【解析】⑴ 设所求的二次函数关系式为2y ax bx c =++.则有1329425c a b c a b c ⎧⎪=⎪⎪++=⎨⎪⎪++=⎪⎩ 解得110a =-,35b =,1c =.∴2131105y x x =-++(0x ≥).⑵ 依题意,得()21032510S y x x x =⨯--=-++(0x ≥). ⑶ 由2256551024S x x x ⎛⎫=-++=--+ ⎪⎝⎭又13x ≤≤,∴当1 2.5x ≤≤时,S 随着x 增大而增大.即当广告费在10万元~25万元时,公司获得的年利润随着广告费的增大而增大.3. 甲、乙两个蔬菜基地,分别向A 、B 、C 三个农贸市场提供同品种蔬菜,按签订的合同规定向A 提供45t ,向B 提供75t ,向C 提供40t .甲基地可安排60t ,乙基地可安排100t .甲、乙与A 、B 、C【解析】设乙基地向A 提供xt ,向B 提供yt ,向C 提供100x y t -+⎡⎤⎣⎦,则甲基地向A 提供)45x t -,向B提供()75y t -,向C 提供()()4010060x y t x y t ---=+-⎡⎤⎡⎤⎣⎦⎣⎦. 依题意,总运费为()()()()10455756604815100W x y x y x y x y =-+-++-+++-+⎡⎤⎡⎤⎣⎦⎣⎦()1965323x y x =-++⎡⎤⎣⎦.因为0xy +≤≤100,045x ≤≤,当且仅当100x y +=,45x =时,W 有最小值,则()min 19653200135960W =-+=元.4. 一座隧道的截面由抛物线和长方形构成,长方形的长为8m ,宽为2m ,隧道最高点P位于AB 的中央且距地面6m ,建立如图所示的坐标系 (1)求抛物线的解析式;(2)一辆货车高4m ,宽2m ,能否从该隧道内通过,为什么?(3) 如果隧道内设双行道,那么这辆货车是否可以顺利通过,为什么?【解析】(1)由题意可知抛物线经过点()()()024682A P B ,,,,, 设抛物线的方程为2yax bx c =++ 将A P D ,,三点的坐标代入抛物线方程. 解得抛物线方程为21224y x x =-++(2)令4y =,则有212244x x -++=解得1244x x =+=-212x x -=>∴货车可以通过.(3)由(2)可知21122x x -=> ∴货车可以通过.5. 如图,E 、F 分别是边长为4的正方形ABCD 的边BC CD ,上的点,413CE CF ==,,直线EF 交AB学习好资料 欢迎下载的延长线于G ,过线段FG 上的一个动点H 作HM AG ⊥,HN AD ⊥,垂足分别为M N ,,设H M x =,矩形AMHN 的面积为y⑴ 求y 与x 之间的函数关系式;⑵ 当x 为何值时,矩形AMHN 的面积最大,最大面积为多少?NM H GF ED CB A 【解析】⑴ ∵正方形ABCD 的边长为4,413CE CF ==,, ∴3BE =又AG CF FEC GEB ∥,△∽△,4CF CE BG BG BE==, 又HM BE ∥ ∴HMG EBG △∽△,MG HM BG BE= ∴44833MG x AM x ==-, ∴()244880433y x x x x x ⎛⎫=-=-+<≤ ⎪⎝⎭ ⑵ ∵()2244831233y x x x =-+=--+ ∴当3x =时,矩形面积最大,最大面积为12。
