(完整版)历年高考立体几何大题试题.doc
2016年-2019年立体几何大题全国卷高考真题

2016年-2019年立体几何大题全国卷高考真题1、(2015年1卷18题)如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF,AE⊥EC.(Ⅰ)证明:平面AFC⊥平面AEC;(Ⅱ)求直线AE与直线CF所成有的余弦值。
(2016年1卷18题)如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD, 2、90AFD ∠=o ,且二面角D -AF -E 与二面角C -BE -F 都是60o .(I )证明:平面ABEF ⊥平面EFDC ;(II )求二面角E -BC -A 的余弦值.3(2016年2卷19题)(本小题满分12分) CA BD EF如图,菱形ABCD 的对角线AC 与BD 交于点O ,5AB =,6AC =,点E ,F 分别在AD ,CD 上,54AE CF ==,EF 交BD 于点H .将△DEF 沿EF 折到△D EF'的位置10OD '=. (I )证明:D H '⊥平面ABCD ;(II )求二面角B D A C '--的正弦值.4、(2017年1卷18题)如图,在四棱锥P ABCD -中,AB CD ∥中,且90BAP CDP ∠=∠=?.(1)证明:平面PAB ⊥平面PAD ;(2)若PA PD AB DC ===,90APD ∠=?,求二面角A PB C --的余弦值.5.(2018年1卷18题)如图,四边形ABCD 为正方形,E ,F 分别为AD ,BC 的中点,以DF 为折痕把DFC △折起,使点C 到达点P 的位置,且PF BF ⊥.⑴证明:平面PEF ⊥平面ABFD ;⑵求DP与平面ABFD所成角的正弦值.6.(2018年新课标Ⅱ理)如图,在三棱锥P-ABC中,AB=BC=22,P A =PB=PC=AC=4,O为AC的中点.(1)求证:PO⊥平面ABC;(2)若点M在棱BC上,且二面角M-P A-C为30°,求PC与平面P AM所成角的正弦值.18.(2019年1卷18题)(12分)如图,直四棱柱ABCD﹣A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.(1)证明:MN∥平面C1DE;(2)求二面角A﹣MA1﹣N的正弦值.8.(12分)(2019年新课标Ⅱ理)如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E 在棱AA1上,BE⊥EC1.(1)证明:BE⊥平面EB1C1;(2)若AE=A1E,求二面角B–EC–C1的正弦值.。
高中数学立体几何测试题(10套)

∴ BD ∥平面 PMN ,
位置关系为
平行
。
∴ O 到平面 PMN 的距离即为 BD 到平面 PMN 的距离。
11 、a,b 为异面直线,且 a,b 所成角为 40 °,直线 c 与 a,b 均异面,且所成角均为
∵ BD ⊥ AC , MN ∥ BD
∵ PA⊥面 ABCD
θ,若这样的 c 共有四条,则 θ的范围为 (70 °, 90° ) 。
D
C
A
B
D1 A1
C1 B1
17 、 已知异面直线 a, b 的公垂线段 AB 的中点为 O,平面 满足 a∥ , b∥ , 且 O , M 、 N 是 a, b 上的任意两点, MN ∩ = P,求证: P 是 MN 的中
点
A aM
O
P
BN b
.
立几面测试 001
参考答 案
一、 1- 8 ACDDBDBA
2、已知 m, n 为异面直线, m∥平面 , n∥平面 , ∩ =l ,则 l( ) ( A)与 m, n 都相交 ( B)与 m,n 中至少一条相交 ( C)与 m, n 都不相交 ( D )与 m, n 中一条相交
3、已知 a, b 是两条相交直线, a∥ ,则 b 与 的位置关系是 ( )
A 、 b∥
PAM
∵ AB=2 , BM=1 , CM=1
∴ AM= 5 ,
P
A H
O
.
B
F M
B
D N C
立几面测试 003
一、选择题
1.异面直线是指
(A) 在空间内不能相交的两条直线
(B) 分别位于两个不同平面的两条直线
(C) 某一个平面内的一条直线和这个平面外的一条直线
历年高考立体几何真题+答案

历年高考真题1、2003(理科)(本题满分12分)已知平行六面体ABCD —A 1B 1C 1D 1中,A 1A ⊥平面ABCD ,AB=4,AD=2.若B 1D ⊥BC ,直线B 1D 与平面ABCD 所成的角等于30°,求平行六面体ABCD —A 1B 1C 1D 1的体积..[解]连结BD ,因为B 1B ⊥平面ABCD ,B 1D ⊥BC ,所以BC ⊥BD.在△BCD 中,BC=2,CD=4,所以BD=32.又因为直线B 1D 与平面ABCD 所成的角等于30°,所以 ∠B 1DB=30°,于是BB 1=31BD=2.故平行六面体ABCD —A 1B 1C 1D 1的体积为S ABCD ·BB 1=38. 2.2005(理科)(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.已知正三棱锥ABC P -的体积为372,侧面与底面所成的二面角的大小为 60. (1)证明:BC PA ⊥;(2)求底面中心O 到侧面的距离.[证明](1)取BC 边的中点D ,连接AD 、PD ,则BC AD ⊥,BC PD ⊥,故⊥BC 平面APD . BCPA ⊥[解](2)如图, 由(1)可知平面⊥PBC 平面APD ,则PDA ∠面所成二面角的平面角.过点O 作E PD OE ,⊥为垂足,则OE 就是点O 到侧面的距离. 设OE 为h ,由题意可知点O 在AD 上,∴ 60=∠PDO ,h OP 2=.h BC h OD 4,32=∴=,∴ 2234)4(43h h S ABC ==∆, ∵ 3233823431372h h h =⋅⋅=,∴ 3=h . 即底面中心O 到侧面的距离为3.3、2006(理科)(本题满分 14分)本题共有 2个小题,第 1小题满分 5分,第 2小题满分满分 9分。
在三棱柱 ABC —A1B1C1 中,∠ABC=90°,AB=BC=1。
(完整)高中数学《立体几何》大题及答案解析.doc

高中数学《立体几何》大题及答案解析( 理)1.( 2009 全国卷Ⅰ)如图,四棱锥S ABCD 中,底面 ABCD 为矩形, SD底面ABCD,AD2 ,DCo SD 2 ,点 M 在侧棱 SC 上,∠ABM=60。
(I )证明:M是侧棱SC的中点;求二面角 S AM B 的大小。
2.( 2009 全国卷Ⅱ)如图,直三棱柱DE ⊥平面 BCC 1(Ⅰ)证明: AB=AC 的角的大小ABC-A 1B1C1中, AB ⊥ AC,D 、E 分别为 AA 1、 B1C 的中点,(Ⅱ)设二面角A-BD-C 为 60°,求 B 1C 与平面 BCD 所成A 1 C1B1D EACB3. ( 2009浙江卷)如图,DC平面ABC,EB / / DC,AC BC EB 2DC 2 ,ACB 120o, P,Q 分别为 AE , AB 的中点.(I)证明: PQ / / 平面ACD;(II)求AD与平面 ABE 所成角的正弦值.4.( 2009 北京卷)如图,四棱锥P ABCD 的底面是正方形,PD 底面 ABCD ,点E在棱PB上.(Ⅰ)求证:平面AEC 平面 PDB ;(Ⅱ)当 PD2AB 且E为PB的中点时,求 AE 与平面 PDB 所成的角的大小.5.( 2009 江西卷)如图,在四棱锥P ABCD 中,底面 ABCD 是矩形, PA平面ABCD,PA AD 4 , AB 2 .以 BD 的中点 O 为球心、 BD 为直径的球面交PD 于点 M .(1)求证:平面ABM⊥平面PCD;(2)求直线PC与平面ABM所成的角;(3)求点O到平面ABM的距离.PMA DOBC6(. 2009 四川卷)如图,正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直,△ ABE 是等腰直角三角形,AB AE , FA FE , AEF 45 (I)求证: EF 平面 BCE ;( II )设线段 CD 、 AE 的中点分别为 P 、 M ,求证: PM ∥平面BCE ( III )求二面角 F BD A 的大小。
高三精选立体几何大题30题(含详细解答)

A BC第1题图ABCD第1题图立体几何大题1.如下图,一个等腰直角三角形的硬纸片ABC中,∠ACB=90°,AC=4cm,CD是斜边上的高沿CD 把△ABC折成直二面角.(1)如果你手中只有一把能度量长度的直尺,应该如何确定A,B的位置,使二面角A-CD-B是直二面角?证明你的结论.(2)试在平面ABC上确定一个P,使DP与平面ABC内任意一条直线都垂直,证明你的结论.(3)如果在折成的三棱锥内有一个小球,求出小球半径的最大值.2.如图,已知正四棱柱ABCD—A1B1C1D1的底面边长为3,侧棱长为4,连结A1B过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E。
(Ⅰ)求证:D1B⊥平面AEC;(Ⅱ)求三棱锥B—AEC的体积;(Ⅲ)求二面角B—AE—C的大小的正弦值.3.如图,正三棱柱ABC—A1B1C1的底面边长为1,点M在BC上,△AMC1是以M为直角顶点的等腰直角三角形.(I)求证:点M为BC的中点;(Ⅱ)求点B到平面AMC1的距离;(Ⅲ)求二面角M—AC1—B 的正切值. 4.如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1,F是CD的中点.(Ⅰ)求证:AF∥平面BCE;(Ⅱ)求多面体ABCDE的体积;(Ⅲ)求二面角C-BE-D 的正切值.5.已知:ABCD是矩形,设PA=a,PA⊥平面ABCD.M、N分别是AB、PC的中点.(Ⅰ)求证:MN⊥AB;(Ⅱ)若PD=AB,且平面MND⊥平面PCD,求二面角P—CD—A的大小;(Ⅲ)在(Ⅱ)的条件下,求三棱锥D—AMN的体积.6.在正方体ABCD—A1B1C1D1中,P、M、N分别为棱DD1、AB、BC的中点。
(I)求二面角B1—MN—B的正切值;(II)证明:PB⊥平面MNB1;(III)画出一个正方体表面展开图,使其满足“有4个正方形面相连成一个长方形”的条件,并求出展开图中P、B两点间的距离。
(完整版)历年高考立体几何大题试题

2015年高考立体几何大题试卷1.【2015高考新课标2,理19】如图,长方体1111ABCD A B C D -中,=16AB ,=10BC ,18AA =,点E ,F 分别在11A B ,11C D 上,114A E D F ==.过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形.(1题图)(Ⅰ)在图中画出这个正方形(不必说出画法和理由); (Ⅱ)求直线AF 与平面α所成角的正弦值.2.【2015江苏高考,16】 如图,在直三棱柱111C B A ABC -中,已知BC AC ⊥,1CC BC =,设1AB 的中点为D ,E BC C B =11 .求证:(1)C C AA DE 11//平面;(2)11AB BC ⊥.(2题图)(3题图)3. 【2015高考安徽,理19】如图所示,在多面体111A B D DCBA ,四边形11AA B B ,11,ADD A ABCD 均为正方形,E 为11B D 的中点,过1,,A D E 的平面交1CD 于F.(Ⅰ)证明:1//EF B C ; (Ⅱ)求二面角11E A D B --余弦值.D D CA EF ABC B AB CD EABC4. 【2015江苏高考,22】如图,在四棱锥P ABCD -中,已知PA ⊥平面ABCD ,且四边形ABCD 为直角梯 形,2ABC BAD π∠=∠=,2,1PA AD AB BC ====(1)求平面PAB 与平面PCD 所成二面角的余弦值;(2)点Q 是线段BP 上的动点,当直线CQ 与DP 所成角最小时,求线段BQ 的长(4题图)G F BACDE(5题图)5 .【2015高考福建,理17】如图,在几何体ABCDE 中,四边形ABCD 是矩形,AB 平面BEC ,BEEC ,AB=BE=EC=2,G ,F 分别是线段BE ,DC 的中点.(Ⅰ)求证://GF 平面ADE ; (Ⅱ)求平面AEF 与平面BEC 所成锐二面角的余弦值.6.【2015高考浙江,理17】如图,在三棱柱111ABC A B C --中,90BAC ∠=,2AB AC ==,14A A =,1A 在底面ABC 的射影为BC 的中点,D 为11B C 的中点.(1)证明:1A D ⊥平面1A B C ;(2)求二面角1A -BD-1B 的平面角的余弦值.P A BCDQ(6题图)(7题图)7.【2015高考山东,理17】如图,在三棱台DEF ABC -中,2,,AB DE G H =分别为,AC BC 的中点. (Ⅰ)求证://BD 平面FGH ;(Ⅱ)若CF ⊥平面ABC ,,AB BC CF DE ⊥= ,45BAC ∠= ,求平面FGH 与平面ACFD 所成的角(锐角)的大小.8 .【2015高考天津,理17】 如图,在四棱柱1111ABCDA B C D 中,侧棱1A A ABCD ⊥底面,AB AC ⊥,1AB ,12,5ACAA AD CD ,且点M 和N 分别为11C D B D 和的中点.(I)求证://MN 平面ABCD ; (II)求二面角11D AC B 的正弦值;(III)设E 为棱11A B 上的点,若直线NE 和平面ABCD 所成角的正弦值为13,求线段1A E 的长NMC 1B 1A 1DABCD 1(8题图)题(19)图PCED BA(9题图)9.【2015高考重庆,理19】 如题(19)图,三棱锥P ABC -中,PC ⊥平面,3,.,2ABC PC ACB D E π=∠=分别为线段,AB BC 上的点,且2,2 2.CD DE CE EB ====(1)证明:DE ⊥平面PCD (2)求二面角A PD C --的余弦值。
高三数学立体几何历年高考题(2011年-2017年)完整版.doc
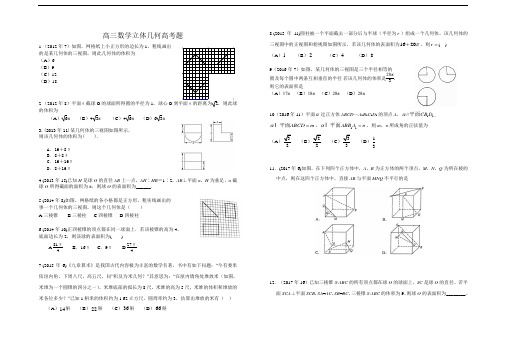
高三数学立体几何高考题1.(2012年7)如图,网格纸上小正方形的边长为1,粗线画出 的是某几何体的三视图,则此几何体的体积为 (A )6 (B )9 (C )12 (D )182.(2012年8)平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为2,则此球的体积为(A )6π (B )43π (C )46π (D )63π3.(2013年11)某几何体的三视图如图所示, 则该几何体的体积为( ).A .16+8πB .8+8πC .16+16πD .8+16π4.(2013年15)已知H 是球O 的直径AB 上一点,AH ∶HB =1∶2,AB ⊥平面α,H 为垂足,α截球O 所得截面的面积为π,则球O 的表面积为______.5.(2014年8)如图,网格纸的各小格都是正方形,粗实线画出的 事一个几何体的三视图,则这个几何体是( ) A.三棱锥 B.三棱柱 C.四棱锥 D.四棱柱6.(2014年10)正四棱锥的顶点都在同一球面上.若该棱锥的高为4, 底面边长为2,则该球的表面积为( )A.81π4 B .16π C .9π D.27π47.(2015年6)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问”积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,米堆的体积和堆放的米各位多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米有( ) (A )14斛 (B )22斛 (C )36斛 (D )66斛8.(2015年11)圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,若该几何体的表面积为1620π+,则r =( ) (A )1 (B )2 (C )4 (D )89(2016年7)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是28π3,则它的表面积是(A )17π (B )18π (C )20π (D )28π10(2016年11)平面α过正方体ABCD —A 1B 1C 1D 1的顶点A ,11//CB D α平面,ABCD m α=I 平面,11ABB A n α=I 平面,则m ,n 所成角的正弦值为(A )32 (B )22 (C )33 (D )1311.(2017年6)如图,在下列四个正方体中,A ,B 为正方体的两个顶点,M ,N ,Q 为所在棱的中点,则在这四个正方体中,直接AB 与平面MNQ 不平行的是12.(2017年16)已知三棱锥S-ABC 的所有顶点都在球O 的球面上,SC 是球O 的直径。
(完整版)高中数学立体几何大题(有答案)

1.(2014•山东)如图,四棱锥P﹣ABCD中,AP⊥平面PCD,AD∥BC,AB=BC=AD,E,F分别为线段AD,PC的中点.(Ⅰ)求证:AP∥平面BEF;(Ⅱ)求证:BE⊥平面PAC.解答:证明:(Ⅰ)连接CE,则∵AD∥BC,BC=AD,E为线段AD的中点,∴四边形ABCE是平行四边形,BCDE是平行四边形,设AC∩BE=O,连接OF,则O是AC的中点,∵F为线段PC的中点,∴PA∥OF,∵PA⊄平面BEF,OF⊂平面BEF,∴AP∥平面BEF;(Ⅱ)∵BCDE是平行四边形,∴BE∥CD,∵AP⊥平面PCD,CD⊂平面PCD,∴AP⊥CD,∴BE⊥AP,∵AB=BC,四边形ABCE是平行四边形,∴四边形ABCE是菱形,∴BE⊥AC,∵AP∩AC=A,∴BE⊥平面PAC.3.(2014•湖北)在四棱锥P﹣ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,E为PC中点,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,CD=2.(Ⅰ)求证:BE∥平面PAD;(Ⅱ)求证:BC⊥平面PBD;(Ⅲ)设Q为侧棱PC上一点,,试确定λ的值,使得二面角Q﹣BD﹣P为45°.解答:解:(Ⅰ)取PD的中点F,连接EF,AF,∵E为PC中点,∴EF∥CD,且,在梯形ABCD中,AB∥CD,AB=1,∴EF∥AB,EF=AB,∴四边形ABEF为平行四边形,∴BE∥AF,∵BE⊄平面PAD,AF⊂平面PAD,∴BE∥平面PAD.(4分)(Ⅱ)∵平面PCD⊥底面ABCD,PD⊥CD,∴PD⊥平面ABCD,∴PD⊥AD.(5分)如图,以D为原点建立空间直角坐标系D﹣xyz.则A(1,0,0),B(1,1,0),C(0,2,0),P(0,0,1).(6分),,∴,BC⊥DB,(8分)又由PD⊥平面ABCD,可得PD⊥BC,∴BC⊥平面PBD.(9分)(Ⅲ)由(Ⅱ)知,平面PBD的法向量为,(10分)∵,,且λ∈(0,1)∴Q(0,2λ,1﹣λ),(11分)设平面QBD的法向量为=(a,b,c),,,由,,得,∴,(12分)∴,(13分)因λ∈(0,1),解得.(14分)4.(2014•江苏)如图,在三棱锥P﹣ABC中,D,E,F分别为棱PC,AC,AB的中点,已知PA⊥AC,PA=6,BC=8,DF=5.求证:(1)直线PA∥平面DEF;(2)平面BDE⊥平面ABC.解答:证明:(1)∵D、E为PC、AC的中点,∴DE∥PA,又∵PA⊄平面DEF,DE⊂平面DEF,∴PA∥平面DEF;(2)∵D、E为PC、AC的中点,∴DE=PA=3;又∵E、F为AC、AB的中点,∴EF=BC=4;∴DE2+EF2=DF2,∴∠DEF=90°,∴DE⊥EF;∵DE∥PA,PA⊥AC,∴DE⊥AC;∵AC∩EF=E,∴DE⊥平面ABC;∵DE⊂平面BDE,∴平面BDE⊥平面ABC.13.(2012•江苏)如图,在直三棱柱ABC﹣A1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D 不同于点C),且AD⊥DE,F为B1C1的中点.求证:(1)平面ADE⊥平面BCC1B1;(2)直线A1F∥平面ADE.解答:解:(1)∵三棱柱ABC﹣A1B1C1是直三棱柱,∴CC1⊥平面ABC,∵AD⊂平面ABC,∴AD⊥CC1又∵AD⊥DE,DE、CC1是平面BCC1B1内的相交直线∴AD⊥平面BCC1B1,∵AD⊂平面ADE∴平面ADE⊥平面BCC1B1;(2)∵△A1B1C1中,A1B1=A1C1,F为B1C1的中点∴A1F⊥B1C1,∵CC1⊥平面A1B1C1,A1F⊂平面A1B1C1,∴A1F⊥CC1又∵B1C1、CC1是平面BCC1B1内的相交直线∴A1F⊥平面BCC1B1又∵AD⊥平面BCC1B1,∴A1F∥AD∵A1F⊄平面ADE,AD⊂平面ADE,∴直线A1F∥平面ADE.16.(2010•深圳模拟)如图,在四棱锥S﹣ABCD中,底面ABCD为正方形,侧棱S D⊥底面ABCD,E、F分别是AB、SC的中点(1)求证:EF∥平面SAD(2)设SD=2CD,求二面角A﹣EF﹣D的大小.解答:(1)如图,建立空间直角坐标系D﹣xyz.设A(a,0,0),S(0,0,b),则B(a,a,0),C(0,a,0),,.取SD的中点,则.平面SAD,EF⊄平面SAD,所以EF∥平面SAD.(2)不妨设A(1,0,0),则B(1,1,0),C(0,1,0),S(0,0,2),,.EF 中点,,,又,,所以向量和的夹角等于二面角A﹣EF﹣D的平面角..所以二面角A﹣EF﹣D的大小为.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015 年高考立体几何大题试卷
1.【 2015 高考新课标2,理 19】
如图,长方体ABCD A1B1C1D1中,AB=16,BC =10, AA18 ,点E,F分别在 A1 B1,C1D1上, A1 E D1F 4 .过点E,F的平面与此长方体的面相交,交线围成一个正方
形.
D F C
A E B
D C
A B ( 1 题图)
(Ⅰ)在图中画出这个正方形(不必说出画法和理由);
(Ⅱ)求直线AF 与平面所成角的正弦值.
2. 【 2015 江苏高考, 16】如图,在直三棱柱ABC A1 B1C1中,已知AC BC ,
BC CC1,设 AB1的中点为D, B1C BC1 E .求证:(1) DE // 平面 AA1C1C ;
(2)BC1AB1.
A C
B
E
D
A C
B ( 2 题图)(3 题图)
3. 【2015 高考安徽,理19】如图所示,在多面体A1 B1 D1 DCBA ,四边形 AA1B1 B ,
ADD A , ABCD 均为正方形, E 为 B D 的中点,过 A1 , D , E 的平面交CD于F.
1 1 1 1 1
(Ⅰ)证明:EF / / B1C ;(Ⅱ)求二面角 E A1 D B1余弦值.
4.【2015江苏高考,22】如图,在四棱锥P ABCD 中,已知 PA平面ABCD,且四边形 ABCD 为直角梯形,ABC BAD,PA AD 2, AB BC 12
( 1)求平面PAB与平面PCD所成二面角的余弦值;
( 2)点Q是线段BP上的动点,当直线CQ 与 DP 所成角最小时,求线段BQ 的长
A
P
D
Q
B F
A D G
B C E C
( 4 题图)( 5 题图)
5 .【 2015 高考福建,理 17】如图,在几何体 ABCDE 中,四边形 ABCD 是矩形, AB ^平
面 BEC, BE^ EC,AB=BE=EC=2 , G,F 分别是线段 BE, DC 的中点 .
( Ⅰ ) 求证:GF / /平面ADE;
( Ⅱ ) 求平面 AEF 与平面 BEC 所成锐二面角的余弦值.
6. 【 2015 高考浙江,理17】如图,在三棱柱ABC A1B1C1 - 中,BAC 90o,
AB AC 2 ,A1A 4 ,A1在底面ABC的射影为BC的中点, D 为B1C1的中点.
(1)证明:A1D平面A1B C;
(2)求二面角A1-BD- B1的平面角的余弦值.
( 6 题图)(7题图)
7. 【 2015 高考山东,理 17】如图,在三棱台DEF ABC 中,AB 2DE ,G , H 分别为AC, BC 的中点. (Ⅰ)求证: BD / / 平面 FGH ;
(Ⅱ)若 CF 平面 ABC ,AB BC, CF DE , BAC 45o , 求平面FGH与平面 ACFD 所成的角(锐角)的大小 .
8 . 【2015 高考天津,理17 】如图,在四棱柱ABCD - A1 B1C1D1中,侧棱
A1 A 底面 ABCD ,AB AC , AB =1 ,
AC = AA1 = 2, AD = CD =5 ,且点M和N分别为B1C和D1D的中点.
(I)求证: MN // 平面 ABCD ;
(II)求二面角 D1 - AC - B1的正弦值;
(III) 设E为棱A1B1上的点,若直线NE和平面ABCD所成角的正弦值为 1 ,求线段
3
A1 E 的长
D1 A1 P
B1
C1
N
M
C E
D A
D
B
A
C 题( 19 )图
题图)
( 8
9. 【 2015 高考重庆,理19】如题( 19)图,三棱锥P ABC 中,
ABC , PC 3, ACB.D , E 分别为线段 AB, BC 上的点,且
2
CD DE2, CE 2EB 2.
B
( 9 题图)PC平面
(1)证明:DE平面PCD(2)求二面角 A PD C 的余弦值。
10 . 【 2015 高考四川,理18】一个正方体的平面展开图及该正方体的直观图的示意图如图所示,在正方体中,设BC 的中点为 M , GH 的中点为 N
(1)请将字母F , G, H标记在正方体相应的顶点处(不需说明理由)
(2)证明:直线MN / /平面BDH
(3)求二面角A EG M的余弦值 .
(10 题图)
11 . 【2015 高考湖北,理19】《九章算术》中,将底面为长方形且有一条侧棱与底面
垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,在阳马 P ABCD 中,侧棱PD底面ABCD,且PD CD ,过棱 PC 的中点 E ,作EF PB 交PB 于点F,连接DE, DF , BD , BE .
(Ⅰ)证明:PB平面DEF.试判断四面体DBEF 是否为鳖臑,若是,写出其每个面
的直角(只需写
出结论);若不是,说明理由;
(Ⅱ)若面 DEF 与面ABCD所成二面角的大小为π
,求
DC
的值.3BC
( 11 题图)
12 .
【2015
高考陕西,理
18 1
,在直角梯形
CD
中,
D// C
, D
,
】如图
2 C
,
D 2
,是
D
的中点,是
C
与的交点.将沿折1
起到 1 的位置,如图 2 .
(I )证明:CD平面1 C ;
(II )若平面1平面CD,求平面1 C 与平面1CD夹角的余弦值.
13.【 2015 高考新课标 1,理 18】如图,,四边形ABCD为菱形,∠ABC=120°,E,F
是平面 ABCD同一侧的两点,BE⊥平面 ABCD, DF⊥平面 ABCD,BE=2 DF,AE⊥EC.
(Ⅰ )证明:平面AEC⊥平面 AFC;
(Ⅱ )求直线 AE 与直线 CF所成角的余弦值.
A
C
F
O
E
B
(13 题图)( 14 题图)
14.【 2015 高考北京,理 17】如图,在四棱锥 A EFCB 中,△ AEF 为等边三角形,平
面 AEF平面EFCB,EF∥BC,BC 4 , EF 2a ,EBC FCB 60 , O 为EF的中点.
( Ⅰ) 求证: AO BE ;(Ⅱ ) 求二面角F AE B 的余弦值;
( Ⅲ) 若BE平面AOC,求a的值.
15.【 2015 高考广东,理 18】如图,三角形PDC所在的平面与长方形ABCD所在的平
面垂直, PD = PC = 4 ,AB = 6 ,BC = 3 .点E是CD边的中点,点F、G分别在线段AB、
BC 上,且AF = 2FB,CG = 2GB.
(1)证明: PE FG ;(2)求二面角P - AD - C的正切值;
(3)求直线 PA 与直线 FG 所成角的余弦值.
P
D
E
C
G
A
F
B
( 15 题图) (16 题图)
图
16 。
2015 高考湖南,理 19 】如图,已知四棱台
ABCD A 1B 1C 1 D 1 上、下底面分别是
边长为 3 和 6 的正方形,1
6 ,且 AA 1 底面
ABCD ,点 P , Q 分别在棱 DD 1 ,
AA
BC 上 . (1)若 P 是 DD 1 的中点,证明: AB 1
PQ ; ( 2)若 PQ / / 平面 1 1
,
ABB A
二面角 P QD A 的余弦值为
3
,求四面体 ADPQ 的体积
7
17. 【2015 高考上海,理 19 】如图,在长方体CD 1 1C 1 D 1 中, 1 1 ,
D 2 , 、 F 分别是
、 C 的中点.证明
1 、 C 1 、 F 、 四点共面,并
求直线 CD 1 与平面
1
C 1F 所成的角的正弦值 .
(17 题图)。
