北京大学高等代数_I+2016+期中考试题+-+答案
高等代数(北大版第三版)习题答案I

高等代数(北大版第三版)习题答案I篇一:高等代数(北大版)第3章习题参考第三章线性方程组1.用消元法解以下线性方程组:?x1?x?1?1)?x1x1x13x25x34x413x22x32x42x2x3x4x54x2x3x4x52x2x3x4x5 x12x23x42x51x5??1?x1x23x3x43x523 2)2x?3x?4x?5x?2x?72345?139x9x6x16x2x252345?11x3?x7?0?3x1?4x2?5?x1?2x2?3x3?4x4?44x3?x2?0?x2?x3?x4??3?2x1?3x2?343)?4)?4x?11x?13x?16x?0x?3x??x?123424?1?17x?3x?x3?7x?2x?x?3x0234234??1?x1?2x2?3x3?x4?1?2x1?x2?x3?x4?1?3x1?2x2?x3?x4?13x1?2x2?2x3?3x4?25)? 6)?2x1?3x2?x3?x4?12x2x2xx15x1x2x32x4123412xxx3x4234?15x1?5x2?2x3?2解1)对方程组得增广矩阵作行初等变换,有111111000033?2?420000?1521112?3?20?1?4?2?11?1?1200101?1?11010001??110??30??3??01?011?200?0000030?5?7?10000?15?3?4?4?400?200423581200001?1?11010001?2?2? ?221?2?0? ?0?0由于rank(A)?rank(B)?4?5,因此方程组有无穷多解,其同解方程组为x1x412x1x52,?2x03x?x?0?24解得x1x2x3x4x51kk0k22k其中k为任意常数。
2)对方程组德增广矩阵作行初等变换,有112910 ??002?1?3?920?3463151632?3221??120?0725022?3?7?27120?346341110?2?5?2?1631?1 5161334512529?8?011??333033?2529??72?10??334?512529? 8001?1?3330000??01?由于rank(A)?4?rank(A)?3,因此原方程无解。
北京师大附中15—16学年高二(上)期中数学试卷(文科)附解析)

2015-2016学年北京师大附中高二(上)期中数学试卷(文科)一、选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.经过(﹣1,2)且与直线x+y﹣1=0垂直的直线是()A.x﹣y+1=0 B.x﹣y+3=0 C.x+y+1=0 D.x+y+3=02.已知两直线l1:(a﹣1)x﹣3y﹣10=0,l2:(a+1)x+y+3=0互相平行,则a=()A.﹣B.C.1 D.﹣13.关于直线a、b、l,以及平面α、β,下列命题中正确的是()A.若a∥α,b∥α,则a∥bB.若a∥α,b⊥a,则b⊥αC.若a⊂α,b⊂α,且l⊥a,l⊥b,则l⊥αD.若a⊥α,a∥β,则α⊥β4.若某空间几何体的三视图如图所示,则该几何体的体积是()A.B.C.D.15.下列说法中正确的是()A.在正三棱锥中,斜高大于侧棱B.有一条侧棱垂直于底面的棱柱是直棱柱C.底面是正方形的棱锥是正四棱锥D.有一个面是多边形,其余各面均为三角形的几何体是棱锥6.长方体ABCD﹣A′B′C′D′中,AB=AD=2,AA′=1,则它的外接球的体积是()A.B.36πC.9πD.π7.一条光线从点(﹣2,﹣3)射出,经y轴反射后经过圆(x+3)2+(y﹣2)2=1的圆心,则反射光线所在直线的斜率为()A.﹣1 B.1 C.D.﹣8.在正四面体P﹣ABC中,D,E,F分别是AB,BC,CA的中点,下面四个结论中不成立的是()A.BC∥平面PDF B.DF⊥平面PAEC.平面PDF⊥平面ABC D.平面PAE⊥平面ABC二、填空题:本大题共6小题,每小题5分,共30分.9.某圆锥的母线和底面半径分别为2,1,则此圆锥的体积是.10.已知某三棱锥的三视图是如图所示的三个直角三角形,那么这个三棱锥最小的一个表面的面积是.11.若直线3x﹣4y+5=0与圆x2+y2=r2(r>0)相交于A,B两点,且∠AOB=120°,(O为坐标原点),则r=.12.正三棱锥的底面边长为2,则经过高的中点且平行于底面的平面截该三棱锥所得的截面面积是.13.已知圆C1:(x﹣1)2+y2=1,圆C2:(x﹣3)2+(y﹣1)2=4,它们的位置关系是.14.如图所示,E是正方形ABCD所在平面外一点,E在面ABCD上的正投影F恰在AC 上,FG∥BC,AB=AE=2,∠EAB=60°.则以下结论中正确的有.(1)CD⊥面GEF.(2)AG=1.(3)以AC,AE作为邻边的平行四边形面积是8.(4)∠EAD=60°.三、解答题:本大题共3小题,共30分.15.如图,在正方体ABCD﹣A1B1C1D1中,E,F分别为棱AD,AB的中点.(1)求证:EF∥平面CB1D1;(2)求证:B1D1⊥平面CAA1C1.16.如图,在四棱锥P﹣ABCD中,四边形ABCD是矩形,平面PCD⊥平面ABCD,M为PC中点.求证:(1)PA∥平面MDB;(2)PD⊥BC.17.设P为直线l1:x﹣2y+4=0与直线l:2x﹣y﹣4=0的交点,圆C:x2+y2﹣4x﹣4y+7=0,l0为过点P且斜率为k的直线,(1)若k=,l0与圆C交于A,B两点,求|AB|;(2)k为何值时,l0与圆C相切?设切点分别为M,N,求cos∠MPN.四、填空题:本大题共3小题,每小题4分,共12分.18.命题p:“存在实数m,使方程x2+mx+1=0有实数根”,则“非p”形式的命题是.19.已知p:不等式ax2+2ax+1>0的解集为R;q:0<a<1.则p是q(充分,必要,充要)条件.20.已知椭圆C:=1(a>b>0)的长轴长为4.若以原点为圆心、椭圆短半轴长为半径的圆与直线y=x+2相切,则椭圆的离心率为.五、解答题:本大题共3小题,共38分.21.已知p:{x|x2﹣8x﹣20≤0};q:{x|x2﹣2x﹣(m2﹣1)≤0,m>0},若非p是非q的必要不充分条件,求实数m的取值范围.22.已知方程x2+y2﹣6x+2y+m=0.(1)若此方程表示圆,求实数m的取值范围;(2)若已知(1)中的圆与直线x+2y﹣2=0相交于A,B两点,并且以线段AB为直径的圆经过坐标原点O,求此时m的值.23.点A、B分别是椭圆+=1长轴的左、右顶点,点F是椭圆的右焦点.点P在椭圆上,且位于x轴上方,PA⊥PF.(1)求P点的坐标;(2)设M是椭圆长轴AB上的一点,M到直线AP的距离等于|MB|,求椭圆上的点到点M 的距离d的最小值.2015-2016学年北京师大附中高二(上)期中数学试卷(文科)参考答案与试题解析一、选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.经过(﹣1,2)且与直线x+y﹣1=0垂直的直线是()A.x﹣y+1=0 B.x﹣y+3=0 C.x+y+1=0 D.x+y+3=0【考点】直线的一般式方程与直线的垂直关系.【专题】方程思想;综合法;直线与圆.【分析】由题意和垂直关系可得直线的斜率,可得点斜式方程,化为一般式即可.【解答】解:∵直线x+y﹣1=0的斜率为﹣1,∴所求垂线的斜率为1,∴方程为y﹣2=x﹣(﹣1),∴x﹣y+3=0,故选:B.【点评】本题考查直线的一般式方程和垂直关系,属基础题.2.已知两直线l1:(a﹣1)x﹣3y﹣10=0,l2:(a+1)x+y+3=0互相平行,则a=()A.﹣B.C.1 D.﹣1【考点】直线的一般式方程与直线的平行关系.【专题】方程思想;综合法;直线与圆.【分析】由直线平行可得a﹣1﹣(﹣3)(a+1)=0,解方程排除重合即可.【解答】解:∵两直线l1:(a﹣1)x﹣3y﹣10=0,l2:(a+1)x+y+3=0互相平行,∴a﹣1﹣(﹣3)(a+1)=0,解得a=,经验证当a=﹣时,两直线平行.故选:A.【点评】本题考查直线的一般式方程和平行关系,属基础题.3.关于直线a、b、l,以及平面α、β,下列命题中正确的是()A.若a∥α,b∥α,则a∥bB.若a∥α,b⊥a,则b⊥αC.若a⊂α,b⊂α,且l⊥a,l⊥b,则l⊥αD.若a⊥α,a∥β,则α⊥β【考点】平面与平面垂直的判定.【分析】利用正方体模型,举出A、B、C三项的反例,得出A、B、C三项均为假命题,通过排除法可得D选项为正确答案.【解答】解:以正方体为例对于A选项,设下底面ABCD为平面α,在上底面A1D1所在直线为a,B1D1所在直线为b,直线a、b都平行于平面α,但直线a、b不平行,故A项不对(如图1)对于B选项,设下底面ABCD为平面α,上底面A1C1所在直线为a,B1D1所在直线为b,直线a是平面α的平行线,直线b与a垂直,但直线b与平面α不垂直,故B选项不对(如图2)对于C选项,设下底面ABCD为平面α,直线AB、CD所在直线分别为a、b,AD1所在直线为l.可见直线a、b是平面α内的平行线,虽然直线a、b都与直线l垂直,但直线l与平面α不垂直,故C选项不对(如图3)由A、B、C都不对,得应该选择D选项.故答案为D【点评】判断空间直线与平面的位置关系时,常常借助于空间几何体如长方体、正方体、三棱锥等,结合立体几何的定理或推论解决问题.4.若某空间几何体的三视图如图所示,则该几何体的体积是()A.B.C.D.1【考点】由三视图求面积、体积.【专题】计算题;空间位置关系与距离.【分析】由三视图知几何体为直三棱柱,且三棱柱的高为,底面是直角边长分别为1,的直角三角形,代入体积公式计算可得答案.【解答】解:由三视图知几何体为直三棱柱,且三棱柱的高为,底面是直角边长分别为1,的直角三角形,∴三棱柱的体积V==1.故选:D.【点评】本题考查了由三视图求几何体的体积,解题的关键是判断几何体的形状及数据所对应的几何量.5.下列说法中正确的是()A.在正三棱锥中,斜高大于侧棱B.有一条侧棱垂直于底面的棱柱是直棱柱C.底面是正方形的棱锥是正四棱锥D.有一个面是多边形,其余各面均为三角形的几何体是棱锥【考点】命题的真假判断与应用.【专题】阅读型;对应思想;分析法;简易逻辑.【分析】由多面体的结构特征逐一核对四个选项得答案.【解答】解:在正三棱锥中,斜高为直角三角形的直角边,侧棱为同一个直角三角形的斜边,∴斜高小于侧棱,A错误;由直棱柱的定义可知,有一条侧棱垂直于底面的棱柱是直棱柱,B正确;底面是正方形的棱锥是正四棱锥错误,还需满足顶点在底面的射影为底面的中心;有一个面是多边形,其余各面均为三角形的几何体是棱锥错误,还需满足三角形由公共顶点.故选:B.【点评】本题考查命题的真假判断与应用,考查了多面体的结构特征,是基础题.6.长方体ABCD﹣A′B′C′D′中,AB=AD=2,AA′=1,则它的外接球的体积是()A.B.36πC.9πD.π【考点】球的体积和表面积;球内接多面体.【专题】计算题;空间位置关系与距离;立体几何.【分析】由已知求出外接球半径,代入球的体积公式,可得答案.【解答】解:∵长方体ABCD﹣A′B′C′D′中,AB=AD=2,AA′=1,∴它的外接球的半径R满足:2R==3,即R=,故它的外接球的体积V==,故选:A【点评】本题考查的知识点是球的体积,球内接多面体,计算出球的半径是解答的关键.7.一条光线从点(﹣2,﹣3)射出,经y轴反射后经过圆(x+3)2+(y﹣2)2=1的圆心,则反射光线所在直线的斜率为()A.﹣1 B.1 C.D.﹣【考点】直线与圆的位置关系.【专题】计算题;规律型;数形结合;直线与圆.【分析】由题意可得反射光线所在的直线经过圆心M(﹣3,2),点P(﹣2,﹣3)关于x 轴的对称点Q(2,﹣3)在反射光线所在的直线上,用斜率公式求解即可.【解答】解:由题意可得反射光线所在的直线经过圆:(x+3)2+(y﹣2)2=1的圆心M(﹣3,2),由反射定律可得点P(﹣2,﹣3)关于y轴的对称点Q(2,﹣3)在反射光线所在的直线上,根据M、Q两点的坐标,所求直线的斜率为:=﹣1.故选:A.【点评】本题主要考查用两点式求直线方程,判断反射光线所在的直线经过圆心M(﹣3,2),是解题的突破口.8.在正四面体P﹣ABC中,D,E,F分别是AB,BC,CA的中点,下面四个结论中不成立的是()A.BC∥平面PDF B.DF⊥平面PAEC.平面PDF⊥平面ABC D.平面PAE⊥平面ABC【考点】平面与平面垂直的判定;直线与平面平行的判定;直线与平面垂直的判定.【专题】计算题;压轴题.【分析】正四面体P﹣ABC即正三棱锥P﹣ABC,所以其四个面都是正三角形,在正三角形中,联系选项B、C、D中有证明到垂直关系,应该联想到“三线合一”.D,E,F分别是AB,BC,CA的中点,由中位线定理可得BC∥DF,所以BC∥平面PDF,进而可得答案.【解答】解:由DF∥BC可得BC∥平面PDF,故A正确.若PO⊥平面ABC,垂足为O,则O在AE上,则DF⊥PO,又DF⊥AE故DF⊥平面PAE,故B正确.由DF⊥平面PAE可得,平面PAE⊥平面ABC,故D正确.故选C.【点评】本小题考查空间中的线面关系,正三角形中“三线合一”,中位线定理等基础知识,考查空间想象能力和思维能力.二、填空题:本大题共6小题,每小题5分,共30分.9.某圆锥的母线和底面半径分别为2,1,则此圆锥的体积是.【考点】棱柱、棱锥、棱台的体积.【专题】计算题;数形结合;函数思想;空间位置关系与距离.【分析】根据圆锥的定义与性质,算出圆锥的高h,再由圆锥的体积公式即可算出此圆锥的体积.【解答】解:∵圆锥的母线长l=52,底面圆的半径r=1,∴圆锥的高h=,因此,圆锥的体积为V=πr2h=π×12×=.故答案为:.【点评】本题给出圆锥的母线长和底面圆的半径,求此圆锥的体积.着重考查了圆锥的定义与性质、圆锥的体积公式等知识,属于基础题.10.已知某三棱锥的三视图是如图所示的三个直角三角形,那么这个三棱锥最小的一个表面的面积是6.【考点】由三视图求面积、体积.【专题】计算题;数形结合;综合法;空间位置关系与距离.【分析】根据三视图还原成原图为四个面都是直角三角形的四面体,然后求出四个面的面积,找出最小面积【解答】解:由三视图可知,该几何体的四个面都是直角三角形的四面体(如图所示),则S ABD=×4×5=10,S ABC=×3×5=7.5,S BCD=×4×3=6,且AD>51,AC>5,CD=5,∴S ACD>S BCD,∴面积最小为6.故答案为:6.【点评】本题考查了由三视图还原成原图,要注意还原前后数量的对应关系,考查了空间想象能力,属于基本题型,难度不大11.若直线3x﹣4y+5=0与圆x2+y2=r2(r>0)相交于A,B两点,且∠AOB=120°,(O为坐标原点),则r=2.【考点】直线与圆相交的性质.【专题】直线与圆.【分析】若直线3x﹣4y+5=0与圆x2+y2=r2(r>0)交于A、B两点,∠AOB=120°,则△AOB为顶角为120°的等腰三角形,顶点(圆心)到直线3x﹣4y+5=0的距离d=r,代入点到直线距离公式,可构造关于r的方程,解方程可得答案.【解答】解:若直线3x﹣4y+5=0与圆x2+y2=r2(r>0)交于A、B两点,O为坐标原点,且∠AOB=120°,则圆心(0,0)到直线3x﹣4y+5=0的距离d=rcos=r,即=r,解得r=2,故答案为:2.【点评】本题考查的知识点是直线与圆相交的性质,其中分析出圆心(0,0)到直线3x﹣4y+5=0的距离d=r是解答的关键.12.正三棱锥的底面边长为2,则经过高的中点且平行于底面的平面截该三棱锥所得的截面面积是.【考点】平面的基本性质及推论.【专题】计算题;转化思想;综合法;空间位置关系与距离.【分析】先求出正三棱锥的底面面积,再由经过高的中点且平行于底面的平面与底面相似,且相似比为,能求出结果.【解答】解:∵正三棱锥的底面边长为2,∴正三棱锥的底面面积S==,∵经过高的中点且平行于底面的平面与底面相似,且相似比为,∴经过高的中点且平行于底面的平面截该三棱锥所得的截面面积S′==.故答案为:.【点评】本题考查三棱锥中截面面积的求法,是基础题,解题时要认真审题,注意正三棱锥的结构特征的合理运用.13.已知圆C1:(x﹣1)2+y2=1,圆C2:(x﹣3)2+(y﹣1)2=4,它们的位置关系是相交.【考点】圆与圆的位置关系及其判定.【专题】计算题;数形结合;直线与圆.【分析】根据两圆的圆心距大于两圆的半径之和,可得两圆的位置关系.【解答】解:由题意可得,两圆的圆心距C1C2==∈[1,3],即两圆的圆心距大于两圆的半径之差,小于半径和,故两圆相交,故答案为:相交.【点评】本题主要考查圆的标准方程,两个圆的位置关系的判定方法,属于中档题.14.如图所示,E是正方形ABCD所在平面外一点,E在面ABCD上的正投影F恰在AC 上,FG∥BC,AB=AE=2,∠EAB=60°.则以下结论中正确的有(1)(2)(4).(1)CD⊥面GEF.(2)AG=1.(3)以AC,AE作为邻边的平行四边形面积是8.(4)∠EAD=60°.【考点】直线与平面垂直的判定.【专题】计算题;转化思想;综合法;空间位置关系与距离.【分析】由已知推导出FG⊥AB,CD⊥GF,EF⊥CD从而得到CD⊥平面GEF;由已知得AB=AE=BE=BC=AC=2,AF=BF=CF,从而得到AG=BG=1,以AC,AE作为邻边的平行四边形面积是4,∠EAD=∠EAB=60°.【解答】解:在(1)中,∵E是正方形ABCD所在平面外一点,FG∥BC,∴BC⊥AB,∴FG⊥AB,∵AB∥CD,∴CD⊥GF,∵E在面ABCD上的正投影F恰在AC上,∴EF⊥平面ABCD,∴EF⊥CD,∵EF∩GF=F,∴CD⊥平面GEF,故(1)正确;在(2)中,∵AB=AE=2,∠EAB=60°,∴AB=AE=BE=BC=AC=2,∴AF=BF=CF,∵FG∥BC,∴AG=BG=1,故(2)正确;在(3)中,∵由(2)得AF=CF=EF=,∴=2,∴以AC,AE作为邻边的平行四边形面积是4,故(3)错误;在(4)中,由(2)得∠EAD=∠EAB=60°,故(4)正确.故答案为:(1)(2)(4).【点评】本题考查命题真假的判断,是基础题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.三、解答题:本大题共3小题,共30分.15.如图,在正方体ABCD﹣A1B1C1D1中,E,F分别为棱AD,AB的中点.(1)求证:EF∥平面CB1D1;(2)求证:B1D1⊥平面CAA1C1.【考点】直线与平面垂直的判定;直线与平面平行的判定.【专题】证明题;数形结合;分析法;空间位置关系与距离.【分析】(1)欲证EF∥平面CB1D1,根据直线与平面平行的判定定理可知只需证EF与平面CB1D1内一直线平行,连接BD,根据中位线可知EF∥BD,则EF∥B1D1,又B1D1⊂平面CB1D1,EF⊄平面CB1D1,满足定理所需条件;(2)欲证平面CAA1C1⊥平面CB1D1,根据面面垂直的判定定理可知在平面CB1D1内一直线与平面CAA1C1垂直,而AA1⊥平面A1B1C1D1,B1D1⊂平面A1B1C1D1,则AA1⊥B1D1,A1C1⊥B1D1,满足线面垂直的判定定理则B1D1⊥平面CAA1C1.【解答】(本题满分为12分)证明:(1)连接BD,因为正方体,所以BB1∥DD1,所以四边形BDD1B1为平行四边形,所以BD∥B1D1,因为EF∥BD,由平行线传递性得:EF∥B1D1,因为B1D1⊄面CB1D1,EF⊂面CB1D1,所以EF∥平面CB1D1.(6分)(2)因为在正方体中,AA1⊥平面A1B1C1D1,而B1D1⊂平面A1B1C1D1,所以AA1⊥B1D1.(10分)又因为在正方形A1B1C1D1中,A1C1⊥B1D1,所以B1D1⊥平面CAA1C1.(12分)【点评】本题主要考查线面平行的判定定理和线面垂直的判定定理.考查对基础知识的综合应用能力和基本定理的掌握能力,考查了空间想象能力和推理论证能力,属于中档题.16.如图,在四棱锥P﹣ABCD中,四边形ABCD是矩形,平面PCD⊥平面ABCD,M为PC中点.求证:(1)PA∥平面MDB;(2)PD⊥BC.【考点】直线与平面平行的判定.【专题】空间位置关系与距离.【分析】(1)连接AC,交BD与点O,连接OM,先证明出MO∥PA,进而根据线面平行的判定定理证明出PA∥平面MDB.(2)先证明出BC⊥平面PCD,进而根据线面垂直的性质证明出BC⊥PD.【解答】证明:(1)连接AC,交BD与点O,连接OM,∵M为PC的中点,O为AC的中点,∴MO∥PA,∵MO⊂平面MDB,PA⊄平面MDB,∴PA∥平面MDB.(2)∵平面PCD⊥平面ABCD,平面PCD∩平面ABCD=CD,BC⊂平面ABCD,BC⊥CD,∴BC⊥平面PCD,∵PD⊂平面PCD,∴BC⊥PD.【点评】本题主要考查了线面平行的判定和线面垂直的判定.判定的关键是先找到到线线平行,线线垂直.17.设P为直线l1:x﹣2y+4=0与直线l:2x﹣y﹣4=0的交点,圆C:x2+y2﹣4x﹣4y+7=0,l0为过点P且斜率为k的直线,(1)若k=,l0与圆C交于A,B两点,求|AB|;(2)k为何值时,l0与圆C相切?设切点分别为M,N,求cos∠MPN.【考点】圆的切线方程.【专题】综合题;数形结合;待定系数法;直线与圆.【分析】(1)联立直线方程可解得P(4,4)可得l0的方程,又可得圆C的圆心为(2,2),半径为1,可得圆心C到直线l0的距离d,由勾股定理可得;(2)由相切可得k的方程,解方程可得k值,由三角函数的定义可得sin∠MPC,由二倍角公式可得cos∠MPN.【解答】解:(1)联立可解得P(4,4),当k=时,l0的方程为y﹣4=(x﹣4),即3x﹣2y﹣4=0,配方可得圆C:x2+y2﹣4x﹣4y+7=0的方程为(x﹣2)2+(y﹣2)2=1,故圆C的圆心为(2,2),半径为1,∴圆心C到直线l0的距离d==,∴|AB|=2=;(2)l0的方程为y﹣4=k(x﹣4),即kx﹣y+4﹣4k=0,由相切可得圆心C到直线l0的距离d==1,平方并整理可得3k2﹣8k+3=0,解得k=,∵sin∠MPC===,∴cos∠MPN=cos2∠MPC=1﹣2sin2∠MPC=1﹣2×=.【点评】本题考查圆的切线方程,涉及圆的弦长和点到直线的距离以及二倍角的余弦公式,属中档题.四、填空题:本大题共3小题,每小题4分,共12分.18.命题p:“存在实数m,使方程x2+mx+1=0有实数根”,则“非p”形式的命题是对任意实数m,方程x2+mx+1=0没有实数根.【考点】复合命题的真假.【专题】规律型.【分析】根据命题的否定可知,存在的否定词为任意,再根据非p进行求解即可.【解答】解:∵p:存在实数m,使方程x2+mx+1=0有实数根,存在的否定词为任意,∴非p形式的命题是:对任意实数m,方程x2+mx+1=0没有实数根,故答案为:对任意实数m,方程x2+mx+1=0没有实数根.【点评】此题主要考查命题的否定,此题是一道基础题.19.已知p:不等式ax2+2ax+1>0的解集为R;q:0<a<1.则p是q必要(充分,必要,充要)条件.【考点】必要条件、充分条件与充要条件的判断.【专题】函数思想;综合法;简易逻辑.【分析】结合二次函数的性质求出a的范围,再由集合的包含关系判断即可.【解答】解:若不等式ax2+2ax+1>0的解集为R,a=0时:1>0,成立,a≠0时:△=4a2﹣4a<0,解得:0<a<1,综上,p:0≤a<1;q:0<a<1,故答案为:必要.【点评】本题考查了充分必要条件,考查二次函数的性质,是一道基础题.20.已知椭圆C:=1(a>b>0)的长轴长为4.若以原点为圆心、椭圆短半轴长为半径的圆与直线y=x+2相切,则椭圆的离心率为.【考点】椭圆的简单性质.【专题】计算题;方程思想;数学模型法;圆锥曲线的定义、性质与方程.【分析】由题意列式求出b,再由椭圆的长轴的长为4求得a,结合隐含条件求出c,则椭圆的离心率可求.【解答】解:由以原点为圆心、椭圆短半轴长为半径的圆与直线y=x+2相切,得b=.又∵2a=4,∴a=2,∴c2=a2﹣b2=2,即c=.∴e=.故答案为:.【点评】本题主要考查了椭圆的标准方程,涉及了椭圆与直线的位置关系,以及点到直线的距离公式,是基础题.五、解答题:本大题共3小题,共38分.21.已知p:{x|x2﹣8x﹣20≤0};q:{x|x2﹣2x﹣(m2﹣1)≤0,m>0},若非p是非q的必要不充分条件,求实数m的取值范围.【考点】必要条件、充分条件与充要条件的判断.【专题】简易逻辑.【分析】结合¬P和¬q的关系,得到不等式组,解出即可.【解答】解:解法一:非p:A={x|x<﹣2或x>10},非q:B={x|x<1﹣m或x>1+m,m>0}.∵非p是非q的必要不充分条件,∴非p推不出非q,非q⇒非p,∴B A,结合数轴分析知,B A的充要条件是:或,解得m≥9,即m的取值范围是m≥9.解法二:∵非p是非q的必要不充分条件,即p是q的充分不必要条件.而p:M={x|﹣2≤x≤10},q:N={x|1﹣m≤x≤1+m,m>0},∴M N,结合数轴分析知,M N的充要条件是:或,解得m≥9,∴m的取值范围是m≥9.【点评】本题考查了充分必要条件,是一道基础题.22.已知方程x2+y2﹣6x+2y+m=0.(1)若此方程表示圆,求实数m的取值范围;(2)若已知(1)中的圆与直线x+2y﹣2=0相交于A,B两点,并且以线段AB为直径的圆经过坐标原点O,求此时m的值.【考点】直线与圆的位置关系.【专题】综合题;转化思想;综合法;直线与圆.【分析】(1)方程表示圆的时候有D2+E2﹣4F>0,代入计算,即可求实数m的取值范围;(2)以线段AB为直径的圆经过坐标原点O得x1x2+y1y2=0,利用根系关系,可得结论.【解答】解:(1)方程x2+y2﹣6x+2y+m=0,由圆的一般方程知识得D=﹣6,E=2,F=m当此方程表示圆的时候有D2+E2﹣4F>0解之得m<10.(2)联立直线和圆的方程,消去x并化简整理得5y2+6y+m﹣8=0设题中直线与圆的交点为A(x1,y1),B(x2,y2),则在上述方程判别式△>0的前提下,由根系关系得到y1+y2=﹣,y1y2=.再由x=2﹣2y可得x1+x2=,x1x2=由以线段AB为直径的圆经过坐标原点O得x1x2+y1y2=0即+=0,解之得m=﹣.验证此时△>0成立.【点评】本题考查圆的方程,考查直线与圆的位置关系,考查根系关系,考查学生分析解决问题的能力,属于中档题.23.点A、B分别是椭圆+=1长轴的左、右顶点,点F是椭圆的右焦点.点P在椭圆上,且位于x轴上方,PA⊥PF.(1)求P点的坐标;(2)设M是椭圆长轴AB上的一点,M到直线AP的距离等于|MB|,求椭圆上的点到点M 的距离d的最小值.【考点】椭圆的简单性质;点到直线的距离公式;椭圆的应用.【专题】计算题.【分析】(1)先求出PA、F的坐标,设出P的坐标,求出、的坐标,由题意可得,且y>0,解方程组求得点P的坐标.(2)求出直线AP的方程,设点M的坐标,由M到直线AP的距离等于|MB|,求出点M 的坐标,再求出椭圆上的点到点M的距离d的平方得解析式,配方求得最小值.【解答】解:(1)由已知可得点A(﹣6,0),F(4,0),设点P(x,y),则=(x+6,y),=(x﹣4,y).由已知可得,2x2+9x﹣18=0,解得x=,或x=﹣6.由于y>0,只能x=,于是y=.∴点P的坐标是(,).(2)直线AP的方程是,即x﹣y+6=0.设点M(m,0),则M到直线AP的距离是.于是=|6﹣m|,又﹣6≤m≤6,解得m=2,故点M(2,0).设椭圆上的点(x,y)到点M的距离为d,有d2=(x﹣2)2+y2 =x2﹣4x+4+20﹣x2 =(x﹣)2+15,∴当x=时,d取得最小值.【点评】本题考查椭圆的简单性质和点到直线的距离公式,两个向量垂直的性质,求出点M 的坐标,是解题的难点.。
2016《高等代数(一)》期中考试试题
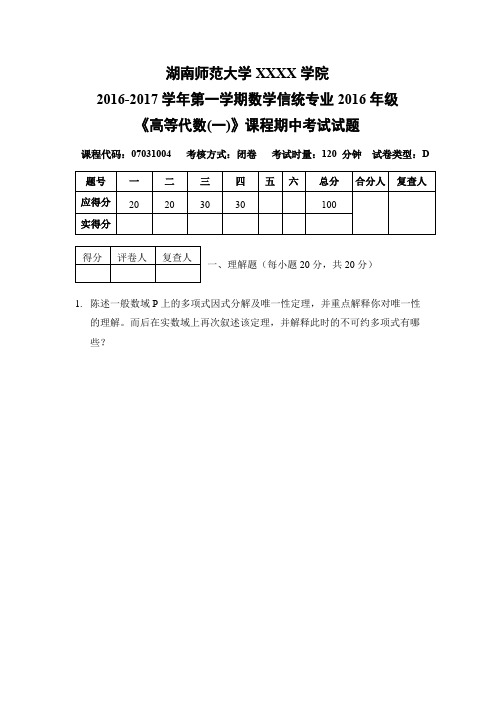
2016-2017学年第一学期数学信统专业2016年级
《高等代数(一)》课程期中考试试题
课程代码:07031004考核方式:闭卷考试时量:120分钟试卷类型:D
题号一二三四 Nhomakorabea五
六
总分
合分人
复查人
应得分
20
20
30
30
100
实得分
得分
评卷人
复查人
一、理解题(每小题20分,共20分)
1.陈述一般数域P上的多项式因式分解及唯一性定理,并重点解释你对唯一性的理解。而后在实数域上再次叙述该定理,并解释此时的不可约多项式有哪些?
得分
评卷人
复查人
二、简答题(下面两题:要求先回答‘对’或‘错’;如果回答‘错’,请给出反举例,如果回答‘对’则简单给出理由。每小题10分,共20分)
1.有人说:对于有理数域上的两个多项式 和 ,它们在有理数域上的最大公因式与它们在实数域上的最大公因式是相等的。这种说法对吗?为什么?
解:
2.有人说:3级行列式
为零的充分必要条件是 这3个数中至少有两个相等。这种说法对吗?为什么?
解:
得分
评卷人
复查人
三、计算题(每小题15分,共30分)
1.在有理数域上将多项式
分解为不可约多项式的乘积。
解:
2.设 ,计算下面 级行列式
解:
得分
评卷人
复查人
四、证明题(每小题15分,共30分)
1.设整数 两两不同,以及整系数多项式 ,证明:
; 如果 , ,一定有 。
证:
2.设两个 级行列式
,
证明:当 时,有 。
证:
高等代数习题北大第四版答案一到四章

从 而 ( f ( x), g( x))h( x) 是 f (x)h(x) 与 g( x)h( x) 的 一 个 最 大 公 因 式 , 又 因 为
( f (x), g( x)) h( x) 的首项系数为1,所以 ( f (x)h(x), g(x)h(x)) = ( f ( x), g( x))h( x) 。
u1(x) f (x) + v1(x)g (x) = 1
(1)
u2 (x) f (x) + v2 (x)h(x) = 1
将(1)(2)两式相乘,得
(2)
[u1(x)u2(x) f (x) + v1(x)u2(x)g (x) + u1(x)v2(x)h(x)] f ( x) , +[v1(x)v2 (x)]g( x)h( x) = 1 所以 ( f ( x), g( x) h( x)) =1 。
即[u(x) − v(x)] f ( x) + v( x)[ f ( x) + g( x)] = 1 ,
所以 ( f (x), f ( x) + g( x)) =1。
同理 ( g( x), f ( x) + g( x)) =1 。
再由 12 题结论,即证 ( f ( x) g( x), f ( x) + g( x)) =1。
2) f (x) = x3 − x2 − x, g( x) = x −1 + 2i 。
q(x) = 2x4 − 6x3 +13x2 − 39x +109
解 1)
;
r (x) = −327
2) q(x) = x2 − 2ix − (5 + 2i ) 。 r (x) = −9 + 8i
高等代数北大编第1章习题参考答案

第一章多项式一、习题及参考解答1 .用g(x)除了(x),求商g(x)与余式r(x):1 ) f (x) = x3 - 3x2 - x -1, g(x) = 3x2 - 2x +1;2 ) f(x) = x4 -2x + 5,g(x) = x2 - x + 2。
解1)由带余除法,可得q(x) =L-Z,“x) =-竺x-2 ;2)同理可得g(x) = / +x-l,r(x) = -5x + 7。
2. 〃?,PM适合什么条件时,有1 ) X2 +/?1¥-1 I X3 + px + c/ 92) x2 + nix + 11 x4 + px2 +q。
解1 )由假设,所得余式为0,即(〃 + l + 〃?2)x + (q-〃?) = O,所以当 1 + 。
时有 /+〃a-11 X* + px +g 0q _ in = 0 .2)类似可得= 于是当〃? = 0时,代入(2)可得〃=夕+ 1;q + 1 —〃一" = 0而当2- 〃 -J = 0时,代入(2)可得4 = 1 04 = ] _, 时,皆有 / + + 1 I X,+ px2 + 9。
综上所诉,当p + nr = 23 .求g(x)除f(x)的商q(x)与余式:1 ) /(x) = 2«?-5x3-8x,g(x) = x + 3 ;2) f(x) = x3-x2 - xg(x) = x-l + 2i o解[)q(x) = 2x4 - 6x3 +13x2 - 39A+ 109 ,r(x) = -327 '2)= x2 -2LV-(5+2/)r(x) = -9 + 8/ °4 .把/1(X)表示成x-%的方幕和,即表成c()+ G(X —“0)+。
2(X — X。
)~ + …+ C n(X — X。
)” + …的形式:1)/(x) = x',x()= 1 ;2) /(X)= X4-2X2+3,X0 =-2 ;3) f (x) = x4 + 2汉3 -(1 + i)x2 -3x + 7 + i,x0 =-i o解 1 ) 由综合除法,可得f(x) = l + 5(x-l) + 10(x-l)2 + 10(x-1)3+5(X-1)4 + (x-1)5 ;2 ) 由综合除法,可得X4-2X2+3=11-24(X + 2) + 22* + 2)2 -8(.r + 2)3 + (x + 2),;3)由综合除法,可得『+2立3_(1 +82_3工+ (7 +,)= (7 + 5i)-5(x + i) + (-l-i)(x + i)2 -2i(x + i)3 + (x + i),。
(完整版)高等代数(北大版第三版)习题答案II

高等代数(北大*第三版)答案目录第一章多项式第二章行列式第三章线性方程组第四章矩阵第五章二次型第六章线性空间第七章线性变换第八章 —矩阵第九章欧氏空间第十章双线性函数与辛空间注:答案分三部分,该为第二部分,其他请搜索,谢谢!12.设A 为一个n 级实对称矩阵,且0<A ,证明:必存在实n 维向量0≠X ,使0<'A X X 。
证 因为0<A ,于是0≠A ,所以()n A rank =,且A 不是正定矩阵。
故必存在非退化线性替换Y C X 1-=使()BY Y ACY CY AX X '=''='-12222122221n p p p y y y y y y ----+++=++ΛΛ,且在规范形中必含带负号的平方项。
于是只要在Y C Z 1-=中,令p y y y ===Λ21,1,021=====++n p p y y y Λ则可得一线性方程组⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=+++=+++=+++=++++++11002211,122,111,122111212111n nn n n n n p p p n pn p p n n x c x c x c x c x c x c x c x c x c x c x c x c ΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛΛ,由于0≠C ,故可得唯一组非零解()ns s s s x x x X ,,,21Λ=使()0111000<--=----+++='p n AX X s sΛΛ, 即证存在0≠X ,使0<'A X X 。
13.如果B A ,都是n 阶正定矩阵,证明:B A +也是正定矩阵。
证 因为B A ,为正定矩阵,所以BX X AX X '',为正定二次型,且 0>'A X X , 0>'B X X ,因此()0>'+'=+'BX X AX X X B A X , 于是()X B A X +'必为正定二次型,从而B A +为正定矩阵。
人大附中2016级高一上期中必修1模块及二卷试题答案

2016~2017学年度第一学期高一年级期中数学练习& 必修1模块考核试卷答案2016年11月6 日说明:本试卷分Ⅰ卷和Ⅱ卷,Ⅰ卷17道题,共100分,作为模块成绩;Ⅱ卷7道题,共50分;Ⅰ卷、Ⅱ卷共24题,合计150分,作为期中成绩;考试时间120分钟;请在密封线内填写个人信息.第Ⅰ卷 (共17题,满分100分)一、选择题(共8个小题,每小题5分,共40分,在每道小题给出的四个备选答案中,只有一个是符合题目要求的,请把所选答案前的字母按规定要求填涂在“机读答题卡”的相应位置上.)1.已知集合{}2|21,M y y x x x R ==−−∈,{}|14P x x =−≤≤,则M 与P 满足( )A .M P =B .M P ⊆C .P M ⊆D .P M =∅ 2.下列各组函数中,()f x 与()g x 表示同一函数的是( )A.2()f x =,()g x =B .()f x x =,2()x g x x=C .||()x f x x=,()1g x = D .()f x x =,()g x =3.下列函数中,在区间(0,1)上是增函数的是( ) A .3y x =− B .1y x=C .24y x =−+D .||y x = 4.已知函数()f x 的图象是两条线段(如图,不含端点),则1[()]3f f =( )A .13−B .13C .23−D .235.在下列区间中,函数()43x f x e x =+−(其中 2.71828e = )的零点所在的区间为( )A.1(,0)4− B.1(0,)2 C.1(,1)2D.(1,2) 6.设13log 2a =,2log 3b =,0.31()2c =,则( )A .a b c <<B .a c b <<C .b c a <<D .b a c <<7.已知二次函数2()4f x x ax =−+,若(1)f x +是偶函数,则实数a 的值为( ) A .1− B .1 C .2− D .28.若函数()(1) (01)x x f x k a a a a −=−−>≠且在R 上既是奇函数,又是减函数,则函数()log ()a g x x k =+的图象是 ( )二、填空题(本大题共6小题,每小题5分,共30分.请把结果填在答题纸中.)9. 若指数函数x y a =的图像经过点(2,4),则a 的值是 ; 10.若集合{}|2Ax x =≤,{}|B x x a =≥满足{}2A B = ,则实数a = ; 11.计算:1241()log 20log 252−+−= ;12.设函数221,0()log ,0x x f x x x − −≤= > ,如果0()1f x >,则0x 的取值范围是 ;13. 某工厂生产某种产品固定成本为2000万元,并且每生产一单位产品,成本增加10万元。
2016年秋季学期高等代数作业(北大有答案)

2 0 1 6年 秋 季 学 期 高 等 代 数 作 业要求:1. 作业必须写出全部求解过程。
计算题必须写出全部 计算过程;证明题必须写出全部证明步骤。
不能只写答案。
2.要独立完成作业,不要抄别人的作业,不要抄《高 等代数教程习题集》的答案。
3.不许抄袭或复制前几个学期的习题解答。
4. 键入数学公式,用数学软件Mathtype .作 业 ( 共 3 1 题 )第 一 章 行 列 式 ( 7 题 )习题 1.3 4、计算行列式0001000270(1)03690410115081375-58002000220003601*(1)*5*(1)036630*512041011041011111048135d =-=--==习题 1.4 (1) 1.计算下列行列式11111111(5)11111111a a b b+-+-D=10111111111111a a a b b-+-=22110101000110001a b = 11010000111000a abb --=221101010001110001a b =221101010*********a b =22a b3.计算n 阶行列式 =D bb bbb a b bb b a bb b b a11...1...1 (00)...0[(1)][(1)][(1)]()1 (00)......0...1 0...n b b b b b b ab bb d a n b a n a n b a b ba b a b a bb b aa b-=+-=+-=+-----5. 计算 N+1 阶行列式112230000000000000n n a a a a a a a bbbbb -⎡⎤⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦11222211230000000000000000000(1)0000023(1)n n n na a a a a a a a D a a a a n ba a a bbbbbbb b nb n b--===⨯+⨯-+习题 1.4(2) 第 4 题 : 计算下列行列式6611145343625313110214210-习题 1.66、计算 2n 阶行列式0...00 0......0...00...0a b a b b a b a答:将第2n 列加和到第一列,将第2n-1列加到第2列,……,第n+1列加到第n 列得到000000000000000000000a b a b a b b a b b a b a a b a a ba++++++(第2n 行减第1行,第2n-1行减第2行……,第n+1行减第n 行)2200000000000000000000000()()()n n n a b b a b b a b b a b a b a ba ba b a b a b =+++--+=--+-复 习 题 1第6题——计算行列式12321213212121n n n n n n ⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥--⎣⎦1120222111110022111110002111111000011211131222210222100221(1)(1)(1)(1)20002100001n n n D nn n n nn n n ++----===-----+--+=-⨯+⨯第二章 线 性 方 程 组 ( 9 题 ) 习题 2.11、用 Cramer 法则解下列线性方程组(3) ⎪⎪⎩⎪⎪⎨⎧-=++-=+-+=---=-++82324223832262324321432143214321x x x x x x x x x x x x x x x x213141123212322581212305813654341083243212041081836745223210745r r D r r r r ----------=-=--==---------习题 2.2(2)1、用消元法解下列线性方程组(4) 12345123451234512345222422334103578221x x x x x x x x x x x x x x x x x x x x -+-+=⎧⎪-+-+=⎪⎨-+-+=⎪⎪+-+-=-⎩习题 2.5(2) 3 .证明:如果 12,,,s ααα 线性无关 ,而 12,,,,s αααβ 线性相关,则β可以由 12,,,s ααα 线性表出 ,并且表法唯一 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京大学数学学院期中试题
一.(16分)
(1)叙述向量组线性相关, 线性无关, 向量组极大无关组的定义 ;
(2)已知向量组α1 , ... , α s 能线性表出β1 , ... , β r , 且α1 , ... , α s 的秩
等于β1 , ... , β r 的秩 . 证明: β1 , ... , β r 也能线性表出α1 , ... , αs .
二.(16分)计算n 级行列式 D = n
n 2n 1n n 2221
2n 1211
1b a n b a n b a n b a b a b a b a b a b a +++++++++
222111. 解:n = 1时,D = 1+ a 1b 1 ;n = 2时,D =(2a 1–a 2 )(b 1–b 2 );
n>2时,D = n
1n 21n 11n n 122121
12n 1211
1b a n a b a n a b a n a b a a b a a b a a b a b a b a )()()()2()2()2(111------+++
= 0 .
三.(24分)设矩阵 A 的列向量依次为α1 , ... , α5 . 已知齐次方程组
A X = 0解空间的一组基为 [ 3 1 1 0 0 ] T , [ 5 6 1 2 -1 ] T .
1) 求A 的简化阶梯型矩阵J ;
2) 求A 列向量组的一个极大无关组, 并用此极大无关组表出A 的
每个列向量;
3) 求 A 行空间的一组基, 并判断当a 取何值时,
β = [ 1 a 0 3 2a –1 ] 落在A 的行空间里, 写出此时β在 基底下的坐标;
4) 将A 写成BC 的形式,B 是列满秩的矩阵,C 是行满秩的矩阵.
解: 1) 矩阵A 的行空间与A 的解空间在R 5中互为正交补 , 即向量 [ a 1 a 2 a 3 a 4 a 5 ] 在A 的行空间中当且仅当 3 a 1 + a 2 + a 3 = 0 且 5a 1 + 6a 2 + a 3 +2 a 4 – a 5 = 0 .
解此方程组得行空间的一组基
⎥⎦
⎤⎢⎣⎡---→⎥⎦⎤⎢⎣⎡-12052001131216500113 得 ⎩⎨⎧++=--=4215
2132523a a a a a a a a 1 , a 2 , a 4为自由变量. ⎥⎥⎥⎥⎥
⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-+⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎥⎥⎦⎤⎢
⎢⎢⎢⎢⎢⎣⎡++--=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡21000501102030125234214214212154321a a a a a a a a a a a a a a a a 故A 的简化阶梯形为 ⎥⎥⎥⎥⎥⎥⎦
⎤⎢⎢⎢⎢⎢
⎢⎣⎡-- 00000
210005*********. 2) A 列向量组的一个极大无关组为α1 , α2 , α4 , 且
α3 = –3 α1 – α2 , α5 = 2 α1 + 5α2 + 2α3 ;
3) A 行空间的一组基为简化阶梯形的前3个行向量;
若 β = [ 1 a 0 3 2a –1 ] 落在A 的行空间里, 则β在
此基底下的坐标只能是 [ 1 a 3 ] T ,且有
–3–a = 0 , 2 + 5 a + 6 =2a –1 .
此条件当且仅当 a = –3 时成立.
故当且仅当 a = –3 时β落在A 的行空间里, 此时β的坐标是
[ 1 –3 3 ] T .
4) A = [ a 1 a 2 a 4 ] ⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡--210005*********.
四.(12分)设A =⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡000100010. 记 C( A) = { X ∈ M 3 (R) | A X = X A }.
1) 证明: 集合C( A )是线性空间M 3 (R) 的子空间;
2) 求子空间C( A ) 的维数和一组基 .
解:
2) C( A ) 的一组基为 I ,A ,A 2 ( A 3 = 0 )。
dim C( A ) = 3.
五.(24分)设α1 , α2 , α3 , α4 , β1 , β2 , β3 依次是A =
的列向量. 设U = < α1 , α2 , α3 , α4 > , W = < β1 , β2 , β3 > 是R 4 的 子空间.
1 ) 求 U + W 与 U ⋂ W 的维数与基底 ;
2) 设 γ = [ 2 3 2 2 ] T . 判断集合 ( γ + W ) ⋂ U 是否非空;
若非空, 将其写为η + V 的形式, 这里η∈ R 4 , V 是R 4 的 子空间 (写出V 的一组基 ).
解:1) 对A 作行变换, 化为简化阶梯形
⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡23
15315311621421
2711333
16416⎥⎥
⎥⎥
⎦⎤
⎢⎢
⎢⎢⎣⎡----→⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡22100001101000
11002100100101
2315315311621421271133316416
由此看出α1 , α2 , α4 , β1 构成U + W 的基, dim( U + W ) = 4 ;
α1 , α2 , α4构成U的基, dim U = 3 ;
β1 , β2 , β3构成W的基, dim W = 3 .
于是dim ( U ⋂ W ) = dim U + dim W – dim( U + W ) = 2 .
由简化阶梯形可看出
β2 – 2β1 = α1 +α2–α4 , β3 + 2β1 = –α2+α4 ∈ U ⋂ W , 且由β1 , β2 , β3线性无关知β1 , β2 – 2β1 , β3 + 2β1线性无关.
故β2 – 2β1 , β3 + 2β1也线性无关,它们构成U ⋂ W的一组基.
2)注意到U + W = R4 , γ可表示成α1 , α2 , α4 , β1的线性组合:γ = α2 + β1 . 以下证明( γ + W ) ⋂ U = α2 + W ⋂ U ,
(这也说明( γ + W ) ⋂ U非空).
由γ + β = α2 + ( β + β1 ) , ∀β∈ W , 知γ + W = α2 + W
故( γ + W ) ⋂ U = ( α2 + W ) ⋂ U .
显然α2 + W ⋂ U⊆α2 + W , 且α2 + W ⋂ U⊆ U .
故α2 + W ⋂ U ⊆ ( α2 + W ) ⋂ U .
若α∈ ( α2 + W ) ⋂ U , 即α∈ U 且α = α2 + β , β∈ W .
则β = α–α2 ∈ U, 故β∈ W⋂ U. 于是α∈α2 + W ⋂ U .
综上所述, 我们有( γ + W ) ⋂ U = α2 + W ⋂ U .
六.(8分)记M n (R)是由全体n级实矩阵构成的线性空间. 设W是M n (R)的线性子空间, 且dimW ≥n2–n + 1 . 证明: W至少包含一个满秩的矩阵.
证: 对W的一组基A1 , ... , A r作以下初等变换:
任取A1的一个非零元素, 比如( i, j )元, 用A1的适当倍数去减其余r - 1个A k,使得每个A k的( i, j )元都取0 . 这个选定的( i, j )元称为A1的主元;再依次对A2 , ... , A r重复以上操作:选
A s的一个非零元作主元, 用A s的适当倍数去减其余r - 1个A k,
使得每个A k在该位置都取0 .
经过以上改造, 得到W的一组基A1 , ... , A r ,每个A k都对应一个主元位置, 在该位置A k的元素不为零, 其它r - 1个矩阵取0.
用适当的系数对A1 , ... , A r作线性组合,可使组合矩阵在这r个主元位置取任意指定的值.
以下用归纳法证明: 当一个n级矩阵有n2–n + 1 个位置的值可以任选时, 总有一种取法可使矩阵满秩(不管其余n–1个位置取什么值).
在n = 1时,命题成立;
假设命题对n -1级的方阵成立, 考察n级方阵的情况.
由抽屉原则, 总有一行, 不妨设是第i行, 该行的n个元素都可任选. 再取一列, 不妨设是第j列, 使得此列中至少有一个元素
不能任选. 在第i行中令( i , j )元为1 , 其余n -1个位置为0 .
由于在( i , j )元的余子阵中至多有n - 2个位置的值不能任选
(其余位置可任选), 应用归纳假设, 存在子阵元素的选法, 使得( i , j )元的余子式不等于零. 在此取法下, 有
n级方阵的行列式= ( i , j )元的代数余子式 0 .
故n级方阵满秩:。
