广东省深圳市2019届高三第一次(2月)调研考试数学理答案

合集下载

数学分类汇编(12)三角函数的化简与求值(含答案)

（山东省德州市2019届高三期末联考数学（理科）试题）8.第24届国际数学家大会会标是以我国古代数学家赵爽的弦图为基础设计的，会标是四个全等的直角三角形与一个小正方形拼成的一个大正方形，如果小正方形的面积为，大正方形的面积为，直角三角形中较小的锐角为，则（）A. B. C. D.【答案】D【解析】【分析】由图形可知三角形的直角边长度差为a，面积为6，列方程组求出直角边得出sinθ，代入所求即可得出答案．【详解】由题意可知小正方形的边长为a，大正方形边长为5a，直角三角形的面积为6，设直角三角形的直角边分别为x，y且x＜y，则由对称性可得y＝x+a，∴直角三角形的面积为S xy＝6，联立方程组可得x＝3a，y＝4a，∴sinθ，tanθ＝．∴===，故选：D．【点睛】本题考查了解直角三角形，三角恒等变换，属于基础题．（山东省潍坊市2019届高三上学期期末测试数学（理科）试题）3.若，则（）A. B. C. D.【答案】C【解析】【分析】本道题化简式子,计算出,结合,即可.【详解】,得到,所以,故选C.【点睛】本道题考查了二倍角公式,难度较小.（山东省烟台市2018届高三下学期高考诊断性测试数学（文）试题）14.已知,则_______【答案】【解析】原式化为，，所以，，填。

（江西省新余市2019届高三上学期期末考试数学（理）试题）15.已知，则______．【答案】【解析】【分析】根据同角的三角函数的关系和二倍角公式即可求出．【详解】解：，，，，，故答案为：．【点睛】本题考查同角的三角函数关系式和二倍角公式的应用，属于基础题．（湖南省长沙市2019届上学期高三统一检测理科数学试题）15.在平面直角坐标系中，角的顶点在原点，始边与轴的非负半轴重合，终边过点，则__________.【答案】【解析】【分析】结合终边过点坐标，计算出，结合二倍角公式和余弦两角和公式，即可。

【详解】，所以【点睛】本道题考查了二倍角公式与余弦的两角和公式，难度中等。

2019年高考真题《不等式(理) 》Word版含解析

2019年高考真题《不等式》1．【2019年高考全国Ⅰ卷理数】已知a ，b ，c 为正数，且满足abc =1．证明：（1）222111a b c a b c++≤++；（2）333()()()24a b b c c a +++≥++．【答案】（1）见解析；（2）见解析．【解析】（1）因为2222222,2,2a b ab b c bc c a ac +≥+≥+≥，又1abc =，故有222111ab bc ca a b c ab bc ca abc a b c++++≥++==++．所以222111a b c a b c++≤++．（2）因为, , a b c 为正数且1abc =，故有333()()()a b b c c a +++++≥=3(+)(+)(+)a b b c a c3≥⨯⨯⨯=24．所以333()()()24a b b c c a +++++≥．【名师点睛】本题考查利用基本不等式进行不等式的证明问题，考查学生对于基本不等式的变形和应用能力，需要注意的是在利用基本不等式时需注意取等条件能否成立． 2．【2019年高考全国Ⅱ卷理数】已知()|||2|().f x x a x x x a =-+-- （1）当1a =时，求不等式()0f x <的解集；（2）若(,1)x ∈-∞时，()0f x <，求a 的取值范围．【答案】（1）(,1)-∞；（2）[1,)+∞【解析】（1）当a =1时，()=|1| +|2|(1)f x x x x x ---．当1x <时，2()2(1)0f x x =--<；当1x ≥时，()0f x ≥．所以，不等式()0f x <的解集为(,1)-∞．（2）因为()=0f a ，所以1a ≥．当1a ≥，(,1)x ∈-∞时，()=() +(2)()=2()(1)<0f x a x x x x a a x x -----．所以，a 的取值范围是[1,)+∞．【名师点睛】本题主要考查含绝对值的不等式，熟记分类讨论的方法求解即可，属于常考题型． 3．【2019年高考全国Ⅲ卷理数】设,,x y z ∈R ，且1x y z ++=．（1）求222(1)(1)(1)x y z -++++的最小值；（2）若2221(2)(1)()3x y z a -+-+-≥成立，证明：3a ≤-或1a ≥-．【答案】（1）43；（2）见详解．【解析】（1）由于2[(1)(1)(1)]x y z -++++222(1)(1)(1)2[(1)(1)(1)(1)(1)(1)]x y z x y y z z x =-+++++-++++++-2223(1)(1)(1)x y z ⎡⎤≤-++++⎣⎦，故由已知得2224(1)(1)(1)3x y z -++++≥，当且仅当x =53，y =–13，13z =-时等号成立．所以222(1)(1)(1)x y z -++++的最小值为43．（2）由于2[(2)(1)()]x y z a -+-+-222(2)(1)()2[(2)(1)(1)()()(2)]x y z a x y y z a z a x =-+-+-+--+--+--2223(2)(1)()x y z a ⎡⎤≤-+-+-⎣⎦，故由已知2222(2)(2)(1)()3a x y z a +-+-+-≥，当且仅当43a x -=，13a y -=，223a z -=时等号成立．因此222(2)(1)()x y z a -+-+-的最小值为2(2)3a +．由题设知2(2)133a +≥，解得3a ≤-或1a ≥-．【名师点睛】两个问都是考查柯西不等式，属于柯西不等式的常见题型． 4．【2019年高考江苏卷数学】设x ∈R ，解不等式||+|2 1|>2x x -．【答案】1{|1}3x x x <->或．【解析】当x <0时，原不等式可化为122x x -+->，解得x <13-；当0≤x ≤12时，原不等式可化为x +1–2x >2，即x <–1，无解；当x >12时，原不等式可化为x +2x –1>2，解得x >1．综上，原不等式的解集为1{|1}3x x x <->或．【名师点睛】本题主要考查解不等式等基础知识，考查运算求解和推理论证能力． 5．【重庆西南大学附属中学校2019届高三第十次月考数学】设函数()333()442f x x x g x x a x =-+-=-++，．（1）解不等式()10f x >；（2）若对于任意1x ∈R ，都存在2x ∈R ，使得12()()f x g x =成立，试求实数a 的取值范围．【答案】（1）4x >或1x <-；（2）40a -≤≤【解析】（1）不等式等价于34610x x >⎧⎨->⎩或13210x x ≤≤⎧⎨>⎩或36410x x <⎧⎨->⎩解得4x >或1x <-．（2）对任意1x ∈R ，都存在2x ∈R ，使得12()=()f x g x 成立，即()g x 的值域包含()f x 的值域．46,3()3332,1364,1x x f x x x x x x ->⎧⎪=-+-=≤≤⎨⎪-<⎩，由图可得1x =时，min ()2f x =，所以()f x 的值域为[2,)+∞．()442(4)(42)2g x x a x x a x a =-++≥--+=+，当且仅当4x a -与42x +异号时取等号，所以()g x 的值域为[2,)a ++∞，由题[2,)+∞⊆[2,)a ++∞，所以22a +≤，解得40a -≤≤．【点睛】本题考查绝对值函数和用绝对值不等式求绝对值函数中参数的范围，是常见考题．6．【山东省郓城一中等学校2019届高三第三次模拟考试数学】已知函数()2f x ax =-，不等式()4f x ≤的解集为{}|26x x -≤≤．（1）求实数a 的值；（2）设()()(3)g x f x f x =++，若存在x ∈R ，使()2g x tx -≤成立，求实数t 的取值范围．【答案】（1）1；（2）1(,1][,)2t ∈-∞-+∞．【解析】（1）由42ax -≤得－4≤2ax -≤4，即－2≤ax ≤6，当a >0时，26x a a -≤≤，所以2266a a ⎧-=-⎪⎪⎨⎪=⎪⎩，解得a ＝1；当a <0时，62x a a ≤≤-，所以6226a a⎧=-⎪⎪⎨⎪-=⎪⎩，无解．所以实数a 的值为1．（2）由已知()()(3)g x f x f x =++＝|x ＋1|＋|x －2|＝()()()211312212x x x x x -+≤-⎧⎪-<<⎨⎪-≥⎩，不等式g （x ）－tx ≤2转化成g （x ）≤tx ＋2，由题意知函数()g x 的图象与直线y ＝tx ＋2相交，作出对应图象，由图得，当t <0时，t ≤k AM ；当t >0时，t ≥k BM ，又因为k AM ＝－1，12BM k =，所以t ≤－1或12t ≥，即t ∈（－∞，－1]∪[12，＋∞）．【点睛】本题主要考查了绝对值不等式的解法及分类思想、方程思想，还考查了思想结合思想及转化能力，考查了作图能力及计算能力，属于中档题．7．【安徽省合肥市2019届高三第一次教学质量检测数学】设函数()|1|f x x =+．（1）若+2>2f x x （），求实数x 的取值范围；（2）设=+>1g x f x f ax a （）（）（）（），若g x （）的最小值为12，求a 的值．【答案】（1）13⎛⎫+∞ ⎪⎝⎭，；（2）2a =．【解析】（1）()22f x x +>，即1>22x x+-⇔101>22x x x +≥⎧⎨+-⎩或10122x x x+<⎧⎨-->-⎩13x ⇔>， ∴实数x 的取值范围是13⎛⎫+∞ ⎪⎝⎭，．（2）∵1a >，∴11a -<-，∴()()()()()121111112a x x g x a x x a a x x a ⎧⎪-+-∈-∞-⎪⎪⎡⎤=-∈--⎨⎢⎥⎣⎦⎪⎪⎛⎫++∈-+∞⎪ ⎪⎝⎭⎩，，，，，，，易知函数()g x 在1a ⎛⎫-∞- ⎪⎝⎭，单调递减，在1a ⎛⎫-+∞ ⎪⎝⎭，单调递增， ∴()min 111g x g a a ⎛⎫=-=- ⎪⎝⎭． ∴1112a -=，解得2a =．【点睛】本道题考查了含绝对值不等式的解法，考查了结合单调性计算函数最值，关键得到函数解析式，难度中等．8．【河南省中原名校（即豫南九校）2018届高三第六次质量考评理科数学】已知函数21f x x a g x x =+=-（），（）．（1）若2f x g x +（）（）的最小值为1，求实数a 的值；（2）若关于x 的不等式1f x g x +<（）（）的解集包含112⎡⎤⎢⎥⎣⎦，，求实数a 的取值范围．【答案】（1）8a =-或4．（2）312⎛⎫ ⎪⎝⎭，．【解析】（1）当1b =时，()()1|||1||1||1|2222a a af xg x x x x x +=-++≥---=+，因为()()12f xg x +的最小值为3，所以132a +=，解得8a =-或4．（2）当1b =-时，()()1f x g x +<即211x a x -+-<，当112x ⎡⎤∈⎢⎥⎣⎦，时，211x a x -+-<2112x a x x a x ⇔-+-<⇔-<，即3ax a <<，因为不等式()()1f x g x +<的解集包含112⎡⎤⎢⎥⎣⎦，，所以1a >且132a <，即312a <<，故实数a 的取值范围是312⎛⎫ ⎪⎝⎭，．【点睛】本题考查不等式的解法及不等式的性质，考查转化思想以及计算能力． 9．【河南省顶级名校2019届高三质量测评数学】已知函数()121f x x x =++-．（1）解不等式()2f x x ≤+；（2）若()3231g x x m x =-+-，对12x x ∀∈∃∈R R ，，使()()12f x g x =成立，求实数m 的取值范围．【答案】（1）{}|01x x ≤≤；（2）1544⎡⎤-⎢⎥⎣⎦，．【解析】（1）不等式等价于132x x x ≤-⎧⎨-≤+⎩或11222x x x ⎧-<≤⎪⎨⎪-+≤+⎩或1232x x x >≤+⎧⎪⎨⎪⎩，解得x φ∈或102x ≤≤或112x <≤，所以不等式2f x x ≤+（）的解集为{}|01x x ≤≤．（2）由311()212132x x f x x x x x ⎧⎪-≤-⎪⎪=-+-<≤⎨⎪⎪>⎪⎩，，，知，当12x =时，min 13()()22f x f ==， 323121g x x m x m ≥---=-（）（）（），当且仅当(32)(31)0x m x --≤时取等号，所以3212m -≤，解得1544m -≤≤．故实数m 的取值范围是1544⎡⎤-⎢⎥⎣⎦，．【点睛】本题考查方程有解问题，考查不等式的解法，考查转化思想以及计算能力． 10．【吉林省吉大附中2018届高三第四次模拟考试数学（理）试卷】已知函数()f x x a =-．（1）当2a =-时，解不等式()1621f x x ≥--；（2）若关于x 的不等式()1f x ≤的解集为[0,2]，求证：()(2)2f x f x ++≥．【答案】（1）17{|3x x ≤-或5}x ≥（2）见解析【解析】（1）当2a =-时，不等式为22116x x ++-≥，当2x ≤-时，原不等式可化为22116x x ---+≥，解得173x ≤-，当122x -<≤时，原等式可化为22116x x +-+≥，解得13x ≤-，不满足，舍去；当12x >时，原不等式可化为22116x x ++-≥，解得5x ≥；不等式的解集为17{|3x x ≤-或5}x ≥．（2）()1f x ≤即1x a -≤，解得11a x a -≤≤+，而()1f x ≤解集是[]02，，所以1012a a -=⎧⎨+=⎩，解得1a =，从而()1f x x =-．于是只需证明()(2)2f x f x ++≥，即证112x x -++≥，因为111x x x -++=-1112x x x ++≥-++= 所以112x x -++≥，证毕．【点睛】本题主要考查了绝对值不等式的解法和证明，主要注意先确定参数的值，进而对定义域进行分类讨论，确定解所在的区间，属于中档题．11．【河北衡水金卷2019届高三12月第三次联合质量测评数学】设函数()2f x x x a =--+．（1）当1a =时，求不等式()2f x <-的解集；（2）当x y ∈R ，时，2()()2()f y f x f y -+≤≤+，求a 的取值范围．【答案】（1）3{|}2x x >；（2）[]31--，【解析】（1）当a =1时，31()121232x f x x x x ≤-⎧⎪=--<≤⎨⎪->⎩，，，，可得()2f x <-的解集为3{|}2x x >；（2）当x y ∈R ，时，[][]ma min 2()()2()()()2()()2x f y f x f y f x f y f x f x -+≤≤+⇔-≤⇔-≤，因为()()222x x a x x a a --+≤--+=+，所以()222a a +--+≤．所以21a +≤，所以31a -≤≤-．所以a 的取值范围是[–3，–1]．【点睛】含绝对值不等式的解法有两个基本方法，一是运用零点分区间讨论，二是利用绝对值的几何意义求解．法一是运用分类讨论思想，法二是运用数形结合思想，将绝对值不等式与函数以及不等式恒成立交汇、渗透，解题时强化函数、数形结合与转化化归思想方法的灵活应用． 12．【河北省衡水中学2019届高三第一次摸底考试数学】已知函数2f x x =-（）．（1）求不等式1f x x x <++（）的解集；（2）若函数()2log 32f x f x f x a ⎡⎤=++-⎣⎦（）（）的定义域为R ，求实数a 的取值范围．【答案】（1）13⎛⎫+∞ ⎪⎝⎭，；（2）32⎛⎫-∞ ⎪⎝⎭，．【解析】（1）由已知不等式()1f x x x <++，得21x x x -<++，当2x >时，绝对值不等式可化为21x x x -<++，解得3x >-，所以2x >；当12x -≤≤时，绝对值不等式可化为21x x x -<++，解得13x >，所以123x <≤；当1x <-时，由21x x x -<--得3x >，此时无解．综上可得所求不等式的解集为13⎛⎫+∞ ⎪⎝⎭，．（2）要使函数()()2log 32y f x f x a ⎡⎤=++-⎣⎦的定义域为R ，只需()()()32g x f x f x a =++-的最小值大于0即可．又()12212232g x x x a x x a a =++--≥+-+-=-，当且仅当[]12x ∈-，时取等号．所以只需320a ->，即32a <．所以实数a 的取值范围是32⎛⎫-∞ ⎪⎝⎭，．【点睛】绝对值不等式的常见解法：①利用绝对值不等式的几何意义求解，体现了数形结合的思想； ②利用“零点分段法”求解，体现了分类讨论的思想；③通过构造函数，利用函数的图象求解，体现了函数与方程的思想．13．【甘肃省兰州市第一中学2019届高三6月最后高考冲刺模拟数学】已知函数()211f x x x =-++．（1）解不等式()3f x ≥；（2）记函数()f x 的最小值为m ，若,,a b c 均为正实数，且232a b c m ++=，求222a b c ++的最小值．【答案】（1）{}11x x x ≤-≥或；（2）914．【解析】（1）由题意，3,11()2,1213,2x x f x x x x x ⎧⎪-≤-⎪⎪=--<<⎨⎪⎪≥⎪⎩，所以()3f x ≥等价于133x x ≤-⎧⎨-≥⎩或11223x x ⎧-<<⎪⎨⎪-≥⎩或1233x x ⎧≥⎪⎨⎪≥⎩．解得1x ≤-或1x ≥，所以不等式的解集为{}11x x x ≤-≥或；（2）由（1）可知，当12x =时，()f x 取得最小值32，所以32m =，即233a b c ++=，由柯西不等式得2222222()(123)(23)9a b c a b c ++++≥++=，整理得222914a b c ++≥，当且仅当123a b c ==时，即369,,141414a b c ===时等号成立．所以222a b c ++的最小值为914．【点睛】本题主要考查含绝对值不等式的解法，以及柯西不等式的应用，熟记不等式解法以及柯西不等式即可，属于常考题型．14．【四川省成都市第七中学2019届高三二诊模拟考试数学】已知000a b c >>>，，设函数f x x b x c a x =-+++∈R （），．（1）若1a b c ===，求不等式5f x <（）的解集；（2）若函数f x （）的最小值为1，证明：14918a b c a b b c c a++≥+++++（）．【答案】（1）(2,2)-；（2）详见解析．【解析】（1）1a b c ===，不等式()5f x <，即|1||1|4x x -++<，当1x ≤-时，11421x x x ---<⇒-<≤-，当11x -<<时，11411x x x -+-<⇒-<<，当1x ≥时，11412x x x -++<⇒≤<，∴解集为(2,2)-；（2）()f x x b x c a =-+++x c x b a ≥+--+（）（）b c a =++，∵000a b c >>>，，，∴min ()1f x a b c =++=， ∴149a b b c c a ++=+++149a b b c c a ⎛⎫++ ⎪+++⎝⎭a b c ++（） 11492a b b c c a ⎛⎫=++ ⎪+++⎝⎭a b b c a c +++++（）22212⎡⎤=++⎢⎥⎢⎥⎣⎦222⎡⎤++⎣⎦212≥1818a b c ==++（）．【点睛】考查了含绝对值不等式的解法，考查了基本不等式，考查了不等式的证明，难度中等偏难．15．【四川省成都市第七中学2019届高三一诊模拟考试数学】已知函数()21f x x x =-+，且a b c ∈R ，，．（1）若1a b c ++=，求()()()f a f b f c ++的最小值；（2）若1x a -<，求证：()()()21f x f a a -<+．【答案】（1）73；（2）见解析【解析】（1）由柯西不等式得，()22221433a b c a b c ++≥++=（当且仅当23a b c ===时取等号），所以()()()()()222473133f a f b f c a b c a b c ++=++-+++≥+=，即()()()f a f b f c ==的最小值为73；（2）因为1x a -<，所以()()()()22•11f x f a x a x a x a x a x a -=---=-+-<+-()()()()212112121x a a x a a a a =-+-≤-+-<++=+，故结论成立．【点睛】本题考查了利用柯西不等式求最值，考查了利用绝对值三角不等式证明的问题，属于中等题．16．【黑龙江省大庆市第一中学2019届高三下学期第四次模拟（最后一卷）数学】已知函数()25f x x a x =-+，其中实数0a >．（1）当3a =时，求不等式()51f x x ≥+的解集；（2）若不等式()0f x ≤的解集为{|1}x x ≤-，求a 的值．【答案】（1）不等式()51f x x ≥+的解集为{|12}x x x ≤≥或；（2）3a =【解析】（1）当3a =时，()51f x x ≥+可化为231x -≥，由此可得1x ≤或2x ≥，故不等式()51f x x ≥+的解集为{|12}x x x ≤≥或；（2）法一：（从去绝对值的角度考虑）由()0f x ≤，得25x a x -≤-，此不等式化等价于2250a x x a x ⎧≥⎪⎨⎪-+≤⎩或()2250a x x a x ⎧<⎪⎨⎪--+≤⎩，解得27a x a x ⎧≥⎪⎪⎨⎪≤⎪⎩或23a x a x ⎧<⎪⎪⎨⎪≤-⎪⎩，因为0a >，所以不等式组的解集为{|}3ax x ≤-，由题设可得13a -=-，故3a =．法二：（从等价转化角度考虑）由()0f x ≤，得25x a x -≤-，此不等式化等价于525x x a x ≤-≤-，即为不等式组5225x x a x a x ≤-⎧⎨-≤-⎩，解得37a x a x ⎧≤-⎪⎪⎨⎪≤⎪⎩，因为0a >，所以不等式组的解集为{|}3a x x ≤-，由题设可得13a -=-，故3a =．法三：（从不等式与方程的关系角度突破）因为{|1}x x ≤-是不等式()0f x ≤的解集，所以1x =-是方程()0f x =的根，把1x =-代入250x a x -+=得37a a ==-或，因为0a >，所以3a =．【点睛】本题考查解绝对值不等式，不等式问题中求参数范围的问题，难度较小．17．【广东省揭阳市2019届高三高考二模数学】已知正实数x ，y 满足x +y =1．（1）解关于x 的不等式522x y x y ++-≤；（2）证明：2211(1)(19x y --≥）．【答案】（1）1[16，）．（2）见解析．【解析】（1）∵1x y +=，且0x >，0y >， ∴0152522212x x y x y x x <<⎧⎪++-≤⇔⎨-+-≤⎪⎩， 01011112121222x x x x x x x <<<<⎧⎧⎪⎪⇔⇔⎨⎨-≤+-+≤-≤+⎪⎪⎩⎩（），解得116x ≤<，所以不等式的解集为1[16，）．（2）解法1：∵1x y +=，且00x y >>，， ∴2222222211()()(1)(1)x y x x y y x y x y+-+---=⋅ 222222xy y xy x x y ++=⋅222222()()y y x x x x y y =++225x y y x =++59≥=．当且仅当12x y ==时，等号成立．解法2：∵1x y +=，且00x y >>，， ∴2222221111(1)(1)x y x y x y----=⋅ 22(1)(1)(1)(1)x x y y x y +-+-=⋅22(1)(1)x y y x x y ++=⋅1x y xy xy+++=21xy =+2219()2x y ≥+=+，当且仅当12x y ==时，等号成立．【点睛】主要考查了绝对值不等式的求解、不等式证明、以及基本不等式的应用，属于中档题．对于绝对值不等式的求解，主要运用零点分段法，也可以运用图像法．而不等式的证明，关键是灵活运用不等式的性质以及基本不等式．。

专题04 二次函数(广东专版)-2019年中考真题数学试题分项汇编(解析版)

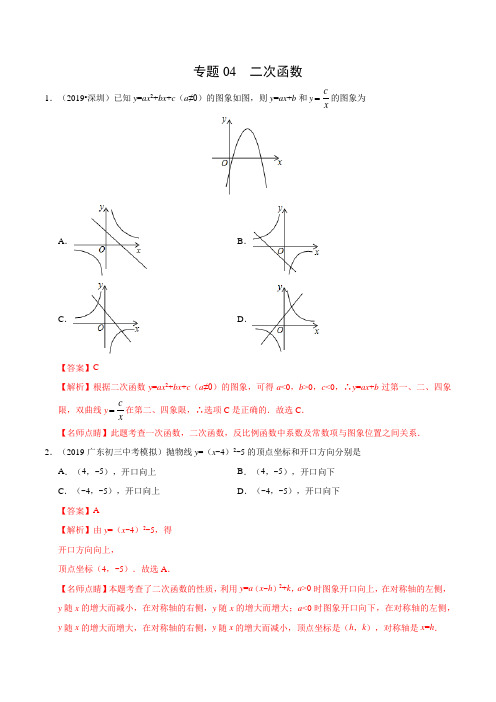
专题04 二次函数1．（2019•深圳）已知y=ax2+bx+c（a≠0）的图象如图，则y=ax+b和ycx=的图象为A．B．C．D．【答案】C【解析】根据二次函数y=ax2+bx+c（a≠0）的图象，可得a<0，b>0，c<0，∴y=ax+b过第一、二、四象限，双曲线ycx=在第二、四象限，∴选项C是正确的．故选C．【名师点睛】此题考查一次函数，二次函数，反比例函数中系数及常数项与图象位置之间关系．2．（2019·广东初三中考模拟）抛物线y=（x-4）2-5的顶点坐标和开口方向分别是A．（4，-5），开口向上B．（4，-5），开口向下C．（-4，-5），开口向上D．（-4，-5），开口向下【答案】A【解析】由y=（x-4）2-5，得开口方向向上，顶点坐标（4，-5）．故选A．【名师点睛】本题考查了二次函数的性质，利用y=a（x-h）2+k，a>0时图象开口向上，在对称轴的左侧，y随x的增大而减小，在对称轴的右侧，y随x的增大而增大；a<0时图象开口向下，在对称轴的左侧，y随x的增大而增大，在对称轴的右侧，y随x的增大而减小，顶点坐标是（h，k），对称轴是x=h．3．（2019·广东初三中考模拟）将抛物线()213y x =-+向左平移1个单位，再向下平移3个单位得到的解析式是A ．()22y x =-B ．()226y x =-+C ．2y x =D ．26y x =+ 【答案】C【解析】∵向左平移1个单位，再向下平移3个单位，∴y =（x -1+1）2+3-3．故得到的抛物线的函数关系式为：y =x 2．故选C ．【名师点睛】主要考查了函数图象的平移，要求熟练掌握平移的规律：左加右减，上加下减．并用规律求函数解析式．4．（2019·广州大学附属中学初三中考模拟）在二次函数221y x x =-++的图象中，若y 随着x 的增大而增大，则x 的取值范围是A ．x <1B ．x >1C ．x <2D ．x >-1【答案】A【解析】∵a =-1<0，∴二次函数图象开口向下，∵对称轴是直线x =1，∴当x <1时，函数图象在对称轴的左边，y 随x 的增大而增大．故选A ．【名师点睛】本题考查了二次函数的性质，解题关键是根据a 的取值判断图象的开口方向，并计算出二次函数的对称轴，根据图象性质判定x 的取值范围．5．（2019·广东初三中考模拟）二次函数y =x 2+bx 的对称轴为直线x =2，若关于x 的一元二次方程x 2+bx -t =0（t 为实数）在-1<x <4的范围内有解，则t 的取值范围是A ．0<t <5B ．-4≤t <5C ．-4≤t <0D ．t ≥-4【答案】B【解析】∵对称轴为直线x =2，∴b =-4，∴y=x2-4x，关于x的一元二次方程x2+bx-t=0的解可以看成二次函数y=x2-4x与直线y=t的交点，∵-1<x<4，∴二次函数y的取值为-4≤y<5，∴-4≤t<5，故选B．【名师点睛】本题考查二次函数图象的性质，一元二次方程的解；将一元二次方程的解转换为二次函数与直线交点问题，数形结合的解决问题是解题的关键．6．（2019·广东初三中考模拟）在同一直角坐标系中，一次函数y=ax-b和二次函数y=-ax2-b的大致图象是A．B．C．D．【答案】A【解析】A、由一次函数y=ax-b的图象可得：a>0，-b>0，此时二次函数y=-ax2-b的图象应该开口向下，顶点的纵坐标-b大于零，故A正确；B、由一次函数y=ax-b的图象可得：a<0，-b>0，此时二次函数y=-ax2-b的图象应该开口向上，顶点的纵坐标-b大于零，故B错误；C、由一次函数y=ax-b的图象可得：a<0，-b>0，此时二次函数y=-ax2-b的图象应该开口向上，故C错误；D、由一次函数y=ax-b的图象可得：a>0，-b>0，此时抛物线y=-ax2-b的顶点的纵坐标大于零，故D错误，故选A．【名师点睛】本题考查了二次函数的图象，应该熟记一次函数y=kx+b在不同情况下所在的象限，以及熟练掌握二次函数的有关性质：开口方向、对称轴、顶点坐标等．7．（2019·广东初三中考模拟）二次函数2y ax bx c =++的部分图象如图，则下列说法：①对称轴是直线x =－1；②c =3：③ab >0；④当x <1时，y >0；⑤方程20ax bx c ++=的根是13x =-和21x =，正确的有A ．2个B ．3个C ．4个D ．5个【答案】C 【解析】由图象可知对称轴为直线x =-1，故①正确，∵抛物线与y 轴的交点为（0，3），∴c =3，故②正确，∵对称轴x =-2b a=-1， ∴ab >0，故③正确，∵对称轴为x =-1，抛物线与x 轴的一个交点为（1，0），∴抛物线与x 轴的另一个交点为（-3，0），∴当-3<x <1时，y >0，故④错误，∴方程ax 2+bx +c =0的两个根为x 1=-3和x 2=1，故⑤正确，综上所述：正确的结论有①②③⑤共4个，故选C ．【名师点睛】本题考查的是二次函数的图象与系数的关系，二次函数y =ax 2+bx +c 系数符号由抛物线开口方向、对称轴、抛物线与y 轴的交点抛物线与x 轴交点的个数确定．8．（2019·广东初三中考模拟）如图，二次函数y =ax 2+bx +c 图象的对称轴是直线x =1，与x 轴一个交点A （3，0），则与x 轴的另一个交点坐标是A ．（0，12-） B ．（12-，0） C ．（0，-1）D ．（-1，0）【答案】D 【解析】∵点A 的坐标为（3，0），∴点A 关于x =1的对称点的坐标为（-1，0）．故选D ．【名师点睛】本题主要考查的是抛物线与x 轴的交点，利用抛物线的对称性求得点A 的对称点的坐标是解题的关键．9．（广东省广州市天河区2019届九年级第一次诊断性检测数学试题）下列关于函数y =x 2-6x +10的四个命题：①当x =0时，y 有最小值10；②n 为任意实数，x =3+n 时的函数值大于x =3-n 时的函数值；③若n >3，且n 是整数，当n ≤x ≤n +1时，y 的整数值有（2n -4）个；④若函数图象过点（x 0，m ）和（x 0-1，n ），则m <n ，其中真命题的个数是A ．0个B ．1个C ．2个D ．3个【答案】B【解析】①y =（x -3）2+1，所以函数的最小值是当x =3时，y 有最小值1，故①错误；②n 为任意实数，x =3+n 与x =3-n 关于对称轴x =3对称，所以函数值相等，故②错误；③若n >3，且n 是整数，当x =n 时，y =（n -3）2+1，当x =n +1时，y =（n -2）2+1，相减得2n -5，所以整数值有（2n -4）个，故③正确；④函数开口向上，所以距离对称轴越近函数值越小，若m <n ，所以（x 0，m ）更靠近对称轴x =3，在不能确定x 0的值时，该项错误，故只有一个正确的真命题，故选B ．【名师点睛】本题考查了命题真假的判断，二次函数的性质，属于简单题，熟悉二次函数的性质是解题关键．10．（2019·广东初三中考模拟）已知抛物线y =ax 2-3ax -4a （a ≠0）．（1）直接写出该抛物线的对称轴．（2）试说明无论a 为何值，该抛物线一定经过两个定点，并求出这两个定点的坐标．【解析】（1）该抛物线的对称轴为x =-32a a -=32．（2）234y ax ax a =--可化为()()14y a x x =+-，当()()140x x +-=，即1x =-或4时，0y =，∴抛物线一定经过点()1,0-，()4,0．【名师点睛】考查了二次函数的性质，解题的关键时了解抛物线的对称轴方程，难度不大．11．（2019·汕头市潮南区阳光实验学校初三中考模拟）某纪念品专卖店上周批发买进100件A 纪念品和300件B 纪念品，花费9600元；本周批发买进200件A 纪念品和100件B 纪念品，花费6200元．（1）求每件A 纪念品和B 纪念品的批发价各为多少元？（2）经市场调研，当A 纪念品每件的销售价为30元时，每周可销售200件；当每件的销售价每增加1元，每周的销售数量将减少10件．当每件的销售价a 为多少时，该纪态品专卖店销售A 纪念品每周获得的利润W 最大？并求出最大利润．【解析】（1）设每件A 纪念品的批发价为x 元，B 纪念品的批发价的为y 元，依题意10030096002001006200x y x y +=⎧⎨+=⎩，解得1826x y =⎧⎨=⎩，即每件A 纪念品的批发价为18元，B 纪念品的批发价的为26元．（2）由（1）知每件A 纪念品的批发价为18元，依题意得W =（a -18+a -30）[200-10（a -30）]=（2a -48）（500-10a ）=-20a 2+1480a -24000整理得W =-20（a -37）2+3380∵-20<0∴W 有最大值，即当a =27时，有最大值3380，即当每件的销售价a 为37元时，该纪态品专卖店销售A 纪念品每周获得的利润W 最大为3380元．【名师点睛】本题考查了二元一次方程组的应用，二次函数的应用，弄清题意，找准各量间的关系，正确列出方程组或解析式是解题的关键．12．（2019·广东初三中考模拟）在2014年巴西世界杯足球赛前夕，某体育用品店购进一批单价为40元的球服，如果按单价60元销售，那么一个月内可售出240套．根据销售经验，提高销售单价会导致销售量的减少，即销售单价每提高5元，销售量相应减少20套．设销售单价为x （x ≥60）元，销售量为y套．[参考公式：抛物线y =ax 2+bx +c （a ≠0）的顶点坐标是（2b a -，244ac b a -）]．（1）求出y 与x 的函数关系式．（2）当销售单价为多少元时，月销售额为14000元；（3）当销售单价为多少元时，才能在一个月内获得最大利润？最大利润是多少？【解析】（1）y =240-60205x -⨯， ∴y =-4x +480（x ≥60）．（2）根据题意可得，x （-4x +480）=14000，解得，x 1=70，x 2=50（不合题意舍去），∴当销售价为70元时，月销售额为14000元．（3）设一个月内获得的利润为w 元，根据题意，得w =（x -40）（-4x +480），=-4x 2+640x -19200，=-4（x -80）2+6400，∵-4<0，∴当x =80时，w 的最大值为6400，∴当销售单价为80元时，才能在一个月内获得最大利润，最大利润是6400元．【名师点睛】本题考查了一元二次方程的应用，二次函数的应用，二次函数的最值，弄清题意，找准各量间的关系并熟练相关的公式是解题的关键．。

2019年深圳市高三年级第二次调研考试数学(理)试题与答案

14． (1, 3) ．
15． 3 ．
三、解答题：本大题共 6 小题，满分 80 分．解答须写出文字说明、证明过程和演算步骤．
16．（本小题满分 12 分）
(本题考查向量的数量积、两角和的正弦公式、三角形的面积公式、三角函数的性质等
知识，考查化归转化的数学思想和运算求角能力
)
解：由已知可知
f x m n cos2 x 3sin x cos x
等知识，考查数形结合、化归转化的数学思想和方法，以及空间想象能力、
推理论证能力和
运算求解能力 )
解: （ 1） (解法一 )：由题意可知 8 3 解得 AD 2 3 ，
2 2 AD ，
………… 1分
在 AOP 中， AP 22 22 2 2 2 cos120O 2 3 ，
B
DE =
．
图3
三、解答题：本大题共 6 小题，满分 80 分．解答须写出
文字说明、证明过程和演算步骤．
16．（本小题满分 12 分）
已知 m cosx, 3sin x ， n cos x,cos x ，设 f x m n ．
（ 1）求函数 f x 的最小正周期及其单调递增区间；
（ 2）若 b、c 分别是锐角 ABC 的内角 B、 C 的对边，且 b c
3 C． 3
2
B．1 D．2
6．设 a 0 ， b 0 ，则以下不等式中，不恒成立的是
A．(a
1 b)(
1 )
4
ab
b2 b B．
a2 a
C． a b
a
1ab 1a
D． aabb abb a
b 1b
俯视图图1
7．已知 a 是实数，则函数 f( x) sin ax 的导函数的图象可能是

(完整版)深圳市2019届高三第一次调研考试理科数学(word精排有答案)

深圳市2019届高三第一次调研考试数学理科2019.02.21一、选择题：本大题共 12小题，每小题5分，每小题的四个选项中，只有一项是符合题目要求 1 .复数zi （2 i ）的共轴复数是（）A. 1 2iB. 1 2iC. 1 2iD. 1 2i2 .已知集合A x|y lg(2 x), B x|2x 3x 0 , 则A B( )A. x 10 x 2B. x|0x 2C. x|2 x 3D. x|2 x 33 ,设S n 为等差数列 a n 的前n 项和. 若S 525, a 3 a 4 8 ,则 a n 的公差为（A. 2 B 1 C.1D. 24 .己知某产品的销售额 y 与广告费用 x 之间的关系如下表：）A . 42万元 B. 45万元 C. 48万元 D . 51万元5.如图所示，网格纸上小正方形的边长为1,粗线画出的是由一个棱柱挖去一个棱锥后的几何体的三视图，则该几何体的体积为（）C. 486 .己知直线x 一是函数f （x ） sin （2x ）（| | ―）与的图象的一条对称轴,62为了得到函数y f （x ）的图象，可把函数y sin 2x 的图象（）A. 2B. 1C. 0D. 1 8.古希腊雅典学派算学家欧道克萨斯提出了 “黄金分割”的理论，利用尺规作图可画出己知线段的黄金分割点，具体方法如下：（l ）取线段AB 2,过点B 作AB 的垂线，并用圆规在垂线上截取 BC -AB ，连接AC; （2）以C 为圆心，BC 为半2径画弧，交 AC 于点D; （3）以A 为圆心，以AD 为半径画弧，交 AB 于点 E.则点E 即为线段AB 的黄金分割点.若在线段 AB 上随贝取一点F ,则使得BE AF AE 的概率约为（）（参考数据：J 5 2.236）A. 0.236B. 0.382C. 0.472D. 0.6189 .已知偶函数f （x ）的图象经过点（1,2），且当0 a b 时，不等式现）一堕 v 0恒成立，则 b a 使得f （x 1） 2成立的x 的取值范困是（）表面积为（）D. 32A .向左平行移动一个单位长度6 C.向左平行移动一个单位长度 12B.向右平行移动一个单位长度6D.向右平行移动一个单位长度127 .在ABC 中,ABC 60 , BC2AB 2, E 为AC 的中点，则AB BEA• (0,2)B.(2,0) y kx （k好经过双曲线的右焦点A. V 210.已知直线C.( .,,,x 20)与双曲线a(2, D • ( , 2) (0,b 2F ,若 ABF 的面积为B.石C. 20,b 0）交于A,B 两点，以4a 2,则双曲线的离心率为（D.灰1(a AB 为直径的圆恰11 .已知A, B,C 为球。

深圳市2019年高三年级第二次调研考试数学(理科)试题(含答案)

学（1）求 ABC 的大小；
（2）求△ ABC 的面积．
科解：（1）(法一)依题意设 ABD = 2CBD = 2 ，
∵ AD = 2CD ， AC = 2 5 ，
∴ AD = 4 5 ， CD = 2 5 ，
育3
3
…………………………………………2 分
在△ BAD 中，由正弦定理，可得 AB = AD ，
Sn
Sn−1
令 bn
=
2n S
+
n
1
，则
bn
− bn−1
=
2（n

2 ），
数列{bn}是以 b1
=
3 S1
=
3 a1
= 1为首项，公差 d
=
2 的等差数列，
bn
=
2n
−1，即
2n +1 Sn
=
2n
−1 ，
Sn
=
2n +1 2n −1
，

S1S2

Sm
=
3
5 3

2m 2m
+1 −1
=
2m
+1
，
由 2m +1 2019 ，解得 m 1009 ，即正整数 m 的最小值为1009 ，故应填1009 ．
三、解答题：解答应写出文字说明，证明过程或演算步骤．
理科数学试题答案及评分参考第2页（共13页）
市教育科
院
17．（本小题满分 12 分）
究
研已知△ ABC 中，AB = 2BC ，AC = 2 5 ，点 D 在边 AC 上，且 AD = 2CD ，ABD = 2CBD ．
教 sin ADB sin ABD

广东省2025届高三上学期毕业班调研考试(一) 数学试卷(含解析)

2025届广东省高三毕业班调研考试（一）数学试卷及答案一、单选题（本大题共8小题）1．已知集合2{|8150},{|5}A x x x B x x =∈-+≤=<Z ，则A B ⋂=（）A．{}3B．{}3,4C．{}4,5D．{}3,4,52．已知1z ，2z 是两个虚数，则“1z ，2z 均为纯虚数”是“12z z 为实数”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件3．已知a和b 的夹角为150︒，且2,a b == ()2a b b +⋅= （）A．9-B．3-C．3D．94．已知π2sin sin 33αα⎛⎫+-= ⎪⎝⎭，则πcos 23α⎛⎫+= ⎪⎝⎭（）A．59-B．19-C．19D．595．已知等比数列{}n a 为递增数列，n nnb a=.记,n n S T 分别为数列{}{},n n a b 的前n 项和，若2133312a a a S T =+=，，则n S =（）A．141n --B．()11414n --C．()14112n-D．24n -6．已知体积为的球O 与正四棱锥的底面和4个侧面均相切，已知正四棱锥的底面边长为则该正四棱锥体积值是（）A．B．C．D．7．斐波那契数列因数学家斐波那契以兔子繁殖为例而引入，又称“兔子数列”.这一数列如下定义：设{}n a 为斐波那契数列，()*12121,1,3,N n n n a a a a a n n --===+≥∈，其通项公式为n n n a ⎡⎤⎛=-⎥ ⎥⎝⎭⎝⎭⎦，设n是2log 1(14(x x x ⎡⎤⎣⎦+-<+的正整数解，则n 的最大值为（）A．5B．6C．7D．88．函数()ln f x x =与函数()212g x mx =+有两个不同的交点，则m 的取值范围是（）A．21,e ⎛⎫-∞ ⎪⎝⎭B．21,2e ⎛⎫-∞ ⎪⎝⎭C．210,e ⎛⎫⎪⎝⎭D．210,2e ⎛⎫ ⎪⎝⎭二、多选题（本大题共3小题）9．现有十个点的坐标为()()()121000,x x x ,,,,,，它们分别与()()()1210101010y y y ,,,,,,关于点(3,5)对称已知1210,,,x x x 的平均数为a ，中位数为b ，方差为c ，极差为d ，则1210,,,y y y 这组数满足（）A．平均数为6a -B．中位数为6b -C．方差为cD．极差为d10．设123,,z z z 是非零复数，则下列选项正确的是（）A． 2211z z =B．1212z z z z +=+C．若122i 2z --=，则116i z +-的最小值为3D．若22i i 4z z ++-=，则2z的最小值为11．已知定义在R 上的函数()f x 的图象连续不间断，当()()0e e e 0x f x f x ≥+--=，，且当>0时，()()e e 0f x f x ''++->，则下列说法正确的是（）A．()e 0f =B．()f x 在(),e -∞上单调递增，在()e,+∞上单调递减C．若()()1212,x x f x f x <>，则212ex x +<D．若12,x x 是()()()2e 2g xf x x =+--在()0,2e 内的两个零点，且12x x <，则()()211ef x f x <<三、填空题（本大题共3小题）12．已知等差数列{}n a 的首项12a =，公差3d =，求第10项10a 的值为.13．若()554325432102x a x a x a x a x a x a +=+++++，则531420a a a a a a ++=++.14．如图，在矩形ABCD 中，8,6,,,,,AB BC E F G H ==分别是矩形四条边的中点，点Q 在直线HF 上，点N 在直线BC 上，,,OQ kOH CN kCF k ==∈R，直线EQ 与直线GN 相交于点R ，则点R 的轨迹方程为.四、解答题（本大题共5小题）15．在ABC 中，角A B C ，，的对边分别为a b c ，，，已知2cos2cos22sin 2sin sin B A C B C-=-(1)求A ；(2)若23b c P Q ==，，，分别为边a b ，上的中点，G 为ABC 的重心，求PGQ ∠的余弦值.16．设A B ，两点的坐标分别为())3,0,3,0.直线AH BH ，相交于点H ，且它们的斜率之积是13-.设点H 的轨迹方程为C .(1)求C ;(2)不经过点A 的直线l 与曲线C 相交于E 、F 两点，且直线AE 与直线AF 的斜率之积是13-，求证：直线l 恒过定点.17．如图所示，四边形ABCD 是圆柱底面的内接四边形，AC 是圆柱的底面直径，PC 是圆柱的母线，E 是AC 与B 的交点，608AB AD BAD AC ∠=== ，，.(1)记圆柱的体积为1V ，四棱锥P ABCD -的体积为2V ，求12V V ；(2)设点F 在线段AP 上，且存在一个正整数k ，使得PA kPF PC kCE ==，，若已知平面FCD 与平面PCD 的夹角的正弦值为1313，求k 的值.18．已知函数()()1ln f x x x =-，(1)已知函数()()1ln f x x x =-的图象与函数()g x 的图象关于直线=−1对称，试求()g x ；(2)证明()0f x ≥；(3)设0x 是()1f x x =+的根，则证明：曲线ln y x =在点()00,ln A x x 处的切线也是曲线e x y =的切线.19．如果函数()F x 的导数为()()F x f x '=，可记为()()d f x x F x =⎰，若()0f x ≥，则()()()baf x dx F b F a =-⎰表示曲线()y f x =，直线x a x b ==，()a b ＜以及x 轴围成的“曲边梯形”的面积.如：22d x x x C =+⎰，其中C 为常数；()()222204xdx C C =+-+=⎰，则表0,1,2x x y x C ===+及x 轴围成图形面积为4.(1)若()()()e1d 02xf x x f =+=⎰，，求()f x 的表达式；(2)求曲线2y x =与直线6y x =-+所围成图形的面积；(3)若()[)e 120,x f x mx x =--∈+∞，，其中m ∈R ，对[)0,a b ∀∈+∞，，若a b >，都满足()()0d d a b f x x f x x >⎰⎰，求m 的取值范围.参考答案1．【答案】B【分析】先解不等式求得集合A ，进而求得A B ⋂.【详解】集合()(){}2{|8150}{|350}3,4,5A x x x x x x =∈-+≤=∈--≤=Z Z .而{|5}B x x =<，故{}3,4A B ⋂=.故选B.2．【答案】A【分析】设12i,i(,R z b z c b c ==∈且,0)b c ≠,可得12z z ∈R ，如121i 12+2i 2z z +==，可得结论.【详解】若12,z z 均为纯虚数，设12i,i(,z b z c b c ==∈R 且,0)b c ≠,则12i i z b b z c c ==∈R ，所以“12,z z 均为纯虚数”是12zz 是实数的充分条件，当121i,22i z z =+=+，121i 12+2i 2z z +==，所以“12,z z 均为纯虚数”是12z z 是实数的不必要条件，综上所述：“12,z z 均为纯虚数”是12z z 是实数的充分不必要条件.故选A.3．【答案】C【分析】根据向量数量积运算求得正确答案.【详解】()222a b b a b b+⋅=⋅+ 2cos1502a b b=⋅⋅︒+2223⎛=+⋅= ⎝⎭.故选C.4．【答案】B【分析】利用两角和差公式以及倍角公式化简求值可得答案.【详解】由题干得2π1sin sin sin cos sin 332ααααα⎛⎫=+-=- ⎪⎝⎭1πsin cos 26ααα⎛⎫-=+ ⎪⎝⎭所以22ππ21cos 22cos 1213639αα⎛⎫⎛⎫⎛⎫+=+-=⨯-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，故选B.5．【答案】C【分析】利用等比数列的通项公式及前n 项和公式求解q 的值，再由数列的单调性进一步判断即可.【详解】2131133141122312a a a a q a S T q q q=⇒=⇒=+=⇒++=，则()()2121294214042q q q q q q -+=--=⇒==，.由于{}n a 为递增数列，则1144q a ==，，所以{}n a 的通项公式为24n n a -=所以()()11414411412nn n S -==--.故选C.6．【答案】A【分析】设正四棱锥P ABCD -的内切球的半径为R ，H 为底面中心，取CD 的中点F ，设O 点在侧面PCD 上的投影为Q 点，则Q 点在PF 上，利用∽ POQ PFH 求出球心到四棱锥顶点的距离h ，再由棱锥的体积公式计算可得答案.【详解】设正四棱锥P ABCD -的内切球的半径为R ，H 为底面中心，由体积为34π3R得R =，连接PH ，PH ⊥平面ABCD ，球心O 在PH 上，OH R =，取CD 的中点F ，连接,HF PF ，设O 点在侧面PCD 上的投影为Q 点，则Q 点在PF 上，且OQ PF ⊥，∽ POQ PFH ，球心到四棱锥顶点的距离为h ，所以=PQ PH OQ FH，h ，所以1181283333==ABCD V S PH .故选A.7．【答案】A【分析】利用给定条件结合对数的性质构造42n a <，两侧同时平方求最值即可.【详解】由题知n是2log 1(14(xx x ⎡⎤⎣⎦-<+的正整数解，故2log (1(14n nn ⎡⎤⎣⎦-<+，取指数得((4112n n n +--<，同除2n得，42n n -<⎝⎭⎝⎭，故42n n ⎡⎤⎫-⨯⎥⎪⎪⎥⎝⎭⎝⎭⎦，即42n a <，根据{}n a 是递增数列可以得到{}2n a 也是递增数列，于是原不等式转化为2812525n a <⨯<.而565,8a a ==可以得到满足要求的n 的最大值为5，故A 正确.故选A.8．【答案】D【分析】利用参变分离将函数图象有两个交点问题转化为y m =和()21ln 2x h x x -=的图象有两个交点，由导数求得ℎ的单调性并求得最大值即可得出结论.【详解】由()21ln 02mx x x +=>得22ln 1m x x -=，则问题转化为y m =和()21ln 2x h x x-=的图象有两个交点，而()()()2232112ln 21ln 2x x x x x h x x x ⎛⎫⋅-- ⎪-'⎝⎭==，令ℎ'>0，解得0e x <<，令ℎ'<0，解得e x >，故ℎ在()0,e 上单调递增，在()e,+∞单调递减，则()()2max 1e 2e h x h ==，ℎ大致图象如下所示：结合图象可知，m 的取值范围是210,2e ⎛⎫ ⎪⎝⎭故选D.9．【答案】ABCD【分析】根据对称知识可得()6110i i y x i i =-∈≤≤Z ，，结合平均数、中位数、方差、极差的性质，即可判断出答案.【详解】由于()()()121,0,,0,,,0x x x ，它们分别与()()()1210,10,,10,,,10y y y 关于点(3,5)对称，则有()6110i i x y i i +=∈≤≤Z ，，即有()6110i i y x i i =-∈≤≤Z ，.则由平均数的性质可得1210,,,y y y 这组数的平均数为6a -，结合中位数性质可知中位数为6b -，结合方差性质可得方差为c ，极差非负，所以极差为d .故选ABCD.10．【答案】CD【分析】利用共轭复数的概念和加减运算性质判断A，举反例判断B，利用复数模的性质得到轨迹方程，结合圆的性质判断C，利用复数模的性质得到轨迹方程，结合椭圆的性质判断D 即可.【详解】对于A.，设1i z a b =+，则1i z a b =-，所以22221(i)2i z a b a b ab =+=-+，2221(i)2i z a b a b ab =-=--，当,a b 有1个为0或全为0时， 2211z z =，当,a b 均不为0时，2211,z z 无法比较大小，故A 错误，对于B，当1i z =，2i z =-时，120z z +=，此时120z z +=，122z z +=，故1212z z z z +=+不成立，故B 错误，对于C，设1i z a b =+，因为122i 2z --=，所以i 22i 2a b +--=，故有2(2)i 2a b -+-=，可得22(2)(2)4a b -+-=,所以1z 的轨迹是以()2,2为圆心，2为半径的圆，而116i i 16i 1(6)i z a b a b +-=++-=++-=，故116i z +-表示点(),a b 到定点()1,6-的距离，由圆的性质可知，1min 16i 23z +-==，故C 正确，对于D，设2z a bi =+，所以2i i i (1)i z a b a b +=++=++=，2i i i (1)i z a b a b -=+-=+-=，而22i i 4z z ++-=，故4，所以得到点(),a b 到两定点()0,1-，()0,1的距离之和为4，故2z 的轨迹是以()0,1-，()0,1为焦点的椭圆，故轨迹方程为22143y x +=，而2z 表示(),a b 到原点的距离，由椭圆的几何性质可得当点B 在椭圆的左右顶点时，2z 取得最小值，此时2z =2min z =D 正确.故选CD .11．【答案】ACD【分析】A 选项，令=0，可求()e f ；B 选项，对()()e e e 0f x f x +--=两边求导，结合()()e e 0f x f x ''++->得()e 0f x '-<，()e 0f x '+>，可判断()f x 单调性；C 选项，12e x x ,,的大小关系进行分类讨论，利用函数单调性，证明不等式；D 选项，证明212e x x +<，利用函数单调性，证明()()12f x f x <且()()21e f x f x <，可得结论.【详解】A 选项，令=0，则有()()()()e e e 1e e 0f f f -=-=，所以()e 0f =，故A 正确.B 选项，对()()e e e 0f x f x +--=两边求导，得()()e e e 0f x f x '++-='，所以()()e e e f x f x +=-'-'，代入()()e e 0f x f x ''++->，得当>0时，()()1e e 0f x '-->，所以()e 0f x '-<.又因为()()e e 0f x f x ''++->，所以，()e 0f x '+>.因此，当e x <时，()0f x '<，()f x 在(),e -∞上单调递减；当e x >时，()0f x '>，()f x 在()e,+∞上单调递增.故B 错误.C 选项，对12e x x ,,的大小关系进行分类讨论：①当12e x x <≤时，()f x 在(),e -∞上单调递减，所以()()12f x f x >，显然有212e x x +<；②当12e x x ≤<时，()f x 在()e,+∞上单调递增，不符合题意；③当12e x x <<时，当0x ≥时，()()e e e f x f x +=-.令()()()()()()122e e,e 2e e 2e t x f t f t f x f x f x ∞=+∈+=->=-，，，又因为()()e 0f x f ≥=，所以()22e 0f x ->，因此()()()()1222e 2e 2e f x f x f x f x >=->-.因为12e 2e e x x <-<，，由()f x 的单调性得，212e x x +<.故C 正确.D 选项，因为()()()()()()2200e 202e 2e e 20e e 220g f g f g f =+->=+->=-=-<，，，所以120e 2e x x <<<<.先证212e x x +<，即证122e x x ->，即()12e 0g x ->，只需证()2112e (2e e)20f x x -+--->，即证()211e (e )20f x x +-->.事实上，()()()()()2211111e e 2e 20f x x f x x g x +-->+--==，因此212e x x +<得证.此时有1210e 2e 2e x x x <<<<-<.因为()()()()()22211122e 22e e 2e 2f x x x x f x =--+=---+<--+=，又()10f x ≠，所以()()211f x f x <，因为()()()2112e e f x f x f x <-=，又()10f x ≠，所以()()21e f x f x <.综上，()()211e f x f x <<，故D 正确.故选ACD.【方法总结】导函数中常用的两种常用的转化方法：一是利用导数研究含参函数的单调性，常化为不等式恒成立问题．注意分类讨论与数形结合思想的应用；二是函数的零点、不等式证明常转化为函数的单调性、极(最)值问题处理．证明不等式，构造一个适当的函数，利用它的单调性进行解题，是一种常用技巧.许多问题，如果运用这种思想去解决，往往能获得简洁明快的思路，有着非凡的功效.12．【答案】29【分析】根据等差数列的通项公式求得正确答案.【详解】依题意101922729a a d =+=+=.故答案为：29.13．【答案】121122【分析】利用赋值法令1x =，1x =-，联立方程组求解即可.【详解】令1x =，得()554321012243a a a a a a +==+++++，令1x =-，得()5543210121a a a a a a -+==-+-+-+，则()()543210543210531243112122a a a a a a a a a a a a a a a +++++--+-+-+-++===，且()()543210543210420243112222a a a a a a a a a a a a a a a ++++++-+-+-++++===，故531420121122a a a a a a ++=++.故答案为：121122.14．【答案】()221,3916y x y -=≠-【分析】以HF 所在直线为x 轴，GE 所在直线为y 轴建立平面直角坐标系，求出直线EQ 的方程与直线GN 的方程，联立求解即可.【详解】以HF 所在直线为x 轴，GE 所在直线为y 轴建立平面直角坐标系.因为8,6AB BC ==，所以()()()()()()0,0,4,0,4,0,0,3,0,3,4,3O H F E G C --，所以()4,0OH =- ()()0,3,4,3CF OC =-= ，又因为,OQ kOH CN kCF == ，所以()()4,0,0,3OQ k CN k =-=-，所以()()4,0,4,33Q k N k --.因为()()0,3,4,0E Q k --，所以直线EQ 的方程为334y x k=--①，因为()()0,3,4,33G N k -，所以直线GN 的方程为334ky x =-+②.由①可得()()3043xk x y =-≠+，代入②化简可得()2210916y x x -=≠，，结合图象易知点R 可到达()0,3G ，但不可到达()0,3E -，所以点R 的轨迹方程为()221,3916y x y -=≠-，故答案为：()221,3916y x y -=≠-.15．【答案】(1)π3；(2)133266-.【分析】(1)根据二倍角公式将已知条件变形转化，再根据正弦定理边角互化，带入到余弦定理即可求得；(2)根据已知设AB c AC b ==，，表达出AP BQ ，，再根据余弦定理可求得结果.【详解】（1）因为2cos2cos22sin 2sin sin B A C B C -=-，所以()()22212sin 12sin 2sin 2sin sin B A C B C ---=-，即222sin sin sin sin sin A B C B C =+-，由正弦定理得222a c b bc =+-，由余弦定理得1cos 2A =，因为()π0π3A A ∈=，，；（2）设AB c AC b== ，，1cos 2332b c b c A ⋅=⋅=⨯⨯= ，依题意可得()1122AP b c BC b c BQ b c =+=-=- ，，，所以AP===，BQ===()221111143917224424424AP BQ b c b c b b c c⎛⎫⋅=+-=-⋅-=--=-⎪⎝⎭，所以cosAP BQPGQAP BQ⋅∠==-⋅.16．【答案】(1)(2213x y x+=≠；(2)证明见解析.【分析】（1）设点H的坐标为(),x y，然后表示出直线,AH BH的斜率，再由它们的斜率之积是13-，列方程化简可得点H的轨迹方程；（2）设()()1122,,,E x yF x y，当直线l斜率不存在时，求得直线l为x=0，当直线l 斜率存在时，设直线:l y kx b=+，由13AE AFk k⋅=-得2213=-，将直线方程代入椭圆方程化简利用根与系数的关系，代入上式化简可得20b=，从而可求得直线恒过的定点.【详解】（1）设点H的坐标为(),x y，因为点A的坐标是()，所以直线AH的斜率AHk x=≠，同理，直线BH的斜率BHk x=，由已知，有(13x-≠±，化简，得点H的轨迹方程为(2213x y x+=≠，即点H的轨迹是除去()),两点的椭圆.（2）证明：设()()1122,,,E x yF x y①当直线l斜率不存在时，可知1221,x x y y==-，且有22111313AE AFx yk k⎧+=⎪⎪⎨⎪⋅=-⎪⎩，解得1101x y==±，，此时直线l为x=0，②当直线l斜率存在时，设直线:l y kxb=+，则此时有：2213AE AFk k+++++⋅==-联立直线方程与椭圆方程2213y kx b x y =+⎧⎪⎨+=⎪⎩，消去y 可得：()222316310kx kbx b +++-=，根据韦达定理可得：122631kb x x k -+=+，21223331b x x k -=+，所以2222222233613131336333131b kbk kb b k k b kb k k --⋅+⋅+++=---++++，所以222222(33)63113k b k b b k --++=-，所以221=-所以20b =，则0b =或b=，当b=时，则直线(:l y k x =+恒过A 点与题意不符，舍去，故0b =，直线l 恒过原点()0,0，结合①，②可知，直线l 恒过原点()0,0，原命题得证.【关键点拨】此题考查椭圆的轨迹方程，考查直线与椭圆的位置关系，考查椭圆中直线过定点问题，解题的关键是设出直线方程代入椭圆方程化简，利用根与系数的关系结合已知条件求解，考查计算能力.17；(2)4k =.【分析】（1）利用圆柱以及棱锥的体积公式，即可求得答案.（2）建立空间直角坐标系，求出相关点坐标，利用空间角的向量求法，结合平面FCD 与平面PCD 的夹角的正弦值，即可求得答案.【详解】（1）在底面ABCD 中，因为AC 是底面直径，所以90ABC ADC ∠=∠=，又AB AD =，故ACB ≌ACD，所以13042BAC DAC BAD BC CD AB AD ∠∠∠=======,,因为PC 是圆柱的母线，所以PC ⊥面ABCD ，所以211π()16π2V AC PC PC ==⨯，211112243232V AB BC PC PC=⨯⨯⨯⋅⋅=⨯⨯⨯⨯=,因此12VV=；（2）以C为坐标原点，以,CA CP为,x z轴正方向，在底面ABCD内过点C作平面PAC的垂直线为y轴，建立如图所示的空间直角坐标系.因为30BAC DAC AB AD∠∠===，，所以ABE≌ADEV，故90AEB AED∠∠== ，所以1622BE DE AB AE CE AC AE=====-=，，2PC kCE k==，因此()()()()()() 0,0,0,8,0,0,2,,0,0,2,2,,0,0,2C AD P k CD CP k==，()8,0,2PA k=-，因为PA kPF=，所以18,0,2PF PAk k⎛⎫==-⎪⎝⎭，则88,0,22,,0,22F k CF kk k⎛⎫⎛⎫-=-⎪ ⎪⎝⎭⎝⎭设平面FCD和平面PCD的法向量分别为()()111222,,,,,n x y z m x y z==，则有:()1111822020n CF x k zkn CD x⎧⋅=+-=⎪⎨⎪⋅=+=⎩，2222020m CP kzm CD x⎧⋅==⎪⎨⋅=+=⎪⎩，取())()221,,1,3,4n k k k k m⎛⎫=----=-⎪⎪⎝⎭，设平面FCD与平面PCD的夹角为θ，则sinθ=所以有：2cos cos,13m nθ==，整理得2120k k--=，2120k k-+=（无解，舍），由于k为正整数，解得4k=.18．【答案】(1)()()()3ln2,(2)g x x x x=----<-；(2)证明见解析；(3)证明见解析.【分析】（1）由()()11f x g x --=-+，得()()()12ln 1g x x x -+=----，再利用换元法求()g x ；（2）分区间讨论各因式的符号或利用导数证明；（3）取曲线e x y =上的一点()11e ,xB x ，设()ln g x x =在A 处的切线即是()ex h x =在B 处的切线，证明直线AB 的斜率等于()ln g x x =在A 处的切线斜率和()e xh x =在B 处的切线斜率即可.【详解】（1）因为()f x 的图象与()g x 的图象关于直线=−1对称，所以()()11f x g x --=-+.又因为()()()()()111ln 12ln 1f x x x x x ⎡⎤--=-----=----⎣⎦，所以()()()12ln 1g x x x -+=----，令1t x =-+，则1x t =+，所以()()][()()()21ln 113ln 2g t t t t t ⎡⎤=--+--+=----⎣⎦，因此()()()3ln 2,(2)g x x x x =----<-.（2）证明：解法1：当1x ≥时，10x -≥且ln 0x ≥，此时()()1ln 0f x x x =-≥；当01x <<时，10x -<且ln 0x <，此时()()1ln 0f x x x =->，故综上()0f x ≥.解法2：()1ln 1f x x x +'=-，令()1ln 1x x xϕ=+-，()2110x x x ϕ'=+>在()0,+∞上恒成立，故()x ϕ在()0,+∞上单调递增，即()f x '在()0,+∞上单调递增，因此当01x <<时，()()10f x f ''<=；当()()110x f x f ''≥≥=，；因此()f x 在()0,1上单调递减，在[)1,+∞上单调递增，故()()10f x f ≥=.（3）证明：不妨取曲线e x y =上的一点()11e ,xB x ，设()ln g x x =在A 处的切线即是()e xh x =在B 处的切线，则()()10101e x g x h x x ''===，得101ln x x =，则B 的坐标0011ln x x ⎛⎫ ⎪⎝⎭，，由于()0001ln 1x x x -=+，所以0001ln 1x xx +=-，则有()()2000000000002000000000011111ln ln 111111ln ln 11ABx x x x x x x x x x k g x x x x x x x x x x x ++-----======++--'++-，综上可知，直线AB 的斜率等于()ln g x x =在A 处的切线斜率和()e xh x =在B 处的切线斜率，所以直线AB 既是曲线ln y x =在点()00n ,l A x x 处的切线也是曲线e x y =的切线.19．【答案】(1)()e 1xf x x =++；(2)1256；(3)12m ≤.【分析】（1）根据新定义及()02f =计算得解；（2）根据新定义，构造函数()26g x x x =-+-即可得出面积；（3）根据所给条件可得()()d F x f x x =⎰在[)0,+∞上单调递增，转化为()0f x ≥在[)0,+∞恒成立，分离参数后利用导数求出函数最值即可得解.【详解】（1）()()e 1d e x xf x x x C =+=++⎰，其中C 为常数.而()02f =，即102C ++=，所以1=C ，所以()e 1xf x x =++.（2）联立26y x y x ⎧=⎨=-+⎩，解得123,2x x =-=，当32x -<<时，26x x -+>，令()26,g x x x =-+-()()2311d 623F x g x x x x x C ==-+-+⎰，则围成的面积()()()2389125d 23212189326S g x x F F -⎛⎫⎛⎫==--=-+----+= ⎪⎪⎝⎭⎝⎭⎰.（3）令()()d F x f x x =⎰，由题意可知，[)0,a b a b ∀∈+∞>，，，满足()()()()00F a F F b F ->-，即()()F a F b >，即()()d F x f x x =⎰在[)0,+∞上单调递增，进而()0f x ≥在[)0,+∞恒成立，e 120x mx --≥在()0,+∞恒成立.由于>0，即e 12x m x -≥，令()e 12x g x x-=，则()22e 2e 24x x x g x x -+'=，令()()2e 2e 22e 0x x xh x x h x x '=-+=≥，，所以ℎ在[)0,+∞上单调递增，所以()()00h x h ≥=，即()0g x '≥，进而()g x 在()0,+∞单调递增，而()000e 1e 1lim lim lim 222x x x x x g x x →+→+→+-===，所以()12g x ≥，所以12m ≤.【关键点拨】本题第三步关键在于利用a b >，都满足()()0d d abf x x f x x >⎰⎰，得出函数()()d F x f x x =⎰在[)0,+∞上单调递增，再转化为()0f x ≥在[)0,+∞恒成立，分离参数求解.。

2019年2月广东省深圳市高2019届高三年级第一次调研考试文科数学及参考答案

深圳市2019届高三第一次调研考试数学文试题2019.02.21一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合A＝{x｜－1≤x≤2}，B＝{1, 2, 3}，则A∩B＝(A) {1} (B) {2} (C) {1,2} (D) {1,2,3}2.设z＝221ii-+，则｜z｜＝（A）2(B) 2(C) 5(D) 33.在平面直角坐标系xoy中，设角α的顶点与原点O重合，始边与x轴的非负半轴重合，若角α终边过点P（2，－1)，则sin(π－2α）的值为（A）一45(B)一35（C）35(D)454.设x，y满足约束条件030426xyx y≤≤⎧⎪≤≤⎨⎪+≥⎩，则z＝3x＋y的最大值为(A) 7 (B）9 (C) 13(D) 155.己知()f x是定义在R上的偶函数，在区间（一∞，0］为增函数，且f（3）＝0，则不等式f (1一2x)＞0的解集为（A）（－l，0）(B) (－1，2)(C) (0，2) (D) (2，+∞)6.如图所示，网格纸上小正方形的边长为1.粗线画出的是由一个棱柱挖去一个棱锥后的几何体的三视图，则该几何体的体积为(A) 64(B) 68(C) 80 (D) 1097.52，则该圆锥的外接球表面积为（A）254π（B) 16π(C) 25π(D) 32π8. 古希腊雅典学派算学家欧道克萨斯提出了“黄金分割”的理论，利用尺规作图可画出己知线段的黄金分割点，具体方法如下：（l ）取线段AB ＝2，过点B 作AB 的垂线，并用圆规在垂线上截取BC ＝12AB ＝1，连接AC ；（2）以C 为圆心，BC 为半径画弧，交AC 于点D ；（3）以A 为圆心，以AD 为半径画弧，交AB 于点E ．则点E 即为线段AB 的黄金分割点．若在线段AB 上随机取一点F ，则使得BE ≤AF ≤AE 的概率约为（参考数据：5≈2.236）（A ）0.236 （B ）0.382 （C ）0.472 （D ）0.6189. 己知直线6x π=是函数f （x ）=sin(2)(||)2x πϕϕ+<与的图象的一条对称轴，为了得到函数 y ＝f （x ）的图象，可把函数y ＝sin2x 的图象（A ）向左平行移动6π个单位长度（B ）向右平行移动6π个单位长度（C ）向左平行移动12π个单位长度（D ）向右平行移动12π个单位长度 10．在长方体ABCD 一A 1B 1C 1D 1中，AB ＝2，BC 2，CC 1＝2，M 为AA 1的中点，则异面直线AC 与B 1M 所成角的余弦值为(A)66（B ）23 （C ）34（D ）23 11．己知F 1，F 2是椭圆22221(0)x y a b a b+=>>的左，右焦点，过F 2的直线与椭圆交于P ，Q 两点，PQ ⊥PF 1，且｜QF 1｜＝2｜PF 1｜，则△PF 1F 2与△QF 1F 2的面积之比为（A ）23 （B 2－1 （C 2+l （D ）312.己知函数ln ,0()1,0x x x f x x x >⎧=⎨+≤⎩，若12x x ≠，且12()()f x f x =，则｜12x x -｜的最大值为 (A) 1 (B)2 (C) 2 2 第II 卷本卷包括必考题和选考题两部分．第13～21题为必考题，每个试题考生都必须作答．第22～23题为选考题．考生根据要求作答．二、填空题：本大题共4小题，每小题5分．13、曲线1x y e x =-在点（1, f(1)）处的切线的斜率为 14.已知平面向量a ，b 满足｜a ｜＝2，｜b ｜＝4，｜2a +b ｜＝43，则a 与b 的夹角为．15.己知F 1，F 2是双曲线的两个焦点，以线段F 1F 2为直径的圆与双曲线的两条渐近线交于A ，B ，C ，D 四个点，若这四个点与F 1，F 2两点恰好是一个正六边形的顶点，则该双曲线的离心率为．16.在△ABC 中，∠ABC ＝150°，D 是线段AC 上的点，∠DBC ＝30°，若△ABC 的面积为3，当BD 取到最大值时，AC ＝三、解答题：解答应写出文字说明，证明过程或演算步骤．17．（本小题满分 12 分）记S n 为等差数列{a n }的前 n 项和．已知a 1 = 4，公差 d > 0 ， a 4 是 a 2 与 a 8 的等比中项．（1）求数列{a n }的通项公式；（2）求数列｛1nS ｝前 n 项和为Tn ．18．（本小题满分 12 分）工厂质检员从生产线上每半个小时抽取一件产品并对其某个质量指标 Y 进行检测，一共抽取了 48 件产品，并得到如下统计表．该厂生产的产品在一年内所需的维护次数与指标 Y 有关，具体见下表．（1）以每个区间的中点值作为每组指标的代表，用上述样本数据估计该厂产品的质量指标 Y 的平均值（保留两位小数）；（2）用分层抽样的方法从上述样本中先抽取 6 件产品，再从 6 件产品中随机抽取 2 件产品，求这 2 件产品的指标 Y 都在[9.8, 10.2]内的概率；（3）已知该厂产品的维护费用为 300 元/次．工厂现推出一项服务：若消费者在购买该厂产品时每件多加 100 元，该产品即可一年内免费维护一次．将每件产品的购买支出和一年的维护支出之和称为消费费用．假设这 48 件产品每件都购买该服务，或者每件都不购买该服务，就这两种情况分别计算每件产品的平均消费费用，并以此为决策依据，判断消费者在购买每件产品时是否值得购买这项维护服务？19．（本小题满分 12 分）已知四棱锥 P －ABCD 的底面 ABCD 为平行四边形， PD =DC ， AD ⊥PC ．（1）求证： AC =AP ；（2）若平面 APD ⊥ 平面 ABCD ， ∠ ADC = 120︒ ， AD = DC = 4 ，求点 B 到平面 PAC 的距离．20．（本小题满分 12 分）设抛物线C ：y 2 = 4x ，直线l : x －my －2= 0与C 交于 A ， B 两点．（1）若|AB ｜ 6 ，求直线l 的方程；（2）点 M 为 AB 的中点，过点 M 作直线 MN 与 y 轴垂直，垂足为 N 。

2019届高三上期末数学分类汇编(18)等差数列与等比数列(含答案)

（山东省德州市2019届高三期末联考数学（理科）试题）4.已知数列为等差数列，且成等比数列，则的前6项的和为（）A. 15B.C. 6D. 3【答案】C【解析】【分析】利用成等比数列,得到方程2a1+5d＝2，将其整体代入 {a n}前6项的和公式中即可求出结果．【详解】∵数列为等差数列，且成等比数列，∴，1，成等差数列，∴2，∴2＝a1+a1+5d，解得2a1+5d＝2，∴{a n}前6项的和为2a1+5d）=．故选：C．【点睛】本题考查等差数列前n项和的求法，是基础题，解题时要认真审题，注意等差数列、等比数列的性质的合理运用．（福建省宁德市2019届高三第一学期期末质量检测数学理科试题）3.等差数列中，，，则数列的前20项和等于（）A. -10B. -20C. 10D. 20【答案】D【解析】【分析】本道题结合等差数列性质，计算公差，然后求和，即可。

【详解】，解得，所以，故选D。

【点睛】本道题考查了等差数列的性质，难度中等。

（江西省新余市2019届高三上学期期末考试数学（理）试题）5.在等差数列中，已知是函数的两个零点，则的前10项和等于( )A. -18B. 9C. 18D. 20【答案】D【解析】【分析】由韦达定理得，从而的前10项和，由此能求出结果.【详解】等差数列中，是函数的两个零点，，的前10项和.故选：D.【点睛】本题考查等差数列的前n项和公式，是基础题，解题时要认真审题，注意等差数列的性质的合理运用.（湖南省长沙市2019届上学期高三统一检测理科数学试题）13.设等差数列的前项和为，且,则__________．【答案】【解析】分析：设等差数列{a n}的公差为d，由S13=52，可得13a1+d=52，化简再利用通项公式代入a4+a8+a9，即可得出．详解：设等差数列{a n}的公差为d，∵S13=52，∴13a1+d=52，化为：a1+6d=4．则a4+a8+a9=3a1+18d=3（a1+6d）=3×4=12．故填12.点睛：本题主要考查等差数列通项和前n项和，意在考查学生等差数列基础知识的掌握能力和基本的运算能力.（湖南省湘潭市2019届高三上学期第一次模拟检测数学（文）试题）3.已知数列是等比数列，其前项和为，，则（）A. B. C. 2 D. 4【答案】A【解析】【分析】由题意，根据等比数列的通项公式和求和公式，求的公比，进而可求解，得到答案。

2020届高考数学(理)一轮必刷题专题48 圆的方程(解析版)

考点48 圆的方程1．（广东省2019届高考适应性考试理）若向量a ，b ，c 满足a b ≠，0c ≠，且()()0c a c b -⋅-=，则a b a bc++-的最小值是（）AB ．C ．2D ．32【答案】C 【解析】设向量a OA =，b OB =，c OC =,则由()()0c a c b -⋅-=得0AC BC ⋅=,即C 的轨迹为以AB 为直径的圆，圆心为AB 中点M ，半径为1||2AB ，因此11||||||(||)||22c OC OM r OA OB AB =≤+=++ 1111(||)(||)(||)(||)2222OA OB OA OB a b a b =++-=++- 从而2a b a bc++-≥，选 C.2．（河南省重点高中2019届高三4月联合质量检测数学理）设是圆上的点，直线与双曲线：的一条斜率为负的渐近线平行，若点到直线距离的最大值为8，则（）A ．9B ．C ．9或D ．9或【答案】C 【解析】因为双曲线的一条斜率为负的渐近线的斜率为，所以，解得. 圆的圆心坐标是，半径为，因为圆心到直线距离为，所以点到直线距离的最大值为，解得或.当时，；当时，.综上，或.故选.3．（广西桂林市、崇左市2019届高三下学期二模联考数学理）过双曲线的右支上一点分别向圆：和圆：作切线，切点分别为，则的最小值为（）A．5 B．4 C．3 D．2【答案】A【解析】圆的圆心为，半径为；圆的圆心为，半径为，设双曲线的左右焦点为，，连接，，，，可得．当且仅当为右顶点时，取得等号，即最小值5．故选：．4．（福建省龙岩市2019届高三5月月考数学理）已知点A 在圆22(2)1x y -+=上，点B 在抛物线28y x=上，则||AB 的最小值为（） A ．1 B ．2 C ．3 D ．4【答案】A 【解析】由题得圆()2221x y -+=的圆心为（2,0），半径为1. 设抛物线的焦点为F(2,0),刚好是圆()2221x y -+=的圆心，由题得|AB|≥|BF|-|AF|=|BF|-1, 设点B 的坐标为(x,y),所以|AB|≥x -(-2)-1=x+1,因为x≥0，所以|AB|≥1，所以|AB|的最小值为1. 故选：A5．（新疆2019届高三第三次诊断性测试数学理）若直线1ax by +=与圆221x y +=有两个公共点，则点(),P a b 与圆221x y +=的位置关系是（）A ．在圆上B ．在圆外C ．在圆内D ．以上都有可能【答案】B 【解析】解：因为直线1ax by +=与圆221x y +=有两个公共点，1<，即1<因为点P 1，所以点P 在圆外，故选B ．6．（河南省焦作市2018-2019学年高三年级第三次模拟考试数学理）已知抛物线E ：y 2＝2px （p ＞0）的准线为l ，圆C ：（x ﹣2p ）2+y 2＝4，l 与圆C 交于A ，B ，圆C 与E 交于M ，N ．若A ，B ，M ，N 为同一个矩形的四个顶点，则E 的方程为（）A ．y 2＝xB ．y 2C ．y 2＝2xD ．y 2＝x【答案】C 【解析】【分析】如图，圆C ：（x ﹣2p ）2+y 2＝4的圆心C （2p ，0）是抛物线E ：y 2＝2px （p ＞0）的焦点， ∵圆C ：（x ﹣2p ）2+y 2＝4的半径为2， ∴|NC|＝2，根据抛物线定义可得：|NA|＝|NC|＝2． ∵A ，B ，M ，N 为同一个矩形的四个顶点， ∴点A ，N 关于直线x ＝2p 对称，即22N A P x x P +=⨯=，∴32N x p =， ∴|NA|＝322p p ⎛⎫-- ⎪⎝⎭＝2，∴2p ＝2，则E 的方程为y 2＝2x ．故选：C ．7．（闽粤赣三省十校2019届高三下学期联考数学理）过抛物线24y x =的焦点F 的直线交抛物线于A B 、两点，分别过A B 、作准线的垂线，垂足分别为A B ''、两点，以线段A B ''为直径的圆C 过点(2,3)-，则圆C 的方程为（）A ．22(1)(1)5x y ++-=B ．22(1)(1)17x y +++=C ．22(1)(2)26x y +++=D ．22(1)(2)2x y ++-=【答案】A 【解析】由抛物线方程可知：()1,0F ，准线方程为：1x =-设直线AB 方程为：1x my =+，代入抛物线方程得：2440y my --= 设()11,A x y ，()22,B x y ，则124y y m +=，124y y = 又()11,A y '-，()21,B y '-，C 在圆上 0A C B C ''∴⋅=即()()()()1211330y y -⨯-+--= ()12121030y y y y ⇒-++= 即101240m -+= 12m ⇒=∴圆心坐标为：()1,2m -，即()1,1-=∴圆的方程为：()()22115x y ++-=本题正确选项：A ．8．（东北三省三校（哈尔滨师大附中、东北师大附中、辽宁省实验中学)2019届高三第一次模拟数学理）Rt ABC ∆中，090ABC ∠=，AB =4BC =，ABD ∆中，0120ADB ∠=，则CD 的取值范围是（） A．2,2] B．(4,2] C．2,2]+ D．2,2]【答案】C 【解析】由题，以点B 为坐标原点，AB 所在直线为x 轴，BC 所在直线为y轴建立直角坐标系；(0,0);(0,4)B A C设点(,)D x y ，因为0120ADB ∠=，所以由题易知点D 可能在直线AB 的上方，也可能在AB 的下方；当点D 可能在直线AB 的上方；直线BD 的斜率1yk x=；直线AD的斜率2k =由两直线的夹角公式可得：2121tan12011k k k k x-=⇒=+⋅化简整理的22((1)4x y ++=可得点D的轨迹是以点1)M -为圆心，半径2r =的圆，且点D 在AB 的上方，所以是圆在AB 上方的劣弧部分；此时CD的最短距离为：22CM r -== 当当点D 可能在直线AB 的下方；同理可得点D的轨迹方程：22((1)4x y +-=此时点D的轨迹是以点N 为圆心，半径2r =的圆，且点D 在AB 的下方，所以是圆在AB 下方的劣弧部分；此时CD的最大距离为：22CN r +==所以CD的取值范围为2⎡⎤⎣⎦．9．（湖北省黄冈市2019届高三上学期元月调研理）已知圆关于对称，则的值为A ．B．1 C．D．0【答案】A【解析】化圆为．则圆心坐标为，圆关于对称，所以直线经过圆心，，得．当时，，不合题意，．故选A．10．（北京市朝阳区2018-2019学年度高三期末）在平面直角坐标系xOy中，过A（4，4），B（4，0），C （0，4）三点的圆被x轴截得的弦长为（）A．2 B．C．4 D．【答案】C【解析】根据题意，设过三点的圆为圆，其方程为,又由，则由，解得，即圆，令，得，解得，即圆M与轴的交点坐标分别为，所以圆M被轴截得的弦长为4，故选C.11．（江西省名校学术联盟2019届高三年级教学质量检测考试12月联考)数学理）已知点，，则以线段为直径的圆的方程为A ．B ．C ．D ．【答案】D 【解析】圆心为的中点，半径为，则以线段为直径的圆的方程为.故选D.12．（四川省南充市2018-2019学年上学期高2019届高三年级第一次高考适应性考试）点，是圆上的不同两点，且点，关于直线对称，则该圆的半径等于A ．B ．C ．1D ．3【答案】D 【解析】圆x 2+y 2+kx+2y-4=0的圆心坐标为（，因为点M ，N 在圆x 2+y 2+kx+2y-4=0上，且点M ，N 关于直线l ：x-y+1=0对称，所以直线l ：x-y+1=0经过圆心，所以．所以圆的方程为：x 2+y 2+4x+2y-4=0，圆的半径为：故选：C ．13．（2017届四川省成都市石室中学高三二诊模拟考试数学理）在直角坐标系xOy 中，点(0,3)A ，直线:24l y x =-，设圆C 的半径为1，圆心在l 上，若圆C 上存在唯一一点M ，使2M A M O =，则圆心C 的非零横坐标是__________．【答案】125【解析】圆心在l 上,设(),24C a a -,点(),M x y ,因为2MA MO ==,化简得:()2214x y ++=,所以点(),M x y 在以()0,1D -为圆心,以2为半径的圆上,又点(),M x y 在圆C 上,所以圆C 与圆D 有唯一公共点,即两圆相切,211CD =-=,或者213CD =+=,即251280a a -+=或25120a a -=,解得0a =(舍)或125,故填125. 14．（广东省肇庆市2019届高中毕业班第三次统一检测数学理）已知椭圆C ：2212x y +=，直线l ：1y x =-与椭圆C 交于A ，B 两点，则过点A ，B 且与直线m ：43x =相切的圆的方程为______．【答案】2211639x y ⎛⎫+-= ⎪⎝⎭．【解析】解：椭圆C ：2212x y +=，直线l ：1y x =-与椭圆C 交于A ，B 两点，联立可得：22121x y y x ⎧+=⎪⎨⎪=-⎩，消去y 可得，2225848y xy x xy x +--+，解得0x =或43x =，可得(0,1)A -，41(,)33B ，过点A ，B 且与直线m ：43x =相切的圆切点为B ，圆的圆心1(0,)3，半径为：43．所求圆的方程为：2211639x y ⎛⎫+-= ⎪⎝⎭．故答案为：2211639x y ⎛⎫+-= ⎪⎝⎭． 15．（宁夏石嘴山市第三中学2019届高三四模考试数学理）点(),M x y 在曲线C ：224210x x y -+-=上运动，22+1212150t x y x y a =+---，且t 的最大值为b ，若,a b R +∈，则111a b++的最小值为_____. 【答案】1 【解析】曲线C 可整理为：()22225x y -+= 则曲线C 表示圆心为()2,0，半径为5的圆()()2222+121215066222t x y x y a x y a =+---=++---设d =d 表示圆上的点到()6,6-的距离则max 515d ==2max 15222t a b ∴=--=，整理得：14a b ++=()111111*********b a a b a b a b a b +⎛⎫⎛⎫∴+=+++=⨯+++ ⎪ ⎪+++⎝⎭⎝⎭又121b a a b ++≥=+（当且仅当11b a a b +=+，即1a =，2b =时取等号） 1114114a b ∴+≥⨯=+，即111a b ++的最小值为1 本题正确结果：116．（贵州省贵阳市2019年高三5月适应性考试二理）圆与曲线相交于，，，四点，为坐标原点，则__________．【答案】.【解析】 ∵圆的圆心为M （-3，2）， ∴圆关于M （-3，2）中心对称，又曲线，关于（-3，2）中心对称， ∴圆与曲线的交点关于（-3，2）中心对称，不妨设与，与关于（-3，2）中心对称，则，,∴，故答案为.17．（北京市房山区2019年高考第一次模拟测试数学理）已知点A （-2，0），B （0，2），若点P 在圆（x-3）2+（y+1）2=2上运动，则面积的最小值为______．【答案】4 【解析】∵点A （-2，0），B （0，2），∴AB 的直线方程为=1，即x-y+2=0．圆心C （3，-1）到直线AB 的距离为d=，因为点P 在圆（x-3）2+（y+1）2=2上运动，所以点P到直线AB距离的最小值为：=，且.则ABP面积的最小值为.故答案为：4．18．（湖南省长沙市第一中学2018届高三下学期高考模拟卷三数学理）已知直线过定点，线段是圆的直径，则________.【答案】7.【解析】直线可化为，联立，解得点，∵线段是圆的直径，∴19．（广西桂林市、崇左市2019届高三下学期二模联考数学理）以抛物线：的顶点为圆心的圆交于两点，交的准线于两点.已知，，则等于__________．【答案】.【解析】如图：，，，，，，，，解得：，故答案为：．20．（北京市大兴区2019届高三4月一模数学理）在极坐标系下，点π(1,)2P 与曲线2cos ρθ=上的动点Q距离的最小值为_________．1 【解析】由题得点P 的直角坐标为（0,1），222222cos 2cos +201)1x y x x y ρθρρθ=∴=∴-=∴-+=，，，（，所以曲线是以点（1，0）为圆心，以1为半径的圆，所以点P 11-=.1．21．（江苏省南京市、盐城市2019届高三第二次模拟考试）在平面直角坐标系xOy 中，已知点()1,0A -，()5,0B .若圆()()22:44M x y m -+-=上存在唯一点P ，使得直线PA ，PB 在y 轴上的截距之积为5，则实数m 的值为______.【答案】【解析】根据题意，设P 的坐标为(,)a b ，直线PA 的方程为(1)1by x a =++，其在y 轴上的截距为1b a +，直线PB 的方程为(5)5b y x a =--，其在y 轴上的截距为55b a --，若点P 满足使得直线PA ，PB 在y 轴上的截距之积为5，则有5()()515b b a a ⨯-=+-，变形可得22(2)9b a +-=，则点P 在圆22(2)9x y -+=上，若圆22:(4)()4M x y m -+-=上存在唯一点P ，则圆M 与22(2)9x y -+=有且只有一个公共点，即两圆内切或外切，2，则两圆只能外切，则有2425m +=，解可得：m =故答案为：22．（湖北省十堰市2019届高三年级元月调研考试理）已知圆22:(6)(6)16M x y -+-=，点(8,4)A ，过点A 的动直线与圆M 交于P ，Q 两点，线段PQ 的中点为N ，O 为坐标原点，则OMN ∆面积的最大值为______．【答案】12 【解析】由题可知MN PQ ⊥，所以点N 在以线段AM 为直径的圆上，OMN ∆的边OM =N 到直线OM 的距离最大时，OMN ∆的面积最大，以线段AM 为直径的圆的圆心为()7,5，直线OM的方程为0x y -=，点()7,5到直线OM=所以N 到直线OM 的距离的最大值为故OMN ∆的面积的最大值为1122⨯=. 故答案为：1223．（江西省名校学术联盟2019届高三年级教学质量检测考试12月联考数学理）已知圆与轴相切于点，与轴正半轴交于点，，且，设点是圆上的动点，则的取值范围是__________．【答案】【解析】由题意，可设圆C 的方程为，则，，所以，则圆C 的方程为，即，可得，设，则== =，由题意可知，，所以.故答案为：. 24．（江苏省苏州市2018届高三调研测试理）在平面直角坐标系中，已知过点的圆和直线相切，且圆心在直线上，则圆的标准方程为__________．【答案】【解析】根据题意，设圆C 的圆心为（m ，n ），半径为r ，则圆C 的标准方程为（x ﹣m ）2+（y ﹣n ）2＝r 2，则有，解可得：m ＝1，n ＝﹣2，r，则圆C 的方程为：（x ﹣1）2+（y +2）2＝2，故答案为：（x ﹣1）2+（y +2）2＝225．（东北三省三校（哈尔滨师大附中、东北师大附中、辽宁省实验中学)2019届高三第一次模拟数学理）已知椭圆1C ：2214x y +=的左、右两个顶点分别为,A B ，点P 为椭圆1C 上异于,A B 的一个动点，设直线,PA PB 的斜率分别为12,k k ，若动点Q 与,A B 的连线斜率分别为34,k k ，且3412(0)kk kk λλ=≠，记动点Q的轨迹为曲线2C .（1）当4λ=时，求曲线2C 的方程；（2）已知点1(1,)2M ，直线AM 与BM 分别与曲线2C 交于,E F 两点，设AMF ∆的面积为1S ，BME ∆的面积为2S ，若[1,3]λ∈，求12S S 的取值范围. 【答案】(1) 224(2)x y x +=≠± (2) []5,7【解析】（1）设()00,P x y ()02x ≠±，则220014x y +=，因为()()2,0,2,0A B -，则2020001222000011422444x y y y k k x x x x -=⋅===-+---(),Q x y 设 ()2x ≠±所以2341222244y y y k k k k x x x λλ=⋅===-+--，整理得 2214x y λ+= ()2x ≠±.所以，当4λ=时，曲线2C 的方程为 ()2242x y x +=≠±.（2）设()()1122,,,E x y F x y . 由题意知，直线AM 的方程为：62x y =-，直线BM 的方程为：22x y =-+.由（Ⅰ）知，曲线2C 的方程为2214x y λ+= ()2x ≠±，联立 ()2262244x y x x y λλ=-⎧≠±⎨+=⎩，消去x ，得()29160y y λλ+-=，得 1691y λλ=+ 联立()2222244x y x x y λλ=-+⎧≠±⎨+=⎩，消去x ，得()2120y y λλ+-=，得 221y λλ=+2212111111sin 91222211111sin 2222MA MF AMF y y MA MF S S MB ME MB ME BME y y λλ∠--+=====+∠-- 设()918911g ，λλλλ+==-++ 则()g λ在[]1,3上递增又()()15,37g g ==，12S S ∴的取值范围为[]5,7 26．（四川省成都市高新区2019届高三上学期“一诊”模拟考试数学理）已知抛物线，过点的直线与抛物线相切，设第一象限的切点为. （Ⅰ）证明：点在轴上的射影为焦点；（Ⅱ）若过点的直线与抛物线相交于两点，圆是以线段为直径的圆且过点，求直线与圆的方程.【答案】（I ）详见解析；（II ）详见解析. 【解析】（Ⅰ）由题意知可设过点的直线方程为，由消去整理得，又因为直线与抛物线相切，所以，解得．当时，直线方程为，可得点坐标为，又因为焦点，所以点在轴上的射影为焦点．（Ⅱ）设直线的方程为，由，其中恒成立.设，，则，所以，．由于圆是以线段为直径的圆过点，则，所以所以，解得或．当时，直线的方程为，圆的方程为；当时，直线的方程为，圆的方程为．27．（江西省抚州市七校2019届高三10月联考数学理）已知圆与直线相切于点，圆心在轴上.（1）求圆的方程；（2）过点且不与轴重合的直线与圆相交于两点，为坐标原点，直线分别与直线相交于两点，记的面积分别是．求的取值范围.【答案】（1）；（2）.【解析】（1）由题可知，设圆的方程为，，解得，，所以圆的方程为．（2）由题意知，，设直线的斜率为，则直线的方程为，由，得，解得或，则点的坐标为．又直线的斜率为，同理可得点的坐标为．由题可知，，．因此，又，同理，所以，当且仅当时取等号．又，所以的取值范围是．。

数学分类汇编(2)命题及其关系、充分条件与必要条件

（山东省德州市2019届高三期末联考数学（理科）试题）6.设且，则是的（）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要【答案】D【解析】【分析】由题意看命题“ab＞1”与“”能否互推，然后根据必要条件、充分条件和充要条件的定义进行判断．【详解】若“ab＞1”当a＝﹣2，b＝﹣1时，不能得到“”，若“”，例如当a＝1，b＝﹣1时，不能得到“ab＞1“，故“ab＞1”是“”的既不充分也不必要条件，故选：D．【点睛】本小题主要考查了充分必要条件，考查了对不等关系的分析，属于基础题．（辽宁省实验中学、大连八中、大连二十四中、鞍山一中、东北育才学校2019届高三上学期期末考试数学（文）试题）3.设，则“”是“函数在定义域上是奇函数”的（）A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件【答案】A【解析】【分析】注意到当时，函数是奇函数，故是函数为奇函数的充分不必要条件.【详解】当时，，，函数为奇函数；当时，，，函数为奇函数.故当时，函数是奇函数，所以是函数为奇函数的充分不必要条件.故选A.【点睛】本小题主要考查充要条件的判断，考查函数奇偶性的定义以及判断，属于基础题.（四川省绵阳市2019届高三第二次（1月）诊断性考试数学理试题）4.“a＝b＝1”是“直线ax－y+1＝0与直线x－by－1＝0平行”的( )A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件【答案】A【解析】【分析】a＝b＝1时，两条直线平行成立，但由ax－y+1＝0与直线x－by－1＝0平行，可得ab＝1，不一定是a＝b＝1．【详解】a＝b＝1时，两条直线ax－y+1＝0与直线x－by－1＝0平行，反之由ax－y+1＝0与直线x－by－1＝0平行，可得：ab＝1，显然不一定是a＝b＝1，所以，必要性不成立，∴“a＝b＝1”是“直线ax－y+1＝0与直线x－by－1＝0平行”的充分不必要条件．故选：A．【点睛】本题考查了直线平行的判定与性质定理、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．（湖南省长沙市2019届上学期高三统一检测理科数学试题）3.在等比数列中，“，是方程的两根”是“”的（）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【答案】A【解析】【分析】结合充分、必要条件判定，即可。

广东省2020届高三数学复习典型题专项训练：统计与概率

广东省2020届高三数学一轮复习典型题专项训练统计与概率一、选择、填空题 1、（广州市2018高三一模）若A ，B ，C ，D ，E 五位同学站成一排照相，则A ，B 两位同学不相邻的概率为A ．45B ．35C ．25D ．152、（珠海市2019届高三9月摸底考试）如图，海水养殖厂进行某水产品的新旧网箱养殖方法产量对比，收获时各随机抽取了100个网箱，测量各箱水产品产量(单位：kg)，其频率分布直方图如图根据频率分布直方图，下列说法正确的是①新网箱产量的方差的估计值高于旧网箱产量的方差的估计值 ②新网箱产量中位数的估计值高于旧网箱产量中位数的估计值 ③新网箱产量平均数的估计值高于旧网箱产量平均数的估计值④新网箱频率最高组的总产量的估计值接近旧网箱频率最高组总产量估计值的两倍 A. ①②③ B. ②③④ C. ①③④ D. ①④3、（华附、省实、广雅、深中2019届高三上学期期末联考）.如图，在正方形区域内任取一点，则此点取自阴影部分的概率是A.21-B.()2421π-C.()2421π+D.164、（深圳市宝安区2019届高三9月调研）某景区在开放时间内，每个整点时会有一趟观光车从景区入口发车，某人上午到达景区入口，准备乘坐观光车，则他等待时间不多于10分钟的概率为（）A．1 10B．16C．15D．565、（佛山市2019届高三教学质量检测（二））下图是1990年～2017年我国劳动年龄（15～64岁）人口数量及其占总人口比重情况：根据图表信息，下列统计结论不正确．．．的是（）A．2000年我国劳动年龄人口数量及其占总人口比重的年增幅均为最大B．2010年后我国人口数量开始呈现负增长态势C．2013年我国劳动年龄人口数量达到峰值D．我国劳动年龄人口占总人口比重极差超过6%6、（广州市2019年普通高中毕业班综合测试（二））某公司生产A，B，C三种不同型号的轿车，产量之比依次为2：3：4，为检验该公司的产品质量，用分层抽样的方法抽取一个容量为n的样本，若样本中A 种型号的轿车比B种型号的轿车少8辆，则n＝A. 96B. 72C. 48D. 367、（广州市2019年普通高中毕业班综合测试（二））从某班6名学生（其中男生4人，女生2人）中任选3人参加学校组织的社会实践活动．设所选3人中女生人数为，则数学期望＝A． B.1 C. D．28、（揭阳市2019届高三第二次模拟）某公司2018年在各个项目中总投资500万元，右图是几类项目的投资占比情况，已知在1万元以上的项目投资中，少于3万元的项目投资占821，那么不少于3万元的项目投资共有A．56万元B．65万元C．91万元D．147万元5千元至1万元的项目投资（占33%）1万元以上的项目投资5千元以下的项目投资（占46%）9、（湛江市2019届高三调研）已知某地区中小学生人数如图所示，用分层抽样的方法抽取200名学生进行调查，则抽取的高中生人数为A ．10B ．40C ．30D ．2010、（汕尾市2019届高三上学期期末）下图是某地某月1日至15日的日平均温度变化的拆线图，根据该拆线图，下列结论正确的是A ．这15天日平均温度的极差为15︒CB ．连续三天日平均温度的方差最大的是7日，8日，9日三天C ．由拆线图能预测16日温度要低于19 ︒CD ．由拆线图能预测本月温度小于25 ︒C 的天数少于温度大于25︒C 的天数 11、（韶关市2019届高三上学期期末）A ，B 两名同学在5次数学考试中的成绩统计如右边的茎叶图所示，若A ，B 两人的平均成绩分别是x A ，x B ，观察茎叶图，下列结论正确的是 A 、x A ＜x B ，B 比A 成绩稳定 B 、x A ＞x B ，B 比A 成绩稳定 C 、x A ＜x B ，A 比B 成绩稳定 D 、x A ＞x B ，A 比B 成绩稳定12、（肇庆市2019届高三上学期期末）太极是中国古代的哲学术语，意为派生万物的本源.太极图是以黑白两个鱼形纹组成的圆形图案，俗称阴阳鱼.太极图形象化地表达了阴阳轮转，相反相成是万物生成变化根源的哲理.太极图形展现了一种互相转化，相对统一的形式美.按照太极图的构图方法，在平面直角坐标系中，圆O 被sin3y x π=的图象分割为两个对称的鱼形图案，图中的两个一黑一白的小圆通常称为“鱼眼”，已知小圆的半径均为1，现在大圆内随机投放一点，则此点投放到“鱼眼”部分的概率为A.89 B. 29 C. 19 D. 11813、（珠海市2019届高三上学期期末）在（0，2π）上随机取一个数x ，使得0＜tanx ＜1成立的概率是（） A 、18 B 、13 C 、12 D 、2π14、（雷州市2019届高三上学期期末）赵爽是我国古代数学家、天文学家，大约在公元222年，赵爽为《周碑算经》一书作序时，介绍了“勾股圆方图”，亦称“赵爽弦图”（以弦为边长得到的正方形是由4个全等的直角三角形再加上中间的一个小正方形组成的）．类比“赵爽弦图”，可类似地构造如图所示的图形，它是由3个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形，设22==AF DF ，若在大等边三角形内部（含边界）随机取一点，则此点取自小等边三角形（阴影部分）的概率是 A ．134 B ．13132 C ．269D ．2613315、（茂名市2019届高三上期末）七巧板是我国古代劳动人民发明的一种智力玩具，它是由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成的．如图1是一个用七巧板拼成的正方形，若在此正方形中任取一点，则此点取自黑色部分的概率为（） A 、14 B 、 38 C 、 316 D 、 71616、（汕头市2019届高三上学期期末）如图所示，半径为1的圆 O 是正方形 MNPQ 的内切圆、将一颗豆子随机地扔到正方形 MNPQ 内，用 A 表示事件 “ 豆子落在圆 O 内”， B 表示事件“ 豆子落在扇形 OEF （阴影部分）内”，则 P (B ｜A ) ＝A.4πB.14C.16πD.1817、（广东省2019届高三3月一模）古希腊数学家欧多克索斯在深入研究比例理论时，提出了分线段的“中末比”问题：将一线段AB 分为两线段AC ，CB ，使得其中较长的一段AC 是全长AB 与另一段CB 的比例中项，即满足＝＝512-≈0.618．后人把这个数称为黄金分割数，把点C 称为线段AB 的黄金分割点在△ABC 中，若点P ，Q 为线段BC 的两个黄金分割点，在△ABC 内任取一点M ，则点M 落在△APQ 内的概率为（）A ．512- B ．﹣2 C ．51- D ．52- 18、（广州市2019届高三3月综合测试（一））刘徽是我因魏晋时期的数学家，在其撰写的《九章算术注》中首创“割圆术”，所谓“割圆术”，是用圆内接正多边形的面积去无限逼近圆面积并以此求取圆周率的方法，如图所示，圆内接正十二边形的中心为圆心O ，圆O 的半径为2，现随机向圆O 内段放a 粒豆子，其中有b 粒豆子落在正十二边形内(,,a b N b a *∈<)，则圆周率的近似值为 A.b a B.a b C.3a b D.3b a19、（深圳市2019届高三第一次（2月）调研考试）己知某产品的销售额y 与广告费用x 之间的关系如下表：若求得其线性回归方程为$ 6.5y x a =+，则预计当广告费用为6万元时的销售额为（A ）42万元（B ）45万元（C ）48万元（D ）51万元20、（肇庆市2019高三二模）太极是中国古代的哲学术语，意为派生万物的本源．太极图是以黑白两个鱼形纹组成的圆形图案，俗称阴阳鱼．太极图形象化地表达了阴阳轮转，相反相成是万物生成变化根源的哲理．太极图形展现了一种互相转化，相对统一的形式美．按照太极图的构图方法，在平面直角坐标系中，圆O 被的图象分割为两个对称的鱼形图案，图中的两个一黑一白的小圆通常称为“鱼眼”，已知小圆的半径均为1，现在大圆内随机投放一点，则此点投放到“鱼眼”部分的概率为（）A ．B ．C ．D ．21、（湛江2019高三一模）某人连续投篮6次，其中3次命中，3次未命中，则他第1次、第2次两次均未命中的概率是 A 、12 B 、310 C 、14 D 、1522、（汕头市2019届高三第一次（3月）模拟考试）将含有甲、乙、丙的6人平均分成两组参加“文明交通”志愿者活动，其中一组指挥交通，一组分发宣传资料，则甲、乙至少一人参加指挥交通且甲、丙不在同一组的概率为（） A ．320 B ．340 C ．920 D ．94023、（湛江2019高三一模）已知空间直角坐标系中的四个点A （4，1，1），B （4，－2，－1），C （－2，－2，－1），D （－2，1，－1），经过A ，B ，C ，D 四点的球记作球M 。

干货提取01(第一篇)- 干货提取之2019届高三数学最新模拟试题精选精析(原卷版)

干货提取之2019届高三数学最新模拟试题精选精析 01一.选择题精选1.【广东省惠州市2019届高三第一次调研考试】已知三棱锥S ABC -的底面是以AB 为斜边的等腰直角三角形，2AB =， 2SA SB SC ===，则三棱锥的外接球的球心到平面ABC 的距离是（）A B ．1 C D 2. 【安徽省合肥市2019届高三第一次教学质量检测】某调查机构对全国互联网行业进行调查统计，得到整个互联网行业从业者年龄分布饼状图、90后从事互联网行业者岗位分布条形图，则下列结论中不一定正确的是( ).注：90后指1990年及以后出生，80后指1980-1989年之间出生，80前指1979年及以前出生.A ．互联网行业从业人员中90后占一半以上B ．互联网行业中从事技术岗位的人数超过总人数的20%C ．互联网行业中从事运营岗位的人数90后比80前多D ．互联网行业中从事技术岗位的人数90后比80后多 3. 【河北省武邑中学2019届高三上学期期末考试】在中，为的中点，，则（） A ． B ．C ．3D ．4. 【河北省武邑中学2019届高三上学期期末考试】设函数，若，则实数的取值范围是（） A ．B ．C ．D ．5. 【安徽省合肥市2019届高三第一次教学质量检测】如图，网格纸上小正方形的边长为1，粗线画出的是某多面体的三视图，则该几何体的体积为( ).A．B．C．D．6.【河北省武邑中学2019届高三上学期期末考试】在三棱锥中，,是线段上一动点，线段长度最小值为，则三棱锥的外接球的表面积是（）A．B．C．D．7.【安徽省定远重点中学2019届高三上学期期末考试】过抛物线（）的焦点作斜率大于的直线交抛物线于，两点（在的上方），且与准线交于点，若，则（）A．B．C．D．8.【安徽省合肥市2019届高三第一次教学质量检测】某商场进行购物摸奖活动，规则是：在一个封闭的纸箱中装有标号分别为1，2，3，4，5的五个小球，每次摸奖需要同时取出两个球，每位顾客最多有两次摸奖机会，并规定：若第一次取出的两球号码连号，则中奖，摸奖结束；若第一次未中奖，则将这两个小球放回后进行第二次摸球.若与第一次取出的两个小球号码相同，则为中奖.按照这样的规则摸奖，中奖的概率为( ).A．B．C．D．9.【河南省周口市2019届高三上学期期末调研考试】函数的图像大致为( )A．B．C．D．10.【河南省周口市2019届高三上学期期末调研考试】如图，图中的大、小三角形分别为全等的等腰直角三角形，向图中任意投掷一飞镖，则飞镖落在阴影部分的概率为( )A．B．C．D．11.【河南省周口市2019届高三上学期期末调研考试】已知双曲线，分别过其左、右焦点，作圆：的切线，四条切线围成的四边形的面积为（），则双曲线的离心率为( )A．B．C．2D．12.【安徽省合肥市2019届高三第一次教学质量检测】设双曲线()的左、右焦点分别为，过的直线分别交双曲线左右两支于点，连结，若，，则双曲线的离心率为( ).A．B．C．D．13.【河南省周口市2019届高三上学期期末调研考试】已知函数，若在区间内无最值，则的取值范围是( )A．B．C．D．14.【河北省武邑中学2019届高三上学期期末考试】函数是定义在上的可导函数，为其导函数，若且，则不等式的解集为（）A．B．C．D．15.【安徽省合肥市2019届高三第一次教学质量检测】已知函数有两个不同的极值点，若不等式恒成立，则实数的取值范围是( ).A．B．C．D．二．填空题精选1．【山西省长治二中、忻州一中、临汾一中、康杰中学、晋城一中2019届高三上学期第一次联考】已知ABC ∆的面积为S ，三内角C B A ,,的对边分别为c b a ,,．若2224c b a S +=+，则)4πco s(si n +-B C 取最大值时C = ．2. 【河北省武邑中学2019届高三上学期期末考试】已知三棱锥的三条侧棱两两互相垂直，且,则该三棱锥的外接球的体积为____．3. 【河南省周口市2019届高三上学期期末调研考试】在中，，，，过作交于，则__________．4. 【安徽省定远重点中学2019届高三上学期期末考试】设函数（是常数，）.若在区间上具有单调性，且，则的最小正周期为_________. 5. 【安徽省合肥市2019届高三第一次教学质量检测】在锐角中，，，则中线AD 长的取值范围是_________.6. 【河北省武邑中学2019届高三上学期期末考试】已知函数的定义域为，若其值域也为，则称区间为的保值区间．若的保值区间是，则的值为_____．7. 【安徽省定远重点中学2019届高三上学期期末考试】设正项等比数列{}n a 的前n 项和为n S ，则以1S ，3S ， 4S 为前三项的等差数列的第8项与第4项之比为________.8. 【河南省周口市2019届高三上学期期末调研考试】已知函数在区间上恒满足，则实数的取值范围是____．9. 【河南省周口市2019届高三上学期期末调研考试】《九章算术》中，将四个面都为直角三角形的四面体称为鳖臑，如图，在鳖臑中，平面，，且，过点分别作于点，于点，连接，则三棱锥的体积的最大值为__________．10. 【安徽省合肥市2019届高三第一次教学质量检测】在平面直角坐标系中，点()()，记的面积为，则____________.二．解答题精选1.【河南省周口市2019届高三上学期期末调研考试】【理】已知函数.（1）讨论函数的单调性；（2）当时，若函数的两个零点分别为，（），证明：.【河南省周口市2019届高三上学期期末调研考试】【文】已知函数.（1）求函数的单调区间；（2）若对任意，函数的图像不在轴上方，求的取值范围.2.【河南省周口市2019届高三上学期期末调研考试】【理】如图，在四棱锥中，底面，，，，为的中点.（1）求证：平面；（2）若点在线段上，且满足，求直线与平面所成角的正弦值.【河南省周口市2019届高三上学期期末调研考试】【文】如图，在四棱锥中，底面，，，，为的中点.（1）求证：平面；（2）若为的中点，求点到平面的距离.3.【安徽省合肥市2019届高三第一次教学质量检测】【理】每年3月21日是世界睡眠日，良好的睡眠状况是保持身体健康的重要基础.为了做好今年的世界睡眠日宣传工作，某社区从本辖区内同一年龄层次的人员中抽取了100人，通过问询的方式得到他们在一周内的睡眠时间(单位：小时)，并绘制出如右的频率分布直方图：(Ⅰ)求这100人睡眠时间的平均数(同一组数据用该组区间的中点值代替，结果精确到个位)；(Ⅱ)由直方图可以认为，人的睡眠时间近似服从正态分布，其中近似地等于样本平均数，近似地等于样本方差，.假设该辖区内这一年龄层次共有10000人，试估计该人群中一周睡眠时间位于区间(39.2，50.8)的人数.附：.若随机变量服从正态分布，则，.【河北省武邑中学2019届高三上学期期末考试】【文】未了解人们对“延迟退休年龄政策”的态度，某部门从年龄在15岁到65岁的人群中随机调查了100人，将这100人的年龄数据分成5组：，，，，，整理得到如图所示的频率分布直方图.在这100人中不支持“延迟退休”的人数与年龄的统计结果如下：（1）由频率分布直方图，估计这100人年龄的平均数；（2）由频率分布直方图，若在年龄，，的三组内用分层抽样的方法抽取12人做问卷调查，求年龄在组内抽取的人数；（3）根据以上统计数据填写下面的列联表，据此表，能否在犯错误的概率不超过5%的前提下，认为以45岁为分界点的不同人群对“延迟退休年龄政策”的不支持态度存在差异？附：，其中.参考数据：4.【广东省雷州市2019届高三上学期期末考试】【文理】已知正项数列满足，且对任意，．（I）求数列的通项公式；（II）设，求数列的前项和．5.【安徽省合肥市2019届高三第一次教学质量检测】【理】设椭圆()的离心率为，圆与轴正半轴交于点，圆在点处的切线被椭圆截得的弦长为．(Ⅰ)求椭圆的方程；(Ⅱ)设圆上任意一点处的切线交椭圆于点，试判断是否为定值？若为定值，求出该定值；若不是定值，请说明理由.【河北省武邑中学2019届高三上学期期末考试】【文】已知抛物线上一点的纵坐标为6，且点到焦点的距离为7.（1）求抛物线的方程；（2）设为过焦点且互相垂直的两条直线，直线与抛物线相交于两点，直线与抛物线相交于点两点，若直线的斜率为，且，试求的值.。

广东深圳2019高三2月第一次调研考试-数学理(扫描版)

广东深圳2019高三2月第一次调研考试-数学理（扫描版）2018年深圳市高三年级第一次调研考试数学(理科)答案及评分标准说明：【一】本解答给出了一种或几种解法供参考，假如考生的解法与本解答不同，可依照试题的要紧考查内容比照评分标准制订相应的评分细那么、【二】对计算题当考生的解答在某一步出现错误时，假如后续部分的解答未改变该题的内容和难度，可视妨碍的程度决定给分，但不得超过该部分正确解承诺得分数的一半；假如后续部分的解答有较严峻的错误，就不再给分、【三】解答右端所注分数，表示考生正确做到这一步应得的累加分数、【四】只给整数分数，选择题和填空题不给中间分数、【一】选择题：本大题每题5分，总分值40分、1 2 3 4 5 6 7 8 C C C D A B B D【二】填空题：本大题每题5分，总分值30分、9、 80； 10、 10； 11、278； 12、1213；13、340≤≤a ； 14、)5,2(； 15、、【三】解答题 16、〔本小题总分值12分〕函数)50)(3π6πsin(2)(≤≤+=x x x f ，点A 、B 分别是函数y f x =（）图像上的最高点和最低点、〔1〕求点A 、B 的坐标以及⋅的值；〔2〕设点A 、B 分别在角α、β的终边上，求)2tan(βα-的值、解：〔1〕50≤≤x ，ππ7π3636x π∴≤+≤， …………………………………1分∴1ππsin()1263x -≤+≤、 ……………………………………………………………2分当πππ632x+=，即1=x 时，ππsin()163x +=，)(x f 取得最大值2；图4当ππ7π636x+=，即5=x 时，ππ1sin(632x +=-，)(x f 取得最小值1-、因此，点A 、B 的坐标分别是(1,2)A 、(5,1)B -、 ………………………………4分152(1)3OA OB ∴⋅=⨯+⨯-=、 ……………………………………………………6分〔2〕点)2,1(A 、)1,5(-B 分别在角α、β的终边上，tan 2α∴=，51tan -=β， …………………………………………8分212()55tan 21121()5β⨯-==---， ………………………………………………10分 ∴52()2912tan(2)5212()12αβ---==+⋅-、 ………………………………………………12分【说明】本小题要紧考查了三角函数)sin()(ϕω+=x A x f 的图象与性质，三角恒等变换，以及平面向量的数量积等基础知识，考查了简单的数学运算能力、 17、〔本小题总分值12分〕一次考试中，五名同学的数学、物理成绩如下表所示：〔1〕请在图4〔2〕要从4名数学成绩在90的同学的物理成绩高于90分的人数，布列及数学期望)(X E 的值、解：〔1〕散点图如右图所示、…………1x =59795939189++++=93，y =59392898987++++=90，,4042 0)2()4()(22222512=+++-+-=-∑=i ix x303422)1(0)1()2()3()4())((51=⨯+⨯+-⨯+-⨯-+-⨯-=--∑=i i iy y x x，300.7540b ==，69.75bx =，20.25a y bx =-=、 ………………………5分故这些数据的回归方程是：ˆ0.7520.25y x =+、………………………6分〔2〕随机变量X 的可能取值为0，，2、 ……………………………………7分22241(0)=6C P X C ==；1122242(1)=3C C P X C ==；22241(2)=6C P X C ==、 …………10分故X 的分布列为：……………11分()E X ∴=610⨯+321⨯+612⨯=、 …………………………………………………12分【说明】此题要紧考察读图表、线性回归方程、概率、随机变量分布列以及数学期望等基础知识，考查运用概率统计知识解决简单实际问题的能力，数据处理能力、 18、〔本小题总分值14分〕如图5，O ⊙的直径4=AB ，点C 、D 为O ⊙上两点，且=45CAB ∠，∠DAB 60=，F 为BC 的中点、沿直径AB 折起，使两个半圆所在平面互相垂直〔如图6〕、〔1〕求证：//OF 平面ACD ；〔2〕求二面角C -AD -B 的余弦值；〔3〕在BD 上是否存在点G ，使得FG //平面ACD ？假设存在，试指出点G 的位置，并求直线AG 与平面ACD 所成角的正弦值；假设不存在，请说明理由、〔法一〕：证明：〔1〕如右图，连接CO ，A BCD⋅O⋅FGE αβ45=∠CAB ，AB CO ⊥∴，又F 为BC 的中点， 45=∠∴FOB ，AC OF //∴、⊄OF 平面ACD ，⊂AC 平面ACD ，∴//OF 平面ACD 、……………………3分解：〔2〕过O 作AD OE ⊥于E ，连CE 、AB CO ⊥ ，平面ABC ⊥平面ABD 、∴CO ⊥平面ABD 、又⊂AD 平面ABD ， AD CO ⊥∴，⊥∴AD 平面CEO ，CE AD ⊥，那么∠CEO 是二面角C -AD -B 的平面角、 ………………………………5分 60=∠OAD ，2=OA ， 3=∴OE 、由CO ⊥平面ABD ，⊂OE 平面ABD ，得CEO ∆为直角三角形，2=CO ，∴7=CE 、∴CEO ∠cos =73=721、 …………………………………………………………8分〔3〕设在BD 上存在点G ，使得FG //平面ACD ，//OF 平面ACD ， ∴平面//OFG 平面ACD ，AD OG //∴，==60BOG BAD ∠∠、因此，在BD 上存在点G ，使得FG //平面ACD ，且点G 为BD 的中点、……10分连AG ，设AG 与平面ACD 所成角为α，点G 到平面ACD 的距离为h 、ACDS∆=CEAD ⨯⨯21=7221⨯⨯=7，OADGAD S S ∆∆==3221⨯⨯=3，∴由ACD-G V=AGD-C V，得h⨯⨯731=2331⨯⨯，得7212=h 、 …………12分在AOG ∆中，2==OG AO ， 120=∠AOG ，由余弦定理得AG =32，…13分AG h =∴αsin =77、…………………………………………………14分〔法二〕：证明：〔1〕如图，以AB 所在的直线为y 轴，以OC 所在的直线为z 轴，以O 为原点，作空间直角坐标系xyz O -，那么()0,20A ,-，()200,,C 、)2,2,0()0,2,0()2,0,0(=--=，点F 为BC 的中点，∴点F 的坐标为(，)2,2,0(=OF 、2OF AC∴=，即//OF AC 、⊄OF 平面ACD ，⊂AC 平面ACD ，∴//OF 平面ACD 、 …………………………………………………………3分解：〔2〕60DAB ∠=，∴点D 的坐标()013,,D -，(3,1,0)AD =、设二面角--C AD B 的大小为θ，()1,,n x y z =为平面ACD 的一个法向量、由110,0,n AC n AD ⎧⋅=⎪⎨⋅=⎪⎩ 有()()()),,0,2,20,,,0,x y z xy z ⎧⋅=⎪⎨⋅=⎪⎩即220,0.y z y +=⎧⎪+=取1=x ，解得3-=y ，3=z 、1n ∴=()331,,-、 ……………………………………………5分取平面ADB 的一个法向量2n =()100,,， ………………………………………6分121210cos n n |n ||n |θ⨯⋅∴==⋅、………………………8分〔3〕设在BD 上存在点G ，使得FG //平面ACD ，//OF 平面ACD ，∴平面//OFG 平面ACD ，那么有AD OG //、设(0)OG AD λλ=>，(3,1,0)AD =，()30OG ,,λλ∴=、又2OG =，2=，解得1λ=±〔舍去1-〕、()310OG ,∴=，那么G 为BD 的中点、因此，在BD 上存在点G ，使得FG //平面ACD ，且点G 为BD 的中点、……11分设直线AG 与平面ACD 所成角为α，(3,1,0)(0,2,0)AG =--=，依照〔2〕的计算(11n=为平面ACD 的一个法向量，113sin cos(90)||||AG n AG n αα⋅∴=-==⋅、因此，直线AG 与平面ACD 、 ……………………………14分【说明】此题要紧考察空间点、线、面位置关系，线面角、二面角及三角函数等基础知识，考查空间想象能力、运算能力和推理论证能力，考查用向量方法解决数学问题的能力、 19、〔本小题总分值14分〕数列{}na 满足：11=a ，2(0)a a a =≠，nn n a a p a 212++⋅=〔其中p 为非零常数，*N n ∈〕、〔1〕判断数列}{1nn a a +是不是等比数列？〔2〕求na ；〔3〕当1=a 时，令2n n nna b a +=，n S 为数列{}n b 的前n 项和，求n S 、解：〔1〕由nn n a ap a 212++⋅=，得nn n n a a p a a 112+++⋅=、 ……………………………1分令1n n na c a +=，那么1c a =，1n n c pc +=、0≠a ，10c ∴≠，pc c nn =+1〔非零常数〕，∴数列}{1n n a a+是等比数列、 ……………………………………………………3分〔2〕数列{}nc 是首项为a ，公比为p 的等比数列，∴111n n n c c p a p --=⋅=⋅，即11n n n aap a -+=、 ……………………………4分当2n ≥时，230121121()()()1n n n n n n n a a aa a ap ap ap a a a -----=⋅⋅⋅⋅=⨯⨯⨯⨯23212n n n ap-+-=， ………………………………………………6分1a 满足上式，2321*2,Nn n n n a ap n -+-∴=∈、 …………………………7分〔3〕12212211()()n n n n n n n n na a a ap ap a p a a a --++++=⋅=⨯=，∴当1=a 时，212n n n nna b nppa -+==、 …………………………………………8分132112n n S p p n p -∴=⨯+⨯++⨯， ① 232121 1(1)n n n p S p n p n p -+=⨯++-⨯+⨯ ②∴当21p ≠，即1p ≠±时，①-②得：22132121212(1)(1)1n n n n n p p p S p p pnpnp p-++--=+++-=--，即221222(1),1(1)1n n n p p np S p p p+-=-≠±--、 …………………………11分而当1p =时，(1)122n n n S n +=+++=， …………………………12分当1p =-时，(1)(1)(2)()2n n n S n +=-+-++-=-、………………………13分综上所述，221222(1),1,2(1),1,2(1), 1.(1)1n n n n n p n n S p p p np p p p +⎧+=⎪⎪+⎪=-=-⎨⎪⎪--≠±⎪--⎩ ……………………………14分【说明】考查了等比数列的通项公式、等比数列求和公式、简单递推数列求通项、错位求和等知识，考查了学生的运算能力，以及化归与转化、分类讨论的思想、 20、〔本小题总分值14分〕两点)0,1(1-F 及)0,1(2F ，点P 在以1F 、2F 为焦点的椭圆C 上，且1PF 、21F F 、2PF 构成等差数列、〔1〕求椭圆C 的方程；〔2〕如图7，动直线:l y kx m =+与椭圆C的两点，且l M F ⊥1，l N F ⊥2、求四边形12F MNF 解：〔1〕依题意，设椭圆C 的方程为2222x y a b+=1122PF F F PF 、、构成等差数列，∴1122224a PF PF F F =+==， 2a =、又1c =，23b ∴=、∴椭圆C 的方程为22143x y +=、 ……………………………………………………4分 (2) 将直线的方程y kx m =+代入椭圆C 的方程223412x y +=中，得01248)34(222=-+++m kmx x k 、…………………………5分由直线与椭圆C 仅有一个公共点知，2222644(43)(412)0k m k m ∆=-+-=，化简得：2243m k =+、 …………………………7分图7设11d F =22d F =〔法一〕当0k ≠时，设直线的倾斜角为θ，那么12tan d d MN θ-=⨯，12d d MN k-∴=，22121212221()221m d d d d S d d k k k --=+==+mm m m 1814322+=+-=，………11分2243m k =+，∴当0k ≠时，3>m ，3343131=+>+m m ，32<S 、当0=k 时，四边形12F MNF 是矩形，S =、 ……………………………13分因此四边形12F MNF 面积S 的最大值为 ………………………………14分〔法二〕2222212222()2(53)11m k k d d k k +++==++，21223331k d d k +=+、MN ∴===、四边形12F MNF 的面积121()2S MN d d =+)(11212d d k ++=， …………11分22221222122)1(1216)2(11++=+++=k k d d d d k S12)211(41622≤-+-=k 、 ………………………………………………13分当且仅当0k =时，212,S S ==，故max S =、因此四边形12F MNF 的面积S 的最大值为、 …………………………14分【说明】此题要紧考查椭圆的方程与性质、直线方程、直线与椭圆的位置关系等基础知识，考查学生运算能力、推理论证以及分析问题、解决问题的能力，考查分类讨论、数形结合、化归与转化思想、 21、〔本小题总分值14分〕)0()(>-=a x ax x f ，bx x x g +=ln 2)(，且直线22-=x y 与曲线)(x g y =相切、〔1〕假设对),1[+∞内的一切实数x ，不等式)()(x g x f ≥恒成立，求实数a 的取值范围；〔2〕当1=a 时，求最大的正整数k ，使得对]3,[e 〔 2.71828e =⋅⋅⋅是自然对数的底数〕内的任意k 个实数k x x x ,,,21 都有)(16)()()(121kk x g x f x f x f ≤+++- 成立；〔3〕求证：)12ln(14412+>-∑=n i ini )(*N n ∈、解：〔1〕设点),(00y x 为直线22-=x y 与曲线)(x g y =的切点，那么有22ln 2000-=+x bx x 、〔*〕b x x g +='2)( ，22=+∴b x 、〔**〕由〔*〕、〔**〕两式，解得0=b ，x x g ln 2)(=、 ……………………………2分由)()(x g x f ≥整理，得xx xaln 2-≤，1≥x ，∴要使不等式)()(x g x f ≥恒成立，必须x x x a ln 22-≤恒成立、设x x x x h ln 2)(2-=，2ln 22)1(ln 22)(--=⋅+-='x x xx x x x h ， xx h 22)(-='' ，∴当1≥x 时，0)(≥''x h ，那么)(x h '是增函数，0)1()(='≥'∴h x h ，)(x h 是增函数，1)1()(=≥h x h ，1≤a 、…………………5分因此，实数a 的取值范围是10≤<a 、 ………………………………………6分〔2〕当1=a 时，xx x f 1)(-=，011)(2>+='xx f ，)(x f ∴在]3,[e 上是增函数，)(x f 在]3,[e 上的最大值为38)3(=f 、要对]3,[e 内的任意k 个实数k x x x ,,,21 都有)(16)()()(121kk x g x f x f x f ≤+++-成立，必须使得不等式左边的最大值小于或等于右边的最小值，当3121====-k x x x 时不等式左边取得最大值，e x k=时不等式右边取得最小值、21638)1(⨯≤⨯-∴k ，解得13≤k 、因此，k 的最大值为13、 ………………………………………10分〔3〕证明〔法一〕：当1=a 时，依照〔1〕的推导有，),1(+∞∈x 时，)()(x g x f >，即)1(21ln xx x -<、 ………………………………………………………11分令1212-+=k k x ，得)12121212(211212ln +---+<-+k k k k k k ，化简得144)12ln()12ln(2-<--+k k k k ， ………………………………13分 ∑∑==-<--+=+n i n i i i i i n 121144)]12ln()12[ln()12ln(、………………………14分〔法二〕数学归纳法：当1=n 时，左边=34，右边=3ln ，依照〔1〕的推导有，),1(+∞∈x 时，)()(x g x f >，即x xx ln 21>-、令3=x ，得3ln 2313>-，即3ln 34>、因此，1=n 时不等式成立、 ………………………………11分〔另解：25>e ，2716625)25(44>=>∴e ，27ln 4>∴，即3ln 34>、〕假设当k n =时不等式成立，即)12ln(14412+>-∑=k i i ki ，那么当1+=k n 时,1)1(4)1(4)12ln(1)1(4)1(41441442212112-++++>-+++-=-∑∑=+=k k k k k i i i i k i k i ，即证1232ln 1)1(4)1(42++>-++k k k k 、在不等式x x x ln 21>-中，令1232++=k k x ，得 1)1(4)1(4)32121232(211232ln 2-++=++-++<++k k k k k k k k 、1+=∴k n 时命题也成立、………………………………………13分依照数学归纳法，可得不等式)12ln(14412+>-∑=n i i ni 对一切*N n ∈成立、…14分【说明】此题要紧考查函数的性质、导数运算法那么、导数的几何意义及其应用、不等式的求解与证明、数学归纳法等综合知识，考查学生的计算推理能力及分析问题、解决问题的能力及创新意识、。

广东省深圳市2019届高三第二次(4月)调研考试数学理试题(WORD版)

深圳市2019年高三年级第二次调研考试数学理 2019.4一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知集合2{|0},{|40},M x x N x x =>=-≥则M N =U ( A ).A. (,2](0,)-∞-+∞UB. (,2][2,)-∞-+∞UC. [3,)+∞D. (0,)+∞2.在复平面内，复数i(1i)12iz +=-所对应的点位于（ C ）. A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限3.2019年是中国成立70周年，也是全面建成小康社会的关键之年.为了迎祖国70周年生日，全民齐心奋力建设小康社会，某校特举办“喜迎国庆，共建小康”知识竞赛活动.下面的茎叶图是参赛两组选手答题得分情况，则下列说法正确的是（ D ）.A.甲组选手得分的平均数小于乙组选手的平均数B.甲组选手得分的中位数小于乙组选手的中位数C.甲组选手得分的中位数等于乙组选手的中位数D.甲组选手得分的方差大于乙组选手的的方差4.已知等比数列{}n a 满足11,2a =且2434(1),a a a =-则5a =（ A ）. A. 8 B.16 C.32 D.64 5.已知函数22()(1)f x ax a x x =+-+是奇函数，则曲线()y f x =在1x =处的切线得倾斜角为（ B ）. A.π4 B.3π4 C.π3 D.2π3 6.在平行四边形ABCD 中，E 为CD 的中点，F 为AE 的中点，设,,AB a AD b ==u u u r r u u u r r则FB =uur （ D ）. A.3142a b -+r r B.1324a b +r r C.1324a b -r r D.3142a b -r r 7. 如图所示，网格上小正方形的边长为1，粗实线和粗虚线画出的是某几何体的三视图，则该几何体的表面积为( A ). A.(842)π+ B. (942)π+ C.(882)π+ D. (982)π+8.十九世纪末，法国学者贝特朗在研究几何概型时提出了“贝特朗悖论”，即“在一个圆内任意选一条弦，这条弦的弦长长于这个圆的内接等边三角形边长的概率是多少？” 贝特朗用“随机半径”、 “随机端点”、 “随机中点”三种方法求解，所得结果均不相同.该悖论的矛头直击概率概念本身，这极大地促进了概率论基础的严格化.已知“随机端点”的方法如下：设A 为圆O 上一个定点，在圆周上随机取一点B,连接AB ，所得弦长AB 大于圆O 的内接等边三角形边长的概率.记该概率为p ，则p =（ C ）. A.15 B.14 C.13 D.129.已知函数()ln 1a f x x x=+-有且仅有一个零点，则实数a 的取值范围为( A ). A. (,0]{1}-∞U B. [0,1] C. (,0]{2}-∞U D. [0,2]10.设12,F F 分别为椭圆2222:1(0)x y C a b a b+=>>的左右焦点，点,A B 分别为椭圆C 的右顶点和下顶点，且点1F 关于直线AB 的对称点为M .若212MF F F ⊥，则椭圆C 的离心率为（ C ）. A.312- B.313- C.512- D.22 11.已知函数()3sin cos (0)f x x x =+>ωωω在区间ππ[,]43-上恰有一个最大值点和最小值点，则实数ω的取值范围为（ B ）. A.8[,7)3 B. C. 20[4,)3 D. 20(,7)312.如图，在四面体ABCD 中，2,3,5,,AB CD AC BD AD BC E F ======分别是 ,AD BC 中点.若用一个与直线EF 垂直，且与四面体的每一个面都相交的平面α去截该四面体，由此得到一个多边形截面，则该多边形截面面积最大值为（ B ）. A.6 B.62 C. 52 D. 54第II 卷（非选择题共90分）本卷包括必考题和选考题两部分，第13-21题为必考题，每个考生都必须作答，第22-23题为选考题，考生根据要求作答.二、填空题：本大题共4个小题，每小题5分，满分20分.13.设实数,x y 满足23,12,4,x y x y ≤≤⎧⎪≤≤⎨⎪+≤⎩则1y x -的最大值为_______.14.已知双曲线2222:1,x y C a b-=且圆22:(2)1E x y -+=的圆心是双曲线C 的右焦点.若圆E 与双曲线C 的渐近线相切，则双曲线C 的方程为____________.15.精准扶贫是全国建成小康社会、实现中华民族伟大“中国梦”的重要保障.某单位拟组成4男3女共7人的扶贫工作队，派驻到3个扶贫地区A 、B 、C 进行精准扶贫工作.若每一个地区至少派驻1男1女两位工作人员，且男性甲必须派驻到A 地区，则不同的派驻方式有_____种.16.设n S 是数列{}n a 的前n 项和，且13,a =当2n ≥时，有1122n n n n n S S S S na --+-=，则使得122019m S S S ≥L 成立的正整数m 的最小值为__________.三、解答题：本大题共7个小题，共70分，解答必须写出必要的文字说明、证明过程或演算步骤.17、（本小题满分12分）已知△ABC 中，AB ＝2BC ，AC ＝25，点D 在边AC 上，且AD ＝2CD ，∠ABD ＝2∠CBD 。

广东省深圳市最新高三第一次(2月)调研考试数学理试题(含解析)

深圳市2019届高三第一次调研考试数学理试题第Ⅰ卷一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.复数的共轭复数是A. B. C. D.【答案】D【解析】【分析】根据复数的运算可知，再根据共轭复数的概念，即可求解。

【详解】由题意，根据复数的运算可知，所以，其共轭复数为：，故选D。

【点睛】本题主要考查了复数的运算，以及共轭复数的概念，其中解答中熟记复数的基本运算法则是解答的关键，着重考查了推理与运算能力，属于基础题。

2.已知集合，{，则A. B. C. D.【答案】B【解析】【分析】由题意，求得集合，，再根据集合的交集的运算，即可求解。

【详解】由题意，求得集合，，所以，【点睛】本题主要考查了对数函数的图象与性质，以及集合的交集运算问题，其中解答中熟记对数函数的图象与性质，以及集合交集的运算是解答的关键，着重考查了运算与求解能力，属于基础题。

3.设为等差数列的前项和．若，，则的公差为A. -2B. -1C. 1D. 2【答案】A【解析】【分析】根据等差数列的前n项和公式和题设条件，求得，进而求解数列的公差，得到答案。

【详解】依题意，可得，解得，又，所以，所以公差，故选A。

【点睛】本题主要考查了等差数列的通项公式，以及前n项和公式的应用，其中解答中熟记等差数列的通项公式和前n项和公式，合理准确运算是解答的关键，着重考查了运算与求解能力，属于基础题。

4.己知某产品的销售额与广告费用之间的关系如下表：（单位：万元）（单位：万元）若求得其线性回归方程为，则预计当广告费用为6万元时的销售额为A. 42万元B. 45万元C. 48万元D. 51万元【答案】C【解析】【分析】根据上表中的数据，求得样本点中心，代入回归直线的方程，求得的值，得到回归直线的方程，即可求解。

【详解】由题意，根据上表中的数据，可得，，即回归方程经过样本点中心，又由线性回归方程为，所以，解得，所以，当时，，故选C.【点睛】本题主要考查了回归直线方程的应用问题，其中解答中熟记回归直线方程的性质，求得回归直线的方程是解答的关键，着重考查了运算与求解能力，属于基础题。

广东省2020届高三数学理一轮复习典型题专项训练：立体几何

广东省2020届高三数学一轮复习典型题专项训练立体几何一、选择、填空题1、（广州市2018高三一模）如图，网格纸上小正方形的边长为1，粗线画出的是某个几何体的三视图，则该几何体的表面积为A ．44223++B ．1442+C ．104223++D ．42、（珠海市2019届高三9月摸底考试）如图，圆锥顶点为P ，底面圆心为O ，过轴PO 的截面PAB ∆，C 为PA 中点，43PA =，6PO =，则从点C 经圆锥侧面到点B 的最短距离为A.215B.21562- C.6D.21563-CBAP3、（华附、省实、广雅、深中2019届高三上学期期末联考）在半径为4的球O 的球面上有不同的四点A ，B ，C ，D ，若4AB AC AD ===，则平面BCD 被球O 所截得的图形的面积为※※.4、（珠海市2019届高三9月摸底考试）S 为顶点的正四面体S ABC -的底面积为3，D 为SC 的中点，则BD 与AC 所成角的余弦值为A.33B.32C.36D.165、（深圳实验、珠海一中等六校2019届高三第二次联考）某几何体的三视图如图所示，则该几何体的体积为()A.32163π-B.16163π-C.3283π-D.1683π-6、（深圳市宝安区2019届高三9月调研）《九章算术》中对一些特殊的几何体有特定的称谓，例如：将底面为直角三角形的直三棱柱称为堑堵，将一堑堵沿其一顶点与相对的棱刨开，得到一个阳马（底面是长方形，且有一条侧棱与底面垂直的四棱锥）和一个鳖臑（四个面均为直角三角形的四面体）．在如图所示的堑堵111C B A ABC -中，4,3,51====BC AB AC AA ，则阳马111A ABB C -的外接球的表面积是7、（佛山市2019届高三教学质量检测（二））已知正方体1111D C B A ABCD -的棱长为2，点P 为对角线11C A 的中点，F E ,分别为对角线11,BC D A （含端点）上的动点，则PE +PF 的最小值为（）A ．2B ．3C ．2D ．228、（广州市2019年普通高中毕业班综合测试（二））有一个底面半径为R ，轴截面为正三角形的圆锥纸盒，在该纸盒内放一个棱长均为a 的四面体，并且四面体在纸盒内可以任意转动，则a 的最大值为____．9、（揭阳市2019届高三第二次模拟）如图是一个长方体ABCD-A 1B 1C 1D 1截去一个角后的多面体的三视图，尺寸如图所示，则这个多面体的体积为A ．12B ．16C ．18D ．2010、（湛江市2019届高三调研）正三棱锥的正视图如图所示，则侧视图的面积为A ．212B ．312C ．26D ．3611、（中山一中等七校2019届高三第二次（11月）联考）中国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器——商鞅铜方升,其三视图如图1所示(单位:寸),若π取3,其体积为13.5(立方寸),则图中的x 为()A .2.4B .1.8C .1.6D .1.212、（肇庆市2019届高三上学期期末）在长方体1111ABCD A B C D -中，124AA AB BC ===，E 是AB 的中点，则三棱锥11E D C C -外接球的表面积为A ．36πB ．32πC ．9πD ．8π13、（珠海市2019届高三上学期期末）如图是某几何体的三视图，其中正视图和侧视图为正方形，俯视图是腰长为2的等腰直角三角形，则该几何体的体积是（）A 、43B 、223C 、83D 、42314、（江门市2019届普通高中高三调研）已知两条直线m n 、，两个平面αβ、，给出下面四个命题：①//,////m n m n αα⇒②//,//,m n m n αβαβ⊥⇒⊥③,//m n m n αα⊥⊥⇒或n α⊂④,//m m αβαβ⊥⇒⊥其中，正确命题的个数是（）A ．1B ．2C ．3D ．415、（揭阳市2019届高三上学期期末）某几何体示意图的三视图如图示，已知其主视图的周长为8，则该几何体侧面积的最大值为A ．πB ．2πC ．4πD ．16π16、（雷州市2019届高三上学期期末）正四面体ABCD 中，CD 在平面α内，点E 是线段AC 的中点，在该四面体绕CD 旋转的过程中，直线BE 与平面α所成角不可能是A ．0B ．6πC ．3πD ．2π17、（茂名市2019届高三上期末）如图2，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则此几何体的体积为（）．A 、6B 、18C 、12D 、3618、（汕尾市2019高三一模）如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的表面积为（）A ．B ．C ．D ．19、（深圳市2019届高三第一次（2月）调研考试）如图所示，网格纸上小正方形的边长为1，粗线画出的是由一个棱柱挖去一个棱锥后的几何体的三视图，则该几何体的体积为（A ）72（B ）64（C ）48（D ）3220、（肇庆市2019高三二模）在长方体ABCD ﹣A 1B 1C 1D 1中，AA 1＝AB ＝2BC ＝4，E 是AB 的中点，则三棱锥E ﹣D 1C 1C 外接球的表面积为（）A ．36πB ．32πC ．9πD ．8π21、（湛江2019高三一模）某几何体的三视图如图所示，则该几何体的体积是A 、113B 、133C 、143D 、16322、（广东省2019届高三3月一模）某几何体的三视图如图所示，则该几何体的体积为（）A ．3πB ．4πC ．6πD ．8π23、（广州市2019届高三3月综合测试（一））一个几何体的三视图如图所示，其中正视图和俯视图中的四边形是边长为2的正方形，则该几何体的表面积为A.132π B.7πC.152π D.8π二、解答题1、（广州市2018高三一模）如图，四棱锥S ABCD -中，△ABD 为正三角形，︒=∠120BCD ，2CB CD CS ===，︒=∠90BSD ．（1）求证：AC ⊥平面SBD ；（2）若BD SC ⊥，求二面角C SB A --的余弦值．2、（珠海市2019届高三9月摸底考试）如图，四边形ABCD 是矩形，AB =2BC ，E 为CD 中点，以BE 为折痕将BEC ∆折起，使C 到C '的位置，且平面BEC '⊥平面ABED (1)求证：AE BC '⊥；(2)求二面角C AE B '--的余弦值．C /EDCBA3、（华附、省实、广雅、深中2019届高三上学期期末联考）等边ABC ∆的边长为3，点D 、E 分别是边AB 、AC 上的点，且满足12AD CE DB EA ==（图1）.将ADE ∆沿DE 折起到1A DE ∆的位置，使二面角1A DE B --成直二面角，连接1A B ，1AC （图2）.（1）求证：1A D ⊥平面BCED ；（2）在线段BC 上是否存在点P ，使直线1PA 与平面1A BD 所成的角为60︒？若存在，求出线段PB 的长；若不存在，请说明理由.4、（深圳实验、珠海一中等六校2019届高三第二次联考）如图所示，在平行四边形ABCD中，04,22,A 45,AB BC BC ==∠=点E 是CD 边的中点，将DAE ∆沿AE 折起，使点D 到达点P 的位置，且26PB =（1）求证;平面PAE ⊥平面ABCE ；（2）若平面PAE 和平面PBC 的交线为l ，求二面角B l E --的余弦值.5、（深圳市宝安区2019届高三9月调研）如图，在多面体ABCDEF 中，四边形ABCD 为菱形，AF ∥DE ，AD AF ⊥，且平面⊥BED 平面ABCD ．(1)求证：CD AF ⊥;(2)若︒=∠60BAD ，ED AD AF 21==，求二面角E FB A --的余弦值．6、（广州市2019年普通高中毕业班综合测试（二））如图，在四棱锥P －ABCD 中，底面ABCD 为菱形，∠BAD ＝60°，∠APD ＝90°，且AD ＝PB ．(l)求证：平面PAD ⊥平面ABCD ；(2)若AD ⊥PB ，求二面角D －PB －C 的余弦值．7、（揭阳市2019届高三第二次模拟）已知如图，四棱锥P ABCD -中，底面ABCD 为矩形，PA ⊥平面ABCD ，E 、F 分别为PC 的三等分点．(1)证明：//AF 平面EBD ；(2)已知1AP AD ==,2AB =，求二面角E BD A --的余弦值.8、（湛江市2019届高三调研）如图，在四棱锥ABCD P -中，△PAB 、△PBC 、△ACD 均为等边三角形，BC AB ⊥．（Ⅰ）求证：BD ⊥平面PAC ；（Ⅱ）求直线CD 与平面PBC 所成角的正弦值．9、（中山一中等七校2019届高三第二次（11月）联考）如图4,在四棱锥E ABCD -中,//AB CD ,90ABC ∠=︒,2CD AB ==24CE =,120BCE ∠=︒,25DE =.(Ⅰ)证明:平面BCE ⊥平面CDE ；(Ⅱ)若4BC =,求二面角E AD B --的余弦值.10、（汕尾市2019届高三上学期期末）如图，在四棱锥P ABCD -中，ABCD 为矩形，△APB 是以∠P 为直角的等腰直角三角形，平面PAB ⊥平面ABCD 。

2020届高考数学(理)一轮必刷题专题62 离散型随机变量均值与方差、正态分布(解析版)

考点62 离散型随机变量均值与方差、正态分布1．（广东省潮州市2019届高三第二次模拟考试数学理）一试验田某种作物一株生长果个数x 服从正态分布()290,N σ，且()700.2P x <=，从试验田中随机抽取10株，果实个数在[]90,110的株数记作随机变量X ，且X 服从二项分布，则X 的方差为（）A ．3B ．2.1C ．0.3D ．0.21【答案】B 【解析】∵290(),x N δ～，且()700.2P x <=，所以()1100.2P x >=∴()901100.50.20.3P x <<=-=， ∴()10,0.3X B ～，X 的方差为()100.310.3 2.1⨯⨯-=．故选B ．2．（湖北省钟祥市2019届高三高考第一次模拟考试理）某班有50名学生，一次数学考试的成绩ξ服从正态分布N （105，102），已知P （95≤ξ≤105）=0.32，估计该班学生数学成绩在115分以上的人数为（）A ．10B ．9C ．8D ．7【答案】B 【解析】∵考试的成绩ξ服从正态分布N （105，102）． ∴考试的成绩ξ关于ξ=105对称， ∵P （95≤ξ≤105）=0.32， ∴P （ξ≥115）=12（1-0.64）=0.18， ∴该班数学成绩在115分以上的人数为0.18×50=9 故选：B ．3．（辽宁省丹东市2019届高三总复习质量测试理）某种种子每粒发芽的概率都为0.85，现播种了1000粒，对于没有发芽的种子，每粒需再补种2粒，补种的种子数记为X ，则X 的数学期望()E X =_______．【答案】300【解析】设没有发芽的种子数为Y ,则有2X Y =,由题意可知Y 服从二项分布，即Y(1000,0.15)B ,()10000.15150E Y =⨯=,()2()300E X E Y ==.4．（河北省石家庄市2019届高三毕业班模拟考试一A 卷理）已知随机变量X 服从正态分布()2,1N ，若()()223P X a P X a ≤-=≥+，则a =__________．【答案】1 【解析】由正态分布的性质可得正态分布的图像对称轴为2X =，结合题意有：()()2232,12a a a -++=⇒=.故答案为：1．5．（湖南省益阳市2019届高三4月模拟考试数学理）某市高三年级26000名学生参加了2019年3月模拟考试，已知数学考试成绩2(100,)XN σ.统计结果显示数学考试成绩X 在80分到120分之间的人数约为总人数的34，则数学成绩不低于120分的学生人数约为__________．【答案】3250 【解析】因为成绩()2100,X N σ~，所以正态分布曲线关于100X =对称，又成绩在80分到120分之间的人数约占总人数的34，由对称性知：成绩不低于120分的学生约为总人数的1311248⎛⎫⨯-= ⎪⎝⎭，所以此次考试成绩不低于120分的学生约有12600032508⨯=.6．（2019届湘赣十四校高三联考第二次考试理）我国2019年新年贺岁大片《流浪地球》自上映以来引发了社会的广泛关注，受到了观众的普遍好评.假设男性观众认为《流浪地球》好看的概率为23，女性观众认为《流浪地球》好看的概率为12.某机构就《流浪地球》是否好看的问题随机采访了4名观众（其中2男2女）. （1）求这4名观众中女性认为好看的人数比男性认为好看的人数多的概率；（2）设ξ表示这4名观众中认为《流浪地球》好看的人数，求ξ的分布列与数学期望. 【答案】（1）736（2）见解析【解析】设X 表示2名女性观众中认为好看的人数，Y 表示2名男性观众中认为好看的人数，则12,2X B ⎛⎫~ ⎪⎝⎭，22,3Y B ⎛⎫~ ⎪⎝⎭. （1）设事件A 表示“这4名观众中女性认为好看的人数比男性认为好看的人数多”，则()()()()2,12,01,0P A P X Y P X Y P X Y ===+==+==,222212022221211123323C C C C ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=⋅+⋅ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭ 21022111722336C C ⎛⎫⎛⎫⎛⎫+⋅= ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭. （2）ξ的可能取值为0，1，2，3，4，()()00,0P P X Y ξ==== 2200221112336C C ⎛⎫⎛⎫=⋅= ⎪ ⎪⎝⎭⎝⎭， ()()()11,00,1P P X Y P X Y ξ====+==，= 2210012222111121223233C C C C ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⋅+⋅ ⎪⎪ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭16=， ()()()()22,01,10,2P P X Y P X Y P X Y ξ====+==+==,2220112222111121232233C C C C ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=⋅+⋅ ⎪ ⎪ ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭ 22022*********C C ⎛⎫⎛⎫+⋅= ⎪ ⎪⎝⎭⎝⎭， ()()()31,22,1P P X Y P X Y ξ====+==,2212212222112*********C C C C ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=⋅+⋅ ⎪⎪ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭13=， ()()42,2P P X Y ξ==== 222222121239C C ⎛⎫⎛⎫=⋅= ⎪ ⎪⎝⎭⎝⎭， ∴ξ的分布列为∴11131170123436636393E ξ=⨯+⨯+⨯+⨯+⨯=. 7．（天津市耀华中学2019届高三第一次模拟考试数学理）在盒子里有大小相同，仅颜色不同的乒乓球共10个，其中红球4个，白球3个，蓝球3个。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

又 f (2) = ln 2 = ln 8 ， f (3) = ln 3 = ln 9 ， f (2) f (3) ，
26
36
只需 f (3) = ln 3 2ln 3 ，即 6 ，即实数的最小值为 6 ，故选 A. 3
（法二） ln x 2ln 3 ，ln x 2ln 3 x ，令 k = 2ln 3 ，则 ln x kx （*），
+ 2)
=
6 y2
(my1
+1) − 2 − 2y1 (my2
（my1 +1）− 2
+1)
+
2
理科数学试题答案及评分参考第6页（共14页）
=
4my1 y2
− 6( y1
+
y2 )
=
4m(−
9 3m2 +
4
)
−
6(−
6m 3m2 +
4
)
=
0，
my1 −1
my1 −1
∴ AN / / AQ ，……………………11 分
ln x

2ln 3 ，
x N* ， 0 ，
x9
x
（法一）
ln x x

2ln 3
，令
f
(x)
=
ln x x
，则
f
(x)
=
1− ln x2
x
，
易知 f (x) 在 (0, e) 上递增，在 (e, +) 上递减，
注意到 2<e<3 ，只需考虑 f (2) 和 f (3) 的大小关系，
)max
=
R+d d
= 3，即 R = 2d
，显然 R2
=
d2
+ r 2 ，故 R
=
2 r， 3
又 2r = AC = 4 ，故 r = 2 ，球 O 的表面积为 4πR2 = 16 πr2 = 64 π ，故选 B.
sin ABC 3
3
3
9
12. 解析：
(
1
)
x

1 ，

xx
9 ，
过 D 做 DG ⊥ BC ，交 BC 于 G ，连接 PG ，则 BC ⊥ 平面角，设为，……………………9 分
P
底面 ABCD 是边长为 1 的菱形， BAD = 45 ，
S
DGC 为等腰直角三角形，
M
DG = 2 ，又 PD = 2， 2
2019 年深圳市高三年级第一次调研考试理科数学试题参考答案及评分标准
第Ⅰ卷
一．选择题
1.D
2.B
3.A
4.C
5.B
6.C
7.B
8.A
9.C
10.D
11.B
12.A
11. 解析:设△ ABC 的外接圆圆心为 O ，其半径为 r ，球 O 的半径为 R ，且| OO |= d ，
依题意可知
( V1 V2
B
PD ⊥ 底面 ABCD ，……………………7 分
如图，以 D 为坐标原点建立空间直角坐标系 D − xyz ，
则 D(0, 0, 0) ， P(0, 0, 2) ， A(1, 0, 0) ， C(−
2, 2
2 , 0) ， 2
Pz
∴ BC = AD = (−1, 0, 0) ，
PC = (− 2 , 2 , −2) ，……………………8 分
E
D
C F
（2）若平面 PDC ⊥ 底面 ABCD ，且 PD ⊥ DC ，求平面 PAD 与平面 PBC 所成锐二面角的余弦值．
A
B
（第 18 题图）
解：（1）证明：（法一）如图，设 DM 中点为 N ，连接 EN ，NF ，BD ，则有 NE / / AD ，
NE 平面 ABCD ， AD 平面 ABCD ， P
5 ，或 AC = − 3
5
（舍去），
5
5
AC 的长为 5 . …………………6 分
理科数学试题答案及评分参考第2页（共14页）
（2） cos BCD = − 3 ， 5
sin BCD = 1− cos2 BCD = 4 ，……………7 分 5
又 CBD = 45 ， sin CDB = sin(180 − BCD − 45)=sin(BCD+45）
（1）若 AC 平分 BCD ，且 AB = 2 ，求 AC 的长；
A
D
（第 17 题图）
（2）若 CBD = 45 ，求 CD 的长．解：（1）若对角线 AC 平分 BCD ，即 BCD = 2ACB = 2ACD ， cos BCD = 2cos2 ACB −1 = − 3 ，
ln 2
ln 2
理科数学试题答案及评分参考第1页（共14页）
二．填空题：
13. 3
14. 15
15. 8
16. 103
16. 解析：
an,1
=1−
1 2n−1
，
an−1,1
=1−
1 2n−2
, (n

2)
下面求数列 an,2 的通项，
由题意可知 an,2 = an−1,1 + an−1,2 , (n 3) ，

an,2
− an−1,2
=
an−1,1
=1−
1 2n−2
, (n

3)
，即 an,2
− an−1,2
=1−
1 2n−2
, (n

3)
，
an,2
=
(an,2
− an−1,2 ) + (an−1,2
− an−2,2 ) + + (a3,2
− a2,2 ) + a2,2
=
1 2n−2
+
n−
5 2
= 2 (sin BCD + cos BCD) = 2 ，…………………………9 分
2
10
在△ BCD 中，由正弦定理 BC = CD ，可得 sin CDB sin CBD
CD = BC sin CBD =5 ，即 CD 的长为 5 .………………………12 分 sin CDB
【说明】本题主要考察正弦定理，余弦定理，三角恒等变换等知识，意在考察考生数形
x

不等式（*）有正整数解，即 y = ln x 在 y = kx 的图象上方（或者图象的交点）存在横坐
标为正整数的点，易知直线 y = x 与曲线 y = ln x e
相切，如右图所示， ln 2 2k ，或 ln 3 3k ，
解得 4ln 3 ，或 6 ，不难判断 4 ln 3 6 ，即实数的最小值为 6 ，故选 A.
=
消去
1，
x
，并整理得：
(3m2
+ 4) y2
+ 6my − 9 = 0 ，
∵ = (6m)2 + 36(3m2 + 4) 0 ，
∴
y1
+
y2
=
−
6m 3m2 +
4
，
y1 y2
=
−
9 3m2 +
4
，……………………7
分
∵直线 BM 的方程可表示为 y = y1 (x − 2) ， x1 − 2
，
数列 an,2 显然递增，又易知 a102,2 100 a103,2 ，
m 的最小值为103 ，故应填103 ．
三、解答题：解答应写出文字说明，证明过程或演算步骤．
（17）（本小题满分 12 分）
如图，在平面四边形 ABCD 中， AC 与 BD 为其对角线，
B
C
已知 BC = 1，且 cos BCD = − 3 ． 5
QF / / ER ，且 QF = 1 PD = ER ，…………………4 分 4
M
即 QFER 为平行四边形， EF / /QR ，………………5 分 E
EF 平面 ABCD ， RQ 平面 ABCD ，
DF
C
EF / / 平面 ABCD ．……………………6 分
R
A
Q
（2）（法一）解：平面 PDC ⊥ 底面 ABCD , 且 PD ⊥ DC ，
2 在椭圆 C 上．
（1）求椭圆 C 的方程；
（2）设椭圆的左、右顶点分别为 A 、B ，M 是椭圆上异于 A ，B 的任意一点，直线 MF
交椭圆 C 于另一点 N ，直线 MB 交直线 x = 4 于 Q 点，求证： A ， N ， Q 三点在同一条直
线上．
y
M
O
B
A
F
N
（第 19 题图）
x2 y2 解：（1）(法一)设椭圆 C 的方程为 a2 + b2 = 1(a b 0) ，
2
m 2n
联立方程①，②，解得 m = 4 ， n = 3 ，
椭圆 C 的方程为 x2 + y2 = 1. ……………………4 分 43
（2）设 M (x1, y1) ， N(x2, y2 ) ，直线 MN 的方程为 x = my +1 ，
x = my +1，
由方程组

x
2
4
+
y2 3
| n1 | | n2 | 3
∴平面 PAD 与平面 PBC 所成锐二面角的余弦值为 2 2 ．……………………12 分 3
（法二）如图，过 A 、P 分别做 PD 、AD 的平行线，交于点 S ，则 SP / / AD / /BC ，