数学必修五数列知识总结概论
人教版高中数学必修五数列基础知识要点总结

①观察法:根据数列的前几项归纳出数列的通项公式;
②公式法:利用 求通项公式
③根据递推公式求通项公式:
(1)迭代法:对于形如 型的递推公式,采取逐次降低“下标”数值的反复迭代方式,最终使 与初始值 (或 )建立联系的方法就是迭代法.
(2)累加法:形如 的递推公式可用 求出通项;
2、等差(比)中项
由三个数 , , 组成的等差数列可以看成最简单的等差数列。这时, 叫做 与 的等差中项.
若 与 的等差中项,则 。
如果在 , 两个数中间插入一个数 ,使 , , 成等比数列。这时, 叫做 与 的等比中项.
①、 与 是两个同号的非零实数
②、若 是 与 的等比中项,则
3、判断等差(比)数列的方法
③裂项相消法:把数列的通项裂成两项之差后求和,正负项相消,剩下首尾若干项.使用此方法时必须搞清楚消去了哪些项,保留了哪些项,一般未被消去的项有前后对称的特点.如:
(1) ,(2) ,
(3) ,(4) 。
④倒序相加法:当把一个数列倒过来排序,与原数列对应项相加后有公因式可提,且余下的项容易求和,这时一般可用倒序相加法求其前 项和.
已知三个数成等比数列,且已知三个数之积时,一般设此三个数分别为 , , ,其中 为公比。
若已知四个数成等比数列及这个四个数的积时,一般不设为 , , , ,因为这种设法使得四个数的公比为 ,就漏掉了公比为负数的情形,造成漏解。
2、求数列最大(小)值的方法
一般方法——解不等式 ;或
特别地,若 为等差数列, 为它的前n项的和时,求 的最大(小)值可以利用①二次函数的性质;② 中项的符号。
第二章 《数列》基础知识小结
一、数列的概念与表示方法
高一数学必修5:数列(知识点梳理)

第二章:数列一、数列的概念1、数列的概念:一般地,按一定次序排列成一列数叫做数列,数列中的每一个数叫做这个数列的项,数列的一般形式可以写成a a a a n ,,,,,123,简记为数列a n {},其中第一项a 1也成为首项;a n 是数列的第n 项,也叫做数列的通项.数列可看作是定义域为正整数集*N (或它的子集)的函数,当自变量从小到大取值时,该函数对应的一列函数值就是这个数列.2、数列的分类:按数列中项的多数分为:(1) 有穷数列:数列中的项为有限个,即项数有限; (2) 无穷数列:数列中的项为无限个,即项数无限.3、通项公式:如果数列a n {}的第n 项a n 与项数n 之间的函数关系可以用一个式子表示成=a f n n (),那么这个式子就叫做这个数列的通项公式,数列的通项公式就是相应函数的解析式.4、数列的函数特征:一般地,一个数列a n {},如果从第二项起,每一项都大于它前面的一项,即>+a a n n 1,那么这个数列叫做递增数列;高一数学必修5:数列(知识点梳理)如果从第二项起,每一项都小于它前面的一项,即1n n a a +<,那么这个数列叫做递减数列; 如果数列的各项都相等,那么这个数列叫做常数列.5、递推公式:某些数列相邻的两项(或几项)有关系,这个关系用一个公式来表示,叫做递推公式.二、等差数列1、等差数列的概念:如果一个数列从第二项起,每一项与前一项的差是同一个常数,那么这个数列久叫做等差数列,这个常数叫做等差数列的公差.即1n n a a d +-=(常数),这也是证明或判断一个数列是否为等差数列的依据.2、等差数列的通项公式:设等差数列的首项为1a ,公差为d ,则通项公式为:()()()11,n m a a n d a n m d n m N +=+-=+-∈、.3、等差中项:(1)若a A b 、、成等差数列,则A 叫做a 与b 的等差中项,且=2a bA +; (2)若数列为等差数列,则12,,n n n a a a ++成等差数列,即1n a +是与2n a +的等差中项,且21=2n n n a a a +++;反之若数列满足21=2n n n a a a +++,则数列是等差数列.4、等差数列的性质:(1)等差数列中,若(),m n p q m n p q N ++=+∈、、、则m n p q a a a a +=+,若2m n p +=,则2m n p a a a +=;(2)若数列和{}n b 均为等差数列,则数列{}n n a b ±也为等差数列;(3)等差数列{}n a 的公差为d ,则{}0n d a >⇔为递增数列,{}0n d a <⇔为递减数列,{}0n d a =⇔为常数列.5、等差数列的前n 项和n S :(1)数列{}n a 的前n 项和n S =()1231,n n a a a a a n N -++++++∈;(2)数列{}n a 的通项与前n 项和n S 的关系:11,1.,2n n n S n a S S n -=⎧=⎨-≥⎩(3)设等差数列{}n a 的首项为1,a 公差为d ,则前n 项和()()111=.22n n n a a n n S na d +-=+6、等差数列前n 和的性质:(1)等差数列{}n a 中,连续m 项的和仍组成等差数列,即12122,,m m m m a a a a a a ++++++++21223m m m a a a +++++,仍为等差数列(即232,,,m m m m m S S S S S --成等差数列);(2)等差数列{}n a 的前n 项和()2111==,222n n n d d S na d n a n -⎛⎫++- ⎪⎝⎭当0d ≠时,n S 可看作关于n 的二次函数,且不含常数项;(3)若等差数列{}n a 共有2n+1(奇数)项,则()11==,n S n S S a S n++-奇奇偶偶中间项且若等差数列{}n a 共有2n (偶数)项,则1==.n nS a S S nd S a +-偶奇偶奇且7、等差数列前n 项和n S 的最值问题:设等差数列{}n a 的首项为1,a 公差为d ,则(1)100a d ><且(即首正递减)时,n S 有最大值且n S 的最大值为所有非负数项之和; (2)100a d <>且(即首负递增)时,n S 有最小值且n S 的最小值为所有非正数项之和.三、等比数列1、等比数列的概念:如果一个数列从第二项起,每一项与前一项的比是同一个不为零的常数,那么这个数列就叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母q 表示(0q ≠).即()1n na q q a +=为非零常数,这也是证明或判断一个数列是否为等比数列的依据.2、等比数列的通项公式:设等比数列{}n a 的首项为1a ,公比为q ,则通项公式为:()11,,n n m n m a a qa q n m n m N --+==≥∈、.3、等比中项:(1)若a A b 、、成等比数列,则A 叫做a 与b 的等比中项,且2=A ab ; (2)若数列{}n a 为等比数列,则12,,n n n a a a ++成等比数列,即1n a +是与2n a +的等比中项,且212=n n n a a a ++⋅;反之若数列{}n a 满足212=n n n a a a ++⋅,则数列{}n a 是等比数列.4、等比数列的性质:(1)等比数列{}n a 中,若(),m n p q m n p q N ++=+∈、、、则m n p q a a a a ⋅=⋅,若2m n p +=,则2m n p a a a ⋅=;(2)若数列{}n a 和{}n b 均为等比数列,则数列{}n n a b ⋅也为等比数列;(3)等比数列{}n a 的首项为1a ,公比为q ,则{}1100101na a a q q ><⎧⎧⇔⎨⎨><<⎩⎩或为递增数列,{}1100011n a a a q q ><⎧⎧⇔⎨⎨<<>⎩⎩或为递减数列, {}1n q a =⇔为常数列.5、等比数列的前n 项和:(1)数列{}n a 的前n 项和n S =()1231,n n a a a a a n N -++++++∈;(2)数列{}n a 的通项与前n 项和n S 的关系:11,1.,2n n n S n a S S n -=⎧=⎨-≥⎩ (3)设等比数列{}n a 的首项为1a ,公比为()0q q ≠,则()11,1.1,11n n na q S a q q q=⎧⎪=-⎨≠⎪-⎩由等比数列的通项公式及前n 项和公式可知,已知1,,,,n n a q n a S 中任意三个,便可建立方程组求出另外两个.6、等比数列的前n 项和性质:设等比数列{}n a 中,首项为1a ,公比为()0q q ≠,则 (1)连续m 项的和仍组成等比数列,即12122,,m m m m a a a a a a ++++++++21223m m m a a a +++++,仍为等比数列(即232,,,m m m m m S S S S S --成等差数列);(2)当1q ≠时,()()11111111111111n n n n n a q a a a a aS q q q qq q q q q -==⋅-=-⋅=⋅-------, 设11a t q =-,则n n S tq t =-.四、递推数列求通项的方法总结1、递推数列的概念:一般地,把数列的若干连续项之间的关系叫做递推关系,把表达递推关系的式子叫做递推公式,而把由递推公式和初始条件给出的数列叫做递推数列.2、两个恒等式:对于任意的数列{}n a 恒有:(1)()()()()12132431n n n a a a a a a a a a a -=+-+-+-++-(2)()23411231,0,nn n n a a a a a a a n N a a a a +-=⨯⨯⨯⨯⨯≠∈3、递推数列的类型以及求通项方法总结: 类型一(公式法):已知n S (即12()n a a a f n +++=)求n a ,用作差法:{11,(1),(2)n n n S n a S S n -==-≥类型二(累加法):已知:数列的首项,且()()1,n n a a f n n N ++-=∈,求n a 通项.给递推公式()()1,n n a a f n n N ++-=∈中的n 依次取1,2,3,……,n-1,可得到下面n-1个式子:()()()()21324311,2,3,,1.n n a a f a a f a a f a a f n --=-=-=-=-利用公式()()()()12132431n n n a a a a a a a a a a -=+-+-+-++-可得:()()()()11231.n a a f f f f n =+++++-类型三(累乘法):已知:数列的首项,且()()1,n na f n n N a ++=∈,求n a 通项. 给递推公式()()1,n na f n n N a ++=∈中的n 一次取1,2,3,……,n-1,可得到下面n-1个式子: ()()()()23412311,2,3,,1.nn a a aa f f f f n a a a a -====- 利用公式()23411231,0,nn n n a a a a a a a n N a a a a +-=⨯⨯⨯⨯⨯≠∈可得: ()()()()11231.n a a f f f f n =⨯⨯⨯⨯⨯-类型四(构造法):形如q pa a n n +=+1、n n n q pa a +=+1(q p b k ,,,为常数)的递推数列都可以用待定系数法转化为公比为k 的等比数列后,再求n a 。
高中数学必修5 第二章 数列 知识整理

第二章 数列2.1 数列1.数列(1)数列的概念按照一定次序排列的一列数称为数列。
数列中的每一个数都叫做这个数列的项,各项依次叫做这个数列的第1项(或首项),第2项,…,第n 项,…,所以,数列的一般形式可以写成:123,,,,,n a a a a ……,简记为{}n a 。
其中数列{}n a 的第n 项n a 也叫做数列的通项。
注意:①数列中每一项都和它的序号有关,排在第一位的数称为这个数列的第1项(通常也叫做首项),排在第二位的数称为这个数列的第2项,…,排在第n 位的数称为这个数列的第n 项。
所以,数列的一般形式可以写成123,,,,n a a a a …,简记为{}n a 。
如:数列1,2,3,4,…,可以简记为{n}。
②数列中的数是按一定次序排列的。
因此,如果组成两个数列的数相同而排列次序不同,那么它们就不是相同的数列。
如:数列1,2,3,4,5与5,4,3,2,1是不同的数列。
③数列的定义中,并没有规定数列中的数必须不同。
因此,同一个数在数列中可以重复出现。
如:1,1,1,1,1,1,---…;2,2,2,2,2,…等。
④{}n a 与n a 是不同的概念。
{}n a 表示数列123,,,,,n a a a a ……,而n a 仅表示数列{}n a的第n 项。
⑤从映射函数的观点看,数列可以看做是一个定义域为正整数N +(或它的有限子集{1,2,3,,}n …)的数与自变量从小到大依次取值时对应的一列函数值,这里的函数是一种特殊函数:它的自变量只能取正整数,由于数列的值是函数值,序号是自变量,数列的通项公式也就是相应函数的解析式。
可以将序号为横坐标,相应的像为纵坐标,通过描点画图来表示一个数列,从数列的图像表示可以直观的看出数列的变化情况。
(2)数列的分类①按照数列的项数的多少可分为:有穷数列与无穷数列。
项数有限的数列叫有穷数列,项数无限的数列叫无穷数列。
②按照数列的每一项随序号变化的情况可分为:递增数列、递减数列、常数列、摆动数列。
(完整版)数学必修五数列知识总结
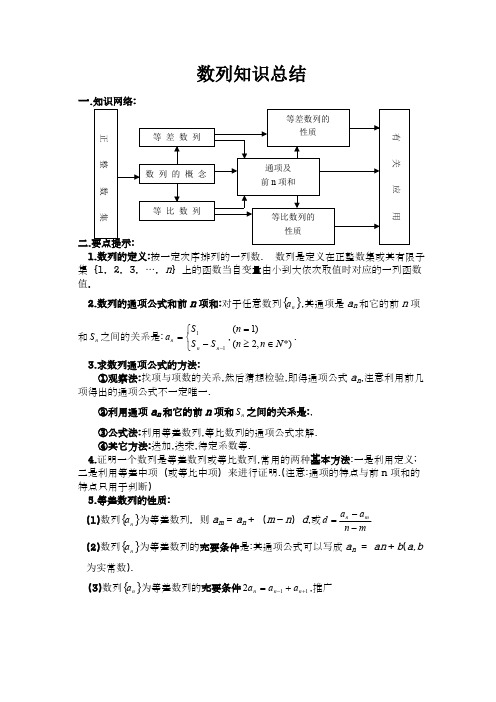
数列知识总结一.知识网络:二. 1.数列的定义:按一定次序排列的一列数. 数列是定义在正整数集或其有限子集{1,2,3,…,n }上的函数当自变量由小到大依次取值时对应的一列函数值.2.数列的通项公式和前n 项和:对于任意数列,其通项是a n 和它的前n 项{}n a 和之间的关系是:,.n S ⎩⎨⎧-=-11n nn S S S a *),2()1(N n n n ∈≥= 3.求数列通项公式的方法:①观察法:找项与项数的关系,然后猜想检验,即得通项公式a n ,注意利用前几项得出的通项公式不一定唯一.②利用通项a n 和它的前n 项和之间的关系是:,n S ③公式法:利用等差数列,等比数列的通项公式求解.④其它方法:迭加,迭乘,待定系数等.4.证明一个数列是等差数列或等比数列,常用的两种基本方法:一是利用定义;二是利用等差中项(或等比中项)来进行证明.(注意:通项的特点与前n 项和的特点只用于判断)5.等差数列的性质:(1)数列为等差数列,则a m = a n +(m -n )d ,或{}n a m n a a d mn--=(2)数列为等差数列的充要条件是:其通项公式可以写成a n = an +b (a,b {}n a 为实常数).(3)数列为等差数列的充要条件,推广{}n a 112+-+=n n n a a a(n>k.>0)k n k n n a a a +-+=2(4)数列为等差数列:若,则.{}n a q p n m +=+q p n m a a a a +=+(5)数列为等差数列,去掉前m 项,剩下的项构成等差数列.{}n a 推广:数列为等差数列,则每隔k 项取m 项的和仍构成等差数列. {}n a (6)数列是公差为d 的等差数列,则奇(偶)数项构成公差为2d 的等差数列.{}n a 推广①:数列为公差为d 等差数列:则在数列中每隔项取一项构成的数{}n a k 列是公差为的等差数列.项数成等差数列的项成等差数列.d k )1(+ 推广②:数列是公差为d 的等差数列,则项下标成等差数列的项也成等差{}n a 数列.(7)数列,项数相同的等差数列:则,,为常{}n a {}n b {}n ka {}n n qb pa +{}q p q pa n ,(+数)仍为等差数列.(8)数列为等差数列,其前n 项和可以写成为常数).{}n a n S b a bn an S n ,(,2+=(9)数列为等差数列:则数列中依次每连续项之和构成的数列也是等差数{}n a k 列.(10)数列为等差数列:表示奇数项的和,表示偶数项的和,{}n a 奇S 偶S 若项数为项时, 则有-= nd , /= a n / a n+1;n 2奇S 偶S 奇S 偶S 若项数为-1项时,则有-= a n ,/= n / (n -1),n 2奇S 偶S 奇S 偶S .n n a n S )12(12-=- 6.等比数列的性质:(1)数列为等比数列:.{}n a m n m n n n m n m n n a a a q a a q a a +---⋅===211,,(2)数列为等比数列: ,推广(n>m >0){}n a 112+-⋅=n n n a a a m n m n n a a a +-⋅=2(3)数列为等比数列:,则.{}n a k p n m +=+k p n m a a a a ⋅=⋅(4)数列为等比数列,取掉前若干项,剩余的项也构成等比数列.{}n a 推广:数列为等比数列,则每隔k 项取m 项的和(积)仍构成等比数列.{}n a (5)数列为等比数列,则奇(偶)数项构成等比数列.{}n a 推广①:数列为公比为 q 等比数列:则在数列中每隔项取一项构成的{}n a k 数列是公比为的等比数列.1+k q 推广②:数列为等比数列,则项数成等差数列的项成等比数列.{}n a (6)数列,为项数相同的等比数列:则,,,,{}n a {}n b }1{n a }{nn b a {}n ka {}n n b a ⋅为常数)等仍为等比数列.{}k a k n((7)数列为公比为q (q ≠±1)的等比数列:则数列中连续项之和(积)构成{}n a k 的数列是等比数列.(8)数列为等比数列: (表示奇数项的和,表示偶数项的和){}n a 奇S 偶S 若项数为项时,则有/=q ;若项数为-1项时,则有(-)/n 2偶S 奇S n 2奇S 1a = q.偶S (9)递推公式为的递推数列,都可以转化为)1(1≠+=+p q pa a n n }{n a 从而构造等比数列.111n n qq a p a p p +⎛⎫+=+ ⎪--⎝⎭7.等差数列与等比数列比较:8.等差数列与等比数列的关系:(1)各项为正的等比数列,其对数数列为等差数列.{}n a )1,0}({log ≠>a a a n a (2)数列为等差数列,则数列为正常数)为等比数列.{}n a C C n a }({9.数列求和的一般方法(结合于具体的示例讲解): ①倒序求和法:(等差数列的求和);②错位相减法:(等比数列和差比数列);例1:求和:.*)(432432N n na a a a a n ∈+++++ ③裂项相消法:(数列中的各项可以拆成几项,然后进行消项);例2:求和:.)12()12(1751531311+⋅-++⨯+⨯+⨯n n 例3:求数列的前n 项和.}11{++n n ④通项化归法:(化出通项,由通项确定求和方法);例4:求数列:的前n 项和. ,3211,,3211,211,1n+++++++n S ⑤分组求和法:(将一个数列分成几组,每组都可以用求和公式来求解);例5:求数列的前n 项之和.,21,,814,413,212,21-+n n ⑥公式法:(应用等差或等比数列的求和公式直接来求解).⑦.累差迭加法例6:已知数列6,9,14,21,30,…,其中相邻两项之差成等差数列,求它的通项.名称等差数列等比数列定义a n+1―a n =d 为等差数⇔{}n a 列为等比数列⇔≠=+)0(1q q a a nn {}n a 通项公式a n = a 1+(n -1)d =a m +(n -m )da n = a 1q n -1= a m q n -m前n 项和公式()21n n a a n S +=()d n n na 211-+=()()()⎪⎩⎪⎨⎧≠--=--==.1111,1111q q qa a q q a q na S n n n 中项a ,A ,b 成等差数列,或2 ⇔2ba A +=A =a +b .a ,G ,b ,成等比数列,或 G 2=ab⇔ab G ±=⑨∑求和记法用= 。
人教版高中数学必修五《数列》基础知识要点总结

9、等差(比)数列的单调性
①若 ,则 为递增数列;
②若 ,则 为递减数列;
③若 ,则 为常数列。
①当 时, 为常数列;
②当 时, 为摆动数列;
③当 , 时, 为递增数列;
④当 , 时, 为递减数列;
⑤当 , 时, 为递减数列;
3、求数列通项的常用方法
①观察法:根据数列的前几项归纳出数列的通项公式;
②公式法:利用 求通项公式
③根据递推公式求通项公式:
(1)迭代法:对于形如 型的递推公式,采取逐次降低“下标”数值的反复迭代方式,最终使 与初始值 (或 )建立联系的方法就是迭代法.
(2)累加法:形如 的递推公式可用 求出通项;
①
②
③
①
②
③
4、等差(比)数列的通项公式
①
②
③ ,其中 、 是常数
①
②
③
5、性质1
在等差数列 中,若已知 与 ,其中 ,则该数列的公差 。
若等比数列 中,公比是 ,则 。
6、性质2
在等差数列 中,若 且 、 、 、 ,则 。
特别地、在等差数列 中,若 且 、 、 ,则 。
在等比数列 中,若 ( , , , ),则 。
等差数列
等比数列
1、定义
一般地,如果一个数列从第二项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做等差数列的公差,公差通常用字母d表示.
一般地,如果一个数列从第二项起,每一项与它的前一项的比都等于同一个常数,那么这个数列就叫做等比数列,这个常数叫做等比数列的公比。公比通常用字母 表示。
数学必修五知识点总结

数学必修五知识点总结1、数列概念①数列是一种特殊的函数。
其特殊性主要表现在其定义域和值域上。
数列可以看作一个定义域为正整数集N某或其有限子集{1,2,3,…,n}的函数,其中的{1,2,3,…,n}不能省略。
②用函数的观点认识数列是重要的思想方法,一般情况下函数有三种表示方法,数列也不例外,通常也有三种表示方法:a、列表法;b、图像法;c、解析法。
其中解析法包括以通项公式给出数列和以递推公式给出数列。
③函数不一定有解析式,同样数列也并非都有通项公式。
等差数列1、等差数列通项公式an=a1+(n—1)dn=1时a1=S1n≥2时an=Sn—Sn—1an=kn+b(k,b为常数)推导过程:an=dn+a1—d令d=k,a1—d=b则得到an=kn+b2、等差中项由三个数a,A,b组成的等差数列可以堪称最简单的等差数列。
这时,A叫做a与b的等差中项(arithmeticmean)。
有关系:A=(a+b)÷23、前n项和倒序相加法推导前n项和公式:Sn=a1+a2+a3+·····+an=a1+(a1+d)+(a1+2d)+······+[a1+(n—1)d]①Sn=an+an—1+an—2+······+a1=an+(an—d)+(an—2d)+······+[an—(n—1)d]②由①+②得2Sn=(a1+an)+(a1+an)+······+(a1+an)(n 个)=n(a1+an)∴Sn=n(a1+an)÷2等差数列的前n项和等于首末两项的和与项数乘积的一半:Sn=n(a1+an)÷2=na1+n(n—1)d÷2Sn=dn2÷2+n(a1—d÷2)亦可得a1=2sn÷n—an=[sn—n(n—1)d÷2]÷nan=2sn÷n—a1有趣的是S2n—1=(2n—1)an,S2n+1=(2n+1)an+14、等差数列性质一、任意两项am,an的关系为:an=am+(n—m)d它可以看作等差数列广义的通项公式。
高中数学必修五第二章《数列》知识点归纳

数列知识点总结一、等差数列与等比数列等差数列等比数列定义a n 1 - a n =d a n 1=q(q 0)通项公式递推公式中项前 n 项和性质a na n = a 1 +( n-1 ) da n = a 1 q n 1 (q 0)a n = a n 1 +d, a n = a m +(n-m)da n = a n 1 qa n = a m q nma b推广: A= a n k a n k ( n,kG 2ab 。
推广:G= a n k a n k ( n,kA=+22 ;n>k>0 )。
任意两数 a 、c 不一定N+有等比中项, 除非有 ac > 0,则等比中N ;n>k>0 )项一定有两个n( a 1 + a n )S n =a 1 (1 q n )S n =1 q2S n =n a 1 +n(n 1)dS n =a 1 a n q21 q( 1)若 m n p q ,则 a m a n a p a q ; (1) 若m np q , 则(2)数列 a2n 1, a 2n, a2n 1 仍为等差数a m ·a n a p ·a q列,S n ,S 2 nS n , S 3 n S 2 n ⋯⋯ 仍为等差数( 2)S n ,S 2n S n ,S 3nS 2n ⋯⋯ 仍列,公差为 n 2d ;为等比数列 ,公比为 q n(3)若三个成等差数列,可设为a d , a , a d( 4)若 a n ,b n 是等差数列,且前 n 项和分别a m S2 m 1为 S n , T n ,则T 2 m 1b m( 5) a n为等差数列S n an 2bn( a , b 为常数,是关于 n 的常数项为 0 的二次函数) ( 6) d=a ma n(m n)m n(7)d>0 递增数列 d<0 递减数列 d=0 常数数列二、求数列通项公式的方法1、通项公式法: 等差数列、等比数列2、涉及前n项和 S n 求通项公式,利用a n 与 S n 的基本关系式来求。
最新人教版高中数学必修五《数列》基础知识要点总结

4、数列求和的常用方法
①公式求和法:公式法是数列求和的最常用方法之一,可直接利用等差数列、等比数列的求和公式,也可利用常见的求前 项和的公式,如: ;
据调查,大学生对此类消费的态度是:手工艺制品消费比“负债”消费更得人心。在等比数列 公比为 中,若 , ,则 , , ,…, ,…构成一个公比为 的等比数列。
8、性质4
若数列 与 分别是公差为 和 的等差数列,则数列 ( , 是常数)是公差为 的等差数列。
若 和 分别是公比为 和 的等比数列,则数列 , 仍是等比数列,它们的公比分别为 , 。
②根据数列项的大小变化分——递增数列、递减数列、常数列、摆动数列
5、数列的递推公式
如果已知数列的第1项(或前几项),且任一项与它的前一项(或前n项)间的关系可以用一个公式来表示,这个公式就叫做这个数列的递推公式。
6、数列前n项和的定义
一般地,我们称 为数列 的前 项和,用 表示,即
二、等差数列与等比数列
当 时, 或
11、前n项和的性质1
①当 时, ,是关于 的一个缺少常数项的一次函数,数列 图象是直线 上一群孤立的点;
②当 时, ,是关于 的一个缺少常数项的二次函数,数列 图象是抛物线 上一群孤立的点。
①当 时, ,数列 的图象是函数 上的一群孤立的点;
②当 时, ,设 ,则 ,此时,数列 的图象是函数 的图象上一群孤立的点。
9、等差(比)数列的单调性
①若 ,则 为递增数列;
②若 ,则 为递减数列;
③若 ,则 为常数列。
①当 时, 为常数列;
②当 时, 为摆动数列;
③当 , 时, 为递增数列;
④当 , 时, 为递减数列;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)数列 为等差数列,
(2)数列 为等差数列的充要条件是:其通项公式可以写成 (a,b为实常数)
(3)数列 为等差数列的充要条件 ,推广 (n>k>0)
(4)数列 为等差数列:若 ,则
(5)数列 为等差数列,去掉前m项,剩下的项构成等差数列
推广:数列 为等差数列,则每隔k项取m项的和仍构成等差数列
例2:求和:
例3:求数列 的前n项和
④通项化归法:(化出通项,由通项确定求和方法,一般可以裂项);
例4:求数列: 的前n项和
⑤公式法:(应用等差或等比数列的求和公式直接来求解)
⑥分组求和法:(将一个数列分成几组,每组都可以用等差数列及或等比数列的求和公式来求解);
例5:求数列 的前n项之和
⑦∑求和记号法
(6)数列 是公差为d的等差数列,则奇(偶)数项构成公差为2d的等差数列
推广①:数列 为公差为d等差数列:则在数列中每隔 项取一项构成的数列a1,ak+2,a2k+3,a3k+4, …是公差为 的等差数列
推广②:数列 是公差为d的等差数列,则项下标成等差数列(公差为k)的项也成等差数列(公差为kd)
2^3-1^3=3*(1^2)+3*1+1.
把这n个等式两端分别相加,得:
(n+1)^3-1=3(1^2+2^2+3^2+....+n^2)+3(1+2+3+...+n)+n,
由于1+2+3+...+n=(n+1)n/2,
代入上式得:
n^3+3n^2+3n=3(1^2+2^2+3^2+....+n^2)+3(n+1)n/2+n
2.数列的通项公式和前n项和:对于任意数列 ,其通项an和它的前n项和 之间的关系是: ,
3.求数列通项公式的方法:
①观察法:找项与项数的关系,然后猜想检验,即得通项公式an,注意利用前几项得出的通项公式不一定唯一
②利用通项 和它的前n项和 之间的关系(详见后面);
③公式法:利用等差数列,等比数列的通项公式求解
推广:数列 为等比数列,则每隔k项取m项的和(积)仍构成等比数列
(5)数列 为等比数列,则奇(偶)数项构成等比数列
推广①:数列 为公比为 q等比数列:则在数列中每隔 项取一项构成的数列是公比为 的等比数列
推广②:数列 为等比数列,则项数成等差数列的项成等比数列
(6)数列 , 为项数相同(可以都是无穷数列)的等比数列:则 , , , , 为常数)等仍为等比数列
(2)数列 为等差数列,则数列 为正常数)为等比数列
9数列求和的一般方法(结合于具体的示例讲解):
①倒序求和法:(等差数列的求和);
②错位相减法:适用于差比数列(如果 等差, 等比,则 叫做差比数列)
例1:求和:
③裂项相消法:适用于数列 和 (其中 等差)。可裂项为: ,
;(小技巧:消项前把加项写在一起,把减项放在一起,便于看出消项的规律)
用 =
已知:
注:(利用恒等式(n+1)^3=n^3+3n^2+3n+1证明1^2+2^2+3^2+....+n^2=n(n+1)(2n+1)/6):
(n+1)^3-n^3=3n^2+3n+1,
n^3-(n-1)^3=3(n-1)^2+3(n-1)+1
..........
3^3-2^3=3*(2^2)+3*2+1
(7)数列 , 项数相同的等差Biblioteka 列:则 , , 为常数)仍为等差数列
(8)数列 为等差数列,其前n项和 可以写成
(9)数列 为等差数列:则数列中依次每连续m项之和构成的数列 (即 )为等差数列,公差 ;
(10)数列 为等差数列: 表示奇数项的和, 表示偶数项的和,
若项数为2n项时, 则有 - = nd, / = an/an+1;
数列知识总结
一.要点提示:
1.数列的定义:按一定次序排列的一列数 数列是定义在正整数集或其有限子集{1,2,3,…,n}上的函数当自变量由小到大依次取值时对应的一列函数值.
数列的分类:①递增数列:对于任何 ,均有 .②递减数列:对于任何 ,均有 .③摆动数列:例如: ④常数数列:例如:6,6,6,6,…….⑤有界数列:存在正数 使 .⑥无界数列:对于任何正数 ,总有项 使得 .
名称
等差数列
等比数列
定义
an+1―an=d 为等差数列
为等比数列
通项公式
an=a1+(n-1)d=am+(n-m)d
an=a1qn-1=amqn-m
前n项和公式
中项
a,A,b成等差数列
,或2A=a+b.
a,G,b,成等比数列
,或G2=ab
8.等差数列与等比数列的关系:
(1)各项为正的等比数列 ,其对数数列 为等差数列
④已知递推公式:迭加,迭乘,待定系数法等(详见后面)
4.证明一个数列是等差数列,常用的两种基本方法:⑴定义法: ( , 是常数) 是等差数列;⑵中项法: ( ) 是等差数列;
证明一个数列是等比数列,常用的两种基本方法:⑴定义法: ( , 是常数) 是等比数列;⑵中项法: ( )且 是等比数列.
(注意:通项的特点与前n项和的特点只用于判断,不用于证明其为等差数列)
若项数为2n-1项时,则有 - = an , / = n/(n-1),
(11)若等差数列 的前 项和 ,则 (即 )为等差数列,公差为 .
6.等比数列的性质:
(1)数列 为等比数列:
(2)数列 为等比数列: ,推广 (n>m>0)
(3)数列 为等比数列: ,则
(4)数列 为等比数列,取掉前若干项,剩余的项也构成等比数列
2、若等差数列 的首项 ,公差 ,则前 项和 有最小值
(ⅰ)若已知通项 ,则 最小 ;
(7)数列 为公比为q(q≠±1)的等比数列:则数列中连续 项之和(积)构成的数列是等比数列
(8)数列 为等比数列: ( 表示奇数项的和, 表示偶数项的和)
若项数为 项时,则有 / = q;
若项数为 -1项时,则有( - )/ = q
(9)递推公式为 的递推数列 ,都可以转化为
从而构造等比数列
7.等差数列与等比数列比较:
整理后得:
1^2+2^2+3^2+....+n^2=n(n+1)(2n+1)/6
例7: 若 , 对n∈N恒成立,求a,b,c的值
补充:
等差数列前 项和的最值问题:
1、若等差数列 的首项 ,公差 ,则前 项和 有最大值。
(ⅰ)若已知通项 ,则 最大 ;
(ⅱ)若已知 ,则当 取最靠近 的非零自然数时 最大;
