山西省长治二中、康杰中学、临汾一中等六校2018届高三第四次名校联合考试数学理
2018届山西省六校(长治二中等)高三第四次名校联合考试(百日冲刺)理科综合试题word

山西省六校2018届高三第四次名校联合考试(百日冲刺)理科综合试题(长治二中,晋城一中、康杰中学、临汾一中等)一、选择题:1.下列关于线粒体和叶绿体的叙述,错误的是A.细胞分化后,不同类型的植物细胞中线粒体和叶绿体的数量不同B.细胞吸收离子物质所需的能fit可来自线粒体和叶绿体C.葡萄糖在叶绿体中合成,其分解产物能在线粒体中被彻底氧化分解D.叶绿体和线粒体中的基因都能转录生成mRNA2.某实验小组在室温条件下,将紫色洋葱鳞片叶外表皮细胞置于一定浓度的某溶液中,测得细胞液浓度与该溶液浓度的比值(P值)随时间的变化曲线如图所示。
下列相关叙述正确的是A.该溶液是一定浓度的蔗糖溶液B.细胞在t1时刻开始从外界溶液中吸收溶质C.若降低温度,则t1〜t2时间段会变长D.t2时刻后P值不再增大主要是由于细胞壁的限制3.同位素标记法是生物学研究中常用的技术手段,下列相关叙述错误的是A.用3H标记的氨基酸来研究抗体的合成和分泌过程中,高尔基体中会出现放射性B.鲁宾和卡门用180分别标记H2O和CO2,证明了光合作用释放的O2来自水C.用15N标记大肠杆菌的DNA和含14N标记的脱氧核苷酸培养液做实验,可证明DNA进行半保留复制D.用32P标记的噬菌体侵染大肠杆菌,适当时间后搅拌离心,检测到沉淀物的放射性很低4.下列关于生物变异及育种的叙述,正确的是A.诱变育种能定向提高突变率,以获得较多的优良变异类型B.通过杂交育种产生的子代个体中会出现新的物种C.一般情况下,基因工程育种不能产生新基因,但能定向改造生物性状D.单倍体植株常表现出长势矮小、种子不饱满等性状5.下列关于人体内环境及其稳态的叙述,错误的是A.血浆中的HCO3-具有维持血浆pH稳定的功能B.组织细胞内液的渗透压与组织液的渗透压差别较大C.抗原与抗体的特异性结合可发生在内环境中D.细胞内液和外液中的Na+、K+分布不均,是兴奋在神经纤维上传导的基础6.人类某遗传病受两对等位基因控制,已知基因A、a为常染色体上,基因B、b位于X染色体上,且基因A、B同时存在时个体表现正常,其余情况下均表现为患病。
【高三数学试题精选】2018山西省高三数学模拟试卷及答案(第四次四校联考理科)

2018山西省高三数学模拟试卷及答案(第四次四校联考理
科)
5 c
(满分150分,考试时间14坐标系与参数方程
在平面直角坐标系中,直线的参数方程为 ( 为参数)若以坐标原点为极点,轴正半轴为极轴建立极坐标系,则曲线的极坐标方程为
(1) 求曲线c的直角坐标方程;
(2) 求直线被曲线所截得的弦长
24(本题满分10分)选修4-5不等式选讲
函数
⑴画出函数的图象;
⑵若不等式恒成立,求实数的范围
高三第四次四校联考理科数学答案
1-5 cBADD 6-10 ABcAc 11-12 BA
13 14 15 16
19解(1)根据茎叶图,有“运动健将”12人,“运动积极分子”18人------------1分
用分层抽样的方法,每个人被抽中的概率为,所以选中的运动健将有
运动积极分子有 -----------------3分
设事至少有1名‘运动健将’被选中,则
-----------5分
(2)由茎叶图知男“运动健将有”8人,女“运动健将”有4人,故的取值为
------------7分
----------9分
的分布列为。
长治二中 康杰中学 临汾一中 忻州一中2013届高三第四次四校联考数学理试题 含答案

山西省长治二中 康杰中学 临汾一中 忻州一中20XX 届高三第四次四校联考数学试题(理)(满分150分,考试时间120分)一、选择题(5×12=60分,在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项用2B 铅笔涂黑机读卡上对应题目的答案标号) 1.已知集合},1|{2R x x y y M ∈-==,}2|{2x y x N -==,则=N MA .),1[+∞-B .]2,1[-C .),2[+∞D .φ2.下列说法错误..的是 A .“1sin 2θ=”是“30θ=”的充分不必要条件 B .命题“若0a =,则0ab =”的否命题是:“若0a ≠,则0ab ≠”C .若命题2:,10p x R x x ∃∈-+=,则 2:,10p x R x x ⌝∀∈-+≠D .若命题“p ⌝”与命题“p 或q ”都是真命题,那么命题q 一定是真命题3.函数)20)(2sin(πϕϕ<<+=x y 图象的一条对称轴在(π6,π3)内,则满足此条件的一个ϕ值为 A .12π B .6π C .3πD . 65π4.一个空间几何体的三视图如右图所示,其中主视图和侧视图都是半径为1的圆,且这个几何体是球体的一部分, 则这个几何体的表面积为A .3πB .4πC .6πD .8π5.若实数x ,y 满足约束条件142x y x y y -≥-⎧⎪+≤⎨⎪≥⎩,则目标函数24z x y =+的最大值为A .10B .12C .13D .146.运行下图所示框图的相应程序,若输入,a b 的值分别为2log 3和3log 2,则输出M 的值是A .0B .1C .2D .-17.已知数列{n a }满足)(log log 1133++∈=+N n a a n n ,且2469a a a ++=,则15793log ()a a a ++的值是M=a ×b +1否是结束开始M=a ×b -1 输入a,b 输入M a ≤bA .15 B . 15- C . 5 D .5- 8.已知一个三棱柱,其底面是正三角形,且侧棱与底面垂直,一个体积为34π的球体与棱柱的所有面均相切,那么这个三棱柱的表面积是A .36B .312C . 318D . 3249.在ABC ∆中,角A 、B 、C 所对的边分别为a ,b ,c 且a=1,B=45°,ABC S ∆=2,则b 等于A .5B .25C .41D .2510.已知函数1)(+-=mx e x f x的图像为曲线C ,若曲线C 存在与直线x y 21=垂直的切线,则实数m 的取值范围是A .2≤mB .2>mC .21-≤m D .21->m 11.若定义在R 上的偶函数()x f 满足()()x f x f =+2且[]1,0∈x 时,(),x x f =则方程()x x f 3log =的零点个数是A .2个B .3个C . 4个D .多于4个12.已知A B P 、、是双曲线22221x y a b-=上的不同三点,且A B 、连线经过坐标原点,若直线PA PB 、的斜率乘积23PA PB k k ⋅=,则该双曲线的离心率e =ABCD二、填空题:(本大题共4小题,每小题5分,共20分,把答案填在答卷纸的相应位置上)13.若函数)1,0(log ≠>=a a x y a 的图象过点(2,-1),且函数)(x f y =的图像与函数)1,0(log ≠>=a a x y a 的图像关于直线xy =对称,则)(x f = .14.i 为虚数单位,则复数i i43105-+的虚部是 .15.某铁路货运站对6列货运列车进行编组调度,决定将这6列列车编成两组,每组3列,且甲与乙两列列车不在同一小组,如果甲所在小组3列列车先开出,那么这6列列车先后不同的发车顺序共有 . 16.已知函数M,最小值为m,则mM= . 三、解答题(本大题6小题,共70分,解答应写出文字说明、证明过程或演算步骤,并把解答写在答卷纸的相应位置上) 17.(本小题满分12分)已知点A (4,0)、B (0,4)、C (ααsin 3,cos 3) (1)若),0(πα∈=,求α的大小;(2)⊥,求αααtan 12sin sin 22++的值.18.(本小题满分12分)为了解甲、乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取12件和5件,测量产品中微量元素x ,y 的含量(单位:毫克).下表是乙厂的5件产品的测量数据:编号 1 23 45 x 169 178 166 175 180 y 75 80 777681( (2)当产品中的微量元素x ,y 满足x ≥175且y ≥75,该产品为优等品,①用上述样本数据估计乙厂生产的优等品的数量;②从乙厂抽出的上述5件产品中,随机抽取2件,求抽取的2件产品中优等品数ξ的分布列及其期望.19.(本小题满分12分)如图,已知长方形ABCD 中,1,2==AD AB ,M 为DC 的中点. 将ADM ∆沿AM 折起,使得平面⊥ADM 平面ABCM .(1)求证:BM AD ⊥ ;(2)若点E 是线段DB 的中点,求二面角D AM E --的余弦值.20.(本小题满分12分)已知21,F F 为椭圆)0(1:2222>>=+b a by a x C 的左,右焦点,M 为椭圆上的动点,且21MF MF ⋅的最大值为1,最小值为-2.(1)求椭圆C 的方程; (2)过点),(056-作不与y 轴垂直的直线l 交该椭圆于N M ,两点,A 为椭圆的左顶点。
山西省六校2018届高三第四次名校联合考试数学(文)试卷(含答案)

2017-2018年度高三第四次名校联合考试(百日冲刺)数学(文科)六校联考 长治二中、鄂尔多斯一中、晋城一中、康杰中学、临汾一中、忻州一中第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合}2,2{},,4{2m B m A ==.若≠⋂B A ∅,则m 的取值可能是( )A .1B .2C .3D .22. 复数3)1(i z +=的虚部为( )A .2-B .2C .i 2-D .i 23.设n S 为等差数列}{n a 的前n 项和,已知88,0112==S a ,则=5a ( )A .6B .7C .9D .104. 已知下表为随机数表的一部分,将其按每5个数字编为一组: 08015 17727 45318 22374 21115 7825377214 77402 43236 00210 45521 6423729148 66252 36936 87203 76621 1399068514 14225 46427 56788 96297 78822已知甲班有60位同学,编号为60~01号,现在利用上面随机数表的某一个数为起点,以简单随机抽样的方法在甲班中抽取4位同学,由于样本容量小于99,所以只用随机数表中每组数字的后两位,得到下列四组数据,则抽到的4位同学的编号不可能是( )A .53,18,27,15B .52,25,02,27C .22,27,25,14D .74,18,27,155. 设)(x f 为定义在R 上的奇函数,当0≥x 时,173)(--=x x f x,则=-)1(f ( )A .5B .5- C. 6 D .6-6. 若41)3sin(=-a π,则=-)62sin(πa ( ) A .87- B .87 C. 1615- D .1615 7. 设变量y x ,满足约束条件⎪⎩⎪⎨⎧≤+≥+≤-3313y x y x y x ,则y x z -=2的取值范围为( )A .]3,1[-B .]6,1[- C. ]5,1[- D .]6,5[8. 已知][x 表示不超过x 的最大整数,如3]4.2[,1]1[,0]4.0[-=-==.执行如图所示的程序框图,则输出的=S ( )A .1B .5 C. 14 D .159. 已知曲线)32sin(:π-=x y C ,则下列结论正确的是( ) A .把C 向左平移125π个单位长度,得到的曲线关于原点对称 B .把C 向右平移6π个单位长度,得到的曲线关于y 轴对称 C. 把C 向左平移3π个单位长度,得到的曲线关于原点对称 D .把C 向右平移12π个单位长度,得到的曲线关于y 轴对称 10.已知倾斜角为ο135的直线l 交双曲线)0,0(1:2222>>=-b a by a x C 于B A ,两点,若线段AB 的中点为)1,2(-P ,则C 的离心率是( )A .3B .2 C. 26 D .25 11.某几何体的三视图如图所示,则该几何体的体积为( )A .34B .1 C. 35 D .2 12.已知R a ∈,函数2225284)(a ax x ae ex f x x +-+-=(e 是自然对数的底数),当)(x f 取得最小值时,则实数a 的值为( )A .4B .58 C. 54 D .52 第Ⅱ卷(共90分) 二、填空题(每题5分,满分20分,将答案填在答题纸上)13.在矩形ABCD 中,2,5==AD AB ,则=+→→||AC AB .14.在正项等比数列}{n a 中,62,a a 是031032=+-x x 的两个根,在=-+2652a a a .15.已知抛物线y x C 8:2=,直线2:+=x y l 与C 交于N M ,两点,则=|MN | .16.在直三棱柱111C B A ABC -中,8,52,4,1===⊥AA AC AB AC AB .若该三棱柱的六个顶点都在球O 的球面上,则球O 的表面积为 . 三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. 在ABC ∆中,角C B A ,,的对边分别为c b a ,,,已知1,sin 2sin 3,12cos 2cos 22=-==-+b a A B C B A . (1)求角C 的大小;(2)求b c 的值. 18. 交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为a 元,在下一年续保时,实行的费率浮动机制,保费是与上一年度车辆发生道路交通安全违法行为或者道路交通事故的情况相联系的.交强险第二年价格计算公式具体如下:交强险最终保费=基准保费⨯a (+1浮动比率t ).发生交通事故的次数越多,出险次数的就越多,费率也就越高,具体浮动情况如下表:上年度出险次数0 1 2 3 4 5≥ 浮动比率t %15- %0 %25+ %50+ %75+ %100+ 某机构为了研究某一品牌普通6座以下私家车的投保情况,为此搜集并整理了100辆这一品牌普通6座以下私家车一年内的出险次数,得到下面的柱状图:已知小明家里有一辆该品牌普通6座以下私家车且需要续保,续保费用为X 元.(1)记A 为事件“a X a ⋅≤≤%175”,求)(A P 的估计值.(2)求X 的平均估计值.19. 如图,在直角梯形ABCD 中,BC AB BC AD ⊥,//,且F E AD BC ,,42==分别为DC AB ,的中点,沿EF 把AEFD 折起,使CF AE ⊥,得到如下的立体图形.(1)证明:平面⊥AEFD 平面EBCF ;(2)若EC BD ⊥,求二面角A CD F --的大小.20. 已知椭圆)0(1:2222>>=+b a by a x C 的左焦点为)0,1(1-F ,点)22,1(M 在椭圆C 上,经过坐标原点O 的直线l 与椭圆C 交于B A ,两点,P 为椭圆C 上一点(P 与B A ,都不重合).(1)求椭圆C 的方程;(2)若直线AB 的斜率为21-,求ABP ∆的面积的最大值. 21. 已知函数x x ax x g ln )(+=(a 是常数). (1)求)(x g 的单调区间与最大值;(2)设)()(x g x x f ⋅=在区间],0(e (e 为自然对数底数)上的最大值为10ln 1--,求a 的值. 请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.选修4-4:坐标系与参数方程在直角坐标系xOy 中,以坐标原点为极点,x 轴为正半轴为极轴建立极坐标系,圆C 的极坐标方程为θρcos 3=.(1)求圆C 的参数方程;(2)设P 为圆C 上一动点,)0,5(A ,若点P 到直线3)3sin(=-πθρ的距离为437,求ACP ∠的大小.23.选修4-5:不等式选讲设函数a a x x f 2||)(++=.(1)若不等式1)(≤x f 的解集为}42|{≤≤-x x ,求实数a 的值;(2)在(1)的条件下,若不等式4)(2--≥k k x f 恒成立,求实数k 的取值范围.。
山西省忻州一中 康杰中学 临汾一中 长治二中高三数学第四次四校联考试题 理 新人教A版
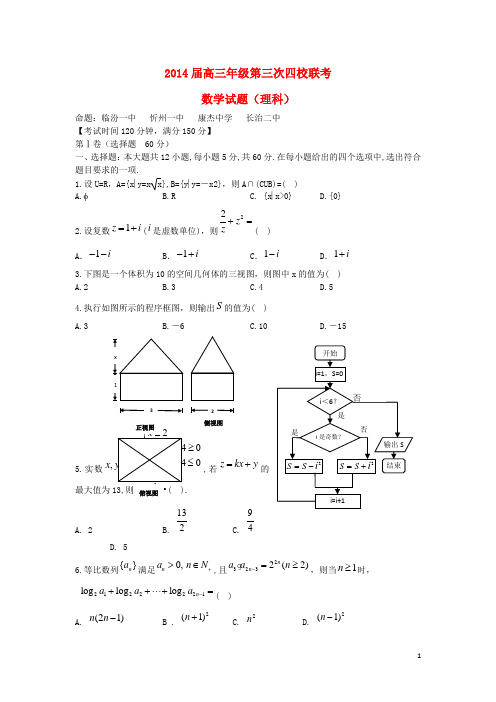
2014届高三年级第三次四校联考数学试题(理科)命题:临汾一中 忻州一中 康杰中学 长治二中 【考试时间120分钟,满分150分】 第Ⅰ卷(选择题 60分) 一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,选出符合题目要求的一项.1.设U=R ,A={x ⎢y=x x},B={y ⎢y=-x2},则A∩(CUB)=( ) A.φ B.R C. {x ⎢x>0}D.{0}2.设复数1z i =+(i 是虚数单位),则22z z +=( )A .1i --B .1i -+C .1i -D .1i +3.下图是一个体积为10的空间几何体的三视图,则图中x 的值为( ) A.2 B.3 C.4 D.54.执行如图所示的程序框图,则输出S 的值为( ) A.3B.-6C.10D.-155.实数,x00≥≤,若z kx y =+的最大值为A. 2 B. 132C. 94D. 56.等比数列{}n a 满足0,n a >n N +∈,且23232(2)n n a a n -=≥g ,则当1n ≥时,2122221log log log n a a a -++⋅⋅⋅+=( )A. (21)n n -B . 2(1)n +C. 2nD. 2(1)n -o7.已知函数f(x)=sin(ωx+ϕ)(ω>0, ⎥ϕ⎢<π2)的部分图象如图所示,则y=f(x+π6)取得最小值时x 的集合为( ) A. {x ⎢x= k π-π6, k ∈Z }B. {x ⎢x= k π-π3, k ∈Z }C. {x ⎢x=2k π-π6, k ∈Z }D. {x ⎢x=2k π-π3, k ∈Z }8.右图可能是下列哪个函数的图象( ) A.y=2x -x2-1 B. y =2xsinx 4x+1C.y=(x2-2x)exD. y=x lnx9.向边长分别为13,6,5的三角形区域内随机投一点M ,则该点M 与三角形三个顶点距离都大于1的概率为( )A .181π-B.121π-C.19π-D.41π-10.航空母舰“辽宁舰”在某次舰载机起降飞行训练中,有5架歼-15飞机准备着舰.如果甲、乙两机必须相邻着舰,而甲、丁两机不能相邻着舰,那么不同的着舰方法有( ) A .12种 B.16种 C.24种 D. 36种11. 三棱锥P —ABC 的四个顶点均在同一球面上,其中△ABC 是正三角形,PA ⊥平面ABC , PA =2AB =6,则该球的体积为( ) A .163πB .323πC .48πD .643π12.已知双曲线()222210,0x y a b a b -=>>,过其左焦点F 作x 轴的垂线,交双曲线于,A B两点,若双曲线的右顶点在以AB 为直径的圆内,则双曲线离心率的取值范围是( )A .()2,+∞B .()1,2C .3,2⎛⎫+∞ ⎪⎝⎭D . 31,2⎛⎫⎪⎝⎭第Ⅱ卷(非选择题 90分)二、填空题:本大题共4小题,每小题5分,共20分.13. 如果(2x -1)6=a0+a1x +a2x2+…+a6x6,那么a1+a2+…+a6的值等于 . 14. 圆O 为△ABC 的外接圆,半径为2,若AB →+AC →=2AO →,且|OA →|=|AC →|,则向量BA →在向量BC →方向上的投影为 .15.已知(0)()(0)x e x f x x x -⎧≤⎪=⎨>⎪⎩,1()()2g x f x x b=--有且仅有一个零点时,则b 的取值范围是 .17π12π3 xoy yx16.若数列{}n a 与{}n b 满足1113(1)(1)1,,2n nn n n n n b a b a b n N -++++-+=-+=∈,且12a =,设数列{}n a 的前n 项和为nS ,则63S = .三、解答题:本大题共6小题,共70分. 解答应写出文字说明,证明过程或演算步骤. 17. (本小题满分12分) 已知∆ABC 中,角A ,B ,C 的对边分别为a ,b ,c .cosA =23,sinB.(1)求tanC 的值;(2)若a∆ABC 的面积.18. (本小题满分12分)学校设计了一个实验学科的考查方案:考生从6道备选题中一次随机抽取3道题,按照题目要求独立完成全部实验操作,并规定:在抽取的3道题中,至少正确完成其中2道题便可通过考查.已知6道备选题中考生甲有4道题能正确完成,2道题不能完成;考生乙每题正确完成的概率都为32,且每题正确完成与否互不影响.(1)求考生甲正确完成题目个数ξ的分布列和数学期望; (2)用统计学知识分析比较甲、乙两考生哪位实验操作能力强及哪位通过考查的可能性大? 19. (本小题满分12分) 如图,在几何体ABCDEF 中,AB ∥CD ,AD =DC =CB =1,∠ABC =60°, 四边形ACFE 为矩形,平面ACFE ⊥平面ABCD ,CF =1. (1)求证:平面FBC ⊥平面ACFE ; (2)点M 在线段EF 上运动,设平面MAB 与平面FCB 所成 二面角的平面角为θ(θ≤90°),试求cosθ的取值范围. 20. (本小题满分12分)抛物线C1:24y x =的焦点与椭圆C2:22221(0)x y a b a b +=>>的一个焦点相同.设椭圆的右顶点为A ,C1, C2在第一象限的交点为B ,O 为坐标原点,且OAB∆的面积为3a .(1)求椭圆C2的标准方程;(2)过A 点作直线l 交C1于C,D 两点,连接OC,OD 分别交C2于E,F 两点,记OEF ∆,OCD ∆的面积分别为1S ,2S .问是否存在上述直线l 使得213S S =,若存在,求直线l 的方程;若不存在,请说明理由.21. (本小题满分12分)设函数-1()=x e f x x (1)判断函数f(x)在(0,+∞)上的单调性;FAB C D EM(2)证明:对任意正数a ,存在正数x ,使不等式f(x)-1<a 成立.请考生在22、23、24中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做第一个题目计分,作答时请用2B 铅笔在答题卡上将所选题号后的方框涂黑.22.(本题满分10分)选修4-1:几何证明选讲 如图,过圆E 外一点A 作一条直线与圆E 交于C B ,两点,且ACAB 31=,作直线AF 与圆E 相切于点F ,连结EF 交BC 于点D ,已知圆E 的半径为2,030=∠EBC (1)求AF 的长;(2)求证:ED AD 3=.23.(本题满分10分)选修4-4:坐标系与参数方程选讲在直角坐标系xoy 中,曲线1C的参数方程为sin x y αα⎧=⎪⎨=⎪⎩(α为参数),以原点O 为极点,x 轴正半轴为极轴建立极坐标系,曲线2C 的极坐标方程为24)4sin(=+πθρ(1)求曲线1C 的普通方程与曲线2C 的直角坐标方程;(2)设P 为曲线1C 上的动点,求点P 到2C 上点的距离的最小值,并求此时点P 的坐标.24.(本题满分10分)选修4-5:不等式选讲 设函数()312--+=x x x f(1)求函数()x f y =的最小值;(2)若272)(-+≥a ax x f 恒成立,求实数a 的取值范围.2014届高三年级第三次四校联考 数学(理科)答案 选择题填空题13. 0 14. 3 15.b ≥1或b=12或b ≤0 16. 560三、解答题17.解:(1)∵cosA =23 ∴sinA =,……………2分=sinB =sin(A +C)=sinAcosC +sinCcosA=cosC +23sinC . ……………5分整理得:tanC ……………6分(2) 由(1)知sinC ,cosC由正弦定理知:sin sin a cA C =,故c = ……………9分又∵sinB 615⋅……………10分∴∆ABC 的面积为:S =B ac sin 21=. ……………12分18.解:(1)设考生甲正确完成实验操作的题目个数分别为ξ,则ξ可能取值为1,2,351)1(362214===C C C P ξ 53)2(361224===C C C P ξ 51)3(360234===C C C P ξ ……………3分ξ 1 2 3P51 53 51所以2513532511=⨯+⨯+⨯=ξE ……………5分(2)设考生乙正确完成实验操作的题目个数为η因为)32,3(~B η,其分布列为:3,2,1,0,)31()32()(33===-k C k P k k k η 所以2323=⨯=ηE ……………6分又因为5251)23(53)22(51)21(222=⨯-+⨯-+⨯-=ξD3231323=⨯⨯=ηD ……………8分 所以ηξD D <又因为8.05153)2(=+=≥ξP , 74.02782712)2(≈+=≥ηP ……………10分所以)2()2(≥>≥ηξP P①从做对题数的数学期望考查,两人水平相当;从做对题数的方差考查,甲较稳定;②从至少完成2题的概率考查,甲获得通过的可能性大,因此,可以判断甲的实验操作能力强. ……………12分 19.(1)证明:在四边形ABCD 中,∵AB ∥CD ,AD=DC=CB=1,∠ABC=60°,∴AB=2,∴AC2=AB2+BC2-2AB·BC·cos60°=3,∴AB2=AC2+BC2,∴BC ⊥AC.∵平面ACFE ⊥平面ABCD ,平面ACFE∩平面ABCD=AC ,BC ⊂平面ABCD ,∴BC ⊥平面ACFE.又因为BC ⊂平面FBC , 所以 平面ACFE ⊥平面FBC , .............5分(2)解:由(1)可建立分别以直线CA ,CB ,CF 为x 轴,y 轴,z 轴的如图所示的空间直角坐标系,令FM=λ(0≤λ≤3),则C(0,0,0),A(3,0,0),B(0,1,0),M(λ,0,1), ∴AB →=(-3,1,0),BM →=(λ,-1,1),设n1=(x,y,z)为平面MAB 的一个法向量,由⎩⎪⎨⎪⎧n1·AB →=0n1·BM →=0,得3x y 0x y z 0,⎧-+=⎪⎨λ-+=⎪⎩,取x=1,则n1=(1,3,3-λ), ∵n2=(1,0,0)是平面FCB 的一个法向量, ∴cos θ=|n1·n2||n1|·|n2|=11+3+(3-λ)2⨯1=1(3-λ)2+4...........10分∵0≤λ≤3,∴当λ=0时,cosθ有最小值77,当λ=3时,cosθ有最大值12.∴cosθ∈[71,2]..............12分20.解:(1)∵24y x =∴焦点()1,0F ∴1c =即221a b =+……………1分又∵1623OAB B S OA y a ∆=⨯⨯= ∴63B y =……………2分 代入抛物线方程得226(,)3B .又B 点在椭圆上得23b =,24a =∴椭圆C2的标准方程为22143x y +=. ……………4分(2)设直线l 的方程为2x my =+,由224x my y x =+⎧⎨=⎩得2480y my --=设1122(,),(,)C x yD x y ,所以12124,8y y m y y +=⋅=-……………6分又因为21211sin 21sin 2E FOC OD COD OC OD S y y S OE OF y y OE OF EOF ∠===⨯∠直线OC 的斜率为1114y x y =,故直线OC 的方程为14y y x =, 由1224143y y x x y ⎧=⎪⎪⎨⎪+=⎪⎩得221364364E y y ⨯=+,同理222364364F y y ⨯=+ 所以22222212364364643()()36436412148EFy y y y m ⨯⨯⨯=⨯=+++则2222212222112148()3E F S y y m S y y ⋅+==⋅, ……………10分所以221214893m +=,所以24840m =-,故不存在直线l 使得213S S = ……………12分21.解:(1) 由题意知:,f '(x)=xex-(ex-1)x2= (x-1)ex+1x2, ……………2分令h(x)=(x-1)ex+1,则h '(x)=x ex>0,∴h(x)在(0,+∞)上是增函数, ……………3分 又h(0)=0,∴h(x)>0,则f '(x)>0,∴f(x)在(0,+∞)上是单调增函数. ……………5分 (2) f(x)-1=ex- x -1x,不等式f(x)-1<a 可化为ex-(a+1)x-1<0,令G(x)= ex-(a+1)x-1, G '(x)=ex-(a+1), ……………7分 由G '(x)=0得:x=ln(a+1),当0<x< (ln(a+1)时,G '(x)<0, 当x>ln(a+1)时,G '(x)>0,∴当x=ln(a+1)时,G(x)min=a-(a+1)ln(a+1), ……………9分 令ϕ(a)=a a+1- ln(a+1),(a≥0) ϕ'(a)=1(a+1)2-1a+1=-a(a+1)2<0,又ϕ(0)=0,∴当a>0时,ϕ(a)< ϕ(0)=0,即当x=ln(a+1)时,G(x)min=a-(a+1)ln(a+1)<0. ……………11分 故存在正数x=ln(a+1),使不等式F(x)-1<a 成立. ……………12分22.(本题满分10分)选修4-1:几何证明选讲 解:(1)延长BE 交圆E 于点M ,连结CM , 则090=∠BCM ,又,42==BE BM 030=∠EBC ,所以32=BC ,又,31AC AB =可知321==BC AB ,所以33=AC根据切割线定理得93332=⨯=⋅=AC AB AF ,即3=AF 证明:过E 作BC EH ⊥于H ,则ADF EDH ∆∆~,从而有AF EH AD ED =,又由题意知,BC CH 321==2=EB 所以1=EH ,因此31=AD ED ,即ED AD 3= 23.(本题满分10分)选修4-4:坐标系与参数方程选讲解:(1)由曲线1C :⎩⎨⎧==ααsin cos 3y x 得⎪⎩⎪⎨⎧==ααsin cos 3y x两式两边平方相加得:1)3(22=+y x即曲线1C 的普通方程为:1322=+y x由曲线2C :24)4sin(=+πθρ得:24)cos (sin 22=+θθρ即8cos sin =+θρθρ,所以08=-+y x 即曲线2C 的直角坐标方程为:08=-+y x(2)由(1)知椭圆1C 与直线2C 无公共点,椭圆上的点)sin ,cos 3(ααP 到直线08=-+y x 的距离为F28)3sin(228sin cos 3-+=-+=παααd所以当1)3sin(=+πα时,d 的最小值为23,此时点P 的坐标为)21,23(24.(本题满分10分)选修4-5:不等式选讲答案:(1)由题意得()()⎪⎪⎪⎩⎪⎪⎪⎨⎧>+⎪⎭⎫ ⎝⎛≤≤---<--=3432123)21(4x x x x x x x f所以 f (x )在⎪⎭⎫ ⎝⎛-∞-21,上单调递减,在⎪⎭⎫⎝⎛+∞-,21上单调递增. 所以当21-=x 时()x f y =取得最小值此时()27min -=x f(2)由(1)及272)(-+=a ax x g 可知()x g y =恒过点过⎪⎭⎫ ⎝⎛--27,21 由图象可知11a -≤≤。
山西省临汾一中、忻州一中、康杰中学、长治二中高三数学第三次四校联考试题 理 新人教A版

1数学试题(理科)(考试时间120分钟 满分150分)一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,选出符合题目要求的一项.1. 集合{}|02P x Z x =∈≤<,{}4|2≤∈=x Z x M ,则PM 等于A.{}1B. {}1,0C. )2,0[D. ]2,0[2. 某教师一天上3个班级的课,每班一节,如果一天共9节课,上午5节、下午4节,并且教师不能连上3节课(第5和第6节不算连上),那么这位教师一天的课的所有排法有A. 474种B. 77种C. 462种D. 79种3. 复数z 1=3+i,z 2=1-i,则复数21z z 的虚部为 A. 2B. -2iC. -2D. 2i4. 过点(2,0)M 作圆221x y +=的两条切线MA ,MB (A ,B 为切点),则MA MB ⋅= A.53B.52 C.33 D.325. 函数()()sin 0,2f x x πωϕωϕ⎛⎫=+><⎪⎝⎭的最小正周期是π,若其图像向右平移3π个单位后得到的函数为奇函数,则函数()f x 的图像A.关于点,012π⎛⎫⎪⎝⎭对称B.关于直线12x π=对称C.关于点5,012π⎛⎫⎪⎝⎭对称D.关于直线512x π=对称 6. 如图所示的算法流程图中输出的最后一个数为-55,则判断框中的条件为A.?11<nB. ?11≥nC.?10<nD. ?10≥n27. 点P 为双曲线1C :()0,012222>>=-b a b y a x 和圆2C :2222b a y x +=+的一个交点,且12212F PF F PF ∠=∠,其中21,F F 为双曲线1C 的两个焦点,则双曲线1C 的离心率为 A.3 B.21+ C.13+ D.2 8. 若某几何体的三视图是如图所示的三个直角三角形, 则该几何体的外接球的表面积为 A.10π B.50π C.25π D.100π9. 对于下列命题:①在△ABC 中,若sin2sin2A B =,则△ABC为等腰三角形;②已知a ,b ,c 是△ABC 的三边长,若2a =,5b =,6A π=,则△ABC 有两组解;③设2012sin3a π=,2012cos 3b π=,2012tan 3c π=,则a b c >>;④将函数2sin 36y x π⎛⎫=+ ⎪⎝⎭图象向左平移6π个单位,得到函数2cos 36y x π⎛⎫=+ ⎪⎝⎭图象.其中正确命题的个数是A.0B.1C. 2D.310. 已知球的直径SC=4,A ,B 是该球球面上的两点,3,30=∠=∠BSC ASC ,则棱锥S —ABC 的体积为 A .33B. 33D. 111. 函数()cos f x x π=与函数()2log 1g x x =-的图像所有交点的横坐标之和为 A .2B. 4C. 6D. 812. 函数)(x f y =为定义在R 上的减函数,函数)1(-=x f y 的图像关于点(1,0)对称, ,x y 满足不等式0)2()2(22≤-+-y y f x x f ,(1,2),(,)M N x y ,O 为坐标原点,则当41≤≤x 时,OM ON ⋅的取值范围为 ( ) A .[)+∞,12 B .[]3,0C .[]12,3D .[]12,0二、填空题:本大题共4小题,每小题5分,共20分.13.在正三角形3AB =中,D 是AB 上的点,3,1AB BD ==,则AB AD ⋅= .314. 实数对(,)x y 满足不等式组20,250,20,x y x y y --≤⎧⎪+-≥⎨⎪-≤⎩则目标函数z=kx -y 当且仅当x=3,y=1时取最大值,则k 的取值范围是 .15.已知xxx f ln )(=,在区间[]3,2上任取一点0x ,使得0'()0f x >的概率为 . 16.已知定义在R 上的函数)(x f 是奇函数且满足)()23(x f x f =-,3)2(-=-f ,数列{}n a 满足11-=a ,且21nnS a nn=⨯+(其中n S 为{}n a 的前n 项和),则=+)()(65a f a f .三、解答题:本大题共6小题,共70分.解答应写出文字说明,演算步骤或证明过程. 17.(本小题满分12分)已知各项均为正数的数列{}n a 前n 项和为n S ,首项为1a ,且n n S a ,,21成等差数列.(1)求数列{}n a 的通项公式; (2)若n b na )21(2=,设n n n a b c =,求数列{}n c 的前n 项和n T .18.(本小题满分12分)某中学参加一次社会公益活动(以下简称活动).该校合唱团共有100名学生,他们参加活动的次数统计如图所示. (1)求合唱团学生参加活动的人均次数;(2)从合唱团中任意选两名学生,求他们参加活动次数恰好相等的概率.(3)从合唱团中任选两名学生,用ξ表示这两人参加活动次数之差的绝对值,求随机变量ξ的分布列及数学期望E ξ.19.(本小题满分12分)如图,四边形PCBM 是直角梯形,90PCB ∠=︒,PM ∥BC ,1,2PM BC ==.又1AC =,120,ACB AB PC ∠=︒⊥,直线AM 与直线PC 所成的角为60︒.(1)求证:PC AC ⊥;(2)求二面角M AC B --的余弦值. 20.(本小题满分12分)已知椭圆,22)0(1:2222=>>=+e b a by a x C 的离心率左、右焦点分别为F 1、F 2,点 1 2 31020 30 40 50 参加人数活动次数4)3,2(P ,点F 2在线段PF 1的中垂线上。
山西省忻州一中 康杰中学 临汾一中 长治二中高三数学第四次四校联考试题 文 新人教A版

2014届高三年级第三次四校联考数学试题(文科)命题:临汾一中 忻州一中 康杰中学 长治二中 【考试时间120分钟,满分150分】 第Ⅰ卷(选择题 60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题列出的四个选项中,只有一项是最符合题目要求的)1. 设全集{}6,5,4,3,2,1=U ,{}3,2,1=M ,{}5,4,3=N ,则=N M C U I )(( ) A.{}3B.{}5,4C.{}5,4,3D.()5,42. 设复数1z i =+(i 是虚数单位),则22z z +=( )A .1i --B .1i -+C .1i -D .1i +3. 函数41++=x x y 的定义域为( )A.[)+∞-,4B.()()+∞-,00,4YC.()+∞-,4D.[)()+∞-,00,4Y4. 已知x 、y 的取值如右表所示: (第4题)从散点图分析,y 与x 线性相关,且a x y +=8.0ˆ,则a =( )A. 0.8B. 1C. 1.2D. 1.55. 某三棱锥的三视图如右图所示,该三棱锥的体积是( )A.4B. 38C.2D.346. 执行如图所示的程序框图,若输入n 的值为7,则输出s 的值是( )A .10B .16C .22D .17x0 1 3 4 y0.91.93.24.47. 直线()31-=-x k y 被圆22(2)(2)4x y -+-=所截得的最短弦长等于( )B.C.8. 若3tan =α,则sin(2)4πα+的值为( ) A .-210B .210C .5210D .72109. 实数,x y 满足2240240x x y x y ≥⎧⎪-+≥⎨⎪--≤⎩,若z kx y =+的最大值为13,则实数k =( )A. 2B. 132C. 94D. 510.设等差数列{}n a 和等比数列{}n b 首项都是1,公差与公比都是2,则=++++54321b b b b b a a a a a ( )A.54B.56C.58D.5711.已知圆锥曲线2244mx y m +=的离心率e 为方程22520x x -+=的根,则满足条件的圆锥曲线的个数为( ) A .4 B .3C .2D .112. 定义在R 上的函数()f x 满足()(),(2)(2),f x f x f x f x -=--=+且(1,0)x ∈-时,1()2,5x f x =+则2(log 20)f =( )A .-1B .45C .1D .-45第Ⅱ卷(非选择题90分)二、填空题(本大题共4小题,每小题5分,共20分)13. 曲线()xe xf =在0x =处的切线方程为 .14. 已知向量()1,2-=,()2,x =,且⊥+的最小值为 .15.已知数列{}n a 的前n 项和为n S ,n a S n n -=2,则=n a .16. 将长、宽分别为4和3的长方形ABCD 沿对角线AC 折起,得到四面体A ﹣BCD ,则四面体A ﹣BCD 的外接球的体积为 . 三、解答题(本大题共70分)17. (本小题满分12分)在ABC ∆中,a ,b ,c 分别为角A ,B ,C 的对边,c b 2=,且=3B C π-.(1) 求角C ;(2) 若1=c ,求ABC ∆的面积.18. (本小题满分12分)某班优秀生16人,中等生24人,学困生8人,现采用分层抽样的方法从这些学生中抽取6名学生做学习习惯调查,(Ⅰ)求应从优秀生、中等生、学困生中分别抽取的学生人数; (Ⅱ)若从抽取的6名学生中随机抽取2名学生做进一步数据分析, (1)列出所有可能的抽取结果;(2)求抽取的2名学生均为中等生的概率. 19. (本小题满分12分)在直三棱柱111ABC A B C -中,13AB AC AA ===,2BC =,D 是BC 的中点,F 是1C C上一点.(1)当2CF =,求证:1B F⊥平面ADF ; (2)若D B FD 1⊥,求三棱锥1B ADF-体积.20. (本小题满分12分)已知函数()x x x ax x f ln 2-+=, (1)若0a =,求函数()x f 的单调区间;(2)若(1)2f =,且在定义域内2()2f x bx x ≥+恒成立,求实数b 的取值范围. 21.(本小题满分12分)已知椭圆C :12222=+b ya x (0>>b a)的右焦点)0,1(F ,右顶点A ,且1||=AF .(1) 求椭圆C 的标准方程;(2)若动直线l :m kx y +=与椭圆C 有且只有一个交点P ,且与直线4=x 交于点Q ,问:是否存在一个定点)0,(t M ,使得0=⋅.若存在,求出点M 坐标;若不存在,说明理由.请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分.答时用2B 铅笔在答题卡上把所选题目的题号涂黑.22. (本小题满分10分) 选修4—1;几何证明选讲.如图,已知⊙O 中,直径AB 垂直于弦CD ,垂足为M ,P 是CD 延长线上一点,PE 切⊙O 于点E ,连接BE 交CD 于点F ,证明:(1)∠BFM =∠PEF ; (2)PF2=PD·PC.23.(本题满分10分)选修4-4:坐标系与参数方程选讲在直角坐标系xoy 中,曲线1C 的参数方程为⎩⎨⎧==ααsin cos 3y x ,(α为参数),以原点O 为极点,x 轴正半轴为极轴,建立极坐标系,曲线2C 的极坐标方程为24)4sin(=+πθρ.(1) 求曲线1C 的普通方程与曲线2C 的直角坐标方程;(2) 设P 为曲线1C 上的动点,求点P 到2C 上点的距离的最小值,并求此时点P 的坐标. 24. (本小题满分10分)选修4-5:不等式选讲 设函数()312--+=x x x f求函数()x f y =的最小值;若272)(-+≥a ax x f 恒成立,求实数a 的取值范围.2014届高三年级第三次四校联考答案 数 学(文科)1-5 BDDBA, 6-10 CCACD, 11-12 BA13. 01=+-y x12-n .16. 1256π17.(1) 由2b c =.又由正弦定理,得2sin b R B =,2sin c R C =,将其代入上式,得sin 2sin B C =. ------------2分∵3B C π-=, ∴3B Cπ=+,将其代入上式,得sin()2sin 3C Cπ+=∴sincos cossin 2sin 33C C Cππ+=,cos C C =. ----- --------4分∴tan C =.∵角C 是三角形的内角,∴6C π=. --------- ------6分(2) ∵6C π=,则2π=B --------- ------8分 又1=c Θ ,3=∴a --------- ------10分∴2321==∆ac S ABC --------- ------12分18. (Ⅰ)优秀生、中等生、学困生中分别抽取的学生人数为2、3、1. ----------4分 (Ⅱ)(1)在抽取到的6名学生中,3名中等生分别记为123,,A A A ,2名优秀生分别记为45,A A ,1名学困生记为6A ,则抽取2名学生的所有可能结果为121314151623242526{,},{,},{,},{,},{,},{,},{,},{,},{,},A A A A A A A A A A A A A A A A A A343536454656{,},{,},{,},{,},{,},{,},A A A A A A A A A A A A 共15种. -------------8分(2)从这6名学生中抽取的2名学生均为中等生(记为事件B )的所有可能结果为121323{,},{,},{,}A A A A A A ,共3种,所以31().155P B == -------------12分19. (1)证明:∵AB AC =,D 是BC 的中点, ∴AD ⊥BC . 在直三棱柱111ABC A B C -中,∵1B B⊥底面ABC ,AD ⊂底面ABC ,∴AD ⊥1B B.∵BC ∩1B B=B ,∴AD ⊥平面11B BCC .∵1B F⊂平面11B BCC ,∴AD ⊥1B F. -------------3分在矩形11B BCC 中,∵11C F CD ==,112B C CF ==,∴Rt DCF ∆≌11Rt FC B ∆.∴∠CFD =∠11C B F.∴∠1B FD=90°,∴1B F FD⊥.∵AD ∩FD =D ,∴1B F⊥平面ADF . -------------6分(2)1AD B DF⊥Q 面,AD =又1B D 1CD =, -------------8分Θ1FD B D ⊥CDF Rt ∆∴∽1Rt BB D ∆,11DF CDB D BB ∴=.133DF ∴==-------------10分111113329B ADF B DF V S AD -∆=⋅=⨯=. -------------12分20. (1)当0a =时,()ln f x x x x =-,函数定义域为(0,)+∞.'()ln f x x =-,由ln 0x -=,得1x =. -------------3分(0,1)x ∈时,'()0f x >,()f x 在(0,1)上是增函数.(1,)x ∈+∞时,'()0f x <,()f x 在(1,)+∞上是减函数; -------------6分(2)由(1)2f =,得21=+a ,1=∴a ,∴ 2()ln f x x x x x =+-,由2()2f x bx x ≥+,得()x x b ln 11≥--,又0>x Θ∴1ln 1xb x x ≤--恒成立, -------------9分 令1ln ()1x g x x x =--,可得2ln )(x x x g =',∴()g x 在(0,1]上递减,在[1,)+∞上递增. ∴min ()(1)0g x g ==即0b ≤,即b 的取值范围是(,0]-∞. ----------12分 21. 由1,1=-=c a c ,,2=∴a 3=∴b ,椭圆C 的标准方程为13422=+y x . -------------4分⎩⎨⎧=++=1243)2(22y x m kx y 由得:01248)43(222=-+++m kmx x k , -------------6分22222243,0)124)(43(464k m m k m k +==-+-=∆∴即.m k k km x p 44342-=+-=,m m m k m kx y p p 342=+-=+=,即P )3,4(m m k -. ---------9分 ΘM )0,(t .又Q()m k +4,4,)3,4(mt m k --=,)4,4(m k t MQ +-=,∴⋅=⋅--)4(t m k ()t -4+)4(3m k m +⋅=0)1(4342=-++-t m kt t 恒成立,故⎩⎨⎧=+-=03412t t t ,即1=t . ∴存在点M (1,0)适合题意. ------------12分22. (1)连接OE ,∵PE 切⊙O 于点E ,∴OE ⊥PE. ∴∠PEF +∠FEO =90°.又∵AB ⊥CD ,∴∠B +∠BFM =90°. 又∵∠B =∠FEO ,∴∠BFM =∠PEF. -------------5分 (2)∵∠EFP =∠BFM , ∴∠EFP =∠PEF. ∴PE =PF.又∵PE2=PD ·PC ,∴PF2=PD ·PC. -------------10分 23.(本题满分10分)选修4-4:坐标系与参数方程选讲解:(1)由曲线1C :⎩⎨⎧==ααsin cos 3y x 得⎪⎩⎪⎨⎧==ααsin cos 3y x两式两边平方相加得:1)3(22=+y x即曲线1C 的普通方程为:1322=+y x由曲线2C :24)4sin(=+πθρ得:24)cos (sin 22=+θθρ即8cos sin =+θρθρ,所以08=-+y x即曲线2C 的直角坐标方程为:08=-+y x ...........5分(2)由(1)知椭圆1C 与直线2C 无公共点,椭圆上的点)sin ,cos 3(ααP 到直线08=-+y x 的距离为28)3sin(228sin cos 3-+=-+=παααd所以当1)3sin(=+πα时,d 的最小值为23,此时点P 的坐标为)21,23( ----------10分24. (1)由题意得()()⎪⎪⎪⎩⎪⎪⎪⎨⎧>+⎪⎭⎫ ⎝⎛≤≤---<--=3432123)21(4x x x x x x x f所以 f (x )在⎪⎭⎫ ⎝⎛-∞-21,上单调递减,在⎪⎭⎫⎝⎛+∞-,21上单调递增. 所以当21-=x 时()x f y =取得最小值此时()27min -=x f -------------5分 (2)272)(-+=a ax x g 的图像恒过点过⎪⎭⎫ ⎝⎛--27,21由图象可知11≤≤-a . -------------10分。
山西省长治二中、康杰中学、忻州一中等五校2018届高三9月摸底考试数学(理)试题+Word版含解析

8. 设 满足约束条件
,则
的最大值为 ( )
A. 1 B. 3 C. 5 D. 6
,故选 B
【点睛】
,高为 ,上下底
本题重点是抓住榫卯的工作原理—榫凸卯凹、榫卯咬合连接,由此发现卯(中空的圆柱体)
中间所缺失的上下表面积刚好由榫的上下表面积补充。故整个构件的上下表积刚好是两个完
整的圆形的面积。
6. 已知函数
的最大值为 ,
的图象的相邻两条对称轴间的距离为 2,与 轴的交点的纵坐标为 1,则
【答案】 C
【解析】
的通项为
,
,根据式子可知当
或
时有常数项,令
;令
; 故所求常数项为
,故选 C.
【点睛】
求解与二项式相关的复杂式子的一般方法及步骤是:
将复杂式子分解转化成与简单的二项式相关的式子
根据条件找到符合条件的二项式的项,
利用二项式的通项求出符合条件的项,
整合最终得出所求
5. 榫卯是在两个木构件上所采用的一种凹凸结合的连接方式,
【解析】
, 结合已知得
,故选 A.
2. 已知集合
A.
B.
C.
【答案】 D 【解析】由
, D.
,则 ( ) ;由
,则有
3. 设等比数列
的前 项和为 ,且
,则
()
A. 4 B. 5 C. 8 D. 9 【答案】 B
【解析】由题设
,
案 B。
4.
的展开式中常数项为 ( )
A.
B.
C.
D. 25
,所以
,故选 D ,应选答
凸出部分叫榫, 凹进部分叫卯,
榫和卯咬合,起到连接作用,代表建筑有:北京的紫禁城、天坛祈年殿、山西悬空寺等,如
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017-2018年度高三第四次名校联合考试(百日冲刺)
数学(理科)
六校联考长治二中、鄂尔多斯一中、晋城一中、
康杰中学、临汾一中、忻州一中
第Ⅰ卷(共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.复数3
)1(i z 的虚部为()
A .2
B .2
C .i 2
D .i
22.设集合}06|{2x x x A ,则满足B B A 的集合B 不可能为()
A .}1,0{
B .)3,0(
C .)2,2(
D .)
1,3(3.已知下表为随机数表的一部分,将其按每5个数字编为一组:
080151772745318223742111578253
772147740243236002104552164237
291486625236936872037662113990
685141422546427567889629778822
已知甲班有60位同学,编号为60~01号,现在利用上面随机数表的某一个数为起点,以简单随机抽样的方法在甲班中抽取4位同学,由于样本容量小于99,所以只用随机数表中每组数字的后两位,得到下列四组数据,则抽到的4位同学的编号不可能是()
A .53,18,27,15
B .52,25,02,27
C .22,27,25,14
D .74
,18,27,154.设)(x f 为定义在R 上的奇函数,当0x 时,b x x f x 273)((b 为常数),则)
2(f (
)A .6 B .6 C.4 D .4
5.若41
)3sin(a ,则)
62sin(a
()
A .1615
B .1615 C.87 D .8
7
6.设变量y x,满足约束条件331
3
y x y x y x ,则y x z 2的取值范围为()
A .]3,1[
B .]6,1[ C.]5,1[ D .]
6,5[7.已知][x 表示不超过x 的最大整数,如3]4.2[,1]1[,0]4.0[.执行如图所示的程序框图,则输出的S ()
A .1
B .5 C.14 D .15
8.已知曲线)
32sin(:x
y C ,则下列结论正确的是()
A .把C 向左平移125
个单位长度,得到的曲线关于原点对称
B .把
C 向右平移6个单位长度,得到的曲线关于y 轴对称
C. 把C 向左平移3个单位长度,得到的曲线关于原点对称
D .把C 向右平移12个单位长度,得到的曲线关于y 轴对称
9.如图,一个水平放置的圆柱形玻璃杯的底面半径为cm 9,高为cm 36.玻璃杯内水深为cm 33,将一个球放在杯口,球面恰好与水面接触,并且球面与杯口密闭.如果不计玻璃杯的厚度,则球的表面积为()。
