数据分析方法与技术-描述性方法统计实验报告讲解
数据分析方法实验报告

数据分析方法实验报告数据分析方法实验报告一、引言数据分析是在当今信息化时代中非常重要的一项技能。
通过对大量数据的收集、整理和分析,我们可以得出有价值的结论和见解,为决策提供支持。
本实验旨在探索数据分析方法的应用,通过实际操作和分析,了解数据分析的过程和技巧。
二、数据收集和整理在本次实验中,我们选择了一份关于消费者购买行为的数据集。
该数据集包含了消费者的年龄、性别、购买金额等信息。
我们首先使用Python编程语言读取数据集,并对数据进行清洗和整理,去除缺失值和异常值,确保数据的准确性和可靠性。
三、描述性统计分析在数据整理完成后,我们进行了描述性统计分析,对数据的基本特征进行了概括和总结。
通过计算平均值、中位数、标准差等统计指标,我们可以了解数据的分布情况和集中趋势。
此外,我们还使用直方图和箱线图等图表形式展示了数据的分布情况,更直观地呈现了数据的特征。
四、相关性分析为了探究不同变量之间的关系,我们进行了相关性分析。
通过计算相关系数,我们可以了解变量之间的线性相关程度。
此外,我们还绘制了散点图和热力图来展示变量之间的关系,帮助我们更好地理解数据的内在联系。
五、回归分析回归分析是一种常用的数据分析方法,用于探究自变量对因变量的影响程度。
在本次实验中,我们选择了线性回归模型进行分析。
通过建立回归模型,我们可以预测因变量的取值,并评估自变量对因变量的影响。
我们使用了最小二乘法来估计回归系数,并进行了模型的显著性检验和残差分析,以确保模型的可靠性和准确性。
六、聚类分析聚类分析是一种无监督学习的方法,用于将数据集中的观测对象划分为不同的类别。
在本次实验中,我们使用了K均值聚类算法对数据进行聚类分析。
通过选择合适的聚类数目和距离度量方法,我们将数据集中的消费者划分为不同的群组,并对每个群组进行了特征分析,以了解不同群组的特点和差异。
七、结论与展望通过本次实验,我们对数据分析方法有了更深入的了解。
通过数据收集和整理、描述性统计分析、相关性分析、回归分析和聚类分析等方法,我们可以从不同的角度和层面对数据进行分析和解读。
描述性数据的分布和度量实验报告分析
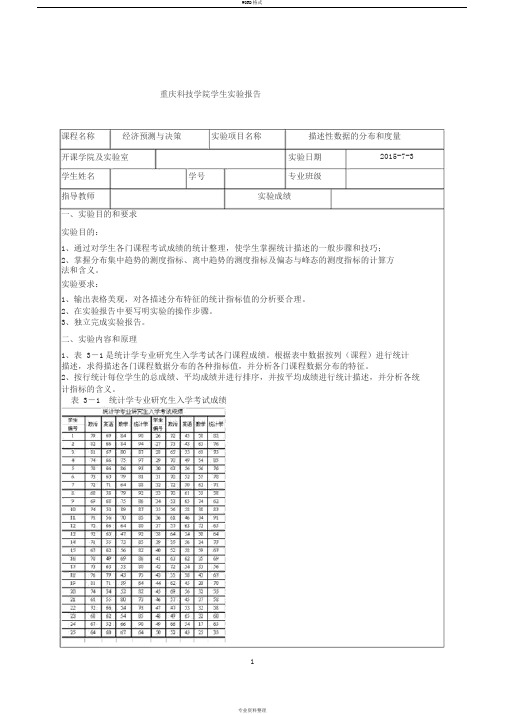
重庆科技学院学生实验报告课程名称经济预测与决策实验项目名称描述性数据的分布和度量开课学院及实验室实验日期2015-7-3 学生姓名学号专业班级指导教师实验成绩一、实验目的和要求实验目的:1、通过对学生各门课程考试成绩的统计整理,使学生掌握统计描述的一般步骤和技巧;2、掌握分布集中趋势的测度指标、离中趋势的测度指标及偏态与峰态的测度指标的计算方法和含义。
实验要求:1、输出表格美观,对各描述分布特征的统计指标值的分析要合理。
2、在实验报告中要写明实验的操作步骤。
3、独立完成实验报告。
二、实验内容和原理1、表 3-1是统计学专业研究生入学考试各门课程成绩。
根据表中数据按列(课程)进行统计描述,求得描述各门课程数据分布的各种指标值,并分析各门课程数据分布的特征。
2、按行统计每位学生的总成绩、平均成绩并进行排序,并按平均成绩进行统计描述,并分析各统计指标的含义。
表 3-1 统计学专业研究生入学考试成绩三、主要仪器设备.实验的基本工具:电脑一台;Microsoft EXCEL 2007 软件一套;四、实验操作方法和步骤操作方法:利用软件数据分析中的统计描述功能,求得描述各门课程数据分布的各种指标值,并分析各门课程数据分布的特征;在进行平均成绩、总成绩的排序以及统计指标的描述。
实验步骤:在工具菜单中—选择数据分析—在数据分析中选择描述统计—选择相应的数据区域—单击确定在数据菜单中—选择排序—框中所选区域—选择主关键字此关键字—单击确定五、实验记录与处理(数据、图表、计算等)按列(课程)进行统计描述按平均成绩进行统计描述统计每位学生的总成绩、平均成绩并进行排序六、实验结果及分析描述各门课程数据分布的各种指标值平均:平均数是表示一组数据集中趋势的量数,是指在一组数据中所有数据之和再除以这组数据的个数。
标准误差:各测量值误差的平方和的平均值的平方根,故又称为均方根误差。
标准误用来衡量抽样误差。
标准误越小,表明样本统计量与总体参数的值越接近,样本对总体越有代表性,用样本统计量推断总体参数的可靠度越大。
社会实践中的统计数据分析方法

社会实践中的统计数据分析方法统计学作为一门科学,广泛应用于社会实践中的各个领域。
它通过收集、整理和分析数据,帮助我们了解现象背后的规律,并为决策提供依据。
在本文中,我们将探讨社会实践中的统计数据分析方法。
一、数据收集与整理在进行统计数据分析之前,首先需要进行数据的收集与整理。
数据的收集可以通过问卷调查、实地观察、实验研究等方式进行。
在选择数据收集方法时,需要根据研究目的和数据的可行性进行合理选择。
而数据的整理则是将收集到的数据进行分类、筛选、清洗和归档,以便后续的分析工作。
二、描述性统计分析描述性统计分析是对数据进行总结和描述的方法。
它通过计算数据的中心趋势(如均值、中位数、众数)、离散程度(如标准差、极差)和数据的分布情况(如频数分布、百分位数)等指标,来描述数据的特征。
描述性统计分析可以帮助我们了解数据的基本情况,为后续的推断性统计分析提供参考。
三、推断性统计分析推断性统计分析是基于样本数据对总体进行推断的方法。
它通过对样本数据进行抽样分析,得出关于总体的概率推断。
常见的推断性统计分析方法包括假设检验和置信区间估计。
假设检验通过对样本数据进行假设检验,判断总体参数是否符合某种假设;置信区间估计则是通过对样本数据进行分析,给出总体参数的一个区间估计,以反映估计结果的不确定性。
四、相关性分析相关性分析是研究两个或多个变量之间关系的方法。
它通过计算相关系数来衡量变量之间的相关程度。
常见的相关系数包括皮尔逊相关系数和斯皮尔曼相关系数。
相关性分析可以帮助我们了解变量之间的相关性质,从而为决策提供依据。
五、回归分析回归分析是研究因果关系的方法。
它通过建立统计模型,分析自变量对因变量的影响程度。
回归分析可以帮助我们预测和解释变量之间的关系,并从中找出影响因素。
常见的回归分析方法包括线性回归、逻辑回归和多元回归等。
六、时间序列分析时间序列分析是研究时间上变化的方法。
它通过对时间序列数据进行建模和分析,揭示数据随时间变化的规律。
技术报告中的实验结果和数据分析方法

技术报告中的实验结果和数据分析方法一、实验结果的展示与说明实验结果是科学研究的重要组成部分,它展示了实验的数据和结果,往往也是评估实验效果的重要指标之一。
在技术报告中,如何准确、清晰地展示实验结果,并进行合理的详细说明,是技术人员必须面对的问题。
本节将介绍实验结果的展示方式和说明方法。
1.1 折线图展示实验数据趋势折线图是一种常用的数据展示方式,能够清晰地表达数据的变化趋势。
在技术报告中,将实验数据以折线图的形式展示出来,能够让读者更直观地了解实验结果。
同时,在折线图下方或旁边,需配以详细的说明文字,解释图中的数据变化趋势以及可能的原因。
1.2 图表的标注和单位的明确无论是折线图、柱状图还是散点图,都需要在图表中清楚地标注数据的含义和单位。
例如,在折线图中,需要标注横坐标和纵坐标的含义,以及所使用的指标或量的单位。
这样做能够使读者能够更加准确地理解实验结果,避免出现误解和歧义。
二、实验数据分析方法的选择与使用实验数据分析是实验研究中必不可少的环节,它能够帮助科研人员从大量的数据中提取有用的信息,揭示数据背后的规律和趋势。
本节将介绍实验数据分析的常用方法和技巧。
2.1 描述性统计分析方法描述性统计分析方法是一种从数据的角度来描述和总结数据特征的方法。
它包括对数据的基本统计指标进行计算,如平均值、方差、标准差等。
在技术报告中,可以通过描述性统计分析方法对实验数据进行整体的量化分析,得到数据的概貌和基本特征,为后续的分析提供依据。
2.2 相关性分析方法相关性分析是一种从数据中找出变量之间相关关系的方法。
它可以帮助科研人员判断两个或多个变量之间的相关性强弱,并进一步分析这种相关性是否具有统计学意义。
在技术报告中,可以通过相关性分析方法探究实验数据中不同因素之间的关联关系,帮助科研人员深入理解数据背后的规律。
三、实验数据分析的结果与讨论实验数据分析的结果是实验报告中最重要的部分之一,它展示了通过数据分析所得到的结论和发现,是对实验的一种科学评价。
常见的数据分析方法与技术介绍

常见的数据分析方法与技术介绍数据分析是指通过对大量数据进行收集、整理、加工和分析,从中获取有用信息、发现规律和趋势的过程。
随着大数据时代的到来,数据分析成为了各行各业的重要工具。
本文将介绍一些常见的数据分析方法和技术。
一、描述性统计分析描述性统计分析是数据分析的基础,它通过对数据的集中趋势、离散程度、分布形态等方面进行统计和描述,帮助人们对数据有一个整体的认识。
常见的描述性统计分析方法包括均值、中位数、众数、标准差、方差等。
二、相关性分析相关性分析是研究两个或多个变量之间关系的方法。
通过计算相关系数,可以判断变量之间的线性相关程度。
常用的相关性分析方法包括皮尔逊相关系数和斯皮尔曼相关系数。
相关性分析可以帮助人们发现变量之间的关联性,为进一步的分析和预测提供依据。
三、回归分析回归分析是研究因变量和自变量之间关系的统计方法。
通过建立回归模型,可以预测因变量的取值。
常见的回归分析方法包括线性回归、多元回归、逻辑回归等。
回归分析在市场营销、经济预测等领域有着广泛的应用。
四、聚类分析聚类分析是将一组对象划分为若干个类别的方法。
通过度量对象之间的相似性或距离,将相似的对象聚在一起,形成一个类别。
聚类分析可以帮助人们发现数据中的隐藏模式和规律。
常见的聚类分析方法包括层次聚类、K均值聚类等。
五、决策树分析决策树分析是一种基于树形结构的分类和回归方法。
通过对数据进行划分和分类,构建决策树模型,可以对未知数据进行分类和预测。
决策树分析具有可解释性强、易于理解和应用的优点。
常见的决策树算法包括ID3、C4.5、CART等。
六、时间序列分析时间序列分析是一种研究时间序列数据的方法。
通过对时间序列数据的趋势、周期性和随机性进行分析,可以预测未来的发展趋势。
时间序列分析在经济预测、股市预测等领域有着广泛的应用。
常见的时间序列分析方法包括移动平均法、指数平滑法、ARIMA模型等。
七、文本分析文本分析是对大量文本数据进行挖掘和分析的方法。
数据分析实验报告分析解析

数据分析实验报告分析解析绪论在信息技术高速发展的时代背景下,数据分析已经成为企业和组织中不可或缺的一部分。
数据分析的目的是利用各种统计方法和工具来解析和挖掘数据中的信息,以此帮助决策者做出更明智的决策。
本实验的目的是通过对一组数据进行分析,提取并解读数据中的相关信息。
实验目的本实验旨在通过对某公司销售数据的分析,了解销售情况与各种因素之间的关系,并从中找出潜在的商业机会和风险。
实验方法与步骤1. 数据采集本次实验采用了某公司最近一年的销售数据,包括销售额、销售地区、产品类别等方面的信息。
2. 数据清洗与预处理在数据分析之前,需要对原始数据进行清洗和预处理。
首先,根据需要删除缺失值和异常值,确保数据的准确性和完整性。
其次,对不规范的数据格式进行调整和标准化,使得数据能够被正确地分析和解读。
3. 数据分析与可视化使用适当的数据分析工具和算法,对清洗后的数据进行分析。
根据实验目的,可以选择不同的分析方法,如描述统计分析、相关性分析、聚类分析等。
同时,使用可视化工具绘制图表,以直观地展示分析结果。
实验结果与讨论1. 销售额分析通过对销售数据的描述统计分析,我们可以得到一些关键指标,如平均销售额、最大销售额、最小销售额等。
进一步,我们可以对销售额进行时间序列分析,探讨销售额的变化趋势和季节性变化规律。
例如,我们可以发现某个季度的销售额呈现上升趋势,而另一个季度则呈现下降趋势,从而为公司的销售策略调整提供参考。
2. 销售地区分析通过对销售数据的地理分布分析,我们可以了解哪些地区是公司的主要销售市场,哪些地区有潜在的市场需求待开发。
通过将销售地区与其他因素(如产品类别、市场规模等)进行交叉分析,可以得出一些有关销售地区的洞察。
例如,我们可以发现某个地区的高销售额主要集中在某个特定产品类别上,从而为公司的地区市场定位提供指导。
3. 产品类别分析通过对销售数据的产品类别分析,我们可以了解公司不同产品类别的销售情况和市场占有率。
实验报告数据分析

实验报告数据分析实验报告数据分析引言实验报告是科学研究中不可或缺的一部分,通过对实验数据的分析可以得出结论,验证假设,推动科学的发展。
本文将围绕实验报告数据分析展开讨论,旨在探索数据分析在科研中的重要性和应用。
数据收集与整理在进行实验之前,首先需要进行数据的收集。
数据可以通过实验仪器、观察、调查问卷等方式获得。
在收集数据时,需要注意数据的准确性和完整性,以确保后续的分析结果可靠。
收集到的数据需要进行整理和清洗,以便后续的分析。
整理数据包括对数据进行分类、排序和归纳等操作,使得数据更加清晰易懂。
同时,还需要对数据进行清洗,剔除异常值和缺失值,以保证数据的准确性。
数据分析方法数据分析是一种对数据进行统计和解读的过程。
常用的数据分析方法包括描述统计、推断统计和数据挖掘等。
描述统计是对数据进行总结和描述的方法。
通过计算平均值、标准差、频率分布等指标,可以对数据的集中趋势、离散程度和分布情况进行描述。
描述统计能够直观地展示数据的特征,为后续的分析提供基础。
推断统计是通过对样本数据进行分析,推断总体特征的方法。
通过构建假设检验和置信区间等方法,可以对总体参数进行估计和推断。
推断统计能够从有限的样本数据中推断出总体的特征,提高数据分析的效率和精度。
数据挖掘是一种通过算法和模型挖掘数据中隐藏信息的方法。
通过数据挖掘技术,可以发现数据中的规律、关联和趋势等。
数据挖掘能够帮助科研人员发现新的问题和解决方案,推动科学的发展。
数据分析应用举例数据分析在科研中有着广泛的应用。
以下是一些常见的数据分析应用举例。
1. 实验结果分析:通过对实验数据进行统计和推断,可以验证实验假设,得出结论。
例如,在药物研发中,科研人员可以通过对药物试验数据的分析,评估药物的疗效和安全性。
2. 趋势分析:通过对时间序列数据的分析,可以揭示数据的趋势和周期性变化。
例如,在经济学研究中,经济学家可以通过对经济指标的时间序列数据进行分析,预测未来的经济发展趋势。
实验报告的数据分析与结果解释

实验报告的数据分析与结果解释一、背景介绍实验报告是科学研究的一个重要组成部分,通过对实验数据的分析和结果的解释,可以帮助研究者深入理解实验结果,验证假设,并得出科学结论。
本文将从数据分析和结果解释两个方面进行详细论述。
二、数据分析1. 数据收集与整理在进行实验研究之前,首先需要明确研究目的,并设计合适的实验方法。
在实验过程中,要准确记录实验数据,包括实验样本的数量、实验时间、实验条件等,确保数据的可靠性和科学性。
2. 数据处理与统计获得实验数据之后,需要进行数据处理和统计。
首先,对数据进行清洗和筛选,去掉异常值和无关数据。
然后,通过统计方法进行数据分析,如平均数、标准差、相关分析等,找出数据的规律和趋势。
3. 数据可视化展示数据可视化是将数据转化为图表的过程,能够直观地展示数据的分布和趋势。
在实验报告中,可以利用表格、柱状图、折线图等形式,将实验数据可视化展示,使读者更容易理解和分析数据。
三、结果解释1. 结果描述通过对实验数据的分析,需要对结果进行描述。
首先,要明确实验结果是什么,是否达到预期目标。
然后,对结果进行客观、准确的描述,包括数据变化趋势、差异分析等。
2. 结果解释解释实验结果是研究者对数据进行深入思考和分析的过程。
通过对数据的解释,可以阐述实验结果的原因、机制和意义。
在解释实验结果时,可以通过对相关研究文献的查阅和对比,提供更充分的理论支持。
3. 结果讨论结果讨论是对实验结果进一步分析和比较的过程。
在讨论中,可以对实验结果与预期目标之间的差距进行分析,并提出可能的原因和改进方法。
此外,还可以对实验结果与其他研究的结果进行比较,揭示新的发现和科学问题。
四、实验误差分析在实验报告中,还需要对实验误差进行分析。
实验误差是指由于实验条件和操作不精确导致的数据偏差。
通过分析实验误差,可以评估实验数据的可靠性和真实性,并提出优化实验方法的建议。
五、结果的影响与应用在实验报告中,可以进一步讨论实验结果的影响和应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电子科技大学政治与公共管理学院本科教学实验报告(实验)课程名称:数据分析技术系列实验电子科技大学教务处制表电 子 科 技 大 学实 验 报 告学生姓名: 学 号:指导教师:一、实验室名称: 电子政务可视化实验室 二、实验项目名称:描述性统计方法 三、实验原理通过调查或观察,采集到样本以后,常用一些统计量描述这些数据的分布状态,并通过这种认识,对数据的总体特征进行总结和归纳。
数据的分布状态常通过数据的进行描写。
本实验主要对数据统计分析的最基础分析——描述性统计分析进行实验,主要包括集中趋势和离中趋势分析,其主要算法原理如下:1. 描述集中趋势的统计(1) 算术平均值(Mean):样本数据的总和除以样本数据的个数即是算术平均值。
∑∑==⨯=n i ini iiff XX 11(2) 中位数(Median ,Me)首先将样本数据(假设有n 个数)按升序或降序排列,如果 n 为奇数,则数列中间的数值为中位数;如果n 为偶数,则中位数为其中两数值的均值。
(3) 众数(Mode ,Mo)样本数据中出现频数(次数)最多的那个数称为众数。
众数不易确定,与中位数一样,它不受极值影响。
但有时会出现两个甚至多个众数,有时又没有众数。
所以,众数的使用受到严格限制。
(4) 几何平均数(Geometric Mean)假定银行每年本利(本金加利率)为 X 1 有 f 1 年,年本利为 X 2 有f 2 年,银行年本利为X 3 有 f 3 年,⋯ ,年本利为X n 有 f n 年,则n 年银行平均本利为G ,银行平均年利率G -1。
∑=⨯⨯⨯⨯=∏=+++niiin n f ni f if f f f nf f f XX X X X G 1)(32121321(5) 四分位数(Quartiles)最低数与中位数之间的中位数是25分位数,原中位数与最高数之间的中位数是75分位数。
类似集中趋势的度量还有十分位数和百分位数。
2. 描述离中趋势的统计量 (1) 极差(Range)是样本数据中最大值与最小值的差值。
极值舍弃了最大值与最小值之间的其他数据信息,仅仅依靠端点值来确定,因而稳定性差。
(2) 平均差(Average Difference)指各样本数据与均值间差异绝对值的均值,也称为平均绝对差。
(3) n 个数据的方差(Variance)2σ 定义如下式,其中X 为这 n 个数的均值。
∑∑==-=ni ini ii ff X X1122)(σ(4) 标准差 (Standard Deviation, Std Dev)是方差的算术平方根 σ 。
标准差是变量与算术平均数的平均离差,也是最常用的反映数据离中趋势的统计量。
但是,在抽样调查中总体标准差往往未知,需要用样本标准差代替总体标准差,总体方差的无偏估计量应该为原方差乘以修正因子 (n / n -1),并由此得到无偏标准差的估计量。
四、实验目的掌握常用的描述性统计方法的原理及操作,包括:算术平均值、中位数、众数、几何平均数、调和平均数、极差、平均差、方差、标准差等。
五、实验内容及步骤使用“Analyze ” 莱单中的“Descriptive Statistics ”功能进行描述性统计分析。
1.频数分析“Frequencies ” 过程通过单个数据的频数分析(Frequencies )来达到整理数据的目的,利用该过程,得到一系列描述数据分布状况的统计量。
单击“Frequencies ”命令则可打开相应对话框(如图示),对对话框中各选项进行设置。
图 2(1)对话框左侧的源变量名列表框中,给出了当前数据文件中所有变量的变量名。
(2)“Variable(s)”列表框,在变量名列表框中单击变量名以后,单击对话框中间的右箭头按钮,将变量名移到该列表框中。
选定变量名以后,将对选定变量的数据进行频数分析。
(3)选择“Display frequency tables”选项,将在浏览器中显示频数分布表,否则只显示直方图,不显示频数表。
(4)若单击“Statistics”按钮,则打开统计量选择对话框,如图示,该对话框中各选项的意义如下。
图 3①“Percentile Values”选项区,可计算并显示如下内容: 四分位数(“Quartiles”)、等间隔n 分位数(“Cut points for”后文本框中输入数值为n ) 和不等间隔“Percentile(s)”分位数p%、q% 。
“Percentile(s)”选项后面的文本框中依次先后输人数值p、q,单击“Add”按钮,显示在文本框中,利用“Change”和“Remove”按钮,可以对文本框中列表进行修改。
②“Central Tendency”将显示样本的集中趋势,如计算并显示样本数据的均值“Mean”,数据的中位值“Median”,数据的众数“Mode”,数据的累加和“sum”。
③“Values are group midpoints”选项,表示假设数据已经分组,数据取值为组中值,选择此项,可计算百分位数统计和数据的中位数。
④“Dispersion”选项区将计算并显示数据的离中趋势,如计算并显示标准差“std. Deviation”,方差“Variance”,极差“Range”,最小值“Minimum”,最大值“Maximum”,和标准误(平均值的标准误差)“S.E. mean”。
⑤“Distribution”选项区设置描述数据样本分布的统计量。
如显示样本数据的偏度“Skewness”和偏度的标准误差,样本数据的峰度“Kurtosis”和峰度的标淮误差。
(5)“Charts”按钮是图形选择对话框,如图所示,各选项的意义如下。
图 4①“Chart Type”确定输出图形的类型。
不生成和显示图形选择“None”单选项(默认选项);生成和显示条形图(横坐标非等距坐标)选择“Bar charts”;生成和显示饼图选择“Pie charts”;生成和显示直方图(横坐标为等距坐标)则选择“Histograms”。
若选择“Histograms”后,“Show normaI curve”选项为可用,选择此项后,在生成和输出直方图时添加正态分布曲线。
②若选择“Bar charts ”或“Pie charts”单选项,对话框底部“Chart Values”选项区内的选项为可用,该选顼要求确定生成图形时所用的数据变量。
若用不同取值的样本数作为分类变量的度量,选“Frequencies”(默认项);若用不同取值对应样本数占总样本的百分数作为分类变量度量,选用“Percentages”选项。
(6)“Format”是频数分析表的输出格式选择对话框,如图所示,各选项的意义如下。
图 5①“Order by”选项区设置表中数据的排列、输出顺序。
若按照变量值的大小做升序排列(默认选项),选“Ascending values”单选项;若按照变量值的大小做降序排列,选“Descnding values”单选项;按照变量值出现的频数做升序排列、输出,选“Λ∞cIldlng cllun‘”单选项;按照变量值出现的频数做降序排列、输出,选“D岱ccnding counts”单选项。
②“Multiple Variables”选项区是多变量的表格显示格式。
若选择“Compare Variables”(默认选项),将对应于各变量的统计量显示在一张单独的表中。
若选择“Organize output by Variables”单选项,将对应于各变量的统计量分别列表显示。
③“Suppress tables with many categories”选项是限定频数表输出的范围,若选择此项,在后面的文本框中输入数值n ,即输出数据的组数不得大于窗口中输入的数值。
默认时该数值为10 。
2. 描述性统计分析在“Analyze”子菜单中单击“Descriptives Statistics”命令(如图示),打开“Descriptives ”对话框(如图55所示),可见如下选择项。
图 6图7①从左边的源变量中选择合适变量,用箭头按钮将其移到“Variables”选项框。
对选项框中所有被选中变量数据的分布特征进行描述。
②“Save standardized values as variables”选项,是将被选中变量的数据进行标准化处理(σXX ZX ii -=),变量名为原变量名前添加字母Z。
新生成的变量和数据保存到当前数据文件内,并显示在数据编辑器最后一列。
③若单击“Options”按钮打开对话框,如右图所示,各选项意义如下。
“Mean”选项、“Sum”选项、“Dispersion”选项区内的选项和“Distribution”选项区内选项意义与前面频数分析中“Statistics”对话框的内容相同。
“Display Order”选项区,用来设置描述表格中数据的显示顺序。
“Variable list”单选项为默认选项,是按照数据文件中变量排列的先后顺序显示表格中的描述统计量;“Alphabetic”单选项,按照变量名的字母顺序显示描述统计量;“Ascending meansⅡ单选项,是按照数据均值的升序显示描述统计量;“DescendiⅡgmeans”单选项,则按照数据均值的降序显示描述统计量。
六、实验器材(设备、元器件):计算机、打印机、硒鼓、碳粉、纸张八、实验数据及结果分析1. 频数分析结果在数据编辑器中打开数据文件“Employee.sav”,在“Frequencies”对话框中的“Variables"选项框中输人“jobcat”变量名,单击“Statistics”按钮,打开对话框,选择全部选项,“Percentile Values”选项区中选择“Percentile(s)”,并在后面文本框中输人数值10,20,25,30,40,50,60,70,75,80,85,90,95,其他对话框中的选项按默认情况设置。
设置完毕后,在“Frequencies”对话框中单击“oK”按钮,生成表格如表所示。
该表为变量“jobcat”数据的频数分析表和数据统计量描述表。
StatisticsEmployment CategoryN Valid 474Missing 0Mean 1.41Std. Error of Mean .036Median 1.00Mode 1Std. Deviation .773Variance .598Skewness 1.456Std. Error of Skewness .112Kurtosis .268Std. Error of Kurtosis .224Range 2Minimum 1Maximum 3Sum 669Percentiles 10 1.0020 1.0025 1.0030 1.0040 1.0050 1.0060 1.0070 1.0075 1.0080 2.0085 3.0090 3.0095 3.00Employment Category2. 描述性统计分析结果打开数据文件“Employee.sav”,在“Descriptive”对话框中的“Variables"选项框中输入变量名“salary”,选择“Options”对话框中的所有选项,单击“OK”按钮,生成九、实验结论SPSS在数据分析方面提供了强大的能力,可以快速地得到丰富的描述性统计分析结果供数据分析人员选用,重点在于理解各输出参量的含义及其与数据分析对象属性之间的关系。
