根据7月20日浙江省教育考试院发布的数据统计分析,2017年
浙江省2017年普通高校招生普通类平行投档(二段)分数线【位次排序】
4366 3728 4519 3714 0025 4206 3748 3742 3288 2323 4305 4206 3702 3120 5148 3748 4408 1404 5017 5027 3425 3235 5024 3227 6111 5003 6205 3760 3145 3705 5321 0024 0012 0024 1156 3714 0024 1216 1138 0004 1216 3605 3442 4414 0009 3714 1223 3742 4001 5107 3425
3720 3728 5304 3605 1216 1422 3725 5204 3714 4019 3434 5307 0018 6205 5220 4096 3728 4206 1138 3605 5017 3511 3288 1329 5304 4206 3159 3719 4402 0015 3627 1229 0027 5304 3516 1216 4211 6111 3649 3728 4206 1216 3622 3737 1135 1418 5139 2104 5304 3242 1315
昆明医科大学 江苏科技大学 天津师范大学 安徽理工大学 浙江科技学院 西华大学 沈阳航空航天大学 吉林财经大学 河南师范大学 浙江外国语学院 南京工程学院 上海商学院 上海工程技术大学 浙江大学城市学院(独立学院) 河北师范大学 上海工程技术大学 南昌航空大学 上海应用技术大学 河南大学 福建中医药大学 长沙理工大学 北京信息科技大学 河南工业大学 江苏科技大学 温州大学 青岛大学 北华大学 湖南中医药大学 山东财经大学 华北理工大学 山东科技大学 安徽理工大学 南昌航空大学 天津工业大学 重庆工商大学 南通大学 西安理工大学 东北师范大学 哈尔滨医科大学 青岛理工大学 武汉轻工大学 武汉工程大学 浙江外国语学院 上海应用技术大学 江苏科技大学 苏州科技大学 中南林业科技大学 淮北师范大学 西安理工大学 青岛大学 浙江中医药大学
浙江省2017年普通高校招生投档分数线(二段)
浙江省2017年普通高校招生普通类平行投档(二段)分数线 学校代号 0012 0012 0012 0012 0012 0012 0013 0013 0014 0014 0014 0014 0014 0014 0014 0014 0014 0014 0014 0014 0014 0014 0014 0014 0014 0014 0014 0014 0014 0014 0014 0014 0014 0014 0014 0014 0014 学校名称 浙江中医药大学 浙江中医药大学 浙江中医药大学 浙江中医药大学 浙江中医药大学 浙江中医药大学 中国计量大学 中国计量大学 浙江万里学院 浙江万里学院 浙江万里学院 浙江万里学院 浙江万里学院 浙江万里学院 浙江万里学院 浙江万里学院 浙江万里学院 浙江万里学院 浙江万里学院 浙江万里学院 浙江万里学院 浙江万里学院 浙江万里学院 浙江万里学院 浙江万里学院 浙江万里学院 浙江万里学院 浙江万里学院 浙江万里学院 浙江万里学院 浙江万里学院 浙江万里学院 浙江万里学院 浙江万里学院 浙江万里学院 浙江万里学院 浙江万里学院 专业代号 015 018 019 020 021 022 029 030 001 002 003 004 005 006 007 008 009 010 011 012 013 014 015 016 017 018 019 020 021 022 023 024 025 026 027 028 029 专业名称 听力与言语康复学 医学信息工程 生物科学 医学实验技术 公共事业管理 健康服务与管理 计算机类(中外合作办学) 金融学类(中外合作办学) 教育创新班1 教育创新班2 电气工程及其自动化 电子信息工程 通信工程 物联网工程 计算机科学与技术 软件工程 机械电子工程 法学 公共事业管理 电子商务及法律 财务管理 国际经济与贸易 国际商务 会计学 金融学 金融工程 统计学 环境工程 环境科学 生物工程 生物制药 食品科学与工程 食品质量与安全 日语 商务英语 英语 汉语言文学 第 3 页,共 270 页 计划数 27 32 32 8 6 7 105 74 40 77 62 48 65 64 101 65 20 74 33 35 91 128 36 115 79 45 28 27 34 31 35 20 17 42 77 44 55 分数线 574 572 573 576 574 574 566 571 530 517 523 526 516 519 527 525 522 532 522 517 521 514 513 530 524 512 520 528 517 523 530 529 527 529 527 539 534 位次 53390 54919 54708 51286 53605 53353 61390 56402 99209 112501 105957 102825 114045 110347 102047 103823 106763 97248 107384 112288 108679 115725 117060 98432 105272 117611 109430 101380 112439 106333 99126 99434 102060 100120 102502 89236 94463
2017年浙江省高考数学试卷(真题详细解析)

2017年浙江省高考数学试卷(真题详细解析)1.已知集合P={x|-1<x<1},Q={x|1<x<2},则P∪Q=(-1,2)。
2.椭圆+1的离心率是1/2.3.几何体的三视图无法确定,无法计算体积。
4.若x、y满足约束条件z=x+2y,则z的取值范围是[4.+∞)。
5.函数f(x)=x^2+ax+b在区间[0,1]上的最大值是M,最小值是m,则M-m与a有关,但与b无关。
6.已知等差数列{an}的公差为d,前n项和为Sn,则d>0是S4+S6>2S5的必要不充分条件。
7.函数y=f(x)的图象可能是B。
8.已知随机变量ξi满足P(ξi=1)=pi,P(ξi=0)=1-pi,i=1,2.若0<p1<p2<1,则E(ξ1)<E(ξ2),D(ξ1)<D(ξ2)。
9.正四面体D-ABC,P、Q、R分别为AB、BC、CA上的点,AP=PB=√2,记二面角D-PR-Q,D-PQ-R,D-QR-P的平面角为α、β、γ,则α<β<γ。
10.平面四边形ABCD,AB⊥BC,AB=BC=AD=2,CD=3,AC与BD交于点O,记I1=OI2/OC,I2=OI3/OD,I3=OI1/OA,则I3<I1<I2.二、填空题:11.XXX创立的“割圆术”可以估算圆周率π,理论上能把π的值计算到任意精度,祖冲之继承并发展了“割圆术”,将π的值精确到小数点后七位。
割圆术的第一步是计算单位圆内接正六边形的面积S6,S6=3√3/2.12.已知a、b∈R,(a+bi)2=3+4i(i是虚数单位),则a2+b2=5,ab=2.13.已知多项式(x+1)(x+2)=x2+3x+2,则a4=34,a5=123.14.已知△ABC,AB=AC=4,BC=2,点D为AB延长线上一点,BD=2,连结CD,则△BDC的面积是2√3,cos∠BDC=1/2.15.已知向量a、b满足||a||=1,||b||=2,则|a+b|+|a-b|-|a|-|b|的最小值是0,最大值是4.16.从6男2女共8名学生中选出队长1人,副队长1人,普通队员2人组成4人服务队,要求服务队中至少有1名女生,共有56种不同的选法。
2017年浙江联考申论真题及答案解析(2)

2017年浙江联考申论真题及答案解析(2)以下材料是某学校暑假致家长的一封信。
尊敬的家长:您好!您的孩子考试结束,顺利离校返家,假期生活已然开启。
学业成绩将由班主任随后发放,敬请查收。
如果我们用庄子“无用方为大用”的观点来谈孩子的教育和成长,或许会被当下的社会斥为无稽之谈,因为实用主义哲学早已深入人心。
成绩至上、目标第一的教育论或已洗去了许多人头脑中培养孩子的乐趣,一些父母总是在盼望孩子快点长大,快一点达成父母心中的期盼。
法国哲学家卢梭说:“大自然希望儿童在成人以前就要像儿童的样子。
如果我们打乱了这个秩序,就会造成一些早熟的果实,既不丰满也不甜美,而且很快就会腐烂;我们将造就一些年纪轻轻的博士和老态龙钟的儿童。
”当我们环视周围,不是可以看到很多实用教育导致的伪成熟的孩子么?学习成为他们生活的唯一,童年的乐趣、少年的轻狂、青春的热情统统因为无用而被压抑。
为了成绩、名次,为了全能的素质而拼尽全力。
待到毕业时他们不知道自己需要什么,不知道生活的乐趣所在,他们只会在压抑的中学之后挎着行囊朝着高校走去,却不是朝着志趣前行。
孩子们在匆促的跋涉中疲于奔命,却无暇慢下来欣赏周边的风景,认真地发现自我。
我们学校从不否定学业和成绩的作用,我们学校还强调的是不断唤醒孩子的自律、自觉、自省,激发他们潜藏的能力、志趣、爱好,以“无用”的阅读、思考、交流来充实他们生命的厚度,拓展他们生命的宽度。
当他们走出校门后,不会因为生活的艰辛而失去创造的灵感,不会因为大学的自由而变得松散怠惰,也不会因为五光十色的诱惑而失去心中的信念。
父母养育孩子,不正是在等待、守护一朵花的盛开么?不管他们是迎春而笑、凌寒而开或是含苞待放,他们都是独一无二的孩子,我们要做的就是慢慢地呵护、静静地等待。
我们是否该像审视自己的生活一样去审视对孩子的教育呢?我们是否会在深沉的思索中看到生活中的无用种种,却是孩子以后人生中宝贵的点点滴滴呢?祝您的孩子在静好的岁月中,自在生长!2017年浙江联考申论试题作答要求(一)根据资料2~3,分析当前社会上“求快”风气产生的原因。
浙江省新高考研究联盟2017届高三上学期考试数学试题Word版含答案

浙江省新⾼考研究联盟2017届⾼三上学期考试数学试题Word版含答案2016学年第⼀学期浙江“七彩阳光”新⾼考研究联盟⾼三联考数学学科试题考⽣须知:1.本试题分为第Ⅰ卷(选择题)和第Ⅱ卷(⾮选择题)两部分,全卷满分150分,考试时间120分钟。
2.考⽣答题前,务必将⾃⼰的姓名、准考证号⽤⿊⾊字迹的签字笔或钢笔填写在答题纸上。
3.选择题的答案须⽤2B 铅笔将答题纸上对应题⽬的答案标号涂⿊,如要改动,须将原填涂处⽤橡⽪擦净。
4.⾮选择题的答案须⽤⿊⾊字迹的签字笔或钢笔写在答题纸相应区域内,答案写在本试题卷上⽆效。
参考公式:如果事件,A B 互斥,那么()()().P A B P A P B +=+ 如果事件,A B 相互独⽴,那么()()().P A B P A P B = 如果事件A 在⼀次试验中发⽣的概率是p,那么n 次独⽴重复试验中事件A 恰好发⽣k次的概率()(1)(0,1,2,,).k kn k n n P k C p p k n -=-= 球的表⾯积公式24,S R π=其中R 表⽰球的半径。
球的体积公式34,3VR π=其中R 表⽰球的半径。
柱体的体积公式,V Sh =其中S 表⽰柱体的表⾯积,h 表⽰柱体的⾼。
锥体的体积公式1,3VSh =其中S 表⽰锥体的表⾯积,h 表⽰锥体的⾼。
台体的体积公式()121,3V h S S =其中12,S S 表⽰台体的上、下⾯积,h 表⽰台体的⾼。
第Ⅰ卷⼀、选择题:本⼤题共10⼩题,每⼩题4分,共40分.在每⼩题给出的四个选项中,只有⼀项是符合题⽬要求的. 1.已知全集U R =,集合{}{}2|3,|13,A x x B x x =≥=<<则()R A C B =B.{|x x x ≤≥C.{|1或x x x ≤≥D.{}|3x x x ≤≥ 2.若,a b 为实数,则“33ab <”是“1a b <+”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.从1,2,3,4,5,6六个数中任取2个数,则取出的两个数不是连续整数的概率是() A.35 B.25C.13D.234.已知等差数列{}na 满⾜22383829a a a a ++=,且0n a <,则其前10项和为()A.-9B.-11C.-13D.-15 5.函数()2cos sin 3f x x x π??=- ?的最⼤值为()A.12 D.26.设圆C的圆⼼与双曲线2221(0)x y a a-=>的右焦点重合,且该圆与此双曲线的渐近线相切,若直线30x y -=被圆C 截得的弦长等于1,则双曲线的离⼼率e 的值是()327.如图,在ABC ?中,D 是BC 的中点,E,F 是AD 两个三等分点,41BA CA BE CE ?=?=- ,,则BF CF的值是()A.-5B.-4C.-3D.-2 8.已知221,0()() (1),0x x x f x y f x x f x x ?--+<==-?-≥?,则的零点有()B.A.1个 B.2个C.3个D.4个()2*0121123sin cos cos ,0...,()(),,2...,n n n n n n n f x x x x x x x x a f x f x n N S a a a a S π-=+≤<<<<≤=-∈=++++9.已知函数则的最⼤值等于()1 D.210.如图,在三棱锥P-ABC 中,AB=AC=PB=PC=5,PA=4,BC=6,点M 在平⾯PBC 内,且α,则cos α的最⼤值为()A.5B.5C.25D.5第Ⅱ卷⼆、填空题:本⼤题共7⼩题,多空题每题6分,单空题每题4分,共36分. 三、11.已知42,lg ,a x a ==则a =;x =.12.正项等⽐数列{}n a 的前n 项和为n S ,公⽐为q ,且4418,a S S =-则1=;=q .13.⼀个⼏何体的三视图如图所⽰,则该⼏何体的最长的棱长为;体积为. 14.已知实数,x y 满⾜320324010x y x y y -+≥??+-≤??+≥?,则z x y =+的最⼤值是15.已知00=2x y xy x y >>+,,,若222x y m m +≥+恒成⽴,则实数m 的取值范围是.16.已知函数2)3,1() 2,1xa x a x f x x -+17.直线,,0x a x b y ===和曲线()y f x =所围成的⾯积称为函数()f x 在区间[],a b 上的⾯积.现已知函数sin y nx =在区间0,n π的⾯积为2n ,则函数3sin 314y x π=-+()在区间5,44ππ上的⾯积为.三、解答题:本⼤题共5个⼩题,共74分.解答应写出⽂字说明,证明过程或演算步骤. 18.(本题满分14分)在ABC ?中,⾓A B C ,,的对边分别为,,a b c ,且tan 21.tan A c B b+=(Ⅰ)求⾓A 的⼤⼩.(Ⅱ)若=2a ,求ABC ?⾯积的最⼤值.19.(本题满分15分)如图,在四棱锥C ABDE-中,F为CD的中点,,//,2D B A B C B D A E B D平⾯且(Ⅰ)求证://.EF ABC 平⾯(Ⅱ)若6AB BC CA DB ====,,求AC 与平⾯ECD 所成⾓的正弦值.20.(本题满分15分)已知函数31() 1.3f x x ax =-+ 1左视图俯视图AEDBF(Ⅰ)若=1a 时,求()f x 在2x =处的切线⽅程.(Ⅱ)求()f x 在[]0,1上的最⼩值()g a 的表达式.21.(本题满分15分)已知椭圆2222:1(0)x y C a b a b+=>>的离⼼率为,并且经过点(M .(Ⅰ)求椭圆的标准⽅程. (Ⅱ)若直线l 与圆22:1O x y +=相切,与椭圆C 相交A,B 两点,求AOB ?D 的⾯积最⼤值.22.(本题满分15分)已知数列{}n a 满⾜12115,6(2)n n n a a a a a n +-===+≥.(Ⅰ)求证:{}12n n a a ++是等⽐数列.(Ⅱ)设33n n n n na b n +=?,且{}n b 的前n 项和为*,n T n N ∈,证明:6n T <.2016学年七彩联盟—⾼三数学试题答案2016.12.1⼀、选择题:本⼤题共10⼩题,每⼩题4分,共40分。
浙江省杭州市萧山区2017年高考模拟命题比赛政治试卷6 含答案

2017年高考模拟试卷政治卷考生须知:满分100分,考试时间90分钟。
其中加试题部分为30分,用【加试题】标出。
一、判断题(本大题共10小题,每小题1分,共10分。
判断下列说法是否正确,正确的请将答题纸相应题号后的T涂黑,错误的请将答题纸相应题号后的F涂黑)1. 通过微信、支付宝“扫码支付”可以减少现金流通量并缓解通货膨胀。
(此题原创)2.“三百六十行,行行出状元”,这启示劳动者应树立多种方式的就业观。
(此题原创)3. 2016年某企业成功在纽约证券交易所挂牌上市,这是“引进来”水平成熟的表现。
(此题原创)4.遵守宪法和法律是我国顺利进行社会主义现代化建设的根本保证。
(此题原创)5. 在某省的村委会选举中实行“不确定候选人”的海选,这是一种直接选举。
(此题根据浙江省新高考联盟高三试卷第4题改编)6.“和平共处五项原则”与“和而不同”理念是一脉相承的,这印证了中华文化的博大精深。
(此题原创)7.“人的完美需要在文化中不断实现”,说明文化对人的影响是潜移默化的。
(此题根据浙江台州学考选考高三政治试卷改编)8.一切生物的反应形式是人类意识产生的前提。
(此题原创)9. 对立统一规律提供了理解一切现存事物“自己运动”的钥匙。
(此题原创)10.党提出“让人们共建共享”理念,表明“全心全意为人民服务”是党的群众路线的基本内容之一。
(此题原创)二、选择题Ⅰ(本大题共22小题,每小题2分,共44分。
每小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不得分)11.当前,一些国有“僵尸企业”问题日益突出。
国家坚持对那些无望恢复生气、但由于获得政府支持而免于倒闭的负债国企进行分类处置,创新发展一批、重组整合一批和清理退出一批。
国家分类处置“负债国企”有利于①有效化解产能不足,促进产业优化升级②企业提高自主创新能力,形成竞争优势③强化企业风险意识,提高资源利用效率④深化国企改革,巩固国有经济主体地位A.②③ B.①③ C.①④ D.②④(此题根据嘉兴市2016届高三测试试卷26题改编)12. 2016年经济下行压力加大的背景下,我国经济总体保持稳健增长,全年城镇新增就业达1300万人以上,同期城乡居民收入稳定增长,民生逐步改善。
2017年高考数学浙江试题及解析
2017年高考数学浙江1.(2017年浙江)已知集合P={x|-1<x <1},Q={0<x <2},那么P ∪Q=( ) A .(1,2)B .(0,1)C .(-1,0)D .(1,2)1.A 【解析】利用数轴,取P ,Q 所有元素,得P ∪Q=(-1,2).2. (2017年浙江)椭圆x29+y24=1的离心率是( )A .133B .53C .23D .592.B 【解析】e=9-43=53.故选B .3. (2017年浙江)某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:cm 3)是( )(第3题图) A .12π+ B .32π+ C .312π+D .332π+ 3. A 【解析】根据所给三视图可还原几何体为半个圆锥和半个棱锥拼接而成的组合体,所以,几何体的体积为V=13×3×(π×122+12×2×1)=π2+1.故选A.4. (2017年浙江)若x ,y 满足约束条件⎩⎪⎨⎪⎧x≥0,x+y-3≥0,x-2y≤0,则z=x+2y 的取值范围是( )A .[0,6]B .[0,4]C .[6,+∞)D .[4,+∞)4. D 【解析】如图,可行域为一开放区域,所以直线过点(2,1)时取最小值4,无最大值,选D .5. (2017年浙江)若函数f (x )=x 2+ ax +b 在区间[0,1]上的最大值是M ,最小值是m ,则M – m ( )A .与a 有关,且与b 有关B .与a 有关,但与b 无关C .与a 无关,且与b 无关D .与a 无关,但与b 有关5. B 【解析】因为最值f (0)=b ,f (1)=1+a+b ,f (-a 2)=b-a24中取,所以最值之差一定与b 无关.故选B.6. (2017年浙江)已知等差数列{a n }的公差为d ,前n 项和为S n ,则“d >0”是“S 4 + S 6>2S 5”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件6. C 【解析】由S 4 + S 6-2S 5=10a 1+21d-2(5a 1+10d )=d ,可知当d >0时,有S 4+S 6-2S 5>0,即S 4 + S 6>2S 5,反之,若S 4 + S 6>2S 5,则d >0,所以“d >0”是“S 4 + S 6>2S 5”的充要条件,选C .7. (2017年浙江)函数y=f (x )的导函数y=f ′(x )的图象如图所示,则函数y=f (x )的图象可能是( )(第7题图)7. D 【解析】原函数先减再增,再减再增,且x=0位于增区间内.故选D.8. (2017年浙江)已知随机变量ξi 满足P (ξi =1)=p i ,P (ξi =0)=1–p i ,i =1,2. 若0<p 1<p 2<12,则( )A .E (ξ1)<E (ξ2),D (ξ1)<D (ξ2)B .E (ξ1)<E (ξ2),D (ξ1)>D (ξ2)C .E (ξ1)>E (ξ2),D (ξ1)<D (ξ2)D .E (ξ1)>E (ξ2),D (ξ1)>D (ξ2)8. A 【解析】∵E (ξ1)=p 1,E (ξ2)=p 2,∴E (ξ1)<E (ξ2),∵D (ξ1)=p 1(1-p 1),D (ξ2)=p 2(1-p 2),∴D (ξ1)- D (ξ2)=(p 1-p 2)(1-p 1-p 2)<0.故选A .9. (2017年浙江)如图,已知正四面体D –ABC (所有棱长均相等的三棱锥),P ,Q ,R 分别为AB ,BC ,CA 上的点,AP=PB ,BQ QC =CRRA =2,分别记二面角D –PR –Q ,D –PQ –R ,D –QR –P 的平面角为α,β,γ,则( )(第9题图)A .γ<α<βB .α<γ<βC .α<β<γD .β<γ<α9. B 【解析】设O 为三角形ABC 中心,则O 到PQ 距离最小,O 到PR 距离最大,O 到RQ 距离居中,而高相等,因此α<γ<β.故选B.10. (2017年浙江)如图,已知平面四边形ABCD ,AB ⊥BC ,AB =BC =AD =2,CD =3,AC 与BD 交于点O ,记I 1=→OA ·→OB ,I 2=→OB ·→OC ,I 3=→OC ·→OD,则( )(第10题图) A .I 1<I 2<I 3B .I 1<I 3<I 2C .I 3<I 1<I 2D .I 2<I 1<I 310. C 【解析】因为∠AOB=∠COD >90°,OA <OC ,OB <OD ,所以→OB ·→OC >0>→OA ·→OB >→OC ·→OD .故选C.11. (2017年浙江)我国古代数学家刘徽创立的“割圆术”可以估算圆周率π,理论上能把π的值计算到任意精度.祖冲之继承并发展了“割圆术”,将π的值精确到小数点后七位,其结果领先世界一千多年.“割圆术”的第一步是计算单位圆内接正六边形的面积S 6,S 6= . 11. 332 【解析】将正六边形分割为6个等边三角形,则S 6=6×(12×1×1×sin 60°)=332.12. (2017年浙江)已知a ,b ∈R ,(a+bi )2=3+4i (i 是虚数单位)则a 2+b 2=___________,ab =___________.12.5 2 【解析】由题意可得a 2-b 2+2abi=3+4i ,则⎩⎨⎧a2-b2=3,ab=2,解得⎩⎨⎧a2=4,b2=1,则a 2+b 2=5,ab=2.13. (2017年浙江)已知多项式(x+1)3(x+2)2=x5+a1x4+a2x3+a3x2+a4x+a5,,则a4=________,a5=________.13. 16 4 【解析】由二项式展开式可得通项公式为C r3x r C m2·22-m= C r3·C m2·22-m·x r+m,分别取r=0,m=1和r=1,m=0可得a4=4+12=16,取r=m,可得a5=1×22=4.14. (2017年浙江)已知△ABC,AB=AC=4,BC=2.点D为AB延长线上一点,BD=2,连结CD,则△BDC的面积是___________,cos∠BDC=___________.14. 152104【解析】取BC中点E,由题意,AE⊥BC,△ABE中,cos∠ABE=BEAB=14,∴cos ∠DBC=-14,sin∠DBC=1-116=154,∴S△BCD=12×BD×BC×sin∠DBC=152.∵∠ABC=2∠BDC,∴cos∠ABC=cos 2∠BDC=2cos2∠BDC-1=14,解得cos∠BDC=104或cos∠BDC=-104(舍去).综上可得,△BCD面积为152,cos∠BDC=10 4.15. (2017年浙江)已知向量a,b满足|a|=1,|b|=2,则|a+b|+|a-b|的最小值是________,最大值是_______.15. 4,2 5 【解析】设向量a,b的夹角为θ,由余弦定理有|a-b|=12+22-2×1×2×co s θ=5-4cos θ,|a+b|=12+22-2×1×2×cos (π-θ)=5+4cos θ,则|a+b|+|a-b|=5+4cos θ+5-4cos θ,令y=5+4cos θ+5-4cos θ,则y2=10+225-16cos2θ∈[16,20],据此可得(|a+b|+|a-b|)max=20=25,(|a+b|+|a-b|)min=16=4,即|a+b|+|a-b|的最小值是4,最大值是25.16. (2017年浙江)从6男2女共8名学生中选出队长1人,副队长1人,普通队员2人组成4人服务队,要求服务队中至少有1名女生,共有______种不同的选法.(用数字作答) 16. 660 【解析】由题意可得,“从8名学生中选出队长1人,副队长1人,普通队员2人组成4人服务队”中的选择方法为C 48×C 1 4×C 1 3(种)方法,其中“服务队中没有女生”的选法有C 4 6×C 1 4×C 1 3(种)方法,则满足题意的选法有C 4 8×C 1 4×C 1 3- C 4 6×C 1 4×C 13=660(种).17. (2017年浙江)已知a ∈R ,函数f (x )=|x+4x -a|+a 在区间[1,4]上的最大值是5,则a 的取值范围是___________.17.(-∞,92]【解析】x ∈[1,4],x+4x ∈[4,5],分类讨论:①当a ≥5时,f (x )=a-x-4x +a=2a-x-4x ,函数的最大值2a-4=5,∴a=92,舍去;②当a ≤4时,f (x )=x+4x -a+a=x+4x≤5,此时命题成立;③当4<a <5时,[f(x)]max =max{|4-a|+a,|5-a|+a},则⎩⎨⎧|4-a|+a≥|5-a|+a ,|4-a|+a=5或⎩⎨⎧|4-a|+a <|5-a|+a ,|4-a|+a=5解得a=92或a <92.综上可得,实数a 的取值范围是(-∞,92].18. (2017年浙江)已知函数f (x )=sin 2x –cos 2x –23sin x cos x (x ∈R ). (1)求f (2π3)的值.(2)求f (x )的最小正周期及单调递增区间. 18.解:(1)由sin 2π3=32,cos 2π3=-12,f (2π3)=(32)2-(-12)2-23×32×(-12).得f (2π3)=2.(2)由cos 2x=cos 2x-sin 2x 与sin 2x=2sin xcos x , 得f(x)=-cos 2x-3sin 2x=-2sin(2x+π6).所以f(x)的最小正周期是π.由正弦函数的性质得π2+2k π≤2x+π6≤3π2+2k π,k ∈Z ,解得π6+k π≤x ≤3π2+2k π,k ∈Z ,所以,f (x )的单调递增区间是[π6+k π,3π2+2k π],k ∈Z .19. (2017年浙江)如图,已知四棱锥P –ABCD ,△PAD 是以AD 为斜边的等腰直角三角形,BC ∥AD ,CD ⊥AD ,PC =AD =2DC =2CB ,E 为PD 的中点.(第19题图)(1)证明:CE ∥平面PAB ;(2)求直线CE 与平面PBC 所成角的正弦值. 19.解:(1)如图,设P A 中点为F ,连接EF ,FB . 因为E ,F 分别为PD ,P A 中点, 所以EF ∥AD 且EF=12AD ,又因为BC ∥AD ,BC=12AD ,所以EF ∥BC 且EF=BC , 即四边形BCEF 为平行四边形, 所以CE ∥BF , 因此CE ∥平面P AB .PABCDE(2)分别取BC ,AD 的中点为M ,N ,连接PN 交EF 于点Q ,连接MQ. 因为E ,F ,N 分别是PD ,PA ,AD 的中点,所以Q 为EF 中点, 在平行四边形BCEF 中,MQ ∥CE. 由△PAD 为等腰直角三角形得PN ⊥AD. 由DC ⊥AD ,N 是AD 的中点得BN ⊥AD . 所以AD ⊥平面PBN , 由BC //AD 得BC ⊥平面PBN , 那么平面PBC ⊥平面PBN .过点Q 作PB 的垂线,垂足为H ,连接MH .MH 是MQ 在平面PBC 上的射影,所以∠QMH 是直线CE 与平面PBC 所成的角. 设CD =1.在△PCD 中,由PC =2,CD =1,PD=2得CE =2, 在△PBN 中,由PN =BN =1,PB =3得QH =14,在Rt △MQH 中,QH=14,MQ =2,所以sin ∠QMH =28, 所以直线CE 与平面PBC 所成角的正弦值是28.20. (2017年浙江)已知函数f (x )=(x –2x-1)e -x (x ≥12).(1)求f (x )的导函数;(2)求f (x )在区间[12,+∞)上的取值范围.20.解:(1)因为(x –2x-1)′=1-12x-1,(e -x )′=-e -x , 所以f (x )=(1-12x-1)e -x -(x –2x-1)e -x =(1-x)(2x-1-2)e -x 2x-1(x >12).(2)由f ′(x )=(1-x)(2x-1-2)e -x2x-1=0解得x=1或x=52.因为 x 12 (12,1) 1 (1,52)52 (52,+∞) f ′(x ) – 0 + 0 – f (x )12e -12↘↗12e -52↘又f (x )=12(2x-1-1)2e -x ≥0,所以f (x )在区间[12,+∞)上的取值范围是[0,12e -12].21. (2017年浙江)如图,已知抛物线x 2=y ,点A (-12,14),B (32,94),抛物线上的点p(x,y)(-12<x <32).过点B 作直线AP 的垂线,垂足为Q .(第19题图)(1)求直线AP 斜率的取值范围; (2)求|PA|·|PQ|的最大值.21. 解:(1)设直线AP 的斜率为k , k=x2-14x+12=x-12,因为-12<x <32,所以直线AP 斜率的取值范围是(-1,1).(2)联立直线AP 与BQ 的方程⎩⎨⎧kx-y+12k+14=0,x+ky-94k-32=0,解得点Q 的横坐标是x Q =-k2+4k+32(k2+1).因为|P A |=1+k2(x+12)=1+k2(k+1),|PQ |=1+k2(x Q -x)=-(k-1)(k+1)2k2+1,所以|PA|·|PQ|=-(k-1)(k+1)3. 令f(k)=-(k-1)(k+1)3, 因为f ′(k)=-(4k-2)(k+1)2,所以f (k )在区间(-1,12)上单调递增,(12,1)上单调递减,因此当k =12时,|PA|·|PQ|取得最大值2716.22. (2017年浙江) 已知数列{x n }满足x 1=1,x n =x n +1+ln(1+x n +1)(n ∈N *). 证明:当n ∈N *时, (1)0<x n +1<x n ; (2)2x n +1− x n ≤xnxn+12;(3)12n-1≤x n ≤12n-2.22.解:(1)用数学归纳法证明x n >0. 当n =1时,x 1=1>0. 假设n =k 时,x k >0,那么n =k +1时,若x k+1≤0,则0<x k = x k +1+ln (1+ x k +1)≤0,矛盾,故x k +1>0. 因此x n >0(n ∈N *).所以x n =x n+1+ln (1+x n+1)>x n+1, 因此0<x n+1<x n (n ∈N *). (2)由x n =x n+1+ln (1+x n+1),得x n x n+1-4x n+1+2x n =x n+12-2x n+1+(x n+1+2)ln (1+x n+1).11 / 11 记函数f (x )=x2-2x+(x+2)ln (1+x )(x ≥0),f ′(x )=2x2+x x+1+ln (1+x )>0(x >0), 函数f (x )在[0,+∞]上单调递增,所以f (x )≥f (0)=0, 因此x n+12-2x n+1+(x n+1+2)ln (1+x n+1)=f (x n+1)≥0, 故2x n+1-x n ≤xnxn+12(n ∈N *). (3)因为x n =x n+1+ln (1+x n+1)≤x n+1+x n+1=2x n+1,所以x n ≥12n-1, 由xnxn+12≥2x n+1-x n , 得1xn+1-12≥2(1xn -12)>0, 所以1xn -12≥2(1xn-1-12)≥…≥2n-1(1x1-12)=2n-2, 故x n ≤12n-2. 综上,12n-1≤x n ≤12n-2(n ∈N *).。
2017年高考有关情况通报
2017年高考有关情况通报6 2017年高考有关情况通报一、今年高考基本情况及组考工作主要措施今年,我省共有高考考生x万人,较上年增加x万人,增长x%。
其中,应届生x万人,占考生总数的x%,往届生x万人,占x%;科考生x万人,占x%,理科考生2182万人,占x%,职高对口类考生x万人,占x%。
除去保送生、高职院校单独招生等提前录取的考生,全省实际参考考生为x万人,比上年增加x万余人。
全省14个市州设有122个考区、x个考点、x间考室,考务工作人员近x万人。
月27日,省政府召开了全省普通高校招生考试暨普通高中学业水平考试工作电视电话会议。
向力力副省长从进一步强化责任担当、强化安全管控、强化保障服务等方面对做好今年高考工作提出了明确要求。
省教育厅肖国安厅长对今年高考工作进行了全面具体的部署,要求进一步统一思想认识、全力以赴确保考试安全、科学调控高校招生计划、切实维护招生录取公平公正。
为落实省委、省政府及省教育厅“保平安、保质量、保公平”和“零差错、零事故”的总体要求,我们坚持以强化责任为重要抓手,进一步完善机制、落实措施、规范管理、优化服务,坚决杜绝失密泄密、大面积有组织舞弊等安全事故和重大工作差错的发生,确保考试安全、招生公平、舆论平稳、社会稳定。
我们采取的主要措施,概括起就是“10个加强”。
1.加强试卷安全保密。
切实抓好试卷运送、保管、分发、回收等试卷流转全过程的监管,加强对涉密场所及相关人员的监控。
严格执行保密室试卷保管“双人双锁”、24小时值班、保密人员出入检查登记、视频监控6小时回放等制度。
同时,采取人技联防、一岗多控等手段,给试卷安全加上多重保险。
2.加强考务精细化管理。
全面细化高考工作流程,全省统一制定了岗位《操作规程》和组考工作日程表,各地、各考点也结合实际层层制定了详实的高考组考和安全工作方案,进一步规范各个环节特别是关键岗位的操作流程,完善组考工作机制,规范考务操作。
3.加强技术防范。
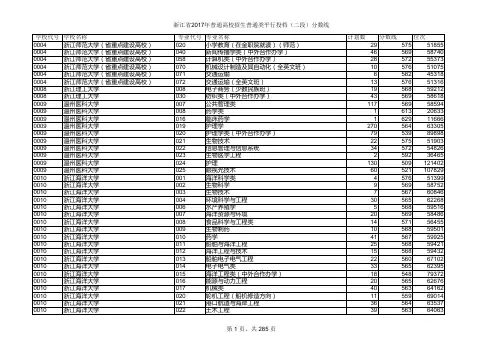
浙江省2017年普通高校招生普通类平行投档(一段)分数线
第 2 页,共 153 页来自浙江省2017年普通高校招生普通类平行投档(一段)分数线 学校代号 学校名称 0004 浙江师范大学(省重点建设高校) 0004 浙江师范大学(省重点建设高校) 0004 浙江师范大学(省重点建设高校) 0004 浙江师范大学(省重点建设高校) 0004 浙江师范大学(省重点建设高校) 0004 浙江师范大学(省重点建设高校) 0004 浙江师范大学(省重点建设高校) 0005 宁波大学(省重点建设高校) 0005 宁波大学(省重点建设高校) 0005 宁波大学(省重点建设高校) 0005 宁波大学(省重点建设高校) 0005 宁波大学(省重点建设高校) 0005 宁波大学(省重点建设高校) 0005 宁波大学(省重点建设高校) 0005 宁波大学(省重点建设高校) 0005 宁波大学(省重点建设高校) 0005 宁波大学(省重点建设高校) 0005 宁波大学(省重点建设高校) 0005 宁波大学(省重点建设高校) 0005 宁波大学(省重点建设高校) 0005 宁波大学(省重点建设高校) 0005 宁波大学(省重点建设高校) 0005 宁波大学(省重点建设高校) 0005 宁波大学(省重点建设高校) 0005 宁波大学(省重点建设高校) 0005 宁波大学(省重点建设高校) 0005 宁波大学(省重点建设高校) 0005 宁波大学(省重点建设高校) 0005 宁波大学(省重点建设高校) 0005 宁波大学(省重点建设高校) 0005 宁波大学(省重点建设高校) 0005 宁波大学(省重点建设高校) 0005 宁波大学(省重点建设高校) 0005 宁波大学(省重点建设高校) 0005 宁波大学(省重点建设高校) 0005 宁波大学(省重点建设高校) 0005 宁波大学(省重点建设高校) 专业代号 071 072 074 076 090 091 092 021 022 023 024 025 026 027 028 029 030 031 032 033 034 036 037 038 039 040 041 042 043 044 045 046 047 048 049 051 052 专业名称 交通运输 交通运输(全英文班) 机电技术教育(师范) 汉语国际教育(师范) 电子商务 应用化学 生物技术 金融学(全英文班) 国际经济与贸易(全英文班) 会计学(ACCA) 会计学(CPACanada) 英语 日语 德语 临床医学 预防医学 通信工程 机械设计制造及其自动化(国贸班) 应用心理学 工商管理(中加学分互认) 建筑学 物流管理 人文与传媒类 经济学类 工商管理类 电子信息类 机械类 数理科学类 海洋科学类 师范类(文科)(师范) 材料化学类 土木建设类 法政类 英语(师范) 小学教育(师范) 数学与应用数学(师范) 食品科学与工程 计划数 分数线 位次 60 577 50696 20 577 50515 30 580 47708 31 606 25174 22 592 36460 12 600 29798 15 594 34562 30 598 31635 30 596 32887 38 602 28287 28 599 30743 70 598 31421 10 597 32558 40 597 32488 130 605 26039 30 599 30449 40 592 36402 42 590 37786 25 596 33284 15 592 36029 30 594 34812 40 590 38513 40 600 30067 150 593 35846 110 594 35065 130 591 37454 60 590 38260 40 592 36317 40 589 39319 15 605 25771 40 591 37442 80 589 39358 100 600 29733 10 607 24860 10 606 25497 20 600 29467 30 592 36758
2017浙江高考一本分数线已公布,2017高考分数线
2017浙江高考一本分数线已公布,2017高考分数线
高考,几家欢喜几家愁,有悔恨的泪,也有成功的笑。
愿落榜的你,鼓起勇气,战胜失败,相信风雨过后,总会有彩虹。
愿金榜题名的你再接再励,永创辉煌。
2017年高考分数线在6月22日公布,高考频道为您提供2017浙江高考一本分数线已公布,希望对您的有所帮助。
2017浙江高考一本分数线已公布
2017年浙江省普通高校招生普通类分段线
分分段线
注:艺术类第一批中,教育部批准的可自主划线的独立设置本科艺术院校和清华大学等15所高校的艺术类本科专业,由学校自主划定艺术类文化分数线;其他高校艺术类本科专业要求考生文化成绩(高考总分)须不低于312分。
2017年浙江省普通高校招生体育类综合分分段线
2017年浙江省单独考试招生分数线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
根据7月20日浙江省教育考试院发布的数据统计分析,2017年新高考普通类第二段总分一分一段表和7月22-23日可参加志愿填报的二段线上的考生90246人,剩余本科计划为7.45万(含公办3.14万、民办及独立学院4.31万),由此从当前理论数据分析约1.6万考生可能进不了本科专业,而进入专科专业。
浙江省普通类二段线480分以上的考生,喜欢我校交通运输类专业,可于7月22日-23日在“浙江省教育考试网”填报我校专业志愿,所有专业录取希望极大,尽管大胆填报,竭尽欢迎考生踊跃报考我校!
浙江交通职业技术学院创建于1958年,隶属于浙江省交通运输厅,是交通运输部与浙江省人民政府共建的公办院校,全国职业教育先进单位,国家优秀骨干高职院校,全国交通职业教育示范院校,浙江省示范高等职业技术学院,教育部首批“中德汽车机电技能型人才培养培训项目”试点院校,四年制高等职业教育人才培养试点院校,“全国定向培养士官”试点院校,全国高等职业院校服务贡献50强院校。
学校位于杭州市,占地622亩,全日制在校学生9000余名,教职员工550余名,具备现代化的教育教学及生活设施,享有全国高职“魅力校园”称号。
学校下设路桥学院、汽车学院、海运学院、航空学院、轨道交通学院、智慧交通学院、运输管理学院、人文学院和继续教育学院等9个分院,以及省交通运输科学研究院和15个院属研究机构,设置41个全日制高职专业,为浙江现代综合交通“大港口、
大路网、大航空、大水运、大物流”五大建设和社会经济发展提供强有力的人才支撑。
学校以“依托交通,服务社会”为办学特色,设置交通基础设施建设、汽车运用工程、国际航运与海洋旅游、高端装备制造、航空技术与服务、智慧交通信息技术、轨道交通技术与管理、现代物流与商贸等8个特色专业群,是国内交通运输类专业设置最全的高校,被誉为“浙江交通人才摇篮”。
2017年面向浙江省普高“普通类”招生计划(院校代码0042)
1. 学生专科升本科的途径?
组织毕业生报考全省普通高校“专升本”统一考试,我校所有专业均列入浙江省“专升本”统一考试专业目录,并设有“专升本”奖学金。
近年来,我校毕业生被杭州电子科技大学、浙江工商大学、浙江理工大学、中国计量大学、杭州师范大学、浙江大学城市学院等本科院校录取率达75%以上。
我校还与武汉理工大学合作建立“专升本”教学点,学生在校期间即可参加武汉理工大学“继续教育学分银行”课程学习,待专科毕业后,凭修满的学分卡换取网络教育本科文凭;与浙江工商大学、宁波工程学院合作开展工商企业管理、汽车营销与售后技术服务专业“专升本”自考助学。
2. 学生公寓住宿条件?
学校具有设施一流的住宿条件,为学生提供了良好的学习和生活环境。
学生住宿由学校统一安排,每间4-6人,室内均配有空调、热水系统、卫生间、电扇、宽带接口、桌椅等设施。
3. 学生入学后调整专业规定?
为满足学生的学习兴趣和职业生涯规划的需求,促进学生个性化发展,经过一个学期学习后,学生可以根据自己的意愿提出调整专业的申请。
学校视学生的实际情形,结合学生第一学期的学习成绩、在校表现、转入分院的教学资源及要求等状况,统一审批学生专业调整
(除汽车运用与维修技术、通信技术两个中外合作专业不能调整到普通类专业外),学生转专业成功率达95%以上。
4. 奖学金和助学帮扶办法?
学校设有国家奖学金、国家励志奖学金、优秀学生奖学金、优秀毕业生奖学金、航海励志奖学金、专升本奖学金、优秀交流生奖学金等,奖励品学兼优学生。
对家庭困难学生设立“绿色通道”,实行国家贴息助学贷款、国家助学金、学费减免、各类困难补助、勤工助学等资助政策,帮扶学生顺利完成学业。
5. 专业优势和人才需求情况?
学校依托交通运输行业的强大优势,构建了与政府、行业、企业、部队、境内外高校等多方联动的紧密型合作平台,产学研合作广泛。
面向交通运输业、装备制造业、高新技术业、管理服务业,设置道桥、铁道、汽车、航运、航空、轨道、通信、物流、邮轮、邮政等41个专业,具有良好的“岗位适应性、专业对口性、技术应用性、服务宽泛性”的特色,用人需求旺盛,供需比例1:4以上,毕业生就业单位稳固,就业质量和满意度高。
其中现代综合交通建设和运输服务类专业是我校历史悠久和特有的品牌专业,与各地交通建设部门、海陆运输系统等单位合作紧密,一直来保持着对接的用人需求。
特别是近几年,随着国家“海洋经济”、“一带一路”、“美丽中国”、“互联网+”、“中国制造2025”等战略的实施,航空、高铁、地铁、城轨、道路、汽车、海运、通信、邮政、邮轮、物流等综合交通建设迎来了快速发展的机遇。
航空公司、上海铁路局、地铁集团、交工集团、海运集团、物流企业、邮轮公司、邮电通信部门等各级各类企事业单位,对我校道路桥梁工程技术、市政工程技术、工程
造价、铁道工程技术、城市轨道交通车辆技术、城市轨道交通运营管理、飞机机电设备维修、通用航空器维修、民航运输、港口与航运管理、国际邮轮乘务管理、物流管理、商务英语、机电一体化技术、通信技术、智能控制技术、邮政通信管理等专业需求量大,校企合作及订单培养广泛。
6. 就业工作和毕业生就业情况?
学校以就业创业为导向,将毕业生就业工作作为人才培养的重要环节纳入教育教学质量提升工程,通过健全组织、完备制度、整合资源,形成了“全校共同关注、全员互动参与”的工作格局,在拓宽合作渠道、深化信息服务、注重指导推荐、强化就业帮扶等方面形成了工作特色。
每年通过“订单培养”、“校企合作”、“校园招聘”、“顶岗实习”、“校友推荐”等途径,助力毕业生充分而高质量就业,每年吸纳上海铁路局、各地地铁集团、交通建设集团、市政工程公司、汽车著名企业、港务航运系统、邮轮旅游公司、物流商贸公司、邮政通信部门、机械电子产业等600多家稳固的企事业单位进校招聘,促进学生高质量就业。
毕业生就业率连续多年保持在98%以上,毕业生薪酬在省内外同类院校中名列前茅。
7. 对外交流与合作办学情况?
学校与浙江科技学院合作开展四年制高等职业教育人才培养,与海军部队合作开展定向培养士官,与美国伯米吉州立大学合作举办“汽车运用与维修技术”、“通信技术”高等专科教育项目,与德国五大汽车生产商(保时捷、宝马、奔驰、奥迪、大众)合作开展中德SGAVE汽车职业教育项目。
学校还与德国外贸交通学院、澳大利亚西海岸科技学院等境外院校开展专业开发、师生交流等合作项目,在校
学生可参加台湾龙华科技大学交换生项目,优秀学生可赴德国外贸交通学院等境外院校交流访学;与丰田公司合作开展“丰田汽车技术培训计划(T-TEP)”;与皇家加勒比游轮公司合作开展邮轮人才培养;与武汉理工大学、浙江工商大学、宁波工程学院合作专升本助学。
学校还与各级各类著名企业校企合作广泛,联合开展订单培养(如:城市轨道交通运营管理、城市轨道交通车辆技术两个专业分别与宁波市轨道交通集团、绍兴市轨道交通集团合作开设订单班;城市轨道交通运营管理专业与温州市铁路与轨道交通投资集团合作开设订单班;城市轨道交通运营管理、城市轨道交通车辆技术、铁道工程技术三个专业与杭州市地铁集团合作开设订单班;城市轨道交通运营管理、城市轨道交通车辆技术、铁道工程技术、机电一体化技术四个专业与浙江省轨道交通运营管理集团合作开设订单班)。
