用落球法测量液体的粘滞系数
落球法测量粘滞系数

01
02
03
绘制粘滞系数(h)-温度(T)曲线
估算间接测量不确定度
实验中误差来源的分析
数据处理
预写实验报告
复习实验步骤
作业
!
CLICK HERE TO ADD A TITLE
单击此处添加文本具体内容
演讲人姓名
这是1个一阶线性微分方程,其通解为:
(A1)
(A2)
(A3)
由(6)式可计算平衡时间。 若钢球直径为10-3m,代入钢球的密度r,蓖麻油的密度r0及40 ºC时蓖麻油的粘度h = 0.231 Pa·s,可得此时的平衡速度约为v0 = 0.016 m/s,平衡时间约为t0 = 0.013 s。 平衡距离L小于平衡速度与平衡时间的乘积,在我们的实验条件下,小于1mm,基本可认为小球进入液体后就达到了平衡速度
1.落球法测定液体的粘度
02
式中d为小球直径
式中r为小球密度,r0为液体密度。由(3)式可解出粘度h的表达式:
(3)
(4)
本实验中,小球在直径为D的玻璃管中下落,液体在各方向无限广阔的条件不满足,(4)式可修正为
(5)
落球法变温粘度测量仪
01
秒表
02
水平仪
03
开放式PID温控实验仪 温控实验仪包含水箱,水泵,加热器,控制及显 示电路等部分
粘滞系数的误差传递函数
壹
贰
小球的密度r
(7.8±0.1)×103 Kg/m3
蓖麻油的密度r0
(0.95±0.01)×103 Kg/m3
玻璃管直径D
(2.0±0.1)×10-2 m
小球直径d
(1.00±0.02)×10-3 m
太原地区重力 加速度g
用落球法测定液体的粘滞系数
用落球法测定液体的粘滞系数液体的粘滞系数又称为内摩擦系数或粘度。
是描述液体内摩擦力性质的一个重要物理量。
它表征液体反抗形变的能力,只有在液体内存在相对运动时才表现出来。
粘滞系数除了因材料而异之外还比较敏感的依赖温度,液体的粘滞系数随着温度升高而减少,气体则反之,大体上按正比例的规律增长。
研究和测定液体的粘滞系数,不仅在材料科学研究方面,而且在工程技术以及其他领域有很重要的作用。
◆【实验目的】1.学习用落球法测定液体的粘滞系数的原理和方法2.熟悉流动液体中的粘滞现象,掌握粘滞现象的一般规律3.测定蓖麻油的粘滞系数◆【仪器及用具】玻璃量筒、待测液体、游标卡尺、秒表、温度计、米尺、小钢球、读数显微镜◆【实验原理】当流体流动时,各层的流速不同,相邻两层中由于流体分子的热运动,流速慢的流层中的分子进入流速快的流层;同时,流速快的流层中的分子进入流速慢的流层,结果流速快的将变慢,流速慢的将变快。
在宏观上就相当于在两流层间产生了相互作用力,我们称这一对相互作用力为内摩擦力或者粘滞力。
流体中的这一现象称为粘滞现象。
一个半径为r的金属小球在无限广延的粘滞液体中自由下落时,它受到3个力的作用:(1)小球W=ρVg(V为小球体积;ρ为小球密度;g为重力加速度),方向向下;(2)液体作用于小球的浮力F=ρ0Vg(ρ0为液体的密度),方向向上;(3)由于附着于球面的液体与周围其他液层之间的摩擦力,即小球受到的粘滞阻力f,方向向上。
由于液体是无限广延的,而且小球的半径r很小,小球下落的速度v也很小,这由斯托克斯公式可知:f=6πrηv=3πdηv式中,d为小球直径;η为该液体在T℃时的粘滞系数,它只与液体性质和温度有关。
一般的,液体温度越高,η越小。
在CGS制中η的单位是泊(P),1P=1g/(cm•s);在SI制中,η的单位是帕斯卡•秒(Pa•s),1Pa•s=1kg/m•s=10P。
小球在液体中下落时重力ρVg和浮力ρ0Vg为恒力,而粘滞阻力f与小球下落的速度v 成正比。
实验11 落球法测量液体的粘滞系数

四、原始数据记ቤተ መጻሕፍቲ ባይዱ表格
组号________ 同组人姓名____________________ 成绩__________ 教师签字_______________
温度/°C 时间 速度 测量值 1 2 3 4 5 平均 温度每上升5°C左右测量一次,依照室温情况,测量范围可以在20°C ~55°C间任意选择,但40°C必做。
实验11 落球法测量液体的粘滞系数
专业___________________ 学号___________________ 姓名___________________
一、预习要点
1. 落球法测定粘滞系数的基本原理是什么?
2. 表示粘滞阻力的斯托克斯公式受到怎样的局限?实验中如何修正?
2. 相对误差保留二位有效数字。
七、思考题
1. 落球法为什么只适用于测量粘滞系数较高的液体?
2. 为什么落球要在圆筒中心轴线垂直下落?如果不满足该条件,会导致测量值偏大还是偏小?
福建农林大学 物理实验要求及原始数据表格
1
二、实验内容
使用变温粘度仪测定不同温度下蓖麻油的粘滞系数。
三、实验注意事项
1. 控温时间至少保证10分钟以上,从而使得样品温度与加热水温一致;
2. 调节样品管的铅直,尽量保证小球沿样品管中心下落;
3. 测量过程中,尽量避免对液体的扰动;
4. 从0刻线开始,小球每下落5cm计时一次,计时要眼明手快,保证视线与管壁刻线水平。
五、数据处理要求
1. 计算出不同温度条件下小球下落的速度及蓖麻油的粘滞系数,结果填入表格中,保留三位有效数字;
【精品】落球法测量液体的粘滞系数

【精品】落球法测量液体的粘滞系数液体的粘滞系数是指单位面积上两层流体在相对运动时所受到的剪切应力的比值,也就是黏性的量度。
在工业、生产和科学研究等领域中,液体的粘滞系数是一个非常重要的参数。
在化学、药品、民用和环保领域中,测定液体的粘滞系数会直接影响到液体的使用和品质。
通过落球法测量液体粘滞系数的方法已经被广泛应用于实际生产和实验研究中。
接下来将详细介绍落球法测量液体粘滞系数的原理、步骤和注意事项。
1.实验原理落球法是通过测量液体对采用特定顺序掉落的球的阻力大小,来推导出液体的粘滞系数,也称为斯托克斯法。
当液体中的一个球在受力平衡下自由落下时,其滑动阻力与重力相等,此时运动的速度达到稳定状态即恒速状态。
斯托克斯公式如下:F=6πηrv其中,F是球所受的阻力,η是流体粘度,r是球半径,v是球的降速度。
所以,液体粘度可以根据公式推算而得。
2.实验步骤2.1 器材准备实验器材准备如下:称量器、物理天平、万能架、滑动卡尺、测定液体、掉球器、支架灵敏度等。
2.2 实验前准备确定采用哪一种球进行实验,并注意该球的重量、半径和密度等参数,并确保球表面必须光滑。
将掉落器的底部设定为垂直于测量板并与水平面相等,并确保测量板的温度稳定。
取一定量的液体,将其转移至规定的容器中,在容器中保留足够的空间让球自由下落。
①将测定液体倒入容器中,确保液面高度超过掉落球轨道的最低位置。
注意,要等待液体温度稳定。
②仔细地沿着轨道掉落球。
③随后根据滑动卡尺得到球的降落距离。
④重复上述实验,至少取3次实验结果,以得到更为准确的粘滞系数。
3.注意事项①实验中必须确保液体温度稳定,并在测量前等待液体温度稳定。
②球表面必须光滑,以确保实验的准确性。
③实验室环境应尽可能减少干扰因素。
④在实验中,控制液体的落球速度必须稳定。
4.实验数据处理通过上述实验步骤所获得的数据,可以根据斯托克斯公式计算液体粘着力值。
如果实验数值有误差,可以通过多次实验,并对数据进行平均数计算,以获得更准确的结果。
实验一 落球法测液体的粘滞系数

第三章 基础性实验实验一 用落球法测量液体的黏滞系数【实验目的】1. 根据斯托克斯公式用落球法测定液体的黏滞系数。
2. 了解斯托克斯公式的修正方法。
【实验仪器】液体黏滞系数仪,米尺,游标卡尺,螺旋测微器,秒表,温度计,小钢球,比重计,镊子,蓖麻油,天平。
【实验原理】当半径为r 的光滑圆球以速度v 在液体中运动时,小球受到与运动方向相反的摩擦阻力的作用,这个阻力称为黏滞(阻)力。
黏滞力并不是小球和液体之间的摩擦力,而是由于黏附在小球表面的液层与相邻液层之间的内摩擦而产生的。
若小球的半径很小,液体是无限广延且黏性较大,如速度不大,在液体中不产生涡流的情况下,根据斯托克斯定律,小球在液体中受到的黏性力F 为:rv F πη6= (1-1)式子中r 为小球的半径,v 为小球的运动速度,η为液体的黏滞系数。
本实验采用落球法测液体的黏滞系数。
一质量为m 的小球落入液体后受到三个力的作用,即重力mg 、浮力gV 0ρ(0ρ为液体的密度,V 为小球的体积)和黏滞力F 。
在小球刚进入液体时,由于重力大于黏滞力和浮力之和,所以小球作加速运动。
随着小球运动速度的增加,黏滞力也增加,设当速度增加到0v 时,小球受到的合外力为零,此时有:gV rv mg 006ρπη+= (1-2)以后小球将以速度0v 匀速下降,此速度称为终极速度。
将小球的体积34()32d Vπ=代入式(1-2)可得: 200()18gd v ρρη-= (1-3) 式(1-3)是奥西斯—果尔斯公式的零级近似,适用于小球在无限广延的液体中运动的情况。
而在本实验中,小球是在半径为R 的装有液体的圆筒内运动的,这时测得的速度v 和理想条件下的速度0v 之间存在如下关系:)3.31)(4.21(0h r R r v v ++= (1-4) 式中,/2rd =,R 为盛液体圆筒的内半径,h 为液体的深度,将式(1-4)代入式(1-3)中,得出: )3.31)(4.21(18)(20hr R r gd ++-='ρρη (1-5) 实验时,先由式(1-3)求出近似值,再用式(1-5)求出经修正的值η'。
《医用物理》落球法测定液体的粘滞系数实验

1υπρηr g V m 6)(排-=2d r =tl =υ实验三落球法测定液体的粘滞系数【实验目的】(1)掌握用落球法测定液体粘滞系数的原理和方法。
(2)学会使用电子天平,并会称量固体、液体密度。
(3)用落球法实验仪测定液体实时温度下的粘滞系数。
【实验仪器】落球法粘滞系数测定仪,激光光电计时仪,电子天平,砝码,2mm 小钢球,蓖麻油,米尺,千分尺,电子秒表,电子温度计等。
【实验原理】当金属小球在粘滞性液体中铅直下落时,由于附着于球面的液层与周围其他液层之间存在着相对运动,因此小球受到粘滞阻力,它的大小与小球下落的速度有关。
如果液体无限深广,在小球下落速度υ较小的情况下斯托克斯给出:6f r πηυ=(1)式中:r 是小球的半径,υ是小球下落的速度;η为液体的粘度,单位是s Pa ⋅。
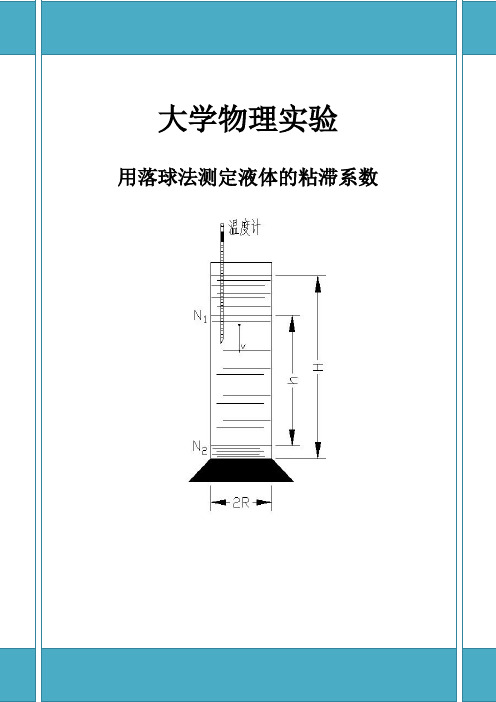
如图(一)所示,小球在液体中下落时受到三个竖直方向的力:小球的重力G =mg (m 为小球的质量);液体作用于小球的浮力F =排gV ρ(V 是小球的体积,ρ是液体的密度);粘滞阻力6f r πηυ=(其方向与小球运动方向相反);D 为量筒直径,H 为量筒中液体高度。
小球开始下落时,由于速度尚小,所以阻力f 也不大;但随着下落速度的增大,阻力也随之增大。
最后三个力达到平衡,即r gV mg πηυρ6+=排,于是,小球做匀速直线运动。
由上式可得:令小球的直径为d ,并用,代入上式得ρπ'=36d m2)6.11)(4.21(18)(2HdD d l tgd ++-'=ρρηlt gd 18)(2ρρη-'=ltgd 18)(2ρρη-'=)6.11)(4.21(1Hd D d ++(2)式中,ρ'为小钢球的密度,l 为小球匀速下落的距离(即两激光束之间的距离),t 为小球下落l 距离所用的时间。
实验时,待测液体盛于量筒中,如图(一)所示,不能满足无限深广的条件。
实验证明,若小球沿筒的中心轴线下降,式(2)需要做如下修正方能符合实际情况:•式中,D 为量筒直径,H 为量筒中液体高度。
落球法测量液体粘滞系数

1.用酒精将小钢球洗净,擦干后用读数显微镜测小球的直径,读数填入表1中并求直径d的平均值。
2.用天平测这些小球的总质量,再除以小球粒数得小球的平均质量m,填入表2中。测后将小球浸在和待测液相同的油中待用。
3.用游标卡尺分别测粘滞系数测量仪上每个圆筒的不同方位内径取平均值D及筒壁上两条刻度线的间距L。填入表2中。
(2)
实验时测定m,ρ,V,r,vT等量,即可计算η值。vT值测量方法:设小球匀速下落时,在时间t内下落距离为L,则
斯托克斯公式应用的条件是小球在无限宽广、均匀的液体中下落,而实验时,液体总要盛放在一定的容器内,其边界不可能是无限宽广的。即小球不可避免受到了容器壁及液体有限深度的影响。下面来介绍两种对容器影响进行修正的方法:
关键词
液体liquid,速度velocity,摩擦系数friction coefficient,密度density,
质量quality,显微镜microscope,直径diameter,磁铁magnet。
实验目的
1.利用斯托克斯公式,用落球法测液体的粘滞系数。
2.巩固使用基本测量仪器的技能。
实验原理
半径为r的光滑小球,以速度v在均匀的无限宽广的液体中运动时,若小球运动速度不大,球也很小,在液体中不产生涡流时,斯托克斯(G.G.Stokes)指出,球在液体中受到的粘滞阻力为
(1)
式(1)称为斯托克斯公式。其中η是液体的粘滞系数;v和r分别为小球的运动速度及半径。需要指出,阻力f不是由小球和液体之间的摩擦所引起,而是由于粘滞附在小球表面的一层液体与不随球运动的流体间的摩擦引起的,因此η也称为液体的内摩擦系数。由式(1)可知η的量纲为[ML-1T-1],在国际单位制中,其单位为“帕斯卡·秒”(Pa·s),C.G.S制中的单位为“帕”(P),1Pa·s=10P。液体的粘滞系数随温度的变化有明显的差异,随温度的升高而减少,气体的粘滞系数则相反。
用落球法测定液体的粘滞系数

1 3 d ( 0 )g=3 dv0 6
粘滞系数
( 0 ) gd 2 ( 0 ) gd 2 = 18v0 18v(1 2.4d / D)
式中:钢球的密度 蓖麻油的密度 重力加速度
7.87 10 Kg m
3
-3
0 (0.96 ~ 0.97) 10 Kg m
L vi ti
2 i
(m ) s
-1
( 0 ) gd i 18vi (1 2.4di / D)
3.测量结果
(P ) a s (P ) a s
相对误差
1 5 i 5 i 1 标 100%
标
0
(标:T C时的粘滞系数)
3
-3
g=9.797m -2 s
圆形容器的内直径。 小球的直径。 小球下落时的速度。
D: d:
v:
【实验内容及步骤】
1.数据记录表格
直径
mm 1
D
2
3
x
ti / s vi / ms1 i / Pa s di D
d1 d2 d3 d4 d5
2。数据处理
各小球下落的速度: 各小球计算的粘滞系数:
:
dv F S dz 粘滞系数(单位 P a s
)
2.运动小球所受的粘滞力
f 3 dv
小球在液体中所受的合力为:
-——斯托克斯公式
F mg B f Vg 0 Vg 3 dv
当
F 0时,小球以速度 v0
匀速下落,即:
Vg 0 Vg=3 dv0
实验4.12
【实验目的】
用落球法测定液体的粘滞系数
1.观察小球在液体中的下落过程,了解液体的内摩擦现象; 2.掌握用落球法测定液体粘滞系数的原理和方法; 3.掌握秒表、密度计等基本测量仪器的使用方法。 【实验仪器】 游标卡尺、螺旋测微器、米尺、秒表、小球、温度计。 【实验原理】 1.粘滞定律
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验报告
实验题目: 落球法测定液体的黏 度
实验目的: 本实验的目的是通过用落球法测量油的粘度,学习并掌握测量的原理和方
法。
实验原理:
1、 斯托克斯公式 粘滞阻力是液体密度、温度和运动状态的函数。
如果小球在液体中下落时的速度 v 很小,球的半径 r 也很小,且液体可以看成在各方向上都是无限广阔的
F 6 vr ( 1)
η 是液体的粘度, SI 制中,η 的单位是 Pa s
2、 雷诺数的影响
雷诺数 R e 来表征液体运动状态的稳定性。
设液体在圆形截面的管中的流速为 v ,液 体的密度为 ρ0,粘度为 η,圆管的直径为 2r ,则
奥西思 - 果尔斯公式反映出了液体运动状态对斯托克斯公式的影响:
F 6 rv (1 3 R e 19 R e 2 ...) 16 e 1080 e 2
式中 3R e 项和 19R e 项可以看作斯托克斯公式的第一和第二修正项 16 1080 随着 R e 的增大,高次修正项的影响变大。
因 F 是很难测定的 ,利用小球匀速下落时重力、 浮力 、粘滞阻力合力等于零 ,由式(4)R e 2v r 2)
3)
3、 容器壁的影响
考虑到容器壁的影响,修正公式为
r3 3.3 )(1 R e h 16 F 6 rv (1 2.4 1080 R e ...) 4)
4、
η 的表示
...) ( 5)
实验内容 :
1、利用三个橡皮筋在靠近量筒下部的地方, 分出两个长度相等的区域, 利用秒表
测 量小球通过两段区域的时间, 调整橡皮筋的位置, 并保持两段区域等长, 寻找两 次测量时间相等的区域,测出两段区域总长度 l 。
2、选用大、中、小三种不同直径的小球进行实验。
3、用螺旋测微器测定 6 个同类小球的直径,取平均值并计算小球直径的误差。
4、将一个小球在量筒中央尽量接近液面处轻轻投下,使其进入液面时初速度为零,
5、分别测出 6 个小球通过匀速下降区 l 的时间 t ,然后求出小球匀速下降的速度。
6、用相应的仪器测出 R 、h 和 ρ0,各测量三次及液体的温度 T ,温度 T 应取实验开
始时的温度和实验结束时的温度的平均值。
应用式( 7)计算 η 0。
7、计算雷诺数 R e ,并根据雷诺数的大小,进行一级或二级修正。
4 r 3( 0)g 6 rv(1 2.4 r )(1 3.3r )(1 3 R e 19 R e 2 3
0 R h 16 e 1080 e 0 )gd 2
η 1 ( η 18 d d 3 19 2 18v(1 2.4 )(1 3.3 )(1 R e R e 2 ...) 2R 2h 16 1080 6)
a. 当 R e <时,可以取零级解,则式( 6)就成为
0 )gd 2 1(
18 v(1 2.42d R )(1 3.32d h ) 7)
即为小球直径和速度都很小时,粘度 η 的零级近似值
时,可以取一级近似解,式( 6)就成为
它可以表示成为零级近似解的函数:
0 3 dv 0 0 16 0 还必须考虑二级修正,则式( 6)变成
c.当 R e >时, 2 21 1[1 1 270 19 (dv 0 )2]
1 8)
9)
...) ( 5)数据记录处理
1、基本数据:
钢球密度 =7. 8g/ cm 3 油的密度 =0. 9615g/ cm 3 重力加速度g=979.47cm/ s 2
2、量筒参数:
1
液面高度 h/cm
匀速下降区 l/cm
量筒直径 D/cm 计算置信度 P=下的不确定度, t=,
量筒直径 D=( ) 3、三种小球直径 d 及下
落时间 t :
d 1/mm
t 1/s
D 2/mm
t 2/s
D 3/mm
t 3/s
(1) 计算直径在置信度 P=下的不确定度, t=, 仪 =0.01 mm ,
C=3 a. d 1 =2.987 mm,U d (t u A )2 ( 仪)2 = 0.003 mm, d 1
= d 2 =2.358
(t u A )2 ( 仪 )2 = 0.003 mm, d 3= 计算小球下落速度 :
mm,U d 2 (t u A 2 )2 ( 仪 )2 = 0.003 mm, d 2= d 3 =1.556
初 始温度 T=o C 实验后温度 T=o C
米尺 =0.05 cm , C =3, 卡尺 =0.002 cm , C 3
a. h =29.92cm U h (t u A h )2 ( C 米尺)2 = 0.02 cm
b. c. 液面高度 h= l =12.81cm U l 匀速下降区 l= ( D =8.794cm U D )cm
(t u A l )2 ( C 米尺)2 =0.02 cm
)cm
(t u A D )2 ( C 卡尺)2 =0.004 cm
cm
d 1 mm,U d 3
计算液体黏度:
a. t 1=t 1 = l t 1 0.0393m/s
b. t 2=t 2 v 2 l t 2 0.0247m/s
c. t 3=t 3 = v 3 t 3 0.0111m/s
a. 第一种球 : 1 18 0 )gd 2 d d = Pa · s, v(1 2.42d R )(1 3.32d h ) R e 2v r 2v r =, 因为 <Re <进行一级修正, 0 3 0 16dv 0= Pa ·s, R e 2v r 0
b. 故利用第一种球测得的黏度 第二种球 : η= Pa ·s. 1 ( 0)gd 2 18 d d v(1 2.4 )(1 3.3 ) 2R 2h = Pa ·s, R e 2v r 2v r =, 因为<Re <进行 一级修 正, 0 3 2v r 0 136dv 0= Pa ·s, R e 2v 0r
c. 故利用第二种球测 得的黏度 η = Pa ·s. 第三种球 : 1 ( 0)gd 2 18v(1 2.42d R )(1 3.32d h
) R e 2v r
=, 因为 Re<, 取零级解,
故利用第三种球测得的黏度η= Pa·s
最终结果:
第一种球测得黏度:η= Pa ·s
第二种球测得黏度:η= Pa ·s 第
三种球测得黏度:η= Pa·s
思考题:
1、假设在水下发射直径为1m的球形水雷,速度为10m/s,水温为10℃, 1.3 10 4Pa
s ,试求水雷附近海水的雷诺数。
答:海水密度近似等于 1.02 g/ cm3, 则R e2v r7.7 107
2、设容器内N1 和N2 之间为匀速下降区,那么对于同样材质但直径较大的球,该区间
也是匀速下降区吗?反过来呢?
答: 不一定,因为半径不同,则球的重力G,所受的浮力 F 和粘滞阻力 f 都会有所不同,达到受力平衡G=F+f 的时间和位移量也不一定不同,因此未必也是打球的匀速下降区。
反过来也未必成立,影响粘滞阻力 f 的因素很多,综合作用也可能使不同半径的球受力平衡G=F+f 的时间和位移量相同,有同样的匀速下降区。
