圆锥曲线综合复习讲义

合集下载

圆锥曲线综合复习讲义

圆锥曲线综合复习讲义【基础概念填空】椭圆1．椭圆的定义：平面内与两定点F 1 ，F 2的距离的和__________________的点的轨迹叫做椭圆。

这两个定点叫做椭圆的_________ , 两焦点之间的距离叫做椭圆的________.2.椭圆的标准方程：椭圆)0b a (1by a x 2222>>=+的中心在______，焦点在_______轴上,焦点的坐标分别是是F 1 ___________，F 2 ____________；椭圆)0b a (1bx a y 2222>>=+的中心在______，焦点在_______轴上,焦点的坐标分别是F 1 ____________，F 2 ____________.3.几个概念：椭圆与对称轴的交点，叫作椭圆的______.a 和b 分别叫做椭圆的______长和______长。

椭圆的焦距是_________. a,b,c 的关系式是_________________。

椭圆的________与________的比称为椭圆的离心率，记作e=_____,e 的范围是_________. 双曲线 1．双曲线的定义：平面内与两定点F 1 ，F 2的距离的差_____________________的点的轨迹叫做双曲线。

这两个定点叫做双曲线的_________ , 两焦点之间的距离叫做双曲线的________.2.双曲线的标准方程：双曲线0)b 0,1(a by a x 2222>>=-的中心在______，焦点在_______轴上,焦点的坐标是____________；顶点坐标是______________,渐近线方程是_____________.双曲线0)b 0,1(a bx a y 2222>>=-的中心在______，焦点在_______轴上,焦点的坐标是____________；顶点坐标是______________,渐近线方程是_____________. 3.几个概念：双曲线与对称轴的交点，叫作双曲线的_____.a 和b 分别叫做双曲线的________长和_______长。

圆锥曲线总复习——上课内容

圆锥曲线总复习一、知识结构 1.方程的曲线在平面直角坐标系中，如果某曲线C(看作适合某种条件的点的集合或轨迹 )上的点与一个二元方程f(x,y)=0的实数解建立了如下的关系：(1)曲线上的点的坐标都是这个方程的解；(2)以这个方程的解为坐标的点都是曲线上的点.那么这个方程叫做曲线的方程；这条曲线叫做方程的曲线.点与曲线的关系若曲线C 的方程是f(x,y)=0，则点P 0(x 0,y 0)在曲线C 上⇔f(x 0,y 0)=0；点P 0(x 0,y 0)不在曲线C 上⇔f(x 0,y 0)≠0两条曲线的交点若曲线C 1，C 2的方程分别为f 1(x,y)=0,f 2(x,y)=0,则 f 1(x 0,y 0)=0 点P 0(x 0,y 0)是C 1，C 2的交点⇔f 2(x 0,y 0) =0方程组有n 个不同的实数解，两条曲线就有n 个不同的交点；方程组没有实数解，曲线就没有交点. 2.圆圆的定义：点集：｛M ｜｜OM ｜=r ｝，其中定点O 为圆心，定长r 为半径. 圆的方程： (1)标准方程圆心在c(a,b)，半径为r 的圆方程是(x-a)2+(y-b)2=r 2 圆心在坐标原点，半径为r 的圆方程是x 2+y 2=r 2(2)一般方程当D 2+E 2-4F ＞0时，一元二次方程x 2+y 2+Dx+Ey+F=0 叫做圆的一般方程，圆心为(-2D ,-2E ），半径是24F-E D 22+.配方，将方程x 2+y 2+Dx+Ey+F=0化为(x+2D )2+(y+2E )2=44F-E D 22+当D 2+E 2-4F=0时，方程表示一个点(-2D ,-2E );当D 2+E 2-4F ＜0时，方程不表示任何图形.点与圆的位置关系已知圆心C(a,b),半径为r,点M 的坐标为(x 0,y 0)，则｜MC ｜＜r ⇔点M 在圆C 内，｜MC ｜=r ⇔点M 在圆C 上，｜MC ｜＞r ⇔点M 在圆C 内，其中｜MC ｜=2020b)-(y a)-(x +. (3)直线和圆的位置关系①直线和圆有相交、相切、相离三种位置关系直线与圆相交⇔有两个公共点直线与圆相切⇔有一个公共点直线与圆相离⇔没有公共点 ②直线和圆的位置关系的判定 (i)判别式法(ii)利用圆心C(a,b)到直线Ax+By+C=0的距离d=22C Bb Aa BA +++与半径r 的大小关系来判定.3.椭圆、双曲线和抛物线基本知识椭圆双曲线抛物线轨迹条件{M ｜｜MF 1｜+｜MF 2｜=2a,｜F 1F 2｜＜2a} {M ｜｜MF 1｜-｜MF 2｜. =±2a,｜F 2F 2｜＞2a}. {M ｜｜MF ｜=点M 到直线l 的距离}. 圆形标准方程22ax +22by =1(a ＞b ＞0)22ax -22by =1(a ＞0,b ＞0)y 2=2px(p ＞0)顶点A 1(-a,0),A 2(a,0);B 1(0,-b),B 2(0,b)A 1(0,-a),A 2(0,a) O(0,0)轴对称轴x=0,y=0长轴长：2a 短轴长：2b对称轴x=0,y=0 实轴长：2a 虚轴长：2b对称轴y=0焦点F 1(-c,0),F 2(c,0) 焦点在长轴上 F 1(-c,0),F 2(c,0) 焦点在实轴上 F(2P ，0)焦点对称轴上焦距｜F 1F 2｜=2c ，c=b2-a2｜F 1F 2｜=2c, c=b2a2+准线x=±ca2x=±ca2x=-2p准线与焦点位于顶点曲线性质准线垂直于长轴，且在椭圆外.准线垂直于实轴，且在两顶点的内侧.两侧，且到顶点的距离相等.离心率e=ac ,0＜e ＜1e=ac ,e ＞1e=14.圆锥曲线的统一定义平面内的动点P(x,y)到一个定点F(c,0)的距离与到不通过这个定点的一条定直线l 的距离之比是一个常数e(e ＞0),则动点的轨迹叫做圆锥曲线.其中定点F(c,0)称为焦点，定直线l 称为准线，正常数e 称为离心率.当0＜e ＜1时，轨迹为椭圆，当e=1时，轨迹为抛物线当e ＞1时，轨迹为双曲线 5.坐标变换坐标变换在解析几何中，把坐标系的变换(如改变坐标系原点的位置或坐标轴的方向)叫做坐标变换.实施坐标变换时，点的位置，曲线的形状、大小、位置都不改变，仅仅只改变点的坐标与曲线的方程.坐标轴的平移坐标轴的方向和长度单位不改变，只改变原点的位置，这种坐标系的变换叫做坐标轴的平移，简称移轴.坐标轴的平移公式设平面内任意一点M ，它在原坐标系xOy 中的坐标是9x,y)，在新坐标系x ′O′y′中的坐标是(x′,y′).设新坐标系的原点O′在原坐标系xOy 中的坐标是(h,k)，则x=x′+h x′=x -h (1) 或(2)y=y′+k y′=y -k 公式(1)或(2)叫做平移(或移轴)公式. 中心或顶点在(h,k)的圆锥曲线方程见下表.方程焦点焦线对称轴椭圆22h)-(x a+22k)-(y b=1(±c+h,k)x=±c a2+hx=h y=k22h)-(x b+22k)-(y a=1 (h,±c+k)y=±ca2+kx=h y=k双曲线22h)-(x a-22k)-(y b=1(±c+h,k)=±c a2+kx=h y=k22k)-(y a-22h)-(x b=1(h,±c+h) y=±ca2+kx=h y=k 抛物线 (y-k)2=2p(x-h)(2p +h,k) x=-2p +hy=k(y-k)2=-2p(x-h) (-2p +h,k)x=2p +hy=k (x-h)2=2p(y-k) (h, 2p +k)y=-2p+kx=h (x-h)2=-2p(y-k)(h,- 2p+k)y=2p +kx=h二、知识点、能力点提示(一)曲线和方程，由已知条件列出曲线的方程，曲线的交点说明在求曲线方程之前必须建立坐标系，然后根据条件列出等式进行化简 .特别是在求出方程后要考虑化简的过程是否是同解变形，是否满足已知条件，只有这样求出的曲线方程才能准确无误.另外，要求会判断曲线间有无交点，会求曲线的交点坐标.求指定的圆锥曲线的方程是高考命题的重点，主要考查识图、画图、数形结合、等价转化、分类讨论、逻辑推理、合理运算及创新思维能力，解决好这类问题，除要求熟练掌握好圆锥曲线的定义、性质外，命题人还常常将它与对称问题、弦长问题、最值问题等综合在一起命制难度较大的题，解决这类问题常用定义法和待定系数法.一般求已知曲线类型的曲线方程问题，可采用“先定形，后定式，再定量”的步骤. 定形——指的是二次曲线的焦点位置与对称轴的位置.定式——根据“形”设方程的形式，注意曲线系方程的应用，如当椭圆的焦点不确定在哪个坐标轴上时，可设方程为mx 2+ny 2=1(m ＞0,n ＞0).定量——由题设中的条件找到“式”中特定系数的等量关系，通过解方程得到量的大小. 直线与圆锥曲线联系在一起的综合题在高考中多以高档题、压轴题出现，主要涉及位置关系的判定，弦长问题、最值问题、对称问题、轨迹问题等.突出考查了数形结合、分类讨论、函数与方程、等价转化等数学思想方法，要求考生分析问题和解决问题的能力、计算能力较高，起到了拉开考生“档次”，有利于选拔的功能.1.直线与圆锥曲线有无公共点或有几个公共点的问题，实际上是研究它们的方程组成的方程是否有实数解成实数解的个数问题，此时要注意用好分类讨论和数形结合的思想方法.2.当直线与圆锥曲线相交时：涉及弦长问题，常用“韦达定理法”设而不求计算弦长(即应用弦长公式)；涉及弦长的中点问题，常用“差分法”设而不求，将弦所在直线的斜率、弦的中点坐标联系起来，相互转化.同时还应充分挖掘题目的隐含条件，寻找量与量间的关系灵活转化，往往就能事半功倍.例题1、已知圆C 1的方程为()()3201222=-+-y x ，椭圆C 2的方程为12222=+by ax ()a b >>0，C 2的离心率为22，如果C 1与C 2相交于A 、B 两点，且线段AB 恰为圆C 1的直径，求直线AB 的方程和椭圆C 2的方程。

高三文科数学圆锥曲线综合复习讲义

高三文科数学圆锥曲线综合复习讲义一、基础知识【理解去记】1.椭圆的定义，第一定义：平面上到两个定点的距离之和等于定长(大于两个定点之间的距离)的点的轨迹，即 |PF i |+|PF 2|=2a (2a>|F i F 2|=2c).第二定义：平面上到一个定点的距离与到一条定直线的距离之比为同一个常数 e(0<e<1)的点的轨迹(其中定点不在定直线上)，即|PF | e (0<e<1).d2 .椭圆的方程，如果以椭圆的中心为原点，焦点所在的直线为坐标轴建立坐标系，由定义可求得它的标准方程，若焦点在x2 2若焦点在y 轴上，列标准方程为：上21(a>b>0)。

a ba 称半长轴长，b 称半短轴长，c 称为半焦距，长轴端点、短轴端点、两个焦点的坐标分别为(土a, 0 ), (0, ± b), ( ±ce 称为离心率，且 e 一，由c 2+b 2=a 2知0<e<1.a椭圆有两条对称轴，分别是长轴、短轴。

2y牙1(a>b>0), F 1 (-c, 0), F 2(c, 0)是它的两焦点。

若 P(x, y)是椭圆上的任意一b1)过椭圆上一点 P(x o , y o )的切线方程为：一字 1 ；a b2)斜率为k 的切线方程为y kx 、a 2k 2 b 2 ； 3)过焦点F 2(c, 0)倾斜角为B 的弦的长为l2ab 2 l 2 2 2。

a c cos6 •双曲线的定义，第一定义：满足 ||PF i |-|PF 2||=2a(2a<2c=|F 1F 2|, a>0)的点 P 的轨迹；第二定义：到定点的距离与到定直线距离之比为常数 e(>｛的点的轨迹。

7.双曲线的方程：中心在原点，焦点在x 轴上的双曲线方程为 3 •椭圆中的相关概念，对于中心在原点，焦点在x 轴上的椭圆:2 x2ab 24 .椭圆的焦半径公式：对于椭圆点，则 |PR|=a+ex, |PF 2|=a-ex. 5.补充知识点：几个常用结论：2x~2a2 2x y——12 . 2a b第五步：把所要解决的问题转化为X1+X2、X1X2，然后代入、化简。

圆锥曲线综合.板块八.圆锥曲线综合问题.教师版普通高中数学复习讲义Word版

【例1】 P 是抛物线22(0)y px p =>上的点，F 是抛物线的焦点，则以||PF 为直径的圆与y 轴位置关系为（）Ａ．相交Ｂ．相离Ｃ．相切Ｄ．不确定【考点】圆锥曲线综合问题【难度】3星【题型】选择【关键字】无【解析】利用抛物线的定义，数形结合，如图，过P 作PA 垂直于准线于A ，交y 轴于B ，设PF 的中点为C ，则C 到y 轴的距离为1111||(||||)(||||)||||2222CH OF BP AB BP AP PF =+=+==，即以||PF 为直径的圆C 与y 轴相切．【答案】C ；【例2】定点(10)N ，，动点A 、B 分别在图中抛物线24y x =及椭圆22143x y +=的实线部分上运动，且AB ∥x 轴，则NAB ∆的周长l 的取值范围是________．A ．223⎛⎫ ⎪⎝⎭，B ．1043⎛⎫⎪⎝⎭，典例分析板块八.圆锥曲线综合问题C ．51416⎛⎫ ⎪⎝⎭， D ．(24)，【考点】圆锥曲线综合问题【难度】3星【题型】选择【关键字】无【解析】易知N 为椭圆的右焦点，且为抛物线的焦点，记抛物线的准线为m ：1x =-；椭圆的右准线n ：4x =；过A 作m 的垂线，垂足为A '，过B 作n 的垂线，垂足为B '，则 AN AA '=，12BN e BB =='，于是12BN BB '=， 11114(1)52222l AA AB BB A B BB BB BB '''''''=++=-=---=-，故只需求出BB '的取值范围即可，显然当B 点为椭圆的长轴的右端点时，有min 422BB '=-=，当B 为椭圆与抛物线的一个交点，即23B x =时，有m a x 210433BB '=-=，但此时都不再构成三角形，故取不到最值，从而有11011055242323l ⎛⎫⎛⎫∈-⨯-⨯= ⎪ ⎪⎝⎭⎝⎭，，．【答案】B ；【例3】已知动圆C 经过点(0,1)F ，并且与直线1y =-相切，若直线34200x y -+=与圆C 有公共点，则圆C 的面积（）A ．有最大值为πB ．有最小值为πC ．有最大值为4πD ．有最小值为4π【考点】圆锥曲线综合问题【难度】4星【题型】选择【关键字】2010年，海淀一模【解析】由抛物线的定义知圆心C 的轨迹为抛物线24x y =，设00(,)C x y ，则204x y =，由【例4】已知P 是抛物线22y x =上的一个动点，过P 作圆22(3)1x y -+=的切线，切点分别为M 、N ，则MN 的最小值是__________．【考点】圆锥曲线综合问题【难度】3星【题型】填空【关键字】2009年，江南十校联合素质测试【解析】记点(3,0)A ，由A 为该圆的圆心．MN 的最小值对应MAN ∠的最小值，而1cos MAP PA =∠，12MAP MAN =∠∠，故PA 取最小值时有MN 的最小值．记00(,)P x y ，则22222000000(3)692(2)5P A x y x x x x =-+=-++=-+，故当02x =时，有min PA =，由,AM PM AP MN ⊥⊥知，此时2MN ==；【例5】已知圆K 过定点(0)(0)A a a >，，圆心K 在抛物线C ：22y ax =上运动，MN 为圆K 在y 轴上截得的弦．⑴试问MN 的长是否随圆心K 的运动而变化？⑵当||OA 是||OM 与||ON 的等差中项时，抛物线C 的准线与圆K 有怎样的位置关系？【考点】圆锥曲线综合问题【难度】4星【题型】解答【关键字】无【解析】⑴设圆心00()K x y ，，且2002y ax =，圆K 的半径||R AK ==∴||2MN a =为定值， ∴弦MN 的长不随圆心K 的运动而变化．⑵设12(0)(0)M y N y ，，，在圆K ：2222000()()x x y y x a -+-=+上，令0x =，得2220020y y y y a -+-=， ∴22120y y y a =-．∵||OA 是||OM 与||ON 的等差中项， ∴12||||||||2||2OM ON y y OA a +=+==．又由⑴，12||||2MN y y a =-=， ∴1212||||||y y y y +=-，∴120≤y y ，因此2200≤y a -，即2020≤ax a -．∴002≤≤ax ．圆心K 到抛物线准线距离02≤ad x a =+，而圆K 半径R a ．且上两式不能同时取等号，故圆K 必与准线相交．【答案】⑴弦MN 的长不随圆心K 的运动而变化．⑵圆K 必与准线相交．【例6】在平面直角坐标系xOy 中，已知圆心在第二象限、半径为C 与直线y x =相切于坐标原点O ．椭圆22219x y a +=与圆C 的一个交点到椭圆两焦点的距离之和为10．⑴求圆C 的方程；⑵试探究圆C 上是否存在异于原点的点Q ，使Q 到椭圆右焦点F 的距离等于线段OF 的长．若存在，请求出点Q 的坐标；若不存在，请说明理由．【考点】圆锥曲线综合问题【难度】4星【题型】解答【关键字】2007年，广东高考【解析】⑴设圆心坐标为()，m n (00)，m n <>，则该圆的方程为22()()8x m y n -+-=已知该圆与直线y x =相切，那么圆心到该直线的距离等于圆的半径，则=即4m n -= ① 又圆与直线切于原点，故10m n -=-- ② 联立方程①和②组成方程组解得22m n =-⎧⎨=⎩故圆的方程为22(2)(2)8x y ++-=．⑵210a =，∴225a =，则椭圆的方程为221259x y +=，其焦距4c ==，右焦点为(40)，，那么4OF =．要探求是否存在异于原点的点Q ，使得该点到右焦点F 的距离等于OF 的长度4，我们可以转化为探求以右焦点F 为圆心，半径为4的圆22(4)16x y -+=与⑴所求的圆的交点数．通过联立两圆的方程解得45x =，125y =．即存在异于原点的点41255，Q ⎛⎫⎪⎝⎭，使得该点到右焦点F 的距离等于OF 的长．或通过圆心距小于半径和得到有两个交点，故Q 存在，且Q 点与原点关于两圆的圆心连线1(4)3y x =--对称，从而求得它的坐标．【答案】⑴22(2)(2)8x y ++-=．⑵存在异于原点的点41255，Q ⎛⎫⎪⎝⎭，使得该点到右焦点F 的距离等于OF 的长．【例7】设0b >，椭圆方程为222212x y b b+=，抛物线方程为28()x y b =-．如图所示，过点(02)F b +，作x 轴的平行线，与抛物线在第一象限的交点为G ．已知抛物线在点G 的切线经过椭圆的右焦点1F ．⑴求满足条件的椭圆方程和抛物线方程；⑵设A ，B 分别是椭圆长轴的左、右端点，试探究在抛物线上是否存在点P ，使得ABP ∆为直角三角形？若存在，请指出共有几个这样的点？并说明理由（不必具体求出这些点的坐标）．【考点】圆锥曲线综合问题【难度】4星【题型】解答【关键字】2008年，广东高考【解析】⑴在抛物线方程28()x y b =-中令2y b =+，解得216x =，又G 为第一象限内的点，故G 点坐标为(42)b +，，又10)F ，即1(0)F b ，，抛物线在G 点处的切线的斜率为4|14x xy ='==，故1214GF b k b --==--，解得1b =，故椭圆方程为2212x y +=，抛物线方程为28(1)x y =-．⑵∵过A 作x 轴的垂线与抛物线只有一个交点P ，∴以PAB ∠为直角的Rt ABP ∆只有一个；同理以PBA ∠为直角的Rt ABP ∆只有一个；若以APB ∠为直角，则P 点必在以AB 为直径的圆上，当且仅当P 点为以AB 为直径的圆与此抛物线的交点．以AB 为直径的圆的方程为222x y +=，联立22228(1)x y x y ⎧+=⎪⎨=-⎪⎩，消去x 得28100y y +-=，解得4y =-±1，故负根舍去，41>，故此根满足，圆与抛物线都关于y 轴对称，故此纵坐标对应两个x ，即此方程组有两组解，对应满足条件的P 点有两个．综上所述抛物线上共存在4个点使ABP ∆为直角三角形．【答案】⑴椭圆方程为2212x y +=，抛物线方程为28(1)x y =-．⑵抛物线上共存在4个点使ABP ∆为直角三角形．【例8】已知：双曲线的顶点坐标()01，，()01-，，离心率e 2=，又抛物线()2:20C x py p =>的焦点与双曲线一个焦点重合．⑴求抛物线C 的方程；⑵已知()0P m ，、()0Q m -，()0m ≠是y 轴上的两点，过P 做直线与抛物线C 交于A 、B 两点，试证：直线QA 、QB 与y 轴所成的锐角相等．⑶在⑵的前提下，若直线AB 的斜率为1，问ABQ △的面积是否有最大值?若有，求出最大值．若没有，说明理由．【考点】圆锥曲线综合问题【难度】4星【题型】解答【关键字】无【解析】⑴ 由题意，设双曲线方程为22221y x a b -=，则1a =，2ca=解得1a =，2c =所以双曲线两焦点为()02±，，即22p=，故4p =，∴抛物线C 的方程为28x y =；⑵ 设直线AB 方程为y kx m =+代入抛物线C 的方程为28x y =得： ()2880*x kx m --=，264320k m ∆=+>，设()11A x y ，，()22B x y ，，则128x x k +=，128x x m =-要证直线QA 、QB 与y 轴所成的锐角相等，只证明0QA QB k k +=，∵()221212121212188088QA QBx m x my m y m m k k x x x x x x m ++++⎛⎫+=+=+=++= ⎪-⎝⎭，所以原命题成立．⑶ 由⑵知，1k =时，()*化为2880x x m --=，由64320m ∆=+>得2m >-，AB =Q 到AB的距离为d =，12ABQ S AB d ==△令()3224f m m m =+，则()2'68f m m m =+，令()2'680f m m m =+>得：0m >或43m <-，∴()3224f m m m =+在423⎛⎫-- ⎪⎝⎭，和()0+∞，上都是增函数，在43⎛⎫-+∞ ⎪⎝⎭，是减函数，所以()3224f m m m =+无最大值．【答案】⑴ 抛物线C 的方程为28x y =；⑵ 设直线AB 方程为y kx m =+代入抛物线C 的方程为28x y =得： ()2880*x kx m --=，264320k m ∆=+>，设()11A x y ，，()22B x y ，，则128x x k +=，128x x m =-要证直线QA 、QB 与y 轴所成的锐角相等，只证明0QA QB k k +=，∵()221212121212188088QA QBx m x my m y m m k k x x x x x x m ++++⎛⎫+=+=+=++= ⎪-⎝⎭，所以原命题成立．⑶ ()3224f m m m =+无最大值．【例9】如图，已知抛物线2:E y x =与圆()222:4M x y r -+=()0r >相交于A 、B 、C 、D 四个点．⑴求r 的取值范围；⑵当四边形ABCD 的面积最大时，求对角线AC 、BD 的交点P 的坐标．【考点】圆锥曲线综合问题【难度】4星【题型】解答【关键字】2009年，全国高考【解析】⑴将2y x =代入()2224x y r -+=，并化简得227160x x r -+-= ………①E 与M 有四个交点的充要条件是方程①有两个不等的正根1x 、2x ．由此得()()22122127416070160.r x x x x r ⎧∆=--->⎪⎪+=>⎨⎪=->⎪⎩，，解得215164r <<，又0r >，所以r 的取值范围是4⎫⎪⎪⎝⎭．⑵不妨设E 与M 的四个交点的坐标为：(1A x 、(1B x ，、(2C x ，、(2D x ．则直线AC 、BD 的方程分别为()121y x x=-，()121y x x +=-，解得点P 的坐标为)0．设t ，由t =⑴知702t <<．由于四边形ABCD 为等腰梯形，因而其面积(2112S x x =⋅⋅-．则(()221212124S x x x x x x ⎡⎤=++⋅+-⎣⎦．将127x x +=t 代入上式，并令()2f t S =，得 ()()()27727202f t t t t ⎛⎫=+⋅-<< ⎪⎝⎭．利用三次均值不等式求解，主要是配凑系数或常数，注意取等号的条件即可． ()()()311727214412872(72)14422323≤t t t f t t t t ++++-⎛⎫⎛⎫=++-= ⎪ ⎪⎝⎭⎝⎭．当且仅当72144t t +=-即76t =时，()f t 有最大值，即四边形ABCD 的面积最大，故所求的点P 的坐标为706⎛⎫⎪⎝⎭，．【答案】⑴r 的取值范围是4⎫⎪⎪⎝⎭． ⑵点P 的坐标为706⎛⎫ ⎪⎝⎭，．【例10】已知动圆过定点(10)P ，，且与定直线l ：1x =-相切，点C 在l 上．⑴求动圆圆心的轨迹M 的方程；⑵设过点P ，且斜率为M 相交于A 、B 两点．①问：ABC ∆能否为正三角形？若能，求点C 的坐标；若不能，说明理由； ②当ABC ∆为钝角三角形时，求这种点C 的纵坐标的取值范围．【考点】圆锥曲线综合问题【难度】4星【题型】解答【关键字】无【解析】⑴法一：依题意，曲线M 是以点P 为焦点，直线l 为准线的抛物线，所以曲线M 的方程为24y x =．法二：设()M x y ，，依题意有MP MN =，所以1x + 化简得：24y x =．⑵①由题意得，直线AB的方程为1)y x =-．由21)4y x y x⎧=-⎪⎨=⎪⎩消去y 得231030x x -+=，解得13x 1=，23x =．所以A点坐标为13⎛ ⎝⎭，B点坐标为(3-，，121623AB x x =++=．假设存在点(1)C y -，，使ABC ∆为正三角形，则BC AB =且AC AB =，即22222216(31)(3116(1)33y y ⎧⎛⎫+++=⎪ ⎪⎝⎭⎪⎨⎛⎪⎛⎫++-= ⎪ ⎪⎝⎭⎝⎩（*）上面两式相减得222244(3y y ⎛⎛⎫++=+ ⎪ ⎝⎭⎝⎭，解得y =y =①，所以方程组（*）无解．因此，直线l 上不存在点C ，使得ABC ∆是正三角形． ②法一：设(1)C y -，使ABC ∆成钝角三角形，由1)1y x x ⎧=-⎪⎨=-⎪⎩得y = 即当点C的坐标为(1-时，A 、B 、C三点共线，故y ≠又2222128139AC y y y ⎛⎛⎫=--+=-+ ⎪ ⎝⎭⎝⎭，2222(31)(28BC y y =+++=++，221625639AB ⎛⎫== ⎪⎝⎭．当CAB ∠为钝角时，222cos 02AB AC BCA AB AC+-=<⋅．即222BC AC AB >+，即22282562899y y y ++>++，即y CAB ∠为钝角．当222AC BC AB >+，即22282562899y y y +>+++，即y <CBA ∠为钝角．又222AB AC BC >+，即22256282899y y >+++，即243y +<，20y ⎛< ⎝．该不等式无解，所以ACB ∠不可能为钝角．因此，当ABC ∆为钝角三角形时，点C 的纵坐标y 的取值范围是y <y y >≠．法二：以AB 为直径的圆的方程为2225833x y ⎛⎫⎛⎛⎫-++= ⎪ ⎪⎝⎭⎝⎝⎭．圆心53⎛ ⎝，到直线l ：1x =-的距离为83，所以，以AB 为直径的圆与直线l 相切于点1G ⎛-- ⎝⎭，．当直线l 上的C 点与G 重合时，ACB ∠为直角，当C 与G 点不重合，且A 、B 、C 三点不共线时，ACB ∠为锐角，即ABC ∆中，ACB ∠不可能是钝角．因此，要使ABC ∆为钝角三角形，只可能是CAB ∠或CBA ∠为钝角．过点A 且与AB 垂直的直线方程为13y x ⎫=-⎪⎝⎭．令1x =-得y =过点B 且与AB 垂直的直线方程为3)y x +-．令1x =-得y =1)1y x x ⎧=-⎪⎨=-⎪⎩，解得y =所以，当点C 的坐标为(1-时，A 、B 、C 三点共线，不构成三角形．因此，当ABC ∆为钝角三角形时，点C 的纵坐标y 的取值范围是y <y >（y ≠）．【答案】⑴24y x =．⑵①直线l 上不存在点C ，使得ABC ∆是正三角形． ②当ABC ∆为钝角三角形时，点C 的纵坐标y 的取值范围是y <y y >≠．【例11】学校科技小组在计算机上模拟航天器变轨返回试验．设计方案如图：航天器运行（按顺时针方向）的轨迹方程为22110025x y +=，变轨（即航天器运行轨迹由椭圆变为抛物线）后返回的轨迹是以y 轴为对称轴、6407，M ⎛⎫⎪⎝⎭为顶点的抛物线的实线部分，降落点为(80)，D ．观测点(40)(60)，，，A B 同时跟踪航天器． ⑴求航天器变轨后的运行轨迹所在的曲线方程；⑵试问：当航天器在x 轴上方时，观测点、A B 测得离航天器的距离分别为多少时，应向航天器发出变轨指令？【考点】圆锥曲线综合问题【难度】4星【题型】解答【关键字】无【解析】⑴设曲线方程为2647y ax =+，由题意可知，640647a =⋅+．∴17a =-．∴曲线方程为216477y x =-+．⑵设变轨点为()，C x y ，根据题意可知22211002516477x y y x ⎧+=⎪⎪⎨⎪=-+⎪⎩，得247360y y --=， 4y =或94y =-（不合题意，舍去）．∴4y =．得6x =或6x =-（不合题意，舍去）．∴C 点的坐标为(64)，，||||4AC BC ==．因此当观测点，A B 测得，AC BC距离分别为4时，应向航天器发出变轨指令．【答案】⑴216477y x =-+．⑵因此当观测点，A B 测得，AC BC 距离分别为4时，应向航天器发出变轨指令．【考点】圆锥曲线综合问题【难度】4星【题型】解答【关键字】2010年，江西高考【解析】⑴ 因为抛物线2C 经过椭圆1C 的两个焦点()10F c -，，()20F c ，，可得22c b =，⑵ 由题设可知M ，N 关于y 轴对称，设()11M x y -，，()11N x y ，，()10x >，则由AMN △的垂心为B ，有0BM AN ⋅=① 由于点()11N x y ，在2C 上，故有2211x by b +=，②2⑵若1AM MB =，求直线⑶若坐标原点O 关于直线求椭圆1C 的长轴长的最小值．【考点】圆锥曲线综合问题【难度】4星【题型】解答【关键字】2010年，海淀一模【解析】⑴由题意，抛物线2C 的方程为：24y x =，…………2分⑵设直线AB 的方程为(4)y k x =-，（k 存在且0k ≠）．联立2(4)4y k x y x=-⎧⎨=⎩，消去x ，得24160ky y k --=，……3分显然216640k ∆=+>，设1122(,),(,)A x y B x y ，12又1AM MB =，所以由①②③消去12,y y ，得22k =，由2222222222(8)4()(16)0k a b a k a k a b ∆=--+-≥，得 242222216()(16)0a k b a k k b -+-≥，即222216a kb k +≥，【答案】⑴24y x =，【例14】已知，，A B C 均在椭圆222:1(1)x M y a a+=>上，直线AB 、AC 分别过椭圆的左右焦点1F 、2F ，当120AC F F ⋅=时，有21219AF AF AF ⋅=． ⑴求椭圆M 的方程；⑵设P 是椭圆M 上的任一点，EF 为圆22:(2)1N x y +-=的任一条直径，求PE PF ⋅的最大值．【考点】圆锥曲线综合问题【难度】4星【题型】解答【关键字】无【解析】⑴∵120AC F F ⋅=，∴12AC F F ⊥，即12△AF F 为直角三角形，∴1122||cos ||AF F AF AF ∠=．于是22212121221199||||cos 9||||AF AF AF AF F AF AF AF AF ⋅=∠===， ∴12||3||AF AF =．又12||||2AF AF a +=，∴123||||22，aAF a AF ==．在12△Rt AF F 中，2221221||||||AF AF F F =+，即22234(1)22a a a ⎛⎫⎛⎫=+- ⎪ ⎪⎝⎭⎝⎭，解得22a =，故所求椭圆M 方程为2212x y +=．⑵()()PE PF NE NP NF NP ⋅=-⋅-222()()()1NF NP NF NP NP NF NP =--⋅-=--=- 从而只需求2NP 的最大值．P 是椭圆M 上的任一点，设00()，P x y ，则有220012x y +=，即220022x y =-．又(02)，N ，所以22222200000(2)22(2)(2)10NP x y y y y =+-=-+-=-++．而0[11]，y ∈-，所以当01y =-时，2NP 取最大值9，故PE PF ⋅的最大值为8．【答案】⑴2212x y +=．⑵PE PF ⋅的最大值为8．【例15】如图，以12A A ，为焦点的双曲线E 与半径为c 的圆O 相交于C ，D ，1C ，1D ，连接1CC 与OB 交于点H ，且有：(323)OH HB =+．其中12A A B ，，是圆O 与坐标轴的交点，c 为双曲线的半焦距． ⑴当1c =时，求双曲线E 的方程；⑵试证：对任意正实数c ，双曲线E 的离心率为常数．⑶连接1A C 与双曲线E 交于F ，是否存在实数λ，使1A F FC λ=恒成立，若存在，试求出λ的值；若不存在，请说明理由．【考点】圆锥曲线综合问题【难度】4星【题型】解答【关键字】无【解析】⑴由1c =知(01)B ，，∵(323)OH HB =+，∴0H H x y ==，，即0H ⎛ ⎝⎭，点C 在单位圆上，∴12C ⎛ ⎝⎭．设双曲线E 的方程为22221(00)x y a b a b-=>>，，由点C 在双曲线E 上，半焦距1c =有： 2222113144a b ab ⎧+=⎪⎨-=⎪⎩，解得221a b == 所以双曲线E221-=．⑵∵1(0)A c -，，(0)B c ，，由(323)OH HB =+，得02c H C ⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，．设双曲线E 的方程为22221(00)x y a b a b-=>>，，C 在双曲线E 上，∴22222223144a b c c c a b ⎧+=⎪⎨-=⎪⎩，化简整理得4224360a a b b +-=，即42630b b a a ⎛⎫⎛⎫--= ⎪ ⎪⎝⎭⎝⎭，解得23b a ⎛⎫=+ ⎪⎝⎭又222214c b e a a ⎛⎫==+=+ ⎪⎝⎭∴1e =，即双曲线E 的离心率是与c 无关的常数．⑶假设存在实数λ，使1A F FC λ=恒成立，1(0)A c -，，2c C ⎛⎫⎪ ⎪⎝⎭，则2211F F c c x y λλλλ-+==++，，即(2)2(1)c F λλ⎛- +⎝⎭．由点C F ，都在双曲线E 上，得 2222222222223144(2)314(1)4(1)c c ab c c a b λλλλ⎧-=⎪⎪⎨-⎪-=⎪++⎩，由上边的式子有222222341443e c c e b b --=⇒=，代入下边的式子化简整理得22210e e λλ-++=，即有2212e e λ-=+，结合⑵的结论可得λ=故存在实数λ=1A F FC λ=恒成立．【答案】221=．⑵∵1(0)A c -，，(0)B c ，，由(323)OH HB =+，得02c H C ⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，．设双曲线E 的方程为22221(00)x y a b a b-=>>，，C 在双曲线E 上，∴22222223144a b c c c a b ⎧+=⎪⎨-=⎪⎩，化简整理得4224360a a b b +-=，即42630b b a a ⎛⎫⎛⎫--= ⎪ ⎪⎝⎭⎝⎭，解得23b a ⎛⎫=+ ⎪⎝⎭又222214c b e a a ⎛⎫==+=+ ⎪⎝⎭∴1e =，即双曲线E 的离心率是与c 无关的常数．⑶存在实数λ=1A F FC λ=恒成立．【例16】在平面直角坐标系xOy中，点P到点(30)F，的距离的4倍与它到直线2x=的距离的3倍之和记为d，当点P运动时，d恒等于点P的横坐标与18之和．⑴求点P的轨迹C；⑵设过点F的直线l与轨迹C相交于M，N两点，求线段MN长度的最大值．【考点】圆锥曲线综合问题【难度】4星【题型】解答【关键字】2009年，湖南理科【解析】⑴设点P的坐标为()x y，，则32d x=-．由题设，18d x=+，即3218x x-=+．……………①当2x>时，由①162x-，……………②化简得2213627x y+=．当2x≤时，由①3x+，……③化简得212y x=．故点P的轨迹C是由椭圆221:13627x yC+=在直线2x=的右侧部分与抛物线22:12C y x=在直线2x=的左侧部分（包括它与直线2x=的交点）所组成的曲线，参见图．⑵如图所示，易知直线2x=与1C，2C的交点都是(2A，，(2B-，，直线AF BF，的斜率分别为AF BF k k =-= 当点P 在1C 上时，由②知1||62PF x =- ……………④当点P 在2C 上时，由③知||3PF x =+ ……………⑤若直线l 的斜率k 存在，则直线l 的方程为(3)y k x =-①当≤AF kk ，或≥BF k k，即≤k -或≥k 时，直线l 与轨迹C 的两个交点11()M x y ，，22()N x y ，都在1C 上，此时由④知1211||6||622MF x NF x =-=-，从而121||||||12()2MN MF NF x x =+=-+将(3)y k x =-代入1C ，得2222(34)24361080k x k x k +-+-=，则12x x ，是这个方程的两根，所以21222434k x x k +=+，于是2212||1234k MNk =-+因为当≤k -≥k 224≥k ，所以2221212100||1212334114≤k MN k k =-=-++，当且仅当k =±②当k -<<时，直线l 与轨迹C 的两个交点11()M x y ，，22()N x y ，分别在12C C ，上，不妨设点M 在1C 上，点N 在2C 上，则由④⑤知，121||6||32MF x NF x =-=+，，设直线AF 与椭圆1C 的另一交点为00()E x y ，，则0122x x x <<， 10211||66||||332||22MF x x EF NF x AF =-<-==+<+=，所以||||||||||||MN MF NF EF AF AE =+<+=．而点A E ，都在1C上，且AE k =-由①的情况知100||11AE =，故100||11MN <．若直线l 的斜率不存在，则123x x ==，此时121100||12()9211MN x x =-+=<综上所述，线段MN 长度的最大值为10011．【答案】⑴点P 的轨迹C 是由椭圆 221:13627x y C +=在直线2x =的右侧部分与抛物线22:12C y x =在直线2x =的左侧部分（包括它与直线2x =的交点）所组成的曲线，参见图．⑵线段MN 长度的最大值为10011．【例17】设0p >是一常数，过点(20)Q p ，的直线与抛物线22y px =交于相异两点A 、B ，以线段AB 为直径作圆H （H 为圆心）． ⑴试证：抛物线顶点在圆H 的圆周上； ⑵求圆H 的面积最小时直线AB 的方程．【考点】圆锥曲线综合问题【难度】4星【题型】解答【关键字】无【解析】⑴由题意，直线AB 斜率不为0，故可设直线方程为：2ky x p =-．又设()A A A x y ，，()B B B x y ，，则其坐标满足222ky x p y px =-⎧⎨=⎩．消去x 得22240y pky p --=，由此得224A B A By y pk y y p +=⎧⎪⎨=-⎪⎩． ∴22224()(42)()4(2)A B A B A B A B x x p k y y k p y y x x p p ⎧+=++=+⎪⎨==⎪⎩，因此0A B A B OA OB x x y y ⋅=+=，即OA OB ⊥．故O 必在圆H 的圆周上．⑵又由题意圆心()H H H x y ，是AB 的中点，故2(2)22A B H A B H x x x k p y y y kp +⎧==+⎪⎪⎨+⎪==⎪⎩，已证OH 是圆H的半径，且OH ===．从而当0k =时，圆H 的半径2p 为最小值，亦使圆H 的面积最小．此时，直线AB 的方程为：2x p =．【答案】⑴由题意，直线AB 斜率不为0，故可设直线方程为：2ky x p =-．又设()A A A x y ，，()B B B x y ，，则其坐标满足222ky x p y px =-⎧⎨=⎩．消去x 得22240y pky p --=，由此得224A B A By y pk y y p +=⎧⎪⎨=-⎪⎩． ∴22224()(42)()4(2)A B A B A B A B x x p k y y k p y y x x p p ⎧+=++=+⎪⎨==⎪⎩，因此0A B A B OA OB x x y y ⋅=+=，即OA OB ⊥．故O 必在圆H 的圆周上． ⑵直线AB 的方程为：2x p =．。

第三章圆锥曲线复习讲义(精心整理、好用、经典)

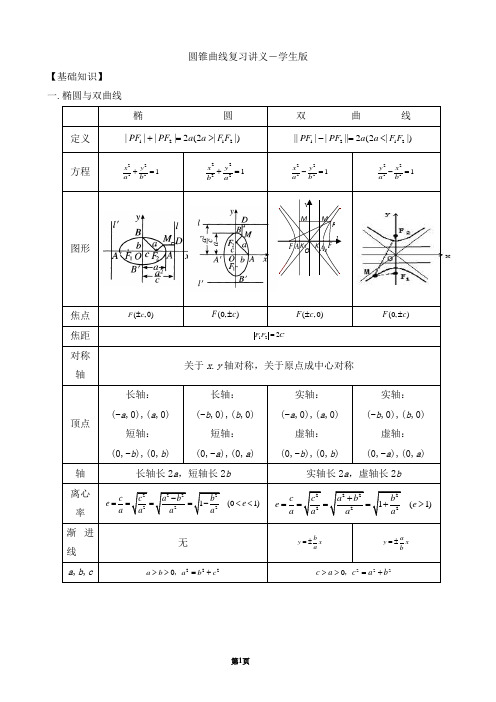
圆锥曲线复习讲义－学生版【基础知识】一.椭圆与双曲线椭圆双曲线定义 1212||||2(2||)PF PF a a F F +=>1212||||||2(2||)PF PF a a F F -=<方程22221x y a b += 22221x y b a+= 22221x y a b -= 22221y x a b -= 图形焦点 (,0)F c ± (0,)F c ±(,0)F c ± (0,)F c ±焦距 C F F 221=对称轴关于x .y 轴对称，关于原点成中心对称顶点长轴：(-a ,0),(a ,0) 短轴：(0,-b ),(0,b )长轴：(-b ,0),(b ,0) 短轴：(0,-a ),(0,a )实轴：(-a ,0),(a ,0) 虚轴：(0,-b ),(0,b )实轴：(-b ,0),(b ,0)虚轴：(0,-a ),(0,a )轴长轴长2a ，短轴长2b实轴长2a ，虚轴长2b离心率 22222221(01)c c a b b e e a a a a-====-<< 22222221(1)c c a b be e a a a a+====+>渐进线无xab y ±= x ba y ±= a ,b ,c 2220c b a b a +=>>，2220b a c a c +=>>，M MPK K 1A A 2F F O yx二．抛物线的性质标准方程22(0)y px p => 22(0)y px p =->22(0)x py p => 22(0)x py p =-> 图形焦点坐标 (,0)2p(,0)2p-(0,)2p (0,)2p -准线方程 2p x =-2p x = 2p y =-2p y =范围 0x ≥ 0x ≤0y ≥ 0y ≤离心率1e = 1e = 1e = 1e = 三、弦长公式： ||14)(1||1||2212212212A k x x x x k x x k AB ∆⋅+=-+⋅+=-+= 其中,∆,A 分别是联立直线方程和圆锥曲线方程,消去 y 后所得关于x 的一元二次方程的判别式和2x 的系数求弦长步骤：（1）求出或设出直线与圆锥曲线方程；（2）联立两方程，消去y,得关于x 的一元二次方程,02=++C Bx Ax 设),(11y x A ，),(22y x B ，由韦达定理求出AB x x -=+21，ACx x =21；（3）代入弦长公式计算。

圆锥曲线的综合问题讲义解析

圆锥曲线的综合问题讲义解析【课前双基巩固】知识聚焦1.(1)没有一个两个(2)对称轴渐近线 Δ>0 Δ=0 Δ<0 2.|y 1-y 2| 对点演练1.√2303[解析] 设A (x 1,y 1),B (x 2,y 2),由{2x -y +1=0,x 24+y 28=1消去y ,化简可得6x 2+4x-7=0,所以x 1+x 2=-23,x 1x 2=-76,所以|AB|=√1+k 2·√(x1+x 2)2-4x 1x 2=√1+22×√(-23)2-4×(-76)=√2303.2.54 [解析] 设A (x 1,y 1),B (x 2,y 2),则x 122-y 12=1,x 222-y 22=1,两式相减,得x 12-x 222=y 12-y 22,即k=y 2-y 1x 2-x 1=x 2+x 12(y 2+y 1),又线段AB 的中点恰好为点P (5,2),所以k=54.3.√3x-y-√3=0 [解析] 抛物线C :y 2=4x 的焦点为F (1,0),设直线l 的方程为y=k (x-1),与抛物线方程联立,得k 2x 2-(2k 2+4)x+k 2=0.设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=2k 2+4k 2,所以|AB|=x 1+x 2+2=2k 2+4k 2+2=163,解得k 2=3,又直线l 的倾斜角为锐角,所以k=√3,所以直线l 的方程为y=√3(x-1),即√3x-y-√3=0.4.(1+√2,+∞) [解析] 由题设条件可知△ABF 2为等腰三角形,只要∠AF 2B 为钝角即可,所以有b 2a>2c ,即b 2>2ac ,所以c 2-a 2>2ac ,即e 2-2e-1>0,所以e>1+√2.5.1或-1 [解析] 由{x 2-y 2=1,y =k(x -√2),得(1-k 2)x 2+2√2k 2x-2k 2-1=0.当1-k 2=0,即k=±1时,方程只有一根,所以直线与双曲线仅有一个公共点;当1-k 2≠0,即k ≠±1时,要满足题意只需Δ=(2√2k 2)2-4(1-k 2)(-2k 2-1)=0,此时无解.所以若直线l :y=k (x-√2)与双曲线x 2-y 2=1仅有一个公共点,则实数k 的值为1或-1.6.[2-2 √2,2+2 √2] [解析] 由椭圆方程得y 2=1-x 22,所以x 2+y 2+2x=12x 2+2x+1=12(x+2)2-1.由x 22+y 2=1,得|x|≤√2,所以当x=√2时,x 2+y 2+2x 有最大值2+2 √2;当x=-√2时,x 2+y 2+2x 有最小值2-2 √2.所以x 2+y 2+2x ∈[2-2 √2,2+2 √2].第1课时直线与圆锥曲线的位置关系【课堂考点探究】例1 [思路点拨] (1)由4a=8,得a=2,再由2×12×2c×b=2√3,b 2+c 2=4,e<√22,可求得b=√3,c=1,即可得椭圆的方程.(2)分类讨论:当y 0=0时,可求得x 0=±2,即可求得直线与曲线的交点; 当y 0≠0时,直线l 的方程可化为y=12−3x 0x 4y 0,代入椭圆方程,再由点P (x 0,y 0)为曲线C 上一点,解得x=x 0,代入直线方程,得y=y 0,故直线l 与曲线C 有且只有一个交点P.解:(1)依题意,设椭圆C 的方程为x 2a +y 2b =1(a>b>0),焦距为2c , 由题设条件知4a=8,得a=2,又2×12×2c×b=2√3,b 2+c 2=a 2=4,所以b=√3,c=1或b=1,c=√3(经检验不合题意舍去),故椭圆C 的方程为x 24+y 23=1.(2)证明:当y 0=0时,由x 024+y 023=1,可得x 0=±2,当x 0=2,y 0=0时,直线l 的方程为x=2,直线l 与曲线C 有且只有一个交点(2,0). 当x 0=-2,y 0=0时,直线l 的方程为x=-2,直线l 与曲线C 有且只有一个交点 (-2,0). 当y 0≠0时,直线l 的方程为y=12−3x 0x 4y 0,联立{y =12−3x 0x4y 0,x 24+y 23=1,消去y ,得(4y 02+3x 02)x 2-24x 0x+48-16y 02=0.①由点P (x 0,y 0)为曲线C 上一点,得x 024+y 023=1,可得4y 02+3x 02=12.于是方程①可以化简为x 2-2x 0x+x 02=0,解得x=x 0,将x=x 0代入方程y=12−3x 0x 4y 0,可得y=y 0,故直线l 与曲线C 有且只有一个交点P (x 0,y 0).综上,直线l 与曲线C 有且只有一个交点,且交点为P (x 0,y 0).变式题 C [解析] 设|F 1F 2|=2c (c>0),△PF 1F 2的内切圆分别与PF 1,F 1F 2,PF 2切于点G ,H ,I ,则|PG |=|PI |,|F 1G|=|F 1H|,|F 2H|=|F 2I|.由双曲线的定义知2a=|PF 1|-|PF 2|=|F 1G|-|F 2I|=|F 1H|-|F 2H|,又|F 1H|+|F 2H|=|F 1F 2|=2c ,故|F 1H|=c+a ,|F 2H|=c-a ,所以H (a ,0),即a=2.若直线l 与双曲线的右支交于A ,B 两点,则当l ⊥x 轴时,|AB|有最小值为2b 2a=b 2(通径长);若直线l 与双曲线的两支分别交于A ,B 两点,则当l ⊥y 轴时,|AB|有最小值为2a.于是,由题意得b 2>2a=4,即b>2,c=√a 2+b 2>2√2,所以双曲线的离心率e=ca >√2.故选C. 例2 [思路点拨] (1)根据题意列出方程组求得a ,b ,c 的值,即可求得椭圆的标准方程;(2)设出直线l 的方程,联立直线与椭圆的方程,同时利用弦长公式求四边形OACB 的面积S ,设OC⃗⃗⃗⃗⃗ =λOM ⃗⃗⃗⃗⃗⃗ (λ>0),结合点到直线的距离公式得到关于λ的方程,解方程即可求得最终结果,注意直线斜率不存在的情况.解:(1)由题意得{ ca =√22,√1+3=c,a 2=b 2+c 2,解得{a =√2,b =1,c =1,故椭圆K 的方程为x 22+y 2=1. (2)由(1)知F 2(1,0),由于直线AB 的倾斜角不能为零,所以设直线AB 的方程为my=x-1, 与x 22+y 2=1联立,可得(m 2+2)y 2+2my-1=0.设M (x 0,y 0),A (x 1,y 1),B (x 2,y 2),则y 1+y 2=-2m m 2+2,可得y 0=-m m 2+2,x 0=my 0+1=2m 2+2.设C (x ,y ),OC ⃗⃗⃗⃗⃗ =λOM⃗⃗⃗⃗⃗⃗ (λ>0),所以x=λx 0,y=λy 0. 因为C 在K 上,故λ2x 022+y 02=1,得m 2+2=λ2.① 设h 1为点O 到直线AB 的距离,h 2为点C 到直线AB 的距离,则h1h 2=|OM⃗⃗⃗⃗⃗⃗⃗ ||MC ⃗⃗⃗⃗⃗⃗ |=1λ-1,得h 2=(λ-1)h 1.又由点到直线的距离公式得h 1=√1+m 2=√λ2-1,而|AB |=√1+m 2·√(y 1+y 2)2-4y 1y 2=2√2(1+m 2)m 2+2=2√2(λ2-1)λ2, 所以S=12|AB |(h 1+h 2)=√2(λ2-1)λ2·√λ2-1=√2√λ2-1λ. 由题意知,S=2√3=√3,所以√2√λ2-1λ=√3,得λ=√3.将λ=√3代入①式,得m=±1,所以直线l 的斜率为±1.变式题解:(1)根据题意可设抛物线C 的标准方程为x 2=2py (p>0).∵|P 1P 2|=4,∴2p=4,∴p=2, ∴抛物线C 的标准方程为x 2=4y. (2)由(1)可知,F (0,1),∴l :y=kx+1, 设M (x 1,y 1),N (x 2,y 2),联立{x 2=4y,y =kx +1,消去y ,得x 2-4kx-4=0,∴x 1+x 2=4k ,∴y 1+y 2=k (x 1+x 2)+2=4k 2+2, ∴|MN|=y 1+y 2+p=4k 2+4.又∵点Q (0,3)到直线l 的距离为d=√1+k 2,∴|AB|=2√8−d 2=4√2k 2+12, ∴√1+k 2|AB|=2√2k 2+1,令√2k 2+1=t (t ∈(1,√3]),则k 2=12(t 2-1),∴√1+k 2|AB|=t 2+12t=12t+1t , 又∵t+1t ∈2,4√33,∴|MN|√1+k 2|AB|的取值范围为1,2√33.例3 [思路点拨] 思路一,首先设出直线方程,代入椭圆方程化为关于x 的一元二次方程,然后结合韦达定理可求得直线的斜率,进而求得直线l 的方程;思路二,利用“点差法”求解. x+2y-4=0 [解析] 方法一:易知直线l 的斜率存在.由题意可设l 的方程为y-1=k (x-2),即y=kx-2k+1.联立{y =kx -2k +1,x 216+y 24=1,整理得(1+4k 2)x 2-8(2k 2-k )x+16k 2-16k-12=0(*).设直线l 与椭圆的交点分别为A (x 1,y 1),B (x 2,y 2), 则x 1+x 2=8(2k 2-k)1+4k 2.因为AB 的中点为M (2,1), 所以8(2k 2-k)1+4k 2=4,解得k=-12.所以所求l 的方程为y-1=-12(x-2),即x+2y-4=0.方法二: 设直线l 与椭圆的交点分别为A (x 1,y 1),B (x 2,y 2),易知x 1≠x 2,则由{x 1216+y 124=1,x 2216+y 224=1,得(x 1-x 2)(x 1+x 2)16+(y 1-y 2)(y 1+y 2)4=0,即(x 1+x 2)+4(y 1+y 2)·y 1-y 2x 1-x 2=0(*).又x 1+x 2=4,y 1+y 2=2,代入(*),得4+4×2×y 1-y 2x 1-x 2=0,所以y 1-y2x 1-x 2=-12,故直线l 的方程为x+2y-4=0.例4 [思路点拨] 首先利用“点差法”求出直线方程,然后联立直线方程与抛物线方程求得交点坐标,进而可求得△ABF 的面积.2 [解析] 易知F (1,0),点M (2,2)是抛物线内的点,设A (x 1,y 1),B (x 2,y 2),易知x 1≠x 2,则{y 12=4x 1,y 22=4x 2,两式相减可得y 12-y 22=4(x 1-x 2),化简得到(y 1+y 2)×y 1-y 2x 1-x 2=4,解得k=y 1-y2x 1-x 2=1,所以直线AB 的方程是y-2=x-2,即y=x ,与y 2=4x 联立,可得{x 1=0,y 1=0,{x 2=4,y 2=4,所以S △ABF =12×1×4=2.例5 [思路点拨] 首先根据条件得出直线PQ 的垂直平分线方程,并代入双曲线方程得到关于x 的一元二次方程,结合韦达定理求得中点M 的坐标,然后利用中点在抛物线上,也在直线y=x+b 上可求得b 的值.A [解析] 因为点P ,Q 关于直线y=x+b 对称,所以PQ 的垂直平分线为y=x+b ,所以直线PQ 的斜率为-1.设直线PQ 的方程为y=-x+m ,由{y =−x +m,x 22-y 23=1,得x 2+4mx-2m 2-6=0,所以x P +x Q =-4m ,所以x M =-2m ,所以M (-2m ,3m ).因为PQ 的中点M 在抛物线y 2=9x 上,所以9m 2=9×(-2m ),解得m=0或m=-2,又PQ 的中点M 也在直线y=x+b 上,所以b=5m ,所以b=0或-10,故选A. 强化演练1.6 [解析] 由抛物线y 2=4x 得p=2,设A (x 1,y 1),B (x 2,y 2),因为线段AB 的中点M 的横坐标为2,所以x 1+x 2=2×2=4,因为直线AB 过焦点,所以|AB |=x 1+x 2+p=4+2=6.2.2x+2y-3=0 [解析] 设A (x 1,y 1),B (x 2,y 2),代入椭圆方程有x 122+y 12=1,x 222+y 22=1,两式相减得(x 2-x 1)(x 2+x 1)2=-(y 2+y 1)(y 2-y 1),即(x 2-x 1)×22=-(y 2-y 1),所以k AB =y 2-y 1x 2-x 1=-1,所以直线l 的方程为y-12=-(x-1),即2x+2y-3=0.3.B [解析] 设M (x 1,y 1),N (x 2,y 2),双曲线方程为x 2a2-y 2b 2=1(a>0,b>0),将y=x-1代入双曲线方程,整理得(b 2-a 2)x 2+2a 2x-a 2-a 2b 2=0,得x 1+x 2=2a 2a -b ,则x 1+x 22=a 2a -b =-23.又c 2=a 2+b 2=7,所以a 2=2,b 2=5,所以双曲线的方程是x 22-y 25=1,故选B.4.x 28+y 24=1 [解析] 抛物线y 2=8x 的焦点为(2,0),∴c=2,设椭圆方程为x 2a2+y 2b2=1(a>0,b>0),A (x 1,y 1),B (x 2,y 2),代入椭圆方程后两式相减,得(x 1+x 2)(x 1-x 2)a 2+(y 1+y 2)(y 1-y 2)b 2=0,由中点M (1,1)及斜率为-12可得a 2b=2.∵a 2-b 2=c 2=4,∴a 2=8,b 2=4,∴椭圆C 的方程为x 28+y 24=1.5.(-2√1313,2√1313) [解析] 设A (x 1,y 1),B (x 2,y 2)是椭圆上关于直线y=4x+m 对称的相异的两点,AB的中点为M (x 0,y 0),则x 124+y 123=1,x 224+y 223=1,由“点差法”得y 0=3x 0,代入y 0=4x 0+m ,解得M 点坐标为(-m ,-3m ).而M 是AB 的中点,∴M 点在椭圆内部,∴m 24+9m 23<1,解得-2√1313<m<2√1313. 第2课时最值﹑范围﹑证明问题【课堂考点探究】例1 [思路点拨] (1)由顶点坐标及椭圆的离心率,即可求得a 和c 的值,进而可求得椭圆方程; (2)分类讨论,当斜率为0时,即可求得m 的值,设直线l 的方程,代入椭圆方程,利用根与系数的关系及弦长公式即可求得m 的表达式,利用导数求得函数的单调性及最值,即可求得m 的最大值.解:(1)因为椭圆C :x 2a2+y 2b 2=1(a>b>0)的顶点坐标为(±√6,0),且离心率为√306, 所以a=√6,且√a 2-b 2a =√306,解得b=1.故椭圆C 的方程为x 26+y 2=1.(2)因为|MN |=4√33>2,所以直线MN 的斜率存在.又因为直线MN 在y 轴上的截距为m ,所以可设直线MN 的方程为y=kx+m , 代入椭圆方程x 26+y 2=1,得(1+6k 2)x 2+12kmx+6(m 2-1)=0,因为Δ=(12km )2-24(1+6k 2)(m 2-1)=24(1+6k 2-m 2)>0,所以m 2<1+6k 2.设M (x 1,y 1),N (x 2,y 2),由根与系数的关系得x 1+x 2=-12km1+6k 2,x 1x 2=6(m 2-1)1+6k 2,则|MN |=√1+k 2|x 1-x 2|=√1+k 2√(x 1+x 2)2-4x 1x 2=√1+k 2√(-12km 1+6k 2)2-24(m 2-1)1+6k 2.因为|MN |=4√33, 所以√1+k 2√(-12km 1+6k 2)2-24(m 2-1)1+6k 2=4√33, 整理得m 2=-18k 4+39k 2+79(1+k 2).令k 2+1=t ≥1,则k 2=t-1, 所以m 2=-18t 2+75t -509t=1975-18t+50t≤75−2×309=53,等号成立的条件是t=53,此时k 2=23,m 2=53,满足m 2<1+6k 2,符合题意.故m 的最大值为√153. 变式题解:(1)曲线C 上的点满足|PF 1|+|PF 2|=2√2>|F 1F 2|=2,∴曲线C 是以F 1,F 2为焦点的椭圆,且a=√2,c=1,b=1,∴曲线C 的方程是x 22+y 2=1.(2)∵F 2M ⃗⃗⃗⃗⃗⃗⃗⃗ =λF 2N ⃗⃗⃗⃗⃗⃗⃗ =μa ,∴M ,N ,F 2三点共线,且直线MN 的斜率为√3,∴直线MN 的方程为y=√3(x-1), 与椭圆方程联立得7x 2-12x+4=0,设M (x 1,y 1),N (x 2,y 2),∴|MN |=2√(x 1+x 2)2-4x 1x 2 =8√27. 设P (√2cos θ,sin θ),∴P 到直线MN 的距离d=|√6cosθ-sinθ-√3|2=|√7sin(θ-φ)+√3|2,∴d max =√7+√32, ∴S △MNP 的最大值为12|MN|·d max =2√14+2√67. 例2 [思路点拨] (1)首先根据抛物线的准线方程可求得a 的值,然后根据椭圆的离心率结合a 2=b 2+c 2可求得b 的值,由此求得椭圆C 1和抛物线C 2的方程;(2)由题意知直线的斜率一定存在,由此设直线l :y=kx+2,代入椭圆的方程,消去y 得到关于x 的一元二次方程,然后利用判别式大于零及根与系数的关系,利用“O 在以线段PQ 为直径的圆的外部”等价于“OP ⃗⃗⃗⃗⃗ ·OQ ⃗⃗⃗⃗⃗ >0”建立不等式,求得k 的取值范围.解:(1)由题意得a 4=12,∴a=2,故抛物线C 2的方程为x 2=-2y.又e=c a =√32,∴c=√3,∴b=1,从而椭圆C 1的方程为x 24+y 2=1.(2)显然直线x=0不满足题设条件,故可设直线l :y=kx+2,P (x 1,y 1),Q (x 2,y 2). 由{x 24+y 2=1,y =kx +2,得(1+4k 2)x 2+16kx+12=0. ∵Δ=(16k )2-4×12(1+4k 2)>0,∴k∈-∞,-√32∪√32,+∞,x 1+x 2=-16k1+4k 2,x 1x 2=121+4k 2,根据题意,得0°<∠POQ<90°,即OP ⃗⃗⃗⃗⃗ ·OQ ⃗⃗⃗⃗⃗ >0,∴OP ⃗⃗⃗⃗⃗ ·OQ ⃗⃗⃗⃗⃗ =x 1x 2+y 1y 2=x 1x 2+(kx 1+2)(kx 2+2)=(1+k 2)x 1x 2+2k (x 1+x 2)+4=12(1+k 2)1+4k 2+2k×-16k 1+4k 2+4=16−4k 21+4k 2>0,解得-2<k<2.综上得k ∈-2,-√32∪√32,2.变式题解:(1) 由题知F p2,0,|FA |=3+2√2+p 2,|FD|=√2|FA|=3√2+4+√22p ,则D 3√2+4+√22p+p2,0,FD 的中点坐标为3√22+2+(2+√2)p4,0,则3√22+2+(2+√2)p4=3+2√2,解得p=2,故C 的方程为y 2=4x.(2)证明:依题可设直线AB 的方程为x=my+x 0(m ≠0),A (x 1,y 1),B (x 2,y 2),则E (x 2,-y 2).由{y 2=4x,x =my +x 0消去x ,得y 2-4my-4x 0=0,因为x 0≥12,所以Δ=16m 2+16x 0>0, y 1+y 2=4m ,y 1y 2=-4x 0.设P 的坐标为(x P ,0),则PE ⃗⃗⃗⃗ =(x 2-x P ,-y 2),PA ⃗⃗⃗⃗⃗ =(x 1-x P ,y 1). 由题知PE ⃗⃗⃗⃗ ∥PA⃗⃗⃗⃗⃗ ,所以(x 2-x P )y 1+y 2(x 1-x P )=0, 即x 2y 1+y 2x 1=y 22y 1+y 12y 24=y 1y 2(y 1+y 2)4=(y 1+y 2)x P ,显然y 1+y 2=4m ≠0,所以x P =y 1y 24=-x 0,即证得点P 的坐标为(-x 0,0).由题知△EPB 为等腰直角三角形,所以k AP =1,即y 1+y2x 1-x 2=1,即y 1+y 214(y 12-y 22)=1,所以y 1-y 2=4,所以(y 1+y 2)2-4y 1y 2=16,即16m 2+16x 0=16,则m 2=1-x 0,x 0<1. 又因为x 0≥12,所以12≤x 0<1.d=002=2=2−x ,令√2−x 0=t ∈1,√62,则x 0=2-t 2,d=2(2−t 2)t=4t-2t ,易知f (t )=4t-2t 在1,√62上是减函数,所以d∈√63,2.例3 [思路点拨] (1)设经过焦点的直线AB 的方程为y=k x-p2(k ≠0),联立直线的方程和抛物线的方程,利用韦达定理以及斜率之积等于-p 求出p 的值,由此求得抛物线方程;(2)利用(1)求得M 点的坐标,利用直线OM 的方程求出D 点的坐标,两者横坐标的比值大于2,得证.解:(1)设A (x 1,y 1),B (x 2,y 2),直线AB (不垂直于x 轴)的方程可设为y=k x-p2(k ≠0). ∵直线AB 过点F 且与抛物线C 交于A ,B 两点,∴y 12=2px 1,y 22=2px 2.∵直线OA 与OB 的斜率之积为-p ,∴y 1y 2x 1x 2=-p ,∴(y 1y 2x 1x 2)2=p 2,得x 1x 2=4.由{y =k (x -p2),y 2=2px,得k 2x 2-(k 2p+2p )x+k 2p 24=0,其中Δ=(k 2p+2p )2-k 2p 2k 2>0,∴x 1+x 2=k 2p+2p k 2,x 1x 2=p 24,∴p=4,∴抛物线C 的方程为y 2=8x.(2)证明:设M (x 0,y 0),D (x 3,y 3),∵M 为线段AB 的中点, ∴x 0=12(x 1+x 2)=k 2p+2p 2k 2=2(k 2+2)k 2,y 0=k (x 0-2)=4k,∴直线OD 的斜率k OD =y 0x 0=2kk 2+2,∴直线OD 的方程为y=2kk 2+2x ,代入抛物线方程y 2=8x ,得x 3=2(k 2+2)2k 2,∴x3x 0=k 2+2,∵k 2>0,∴|OD||OM|=x3x 0=k 2+2>2.变式题解:(1)依题意得c a =√22,3a 2+12b 2=1,a 2=b 2+c 2,解得a 2=4,b 2=2,故椭圆C 的方程为x 24+y 22=1.(2)证明:由椭圆的对称性,不妨假设存在k>0,使得|BP||BQ|=12. 由题意得a 2=2b 2,则椭圆C :x 22b 2+y 2b 2=1,联立直线l 与椭圆C 的方程可得(1+2k 2)x 2+4kbx=0,解得x P =-4kb 1+2k 2,所以|BP |=√1+k 2×4kb1+2k 2,因为BP ⊥BQ ,所以|BQ |=√1+(-1k)2×4(-1k)b1+2(-1k)2=√1+k 2×4bk 2+2,因为|BP||BQ|=12,所以2√1+k 2×4kb 1+2k 2 =√1+k 2×4bk 2+2,即2k 3-2k 2+4k-1=0.记f (x )=2x 3-2x 2+4x-1,因为f (14)<0,f (12)>0,所以函数f (x )存在零点,所以存在k ∈R ,使得|BP||BQ|=12.第3课时定点﹑定值﹑探索性问题【课堂考点探究】例1 [思路点拨] (1)设C (x ,y )(y ≠0),由题意与两点间的距离公式可得结论;(2)设直线MN 的方程为x=my+n ,M (x 1,y 1),N (x 2,y 2),联立直线与抛物线的方程结合韦达定理可得y 1y 2的表达式,结合条件中的斜率关系可得到y 1y 2的值,进而建立一个等式,可求得结果.解:(1)设C (x ,y )(y ≠0),因为B 在x 轴上且BC 的中点在y 轴上,所以B (-x ,0),由|AB |=|AC |,得(x+1)2=(x-1)2+y 2,化简得y 2=4x ,所以点C 的轨迹Γ的方程为y 2=4x (y ≠0).(2)证明:设直线MN 的方程为x=my+n ,M (x 1,y 1),N (x 2,y 2), 由{y 2=4x,x =my +n,得y 2-4my-4n=0,所以y 1y 2=-4n. k MP =y 1-2x 1-1=y 1-2y 124-1=4y1+2,同理k NP =4y 2+2,所以4y1+2+4y2+2=2,化简得y 1y 2=4,又因为y 1y 2=-4n ,所以n=-1, 所以直线MN 过定点(-1,0).变式题解:(1)如图,因为☉C 1内切☉C 2于点A ,所以r-1=2,解得r=3,所以☉C 2的方程为(x-1)2+y 2=9.因为直线PQ ,PR 分别切☉C 1,☉C 2于Q ,R ,所以C 1Q ⊥PQ ,C 2R ⊥PR ,连接PM ,在Rt △PQM 与Rt △PRM 中,|PQ |=|PA |=|PR |,|PM |=|PM |,所以|QM |=|RM |,所以|MC 1|+|MC 2|=|MQ |+|C 1Q|+|MC 2|=|MR |+|C 1Q|+|C 2M|=|C 1Q|+|C 2R|=4>2=|C 1C 2|, 所以点M 的轨迹C 是以C 1,C 2为焦点,长轴长为4的椭圆(除去长轴端点), 所以M 的轨迹C 的方程为x 24+y 23=1(y ≠0).(2)证明:依题意,设直线MN 的方程为x=ty-1(t ≠0),M (x 1,y 1),N (x 2,y 2), 则M'(x 1,-y 1)且x 1≠x 2,y 1+y 2≠0, 联立{x =ty -1,x 24+y 23=1,消去x ,并整理得(3t 2+4)y 2-6ty-9=0, Δ=(-6t )2-4×(-9)(3t 2+4)=144t 2+144>0,则y 1+y 2=6t 3t 2+4,y 1y 2=-93t 2+4,直线M'N 的方程为y+y 1=y 2+y 1x 2-x 1(x-x 1),令y=0,得x=y 1(x 2-x 1)y 2+y 1+x 1=y 1x 2+x 1y 2y 2+y 1=y 1(ty 2-1)+y 2(ty 1-1)y 2+y 1=2ty 1y 2y 2+y 1-1=-18t 3t 2+46t 3t 2+4-1=-4,故直线M'N 过定点(-4,0).例2 [思路点拨] (1)由题意求得a 2,c 2,再由b 2=a 2-c 2求得b 2,从而可得椭圆的标准方程;(2)证明:设C (x 3,y 3),D (x 4,y 4),可求得直线AR 的方程,与椭圆方程联立,由韦达定理可求得y 1y 3=-4y 125−x 1,进一步可求C 的坐标,同理得D 的坐标,从而可得k 2与k 1的关系式,化简运算即可.解:(1)由题意得{c a =23,a -c =1,解得{a =3,c =2,∴b 2=a 2-c 2=5,故椭圆E 的标准方程为x 29+y 25=1.(2)证明:设C (x 3,y 3),D (x 4,y 4), 由已知得,直线AR 的方程为y=y 1x 1-1(x-1),即x=x 1-1y 1y+1.联立{x =x 1-1y 1y +1,x 29+y 25=1,消去x 并整理,得5−x 1y 12y 2+x 1-1y 1y-4=0,则y 1y 3=-4y 125−x 1,∵y 1≠0,∴y 3=4y1x 1-5, ∴x 3=x 1-1y 1y 3+1=x 1-1y 1·4y 1x 1-5+1=5x 1-9x 1-5, ∴C5x 1-9x 1-5,4y 1x 1-5.同理D5x 2-9x 2-5,4y 2x 2-5, ∴k 2=4y 1x 1-5-4y 2x 2-55x 1-9x 1-5-5x 2-9x 2-5=4y 1(x 2-5)-4y 2(x 1-5)(5x1-9)(x 2-5)-(5x 2-9)(x 1-5)=4y 1(x 2-5)-4y 2(x 1-5)16(x 2-x 1),∵y 1=k 1(x 1+2),y 2=k 1(x 2+2), ∴k 2=4k 1(x 1+2)(x 2-5)-4k 1(x 2+2)(x 1-5)16(x 2-x 1)=7k 1(x 2-x 1)4(x 2-x 1)=7k 14,∴k1k 2=47为定值.变式题解:(1)设点P 的坐标为(x ,y ),因为定点F12,0在定直线l : x=-2的右侧,且动点P 到定直线l : x=-2的距离比到定点F 12,0的距离大32,所以x>-2且√(x -12)2+y 2=|x+2|-32,化简得√(x -12)2+y 2=x+12,即y 2=2x ,所以轨迹C 的方程为y 2=2x.(2)证明:设A (2t 12,2t 1),B (2t 22,2t 2)(t 1·t 2≠0),则DA ⃗⃗⃗⃗⃗ =(2t 12-2,2t 1),DB ⃗⃗⃗⃗⃗ =(2t 22-2,2t 2),因为A ,D ,B 三点共线,所以2t 2(2t 12-2)=2t 1(2t 22-2),所以(t 1-t 2)(t 1t 2+1)=0,又t 1≠t 2,所以t 1t 2=-1.直线OA 的方程为y=1t 1x ,令x=-2,得M -2,-2t 1.同理可得N -2,-2t 2,所以以线段MN 为直径的圆的方程为(x+2)(x+2)+y+2t1y+2t2=0,即(x+2)2+y 2+2t 1+t 2t 1t 2y+4t 1t 2=0.将t 1t 2=-1代入上式,可得(x+2)2+y 2-2(t 1+t 2)y-4=0, 令y=0,得x=0或x=-4,故以线段MN 为直径的圆被x 轴截得的弦长为定值4.例3 [思路点拨] (1)设M 点坐标为(x ,y ),直接找出关于x ,y 的方程,这就是曲线C 的轨迹方程;(2)设P (m ,0),由∠APF=∠BPF 可知直线BP 与AP 的倾斜角互补,即k BP +k AP =0,得到关于m 的方程,求出m 的值即可.解:(1)设M (x ,y ),则依题意有√(x -1)2+y 2|x -4|=12,整理得x 24+y 23=1,即为曲线C 的方程. (2)存在.设直线AB 的方程为x=ty+1(t ≠0),A (ty 1+1,y 1),B (ty 2+1,y 2),P (m ,0), 则由{x =ty +1,3x 2+4y 2=12,消去x ,得3(ty+1)2+4y 2=12,即(3t 2+4)y 2+6ty-9=0, 则y 1+y 2=-6t3t 2+4,y 1y 2=-93t 2+4, 由∠APF=∠BPF ,得k AP +k BP =0,即y 1ty 1+1−m +y 2ty 2+1−m=0,整理得2ty 1y 2+(1-m )(y 1+y 2)=0, 所以2t ·-93t 2+4+(1-m )·-6t3t 2+4=0,解得m=4.综上知,在x 轴上存在点P (4,0)满足题意.变式题解:(1)依题意可知,△PF 1F 2的周长为|PF 1|+|PF 2|+|F 1F 2|,由于|F 1F 2|=2,故|PF 1|+|PF 2|=4,由于|PF 1|+|PF 2|>|F 1F 2|,故点P 的轨迹C 1是以F 1,F 2为焦点的椭圆的一部分,且a=2,c=1,故b=√3,故C 1的方程为x 24+y 23=1(x ≠±2),C 2的方程为y 2=4x.(2)假设存在.设A (x 1,y 1),B (x 2,y 2),M (x 0,y 0),设直线AB 的方程为x=my+1, 由{x =my +1,y 2=4x,得y 2-4my-4=0,故y 1+y 2=4m ,y 1y 2=-4, 又k MA +k MB =y 0-y 1x 0-x 1+y 0-y 2x 0-x 2=2k MF 2=2y0x 0-1, 所以(y 0-y 1)(x 0-my 2-1)+(y 0-y 2)(x 0-my 1-1)(x 0-my 1-1)(x 0-my 2-1)=2y 0x 0-1,即-(y 1+y 2)(x 0-1)2+my 0(y 1+y 2)(x 0-1)+2my 1y 2(x 0-1)=2m 2y 0y 1y 2, 即m (x 0+1)(x 0-my 0-1)=0,因为直线AB 不经过点M ,所以x 0-my 0-1≠0,故m=0或x 0+1=0. 当m=0时,C 1上除点1,±32外,均符合题意; 当m ≠0时,M 为-1,32和-1,-32都符合题意.。

高中圆锥曲线综合部分总复习

圆锥曲线与方程综合部分一、知识点梳理椭圆、双曲线：二、章节知识点回顾：椭圆、双曲线、抛物线分别是满足某些条件的点的轨迹，由这些条件可以求出它们的标准方程，并通过分析标准方程研究这三种曲线的几何性质1．椭圆定义：在平面内，到两定点距离之和等于定长（定长大于两定点间的距离）的动点的轨迹2．椭圆的标准方程：12222=+b y a x ，12222=+b x a y （0>>b a ）3．椭圆的性质：由椭圆方程12222=+by a x (0>>b a )(1)范围: a x a ≤≤-,b y b ≤≤-，椭圆落在b y a x ±=±=,组成的矩形中． (2)对称性:图象关于y 轴对称．图象关于x 轴对称．图象关于原点对称原点叫椭圆的对称中心，简称中心．x 轴、y 轴叫椭圆的对称轴．从椭圆的方程中直接可以看出它的范围，对称的截距（3）顶点：椭圆和对称轴的交点叫做椭圆的顶点椭圆共有四个顶点： )0,(),0,(2a A a A -，),0(),,0(2b B b B -加两焦点)0,(),0,(21c F c F -共有六个特殊点21A A 叫椭圆的长轴，21B B 叫椭圆的短轴．长分别为b a 2,2 b a ,分别为椭圆的长半轴长和短半轴长椭圆的顶点即为椭圆与对称轴的交点(4)离心率: 椭圆焦距与长轴长之比a c e =⇒2)(1abe -=10<<e椭圆形状与e 的关系：0,0→→c e ，椭圆变圆，直至成为极限位置圆，此时也可认为圆为椭圆在0=e 时的特例,,1a c e →→椭圆变扁，直至成为极限位置线段21F F ，此时也可认为圆为椭圆在1=e 时的特例4．双曲线的定义：平面内到两定点21,F F 的距离的差的绝对值为常数（小于21F F ）的动点的轨迹叫双曲线即a MF MF 221=- 这两个定点叫做双曲线的焦点，两焦点间的距离叫做焦距在同样的差下，两定点间距离较长，则所画出的双曲线的开口较开阔（→两条平行线）两定点间距离较短（大于定差），则所画出的双曲线的开口较狭窄（→两条射线）双曲线的形状与两定点间距离、定差有关 5．双曲线的标准方程及特点：（1）双曲线的标准方程有焦点在x 轴上和焦点y 轴上两种：焦点在x 轴上时双曲线的标准方程为：12222=-b y a x (0>a ,0>b )；焦点在y 轴上时双曲线的标准方程为：12222=-bx a y (0>a ,0>b )6.c b a ,,有关系式222b a c +=成立，且0,0,0>>>c b a 其中a 与b 的大小关系:可以为b a b a b a ><=,,7焦点的位置:从椭圆的标准方程不难看出椭圆的焦点位置可由方程中含字母2x 、2y 项的分母的大小来确定，分母大的项对应的字母所在的轴就是焦点所在的轴而双曲线是根据项的正负来判断焦点所在的位置，即2x 项的系数是正的，那么焦点在x 轴上；2y 项的系数是正的，那么焦点在y 轴上 8．双曲线的几何性质：（1）范围、对称性由标准方程12222=-by a x ，从横的方向来看，直线x=-a,x=a 之间没有图象，从纵的方向来看，随着x 的增大，y 的绝对值也无限增大，所以曲线在纵方向上可无限伸展，不像椭圆那样是封闭曲线双曲线不封闭，但仍称其对称中心为双曲线的中心（2）顶点顶点：()0,),0,(21a A a A -，特殊点：()b B b B -,0),,0(21实轴：21A A 长为2a, a 叫做半实轴长虚轴：21B B 长为2b ，b 叫做虚半轴长双曲线只有两个顶点，而椭圆则有四个顶点，这是两者的又一差异（3）渐近线过双曲线12222=-by a x 的渐近线x a b y ±=（0=±b y a x ）（4）离心率双曲线的焦距与实轴长的比aca c e ==22，叫做双曲线的离心率范围：1>e 双曲线形状与e 的关系：1122222-=-=-==e a c a a c a b k ，e 越大，即渐近线的斜率的绝对值就大，这是双曲线的形状就从扁狭逐渐变得开阔由此可知，双曲线的离心率越大，它的开口就越阔 9．等轴双曲线定义：实轴和虚轴等长的双曲线叫做等轴双曲线，这样的双曲线叫做等轴双曲线等轴双曲线的性质：（1）渐近线方程为：x y ±=；（2）渐近线互相垂直；（3）离心率2=e 10．共渐近线的双曲线系如果已知一双曲线的渐近线方程为x a b y ±=)0(>±=k x kakb，那么此双曲线方程就一定是：)0(1)()(2222>±=-k kb y ka x 或写成λ=-2222b y a x 11．共轭双曲线以已知双曲线的实轴为虚轴，虚轴为实轴，这样得到的双曲线称为原双曲线的共轭双曲线区别：三量a,b,c 中a,b 不同（互换）c 相同共用一对渐近线双曲线和它的共轭双曲线的焦点在同一圆上确定双曲线的共轭双曲线的方法：将1变为-112．双曲线的焦点弦：定义：过焦点的直线割双曲线所成的相交弦焦点弦公式：当双曲线焦点在x 轴上时，过左焦点与左支交于两点时： )(221x x e a AB +--= 过右焦点与右支交于两点时：)(221x x e a AB ++-= 当双曲线焦点在y 轴上时，过左焦点与左支交于两点时：)(221y y e a AB +--= 过右焦点与右支交于两点时：)(221y y e a AB ++-=13．双曲线的通径：定义：过焦点且垂直于对称轴的相交弦 ab d 22=14 抛物线定义：平面内与一个定点F 和一条定直线l 的距离相等的点的轨迹叫做抛物线定点F 叫做抛物线的焦点，定直线l 叫做抛物线的准线 15．抛物线的准线方程：(1))0(22>=p px y , 焦点:)0,2(p ，准线l ：2px -=(2))0(22>=p py x , 焦点:)2,0(p ，准线l ：2py -=(3))0(22>-=p px y , 焦点:)0,2(p -，准线l ：2px =(4) )0(22>-=p py x , 焦点:)2,0(p -，准线l ：2py =相同点：(1)抛物线都过原点；(2)对称轴为坐标轴；(3)准线都与对称轴垂直，垂足与焦点在对称轴上关于原点对称它们到原点的距离都等于一次项系数绝对值的41，即242pp = 不同点：(1)图形关于X 轴对称时，X 为一次项，Y 为二次项，方程右端为px 2±、左端为2y ；图形关于Y 轴对称时，X 为二次项，Y 为一次项，方程右端为py 2±，左端为2x （2）开口方向在X 轴（或Y 轴）正向时，焦点在X 轴（或Y 轴）的正半轴上，方程右端取正号；开口在X 轴（或Y 轴）负向时，焦点在X 轴（或Y 轴）负半轴时，方程右端取负号 16．抛物线的几何性质（1）范围因为p ＞0，由方程()022>=p px y 可知，这条抛物线上的点M 的坐标(x ，y)满足不等式x≥0，所以这条抛物线在y 轴的右侧；当x 的值增大时，|y|也增大，这说明抛物线向右上方和右下方无限延伸．（2）对称性以－y 代y ，方程()022>=p px y 不变，所以这条抛物线关于x 轴对称，我们把抛物线的对称轴叫做抛物线的轴．（3）顶点抛物线和它的轴的交点叫做抛物线的顶点．在方程()022>=p px y 中，当y=0时，x=0，因此抛物线()022>=p px y 的顶点就是坐标原点．（4）离心率抛物线上的点M 与焦点的距离和它到准线的距离的比，叫做抛物线的离心率，用e 表示．由抛物线的定义可知，e=1． 17抛物线的焦半径公式：抛物线)0(22>=p px y ，0022x pp x PF +=+= 抛物线)0(22>-=p px y ，0022x pp x PF -=-= 抛物线)0(22>=p py x ，0022y pp y PF +=+= 抛物线)0(22>-=p py x ，0022y pp y PF -=-= 18．直线与抛物线：（1）位置关系：相交（两个公共点或一个公共点）；相离（无公共点）；相切（一个公共点）将b kx y l +=:代入0:22=++++F Ey Dx Cy Ax C ，消去y ，得到关于x 的二次方程02=++c bx ax （*）若0>∆，相交；0=∆，相切；0<∆，相离综上，得：联立⎩⎨⎧=+=px y b kx y 22，得关于x 的方程02=++c bx ax当0=a （二次项系数为零），唯一一个公共点（交点）当0≠a ，则若0>∆，两个公共点（交点） 0=∆，一个公共点（切点） 0<∆，无公共点（相离）（2）相交弦长：弦长公式：21k ad +∆=，（3）焦点弦公式：抛物线)0(22>=p px y ， )(21x x p AB ++= 抛物线)0(22>-=p px y ， )(21x x p AB +-= 抛物线)0(22>=p py x ， )(21y y p AB ++= 抛物线)0(22>-=p py x ，)(21y y p AB +-=（4）通径：定义：过焦点且垂直于对称轴的相交弦通径：p d 2= （5）若已知过焦点的直线倾斜角θ则⎪⎩⎪⎨⎧=-=px y p x k y 2)2(20222=--⇒p y k p y ⎪⎩⎪⎨⎧-==+⇒221212p y y k p y y θsin 24422221p p kp y y =+=-⇒θθ221sin 2sin 1p y y AB =-=⇒ （6）常用结论：⎪⎩⎪⎨⎧=-=pxy p x k y 2)2(20222=--⇒p y k p y 和04)2(22222=++-p k x p p k x k 221p y y -=⇒和421px x =----------------------------------------------------------------------------------------------------------------- 椭圆习题：选择题1．已知椭圆1162522=+y x 上的一点P 到椭圆一个焦点的距离为3，则P 到另一焦点距离为（）A ．2B ．3C ．5D ．72．若椭圆的对称轴为坐标轴，长轴长与短轴长的和为18，焦距为6，则椭圆的方程为（）A ．116922=+y x B ．1162522=+y x C ．1162522=+y x 或1251622=+y x D ．以上都不对 3．如果222=+ky x 表示焦点在y 轴上的椭圆，那么实数k 的取值范围是（）A ．()+∞,0B ．()2,0C ．()+∞,1D ．()1,04．以椭圆1162522=+y x 的顶点为顶点，离心率为2的双曲线方程（） A ．1481622=-y x B ．127922=-y x C ．1481622=-y x 或127922=-y x D ．以上都不对 5．椭圆1244922=+y x 上一点P 与椭圆的两个焦点1F 、2F 的连线互相垂直，则△21F PF 的面积为（）A ．20B ．22C ．28D ．246．与椭圆1422=+y x 共焦点且过点(2,1)Q 的双曲线方程是（） A ．1222=-y x B ．1422=-y x C ．13322=-y x D ．1222=-y x 填空题：7．若椭圆221x my +=_______________. 8．椭圆5522=+ky x 的一个焦点是)2,0(，那么=k 。

圆锥曲线复习讲义(1)

圆锥曲线复习讲义（1）椭圆一．复习目标：1．正确理解椭圆的两种定义，能运用定义解题，能根据条件，求出椭圆的标准方程；2．掌握椭圆的几何性质，能利用椭圆的几何性质，确定椭圆的标准方程；3．理解椭圆的参数方程，并掌握它的应用；4．掌握直线与椭圆位置关系的判定方法，能解决与弦长、弦的中点有关的问题.二．基础训练：1．已知椭圆的方程为191622=+y x ，1F 、2F 分别为它的焦点，CD 为过1F 的弦，则△CD F 2 的周长为．2．已知椭圆的离心率32=e ，焦距是16，则椭圆的标准方程是 . 3．已知方程12322=-++ky k x 表示椭圆，则k 的取值范围为 . 4．椭圆2225161x y +=的焦点坐标为 .三．例题分析：例1．如图，PMN ∆中，1tan 2PMN ∠=,tan 2PNM ∠=-,PMN ∆面积为1，建立适当的坐标系，求以M 、N 为焦点，经过点P 的椭圆方程.M NP例2．已知椭圆的中心在坐标原点O ，一条准线方程为1x =，倾斜角为45的直线交椭圆于A 、B 两点,设线段AB 的中点为M ，直线AB 与OM 的夹角为α，(1)当arctan 2α=时，求椭圆的方程；(2)当2tan 3α<<时，求椭圆的短轴长的取值范围.例3.已知椭圆的一个顶点为()0,1A ,焦点在x 轴上，且右焦点到直线0x y -+=的距离为3，试问能否找到一条斜率为(0)k k ≠的直线l ,使l 与已知椭圆交于不同的两点M 、N 且满足||||AM AN =，并说明理由.四．课后作业：班级学号姓名1．ABC ∆的一边BC 在x 轴上，BC 的中点在原点，||16BC =，AB 和AC 两边上中线长的和为30，则此三角形重心G 的轨迹方程是 .2．直线10y kx --=与椭圆2215x y m+=恒有共点时，则m 的取值范围是___ _____. 3．已知1F 、2F 是椭圆1486422=+y x 的左、右焦点，P 为椭圆上一点，若213PF PF =，则P 到左准线的距离为．4．方程221616x ky k +=的曲线是焦点在y 轴上的椭圆，则k 的取值范围是 .5．(,)P x y 是椭圆123222=+y x 上的一个动点，则2x y +的最大值是，最小值是。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

圆锥曲线综合复习题精选1 ．已知圆22670xy x +--=与抛物线()220y px p =>的准线相切,则p 的值为A.1B.2C.12D.42 ．已知圆22104xy mx ++-=与抛物线214y x =的准线相切,则m= (A)±22 (B)3 (C) 2 (D)±33 ．已知与向量v=(1,0)平行的直线l 与双曲线2214x y -=相交于A 、B 两点,则A B 的最小值为A.2B.5C.4D.254 ．若抛物线)0(22>=p px y 的焦点在直线022=--y x 上,则该抛物线的准线方程为A.2x =-B. 4=xC. 8-=xD. 4-=y5 ．已知椭圆:)20(14222<<=+b by x ,左右焦点分别为21F F ，,,过1F 的直线l 交椭圆于A,B 两点,若||||22AF BF +的最大值为5,则b 的值是A.1 B.2 C.23D.36 ．已知点P 是抛物线x 2=4y 上的动点,点P 在直线y+1=0上的射影是点M,点A 的坐标(4,2),则P A P M+的最小值是( ) A.17B.13C.3D.27 ．已知双曲线22221(0,0)x y a b a b-=>>的两条渐近线均与22:650C x y x +-+=相切,则该双曲线离心率等于（）356C.3258．已知双曲线()0,012222>>=-b a by a x 的一条渐近线的斜率为2,且右焦点与抛物线x y 342=的焦点重合,则该双曲线的离心率等于 (A)2(B)3(C)2(D)239．已知抛物线22(0)y px p =>的焦点F 与双曲22145x y -=的右焦点重合,抛物线的准线与x 轴的交点为K,点A 在抛物线上且AK =A 点的横坐标为(A) (B)3 (C) (D)410．已知双曲线的方程为()222210,2x y a b a b -=>>,(其中c为双曲线的半焦距长),则该双曲线的离心率为A.32D.5211．已知三个数2,8m ，构成一个等比数列,则圆锥曲线2212x y m +=的离心率为12．设双曲线2221()9x y a o a -=>的焦点为(5,0),则该双曲线的离心率等于( )A.32 B.43C.54D.5313．以双曲线22163x y -=的右焦点为圆心且与双曲线的线相切的圆的方程是A.(22x y +=B.(223x y +=C.()223x y -+=D.()2233x y -+=14．已知抛物线y 2 =2px (p>0)上一点M(1,m)(m>0)到其焦点F 的距离为5,则以M 为圆心且与y 轴相切的圆的方程为A.(x-1)2+(y-4)2=1 B.(x-1)2+(y+4)2=1C.(x-l)2+(y-4)2=16 D.(x-1)2+(y+4)2=1615．抛物线)0(42>=p px y 与双曲线)0,0(12222>>=-b a by a x 有相同的焦点F ,点A 是两曲线的交点,且AF ⊥x 轴,则双曲线的离心率为A.215+ B.12+ C.13+ D.2122+ 16．已知抛物线x y 42=的焦点为F ,准线为l ,点P 为抛物线上一点,且在第一象限,l PA ⊥,垂足为A ,4PF =,则直线AF 的倾斜角等于A.712πB.23π C.34π D.56π17．若抛物线y 2=2px 的焦点与椭圆2262x y +=1的右焦点重合,则p 的值为A.-2B.2C.-4D.418．已知双曲线22221x y a b-=的实轴长为2,焦距为4,则该双曲线的渐近线方程是A.3y x =±B.y x =C.y =D.2y x =± 19．已知椭圆方程22143x y +=,双曲线的焦点是椭圆的顶点,顶点是椭圆的焦点,则双曲线的离心率C. 2D. 320．过点P(0,2)的双曲线C 的一个焦点与抛物线216xy 的焦点相同,则双曲线C 的标准方程是( )A.221124x y B.221204x yC.221412y xD.221420y x21．已知双曲线2219x y a-=的右焦点为则该双曲线的渐近线方程为_______·22．已知抛物线22(0)xpy p =>与圆221x y +=有公共的切线y x b =+,则p =_____.23．若双曲线221y x m-=的一个焦点与抛物线28y x =的焦点重合,则m 的值为__________.24．已知双曲线223x y m m -=1的一个焦点是(0,2),椭圆221y x n m-=的焦距等于4,则n=________25．已知双曲线22221(0,0)x y a b a b-=>>的一条渐近线与直线210x y +-=垂直,则曲线的离心率等于______________.26．设双曲线221x y m n+=的离心率为2,且一个焦点与抛物线28x y =的焦点相同,则此双曲线的方程为______.27．已知抛物线28y x =-的准线过双曲线2213x y m -=的右焦点,则双曲线的离心率为______. 28．若双曲线()222210x y a b a b-=>>的左、右焦点分别为F 1,F 2,线段F 1F 2被抛物线22y bx =的焦点分成5:3两段,则此双曲线的离心率为______.29．已知双曲线22221(0,0)x y a b a b-=＞＞的左顶点与抛物线22(0)y px p =＞的焦点的距离为4,且双曲线的一条渐近线与抛物线准线的交点坐标为(2,1--),则双曲线的焦距为____________.30．设21F F ，分别是椭圆:)0(2222>>+b a by a x 的左、右焦点,过1F 倾斜角为45的直线l 与该椭圆相交于P,Q 两点,且a PQ 34||=. (Ⅰ)求该椭圆的离心率;(Ⅱ)设点)10(-，M 满足||||MQ MP =,求该椭圆的方程.31．如图,椭圆22221(0)x y a b a b +=>>的左、右焦点分别为1(0)F c -，,2(0)F c ，.已知点M 在椭圆上, 且点M 到两焦点距离之和为4.(1)求椭圆的方程;(2)设与MO (O 为坐标原点)垂直的直线交椭圆于,A B (,A B 不重合),求OB OA ⋅的取值范围.32．已知椭圆()0,012222>>=+b a by a x 的左焦点F 为圆0222=++x y x 的圆心,且椭圆上的点到点F 的距离最小值为12-. (I)求椭圆方程;(II)已知经过点F 的动直线l 与椭圆交于不同的两点A 、B,点M(0,45-),证明:MB MA ⋅为定值. 33．已知椭圆221:1164y x C +=,椭圆C 2以C 1的短轴为长轴,且与C 1有相同的离心率. (I)求椭圆C 2的方程;(II)设直线l 与椭圆C 2相交于不同的两点A 、B,已知A 点的坐标为()2,0-,点()00,Q y 在线段AB 的垂直平分线上,且4QA QB ⋅=,求直线l 的方程.34．设椭圆的中心为坐标原点O,焦点在x 轴上,焦距为2,F 为右焦点,1B 为下顶点,2B 为上顶点,121B FB S ∆=.(I)求椭圆的方程;(Ⅱ)若直线l 同时满足下列三个条件:①与直线1B F 平行;②与椭圆交于两个不同的点P Q 、;③23POQ S ∆=,求直线l 的方程.35．已知椭圆2222:1x y C a b +=()0a b >>1F 、2F 分别为椭圆C 的左、右焦点,过F 2的直线l 与C 相交于A 、B 两点,1F AB ∆的周长为(I)求椭圆C 的方程;(II)若椭圆C 上存在点P,使得四边形OAPB 为平行四边形,求此时直线l 的方程.36．已知椭圆C 的中心在坐标原点焦点在x 轴上,左、右焦点分别为F 1、F 2,且1232,1,2F F P ⎛⎫= ⎪⎝⎭点在椭圆C 上.(I)求椭圆C 的方程;(II)过F 1的直线l 与椭圆C 相交于A,B 两点,且2AF B ∆,求直线l 的方程. 37．已知椭圆M:2221(0)3x y a a +=>的一个焦点为F(-1,0),左右顶点分别为A,B.经过点F 的直线l 与椭圆M交于C,D 两点.(1)求椭圆方程;(2)当直线l 的倾斜角为45o时,求线段CD 的长;(3)记△ABD 与△ABC 的面积分别为S 1和S 2,求|s 1-S 2|的最大值.38．已知圆的方程为224xy +=,过点(2,4)M 作圆的两条切线,切点分别为1A 、2A ,直线12A A 恰好经过椭圆22221(0)x y a b a b+=>>的右顶点和上顶点. (Ⅰ)求椭圆的方程;(Ⅱ)设直线1x =-与椭圆相交于A B 、两点,P 是椭圆上异于A 、B 的任意一点,直线AP 、BP 分别交定直线:4l x =-于两点Q 、R , 求证OQ OR ⋅为定值.39．已知椭圆2222:1(0)x y C a b a b +=>>.(1)求椭圆C 的方程:(2)设直线l 与椭圆C 交于A 、B 两点,坐标原点O 到直线l,求△AOB 面积的最大值.40．已知椭圆C:22221(0)x y a b a b+=>>的离心率e =,短轴长为 2.(1)求椭圆C 的方程o(2)设1122(,),(,)A x y B x y 为椭圆C 上的不同两点,已知向量1122(,),(,)x y x ym n b a b a==,且0.m n ⋅=已知O 为坐标原点,试问△AOB 的面积是否为定值?如果是,请给予证明;如果不是,请说明理由,41．如图,已知圆C 与y 轴相切于点T(0,2),与x 轴正半轴相交于两点M,N(点M 必在点N 的右侧),且3MN =,已知椭圆D:22221(0)x y a b a b +=>>的焦距等于2ON ,且过点6(2,)2( I ) 求圆C 和椭圆D 的方程;(Ⅱ) 若过点M 斜率不为零的直线l 与椭圆D 交于A 、B 两点,求证:直线NA 与直线NB 的倾角互补.42．椭圆2222:1(0)x y E a b b a+=>>的焦点到直线30x y -=的距离为10,离心率为25,抛物线2:2(0)G y px p =>的焦点与椭圆E 的焦点重合;斜率为k 的直线l 过G 的焦点与E 交于A,B,与G 交于C,D.(1)求椭圆E 及抛物线G 的方程; (2)是否存在学常数λ,使1||AB CD λ+为常数,若存在,求λ的值,若不存在,说明理由. 43．已知椭圆)0(12222>>=+b a by a x 的左右焦点分别为F 1和F 2,由4个点M(-a ,b )、N(a ,b )、F 2和F 1组成了一个高为3,面积为33的等腰梯形.(1)求椭圆的方程;(2)过点F 1的直线和椭圆交于两点A 、B,求∆F 2AB 面积的最大值.44．已知椭圆2222:1(0)x y C a b a b +=>>3,直线:2l y x =+与以原点为圆心,椭圆的短半轴为半径的圆O 相切.(Ⅰ)求椭圆C 的方程;(Ⅱ)设椭圆C 与曲线||(0)y kx k =>的交点为A 、B ,求OAB 面积的最大值.45．已知椭圆2222:1(0)x y C a b ab ,焦点到短轴端点的距离为2,2,过点 (m,o)作圆221xy 的切线l 交椭圆C 于,A,B 两点.(1)求椭圆C 的标准方程:(2)将|AB|表示为m 的函数,并求|AB|的最大值46.已知椭圆22122:1(0),(,0)x y C a b F c a b+=-＞＞、2(,0)F c 分别为其左、右焦点,A 、B 分别为其上顶点、右顶点,且满足190F AB ∠=. (1)求椭圆C 的离心率e;(2)若P 为椭圆C 上的任意一点,是否存在过点F 2、P 的直线l ,使l 与y 轴的交点R 满足22?RP PF =-若存在,求出直线l 的斜率k;若不存在,请说明理由.47．如图，已知椭圆C ：22221(0)x y a b a b +=＞＞的左、右焦点分别为F 1、F 2，点A 是椭圆上任一点，△AF 1F 2的周长为. （Ⅰ）求椭圆C 的方程；（Ⅱ）过点Q （-4,0）任作一动直线l 交椭圆C 于M ，N 两点，记MQ QN λ=，若在线段MN 上取一点R ，使得MR RN λ=-，则当直线l 转动时，点R 在某一定直线上运动，求该定直线的方程.1 ．解:圆的标准方程为22(3)16x y -+=,圆心为(3,0),半径为4.抛物线的准线为3()42p--=.所以解得=2p ,选B.2 ．抛物线的标准方程为24x y =,所以准线为1y =-.圆的标准方程为2221()24m m x y +++=,所以圆心为(,0)2m -,.所以圆心到直线的距离为11=,解的m =,选D. 3 ．由题意可设直线l 的方程为y b =,代入2214x y -=得224(1)x b =+,所以1x ==2x =-所以12A B x x =-=,所以4A B =≥,即当0b =时,A B 有最小值4,选C.4 ．抛物线的焦点坐标为(,0)2p ,代入直线220x y --=得202p-=,即4p =,所以抛物线的准线方程为4222p x =-=-=-,选A. 5 ．由题意知2a =,所以22||||48BF AF AB a ++==因为22||||BF AF +的最大值为5,所以AB 的最小值为3,当且仅当AB x ⊥轴时,取得最小值,此时33(,),(,)22A c B c ---,代入椭圆方程得229144c b+=,又22224c a b b =-=-,所以2249144b b -+=,即2291144b b -+=,所以22944b b=,解得23b =,所以b =,选D.6 ．抛物线的焦点坐标(1,0)F ,准线方程为1y =-.根据抛物线的定义可知PM PF =,所以P A P M P A P F AF +=+≥,即当A,P,F 三点共线时,=选A.7 ．圆的标准方程为22(3)4x y -+=,所以圆心坐标为(3,0)C ,半径2r =,双曲线的渐近线为by x a=±,不妨取by x a =,即0bx ay -=,因为渐近线与圆相切,所以圆心到直线的距离2d ==,即22294()b a b =+,所以2254b a =,222245b a c a ==-,即2295a c =,所以29,5e e ==选A.8．抛物线的焦点为,即c =.双曲线的渐近线方程为b y x a =,由ba=,即b =,所以22222b a c a ==-,所以223c a =,即23,e e ==即离心率为3,选B.9． B 抛物线的焦点为(,0)2p ,准线为2p x =-.双曲线的右焦点为(3,0),所以32p=,即6p =,即26y x =.过F 做准线的垂线,垂足为M,则AK AM =,即KM AM =,设(,)A x y ,则3y x =+代入26y x =,解得3x =.选B.10．不妨取双曲线的右焦点为(,0)c ,双曲线的渐近线为by x a=,即0bx ay -=.则焦点到准线的距离为=,即b =,222259b c c a ==-,所以2249c a =,即294e =,所以离心率32e =,选A. 11．因为三个数2,8m ，构成一个等比数列,所以22816m =⨯=,即4m =±.若4m =,则圆锥曲线方程为22142x y +=,此时为椭圆,其中2224,2,422a b c ===-=,所以2,a c ==,离心率为c e a ==.若4m=-,则圆锥曲线方程为22124y x-=,此时为双曲线,其中2222,4,426a b c===+=,所以a c==,离心率为cea===所以选C.12．因为双曲线的焦点为(5,0),所以5c=,又22925a c+==,所以216,4a a==,所以离心率为54cea==,选C.13．双曲线的右焦点为(3,0),双曲线的渐近线为y x=,不妨取渐近线y x=,20y-=,所以圆心到直线的距离等于圆的半径,即r====,所以圆的标准方程为22(3)3x y-+=,选D.14．抛物线的焦点为(,0)2pF,准线方程为2px=-,所以1()52pMF=--=,解得8p=,即抛物线为216y x=,又216m=,所以4m=,即(1,4)M,所以半径为1,所以圆的方程为22(1)(4)1x y-+-=,选A. 15．解:抛物线的焦点为(,0)F p,即p c=.当x c=时,2244y pc c==,所以2y c=±,不妨取2y c=,即(,2)A c c.又因为点A在双曲线上,所以222241c ca b-=,即22ac b=,所以2222ac b c a==-,即2210e e--=,解得1e=±所以双曲线的离心率为12+,选B.16．抛物线的焦点坐标为(1,0)F,准线方程为1x=-.由题意4PF PA==,则(1)4Px--=,即3Px=,所以243Py=⨯,即Py=±不妨取(1,P-,则设直线AF的倾斜角等于θ,则tanθ==所以23πθ=,选B.17．抛物线的焦点坐标为(,0)2p,椭圆的右焦点为(2,0),所以由22p=得4p=,选D.18．由题意知22,24a c==,所以1,2a c==,所以b==又双曲线的渐近线方程是by xa=±,即y=,选C.19．椭圆的焦点为(1,0),顶点为(2,0),即双曲线中1,2a c==,所以双曲线的离心率为221cea===,选C. 20．抛物线的焦点为(0,4)-,所以双曲线的焦点在y轴上,且4c=,又双曲线过点(0,2)P,所以P为双曲线的一个顶点,所以2a =,22216412b c a =-=-=,所以双曲线的标准方程为221412y x ,选C.21．双曲线的右焦点为,即c =,所以2913a c +==,所以4a =.即双曲线为22194x y -=,所以双曲线的渐近线为23y x =±.22．圆心到直线的距离1d ,所以b =抛物线的方程为22x y p =,函数的导数为21'2x y x p p ==,即1'1y x p ==,所以x p =,代入得2p y =,代入切线y x b =+得2p b p =+,即2p b =-,所以2p-=,所以p =,即p =.23．抛物线28yx =的焦点为(2,0),双曲线的一个焦点如抛物线的焦点重合,所以2c =.又221,a b m ==,所以222c a b =+,即41,3m m =+=.24．因为双曲线的焦点为(0,2),所以焦点在y 轴,所以双曲线的方程为2213y x m m -=--,即2223,,344a m b m c m m m =-=-=--=-=,解得1m =-,所以椭圆方程为21y x n+=,且0n >,椭圆的焦距为24c =,即2c =,所以214c n =-=,解得5n =.25．双曲线的渐近线为b y x a =±.直线210x y +-=的斜率为12y =-.因为by x a=与直线210x y +-=垂直,所以1()12b a ⋅-=-,即2b a =.所以22225c a b a =+=,即25,e e ==. 26．抛物线的焦点坐标为(0,2),所以双曲线的焦点在y 轴上且2c =,所以双曲线的方程为221y x n m-=-,即220,0a n b m =>=->,所以a =,又2c ea ===,解得1n =,所以222413b c a =-=-=,即3,3m m -==-,所以双曲线的方程为2213x y -=. 27．抛物线的焦点坐标为(2,0)-,准线方程为2x =.则2c =.所以234c m =+=,解得1m =,所以双曲线的离心率为2ce a==.28．抛物线的焦点坐标为(,0)2b,由题意知()5232bc b c --=-,2c b =,所以222244()c b c a ==-,即2243a c =,所以2a =,所以c e a ===. 29．双曲线的左顶点为(,0)a -,抛物线的焦点为(,0)2p ,准线方程为2p x =-.由题意知()42pa --=,即42p a +=.又双曲线的一条渐近线与抛物线准线的交点坐标为(2,1)--,所以22px =-=-,解得4p =,代入42p a +=得2a =.且点(2,1)--也在渐近线b y x a =上,即1(2)2b -=⨯-,解得1b =,所以c ===所以双曲线的焦距为2c =.30．解:(Ⅰ)直线PQ 斜率为1,设直线l 的方程为c x y +=,其中22b a c -=设),(),,(2211y x Q y x P ,则Q P ,两点坐标满足方程组⎪⎩⎪⎨⎧=++=12222b y ax cx y 化简得0)(2)(2222222=-+++b c a cx a x b a ,则222212b a c a x x +-=+,.2222221b a b c a x x +-=因为,所以a x x x x x x PQ 34]4)[(2||2||2122112⋅-+=-=得222434b a ab a +=,故222b a =,所以椭圆的离心率2222=-==a b a a c e (Ⅱ)设PQ 的中点为),(00y x N ,由(1)知.3,32200222210c c x y c b a c a x x x =+=-=+-=+=由||||MQ MP =得1-=MN k 即1100-=+x y ,得3=c ,从而3,23==b a .故椭圆的方程为191822=+y x31【答案】解:(1)∵2a=4, ∴a=2又M 在椭圆上,∴231142b+=解得:22=b ,∴所求椭圆方程12422=+y x (2)66=MO k ,∴6-=AB k .设直线AB 的方程:m x y +-=6,联立方程组⎪⎩⎪⎨⎧+-==+m x y y x 612422消去y得:042641322=-+-m mx x 0)261312(8)42(134)64(2222>+-=-⨯-=∆m m m m ,∴262<m .136421mx x =+,1342221-=m x x 设),(),,(2211y x B y x A ,则13283)(672221212121-=++-=+=⋅m m x x m x x y y x x OB OA ∴OB OA ⋅的取值范围2850[,)1313- 32．【答案】33．【答案】34．【答案】35．【答案】36．【答案】37．【答案】38．【答案】解:(Ⅰ)观察知,2x =是圆的一条切线,切点为1(2,0)A ,设O 为圆心,根据圆的切线性质,12MO A A ⊥,所以12112A A MOk k =-=-,所以直线12A A 的方程为1(2)2y x =--直线12A A 与y 轴相交于(0,1),依题意2,1a b ==,所求椭圆的方程为2214x y +=(Ⅱ)椭圆方程为2214x y +=,设),,(00y x P (1,),A t -(1,),B t --则有2200440x y +-=,22440m n +-=在直线AP 的方程0(1)1t y y t x x --=+--中,令4x =-,整理得000(4)3.(1)Q x t y y x +-=+ ①同理,0003(4).(1)R y x ty x --+=+ ②①⨯②,并将220011,4y x=-234t=代入得RQyy⋅2220029(4)(1)y x tx-+=+=22002139(1)(4)44(1)x xx--+⋅+=223(1)(1)xx-++=3-而()()4,4,16Q R Q ROQ OR y y y y=-⋅-=+⋅=13为定值39．40．【答案】41．【答案】解:(Ⅰ)设圆的半径为r ,由题意,圆心为(,2)r ,因为||3MN =,所以2223255()2,,242r r =+==故圆C的方程是22525()(2)24x y -+-= ①在①中,令0y =解得1x =或4x =,所以(1,0),(4,0).N M 由2212c c e a =⎧⎪⎨==⎪⎩得1,2c a ==,故23b =所以椭圆D 的方程为22143x y +=(Ⅱ)设直线l 的方程为(4).y k x =-由22143(4)x y y k x ⎧+=⎪⎨⎪=-⎩得2222(34)3264120k x k x k +-+-=○*设1122(,),(,),A x yB x y 则22121222326412,.3434k k x x x x k k -+==++因为12121212(4)(4)1111AN BN y y k x k x k k x x x x --+=+=+----122112(4)(1)(4)(1)(1)(1)x x x x k x x --+--=⋅--121212[25()8](1)(1)k x x x x x x =⋅-++--2222122(6412)160[8](1)(1)3434k k k x x k k -=⋅-+--++=0.所以AN BN k k =-,当11x =或21x =时,12k =±,此时,对方程○*,0∆=,不合题意. 所以直线AN 与直线BN 的倾斜角互补 42．【答案】43．【答案】解:(1)由条件,得b=3,且333222=+ca ,所以a+c=3又322=-c a ,解得a=2,c=1. 所以椭圆的方程13422=+y x (2)显然,直线的斜率不能为0,设直线方程为x=my -1,直线与椭圆交于A(x 1,y 1),B(x 2,y 2).联立方程 221431x y x my ⎧+=⎪⎨⎪=-⎩,消去x 得, 096)43(22=--+my y m ,因为直线过椭圆内的点,无论m为何值,直线和椭圆总相交..439,436221221+-=+=+∴m y y m m y y ABF S 2∆=21212121y y y y F F -=-22222221221)311(14)43(1124)(+++=++=-+=m m m m y y y y ,)1(913211422++++=m m 令112≥+=m t ,设t t y 91+=,易知)31,0(∈t 时,函数单调递减, ),31(+∞∈t 函数单调递增所以当t=12+m =1即m=0时,910min =y AB F S 2∆取最大值3 44．【答案】45．【答案】46.【答案】47．【答案】解（Ⅰ）∵△AF 1F 2的周长为4+，∴224a c +=+即2a c +=+. ……………………（1分）又c e a ==解得2222, 1.a c b a c ===-=………………（3分） ∴椭圆C 的方程为22 1.4x y +=………………………………（4分）（Ⅱ）由题意知，直线l 的斜率必存在，设其方程为1122(4),(,),(,).y k x M x y N x y =+由221,4(4)x y y k x ⎧+=⎪⎨⎪=+⎩得2222(14)326440.k x k x k +++-=…………………（6分）则2212122232644,1414k k x x x x k k--+==++……………………………………（7分）由MQ QN λ=，得1122(4,,)(4,)x y x y λ---=+∴124(4),x x λ--=+∴1244x x λ+=-+.……………………………………（8分）设点R 的坐标为（00,x y ），由MR RN λ=，得01012020(,)(,),x x y y x x y y λ--=---∴0120(),x x x x λ-=-- 解得1121221212011224424().41()814x x x x x x x x x x x x x x x λλ++⋅-+++===+-++++………………（10分）而22121222264432824()24,141414k k x x x x k k k --++=⨯+⨯=-+++ 21222328()88,1414k x x k k-++=+=++ ∴2028141,814k x k -+==-+…………………………………………………（13分）故点R 在定直线1x =-上. ………………………………………………（14分）。

圆锥曲线综合复习讲义