清华丘成桐数学英才班2018-2020届考试真题
2020年清华大学丘成桐数学英才班招生考试复试笔试试题全

专注名名校自主选拔 2
专注名校自主选拔
复试 笔试二
丘成桐数学英才班第二日的测试采用的是现学现考形式。这种形式非常常见,在小升初、 初升高、大学自主选拔活动中都有出现,这样的考试形式对于高中生来说难以提前准备,侧 重于考察学生的快速学习能力和数学研究能力。
清华本次安排为上午进行两场授课讲座,下午直接对所学内容笔试,笔试时间为 13:00-16:00,共 3 个小时,题目分 A、B 组,其中 A 组共 5 道大题;B 组共 3 道大题(7 道小题),内容主要为纽结理论和代数表示论,均是大学数学知识。
丘成桐英才班考试范围

丘成桐英才班考试范围全文共四篇示例,供读者参考第一篇示例:一、数学1. 初等数论:包括整数、有理数等基本概念的考察,以及一些中级数论题目的解答。
2. 数列与数学归纳法:包括等差数列、等比数列等常见数列的求和公式,以及数列与数学归纳法在解题中的应用。
3. 平面几何:包括角度、三角形、四边形、圆等几何图形的性质和相关定理的考察。
4. 进阶数学:包括微积分、线性代数等高阶数学概念和定理的考察。
5. 竞赛数学:包括奥赛数学中的高难度题目和解题技巧的练习。
二、物理1. 力学:包括牛顿三大定律、摩擦力、弹簧力等力学知识和题目。
2. 热学:包括热力学、温度、热平衡等热学基础知识和问题。
3. 电磁学:包括电场、磁场、电流等电磁学基础知识和问题。
4. 光学:包括光的传播、反射、折射等光学知识和问题。
5. 现代物理:包括相对论、量子力学等现代物理领域的知识。
三、信息学1. 基本算法:包括排序算法、查找算法等常见算法的实现和应用。
2. 数据结构:包括链表、树、图等数据结构的基本概念和应用。
3. 计算机原理:包括计算机组成原理、操作系统、编程语言等计算机基础知识。
4. 算法设计:包括贪心算法、动态规划、回溯法等高级算法设计和分析。
5. 程序设计:包括编程能力、程序调试、算法实现等计算机编程技能的练习。
以上是丘成桐英才班考试范围的主要内容,学生们需要在这些领域取得一定的基础才能进入这个特殊的班级学习。
通过参加丘成桐英才班的学习,学生们将能够更好地提高自己的数学、物理和信息学能力,为未来参加奥赛比赛和科研工作打下坚实基础。
希望学生们在这个班级的学习过程中,不断努力,不断挑战自己,取得更好的成绩。
【2000字】第二篇示例:【丘成桐英才班考试范围】丘成桐英才班作为国内著名的数学培训机构,向来以其严格的教学标准和高质量的教育服务而闻名。
对于学生来说,通过丘成桐英才班的培训,不仅可以提高数学水平,更可以为未来的学业和职业发展打下坚实的基础。
2020清华大学丘成桐数学英才班招生考试笔试题
免费下载站
2019-12-08原文
“丘成桐数学英才班”,这个班,由清华大学丘成桐主导创建”。
丘成桐教
授被誉为几何分析学科的奠基人,菲尔兹奖首位华人获得者、美国国家科学院院士、哈佛大学教授、清华大学丘成桐数学科学中心主任,目前在清
华英才班担任首席教授。
是当代公认的最具影响力的数学家之一。
“丘成桐数学英才班”建立仅有三年时间,2018年首次全国招生15人;2019年录取17名学生,其中高二学生6名,高三学生11名。
授课教师主要由普林思顿大学、哈佛大学毕业的多位数学学科的领军人物组成,而且每一位都是大名鼎鼎,比如李思、于品教授等。
2020年清华大学“丘成桐数学英才班”招生考试复试于12月7日-12月9日举行。
12月7日进行了笔试一测试与心理测试,其中笔试一共8道数学试题。
这题没答案
是不是很厉害,但他不是最厉害的,最厉害的是清华的姚班,全国数学应用领域最厉害的人物,一半都来自这个班。
用户设置不下载评论。
清华数学试题及答案

清华数学试题及答案一、选择题(每题4分,共20分)1. 下列哪个函数是奇函数?A. \( f(x) = x^2 \)B. \( f(x) = x^3 \)C. \( f(x) = |x| \)D. \( f(x) = \cos(x) \)答案:B2. 求极限 \(\lim_{x \to 0} \frac{\sin(x)}{x}\) 的值是多少?A. 0B. 1C. \(\frac{1}{2}\)D. \(\infty\)答案:B3. 以下哪个矩阵是可逆的?A. \(\begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix}\)B. \(\begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix}\)C. \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\)D. \(\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}\)答案:C4. 计算定积分 \(\int_{0}^{1} x^2 dx\) 的结果是多少?A. \(\frac{1}{3}\)B. \(\frac{1}{2}\)C. \(\frac{1}{4}\)D. \(\frac{1}{6}\)答案:A5. 以下哪个方程的解是 \(x = 2\)?A. \(x^2 - 4x + 4 = 0\)B. \(x^2 - 3x + 2 = 0\)C. \(x^2 - 5x + 6 = 0\)D. \(x^2 - 6x + 9 = 0\)答案:A二、填空题(每题4分,共20分)1. 函数 \(y = \ln(x)\) 的导数是 ________。
答案:\(\frac{1}{x}\)2. 向量 \(\vec{a} = (3, -2)\) 和 \(\vec{b} = (-1, 4)\) 的点积是 ________。
2018年清华大学自主招生数学真题选集

清华大学本试卷数学部分共有40道选择题.1.【真题】已知定义在R上的函数()fx={2x+a,x≤0lnx+a,x>0若方程f(x)=12有两个不相等的实数根,则a的取值范围是()A.−12≤a≤12B.0≤a<12C.0≤a<1D.−12<a≤04.【真题】已知抛物线C:y2=8x的焦点为F,准线为I,P是I上一点,Q是直线PF与C的一个交点,若FP=3FQ,则|QF|=()A.83B.52C.3D.27.【真题】我们把焦点相同,且离心率互为倒数的椭圆和双曲线称为一对“相关曲线”,已知F1、F2是一对相关曲线的焦点,P是它们在第一象限的交点,当∠F1PF2=30∘时,这一对相关曲线中椭圆的离心率是()A.7−4√3B.2−√3C.√3−1D.4−2√311.【真题】如图所示,为测一树的高度,在地面上选取A、B两点,从A、B两点分别测得树尖的仰角为30∘,45∘,且A、B两点之间的距离为60m,则树的高度为()A.(15+3√3)mB.(30+15√3)mC.(30+30√3)mD.(15+30√3)m14.【真题】在复平面内,复数z=2i(为虚数单位)的共轭复数对应的点位于()1+iA.第一象限B.第二象限C.第三象限D.第四象限15.【真题】设X−N(μ1,σ12),Y−N(μ2,σ22),这两个正态分布密度曲线如图所示.下列结论中正确的是()A.P(Y≥μ2)≥P(Y≥μ1)B.P(X≤σ2)≤P(X≤σ1)C.对任意正数t,P(X≤t)≥P(Y≤t) D对任意正数t,P(X≥t)≥P(Y≥t)20.【真题】如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为()cm3A.500π3cm3B.866π3cm3C.1372π3D.2048π3 cm 321.【真题】已知x,y,z 为正实数,则xy+yz x 2+y 2+z 2的最大值为()A.1B.2C.√22D.√229.【真题】已知e 1,e 2为平面上的单位向量,e 1与e 2的起点均为坐标原点O,e 1与e 2夹角为π3.平面区域D 由所有满足OP ⃗⃗⃗⃗⃗ =λe 1+μe 2的点P 组成,其中{λ+μ≤10≤λ0≤μ,那么平面区域D 的面积为()A.12B.√3C.√32D.√3431.【真题】已知α是第二象限角,且sin (π2+α)=−√55,则cos 3α+sinαcos(α−π4)=() A.−11√215 B.−9√25 C.9√25 D.11√215)的图象,只需把函数y=sin2x的图象上所有的33.【真题】为了得到函数y=sin(2x−π3点()个单位长度A.向左平行移动π3B.向右平行移动π个单位长度3C.向左平行移动π个单位长度 6个单位长度D.向右平行移动π636.【真题】若a<b<c,则函数f(x)=(x−a)(x−b)+(x−b)(x−c)+(x−c)(x−a)两个零点分别位于区间()A.(a,b)和(b,c)内B.(−∞,a)和(a,b)内C.(b,c)和(c,+∞)内D.(−∞,a)和(c,+∞)内37.【真题】设A,B是有限集,定义d(A,B)=card(A∪B)−card(A∩B),其中card(A)表示有限集A中的元素个数,命题①:对任意有限集A,B,“A≠B”是“d(A,B)>0”的充分必要条件:命题②:对任意有限集A,B,C,d(A,C)≤d(A,B)+d(B,C)()A.命题①和命题②都成立B.命题①和命题②都不成立C.命题①成立,命题②不成立D.命题①不成立,命题②成立39.【真题】已知f(x)=x5+2x3+3x2+x+1,应用秦九韶算法计算x=3时的值时需要()次乘法运算A.9B.8C.5D.4。
2024年湖北武汉华中师大一附中丘成桐少年班选拔数学试题

2024年湖北省武汉市华中师范大学第一附属中学丘成桐少年班选拔真题1、解方程:[x]= 3x-2,x=____________。
2、15转化成2进制是_______,10位的2进制数有___________。
3、Φ(x)表示不超过x的非0自然数中与x互质的自然数的个数,Ф(25)=______;Ф(77)=_____.4、甲、乙、丙3人从A地出发去270km 远的B地,每天走10km,每人最多带36 天的食物。
可以把食物分给他人。
(1)、若甲、乙两人出发,甲距离A地100km 时返回,乙可以走_____千米就要返回;(2)、若甲、乙两人出发,乙最多可以走_______千米就要返回;(3)、请设计一种方案,可以互相补给,不可以存放,如何让乙走到B再返回。
5、一批衣服进价40 元,打算以40%的利润卖出,卖了80%后打折,卖完后的总利润只有原来的86%,则打了_________折。
6、对于一些数a1,a2,…, a n,若a i>a j,且i<j则成a i,a j为逆序,a i到a n的逆序数量叫逆序数(1)、1,2,3,4的任意排列中,逆序数恰好为2的排列有_______个;(2)、设a1,a2,…, a10的逆序数为k,则a10,a9,…, a1的逆序数为_______(用k表示)。
7、计算=_____________.8、小明一步跨2级或3级台阶,一共20级台阶有种___________不同的走法。
9、有一堆石子,甲乙两人轮流取,甲先取,乙后取,每次1-5颗,如果一共12颗,______必胜;如果一共2024颗,________必胜。
10、有一个水池,单开甲管12个小时可以注满,单开乙管20个小时可以注满,现在甲开1个小时,乙开1个小时,轮流下去,注满水池要_______小时。
11、把圆柱体切成2个小的圆柱体,它的表面积增加了25.12平方分米,把它切成两个半圆柱体,它的表面积增加80平方分米,这个圆柱体的体积是_________立方分米。
清华丘成桐大学生数学竞赛2021年笔试真题computational_and_applied_21s

min
x ∈Rn
Ax − b 2 .
(a) Show that all solutions x can be written as
x = V1Σ−1 1UT1 b + V2z2,
with z2 an arbitrary vector. (b) Show that the solution x has minimal norm x 2 precisely when z2 = 0, and in which case,
=
π 6
,
determine
an
n
that
guarantees
|
xn
−
x∗|
<
1 2
× 10−8.
For
the
fixed
point
iteration
in
(b)
with
x0
=
20,
determine
an
n
that
guarantees
| xn
−
x∗|
<
1 4
.
Problem 4. Let matrix A ∈ Rm×n with m ≥ n and r = rank(A) < n, and assume A has the following SVD
(e) Prove an a priori error estimate for this method in the L2 norm:
∫1
1 2
e L2 =: e =
e2dx .
0
(b) Prove that the sequence defined by the fixed point iteration
2018年秋季精英班数学选拔测试题
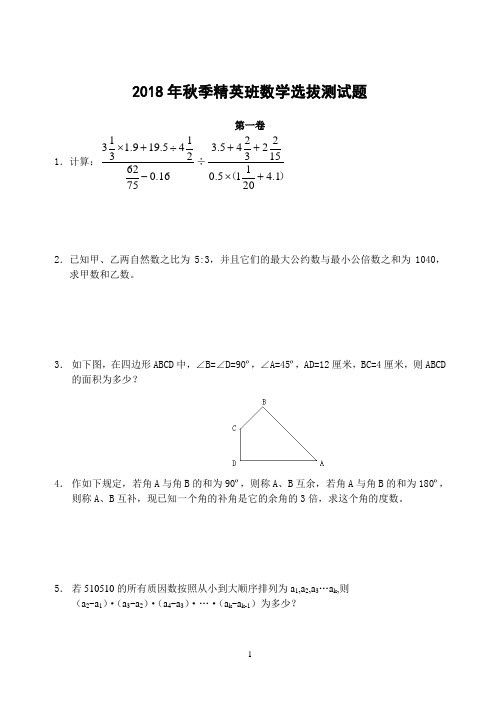
2018年秋季精英班数学选拔测试题第一卷1.计算:16.075622145.199.1313-÷+⨯÷)(1.420115.015223245.3+⨯++2.已知甲、乙两自然数之比为5:3,并且它们的最大公约数与最小公倍数之和为1040,求甲数和乙数。
3. 如下图,在四边形ABCD 中,∠B=∠D=90º,∠A=45º,AD=12厘米,BC=4厘米,则ABCD 的面积为多少?4. 作如下规定,若角A 与角B 的和为90º,则称A 、B 互余,若角A 与角B 的和为180º,则称A 、B 互补,现已知一个角的补角是它的余角的3倍,求这个角的度数。
5. 若510510的所有质因数按照从小到大顺序排列为a 1,a 2,a 3…a k ,则(a 2-a 1)·(a 3-a 2)·(a 4-a 3)·…·(a k -a k-1)为多少?6.用1到6这六个不同的数字组成一个各个数位上数字均不相同的六位数abcdef,且4|abc,5|bcd,3|cde,11|def。
那么满足上述要求的六位数是多少?第二卷1.甲乙两瓶浓度未知的酒精分别含纯酒精200毫升和450毫升,如果把它们均匀混合(忽略体积变化)则混合后的浓度比原来甲瓶的浓度高7%,但比原来乙瓶的浓度低14%,问混合后的浓度是多少2.一次象棋比赛共有10名选手参赛,他们分别来自甲、乙、丙3个队,每个人都与其余9名选手各赛一盘,每盘棋胜者都得1分,负者得0分,平局各得0.5分,结果甲队选手平均得4.5分,乙队选手平均得分3.6分,丙队选手平均得9分,那么甲、乙、丙3队各派参赛选手多少名?3.组织集体订阅,有《数理天地》月刊,全年共出12期,每期定价2.50元,其小学六年级些学生订半年而另一些学生订全年,共需1320元,若订全年的同学与订半年的同学人数交换,共需订费1245元,由该小学六年级订阅《数理天地》的学生共有多少人?4.箱子里有乒乓球若干,其中25%是一级品,五分之几是二级品,其余91是三级品。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年试题
2020年“丘成桐数学英才班”招生考试形式内容
英才班考试内容包括综合考核、学术能力测试(两场笔试、一场面试)和心理测评,其中对学术能力的考查是关键。
针对考试形式和往届真题解析如下,供大家参考。
笔试第一场考查中学数学常见内容和微积分及线性代数。
主要考查数学基础知识是否扎实,以及对微积分、线性代数等未来研究数学真正的基础方法和工具的掌握程度。
笔试第二场采取现学现考的形式,考试当天上午两位教授讲授两个专题,着重讲解中学数学未涉及的概念或者定理,下午考核上午所学内容。
重点考查学生对新知识的接受程度,学习理解能力和分析解决问题能力,而非解题技巧的运用。
两场笔试的优胜者获得面试资格,面试采取考生和评委面对面的方式进行,评委
由三至五位教授组成,进一步了解学生的数学知识体系以及现场沟通、临场反应能力。
考生要在短时间内抓住重点、讲清要点、流畅沟通、有效反馈。
2019年试题
2018年试题
(一)初试
综合测试(语数英一起考210分钟理化一起考120分钟)
(二)复试
复试一:一个数论、一个不等式、个求不定方程解个数、一个积分一个组合几何一个证明欧拉定理(边点面关系那个)都是代数数论
真题还原:积分那道是证明pi的无理性,分两个小题(相当于提示)(证明方法和数论书(闵嗣鹤)里基本一样);最后一道是类似欧拉定理在空间中的一些推广。
复试二:群论和简单随机游走,讲完测评。
往年试题(官方版)
针对英才班考试特点,以下管中窥豹,对往届试题略加分析,进一步帮助考生了解如何应考。
笔试第一场真题包括以下三个题目。
例1是不等式题目,例2是立体几何与组合相结合的问题,都是中学数学的常见内容。
例3是微积分题目。
例1.
例2.
例3.
这道题要求考生能真正掌握一元Riemann积分的概念以及分部积分等重要技术手段。
笔试第二场现学现考真题包括以下两个题目。
例4是关于平面整点上随机游动的专题,例5是关于群的作用的专题。
例4.
这道试题的还有一个不同于传统考试的特点:它由一系列的小问题组成,每一小问都可以利用前面已经得到的结论作答。
这通常将一个困难的命题分拆为若干
步骤,要求考生一步一步接近最终的目标,这种类型的题目在法国广泛流行。
例5.
这是得分率最低的一道题目,几百名考生中只有两位同学能够完整地给出解答。
该问题期望考生利用所学到的关于群作用的知识进行解答,大多考生纠缠于初等的技巧而不得要领。
