高中数学典型例题解析汇报平面向量与空间向量
高中数学素材:平面向量与空间向量类比

平面向量与空间向量类比 某某 王建宏 某某 X 金龙 平面向量与空间向量有诸多相似之处,学习空间向量时若能与平面向量类比,往往会收到事半功倍的效果.本文以向量的线性表示为例(例1与例2)作简单介绍. 例1 已知:如图1,在平面中,1OA OB OA ==,与OB 的夹角为120OC ,与OA 的夹角为25,5OC =.用OAOB ,表示OC . 解法一:OA OCcos OA OC AOC =∠5cos 25=.设OC OA OB λμ=+,则212OA OC OA OA OB λμλμ=+=-. 15cos 252λμ-=①同理由OB OC ,可得15cos952λμ-+=.② 由①②,可得103103sin 95sin 2533λμ==,, 103103sin 95sin 2533OC OA OB =+. 解法二:如图2,以OA 所在直线为x 轴,点O 为坐标原点建立直角坐标系,则(5cos 255sin 25)OC ,. 设OC OA OB λμ=+,则13(10)22OC λμ⎛⎫=+- ⎪ ⎪⎝⎭,,.解得103103sin 95sin 2533OC OA OB =+. 解法三:如图3,作平行四边形OM ,设OM OAON OB λμ==,, 由正弦定理得103103sin 95sin 2533OC OA OB =+(过程略). 例2 已知:正四面体O ABC -中,OA OB OC a ===,点O 在底面上的射影为G ,试用向量OAOB OC ,,表示OG . 解法一:如图4,∵OA =OB =OC ,∴点O 在底面的射影点G 为△ABC 的中心.取AB 的中点D ,则DG =13DC . ∵13OG OD DG OD DC =+=+ 1()3OD OC OD =+-, 又∵1()2OD OA OB =+, ∴2133OG OD OC =+ 111333OA OB OC =++. 故111333OG OA OB OC =++. 解法二:如图5,以点O 为原点,建立空间直角坐标系,设111222333()()()A x y z B x y z C x y z ,,,,,,,,,由定比分点坐标公式,可得点G 的坐标123123123333x x x y y y z z z ++++++⎛⎫ ⎪⎝⎭,,. 111333OG OA OB OC ∴=++. 解法三:如图6,作平行六面体CENF OBMA -,使得正四面体O ABC -为其一个角上的小三棱锥,则ON OA OB OC =++.可证13OG ON =(过程略). 提起空间向量,许多同学会习惯于空间向量的直角坐标运算,忽略了空间向量本身的应用.2005年全国高中数学联赛第2题(例3),是利用空间向量(不建立空间直角坐标系)解立体几何问题的典型,应培养空间向量的应用意识.例3 如图7,空间四点AB C D ,,,满足 37119AB BC CD DA ====,,,,则AC BD 的取值( )(A )只有一个 (B )有两个(C )有四个 (D )有无穷多个此题设计精巧,构思奇妙,其来源于课本习题(具体化,并向空间推广),思维含量颇高.试题组提供的解答过程比较麻烦,此处从略.课本上有这样一道习题:已知四边形一组对边的平方和等于另一组对边的平方和,求证它的对角线互相垂直.这道习题有很多种证明方法,向量法简证如下:设AD AC AB ===,,a b c 则BD =-a c ,条件2222AB CD BC AD +=+即22()()+-=-+22c a b b c a ,展开整理可得a b =b c ,即()0-=b c a ,也就是0AC BD =,从而AC BDAC BD ,⊥⊥.上述证明与四边形ABCD 是平面图形还是立体图形无关,该结论也适合于空间问题.该试题可追溯到一道匈牙利数学竞赛试题:证明四边形一组对边的平方和等于另一组对边的平方和的充要条件是它的两条对角线互相垂直.该联赛试题的解答可简化为:由222231179+=+,则0AC BD AC BD =,⊥.故此题选(A).阿波罗尼斯圆比例为0.5阿波罗尼斯(Apollonius )圆,简称阿氏圆。
高二数学空间向量及其运算1

必修4 第二章 平面向量
第二课时 向量的字符运算与坐标运算
学习目标 1.知道平面向量的基本定理及其意义,理
解平面向量的正交分解及其坐标表示,理解 用坐标表示平面向量的加、减及数乘运算, 了解用坐标表示平面向量共线的条件.
2.了解平面向量数量积的含义及其物理意 义,了解平面向量的数量积与向量投影的关 系,理解平面向量数量积的坐标表达式及其 运算,理解运用数量积表示两个向量的夹角, 并判断两个平面向量的垂直关系,掌握平面 向量的应用,并关注学科内综合.【问题源自】向量的字符运算 tp
1 2
5730
例1 已知|a|=1,|b|=2,c=a+b, 且 c⊥a,求向量 a与b的夹角. 120°
Auu=Bur例22a+设kab,,b是Cu两u=Bur 个a+不3共b,线的Cu=uD向ur2量a-,b,
若A,B,D三点共线,求实数k的值.
-8
例3 已知a、b是平面内两个互相垂直
的单位向量,若非零向量c满足(a-c)·(b
-c)=0,求|c|的最大值.
2
; 快速阅读加盟
;
厥极疾。时则有草妖,时则有蠃虫之孽,时则有羊祸,时则有目痾,时则有赤眚赤祥。惟水沴火”“视之不明,是谓不哲”,悊,知也。《诗》云“尔德不明,以亡陪亡卿。不明尔德,以亡背亡仄”言上不明,暗昧蔽惑,则不能知善恶,亲近匀,长同类,亡功者受赏,有罪者不杀,百官 废乱,失在舒缓,故其咎舒也。盛夏日长,暑以养物,政弛缓,故其罚常奥也。奥则冬温,春夏不和,伤病民人,故极疾也。诛不行则霜不杀草,繇臣下则杀不以时,故有草妖。凡妖,貌则以服,言则以诗,听则以声。视则以色者,五色物之大分也,在於眚祥,故圣人以为草妖,失秉之 明者也。温奥生虫,故有蠃虫之孽,谓螟螣之类当死不死,
高中空间向量练习题及讲解讲解

高中空间向量练习题及讲解讲解### 高中空间向量练习题及讲解#### 练习题一:空间向量的坐标运算题目:设空间向量\( \vec{a} \)和\( \vec{b} \)的坐标分别为\( (1, 2, 3) \)和\( (4, -1, 2) \),求向量\( \vec{a} + \vec{b} \)的坐标。
解答:向量加法遵循坐标的分量相加原则。
对于向量\( \vec{a} \)和\( \vec{b} \),其坐标分别为\( (a_1, a_2, a_3) \)和\( (b_1,b_2, b_3) \),向量和的坐标为\( (a_1 + b_1, a_2 + b_2, a_3 +b_3) \)。
将给定的向量坐标代入公式,得到:\[ \vec{a} + \vec{b} = (1 + 4, 2 - 1, 3 + 2) = (5, 1, 5) \]#### 练习题二:空间向量的模长题目:已知空间向量\( \vec{c} \)的坐标为\( (2, 3, -1) \),求向量\( \vec{c} \)的模长。
解答:空间向量的模长可以通过以下公式计算:\[ |\vec{c}| = \sqrt{c_1^2 + c_2^2 + c_3^2} \]将向量\( \vec{c} \)的坐标代入公式,得到:\[ |\vec{c}| = \sqrt{2^2 + 3^2 + (-1)^2} = \sqrt{4 + 9 + 1} = \sqrt{14} \]#### 练习题三:空间向量的夹角题目:设空间向量\( \vec{d} \)和\( \vec{e} \)的坐标分别为\( (1, 2, 1) \)和\( (2, 1, 3) \),求向量\( \vec{d} \)和\( \vec{e} \)的夹角。
解答:空间向量\( \vec{d} \)和\( \vec{e} \)的夹角可以通过向量的点积来求得,公式为:\[ \cos \theta = \frac{\vec{d} \cdot \vec{e}}{|\vec{d}||\vec{e}|} \]首先计算点积:\[ \vec{d} \cdot \vec{e} = 1 \times 2 + 2 \times 1 + 1 \times 3 = 2 + 2 + 3 = 7 \]然后计算模长:\[ |\vec{d}| = \sqrt{1^2 + 2^2 + 1^2} = \sqrt{6} \]\[ |\vec{e}| = \sqrt{2^2 + 1^2 + 3^2} = \sqrt{14} \]代入公式计算夹角的余弦值:\[ \cos \theta = \frac{7}{\sqrt{6} \times \sqrt{14}} \]最后,通过反余弦函数求得夹角\( \theta \)。
高中数学典型例题解析平面向量与空间向量(可编辑修改word版)

b b 0 高中数学典型例题分析 第八章 平面向量与空间向量一、、疑难知识导析§8.1 平面向量及其运算1. 向量的概念的理解,尤其是特殊向量“零向量”向量是既有大小,又有方向的量.向量的模是正数或 0,是可以进行大小比较的, 由于方向不能比较大小,所以向量是不能比大小的.两个向量的模相等,方向相同,我们称这两个向量相等,两个零向量是相等的,零向量与任何向量平行,与任何向量都是共线向量;2. 在运用三角形法则和平行四边形法则求向量的加减法时要注意起点和终点;3. 对于坐标形式给出的两个向量,在运用平行与垂直的充要条件时,一定要区分好两个公式,切不可混淆。
因此,建议在记忆时对比记忆;4. 定比分点公式中则要记清哪个点是分点;还有就是此公式中横坐标和纵坐标是分开计算的;5. 平移公式中首先要知道这个公式是点的平移公式,故在使用的过程中须将起始点的坐标给出,同时注意顺序。
二知识导学1. 模(长度):向量 的大小,记作| |。
长度为0的向量称为零向量,长度等于1个单位长度的向量,叫做单位向量。
2. 平行向量:方向相同或相反的非零向量叫做平行向量,又叫做共线向量。
3. 相等向量:长度相等且方向相同的向量。
4. 相反向量:我们把与向量 a 长度相等,方向相反的向量叫做 a 的相反向量。
记作- a。
5. 向量的加法:求两个向量和的运算。
已知 a ,。
在平面内任取一点,作 AB = a, BC = b ,则向量 AC 叫做 a 与 的和。
b b 记作 a + 。
6. 向量的减法:求两个向量差的运算。
已知 , a b 。
在平面内任取一点 O ,作OA = a , OB = b ,则向量 BA 叫做 a 与b 的差。
记作 a - 。
7. 实数与向量的积:(1) 定义: 实数 λ 与向量 a 的积是一个向量,记作 λ a,并规定:①λ a 的长度|λ a |=|λ|·| a|;②当 λ>0 时,λ a 的方向与 a的方向相同;当 λ<0 时,λ a 的方向与 a的方向相反;当 λ=0 时,λ a =(2) 实数与向量的积的运算律:设 λ、μ 为实数,则①λ(μ a)=(λμ) ab b 1 1 b 2 2 b 1 2 2 1b b b b b2 ②(λ+μ) a =λ a +μ a③λ( a + b )=λ a+λ b8. 向量共线的充分条件:向量 与非零向量 a共线的充要条件是有且只有一个实数 λ, 使得 =λ a 。
高三数学空间向量试题答案及解析

高三数学空间向量试题答案及解析1.如图,长方体中,分别为中点,(1)求证:.(2)求二面角的正切值.【答案】(1)见解析(2)【解析】(1)由长方体及E、F分别为AB、C1D1的中点知,AE平行且等于C1F,所以AEC1F是平行四边形,所以C1E∥AF,由线面平行的判定定理知,C1E∥面ACF;(2)易证FG⊥面ABCD,过F作FH⊥AC于H,连结HG,因为FG⊥面ABCD,则FG⊥AC,所以∠FHG为二面角F—AC—G的平面角,然后通过解三角形,求出FG、GH的长,即可求出∠FHG的正切值,即为二面角F-AC-G的正切值.试题解析:(1)证明:在长方体中,分别为中点,且四边形是平行四边形3分,5分(2).长方体中,分别为中点,7分过做于,又就是二面角的平面角 9分,在中, 11分直角三角形中 13分二面角的正切值为 14分考点:线面平行的判定定理;二面角的计算;逻辑推理能力2.如图,在直三棱柱A1B1C1-ABC中,AB⊥AC,AB=AC=2,A1A=4,点D是BC的中点.(1)求异面直线A1B与C1D所成角的余弦值;(2)求平面ADC1与平面ABA1夹角的正弦值.【答案】(1)(2)【解析】解:(1)以A为坐标原点,建立如图所示的空间直角坐标系A-xyz,则A(0,0,0),B(2,0,0),C(0,2,0),D(1,1,0),A1(0,0,4),C1(0,2,4),∴=(2,0,-4),=(1,-1,-4).∵cos〈,〉===,∴异面直线A1B与C1D所成角的余弦值为.(2)设平面ADC1的法向量为n1=(x,y,z),∵=(1,1,0),=(0,2,4),∴n1·=0,n 1·=0,即x+y=0且2y+4z=0,取z=1,得x=2,y=-2,∴n1=(2,-2,1)是平面ADC1的一个法向量.取平面AA1B的一个法向量为n2=(0,1,0),设平面ADC1与平面ABA1夹角的大小为θ.由cosθ===,得sinθ=.因此,平面ADC1与平面ABA1夹角的正弦值为.3.已知正方体ABCD-A1B1C1D1中,点E为上底面A1C1的中心,若=+x+y,则x、y的值分别为()A.x=1,y=1B.x=1,y=C.x=,y=D.x=,y=1【答案】C【解析】如图,=+=+=+ (+).4.如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E、F、G分别是AB、AD、CD的中点,计算:(1)·;(2)·;(3)EG的长;(4)异面直线AG与CE所成角的余弦值.【答案】(1)(2)-(3)(4)【解析】解:设=a,=b,=c.则|a|=|b|=|c|=1,〈a,b〉=〈b,c〉=〈c,a〉=60°.=BD=c-a,=-a,=b-c,(1)·=(c-a)·(-a)=a2-a·c=;(2)·= (c-a)·(b-c)= (b·c-a·b-c2+a·c)=-;(3)=++=a+b-a+c-b=-a+b+ c.||2=a2+b2+c2-a·b+b·c-c·a=.即||=,所以EG的长为.(4)设、的夹角为θ.=b+c,=+=-b+a,cosθ==-,由于异面直线所成角的范围是(0°,90°],所以异面直线AG与CE所成角的余弦值为.5.在如图所示的空间直角坐标系中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为()A.①和②B.③和①C.④和③D.④和②【答案】D【解析】设,在坐标系中标出已知的四个点,根据三视图的画图规则判断三棱锥的正视图为④与俯视图为②,故选D.【考点】空间由已知条件,在空间坐标系中作出几何体的形状,再正视图与俯视图,容易题.6.如图,直四棱柱底面直角梯形,∥,,是棱上一点,,,,,.(1)求异面直线与所成的角;(2)求证:平面.【答案】(1);(2)证明见解析.【解析】(1)本题中由于有两两垂直,因此在求异面直线所成角时,可以通过建立空间直角坐标系,利用向量的夹角求出所求角;(2)同(1)我们可以用向量法证明线线垂直,以证明线面垂直,,,,易得当然我们也可直线用几何法证明线面垂直,首先,这由已知可直接得到,而证明可在直角梯形通过计算利用勾股定理证明,,,因此,得证.(1)以原点,、、分别为轴、轴、轴建立空间直角坐标系.则,,,. 3分于是,,,异面直线与所成的角的大小等于. 6分(2)过作交于,在中,,,则,,,, 10分,.又,平面. 12分【考点】(1)异面直线所成的角;(2)线面垂直.7.(2013•天津)如图,四棱柱ABCD﹣A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.(1)证明B1C1⊥CE;(2)求二面角B1﹣CE﹣C1的正弦值.(3)设点M在线段C1E上,且直线AM与平面ADD1A1所成角的正弦值为,求线段AM的长.【答案】(1)见解析(2)(3)【解析】(1)证明:以点A为原点建立空间直角坐标系,如图,依题意得A(0,0,0),B(0,0,2),C(1,0,1),B1(0,2,2),C1(1,2,1),E(0,1,0).则,而=0.所以B1C1⊥CE;(2)解:,设平面B1CE的法向量为,则,即,取z=1,得x=﹣3,y=﹣2.所以.由(1)知B1C1⊥CE,又CC1⊥B1C1,所以B1C1⊥平面CEC1,故为平面CEC1的一个法向量,于是=.从而==.所以二面角B1﹣CE﹣C1的正弦值为.(3)解:,设0≤λ≤1,有.取为平面ADD1A1的一个法向量,设θ为直线AM与平面ADD1A1所成的角,则==.于是.解得.所以.所以线段AM的长为.8.如图,四棱锥P-ABCD中,PA⊥平面ABCD,E为BD的中点,G为PD的中点,△DAB≌△DCB,EA=EB=AB=1,PA=,连接CE并延长交AD于F.(1)求证:AD⊥平面CFG;(2)求平面BCP与平面DCP的夹角的余弦值.【答案】(1)见解析(2)【解析】(1)因为△DAB ≌△DCB,EA=EB=AB=1,所以△ECB是等边,,(2)建立空间坐标系如图,取向观点的坐标为, 向量设平面PBC的法向量平面PDC的法向量则【考点】本题主要考查空间垂直关系的证明、平行关系的运用,考查空间角的求解方法,考查空间想象能力、推理论证能力、计算能力.9.如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.(1)证明:PA⊥BD;(2)若PD=AD,求二面角A-PB-C的余弦值。
平面向量与空间向量重要概念解析

平面向量与空间向量重要概念解析向量是数学中常见的概念,它在平面几何和空间几何中都扮演着重要的角色。
本文将对平面向量和空间向量的概念进行解析,并探讨它们在几何学和物理学中的应用。
一、平面向量的概念解析平面向量是指在平面上具有大小和方向的量。
平面向量通常用符号表示,如AB表示从点A指向点B的向量。
平面向量有两个重要的性质,即大小和方向。
平面向量的大小可以用模长来表示,通常用两个坐标差的平方和的开方来计算。
设向量AB的坐标为(x1, y1)和(x2, y2),则向量AB的模长记作||AB||,计算公式为:||AB|| = √((x2 - x1)^2 + (y2 - y1)^2)平面向量的方向可以用角度或方向角来表示。
与x轴的正向之间的夹角称为向量的方向角。
方向角的计算可以通过与x轴的夹角的三角函数比值来得到。
如果向量AB的方向角为α,则有:tanα = (y2 - y1) / (x2 - x1)平面向量的加法、减法和数量乘法等运算规则也是平面向量的重要性质。
向量的加法按照平行四边形法则进行,向量的减法可以通过加上负向量来实现,向量的数量乘法是将向量的模长与一个标量相乘。
二、空间向量的概念解析空间向量是指在空间中具有大小和方向的量。
与平面向量相比,空间向量多了一个维度,即在三维空间中进行描述。
空间向量通常用符号表示,如AB表示从点A指向点B的向量。
空间向量也有大小和方向两个重要的性质。
空间向量的大小可以用模长来表示,计算公式同平面向量。
设向量AB的坐标为(x1, y1, z1)和(x2, y2, z2),则向量AB的模长记作||AB||,计算公式为:||AB|| = √((x2 - x1)^2 + (y2 - y1)^2 + (z2 - z1)^2)空间向量的方向可以用方向角来表示。
与x轴的正向之间的夹角称为向量的方向角,与xOy平面的法线向量之间的夹角称为倾斜角。
空间向量的方向可以通过方向角和倾斜角来确定。
高中数学空间向量经典例题及解析

高中数学空间向量经典例题及解析一、引言空间向量是高中数学的一个重要知识点,它涉及到三维空间中向量的加法、数乘、数量积和向量积等运算。
这些运算在解决实际问题中有着广泛的应用,因此学好空间向量对于学生来说至关重要。
本篇文章将通过经典例题的方式,对空间向量的相关知识点进行深入解析,以期帮助学生更好地掌握这一知识点。
二、经典例题及解析【例题1】在空间四边形中,已知两个向量,,求异面直线的夹角(锐角或直角)。
【解析】本题考查空间向量的夹角问题,需要利用两个向量的夹角公式。
【解答】首先根据向量的定义,可得到向量,的坐标分别为(, )。
根据向量的加法,可得向量的坐标为(, )。
又因为两个向量垂直,所以它们的数量积为0,即,所以。
根据异面直线夹角公式,可得异面直线的夹角为。
【例题2】在长方体中,已知三个向量,,求异面直线的夹角(锐角或直角)。
【解析】本题除了需要用到向量的加法、数乘、数量积和向量积等运算,还需要用到长方体的性质。
【解答】首先根据向量的定义,可得到向量的坐标分别为(, , )。
又因为长方体中,所以可以表示为和的线性组合,即或。
设所在直线的方向向量,所在平面的法向量,则的坐标分别为(, )。
根据向量夹角公式和向量垂直的条件,可得垂直于平面,所以。
又因为两个向量垂直,所以它们的数量积为0,即,所以。
根据异面直线夹角公式,可得异面直线AB与CD的夹角为。
【例题3】已知长方体,设点,求与平面之间的距离。
【解析】本题需要利用长方体的性质和向量的数量积求解。
【解答】设平面的法向量,则所在直线的方向向量。
因为点在平面内,所以点在平面外,所以向量,即。
又因为向量与平面共线,所以向量,即。
根据向量的数量积和点到平面的距离公式,可得与平面之间的距离为。
三、总结空间向量是高中数学的一个难点也是重点,通过经典例题的解析,我们可以更好地掌握空间向量的相关知识点。
在解决实际问题时,我们需要灵活运用向量的加法、数乘、数量积和向量积等运算,同时还要注意向量的表示和坐标的确定。
2021-2022学年高中数学经典解析-空间向量单元
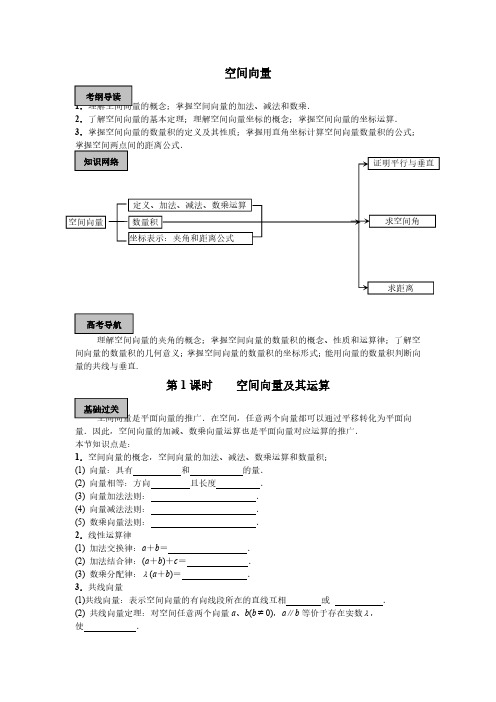
空间向量1.理解空间向量的概念;掌握空间向量的加法、减法和数乘.2.了解空间向量的基本定理;理解空间向量坐标的概念;掌握空间向量的坐标运算.3.掌握空间向量的数量积的定义及其性质;掌握用直角坐标计算空间向量数量积的公式;掌握空间两点间的距离公式.理解空间向量的夹角的概念;掌握空间向量的数量积的概念、性质和运算律;了解空间向量的数量积的几何意义;掌握空间向量的数量积的坐标形式;能用向量的数量积判断向量的共线与垂直.第1课时空间向量及其运算空间向量是平面向量的推广.在空间,任意两个向量都可以通过平移转化为平面向量.因此,空间向量的加减、数乘向量运算也是平面向量对应运算的推广.本节知识点是:1.空间向量的概念,空间向量的加法、减法、数乘运算和数量积;(1)向量:具有和的量.(2)向量相等:方向且长度.(3)向量加法法则:.(4)向量减法法则:.(5)数乘向量法则:.2.线性运算律(1)加法交换律:a +b =.(2)加法结合律:(a +b )+c =.(3)数乘分配律:λ(a +b )=.3.共线向量(1)共线向量:表示空间向量的有向线段所在的直线互相或.(2)共线向量定理:对空间任意两个向量a 、b (b ≠0),a ∥b 等价于存在实数λ,使.基础过关知识网络考纲导读高考导航空间向量定义、加法、减法、数乘运算数量积坐标表示:夹角和距离公式求距离求空间角证明平行与垂直(3)直线的向量参数方程:设直线l 过定点A 且平行于非零向量a ,则对于空间中任意一点O ,点P 在l 上等价于存在R t ∈,使.4.共面向量(1)共面向量:平行于的向量.(2)共面向量定理:两个向量a 、b 不共线,则向量P 与向量a 、b 共面的充要条件是存在实数对(y x ,),使P .共面向量定理的推论:.5.空间向量基本定理(1)空间向量的基底:的三个向量.(2)空间向量基本定理:如果a ,b ,c 三个向量不共面,那么对空间中任意一个向量p ,存在一个唯一的有序实数组z y x ,,,使.空间向量基本定理的推论:设O ,A ,B ,C 是不共面的的四点,则对空间中任意一点P ,都存在唯一的有序实数组z y x ,,,使.6.空间向量的数量积(1)空间向量的夹角:.(2)空间向量的长度或模:.(3)空间向量的数量积:已知空间中任意两个向量a 、b ,则a ·b =.空间向量的数量积的常用结论:(a)cos 〈a 、b 〉=;(b)⎪a ⎪2=;(c)a ⊥b ⇔.(4)空间向量的数量积的运算律:(a )交换律a ·b =;(b )分配律a ·(b +c )=.例1.已知正方体ABCD—A 1B 1C 1D 1中,点F 是侧面CDD 1C 1的中心,若1AA y AB x AD AF ++=,求x -y 的值.变式训练1.在平行六面体1111D C B A ABCD -中,M 为AC 与BD 的交点,若=11B A a ,=11D A b ,=A A 1c ,则下列向量中与M B 1相等的向量是()A .-21a +21b +c B .21a +21b +c C .21a -21b +cD .-21a -21b +c典型例题ABCD ACB例2.底面为正三角形的斜棱柱ABC -A 1B 1C 1中,D 为AC 的中点,求证:AB 1∥平面C 1BD.变式训练2:正方体ABCD -EFGH 中,M 、N 分别是对角线AC 和BE 上的点,且AM =EN .(1)求证:MN ∥平面FC ;(2)求证:MN ⊥AB ;(3)当MA 为何值时,MN 取最小值,最小值是多少?例3.已知四面体ABCD 中,AB ⊥CD ,AC ⊥BD ,G 、H 分别是△ABC 和△ACD 的重心.求证:(1)AD ⊥BC ;(2)GH ∥BD .变式训练3:已知平行六面体1111D C B A ABCD ,E 、F 、G 、H 分别为棱AB C C C D D A 和11111,,的中点.求证:E 、F 、G 、H 四点共面.例4.如图,平行六面体AC1中,AE=3EA1,AF=FD,AG=GB21,过E、F、G的平面与对角线AC1交于点P,求AP:PC1的值.变式训练4:已知空间四边形OABC中,M为BC的中点,N为AC的中点,P为OA的中点,Q为OB的中点,若AB=OC,求证QNPM⊥.1.立体几何中有关垂直和平行的一些命题,可通过向量运算来证明.对于垂直,一般是利用a⊥b⇔a·b=0进行证明.对于平行,一般是利用共线向量和共面向量定理进行证明.2.运用向量求解距离问题,其一般方法是找出代表相应距离的线段所对向量,然后计算这个向量对应的模.而计算过程中只要运用好加法法则,就总能利用一个一个的向量三角形,将所求向量用有模和夹角的已知向量表示出来,从而求得结果.3.利用向量求夹角(线线夹角、线面夹角、面面夹角)有时也很方便.其一般方法是将所求的角转化为求两个向量的夹角,而求两个向量的夹角则可以利用公式c osθb a.4.异面直线间的距离的向量求法:已知异面直线l1、l2,AB为其公垂线段,C、D分别为l1、l2上的任意一点,n为与AB共线的向量,则|AB||n nCD.5.设平面α的一个法向量为n,点P是平面α外一点,且P o∈α,则点P到平面α的距离是d||n nPP o.1小结归纳第2课时空间向量的坐标运算设a =),,(321a a a ,b =),,(321b b b (1)a ±b =(2)λa =.(3)a ·b =.(4)a ∥b ⇔;a ⊥b ⇔.(5)设),,(),,,(222111z y x B z y x A ==则AB =,=AB .AB 的中点M 的坐标为.例1.若a =(1,5,-1),b =(-2,3,5)(1)若(k a +b )∥(a -3b ),求实数k 的值;(2)若(k a +b )⊥(a -3b ),求实数k 的值;(3)若a k 取得最小值,求实数k 的值.变式训练1.已知O 为原点,向量()()3,0,1,1,1,2,,OA OB OC OA BC ==-⊥ ∥OA,求AC .典型例题基础过关例2.如图,直三棱柱111C B A ABC -,底面ABC ∆中,CA =CB =1, 90=∠BCA ,棱21=AA ,M 、N 分别A 1B 1、A 1A 是的中点.(1)求BM 的长;(2)求〉〈11,cos CB BA 的值;(3)求证:C B A 11⊥.变式训练2.在四棱锥P-ABCD 中,底面ABCD 为矩形,侧棱PA ⊥底面ABCD ,AB =3,BC =1,PA =2,E 为PD 的中点.(1)在侧面PAB 内找一点N ,使NE ⊥面PAC ,并求出N 点到AB 和AP 的距离;(2)求(1)中的点N 到平面PAC 的距离.例3.如图,在底面是棱形的四棱锥ABCD P -中,,,60a AC P A ABC ===∠ a PD PB 2==,点E 在PD 上,且PE :ED =2:1.(1)证明⊥P A 平面ABCD ;(2)求以AC 为棱,EAC 与DAC 为面的二面角θ的大小;(3)在棱PC 上是否存在一点F ,使BF ∥平面AEC xyABCP E D·例4.如图,多面体是由底面为ABCD 的长方体被截面AEFG 所截而得,其中AB =4,BC =1,BE =3,CF =4.(1)求EF 和点G 的坐标;(2)求GE 与平面ABCD 所成的角;(3)求点C 到截面AEFG 的距离.变式训练4.如图四棱锥P —ABCD 中,底面ABCD 是平行四边形,PG ⊥平面ABCD ,垂足为G ,G 在AD 上,且PG =4,GD AG 31,BG ⊥GC ,GB =GC =2,E 是BC 的中点.(1)求异面直线GE 与PC 所成的角的余弦值;(2)求点D 到平面PBG 的距离;(3)若F 点是棱PC 上一点,且DF ⊥GC ,求FCPF的值.对于以下几类立体几何问题:(1)共线与共面问题;(2)平行与垂直问题;(3)夹角问题;(4)距离问题;(5)探索性问题.运用向量来解决它们有时会体现出一定的优势.用空间向量解题的关键步骤是把所求向量用某个合适的基底表示,本节主要是用单位正交基底表示,就是适当地建立起空间直角坐标系,把向量用坐标表示,然后进行向量与向量的坐标运算,最后通过向量在数量上的关系反映出向量的空间位置关系,从而使问题得到解决.在寻求向量间的数量关系时,一个基本的思路是列方程,解方程.Z AD GE FCBxyPAGBCDFE空间向量章节测试题1.在正三棱柱ABC-A 1B 1C 1中,若AB=2,A A 1=1,则点A 到平面A 1BC 的距离为()A .43B .23C .433D .32.在正三棱柱ABC-A 1B 1C 1中,若AB=2BB 1,则AB 1与C 1B 所成的角的大小为A.60ºB.90ºC.105ºD.75º3.正方体ABCD—A 1B 1C 1D 1中,E 、F 分别是AA 1与CC 1的中点,则直线ED 与D 1F 所成角的大小是()A .15B 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实用文档文案大全高中数学典型例题第八章平面向量与空间向量§8.1平面向量及其运算一、、疑难知识导析1.向量的概念的理解,尤其是特殊向量“零向量”向量是既有大小,又有方向的量.向量的模是正数或0,是可以进行大小比较的,由于方向不能比较大小,所以向量是不能比大小的.两个向量的模相等,方向相同,我们称这两个向量相等,两个零向量是相等的,零向量与任何向量平行,与任何向量都是共线向量;2.在运用三角形法则和平行四边形法则求向量的加减法时要注意起点和终点;3.对于坐标形式给出的两个向量,在运用平行与垂直的充要条件时,一定要区分好两个公式,切不可混淆。
因此,建议在记忆时对比记忆;4.定比分点公式中则要记清哪个点是分点;还有就是此公式中横坐标和纵坐标是分开计算的;5.平移公式中首先要知道这个公式是点的平移公式,故在使用的过程中须将起始点的坐标给出,同时注意顺序。
二知识导学1.模(长度):向量AB的大小,记作|AB|。
长度为0的向量称为零向量,长度等于1个单位长度的向量,叫做单位向量。
2.平行向量:方向相同或相反的非零向量叫做平行向量,又叫做共线向量。
3.相等向量:长度相等且方向相同的向量。
4.相反向量:我们把与向量a?长度相等,方向相反的向量叫做a?的相反向量。
记作-a?。
5.向量的加法:求两个向量和的运算。
已知a?,b?。
在平面内任取一点,作AB=a?,BC=b,则向量AC 叫做a与b?的和。
记作a?+b?。
6. 向量的减法:求两个向量差的运算。
已知a?,b?。
在平面内任取一点O,作OA=a?,OB=b?,则向量BA 叫做a?与b?的差。
记作a?-b?。
7.实数与向量的积:(1)定义:实数λ与向量a?的积是一个向量,记作λa?,并规定:①λa?的长度|λa?|=|λ|·|a?|;②当λ>0时,λa?的方向与a?的方向相同;当λ<0时,λa?的方向与a?的方向相反;当λ=0时,λa?=0?(2)实数与向量的积的运算律:设λ、μ为实数,则①λ(μa?)=(λμ) a?实用文档文案大全②(λ+μ) a?=λa?+μa?③λ(a?+b)=λa?+λb8.向量共线的充分条件:向量b?与非零向量a?共线的充要条件是有且只有一个实数λ,使得b?=λa?。
另外,设a?=(x1 ,y1), b?= (x2,y2),则a?//b??x1y2-x2y1=09.平面向量基本定理:如果1e?、2e?是同一平面内的两个不共线向量,那么对于这一平面内的任一向量a?,有且只有一对实数λ1、λ2使a?=λ11e?+λ22e?,其中不共线向量1e?、2e?叫做表示这一平面内所有向量的一组基底。
10.定比分点设P1,P2是直线l上的两点,点P是不同于P1,P2的任意一点则存在一个实数λ,使21PP=λ21PP,λ叫做分有向线段所成的比。
若点P1、P、P2的坐标分别为(x1,y1),(x,y),(x2,y2),则有特别当λ=1,即当点P是线段P1P2的中点时,有?????????222121yyyxxx11.平面向量的数量积(1)定义:已知两个非零向量a?和b?,它们的夹角为θ,则数量|a?||b?|cosθ叫做a?与b?的数量积(或内积),记作a?·b?,即a?·b=|a?||b?|cosθ规定:零向量与任一向量的数量积是0。
(2)几何意义:数量积a?·b?等于a?的长度|a?|与b?在a?的方向上的投影|b?|cos θ的乘积。
(3)性质:设a?,b?都是非零向量,e?是与b?方向相同的单位向量,θ是a?与e?的夹角,则e?·a?=a?·e?=|a?|cosθ,a?⊥b??a?·b?=0 当a?与b?同向时,a?·b?=|a?||b?| 当a?与b?反向时,a?·b?=-|a?||b?|实用文档文案大全特别地,a?·a?=|a?|2或|a?|=aa???cosθ=baba?????? |a?·b?|≤|a?||b?|(4)运算律:a?·b?=b?·a? (交换律)(λa?)·b?=λ(b?·a?)=a?·(λb?)(a?+b?)·c?=a?·c?+b?·c?(5)平面向量垂直的坐标表示的充要条件:设a?=(x1 ,y1), b?= (x2,y2),则a??b??a?·b?=|a?|·|b?|cos90°=0a??b??x1x2+y1y2=012.平移公式:设P(x,y)是图形F上的任意一点,它在平移后图形F/上对应点为P/(x/,y/),且设/PP的坐标为(h,k),则由/OP=OP+/PP,得:(x/,y/)=(x,y)+(h,k)三、经典例题导讲[例1]和a= (3,-4)平行的单位向量是_________;错解:因为a的模等于5,所以与a平行的单位向量就是51 a,即 (35 ,-45 )错因:在求解平行向量时没有考虑到方向相反的情况。
正解:因为a的模等于5,所以与a平行的单位向量是?51 a,即(35 ,-45 )或(-35 ,45 )点评:平行的情况有方向相同和方向相反两种。
读者可以自己再求解“和a=(3,-4)垂直的单位向量”,结果也应该是两个。
[例2]已知A(2,1),B(3,2),C(-1,4),若A、B、C是平行四边形的三个顶点,求第四个顶点D的坐标。
错解:设D的坐标为(x,y),则有x-2=-1-3,y-1=4-2 ,即x=-2,y=3。
故所求D的坐标为(-2,3)。
错因:思维定势。
习惯上,我们认为平行四边形的四个顶点是按照ABCD的顺序。
其实,在这个题目中,根本就没有指出四边形ABCD。
因此,还需要分类讨论。
正解:设D的坐标为(x,y)实用文档文案大全当四边形为平行四边形ABCD时,有x-2=-1-3,y-1= 4-2 ,即x= -2,y= 3。
解得D的坐标为(-2,3);当四边形为平行四边形ADBC时,有x-2=3-(-1),y-1= 2-4 ,即x= 6,y= -1。
解得D 的坐标为(6,-1);当四边形为平行四边形ABDC时,有x-3=-1-2,y-2= 4-1 ,即x= 0,y= 5。
解得D的坐标为(0,5)。
故第四个顶点D的坐标为(-2,3)或(6,-1)或(0,5)。
[例3]已知P1(3,2),P2(8,3),若点P在直线P1P2上,且满足|P1P|=2|PP2|,求点P的坐标。
错解:由|P1P|=2|PP2|得,点P 分P1P2所成的比为2,代入定比分点坐标公式得P(38,319)错因:对于|P1P|=2|PP2|这个等式,它所包含的不仅是点P为 P1,P2的内分点这一种情况,还有点P是 P1,P2的外分点。
故须分情况讨论。
正解:当点P为 P1,P2的内分点时,P 分P1P2所成的比为2,此时解得P(38,319);当点P为 P1,P2的外分点时,P 分P1P2所成的比为-2,此时解得P(13,4)。
则所求点P的坐标为(38,319)或(13,4)。
点评:在运用定比分点坐标公式时,要审清题意,注意内外分点的情况。
也就是分类讨论的数学思想。
[例4]设向量),(11yxa? ,),(22yxb? ,0???b,则“ba??//”是“1221yxyx?”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件分析:根据向量的坐标运算和充要条件的意义进行演算即可.解:若ba??//,∵0???b,则bra???,代入坐标得:),(),(2211yxryx?,即21rxx?且21ryy?消去r,得1221yxyx?;反之,若1221yxyx?,则21rxx?且21ryy?,即),(),(2211yxryx?则bra???,∴ba??//故“ba??//”是“1221yxyx?”的充要条件.答案:C点评:本题意在巩固向量平行的坐标表示.[例5]..已知a?=(1,-1),b?=(-1,3),c?=(3,5),求实数x、y,使c?=x a?+y b?分析:根据向量坐标运算和待定系数法,用方程思想求解即可.解:由题意有实用文档文案大全 x a? +y b =x(1,-1)+y(-1,3)=(x-y,-x+3y).又c? =(3,5)∴x-y=3且-x+3y=5 解之得 x=7 且y=4点评:在向量的坐标运算中经常要用到解方程的方法.[例6]已知A(-1,2),B(2,8),AC=31AB,DA= -31BA,求点C、D和向量CD的坐标.分析:待定系数法设定点C、D的坐标,再根据向量AC AB,DA和CD关系进行坐标运算,用方程思想解之.解:设C、D的坐标为),(11yx、),(22yx,由题意得AC=(2,111??yx),AB=(3,6),DA=(222,1yx???),BA=(-3,-6)又AC=31AB,DA= -31BA∴(2,111??yx)=31(3,6),(222,1yx???)=-31(-3,-6)即 (2,111??yx)=(1,2) , (222,1yx???)=(1,2) ∴111??x且221??y,112???x 且222??y∴01?x且41?y,且22??x02?y∴点C、D和向量CD的坐标分别为(0,4)、(-2,0)和(-2,-4)小结:本题涉及到方程思想,对学生运算能力要求较高.§8.2平面向量与代数、几何的综合应用一、疑难知识导析1.初中学过的勾股定理只是余弦定理的一种特殊情况。
如当C=2?时,C cos=0,此时有222bac??;2.由于本节内容与代数、几何联系比较紧,故读者需对解斜三角形、解析几何中的圆锥曲线等知识非常熟悉方可。
二、知识导学1.余弦定理:三角形任何一边的平方等于其他两边平方的和,减去这两边与它们夹角的余弦的积的2倍,即实用文档文案大全Abccbacos2222???Baccabcos2222???Cabbaccos2222???2.正弦定理在一个三角形中,各边和它所对角的正弦的比相等,并且都等于外接圆的直径,即RCcBbAa2sinsinsin???三经典例题导讲[例1]在ABC中,已知a2=b2+bc+c2,则角A为( )A3? B6? C32? D3?或32?错解:选A错因:公式记不牢,误将余弦定理中的“减”记作“加”。
正解:∵a2=b2+bc+c2=b2+c2-2bc(-21)=b2+c2-2bc·cos32?∴∠A=32?选 C.[例2]在△ABC中,已知BbAacoscos?,试判别其形状。
错解:等腰三角形。
错因:忽视了两角互补,正弦值也相等的情形。
