7梯形-一般梯形基础题和培优题
梯形基础习题

梯形基础习题一、梯形的定义梯形是一个四边形,具有两边平行的特点。
它的两个平行边被称为梯形的上底和下底,两边非平行的边被称为梯形的斜边,而两个非平行边之间的夹角被称为梯形的夹角。
二、梯形的性质1. 梯形的对角线互相垂直,即上底和下底的中点连线与斜边互相垂直。
2. 梯形的对角线相等,即上底和下底的中点连线的长度相等。
3. 梯形的夹角互补,即上底和下底的夹角加起来等于180度。
4. 梯形的面积可以通过上底、下底和高的关系计算,公式为:面积 = (上底 + 下底) ×高 ÷ 2。
三、梯形的基础题以下是一些梯形的基础题,帮助加深理解和掌握梯形的性质。
1. 已知一梯形的上底为 6 cm,下底为 10 cm,高为 4 cm,求该梯形的面积。
根据面积公式,可以得到:面积 = (6 + 10) × 4 ÷ 2 = 16 cm²因此,该梯形的面积为 16 平方厘米。
2. 已知一梯形的对角线长度为 8 cm,上底与下底的差为 2 cm,求该梯形的上底和下底的长度。
设上底为 x cm,则下底为 x + 2 cm。
根据梯形的对角线相等性质,可以得到:x² + 4² = (x + 2)²化简后得到:x² + 16 = x² + 4x + 4继续化简得到:12 = 4x解方程可得:x = 3因此,该梯形的上底长度为 3 cm,下底长度为 5 cm。
3. 已知一梯形的上底为 8 cm,下底为 12 cm,面积为 40 平方厘米,求该梯形的高。
根据面积公式,可以得到:40 = (8 + 12) ×高 ÷ 2化简得到:40 = 20 ×高 ÷ 2继续化简得到:80 = 20 ×高解方程可得:高 = 4因此,该梯形的高为 4 cm。
以上是关于梯形基础题的内容,希望能对您理解和掌握梯形的性质有所帮助。
梯形培优提高训练题
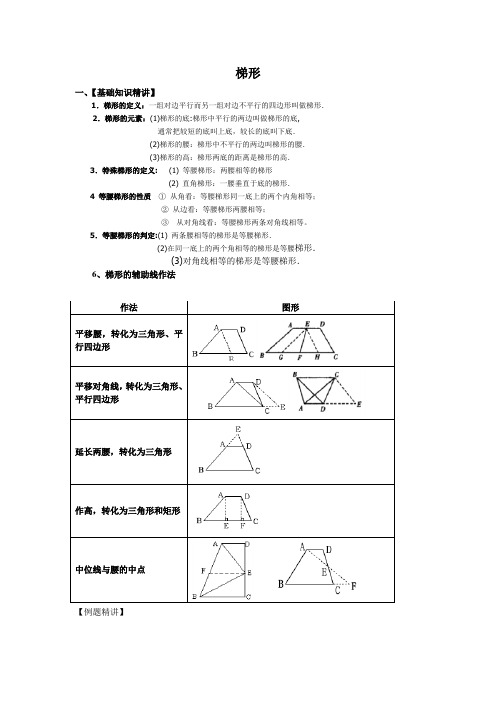
梯形一、【基础知识精讲】1.梯形的定义:一组对边平行而另一组对边不平行的四边形叫做梯形.2.梯形的元素:(1)梯形的底:梯形中平行的两边叫做梯形的底,通常把较短的底叫上底,较长的底叫下底.(2)梯形的腰:梯形中不平行的两边叫梯形的腰.(3)梯形的高:梯形两底的距离是梯形的高.3.特殊梯形的定义: (1) 等腰梯形:两腰相等的梯形(2) 直角梯形:一腰垂直于底的梯形.4 等腰梯形的性质①从角看:等腰梯形同一底上的两个内角相等;②从边看:等腰梯形两腰相等;③从对角线看:等腰梯形两条对角线相等。
5.等腰梯形的判定:(1) 两条腰相等的梯形是等腰梯形.(2)在同一底上的两个角相等的梯形是等腰梯形.(3)对角线相等的梯形是等腰梯形.6、梯形的辅助线作法【例题精讲】平移梯形一腰或两腰,把梯形的腰、两底角等转移到一个三角形中,同时还得到平行四边形例1 如图,梯形ABCD中,AB∥DC,∠ADC+∠BCD=90°,且DC=2AB,分别以DA、AB、BC为边向梯形外作正方形,其面积分别为S1、S2、S3,则S1、S2、S3之间的关系为__________。
例2、(希望杯邀请赛)如如图,在四边形ABCD中,AB//CD,∠D=2∠B,若AD=a,AB=b,则CD的长为____________。
例3 如图,在梯形ABCD中,AD//BC,AD<BC,E、F分别为AD,BC的中点,且EF⊥BC,求证:∠B=∠C。
例4 已知一个梯形的4条边长分别是1、2、3、4,则此梯形的面积等于_______。
【变式练习】1、如图,梯形ABCD 中, AB∥CD,∠D=70 °,∠C=40 °AB=4cm,CD=11cm,求BC。
2、在梯形ABCD中 AD∥BC AD<BC E、F分别为AD、BC的中点 且EF⊥BC 梯形ABCD 是等腰梯形吗?为什么?3、在梯形ABCD中,AD//BC,∠A+∠D90°,M,N分别是BC和AD的中点,.已知AD=7,BC=2,试MN长。
(完整版)梯形练习题

(完整版)梯形练习题1. 梯形的定义和性质梯形是指有两边平行的四边形。
其性质如下:- 梯形的对边平行,即上底和下底平行。
- 梯形的两条斜边不相等。
- 梯形的两条斜边之和大于上底和下底之差。
- 梯形的两个底角相等,两个顶角相等。
2. 梯形的面积公式梯形的面积可以通过以下公式计算:$$\text{面积} = \frac{(\text{上底} + \text{下底}) \times \text{高}}{2}$$3. 梯形的练题下面是一些梯形的练题,供你练梯形的面积计算:练题1已知一个梯形的上底为5cm,下底为9cm,高为4cm,求其面积。
练题2已知一个梯形的面积为36cm²,上底为6cm,高为9cm,求其下底的长度。
练题3一个梯形的上底和下底之差为7cm,上底和下底的和为15cm,求该梯形的面积。
请按照上述公式和给出的条件,计算并填写答案。
答案及解析练题1:根据梯形面积公式,代入已知条件计算:$$\text{面积} = \frac{(5 + 9) \times 4}{2} = 28 \, \text{cm²}$$练题2:根据梯形面积公式,代入已知条件计算下底长度:$$36 = \frac{(6 + \text{下底}) \times 9}{2}$$化简方程,得到:$$72 = 6 + \text{下底} \quad \Rightarrow \quad \text{下底} = 66 \, \text{cm}$$练题3:设上底为 $x$,下底为 $x - 7$。
根据梯形面积公式,代入已知条件计算:$$\text{面积} = \frac{(x + (x - 7)) \times 4}{2} = 15$$化简方程,得到:$$2x - 7 = 15 \quad \Rightarrow \quad x = 11$$上底为 11cm,下底为 4cm,高为 4cm,面积为:$$\text{面积} = \frac{(11 + 4) \times 4}{2} = 30 \, \text{cm²}$$以上是梯形的练习题及其答案解析。
梯形练习题及答案

梯形练习题及答案答案一:梯形练习题及答案一、选择题1. 梯形的两边是平行边,且不等长的四边形,其中不等长的一对边称为()。
A. 平行边B. 高C. 长边D. 短边2. 梯形中,非平行边的夹角互补,则该梯形是()。
A. 直角梯形B. 等腰梯形C. 普通梯形D. 等边梯形3. 若梯形的一组对边的夹角为75°,则该梯形的另一组对边的夹角为()A. 15°B. 30°C. 45°D. 60°4. 若梯形的一组对边的夹角为120°,则该梯形的另一组对边的夹角为()A. 60°B. 75°C. 90°D. 105°5. 梯形的高等于上底和下底的差,且上底为10 cm,下底为20 cm,那么该梯形的面积为()㎠。
A. 90B. 100C. 110D. 120二、计算题1. 已知一个梯形的上底长为8 cm,下底长为14 cm,高为6 cm,求该梯形的面积。
解:面积 = (上底长 + 下底长) ×高 ÷ 2= 22 × 6 ÷ 2= 132 ÷ 2= 66 cm²该梯形的面积为66平方厘米。
2. 已知一个梯形的上底长为16 cm,下底长为12 cm,面积为160平方厘米,求该梯形的高。
解:面积 = (上底长 + 下底长) ×高 ÷ 2160 = (16 + 12) ×高 ÷ 2320 = 28 ×高高 = 320 ÷ 28高≈ 11.43 cm该梯形的高约为11.43厘米。
三、综合题在一个梯形中,上底长是下底长的3倍,梯形的高是7 cm,求该梯形的面积。
解:设下底长为x,则上底长为3x。
面积 = (上底长 + 下底长) ×高 ÷ 2= 4x × 7 ÷ 2= 14x ÷ 2= 7x根据题意可得 7x = 7 cm解得 x = 1下底长为1 cm,上底长为3 cm。
梯形典型题目汇编

题目:一个直角梯形,上底是4cm,下底是6cm,高是5cm,求这个直角梯形的面积。
题目:一个等腰梯形的上底是4cm,下底是6cm,高是5cm,求这个等腰梯形的面积。
题目:一个梯形的上底是4cm,下底是6cm,高是5cm,求这个梯形的周长。
高难度题目解析
题目:一个直角梯形的上底是2厘米,下底是4厘米,高是3厘米,求梯形的面积。
题目:等腰梯形的性质
解析:等腰梯形两腰相等,上下底平行,内角和为360度,对角线相等。
解题思路:利用等腰梯形的性质,结合已知条件,推导出相关结论。
解题技巧:利用辅助线,将等腰梯形转化为三角形或平行四边形,简化计算过程。
中等难度题目解析
题目:一个等腰梯形的上底是4cm,下底是6cm,高是5cm,求这个等腰梯形的周长。
题目:一个等腰梯形的上底是5厘米,下底是7厘米,高是4厘米,求梯形的周长。
题目:一个梯形的上底是4厘米,下底是6厘米,高是5厘米,求梯形的面积。
题目:一个梯形的上底是3厘米,下底是7厘米,高是5厘米,求梯形的周长。
汇报人:XX
感谢观看
特殊四边形的判定
正方形的判定:四边相等且有一个角为直角
矩形的判定:有一个角为直角且对角线相等
梯形的判定:一组对边平行且不相等
菱形的判定:四边相等
05
梯形的实际应用
生活中的梯形应用
桥梁结构:桥梁的斜拉索、桥墩等结构中常采用梯形设计,以提高结构的稳定性和承重能力。
机械零件:梯形螺纹在许多机械零件中都有应用,例如螺钉、螺栓等,可以实现精确的配合和传动。
XX,a click to unlimited possibilities
梯形典型题目汇编
目录
01
梯形相关练习题

梯形相关练习题梯形是一种特殊的四边形,其中有两边是平行的,被称为上底和下底,而另外两边则不平行,被称为斜边或者腰。
本文将介绍一些梯形的相关练习题,帮助读者巩固对梯形的理解和应用。
练习题一:计算梯形的面积已知一梯形的上底长度为a,下底长度为b,高为h,请计算其面积。
解答:梯形的面积计算公式为:面积 = (上底 + 下底) ×高 ÷ 2代入已知条件,即可计算出梯形的面积。
练习题二:求解梯形的周长已知一梯形的上底长度为a,下底长度为b,斜边长度为c,请计算其周长。
解答:梯形的周长计算公式为:周长 = 上底 + 下底 + 两边之和代入已知条件,即可计算出梯形的周长。
练习题三:寻找梯形的等腰性质已知一梯形的上底长度为a,下底长度为b,斜边长度为c,高为h。
观察该梯形的特点,判断并证明是否存在两边相等的情况。
解答:根据梯形的定义,我们可以发现一条重要性质:梯形的两个底角和两个顶角的和都是180度。
假设上底角为A,下底角为B,则有A + B + 两个顶角的和 = 180度。
由于梯形的两边不平行,所以两个顶角一定相等,即上底角A和下底角B相等。
练习题四:求解梯形的中线长度已知一梯形的上底长度为a,下底长度为b,高为h。
求解梯形的中线长度。
解答:梯形的中线长度计算公式为:中线长度 = (上底 + 下底) ÷ 2代入已知条件,即可计算出梯形的中线长度。
练习题五:求解梯形的对角线长度已知一梯形的上底长度为a,下底长度为b,斜边1长度为c1,斜边2长度为c2。
求解梯形的对角线长度。
解答:梯形的对角线长度计算公式为:对角线长度= √(c1² + c2² -2c1c2cos(θ))其中,θ为斜边1和斜边2之间的夹角。
练习题六:有关梯形的面积比已知两个梯形,其上底分别为a1和a2,下底分别为b1和b2,高分别为h1和h2。
假设这两个梯形的面积满足比例关系,即:面积1:面积2 = k:1。
梯形经典题型(培优提高)

梯形知识归纳1、梯形的有关概念:梯形:一组对边平行而另一组对边不平行的四边形叫做梯形。
等腰梯形:两腰相等的梯形叫做等腰梯形。
直角梯形:一腰和底垂直的梯形叫做直角梯形。
2、等腰梯形的性质以及应用:等腰梯形是轴对称图形,对称轴是连接两底中点的直线。
等腰梯形同一底上的两个内角相等,两条对角线相等。
3、等腰梯形的判别方法:定义判定,即“两腰相等的梯形是等腰梯形”。
同一底上的两个内角相等的梯形是等腰梯形。
4、梯形问题常见辅助线做法(见例题)5、三角形和梯形的中位线定理:(1)三角形的中位线________于第三边且等于第三边的_______.(2)梯形的中位线_______于两底且等于两底和的_______.6、梯形的面积:如图所示,S梯形ABCD=12(AB+CD)·DE=________(用L表示中位线,h表示高).在该梯形中,面积相等的三角形有:_____________;_____________;_____________.例题讲解在解(证)有关梯形的问题时,常常要添作辅助线,把梯形问题转化为三角形或平行四边形问题。
一、平移1、平移一腰:从梯形的一个顶点作一腰的平行线,把梯形转化为一个三角形和一个平行四边形。
例1:如图,梯形ABCD的上底AB=3,下底CD=8,腰AD=4,求另一腰BC的取值范围。
2、平移两腰:利用梯形中的某个特殊点,过此点作两腰的平行线,把两腰转化到同一个三角形中。
例2:如图,在梯形ABCD中,AD//BC,∠B+∠C=90°,AD=1,BC=3,E、F分别是AD、BC的中点,连接EF,求EF的长。
3、平移对角线:过梯形的一个顶点作对角线的平行线,将已知条件转化到一个三角形中。
例3:如图,在梯形ABCD中,AD//BC,BD=15cm,AC=20cm,高AE=12cm,求梯形ABCD的面积。
【变式1】已知梯形ABCD的面积是32,两底与高的和为16,如果其中一条对角线与两底垂直,则另一条对角线长为_____________【变式2】在梯形ABCD中,AD∥BC,AC⊥BD,若AD=2,BC=8,BD=6.求:(1)对角线AC的长;(2)梯形ABCD的面积.二、延长即延长两腰相交于一点,可使梯形转化为三角形。
梯形性质及判定练习题

梯形性质及判定练习题梯形是一种四边形,其两边边平行,而另外两边不平行。
在本练题中,我们将探讨梯形的性质以及如何判定一个四边形是否为梯形。
梯形的性质梯形具有以下性质:1. 两底角相等:梯形的两个底角(与较长边相对的两个角)是相等的。
两底角相等:梯形的两个底角(与较长边相对的两个角)是相等的。
2. 两腰相等:梯形的两条斜边(与底平行的两边)是相等的。
两腰相等:梯形的两条斜边(与底平行的两边)是相等的。
3. 对角线交点连线平分底角:梯形的对角线交点连线将底角平分。
对角线交点连线平分底角:梯形的对角线交点连线将底角平分。
4. 底角与顶角之和等于180度:梯形的底角和顶角之和总是等于180度。
底角与顶角之和等于180度:梯形的底角和顶角之和总是等于180度。
判定一个四边形是否为梯形要判定一个四边形是否为梯形,可以根据以下条件进行判断:1. 两对边平行:如果一个四边形的两对边都是平行的,那么它就是一个梯形。
两对边平行:如果一个四边形的两对边都是平行的,那么它就是一个梯形。
2. 底角相等:如果一个四边形的两个底角是相等的,那么它就是一个梯形。
底角相等:如果一个四边形的两个底角是相等的,那么它就是一个梯形。
如果一个四边形同时满足上述两个条件,那么我们可以确定它是一个梯形。
练题让我们来练一下判定一个四边形是否为梯形。
1. 判定以下四边形是否为梯形:*使用上述判定条件,来判断这个四边形是否为梯形,并解释理由。
*这个四边形是一个梯形。
它满足两对边平行的条件(上边和下边平行,左边和右边平行),同时底角相等。
2. 判定以下四边形是否为梯形:*使用上述判定条件,来判断这个四边形是否为梯形,并解释理由。
*这个四边形不是一个梯形。
虽然两对边平行(上边和下边平行,左边和右边平行),但底角并不相等。
练题结束。
通过不断练判定梯形的条件,我们可以更好地理解和应用梯形的性质。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
梯形一般梯形【基础练习】1. 在梯形ABCD 中,AD ∥BC ,AB=AC ,若∠D=110°,∠ACD=30°,则∠BAC 等于A. 80°B. 90°C. 100°D. 110°2. 若梯形的上底边长为4,中位线长为6,则此梯形的下底长为A.5B.8C.12D.163. 如果梯形中位线长20,它被一条对角线分成两段的差为5,那么两底的长分别为A.15,30B.25,15C.30,20D.以上都不对 4. 已知梯形的两个对角分别是78°和120°,则另两个角分别是( )A.78°或120°B.102°或60°;C.120°或78°D.60°或120° 5. 直角梯形的斜腰和下底长都等于a,斜腰和下底的夹角是60°,则梯形的上、 下底之差是( )A.aB.32a C.34a D.22a 6. 在梯形ABCD 中,AD ∥BC ,AB=AD=DC=2,∠C=45°,则梯形ABCD 的周长是( )A 、10B 、8C 、228+D 、2210-7. 在下列图形中,沿着虚线将长方形剪成两部分,那么由这两部分既能拼成平行四边形,又能拼成三角形和梯形的是 ( ).A B C D8. 在梯形ABCD 中,AB ∥CD ,AB>CD ,如果∠D>∠C ,那么AD 和BC 的关系是( )A.AD>BCB.AD=BCC.AD<BCD.不能确定9. 梯形的一腰和上底所成的角为150°,若这腰的长为5cm ,中位线为4cm ,则这个梯形的面积为()A 、10cmB 、5cmC 、20cmD 、40cm10.如图,在梯形ABCD中,AD∥BC,CA平分∠BCD,CD=5,则AD的长是()A. 6B. 5C. 4D. 311.如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是()A. 1B. 2C. 3D. 不能确定12.若梯形的中位线长为5,面积为20,则这个梯形的高为.13.已知直角梯形的一腰与下底的夹角为60º,下底与其中的一腰都等于6,则梯形的中位线的长为以线段16=a、13=b为梯形的两底,以10=c为一腰,则另一腰长d的范围是________;14.在梯形中,不是同一底上的两组角的比值分别为1:3和3:7,则四个角的度数为___________________15.如果一个直角梯形的两底长分别为7 cm,12 cm,斜腰长为13 cm,那么这个梯形的面积等于_______.16.已知一个梯形的面积为22 cm2,高为2 cm,则该梯形的中位线的长等于________cm.17.梯形ABCD中,AD∥BC,∠B=72°,∠C=48°,则∠A=____, ∠D=_____.18.如图2,a∥b∥c∥d,AB=BC=CD,O是AB的中点,EF=6cm,那么OH=____DCBAHGFE abcdACED FGADE19.如图3,△ABC中,D、E三等分AB,DE∥BC,EG∥BC,AC=15cm,则FC=_____.20.如图4,△ABC中,∠C=90°,∠A=45°,AC=10cm,D是AB中点,DE⊥BC于E,则DE=_______.21.如图,梯形ABCD中,AB//CD,∠ABC=90°,AB=9cm,BC=8cm,CD=7cm,M是AD的中点,过M作AD的垂线交BC于N,则BN等于_____cm.21题图22题图22.如图,梯形ABCD中,AD∥BC,若∠B=60°,AC⊥AB,那么∠DAC= .23.如图,在梯形ABCD中,∠DCB=90°,AB∥CD,AB=25,BC=24. 将该梯形折叠,点A恰好与点D重合,BE为折痕,那么AD的长度为________.24.如图所示,图(1)中梯形符合_________条件时,可以经过旋转和翻折形成图(2).25.如图所示,梯形纸片ABCD,∠B=60°,AD∥BC,AB=AD=2,BC=6,将纸片折叠,使点B与点D重合,折痕为AE,则CE=________.26. 如图,已知梯形ABCD 中,AB ∥CD ,AD ⊥CD ,若腰BC =15,对角线AC =20,且AC ⊥BC ,则AB = ,AD = ,CD = , ABCDS 梯形 .ABCD27. 如图,已知:直线m ∥n ,A 、B 为直线n 上两点,C 、P 为直线m 上两点. ⑴请写出图中面积相等的各对三角形:____________.⑵如果A 、B 、C 、为三个定点,点P 在m 上移动,那么,无论P 点移动到任何位置,总有_______与△ABC 的面积相等.ABCPO m n28. 如图,梯形ABCD 中,AB ∥CD, EF 是中位线,EF 分别交AC 、BD 于M 、N ,若AB=8,CD=6,则MN =_______.29. 在梯形ABCD 中,AD//BC ,∠B=90°,∠C=45°,AD=1,BC=4,E 为AB 中点,EF//DC交BC 于点F ,求EF 的长。
30. 如图,梯形 ABCD 中,AD //BC ,E 是CD 的中点,EF ⊥AB 于点F ,AB =6cm ,EF =5cm ,试求梯形 ABCD 的面积.A BCD EF31. 如图,在梯形ABCD 中,AD ∥BC ,AB=CD ,AD=2,BC=6,∠B =45°。
求此梯形的面积。
(8分)32. 如图,在梯形ABCD 中,AD ∥BC ,∠B =50°,∠C =80°AB CD33. 如图,在梯形ABCD 中,AD//BC ,∠B=50°,∠C=80°,AD=2,BC=5,求CD 的长。
34. 四边形ABCD,∠ABC=∠BCD ,AD//BC ,AC 与BD 相交于O ,∠BOC=120°,且AD=7,BD=10.求四边形的面积。
35. 如图,在直角梯形ABCD 中,AD//BC ,AB ⊥AD ,BC=CD ,BE ⊥CD 于点E ,求证:AD=DE 。
ABCDABCDE36. 已知:在梯形ABCD 中,点E 、F 是AB 、CD 的中点,求证:EF ∥AB ∥CD 且)(21BC AD EF +=37. 同学们对公园的滑梯很熟悉吧!如图,是某公园(六•一)前新增设的一台滑梯,该滑 梯高度AC =2m ,滑梯着地点B 与梯架之间的距离BC =4m 。
(1)求滑梯AB 的长(精确到0.1m );(2)若规定滑梯的倾斜角(∠ABC )不超过45°属于安全范围。
请通过计算说明这架滑梯的倾斜角是否要求?38. 如图,在直角梯形ABCD 中,AB ∥DC,∠ABC=90°,AB=2DC,对角线AC ⊥BD,垂足为F,过点F 作EF ∥AB,交AD 于点E,CF=4cm. ⑴求证:四边形ABFE 是等腰梯形; ⑵求AE 的长.39. 如图,在梯形ABCD 中,AD ∥BC ,AB=DC=AD ,∠ADC=120°.求证:(1)BD ⊥DC ;(2)若AB=4,求梯形ABCD 的面积.A BCD E F40. 如图,在梯形ABCD 中,AB//DC ,O 是BC 的中点,∠AOD=90°,求证:AB +CD=AD 。
【培优练习】41. 如图,在梯形ABCD 中,边AB 与CD 平行,对角线BD 与边AD 的长相等. 若DCB∠=110°,30=∠CBD °,那么ADB ∠等于A. 80°B. 90°C. 100°D. 110°42.观察下列图形并填表:梯形个数 1 2 3 4 5 6 ... n 周 长 591317...43. 如图,在梯形ABCD 中,AB CD ∥, 90A B ∠+∠=°, 511CD AB ==,,点M N 、分别为AB CD 、的中点,则线段MN = .ABCDN MCB44. 如图,梯形ABCD 中,AD //BC ,M 、N 分别是底AD 和BC 的中点,∠B +∠C =90°,BC=18,AD =6,求EF 的长.进而探究一般规律,若BC =x ,AD =y ,那么 EF 为多少?BCDEFA45. 如图,梯形ABCD 中,AD ∥BC ,对角线AC 与BD ∠DBC=30°.求证:AC=MN 。
(10分)46. 如图,梯形ABCD 中,120AD BC AB DC ADC =∠=o∥,,,对角线CA 平分DCB ∠,E 为BC 的中点,试求DCE △与四边形ABED 面积的比.47. 如图,在梯形ABCD 中,AD//BC ,E 、F 分别是BD 、AC 的中点,求证:(1)EF//AD ;(2))(21AD BC EF -=。
A DBECEFBCGAN MOA DB C48. 在梯形ABCD 中,AD ∥BC , ∠BAD=900,E 是DC 上的中点,连接AE 和BE ,求∠AEB=2∠CBE 。
49. 如图,在梯形ABCD 中,AD//BC ,AC=15cm ,BD=20cm ,高DH=12cm ,求梯形ABCD的面积。
50. 在梯形ABCD 中,AD ∥BC, E 为CD 的中点,求证:S △ABE=21S 梯形ABCDDACNM51.(选做)如图所示,在直角梯形ABCD中,AD//BC,∠A=90°,AB=12,BC=21,AD=16。
动点P从点B出发,沿射线BC的方向以每秒2个单位长的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位长的速度向点D运动,当其中一个动点到达端点时另一个动点也随之停止运动。
设运动的时间为t(秒)(1)设△DPQ的面积为S,求S与t之间的函数关系式;(2)当t为何值时,四边形PCDQ是平行四边形?(3)当t为何值时PD=PQ?当t为何值时DQ=PQ?52.如图,直角梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm,动点P 从A开始沿AD边向D以1cm/s的速度运动,动点Q从点C开始沿CB以3cm/s的速度向点B运动.P、Q同时出发,当其中一点到达顶点时,另一点也随之停止运动,设运动时间为ts, 问t为何值时.(1)四边形PQCD是平行四边形.(2)当t为何值时,四边形PQCD为等腰梯形.。
