人教版八年级数学第23讲菱形培优训练

合集下载

2018春人教版数学八年级下册《菱形》提升练习

菱形一、选择题（每小题4分，共12分)1、（2013·海南中考）如图，将△ABC沿BC方向平移得到△DCE,连接AD,下列条件中能够判定四边形ACED为菱形的是（)A、AB=BCB、AC=BCC、∠B=60°D、∠ACB=60°2、如图，两条笔直的公路l1,l2相交于点O，村庄C的村民在公路的旁边建三个加工厂A，B,D，已知AB=BC=CD=DA=5千米，村庄C到公路l1的距离为4千米，则村庄C到公路l2的距离是（）A、3千米B、4千米C、5千米D、6千米3、（2013·玉林中考)如图，在给定的一张平行四边形纸片上作一个菱形、甲、乙两人的作法如下：甲：连接AC，作AC的垂直平分线MN分别交AD,AC,BC于M，O，N,连接AN，CM，则四边形ANCM是菱形、乙：分别作∠A，∠B的平分线AE，BF,分别交BC，AD于E，F,连接EF，则四边形ABEF是菱形、根据两人的作法可判断（)A、甲正确，乙错误B、乙正确,甲错误C、甲、乙均正确D、甲、乙均错误二、填空题(每小题4分，共12分）4、(2013·潍坊中考)如图,ABCD是对角线互相垂直的四边形,且OB=OD,请你添加一个适当的条件，使ABCD成为菱形、（只需添加一个即可)5、如图，在四边形ABCD中,AC=BD=6，E，F，G，H分别是AB,BC，CD，DA的中点，则EG2+FH2= 、6、（2013·宜宾中考)如图，在△ABC中，∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线，交CE的延长线于点F，在AF的延长线上截取FG=BD,连接BG,DF、若AG=13,CF=6，则四边形BDFG的周长为、三、解答题(共26分)7、(8分）已知:如图所示，平行四边形ABCD中，M，N分别是DC,AB的中点,若∠A=60°，AB=2AD、求证：MN⊥BD、8、（8分)（2013·盐城中考）如图,在平行四边形ABCD中,E为BC边上的一点，连接AE，BD且AE=AB、（1)求证：∠ABE=∠EAD、(2)若∠AEB=2∠ADB,求证：四边形ABCD是菱形、【拓展延伸】9、(10分）△ABC是等边三角形,点D是射线BC上的一个动点(点D 不与点B,C重合）,△ADE是以AD为一边的等边三角形，过点E作BC 的平行线，分别交射线AB，AC于点F，G，连接BE、(1）如图（a)所示,当点D在线段BC上时、①求证:△AEB≌△ADC、②探究四边形BCGE是怎样的特殊四边形?并说明理由、（2）如图(b)所示，当点D在BC的延长线上时,直接写出(1）中的两个结论是否成立、（3）在（2)的情况下,当点D运动到什么位置时,四边形BCGE是菱形?并说明理由、答案解析1、【解析】选B、由平移，得AC∥DE，AC=DE,∴四边形ACED是平行四边形；又∵BC=CE,∴当AC=BC时，AC=CE，∴四边形ACED是菱形、2、【解析】选B、如图，连接AC,作CF⊥l1，CE⊥l2; ∵AB=BC=CD=DA=5千米，∴四边形ABCD是菱形，∴∠CAE=∠CAF,∴CE=CF=4千米、3、【解析】选C、甲的作法正确；∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DAC=∠ACN,∵MN是AC的垂直平分线,∴AO=CO，在△AOM和△CON中,∴△AOM≌△CON（ASA），∴MO=NO,∴四边形ANCM是平行四边形，∵AC⊥MN，∴四边形ANCM是菱形、乙的作法正确;∵AD∥BC，∴∠1=∠2,∠6=∠7，∵BF平分∠ABC,AE平分∠BAD，∴∠2=∠3,∠5=∠6,∴∠1=∠3，∠5=∠7，∴AB=AF，AB=BE，∴AF=BE、∵AF∥BE,且AF=BE,∴四边形ABEF是平行四边形、∵AB=AF,∴平行四边形ABEF是菱形、4、【解析】根据对角线互相垂直的平行四边形是菱形，已知AC⊥BD,所以只需添加条件使四边形ABCD为平行四边形即可，答案不唯一,如OA=OC等、答案：OA=OC（答案不唯一)5、【解析】连接EF，FG，GH,HE,∵点E,F,G,H分别是AB,BC，CD,DA的中点,∴EF∥AC∥GH，EF=GH=AC=3,EH∥BD∥FG，EH=FG=BD=3，所以四边形EFGH是菱形，∴EG⊥FH、设EG,FH的交点为O、∴EG2+FH2=(2OE)2+(2OH)2=4OE2+4OH2=4(OE2+OH2)=4EH2=36、答案:366、【解析】∵AG∥BD,BD=FG,∴四边形BGFD是平行四边形，∵CF⊥BD,∴CF⊥AG,又∵点D是AC的中点，∴BD=DF=AC,∴四边形BGFD是菱形，设GF=x,则AF=13—x，AC=2x,在Rt△ACF中,AF2+CF2=AC2，即（13—x）2+62=(2x）2,解得：x=5，故四边形BDFG的周长=4GF=20、答案:207、【证明】连接DN，BM、∵四边形ABCD是平行四边形，∴AB CD，∵M,N分别是DC，AB的中点，∴DM=DC，BN=AB=AN，∴DM BN，∴四边形BMDN是平行四边形、∵AB=2AD，AB=2AN，∴AD=AN、∵∠A=60°，∴△ADN是等边三角形,∴DN=AN=BN,∴平行四边形BMDN是菱形，∴MN⊥BD、8、【证明】（1)∵四边形ABCD为平行四边形，∴AD∥BC,∴∠AEB=∠EAD、又∵AE=AB,∴∠ABE=∠AEB、∴∠ABE=∠EAD、（2)∵AD∥BC，∴∠ADB=∠DBC、又∵∠AEB=2∠ADB，∠AEB=∠ABE，∴∠ABE=2∠DBC,∴∠ABD=∠DBC、∴∠ABD=∠ADB,∴AB=AD、又∵四边形ABCD为平行四边形，∴四边形ABCD是菱形、9、【解析】（1)①∵△ABC和△ADE都是等边三角形，∴AE=AD，AB=AC，∠EAD=∠BAC=60°、又∵∠EAB=∠EAD—∠BAD，∠DAC=∠BAC-∠BAD,∴∠EAB=∠DAC，∴△AEB≌△ADC、②四边形BCGE是平行四边形,理由：由①得△AEB≌△ADC,∴∠ABE=∠C=60°、又∵∠BAC=∠C=60°，∴∠ABE=∠BAC，∴EB∥GC、又∵EG∥BC，∴四边形BCGE是平行四边形、（2)①②都成立、（3）当CD=CB(∠CAD=30°或∠BAD=90°或∠ADC=30°）时，四边形BCGE是菱形、理由：由①得△AEB≌△ADC，∴BE=CD、又∵CD=CB,∴BE=CB、由②得四边形BCGE是平行四边形,∴四边形BCGE是菱形、7C学科网，最大最全的中小学教育资源网站，教学资料详细分类下载！。

2024年人教版八年级下册数学同步培优训练第十八章平行四边形第2节菱形第1课时

18.2.2菱形第1课时【基础达标练】课时训练夯实基础【易错诊断】(打“√”或“×”)1.菱形是特殊的平行四边形.(√)2.菱形的四个角都相等.(×)3.菱形的对角线互相垂直且相等.(×)4.菱形的对角线把菱形分成四个全等的直角三角形.(√)5.菱形的面积等于两条对角线长乘积的一半.(√)【对点达标】知识点1菱形的性质1.下列关系中,是菱形的性质但不是平行四边形的性质的是(A)A.对角线垂直B.两组对边分别平行C.对角线互相平分D.两组对角分别相等2.(2023·湘潭中考)如图,菱形ABCD中,连接AC,BD,若∠1=20°,则∠2的度数为(C)A.20°B.60°C.70°D.80°3.(2023·丽水中考)如图,在菱形ABCD中,AB=1,∠DAB=60°,则AC的长为(D)A.12B.1 C.√32D.√34.菱形的对角线的一半的长分别为8 cm和11 cm,则菱形的面积是176 cm2.5.(一题多解)如图,菱形ABCD的对角线AC,BD相交于点O,E为DC的中点,若OE=2,则菱形的周长为16.6.如图,在菱形ABCD 中,点M ,N 分别在AB ,CB 上,且∠ADM =∠CDN ,求证:BM =BN.【证明】∵四边形ABCD 为菱形,∴AD =CD =AB =BC ,∠A =∠C.在△AMD 和△CND 中,{∠A =∠C ,AD =CD ,∠ADM =∠CDN ,∴△AMD ≌△CND (ASA),∴AM =CN ,∴AB -AM =BC -CN ,即BM =BN. 知识点2 菱形性质的实际应用7.(情境应用题)如图,已知某菱形花坛ABCD 的周长是24米,∠BAC =60°,则花坛对角线AC 的长等于 (B)A.6√3米B.6米C.3√3米D.3米8.(2023·贵阳白云区质检)中国结,象征着中华民族的历史文化与精神.小明家有一中国结挂饰,他想求两对边的距离,利用所学知识抽象出如图所示的菱形ABCD ,测得BD =12 cm,AC =16 cm,直线EF ⊥AB 交两对边于E ,F ,则EF 的长为485cm .【综合能力练】巩固提升迁移运用9.如图,在菱形ABCD 中,对角线AC ,BD 相交于点O ,下列结论:①AC ⊥BD ;②OA =OB ;③∠ADB =∠CDB;④△ABC是等边三角形,其中一定成立的是(D)A.①②B.③④C.②③D.①③10.如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=4,S菱=36,则OH的长为(B)形ABCDA.5B.4.5C.4D.2.511.(2023·河北中考)如图,直线l1∥l2,菱形ABCD和等边△EFG在l1,l2之间,点A,F分别在l1,l2上,点B,D,E,G在同一条直线上.若∠α=50°,∠ADE=146°,则∠β=(C)A.42°B.43°C.44°D.45°12.(情境应用题)如图是一个利用四边形的不稳定性制作的菱形晾衣架.已知其中每个菱形的边长为20 cm,∠1=60°,则墙上悬挂晾衣架的两个铁钉A,B之间的距离等于 (D)A.10 cmB.10√3 cmC.20 cmD.20√3 cm13.(素养提升题)如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF ⊥AB,OG∥EF.(1)求证:四边形OEFG 是矩形; (2)若AD =10,EF =4,求OE 和BG 的长.【解析】(1)∵四边形ABCD 是菱形,∴BD ⊥AC ,∠DAO =∠BAO. ∵E 是AD 的中点,∴AE =OE =12AD ,∴∠EAO =∠AOE ,∴∠AOE =∠BAO , ∴OE ∥FG.∵OG ∥EF ,∴四边形OEFG 是平行四边形. ∵EF ⊥AB ,∴∠EFG =90°,∴四边形OEFG 是矩形; (2)∵四边形ABCD 是菱形,∴BD ⊥AC ,AB =AD =10,∴∠AOD =90°, ∵E 是AD 的中点,∴OE =AE =12AD =5; 由(1)知,四边形OEFG 是矩形,∴FG =OE =5,∵AE =5,EF =4,∴AF =√AE 2-EF 2=3,∴BG =AB -AF -FG =10-3-5=2.模型1 菱形+60°(或120°)+对角线→等边三角形,含30°角的直角三角形如图(1),已知菱形ABCD 中∠BAD =60°,对角线AC ,BD 相交于点O ,则△ABD ,△CBD 均为等边三角形;△ADO ,△AOB ,△BOC ,△COD 都是含30°角的直角三角形. 模型2 菱形对角线交点+ 一边中点→构造三角形中位线:如图(2),菱形ABCD 的对角线AC ,BD 相交于点O ,E 为DC 的中点,则OE 是△ACD (或△BDC )的中位线,则OE =12AD =12BC.。

部编数学八年级下册菱形的判定专项提升训练(重难点培优)【拔尖特训】2023年培优含答案

【拔尖特训】2022-2023学年八年级数学下册尖子生培优必刷题【人教版】专题18.3菱形的判定专项提升训练（重难点培优）班级：___________________ 姓名：_________________ 得分：_______________注意事项：本试卷满分120分，试题共24题，其中选择10道、填空8道、解答6道．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．1．（2022春•杜尔伯特县期中）菱形的周长为12，一个内角为60°，则较短的对角线长为（）A．2B．3C．1D．【分析】根据已知可得较短的对角线与两邻边组成等边三角形，则菱形较短的对角线长＝菱形的边长，根据周长可求得菱形的边长从而较短的对角线也就求得了．【解答】解：由已知得，较短的对角线与两邻边组成等边三角形，则菱形较短的对角线长＝菱形的边长＝12÷4＝3，故选：B．2．（2022春•南岗区校级期中）如图，菱形ABCD的两条对角线长分别为AC＝9和BD＝6，那么菱形ABCD 的面积为（）A．4B．30C．54D．27【分析】直接根据菱形面积等于两条对角线的长度乘积的一半进行计算即可．【解答】解：∵四边形ABCD是菱形，∴菱形ABCD的面积＝BD•AC＝×6×9＝27，故选：D．3．（2022春•墨玉县期末）如图，菱形ABCD中，AC＝8．BD＝6．则菱形的面积为（）A．20B．40C．28D．24【分析】根据菱形的面积等于对角线乘积的一半可得答案．【解答】解：菱形的面积为6×8÷2＝24，故选：D．4．（2022春•南召县期末）四边形具有不稳定性，小明将一个菱形ABCD转动，使它形状改变，当转动到使∠B＝60°时（如图），测得AC＝2；当转动到使∠B＝120°时，AC的值为（）A．2B．C．D．【分析】根据有一个角是60°的等腰三角形是等边三角形可得菱形的边长为2，再根据菱形的性质以及勾股定理解答即可．【解答】解：因为菱形ABCD，∠B＝60°时，测得AC＝2，所以△ABC是等边三角形，所以菱形的边长为2，当转动到使∠B＝120°时，如图所示：因为AC⊥BD，∠ABC＝120°，所以∠ABO＝60°，所以∠OAB＝30°，所以，所以，所以AC＝2AO＝．故选：B．5．（2022春•博兴县期末）如图，菱形ABCD的对角线AC、BD相交于点O，DE⊥AB于点E，若AB＝5，DE＝4，则在下列结论中正确的是（）A．DB＝5B．AE＝4C．BE＝2D．OA＝3【分析】根据菱形的性质可知AB＝AD，AO＝OC，OD＝OB，由于DE⊥AB于点E，所以在Rt△AED中，利用勾股定理可以求出AE，进而求出BE、BD，再在Rt△AOB中求出OA即可作出判断．【解答】解：∵四边形ABCD是菱形，∴AB＝AD，AO＝OC，OD＝OB，∵AB＝5，∴AD＝5，∵DE⊥AB于点E，DE＝4在Rt△AED中，根据勾股定理得，AE＝＝3，故B错误；∴BE＝AB﹣AE＝5﹣3＝2，故C正确；在Rt△BDE中，根据勾股定理得，BD＝，故A错误；∴OB＝BD＝，在Rt△AOB中，根据勾股定理得，OA＝，故D错误．故选：C．6．（2022春•承德县期末）如图，在平面直角坐标系中，菱形ABCD的顶点D在x轴上，边BC在y轴上，若点A的坐标为（12，13），则点C的坐标是（）A．（0，﹣8）B．（0，﹣5）C．（﹣5，0）D．（0，﹣6）【分析】在Rt△ODC中，利用勾股定理求出OC即可解决问题．【解答】解：∵A（12，13），∴OD＝12，AD＝13，∵四边形ABCD是菱形，∴CD＝AD＝13，在Rt△ODC中，OC＝，∴C（0，﹣5）．故选：B．7．（2022春•丰泽区校级月考）如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DH⊥AB于点H，连接OH，OH＝2，若菱形ABCD的面积为12，则AB的长为（）A．10B．4C．D．6【分析】由菱形的性质得OA＝OC，OB＝OD，AC⊥BD，再求出BD＝4，则OB＝2，然后由菱形面积求出AC＝6，则OA＝3，即可解决问题．【解答】解：∵四边形ABCD是菱形，∴OA＝OC，OB＝OD，AC⊥BD，∵DH⊥AB，∴∠BHD＝90°，∴BD＝2OH，∵OH＝2，∴BD＝4，∴OB＝2，∵菱形ABCD的面积＝AC•BD＝AC×4＝12，∴AC＝6，∴OA＝3，在Rt△AOB中，由勾股定理得：AB＝＝＝，故选：C．8．（2022秋•合川区校级月考）如图，在菱形ABCD中，M．N分别在AB，CD上，且AM＝CN，MN与AC 交于点O，连接BC若∠DAC＝28°，则∠OBC的度数为（）A．28°B．52°C．62°D．72°【分析】根据菱形的性质以及AM＝CN，再由ASA可得△AMO≌△CNO，得AO＝CO，然后证BO⊥AC，继而可求得∠OBC的度数【解答】解：∵四边形ABCD为菱形，∴AB∥CD，AB＝BC，∴∠MAO＝∠NCO，∠AMO＝∠CNO，在△AMO和△CNO中，，∴△AMO≌△CNO（ASA），∴AO＝CO，∵AB＝BC，∴BO⊥AC，∴∠BOC＝90°，∵∠DAC＝28°，∴∠BCA＝∠DAC＝28°，∴∠OBC＝90°﹣28°＝62°．故选：C．9．（2022秋•胶州市校级月考）如图，在菱形ABCD中，∠A＝60°，E、F分别是AB，AD的中点，DE、BF相交于点G，连接BD，CG．有下列结论：①∠BGD＝120°；②BG+DG＝CG；③△BDF≌△CGB；④，其中正确的结论有（）A．①②③B．①②④C．①③④D．②③④【分析】根据菱形的性质和∠A＝60°，可知△ABD是等边三角形，△BDC是等边三角形，根据等边三角形的性质可得∠BFD＝∠DEB＝90°，∠GDB＝∠GBD＝30°，即可判断①选项；根据SSS可证△CDG ≌△CBG，根据全等三角形的性质可得∠DGC＝∠BGC＝60°，再根据含30°角的直角三角形的性质可判断②选项；根据△GBC为直角三角形，可知CG＞BC，进一步可知CG≠BD，即可判断③选项；根据勾股定理可得DE＝AB，再根据三角形面积的求法即可判断④选项．【解答】解：在菱形ABCD中，AB＝BC＝CD＝AD，∵∠A＝60°，∴∠BCD＝∠A＝60°，∴△ABD是等边三角形，△BDC是等边三角形，∴∠ADB＝∠ABD＝60°，∠CDB＝∠CBD＝60°，∵E，F分别是AB，AD的中点，∴∠BFD＝∠DEB＝90°，∴∠GDB＝∠GBD＝30°，∴∠GDC＝∠GBC＝90°，DG＝BG，∴∠BGD＝180°﹣30°﹣30°＝120°，故①选项正确；在△CDG和△CBG中，，∴△CDG≌△CBG（SSS），∴∠DGC＝∠BGC＝60°，∴∠GCD＝30°，∴CG＝2GD，∵DG＝BG，∴CG＝DG+BG，故②选项正确；∵△GBC为直角三角形，∴CG＞BC，∴CG≠BD，∴△BDF与△CGB不全等，故③选项错误；∵BE＝AB，BD＝AB，∠DEB＝90°，根据勾股定理，得DE＝AB，＝＝，∴S△ABD故④选项正确，故正确的有①②④，故选：B．10．（2022春•新抚区期末）如图，点P是菱形ABCD的对角线AC延长线上一点，过点P分别作AD，DC延长线的垂线，垂足分别为点E，F．若∠B＝120°，AB＝，则PE﹣PF的值为（）A．2B．3C．4D．6【分析】连接BD交AC于O，由菱形的性质和勾股定理得OA＝3，则AC＝6，再由含30°角的直角三角形的性质得PF＝CP，则PE﹣PF＝（AP﹣CP）＝AC，即可得出答案．【解答】解：连接BD交AC于O，如图所示：∵四边形ABCD是菱形，∠ABC＝120°，AB＝2，∴∠BAD＝∠BCD＝180°﹣120°＝60°，∠DAC＝∠DCA＝∠BAD＝×60°＝30°，AD＝AB＝2，BD⊥AC，在Rt△AOD中，OD＝AD＝×＝，∴OA＝＝＝3，∴AC＝2OA＝2×3＝6，Rt△APE中，∠DAC＝30°，∴PE＝AP，在Rt△CPF中，∠PCF＝∠DCA＝30°，∴PF＝CP，∴PE﹣PF＝AP﹣CP＝（AP﹣CP）＝AC＝×6＝3，故选：B．二、填空题（本大题共8小题，每小题3分，共24分）请把答案直接填写在横线上11．（2022秋•牡丹区校级月考）如图，菱形ABCD的对角线相交于点O，若AC＝24，AB＝13，则菱形ABCD 的面积是　120　．【分析】由菱形的性质得AC⊥BD，OA＝OC＝AC＝12，OB＝OD＝BD，再由勾股定理求出OB，得出BD的长，即可解决问题．【解答】解：∵四边形ABCD是菱形，∴AC⊥BD，OA＝OC＝AC＝12，OB＝OD＝BD，∴∠AOB＝90°，∴OB＝＝＝5，∴BD＝2OB＝10，∴菱形ABCD的面积＝AC•BD＝×24×10＝120，故答案为：120．12．（2022秋•东明县校级月考）已知菱形的两条对角线长为10cm和24cm，那么这个菱形的周长为　52cm　，面积为　120cm2　．【分析】由菱形的性质得AC⊥BD，OA＝OC＝AC＝12（cm），OB＝OD＝BD，再由勾股定理求出OB，得出BD的长，即可解决问题．【解答】解：如图，∵四边形ABCD是菱形，AC＝24cm，BD＝10cm，∴AB＝BC＝CD＝AD，AC⊥BD，OA＝OC＝AC＝12（cm），OB＝OD＝BD＝5（cm），∴S＝AC•BD＝×24×10＝120（cm2），∠AOB＝90°，菱形ABCD∴AB＝＝＝13（cm），∴菱形ABCD的周长＝4AB＝4×13＝52（cm），故答案为：52cm，120cm2．13．（2022春•杭州期中）如图，菱形ABCD中，AC，BD相交于O，DE⊥BC于E，连接OE，若∠BAD＝40°，则∠ODE的度数为　20°　．【分析】根据菱形的性质得出∠DAO＝BAD＝20°，AC⊥BD，DO＝BO，AD∥BC，求出DE⊥AD，根据垂直的定义求出∠ADE＝90°，∠DEB＝90°，求出∠ADO，∠ODE的度数，根据直角三角形斜边上的中线的性质得出OD＝OE，求出∠ODE＝∠OED即可．【解答】解：∵四边形ABCD是菱形，∠BAD＝40°，∴∠DAO＝BAD＝20°，AC⊥BD，DO＝BO，AD∥BC，∴∠DOA＝90°，∴∠ADO＝90°﹣∠DAO＝70°，∵AD∥BC，DE⊥BC，∴DE⊥AD，∴∠ADE＝90°，∴∠ODE＝∠ADE﹣∠ADO＝20°，∵DE⊥BC，∴∠DEB＝90°，∵DO＝BO，∴OE＝BD＝OD，∴∠OED＝∠ODE＝20°，故答案为：20°．14．（2022春•吴中区校级期中）如图，在菱形ABCD中，AB＝2，∠A＝120°，E，F分别是边AB和CD 上的点，EF⊥CD于点F，则线段EF的长度为．【分析】连接AC，BD，根据菱形的性质和等边三角形的性质得出AC，进而得出BD，利用菱形的面积解答即可．【解答】解：连接AC，BD，相交于O，∵四边形ABCD是菱形，AB＝2，∠A＝120°，∴AB＝BC，∠ABC＝60°，∴△ABC是等边三角形，∴AC＝AB＝2，BO＝，∴BD＝2，∴菱形ABCD的面积＝，∴EF＝，故答案为：．15．（2022春•集美区校级期中）如图，在菱形ABCD中，∠B＝60°，AB＝a，点E，F分别是边AB，AD 上的动点，且AE+AF＝a，则△CEF面积的最小值为．【分析】由在边长为a的菱形ABCD中，易得△ABC、△CAD都是边长为a的正三角形，继而证得△ACE ≌△DCF，继而证得△CEF是正三角形，继而可得当动点E运动到点B或点A时，CE的值最大，当CE ⊥AB，即E为AB的中点时，EF的值最小，△CEF面积的最小值最小．【解答】解：连接AC、CE、CF，如图所示：∵四边形ABCD是边长为a的菱形，∠B＝60°，∴△ABC、△CAD都是边长为a的正三角形，∴AB＝BC＝CD＝AC＝AD，∠CAE＝∠ACB＝∠ACD＝∠CDF＝60°，∵AE+AF＝a，∴AE＝a﹣AF＝AD﹣AF＝DE，在△ACE和△DCF中，，∴△ACE≌△DCF（SAS），∴∠ACE＝∠DCF，∴∠ACE+∠ACF＝∠DCF+∠ACF，∴∠ECF＝∠ACD＝60°，∴△CEF是正三角形，∴EF＝CE＝CF，当动点E运动到点B或点A时，CE的最大值为a，当CE⊥AB，即E为BD的中点时，CE的最小值为a，∵EF＝CE，∴EF的最小值为a，∴△CEF面积的最小值为：，故答案为：．16．（2022•温江区校级自主招生）如图，四边形ABCD是菱形，对角线AC，BD交于点O，E是边AD的中点，过点E作EF⊥BD，EG⊥AC，点F，G为垂足，若AC＝10，BD＝24，则FG的长为　6.5　．【分析】由菱形的性质得出OA＝OC＝5，OB＝OD＝12，AC⊥BD，根据勾股定理求出AD＝13，由直角三角形斜边上的中线等于斜边的一半求出OE＝6.5，证出四边形EFOG是矩形，得到EO＝GF即可得出答案．【解答】解：连接OE，∵四边形ABCD是菱形，∴OA＝OC＝5，OB＝OD＝12，AC⊥BD，在Rt△AOD中，AD＝＝13，又∵E是边AD的中点，∴OE＝AD＝6.5，∵EF⊥BD，EG⊥AC，AC⊥BD，∴∠EFO＝90°，∠EGO＝90°，∠GOF＝90°，∴四边形EFOG为矩形，∴FG＝OE＝6.5．故答案为：6.5．17．（2022春•南岗区校级期中）如图，在边长为5的菱形ABCD中，∠BAD＝60°，点E、点F分别在AD、CD上，且∠EBF＝60°，连接EF，若AE＝2，则EF的长度为．【分析】连接BD，过E点作EH⊥AB于H点，如图，先根据菱形的性质得到AB＝AD＝5，AB∥CD，则可判断△ABD为等边三角形，所以BD＝AB，∠ABD＝60°，再证明∠ABE＝∠DBF，∠FDB＝∠EAB，则可判断△BDF≌△BAE，所以BF＝BE，于是可证明△BEF为等边三角形得到EF＝BE，接着利用含30度角的直角三角形三边的关系得到AH＝1，EH＝，然后利用勾股定理计算出BE，从而得到EF的长．【解答】解：连接BD，过E点作EH⊥AB于H点，如图，∵四边形ABCD为菱形，∴AB＝AD＝5，AB∥CD，∵∠BAD＝60°，∴△ABD为等边三角形，∴BD＝AB，∠ABD＝60°，∵∠EBF＝60°，∴∠ABD﹣∠EBD＝∠EBF﹣∠EBD，即∠ABE＝∠DBF，∵CD∥AB，∴∠FDB＝∠ABD＝60°，∴∠FDB＝∠EAB，在△BDF和△BAE中，，∴△BDF≌△BAE（ASA），∴BF＝BE，而∠EBF＝60°，∴△BEF为等边三角形，∴EF＝BE，在Rt△AEH中，∵∠A＝60°，∴AH＝AE＝1，∴EH＝AH＝，在Rt△BEH中，∵EH＝，BH＝BA﹣AH＝5﹣1＝4，∴BE＝＝，∴EF＝BE＝．故答案为：．18．（2022春•鼓楼区校级期中）如图，在菱形ABCD中，AB＝6，∠ABC＝120°，点E在边BC上（不与端点重合），AE交BD于点F，以EF为边向外作等边△EFG，连接CF，BG，现给出以下结论：①∠EAB＝30°；②△ABF≌△CBF；③直线AB与直线DC的距离是9；④BF+BG＝BE．其中正确的是　②③④　（写出所有正确结论的序号）．【分析】连接AC，先证明△ABD和△CBD都是等边三角形，再证明△ADC≌△ABC，则∠CAD＝∠CAB ＝30°，假设∠EAB＝30°，则∠EAB＝∠CAB，所以点E与点C重合，这与已知条件相矛盾，所以∠EAB≠30°，可判断①错误；由AB＝CB，∠ABF＝∠CBF，BF＝BF根据全等三角形的判定定理“SAS”可证明△ABF≌△CBF，可判断②正确；作DI⊥AB于点I，则∠AID＝90°，所以∠ADI＝30°，则AI＝×6＝3，可根据勾股定理求得DI＝9，可判断③正确；在BC上截取BH＝BF，连接FH，则△BFH是等边三角形，而△EFG是等边三角形，可证明△BFG≌△HFE，得BG＝HE，所以BF+BG＝BH+HE＝BE，可判断④正确．【解答】解：如图，连接AC，∵四边形ABCD是菱形，∠ABC＝120°，AB＝6，∴AD＝AB＝CD＝CB＝6，AD∥BC，AB∥CD，∴∠DAB＝∠DCB＝180°﹣∠ABC＝60°，∴△ABD和△CBD都是等边三角形，∴∠ABF＝∠CBF＝60°，在△ADC和△ABC中，，∴△ADC≌△ABC（SSS），∴∠CAD＝∠CAB＝∠DAB＝30°，假设∠EAB＝30°，则∠EAB＝∠CAB，∴AE与AC重合，点E与点C重合，与已知条件相矛盾，∴假设不成立，即∠EAB≠30°，故①错误；在△ABF和△CBF中，，∴△ABF≌△CBF（SAS），故②正确；作DI⊥AB于点I，则∠AID＝90°，∵∠DAI＝60°，∴∠ADI＝30°，∴AI＝AD＝×6＝3，∴DI＝＝＝9，∴直线AB与直线DC的距离是9，故③正确；在BC上截取BH＝BF，连接FH，则△BFH是等边三角形，∵△EFG是等边三角形，∴FB＝FH，FG＝FE，∠BFH＝∠GFE＝60°，∴∠BFG＝∠HFE＝60°﹣∠GFH，在△BFG和△HFE中，，∴△BFG≌△HFE（SAS），∴BG＝HE，∴BF+BG＝BH+HE＝BE，故④正确，故答案为：②③④．三、解答题（本大题共6小题，共66分．解答时应写出文字说明、证明过程或演算步骤）19．（2022秋•薛城区月考）如图，已知A，F，C，D四点在同一条直线上，AF＝CD，AB∥ED，且AB＝ED．（1）求证：△ABC≌△DEF．（2）如果四边形EFBC是菱形，已知EF＝3，DE＝4，∠DEF＝90°，求AF的长度．【分析】（1）根据SAS即可证明△ABC≌△DEF；（2）解直角三角形求出DF、OE、OF的长，即可解决问题．【解答】（1）证明：∵AB∥DE，∴∠A＝∠D，∵AF＝CD，∴AF+FC＝CD+FC，即AC＝DF，在△ABC和△DEF中，，∴△ABC≌△DEF（SAS）．（2）解：如图，连接EB交AD于O．在Rt△EFD中，∠DEF＝90°，EF＝3，DE＝4，∴DF＝＝＝5，∵四边形EFBC是菱形，∴OF＝OC，BE⊥CF，∴EO＝＝＝，∴OF＝OC＝＝＝，∴CF＝2OF＝，∴AF＝CD＝DF﹣FC＝5﹣＝．20．（2022春•姑苏区校级期中）如图，已知菱形ABCD的对角线AC、BD相交于点O，延长AB至点E，使BE＝AB，连接CE．（1）求证：四边形BECD是平行四边形；（2）若∠E＝60°，BD＝8，求菱形ABCD的面积．【分析】（1）根据菱形的对边平行且相等可得AB＝CD，AB∥CD，然后证明得到BE＝CD，BE∥CD，从而证明四边形BECD是平行四边形；（2）欲求菱形ABCD的面积，求得AC、BD的长度即可．【解答】（1）证明：∵四边形ABCD是菱形，∴AB＝CD＝BC，AB∥CD，又∵BE＝AB，∴BE＝CD，BE∥CD，∴四边形BECD是平行四边形；（2）解：由（1）知，四边形BECD是平行四边形，则BD∥CE．∵∠E＝60°，∴∠ABD＝60°．∵四边形ABCD是菱形，∴AD＝AB．∴△ABD是等边三角形．∴AB＝BD＝8．又∵四边形ABCD是菱形，∴AC⊥BD，OB＝BD＝4．∴OA＝＝＝4．∴AC＝8．∴菱形ABCD的面积＝AC•BD＝×8×8＝32．21．（2022•雨花区校级开学）如图，四边形ABCD是菱形，AE⊥BC于点E，AF⊥CD于点F．（1）求证：△ABE≌△ADF；（2）若AE＝4，CF＝2，求菱形的面积．【分析】（1）由菱形ABCD的四条边相等、对角相等的性质知AB＝AD，∠B＝∠D；然后根据已知条件“AE⊥BC，AF⊥CD”知∠AEB＝∠AFD；最后由全等三角形的判定定理AAS证明△ABE≌△ADF；（2）由全等三角形△ABE≌△ADF的对应边相等知BE＝DF，然后根据菱形的四条边相等求得AB＝CD，设AB＝CD＝x，已知CF＝2，则BE＝DF＝x﹣2，利用勾股定理即可求出菱形的边长，进而可以求菱形的面积．【解答】（1）证明：∵四边形ABCD是菱形，∴AB＝BC＝CD＝AD，∠B＝∠D，∵AE⊥BC，AF⊥CD，∴∠AEB＝∠AFD，在△ABE和△ADF中，，∴△ABE≌△ADF（AAS）；（2）解：设菱形的边长为x，∵AB＝CD＝x，CF＝2，∴DF＝x﹣2，∵△ABE≌△ADF，∴BE＝DF＝x﹣2，在Rt△ABE中，根据勾股定理得，AE2+BE2＝AB2，即42+（x﹣2）2＝x2，解得x＝5，∴菱形的边长是5，∴菱形的面积＝BC•AE＝5×4＝20．22．（2022春•南浔区期末）如图，已知四边形ABCD是菱形，点E、F分别是边AB、BC的中点，连结DE、EF、DF．（1）求证：△DEF是等腰三角形；（2）若AD＝10，EF＝8，求菱形ABCD的面积．【分析】（1）根据菱形的性质得到∠A＝∠C，AD＝CD＝AB＝BC，根据全等三角形的性质即可得到结论；（2）连接AC，BD交于O，根据三角形中位线定理得到AC＝16，根据菱形的性质得到AO＝AC＝8，AC⊥BD，根据勾股定理得到OB＝＝6，根据菱形的面积公式即可得到结论．【解答】（1）证明：∵四边形ABCD是菱形，∴∠A＝∠C，AD＝CD＝AB＝BC，∵点E、F分别是边AB、BC的中点，∴AE＝AB，CF＝BC，∴AE＝CF，∴△ADE≌△CDF（SAS），∴DE＝DF，∴△DEF是等腰三角形；（2）解：连接AC，BD交于O，∵点E、F分别是边AB、BC的中点，∴EF是△ABC的中位线，∵EF＝8，∴AC＝16，∵四边形ABCD是菱形，∴AO＝AC＝8，AC⊥BD，∴OB＝＝6，∴BD＝12，∴菱形ABCD的面积＝AC•BD＝×16×12＝96．23．（2022春•重庆期末）如图，在菱形ABCD中，∠C＝60°，E是对角线BD上一点．（1）如图1，若E是线段BD的中点，且AB＝6，求AE的长度；（2）如图2，F是线段AB延长线上一点，且DE＝BF，连接AE，EF．求证：AE＝EF．【分析】（1）由四边形ABCD是菱形，且∠DAB＝60°，证明△ABD是等边三角形，根据E是线段BD 的中点，进而可以解决问题；（2）作EG∥AB交AD于点G，先证明△DGE是等边三角形，得DG＝DE＝GE，再证明△AGE≌△EBF，得AE＝EF．【解答】（1）解：如图1，∵四边形ABCD是菱形，∴∠DAB＝∠C＝60°，AB＝AD，∴△ABD是等边三角形，∴AD＝BD＝AB＝6，∵E是线段BD的中点，∴BE＝DE＝3，∴AE＝BE＝3；（2）证明：如图2，作EG∥AB交AD于点G，∵△DAB是等边三角形，∴∠GDE＝60°，∠DGE＝∠DAB＝60°，∠DEG＝∠DBA＝60°，∴△DGE是等边三角形，∴DG＝DE＝GE，∵BF＝DE，∴GE＝BF，∵AD＝BD，∴AD﹣DG＝BD﹣DE，∴AG＝EB，∵∠AGE＝180°﹣∠DGE＝120°，∠EBF＝180°﹣∠DBA＝120°，∴∠AGE＝∠EBF，在△AGE和△EBF中，，∴△AGE≌△EBF（SAS），∴AE＝EF．24．（2022春•抚远市期末）在菱形ABCD中，∠ABC＝60°，P是射线BD上一动点，以AP为边向右侧作等边三角形APE，点E的位置随点P位置的变化而变化，连接CE．（1）如图①，当点E在菱形ABCD内部或边上时，求证：BD＝CE+PD；（2）如图②、图③，请分别写出线段BD，CE，PD之间的数量关系，不需证明．【分析】（1）先判断出∠BAP＝∠CAE，进而判断出△BAP≌△CAE，得出BP＝CE，∠ABP＝∠ACE＝30°，再判断出∠CAH+∠ACH＝90°，即可得出结论；（2）同（1）的方法即得出结论；【解答】（1）证明：如图1，连接AC，延长CE交AD于H，∵四边形ABCD是菱形，∠ABC＝60°，∴△ABC，△ACD都是等边三角形，∠ABD＝∠CBD＝30°，∴AB＝AC，∠BAC＝60°，∠CAH＝60°，∵△APE是等边三角形，∴AP＝AE，∠PAE＝60°，∵∠BAC＝∠PAE，∴∠BAP＝∠CAE，∴△BAP≌△CAE（SAS），∴BP＝CE，∵BD＝BP+PD，∴BD＝CE+PD；（2）解：如图2，BD＝CE+PD，连接AC，AC与BD交于点O，∴△ABC，△ACD为等边三角形，在△ABP和△ACE中，AB＝AC，AP＝AE，又∵∠BAP＝∠BAC+∠CAP＝60°+∠CAP，∠CAE＝∠EAP+∠CAP＝60°+∠CAP，∴∠BAP＝∠CAE，∴△ABP≌△ACE（SAS），∴BP＝CE，∵BD＝BP+PD，∴BD＝CE+PD；如图3，BD＝CE﹣PD，连接AC，AC与BD交于点O，∴△ABC，△ACD为等边三角形，在△ABP和△ACE中，AB＝AC，AP＝AE，又∵∠BAP＝∠BAD+∠DAP＝120°+∠DAP，∠CAE＝∠CAD+∠DAP+∠PAE＝120°+∠DAP，∴∠BAP＝∠CAE，∴△ABP≌△ACE（SAS），∴BP＝CE，∵BD＝BP﹣PD，∴BD＝CE﹣PD．。

人教版八年级数学下册18.2.2.2菱形的判定培优训练(含答案)

人教版八年级数学下册菱形的判断培优训练一、选择题（共 10 小题， 3*10=30 ）1．以下命题中，正确的选项是()A ．有一个角是60°的平行四边形是菱形B．有一组邻边相等的四边形是菱形C．有两边相等的平行四边形是菱形D．四条边相等的四边形是菱形2．如图，在 ?ABCD 中， AC ，BD 交于点 O，AB ＝13， AC ＝24， DB＝ 10，则四边形ABCD 是 () A ．一般的平行四边形B．长方形C．菱形 D ．形状不可以确立3. 如图，以下条件之一能使平行四边形ABCD 是菱形的为 ()①AC ⊥ BD ；②∠ BAD=90°；③ AB=BC ；④ AC=BD ．A 、①③B 、②③C、③④D、①②③4.如图，四边形 ABCD 的两条对角线订交于点 O，且相互均分．增添以下条件，仍不可以判断四边形ABCD 为菱形的是 ()A ．AC ⊥BD B．AB ＝ADC． AC ＝ BD D．∠ ABD ＝∠ CBD5. 如图，在 ?ABCD 中，对角线AC ，BD 订交于点O，增添以下条件不可以判断 ? ABCD 是菱形的只有()C．AC＝BD D．∠ 1＝∠ 26.如图，四边形 ABCD 的两条对角线订交于点 O，且相互均分，增添以下条件，仍不可以判断四边形ABCD 为菱形的是 ()A ．AC ⊥BD B．AB ＝ADC． AC ＝ BD D ．∠ ABD ＝∠ CBD7. 如图，将?ABCD 沿 AE 翻折，使点 B 恰巧落在 AD 上的点 F 处，则以下结论不必定建立的是()A ．AF＝EF B．AB ＝EFC．AE＝AF D．AF ＝BE8. 四边形的四边长按序为a、b、 c、 d，且 a2+b2+c2+d2=ab+bc+cd+ad ，则此四边形必定是()A.平行四边形B. 矩形C. 菱形D. 正方形9．如图，四边形ABCD 的四边相等，且面积为120 cm2，对角线AC ＝24 cm，则四边形ABCD 的周长为()A ． 52 cmB ．40 cmC． 39 cm D ．26 cm10.如图，分别以 Rt△ABC 的斜边 AB 和直角边 AC 为边向△ABC 外作等边三角形 ABD 和等边三角形 ACE ， F 为 AB 的中点， DE 与 AB 交于点 G，EF 与 AC 交于点 H，∠ BAC ＝ 30°给.出以下结论：1二．填空题（共 8 小题， 3*8=24 ）11.如图，假如要使平行四边形ABCD成为一个菱形，需要增添一个条件，那么你增添的条件是_________．12.如图在矩形 ABCD 中，对角线 AC 、 BD 订交于点 O，且 DE ∥AC ， CE∥ BD ，则四边形 OCED 的形状是 _________．13. 如图 ,在长方形 ABCD 中,AB=12,AD=14,E为AB的中点,点F,G分别在CD,AD上,若CF=4,且△EFG 为等腰直角三角形,则 EF 的长为 _________．14. 如图 ,在周长为 12 的菱形 ABCD 中 ,AE=1,AF=2, 若 P 为对角线BD 上一动点 ,则 EP+FP 的最小值为_________．15．以下命题：①四边都相等的四边形是菱形；②两组邻边分别相等的四边形是菱形；③对角线相互垂直的平行四边形是菱形；④对角线相等的四边形是菱形；⑤一条对角线均分一组对角的平行四边形是菱形．此中正确的选项是__________( 填序号 )．16.把一张矩形纸片 ABCD 按如图方式折叠，使极点 B 和极点 D 重合，折痕为 EF．若 BF=4 ，FC=2 ，17.如图 ,把长方形纸片 ABCD 折叠 ,使其对角极点 C 与 A 重合 .若长方形的长 BC 为 8,宽 AB 为 4,则折痕 EF 的长度为 _________．18. 在菱形 ABCD 中， AE 为 BC 边上的高，若AB=5 ， AE=4 ，则线段CE 的长为．三．解答题（共 7 小题，46 分）19．(6 分 )如图，在平行四边形ABCD 中， AC 均分∠ DAB ，AB ＝ 2 cm，求平行四边形ABCD 的周长为 .20． (6 分 ) 如图， E， F 是菱形 ABCD 对角线上的两点，且AE ＝ CF.求证：四边形BEDF 是菱形；21． (6 分 ) 如图，在△ABC 中， AD 均分∠ BAC ，过点 D 分别作 DE∥ AC 、 DF ∥AB ，分别交 AB 、 AC 于点 E、 F.求证：四边形 AEDF 是菱形．22． (6 分 ) 如图，在△ABC 中， AD 均分∠ BAC ，将△ABC 折叠，使点 A 与点 D 重合，睁开后折痕分别交AB ， AC 于点 E， F，连结 DE，DF.求证：四边形AEDF 是菱形．23． (6 分 ) 如图，在 ?ABCD 中，对角线AC ， BD 订交于点O，AB ＝ 5， AC ＝ 6， BD ＝ 8.(1)求证：四边形 ABCD 是菱形；(2)过点 A 作 AH ⊥BC 于点 H，求 AH 的长．24． (8 分 ) 如图，在矩形ABCD 中， E， F 分别是 BC ， AD 边上的点，且AE ＝ CF.(1)求证：△ABE ≌△ CDF；(2)当 AC⊥ EF 时，四边形 AECF 是菱形吗？请说明原因．25． (8 分 ) 如图，将一张矩形纸片ABCD 进行折叠，详细操作以下：第一步：先对折，使AD 与 BC 重合，获得折痕MN ，睁开；第二步：再折叠一次，使点 A 落在 MN 上的点 A′处，并使折痕经过点B，获得折痕BE，同时，获得线段 BA′， EA′，睁开，如图①；第三步：再沿EA′所在的直线折叠，点 B 落在 AD 上的点B′处，获得折痕EF，同时获得线段B′F，睁开，如图②.求证： (1) ∠ ABE ＝30°； (2)四边形 BFB′E为菱形．参照答案1-5DCACC6-10 CCCAC11.AB=AD 或 AC ⊥BD12.菱形13.10214.315.①③⑤16.6017.2518.2 或 819.解：如图．∵四边形 ABCD 为平行四边形，∴∠ 1＝∠ 4，∠ 2＝∠ 3，∵ AC 均分∠ DAB ，∴∠ 1＝∠ 2，∴∠ 1＝∠ 3，∴ AD ＝DC，四边形 ABCD 为菱形，∴四边形 ABCD 的周长＝ 4×2＝ 8.20.证明：连结 BD ，交 AC 于 O.∵四边形ABCD 是菱形，∴OA ＝ OC，OB＝ OD ， AC ⊥BD ，∵ AE ＝ CF，∴ OE＝ OF，∴四边形 BEDF 是平行四边形，∵ EF⊥ BD ，∴四边形 BEDF 是菱形；21.证明：∵DE∥AC ，DF∥AB ，∴四边形 AEDF 是平行四边形．∵ AD 均分∠ BAC ，∴∠ BAD ＝∠ CAD.∵DE ∥ AC ，∴∠ EDA ＝∠ CAD ，∴∠ EDA ＝∠ BAD ，∴四边形AEDF 是菱形．22.证明： (方法不独一 )由折叠性质知： AE ＝ DE，AF ＝ DF，∴∠ DAE ＝∠ EDA ，∠ ADF ＝∠ FAD ，∵∠ DAE ＝∠ FAD ，∴∠ DAE ＝∠ ADF ，∠ DAF ＝∠ EDA ，∴DF∥AE，DE∥AF ，∴四边形 AEDF 是平行四边形，∵ AE ＝ DE，∴四边形 AEDF 是菱形1 23. (1) 证明：∵在 ?ABCD 中，对角线AC ， BD 订交于点O， AB ＝ 5，AC ＝ 6， BD ＝8，∴ AO ＝2AC1＝ 3， BO＝2BD ＝ 4，∵AB ＝ 5，且 32＋ 42＝ 52，∴AO 2＋BO2＝AB 2，∴△ AOB 是直角三角形，且∠ AOB ＝ 90°，∴ AC ⊥ BD ，∴四边形 ABCD 是菱形．(2)解：∵四边形 ABCD 是菱形，∴BC＝AB ＝ 5，1111∵ S△ABC＝2AC· BO＝2BC· AH，∴2× 6×4＝2× 5× AH，解得： AH ＝24 5.24.解： (1) 证明：∵四边形 ABCD 是矩形，∴∠ B ＝∠ D ＝ 90°，AB ＝ CD， AD ＝BC ， AD ∥ BC，AE ＝ CF，在 Rt△ABE 和 Rt△CDF 中，AB ＝CD ，∴Rt△ABE ≌ Rt △CDF(HL)(2)解：当 AC ⊥ EF 时，四边形 AECF 是菱形，原因以下：∵△ ABE ≌△ CDF ，∴ BE ＝ DF，∵BC＝AD ，∴ CE＝AF ，∵CE∥ AF，∴四边形AECF 是平行四边形，又∵ AC ⊥ EF，∴四边形AECF 是菱形∴∠ AEB ＝∠ A′EB.∵第三步折叠，点 B 落在 AD 上的点 B′处，获得折痕EF，同时获得线段B′F，∴∠ A′EB＝∠ FEB′.∵∠ AEB ＋∠ A′EB＋∠ FEB′＝ 180°，∴∠ AEB ＝∠ A′EB＝∠ FEB′＝ 60°，∴∠ ABE ＝30°(2) ∵沿 EA′所在的直线折叠，点 B 落在 AD 上的点 B′处，∴BE ＝ B′E， BF＝B′F.∵AD ∥ BC，∴∠ BFE ＝∠ FEB′＝60°，∴△ BEF 是等边三角形，∴ BE ＝ BF，∴ BE ＝ B′E＝ B′F＝BF，∴四边形 BFB′E为菱形。

人教版八年级数学下册 18.2.2.2菱形的判定培优训练(含答案)

人教版八年级数学下册18.2.2.2 菱形的判定培优训练一、选择题（共10小题，3*10=30）1．下列命题中，正确的是( )A．有一个角是60°的平行四边形是菱形B．有一组邻边相等的四边形是菱形C．有两边相等的平行四边形是菱形D．四条边相等的四边形是菱形2．如图，在▱ABCD中，AC，BD交于点O，AB＝13，AC＝24，DB＝10，则四边形ABCD是() A．一般的平行四边形B．长方形C．菱形D．形状不能确定3. 如图，下列条件之一能使平行四边形ABCD是菱形的为( )①AC⊥BD；②∠BAD=90°；③AB=BC；④AC=BD．A、①③B、②③C、③④D、①②③4. 如图，四边形ABCD的两条对角线相交于点O，且互相平分．添加下列条件，仍不能判定四边形ABCD为菱形的是( )A．AC⊥BD B．AB＝ADC．AC＝BD D．∠ABD＝∠CBD5. 如图，在▱ABCD中，对角线AC，BD相交于点O，添加下列条件不能判定▱ABCD是菱形的只有()C．AC＝BD D．∠1＝∠26. 如图，四边形ABCD的两条对角线相交于点O，且互相平分，添加下列条件，仍不能判定四边形ABCD为菱形的是()A．AC⊥BD B．AB＝ADC．AC＝BD D．∠ABD＝∠CBD7. 如图，将▱ABCD沿AE翻折，使点B恰好落在AD上的点F处，则下列结论不一定成立的是() A．AF＝EF B．AB＝EFC．AE＝AF D．AF＝BE8. 四边形的四边长顺次为a、b、c、d，且a2+b2+c2+d2=ab+bc+cd+ad，则此四边形一定是( )A. 平行四边形B. 矩形C. 菱形D. 正方形9．如图，四边形ABCD的四边相等，且面积为120 cm2，对角线AC＝24 cm，则四边形ABCD的周长为()A．52 cm B．40 cmC．39 cm D．26 cm10. 如图，分别以Rt△ABC的斜边AB和直角边AC为边向△ABC外作等边三角形ABD和等边三角形ACE，F为AB的中点，DE与AB交于点G，EF与AC交于点H，∠BAC＝30°.给出以下结论：①EF⊥AC；②四边形ADFE为菱形；③AD＝4AG; ④FH＝14BD.其中正确的结论是()二．填空题（共8小题，3*8=24）11.如图，如果要使平行四边形ABCD成为一个菱形，需要添加一个条件，那么你添加的条件是_________．12. 如图在矩形ABCD中，对角线AC、BD相交于点O，且DE∥AC，CE∥BD，则四边形OCED 的形状是_________．13. 如图,在长方形ABCD中,AB=12,AD=14,E为AB的中点,点F,G分别在CD,AD上,若CF=4,且△EFG 为等腰直角三角形,则EF的长为_________．14. 如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为_________．15．下列命题：①四边都相等的四边形是菱形；②两组邻边分别相等的四边形是菱形；③对角线互相垂直的平行四边形是菱形；④对角线相等的四边形是菱形；⑤一条对角线平分一组对角的平行四边形是菱形．其中正确的是__________(填序号)．16. 把一张矩形纸片ABCD按如图方式折叠，使顶点B和顶点D重合，折痕为EF．若BF=4，FC=2，17. 如图,把长方形纸片ABCD折叠,使其对角顶点C与A重合.若长方形的长BC为8,宽AB为4,则折痕EF的长度为_________．18. 在菱形ABCD中，AE为BC边上的高，若AB=5，AE=4，则线段CE的长为．三．解答题（共7小题，46分）19．(6分)如图，在平行四边形ABCD中，AC平分∠DAB，AB＝2 cm，求平行四边形ABCD的周长为.20．(6分) 如图，E，F是菱形ABCD对角线上的两点，且AE＝CF.求证：四边形BEDF是菱形；21．(6分) 如图，在△ABC中，AD平分∠BAC，过点D分别作DE∥AC、DF∥AB，分别交AB、AC于点E、F.求证：四边形AEDF是菱形．22．(6分) 如图，在△ABC中，AD平分∠BAC，将△ABC折叠，使点A与点D重合，展开后折痕分别交AB，AC于点E，F，连接DE，DF.求证：四边形AEDF是菱形．23．(6分) 如图，在▱ABCD中，对角线AC，BD相交于点O，AB＝5，AC＝6，BD＝8.(1)求证：四边形ABCD是菱形；(2)过点A作AH⊥BC于点H，求AH的长．24．(8分) 如图，在矩形ABCD中，E，F分别是BC，AD边上的点，且AE＝CF.(1)求证：△ABE≌△CDF；(2)当AC⊥EF时，四边形AECF是菱形吗？请说明理由．25．(8分) 如图，将一张矩形纸片ABCD进行折叠，具体操作如下：第一步：先对折，使AD与BC重合，得到折痕MN，展开；第二步：再折叠一次，使点A落在MN上的点A′处，并使折痕经过点B，得到折痕BE，同时，得到线段BA′，EA′，展开，如图①；第三步：再沿EA′所在的直线折叠，点B落在AD上的点B′处，得到折痕EF，同时得到线段B′F，展开，如图②.求证：(1)∠ABE＝30°；(2)四边形BFB′E为菱形．参考答案1-5DCACC 6-10 CCCAC11. AB=AD或AC⊥BD12. 菱形13.10 214.315. ①③⑤16. 6017.2 518. 2或819. 解：如图．∵四边形ABCD为平行四边形，∴∠1＝∠4，∠2＝∠3，∵AC平分∠DAB，∴∠1＝∠2，∴∠1＝∠3，∴AD＝DC，四边形ABCD为菱形，∴四边形ABCD的周长＝4×2＝8.20. 证明：连接BD，交AC于O.∵四边形ABCD是菱形，∴OA＝OC，OB＝OD，AC⊥BD，∵AE＝CF，∴OE＝OF，∴四边形BEDF是平行四边形，∵EF⊥BD，∴四边形BEDF是菱形；21. 证明：∵DE∥AC，DF∥AB，∴四边形AEDF是平行四边形．∵AD平分∠BAC，∴∠BAD＝∠CAD.∵DE∥AC，∴∠EDA＝∠CAD，∴∠EDA＝∠BAD，∴四边形AEDF 是菱形．22. 证明：(方法不唯一)由折叠性质知：AE ＝DE ，AF ＝DF ， ∴∠DAE ＝∠EDA ，∠ADF ＝∠FAD ， ∵∠DAE ＝∠FAD ，∴∠DAE ＝∠ADF ，∠DAF ＝∠EDA ， ∴DF ∥AE ，DE ∥AF ， ∴四边形AEDF 是平行四边形， ∵AE ＝DE ，∴四边形AEDF 是菱形23. (1)证明：∵在▱ABCD 中，对角线AC ，BD 相交于点O ，AB ＝5，AC ＝6，BD ＝8，∴AO ＝12AC＝3，BO ＝12BD ＝4，∵AB ＝5，且32＋42＝52， ∴AO 2＋BO 2＝AB 2，∴△AOB 是直角三角形，且∠AOB ＝90°， ∴AC ⊥BD ，∴四边形ABCD 是菱形． (2)解：∵四边形ABCD 是菱形， ∴BC ＝AB ＝5，∵S △ABC ＝12AC·BO ＝12BC·AH ，∴12×6×4＝12×5×AH ，解得：AH ＝245.24. 解：(1)证明：∵四边形ABCD 是矩形，∴∠B ＝∠D ＝90°， AB ＝CD ，AD ＝BC ，AD ∥BC ，在Rt △ABE 和Rt △CDF 中，⎩⎪⎨⎪⎧AE ＝CF ，AB ＝CD ，∴Rt △ABE ≌Rt △CDF(HL)(2)解：当AC ⊥EF 时，四边形AECF 是菱形，理由如下： ∵△ABE ≌△CDF ，∴BE ＝DF ， ∵BC ＝AD ，∴CE ＝AF ， ∵CE ∥AF ，∴四边形AECF 是平行四边形，又∵AC ⊥EF ，∴四边形AECF 是菱形∴∠AEB＝∠A′EB.∵第三步折叠，点B落在AD上的点B′处，得到折痕EF，同时得到线段B′F，∴∠A′EB＝∠FEB′.∵∠AEB＋∠A′EB＋∠FEB′＝180°，∴∠AEB＝∠A′EB＝∠FEB′＝60°，∴∠ABE＝30°(2)∵沿EA′所在的直线折叠，点B落在AD上的点B′处，∴BE＝B′E，BF＝B′F.∵AD∥BC，∴∠BFE＝∠FEB′＝60°，∴△BEF是等边三角形，∴BE＝BF，∴BE＝B′E＝B′F＝BF，∴四边形BFB′E为菱形。

八年级数学下册菱形培优专题练习

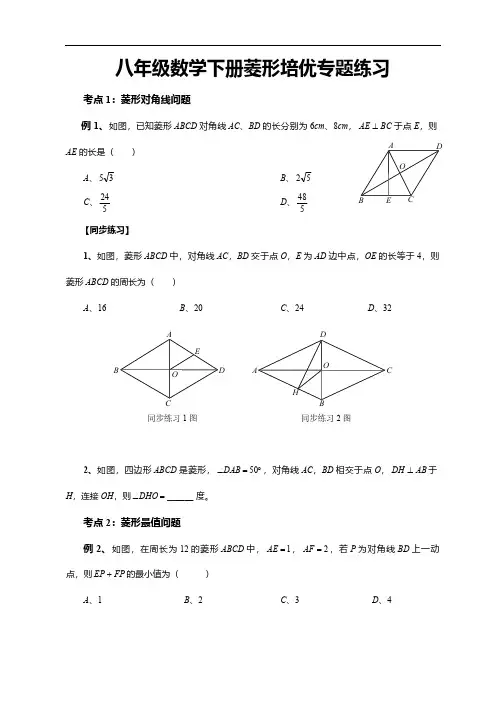
同步练习2图同步练习1图B八年级数学下册菱形培优专题练习考点1：菱形对角线问题例1、如图，已知菱形ABCD 对角线AC 、BD 的长分别为6cm 、8cm ，于点E ，则BC AE ⊥AE 的长是（）A 、B 、3552C 、D 、524548【同步练习】1、如图，菱形ABCD 中，对角线AC ，BD 交于点O ，E 为AD 边中点，OE 的长等于4，则菱形ABCD 的周长为（）A 、16B 、20C 、24D 、322、如图，四边形ABCD 是菱形，，对角线AC ，BD 相交于点O ，于︒=∠50DAB AB DH ⊥H ，连接OH ，则度。

______=∠DHO 考点2：菱形最值问题例2、如图，在周长为12的菱形ABCD 中，，，若P 为对角线BD 上一动1=AE 2=AF 点，则的最小值为（）FP EP +A 、1B 、2C、3D 、4例2图B同步练习2图例3图同步练习1图同步练习2图【同步练习】1、如图，在菱形ABCD 中，，，E 是AB 的中点，P 是对角线AC 上的一2=AB ︒=∠60BAD 个动点，则的最小值为（）PB PE +A 、1B 、C 、2D 、35例3、如图，将两张长为9，宽为3的矩形纸条交叉，使重叠部分是一个菱形，容易知道当两张纸条垂直时，菱形的面积有最小值9，那么菱形面积的最大值是 .【同步练习】1、如图，将两张长为8，宽为3的矩形纸条交叉，使重叠部分是一个菱形，容易知道当两张纸条垂直时，菱形的周长有最小值12，那么菱形周长的最大值是 .2、如图，由两个长为9，宽为3的全等矩形叠合而得到四边形ABCD ，则四边形ABCD 面积的最大值是（）A 、15B 、16C 、19D 、20考点3：菱形与直角坐标系问题同步练习1图同步练习2图同步练习3图例4、如图，正方形ABCD 的边长为10，点A 的坐标为（0， 8），点B 在x 轴上，若反比例函数（）的图象过点C ，则该反比例函数的表达式为（）x ky =0≠k A 、 B 、x y 6=x y 12-=C 、D 、xy 10=xy 10-=【同步练习】1、如图，平面直角坐标系中，菱形ABCD 的顶点A （3，0），B （ 2，0），顶点D 在y 轴正半轴上，则点C 的坐标为（）A 、（ 3，4）B 、（ 4，5）C 、（ 5，5）D 、（ 5，4）2、在平面直角坐标系中，菱形OABC 的OC 边落在x 轴上，，.若︒=∠60AOOC 360=OA 菱形OABC 内部（边界及顶点除外）的一格点P （x ，y ）满足：，就称格点P y x y x 909022-=-为“好点”，则菱形OABC 内部“好点”的个数为（）（注：所谓“格点”，是指在平面直角坐标系中横、纵坐标均为整数的点。

新人教版八年级下册菱形基础知识点及同步练习、含答案

学科：数学教学内容：菱形【基础知识精讲】定义：有一组邻边相等的平行四边形是菱形．定理1：四边都相等的四边形是菱形．定理2：对角线互相垂直的平行四边形是菱形．【重点难点解析】1．菱形的性质(1)菱形具有平行四边形的一切性质；(2)菱形的四条边都相等；(3)菱形的对角线互相垂直，并且每一条对角线平分一组对角；(4)菱形是轴对称图形．2．菱形的面积=底×高=对角线乘积的一半．A．重点、难点提示1．理解并掌握菱形的概念，性质和判别方法；（这是重点，也是难点，要掌握好）2．经历探索菱形的性质和判别条件的过程，在操作活动和观察、分析过程中发展学生的主动探究习惯和初步的审美意识，进一步了解和体会说理的基本方法；3．了解菱形的现实应用和常用的判别条件；4．体会特殊与一般的关系．B．考点指要菱形是特殊的平行四边形，其性质和判别方法是中考的重要内容之一．一组邻边相等的平行四边形叫做菱形．菱形是特殊的平行四边形，具有平行四边形的一切性质．除具有平行四边形的一切性质外，菱形还具有以下性质：①菱形的四条边都相等；②两条对角线互相垂直平分；（出现了垂直，常与勾股定理联系在一起）③每一条对角线都平分一组内角．（出现了相等的角，常与角平分线联系在一起）菱形是轴对称图形，它的两条对角线所在直线是它的两条对称轴．（不是对角线，而是其所在直线，因为对称轴是直线，而对角线是线段）菱形的判别方法：（学会利用轴对称的方法研究菱形）①一组邻边相等的平行四边形是菱形；②对角线互相垂直的平行四边形是菱形；③四条边都相等的四边形是菱形．【难题巧解点拨】例1：如图4-24，在△ABC中，∠BAC=90°，AD⊥BC于D，CE平分∠ACB，交AD于G，交AB于E，EF⊥BC于F．求证：四边形AEFG是菱形．思路分析由已知可知，图中有平行线，就可证角相等、线段相等，因此，可先证四边形AEFG 是平行四边形，再证一组邻边相等．证明：∵∠BAC=90°，EF⊥BC，CE平分∠ACB，∴AE=EF，∠CEA=∠CEF．（这是略证，并不是完整的证明过程）∵AD⊥BC，EF⊥BC，∴EF∥AD，（垂直于同一条直线的两条直线互相平行）∴∠CEF=∠AGE，（两直线平行，内错角相等）∴∠CEA=∠AGE，∴AE=AG，∴EF∥AG，且EF=AG，∴四边形AEFG是平行四边形．（一组对边平行且相等的四边形是平行四边形）又∵AE=EF，∴平行四边形AEFG是菱形．例2：已知菱形的周长为20cm，一条对角线长为5cm，求菱形各个角的度数．已知：菱形ABCD中，AB+BC+CD+DA=20cm，对角线AC=5cm．求∠ADC、∠ABC、∠BCD、∠DAB的度数．思路分析利用菱形的四条边相等，可求出各边长，从而得到等边三角形，如图4-25．解：在菱形ABCD中，∵AB=BC=CD=DA，又AB+BC+CD+DA=20cm，∴AB=BC=CD=DA=5cm，又∵AC=5cm，∴AB=BC=AC，CD=DA=AC，∴△ABC和△DAC都是等边三角形，（本题将边之间的长度关系转化为角的关系）∴∠ADC=∠ABC=60°，∠BCD=∠DAB=120°．例3：如图4-26，在平行四边形ABCD中，∠BAE=∠FAE，∠FBA=∠FBE．求证：四边形ABEF是菱形．证法一：∵AF∥BE，∴∠FAE=∠AEB （两直线平行，内错角相等）又∵∠BAE=∠FAE，∴∠BAE=∠AEB，∴AB=BE．（等角对等边）同理，AB=AF，BE=EF，∴AB=BE=EF=AF，∴四边形ABEF是菱形．（四条边都相等的四边形是菱形）证法二：∵AF∥BE，∴∠FAE=∠AEB，又∵∠BAE=∠FAE，∴∠BAE=∠AEB，∴AB=BE．又∵∠FBA=∠FBE，∴AO=OE，AE⊥FB，（等腰三角形三线合一）同理，BO=OF，∴四边形ABEF是菱形．（对角线互相垂直平分的四边形是菱形）（你还有其他的证明方法吗？不妨试一下）例4：菱形的两邻角之比为1：2，边长为2，则菱形的面积为__________．思路分析本题主要考查菱形的性质和面积公式的应用：解法一：如图4-27，∠B：∠A=1：2，∵四边形ABCD 是菱形， ∴AD ∥BC ，∴∠A+∠B=180°，∴∠B=60°，∠A=120°，过A 作AE ⊥BC 于E ， ∴∠BAE=30°，1AB 21BE ==∴，（直角三角形中，30°角所对的直角边等于斜边的一半） 312B E AB AE 2222=-=-=∴，（勾股定理） 32AE BC S ABCD =⋅=∴菱形．（平行四边形的面积计算方法是：底乘以高）解法二：如图4-28，∠B ∶∠A=1∶2，∵四边形ABCD 是菱形， ∴AD ∥BC ，∴∠A+∠B=180°，∴∠B=60°，∠A=120°，连结AC 、BD 交于点O ，︒=∠=∠∴30B 21ABD ，AC ⊥BD ．（菱形的性质：对角线平分一组对角，对角线互相垂直）在Rt △ABO 中，1AB 21AO ==， 312AO AB B O 2222=-=-=∴，∴AC=2，32BD =， 3232221BD AC 21S ABCD =⨯⨯=⋅=∴菱形．答：菱形的面积为32．【典型热点考题】例1 如图4-13，已知菱形ABCD 中，E 、F 分别是BC 、CD 上的点，且∠B=∠EAF=60°，∠BAE=18°，求∠CEF 的度数．点悟：由∠B=60°知，连接AC得等边△ABC与△ACD，从而△ABE≌△ADF，有AE=AF，则△AEF为等边三角形，再由外角等于不相邻的两个内角和，可求∠CEF．解：连接AC．∵四边形ABCD为菱形，∴∠B=∠D= 60°，AB=BC=CD=DA，∴△ABC与△CDA为等边三角形．∴ AB=AC，∠B=∠ACD=∠BAC=60°，∵∠EAF=60°，∴∠BAE=∠CAF．∴ AE=AF．又∵∠EAF=60°，∴△EAF为等边三角形．∴∠AEF=60°，∵∠AEC=∠B+∠BAE=∠AEF+∠CEF，∴ 60°+18°=60°+∠CEF，∴∠CEF=18°．例2已知如图4-14，在△ABC中，∠BAC=90°，AD⊥BC于D，CE平分∠ACB，交AD 于G，交AB于E，EF⊥BC于F，求证：四边形AEFG为菱形．点悟：可先证四边形AEFG为平行四边形，再证邻边相等(或对角线垂直)．证明：∵∠BAC=90°，EF⊥BC，CE平分∠BCA，∴ AE=FE，∠AEC=∠FEC．∵ EF⊥BC，AD⊥BC，∴ EF∥AD．∴∠FEC=∠AGE，∴∠AEC=∠AGE∴ AE=AG，∴∴四边形AEFG为平行四边形．又∵ AE=AG．∴四边形AEFG为菱形．点拨：此题还可以用判定菱形的另两种方法来证．例3 已知如图4-15，E为菱形ABCD边BC上一点，且AB=AE，AE交BD于O，且∠DAE=2∠BAE．求证：EB=OA证明：∵四边形ABCD为菱形，∴∠ABC=2∠ABD， AD∥BC，∴∠DAE=∠AEB，∵ AB=AE，∴∠ABC=∠AEB．∴∠DAE=2∠ABD．∵∠DAE=2∠BAE，∴∠ABD=∠BAE，∴ OA=OB．∵∠BOE=∠ABD+∠BAE，∴∠BOE=2∠BAE．∴∠BEA=∠BOE，∴ OB=BE，∴ AO=BE．说明：利用菱形性质证题时，要灵活选用，选不同性质，就会有不同思路．例4已知菱形的一边与两条对角线构成的两角之比为5：4，求菱形的各内角的度数．点悟：先作出菱形ABCD和对角线AC、BD(如图4-16)．解：∵四边形ABCD是菱形，∴ AC⊥BD，∴∠1+∠2=90°，又∵∠1：∠2=4：5，∴∠1=40°，∠2=50°，∴∠DCB=∠DAB=2∠2=100°，故∠CBA=∠CDA=2∠1=80°．【同步达纲练习一】一、选择题1．已知菱形的一条对角线与边长相等，则菱形的邻角度数分别为 ( ) (A)45°， 135° (B)60°， 120° (C)90°， 90° (D)30°， 150°2．若菱形的一条对角线长是另一条对角线的2倍，且此菱形的面积为S ，则它的边长为( )(A)S (B)S 21 (c)S 321 (D)S 521二、填空题3．已知：菱形ABCD 中，E 、F 是BC 、CD 上的点，且AE=EF=AF=AB ，则∠B=________. 4．已知：菱形的两条对角线长分别为a 、b ，则此菱形周长为_______，面积为__________.5．菱形具有而矩形不具有的性质是_______.6．已知一个菱形的面积为38平方厘米，且两条对角线的比为1：3，则菱形的边长为_________.三、解答题 7．已知：O 为对角线BD 的中点，MN 过O 且垂直BD ，分别交CD 、AB 于M 、N ．求证：四边形DNBM 是菱形．8．如图4-17，已知菱形ABCD 的对角线交于点O ，AC=16cm ，BD=12cm ，求菱形的高．【同步达纲练习二】1．在菱形ABCD 中，若∠ADC=120°，则BD ：AC 等于( ) A ．2:3B ．3:3C ．1：2D ．1:32．已知菱形的周长为40cm ，两对角线的长度之比为3：4，则两对角线的长分别为( ) A ．6cm ，8cm B ．3cm ，4cm C ．12cm ，16cm D ．24cm ，32cm 3．菱形的对角线具有( ) A ．互相平分且不垂直B ．互相平分且相等C ．互相平分且垂直D ．互相平分、垂直且相等（掌握菱形对角线的性质，注意不要增加性质）4．已知菱形的面积等于2cm 160，高等于8cm ，则菱形的周长等于____________． 5．已知菱形的两条对角线的长分别是6和8，那么它的边长是______________． 6．菱形的周长是40cm ，两邻角的比是1：2，则较短的对角线长是_________cm ． 7．如图4-29，在△ABC 中，∠BAC=90°，BD 平分∠ABC ，AG ⊥BC ，且BD 、AG 相交于点E ，DF ⊥BC 于F ．求证：四边形AEFD 是菱形．8．如图4-30，平行四边形ABCD 的对角线AC 的垂直平分线与AD 、BC 、AC 分别交于点E 、F 、O ．求证：四边形AFCE 是菱形．参考答案【同步达纲练习一】一、1．B ； 2．D ；二、3．80°；4．222b a +，ab 21；5．对角线互相垂直，各边长相等． 6．4厘米．三、7．由已知MN 为BD 的垂直平分线，有 DM=BM ，DN=BN ，又由△DOM ≌△BON ，得DM=BN ，∴ DM=BM=BN=DN ．∴四边形DNBM 是菱形.8．过点D 作DH ⊥AB 于H ，则DH 为菱形的一条高．又∵ AC 、BD 互相垂直平分于O ，∴ 821==AB OA 厘米，621==BD OB 厘米．由勾股定理，得 1022=+=BO AO AB (厘米)．又∵OA BD DH AB ⋅=⋅2121， ∴812211021⨯⨯=⨯⨯DH ，DH=9.6厘米．【同步达纲练习二】1．B ； 2．C ； 3．C ； 4．80cm ； 5．5； 6．10； 7．证法一：在Rt △ABD 和Rt △FBD 中，∵BD 为∠ABC 的平分线，∴∠ABD=∠FBD ，∠DAB=∠DFB=90°，又∵BD=BD ，∴Rt △ABD ≌Rt △FBD ∴AD=DF ，∠ADE=∠EDF又∵DF ⊥BC ，AG ⊥BC ，∴DF//AE ，∴∠EDF=∠DEA ，∴∠ADE=∠DEA ，∴AD=AE ， ∴AE=DF ，∴四边形AEFD 是平行四边形． ∵AD=DF ，∴四边形AEFD 为菱形．证法二：同证法一得DF=DA=AE ，∵Rt △ABD ≌Rt △FBD ，∴AB=BF ，∴△ABE ≌△FBE ， ∴AE=EF ，∴DF=DA=AE=EF ，∴四边形AEFD 是菱形．证法三：同证法一：Rt △ABD ≌Rt △FBD ，∴AB=BF ， ∴△ABE ≌△FBE ，∴∠GAB=∠EFB ，又∵∠C+∠ABC=90°，∠GAB+∠ABC=90°， ∴∠C=∠GAB ，∴∠C=∠EFB ，∴EF ∥AC ，又∵DF ∥AG ，∴四边形AEFD 是平行四边形， ∵AD=DF ，∴四边形AEFD 是菱形．8．∵AD ∥BC ，∴∠OAE=∠OCF ，又∵∠AOE=∠COF=90°，AO=CO ， ∴△AOE ≌△COF ，∴AE=CF ，又∵AE ∥CF ， ∴四边形AFCE 是平行四边形．又∵EF 是AC 的垂直平分线，∴AE=CE ．（垂直平分线上的点到线段两端距离相等）∴四边形AFCE是菱形．。

2020-2021 学年人教版八年级数学下册18.2.2菱形双基培优练习

第11题图人教版八年级数学下册第18章第2节菱形双基培优练习一、选择题(12×3=36分)1. 下列命题中，是真命题的是（）A．对角线相等的平行四边形是菱形B．一组邻边相等的四边形是菱形C．对角线互相垂直的平行四边形是菱形D．四个角相等的四边形是菱形2. 如图所示，四边形ABCD的对角线AC，BD互相垂直，则下列条件中能判定四边形ABCD为菱形的是( )A．BA＝BC B．AC，BD互相平分 C．AC＝BD D．AB∥CD3. 如图，纸片ABCD是一张平行四边形纸片，要求利用所学知识作出一个菱形，甲、乙两名同学的作法分别如下：甲：连接BD，作BD的垂直平分线分别交AD，BC于点E，F，则四边形BFDE是菱形．乙：分别作∠A与∠B的平分线AE，BF，分别交BC于点E，交AD于点F，则四边形ABEF是菱形．对于甲、乙两人的作法，下列判断正确的为( )A．甲正确，乙错误 B．甲错误，乙正确 C．甲、乙均正确 D．甲、乙均错误4. 如图，在菱形ABCD中，对角线AC与BD相交于点O，若AB＝2，∠ABC＝60°，则BD的长为()A．2 B．3 C.√3D． 2√35. 如图，在菱形ABCD中，E，F分别是AB，AC的中点，若EF＝3，则菱形ABCD的周长是( )A．12 B．16 C．20 D．246. 如图，菱形ABCD的边长为√5，对角线AC，BD交于点O，OA=1，则菱形ABCD的面积为（）A．√5B．2√5C．2 D．47. 如图，在菱形ABCD中，AB的垂直平分线交对角线AC于点F，垂足为E，连结DF，若∠BAD＝70°，则∠CFD等于（）A．50°B．60°C．70°D．80°8. 如图，菱形ABCD对角线AC，BD交于点O，∠ACB=15°，过点C作CE⊥AD交AD的延长线于点E．若菱形ABCD的面积为4，则菱形的边长为（）A．2√2B．2 C．42D．4 9. 菱形ABCD中，∠D=60°．点E、F分别在边BC、CD上，且DF=CE．若EF=4，则△AEF 的面积为（）．A．4√3B．3√3C．2√3D．√310. 如图，菱形ABCD的边长为4，过点A、C作对角线AC的垂线，分别交CB和AD的延长线于点E、F，AE=3，则四边形AECF的周长为( )A.22 B.18 C.14 D.1111. 如图，菱形ABCD的对角线AC，BD相交于点O，点E，F分别是AB，BC边上的中点，连接EF，若EF=√3，BD=4，则菱形ABCD的周长为（）A.2√7B.4√7 C.12 D.912. 用四个全等的直角三角形无空隙、无重叠地拼成一个菱形，该菱形的边长的平方等于两条对角线的积，则这四个直角三角形的最小内角是（）A．60° B．45° C．30° D．15°二、填空题(5×3=15分)13. 如图,小红在作线段AB的垂直平分线时,是这样操作的:分别以点A,B为圆心,大于线段AB第2题图第3题图第4题图第6题图第5题图第7题图第8题图第9题图第10题图第13题图第14题图第15题图第16题图第17题图长度一半的长为半径画弧,相交于点C,D,则直线CD即为所求.连接AC,BC,AD,BD,根据她的作图方法可知,四边形ADBC一定是 .14. 如图，四边形ABCD是菱形，AC＝8，DB＝6，DH⊥AB于点H，则DH＝_ _．15. 如图，菱形ABCD的两条对角线分别长为6和8，点P是对角线AC上的一个动点，点M，N分别是边AB，BC的中点，则PM+PN的最小值为 .16. 如图，在边长为2的菱形ABCD中，∠B=45°，AE为BC边上的高，将△ABE沿AE所在直线翻折得△AB1E，则△AB1E与四边形AECD重叠部分的面积为___.17. 如图，在菱形纸片ABCD中，AB=4，∠A=60°，将菱形纸片翻折，使点A落在CD的中点E处，折痕为FG，点F、G分别在边AB、AD上，则BFAF的值为________．三、解答题(8+9+10+10+10+10+12)18. 如图，菱形ABCD的较短对角线BD的长为4，∠ADB＝60°，E，F分别是AD，CD边上的动点，且∠EBF＝60°.(1)求证：△ABE≌△DBF；(2)判断△BEF的形状，并说明理由；19. 如图，▱ABCD中，AB=2，AD=1，∠ADC=60°，将▱ABCD沿过点A的直线l折叠，使点D落到AB边上的点D′处，折痕交CD边于点E．（1）求证：四边形BCED′是菱形；（2）若点P时直线l上的一个动点，请计算PD′+PB的最小值．20. 如图，菱形ABCD中，点E为AC上一点，且DE⊥BE。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

人教版八年级第23讲菱形培优训练
姓名:________ 班级:________ 成绩:________
一、单选题
1 . 如图，四边形ABCD是菱形，DH⊥AB于点H，若AC=8cm，BD=6cm，则DH=（）
A．5cm B．cm
C．cm D．cm
2 . 如图，已知中，DE、FG分别是AB，AC边上的垂直平分线，，，则
的度数是
A．B．C．D．
二、填空题
3 . 如图，Rt△ABC中，∠C＝90°，AB＝5，BC＝4，点G为边BC的中点，点D从点C出发沿CA向点A运动，
到点A停止，以GD为边作正方形DEFG，则点E运动的路程为_______．
4 . 如图，四边形ABCD是菱形，AC=24，BD=10，DH⊥AB于点H，则线段BH的长为
______．
5 . 如图,边长为2的菱形ABCD中,BD=2,E、F分别是AD,CD上的动点(包含端点)，且AE+CF=2，则线段EF长
的最小值是__________.
6 . 如图，在菱形中，，点是边的中点，是对角线上的一个动点，若，
则的最小值是_____.
三、解答题
7 . 如图，已知的对角线AD和BC交于点O，，分别过点A、C作，，AE和CE交于点E，连接BE.
（1）求证：四边形AECO是矩形；
（2）当，时，求的值.
8 . 如图，，，点、、、在同一直线上，．
(1)求证：；
(2)连结、，若，试猜想四边形是什么四边形，并证明你的结
论．
参考答案一、单选题
1、
2、
二、填空题
1、
2、
3、
4、
三、解答题
1、
2、。