资料分析最全公式
资料分析公式汇总

资料分析公式汇总在进行资料分析时,掌握一些关键的公式可以帮助我们更高效、准确地处理和解读数据。
以下是为大家汇总的一些常用公式:一、增长相关公式1、增长量=现期量基期量增长量用于衡量数据在一定时期内的绝对增长幅度。
2、增长率=增长量÷基期量×100%这个公式反映了数据增长的相对速度。
3、基期量=现期量÷(1 +增长率)当我们已知现期量和增长率,要求出之前某个时期的量时,就会用到这个公式。
4、现期量=基期量×(1 +增长率)通过基期量和增长率来计算当前时期的量。
二、比重相关公式1、比重=部分÷整体×100%比重表示部分在整体中所占的比例。
2、整体=部分÷比重已知部分和其占整体的比重,可求出整体的量。
3、部分=整体×比重根据整体的量和部分所占的比重,能计算出部分的量。
三、平均数相关公式1、平均数=总数÷个数这是计算平均数最基本的公式。
2、总数=平均数×个数当已知平均数和个数时,可求出总数。
四、倍数相关公式1、 A 是 B 的几倍:A÷B直接用 A 的数值除以 B 的数值,得到 A 是 B 的倍数。
2、 A 比 B 多几倍:(A B)÷B先计算 A 与 B 的差值,再除以 B 的数值。
五、隔年增长相关公式1、隔年增长率=现期增长率+间期增长率+现期增长率×间期增长率例如,今年的增长率为 r1,去年的增长率为 r2,那么隔年增长率就是 r1 + r2 + r1×r2 。
2、隔年基期量=现期量÷(1 +隔年增长率)六、年均增长相关公式1、年均增长量=(末期量初期量)÷年份差用于计算在一定年份内平均每年的增长量。
2、年均增长率=(末期量÷初期量)^(1÷年份差) 1七、混合增长率相关公式整体增长率介于部分增长率之间,且偏向于基期量大的部分增长率。
(完整版)资料分析计算公式

资料分析计算公式
基本概念:
基期:统计中计算指数或变化情况等动态指标时,作为参照标准的时期。
(参照物)现期:相对基期而言,是与基期相比较的后一时期。
同比增长:与上一年同一时期相比的增长情况。
环比增长:与之紧紧相邻的上一个统计周期相比较的增长情况。
贸易顺差与贸易逆差
贸易顺差:进口额< 出口额
贸易顺差= 出口额—进口额
贸易逆差:进口额> 出口额
贸易逆差= 进口额—出口额
年均增长率、年均增长量:
现期量= 基期量()N
⨯,其中n为相差年数;
+
1年均增长率
年均增长量= ()n÷
现期量,其中n为相差年数;
-基期量。
资料分析公式汇总
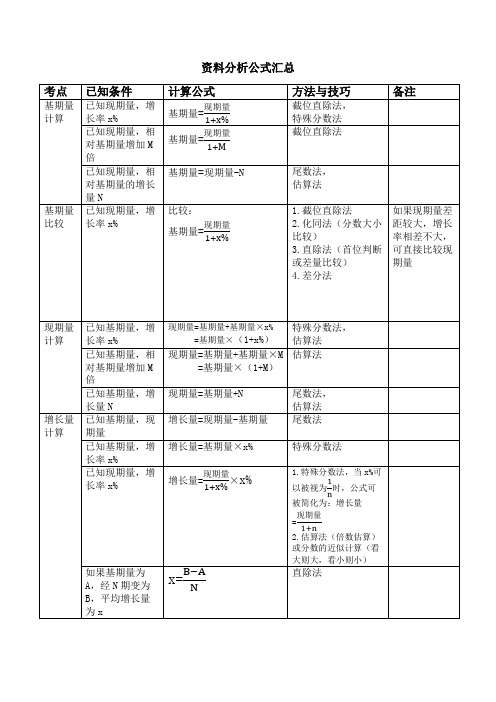
资料分析公式汇总速算技巧一、估算法精度要求不高的情况下,进行粗略估值的速算方式。
选项相差较大,或者在被比较的数字相差必须比较大,差距的大小将直接决定对“估算”时对精度的要求。
二、直除法在比较或者计算较复杂的分数时,通过“直接相除”的方式得到商的首位(首一位、首两位、首三位),从而得出正确答案的速算方式。
常用形式: 1.比较型:比较分数大小时,若其量级相当,首位最大∕小数为最大∕小数2.计算型:计算分数大小时,选项首位不同,通过计算首位便可得出答案。
难易梯度:1.基础直除法:①可通过直接观察判断首位的情形;②需要通过手动计算判断首位的情形。
2.多位直除法:通过计算分数的“首两位”或“首三位”判断答案情形。
三、插值法1.“比较型”插值法如果A与B的比较,若可以找到一个数C,使得A﹥C,而B﹤C,既可以判定A﹥B;若可以找到一个数C,使得A﹤C,而B﹥C,既可以判定A﹤B;2.“计算型”插值法若A﹤C﹤B,则如果f﹥C,则可以得到f=B;如果f﹤C,则可以得到f=A;若A﹥C﹥B,则如果f﹥C,则可以得到f=A;如果f﹤C,则可以得到f=B。
四、放缩法当计算精度要求不高时,可以将中间结果进行大胆的“放”(扩大)或者“缩”(缩小),从而迅速得到精度足够的结果。
常用形式:1. A﹥B,C﹥D,则有A+C﹥B+D;A-D﹥B-C;2. A﹥B﹥0,C﹥D﹥0,则有A×C﹥B×D;A÷D﹥B÷C五、割补法在计算一组数据的平均值或总和值时,首先选取一个中间值,根据中间值将这组数据“割”(减去)或“补”(追上),进而求取平均值或总和值。
常用形式:1.根据该组数据,粗略估算一个中间值;2.将该组值分别减去中间值得到一组数值;3.将得到的新数值相加得到和值,用和值除以该组数值的项数得到商值,将商值加上中间值,即为该组数值的精确平均值;4.用中间值乘以数据项数再加上最后的和值即为总和值。
资料分析公式汇总

资料分析公式汇总资料分析公式的汇总在社会科学、自然科学、工程技术等领域,资料分析是一项非常重要的研究方法。
通过对大量的数据进行收集、整理和处理,可以得出对问题的解释和预测。
而资料分析公式则是在这个过程中广泛应用的一种工具。
本文将对一些常见的资料分析公式进行汇总和解释。
一、中心趋势测量公式1. 平均数公式:平均数是将一组数据的总和除以数据的个数得出的数值,用来代表这组数据的中心趋势。
计算公式如下:平均数 = 总和 / 数据个数2. 中位数公式:中位数是将一组数据按大小顺序排列后,位于中间位置的数值。
如果数据个数为奇数,则中位数就是中间的数值;如果数据个数为偶数,则中位数是中间两个数值的平均值。
3. 众数公式:众数是指在一组数据中出现频率最高的数值。
有时候一组数据中可能存在多个众数,这时可以将所有的众数列举出来。
二、离散程度测量公式1. 范围(R)公式:范围是用于度量一组数据的离散程度的指标,其计算公式如下:范围 = 最大值 - 最小值2. 方差(S²)公式:方差是一组数据偏离平均数的平方差的平均值,用于度量一组数据的离散程度。
计算公式如下:方差= ∑(Xi - 平均数)² / 数据个数3. 标准差(S)公式:标准差是方差的平方根,用于度量一组数据的离散程度的更常用指标。
计算公式如下:标准差= √方差三、相关关系测量公式1. 相关系数(r)公式:相关系数用于度量两组数据之间的相关性,其取值范围在-1到1之间。
相关系数越接近于1或-1,表示两组数据之间的相关性越强,越接近于0则表示两组数据之间的相关性越弱。
计算公式如下:相关系数r = ∑(Xi - 平均数X)(Yi - 平均数Y)/ √[∑(Xi - 平均数X)²] * √[∑(Yi - 平均数Y)²]2. 斯皮尔曼相关系数公式:斯皮尔曼相关系数也是度量两组数据之间的相关性的指标,但它适用于非线性关系的数据。
计算公式如下:斯皮尔曼相关系数 rs = 1 - 6 * ∑(Di²) / (n³ - n)四、回归关系测量公式1. 简单线性回归公式:简单线性回归是通过拟合一条直线来建立两组数据之间的线性关系,从而进行预测和解释的方法。
资料分析公式大全

一、与增长有关的基本公式
1、增长量= 今年的量- 去年的量
2、
3、
4、增长率=去年的量×增长率
5、
6、
7、今年的量=去年的量×(1+增长率)
、
、
二、与隔年增长有关的基本公式(ql表示今年的增长率,q2表示去年的增长率) 1、
2、
3、隔年的增长率=(1+ql)×(1+q2)- 1
4、
三、与比重有关的公式(ql表示部分的增长率,q2表示整体的增长率)
1、
2、部分的量=比重×整体的量
3、
比重的差(百分点)=今年的比重
4、
5、比重的递推
已知则,
已则
四、与平均量有关的公式(q1表示总数的增长率,q2表示份数的增长) 1、
平均量的增长量=今年的平均量)
2、
3、
五、与倍数有关的公式
1、
2、
3、"是"几倍-1="多"几倍=增长率
六、与指数有关的公式
1、(指数-100)%=增长率
2、
七、与拉动增长、贡献率有关的公式1、
2、
3、
八、与去年的和或差有关的公式。
资料分析满分必备计算公式

相当于分数大小比较,同上述做法
当部分增长率大于整体增长率,则现期比 重大于基期比重。 (方法为“看”增长率)
凑整法
增长量
现期量 x%
1 x%
( 11)如果基期量为 A ,经 N 期变为 B,平均 增长量为 x
BA x
N
增长量比较 ( 12)已知现期量与增长率 x%
增长量 现期量 x% 1 x%
估算法
尾数法,估算法 尾数法
特殊分数法
( 1)特殊分数法, 当 x%可以被视为 1 时, n
公式可被化简为: 增长量
现期量
计算公式整理
考点
已知条件
( 1)已知现期量,增长率 x%
基期量计算 ( 2)已知现期量,相对基期量增加 M 倍
( 3)已知现期量,相对基期量的增长量 N
计算公式
现期量 基期量
1 x% 现期量 基期量 1M
基期量 现期量 - N
基期量比较 ( 4)已知现期量,增长率 x% 现期量计算 ( 5)已知基期量,增长率 x%
A a% B b% r%
AB
则 rA 介于 rB 和 rC 之间
( 19)已知现期量与增长量
比较 增长率
现期量
代替增长率进行
基期量
大小比较
x% 为增函数, 所以现期量大, 增长率 1 x%
大的情况下,增长量一定大。 ( 1)截位直除法 ( 2)插值法
截位直除法
代入法或公式法
简单记忆口诀:连续增长,最终增长大于 增长率之和;连续下降,最终下降小于增 长率之和
增长率 现期量 - 基期量 基期量
增长率计算
( 15)如果基期量为 A ,经 N 期变为 B ,平均 增长率为 x%
资料分析公式及例题(最全)

A B 一、增长增长量 = 现期量 — 基期量增长率 = 增幅 = 增速 = 增长量 ÷ 基期量 = (现期量 — 基期量) ÷基期量 年均增长量、年均增长率:如果初值为 A ,第 n+1 年增长为 B ,年均增长量为 M ,年均增长率为 %,则:M=B −A = A( +x %)nn 增长量 = A × m , 当 m>0B 时, m 越大, m% 越大。
%现期量高,增长率高,则增长量高。
同比增长、环比增长同比增长:与上一年的同一时期相比的增长速度。
环比增长:与紧紧相邻的上一期相比的增长速度。
乘除法转化法: 当0 <x < 5%时, = ≈ × (1 ∓ x)B【例 1】2011 年全国农民工总量达到 25278 万人,比上年增加 1055 万人,增长 4.4%。
农民工从业仍以制造业、 建筑业和服务业为主, 从事建筑业的比重明显提 高。
从农民工的就业地区来看, 2011 年在东部地区务工的农民工 16537 万人, 比上年增加 324 万人;在中部地区务工的农民工 4438 万人,比上年增加 334 万 人, 增长 8.1%;在西部地区务工的农民工 4215 万人, 比上年增加 370 万人, 增 长 9.6%。
问题: 与上一年相比, 2011 年在东部地区务工的农民工人数增长率约为( )A . 2.0%B . 4.4%C . 5.2%D . 8.1%【例 2】2010 年,我国进出口贸易总额为 29727.6 亿美元,同比增长 34.7%。
其 中,出口额 15779.3 亿美元,同比增长 31.3%;进口额 13948.3 亿美元,同比增 1+m% 1+m%1±x 1长 38.7%。
问题: 2009 年我国进出口贸易总额约为( )万亿美元。
A.1.6B.2.2C.2.6D.3.0二、比重比重 = 分量÷总体量× 100%已知本期分量为 A,增长率为 a%,总量为 B,增长率为 b%,则:基期分量占总量的比重:A ÷ (1 + a%) A 1 + b%= ×B ÷ (1 + b%) B 1 + a%如果 a%>b%,则本期 A 占 B 的比重(B A)相较基期(B A× )有所上升。
资料分析必备公式

给人改变未来的力量版权所有 翻印必究资料分析必备公式1. 增长量 ①.增长量=增长后的量-增长前的量 ②.本期比上期增长的量= 2. 年均增长量本期的量 × 增长率 1 + 增长率m=b − a 总增长量 = n 增长次数其中,m 代表年均增长量,n 代表增长次数,b 代表增长后的量,a 代表增长前的量 3. 增长率 ①.增长率=增长后的量 − 增长前的量 增长量 × 100% = × 100% 增长前的量 “比”字后面的量 减少前的量 − 减少后的量 减少量 × 100% = × 100% 减少前的量 “比”字后面的量②.减少率=③.总体的增长率数值介于部分增长率之间 一个整体中包含两个部分。
已知总体增长率为 f%,两个部分增长率分别为 x%,y%, 其中 x%<y% 那么它们之间满足关系式:x%<f%<y% 4. 年均增长率 ①.x%= n (b − 1) 100% × a其中 x%代表年均增长率,b 代表增长后的量,a 代表增长前的量,n 代表增长次数 ②.a×(1+x%)n=b 其中 a 代表增长前的量,x%代表年均增长率,n 代表增长次数,b 代笔增长后的量 5. 倍数b ,其中 k 代表 b 是 a 的多少倍(a<b) a b−a b ②. × 100% = − 1 (a<b) a a①.k= 即:增长率 6. 比重 比重= = 倍数-1部分的量 × 100% 整体的量 整体 = 部分的量 部分占整体的比重部分= 整体 × 部分占整体的比重 7. 比重的变化全国客服:4006 300 9991中公教育学员内部专用资料给人改变未来的力量版权所有 翻印必究对比: ①:本期比重=部分的量 × 100% 整体的量增长后的比重=部分的量(1 + x%) × 100% 整体的量(1 + y %)其中 x%代表部分的增长率,y%代表整体的增长率 如果 x%>y%,那么增长后的比重>本期比重 如果 x%<y%,那么增长后的比重<本期比重②:本期比重=部分的量 × 100% 整体的量部分的量 增长前的比重= 1 + x % × 100% 整体的量 1 + y%其中 x%代表部分的增长率,y%代表整体的增长率 如果 x%>y%,那么本期比重>增长前的比重 如果 x%<y%,那么本期比重<增长前的比重 8. 平均数 平均数=总量/份数,人均=总量/人数 9. 计算公式 ①.1 1 ≈ 1 − x%, ≈ 1 + x% ,其中 x%在比较小的情况下的近似,一般 x%<3%。
