连续时间信号的卷积实验报告
连续时间信号实验报告

一、实验目的1. 理解连续时间信号的基本概念和特性。
2. 掌握连续时间信号的时域分析方法和基本运算。
3. 学会使用MATLAB软件进行连续时间信号的时域分析和图形绘制。
4. 通过实验加深对连续时间信号理论知识的理解和应用。
二、实验原理连续时间信号是指信号在任意时刻都有确定的取值。
本实验主要涉及以下内容:1. 基本连续时间信号的时域表示,如单位冲激信号、单位阶跃信号、正弦信号等。
2. 连续时间信号的时域运算,如卷积、微分、积分等。
3. 连续时间信号的时域分析方法,如时域波形分析、时域频谱分析等。
三、实验设备1. PC机2. MATLAB软件3. 连续时间信号发生器4. 示波器四、实验内容与步骤1. 基本连续时间信号的时域表示(1)在MATLAB中编写程序,生成单位冲激信号、单位阶跃信号和正弦信号。
(2)绘制这些信号的时域波形图,观察其特性。
2. 连续时间信号的时域运算(1)编写程序,实现两个连续时间信号的卷积运算。
(2)绘制卷积结果的时域波形图,观察其特性。
3. 连续时间信号的时域分析方法(1)编写程序,对连续时间信号进行微分和积分运算。
(2)绘制微分和积分结果的时域波形图,观察其特性。
4. 使用MATLAB进行连续时间信号的时域分析(1)使用MATLAB中的函数进行连续时间信号的时域分析,如fft、ifft、diff、int等。
(2)绘制分析结果的时域波形图和频谱图,观察其特性。
五、实验结果与分析1. 基本连续时间信号的时域表示通过实验,我们成功生成了单位冲激信号、单位阶跃信号和正弦信号,并绘制了它们的时域波形图。
观察波形图,我们可以发现这些信号具有不同的特性,如单位冲激信号具有脉冲性质,单位阶跃信号具有阶跃性质,正弦信号具有周期性质。
2. 连续时间信号的时域运算通过实验,我们成功实现了两个连续时间信号的卷积运算,并绘制了卷积结果的时域波形图。
观察波形图,我们可以发现卷积运算的结果具有以下特性:(1)卷积运算的结果是两个信号的叠加。
实验报告信号卷积实验

一、实验目的1. 理解卷积的概念及其物理意义。
2. 掌握卷积运算的原理和方法。
3. 通过实验加深对卷积运算在实际应用中的理解。
二、实验原理1. 卷积的定义:卷积是一种线性运算,它描述了两个信号在时域上的相互作用。
对于两个连续时间信号f(t)和g(t),它们的卷积定义为:F(t) = ∫f(τ)g(t-τ)dτ其中,F(t)是卷积结果,f(τ)是信号f(t)的任意时刻的值,g(t-τ)是信号g(t)在时刻t-τ的值。
2. 卷积的性质:卷积具有交换律、结合律和分配律等性质。
其中,交换律是指f(t)和g(t)的卷积与g(t)和f(t)的卷积相等;结合律是指三个信号f(t)、g(t)和h(t)的卷积可以分别进行两两卷积后再进行一次卷积;分配律是指一个信号与两个信号的卷积等于该信号分别与两个信号卷积后的和。
三、实验内容1. 实验一:连续时间信号卷积实验(1)选用信号:选取两个连续时间信号f(t)和g(t),其中f(t)为矩形脉冲信号,g(t)为指数衰减信号。
(2)卷积计算:根据卷积的定义,计算f(t)和g(t)的卷积F(t)。
(3)结果分析:观察F(t)的波形,分析卷积结果的物理意义。
2. 实验二:离散时间信号卷积实验(1)选用信号:选取两个离散时间信号f[n]和g[n],其中f[n]为单位阶跃信号,g[n]为矩形脉冲信号。
(2)卷积计算:根据离散时间信号卷积的定义,计算f[n]和g[n]的卷积F[n]。
(3)结果分析:观察F[n]的波形,分析卷积结果的物理意义。
3. 实验三:MATLAB仿真实验(1)选用信号:选取两个连续时间信号f(t)和g(t),其中f(t)为正弦信号,g(t)为余弦信号。
(2)MATLAB编程:利用MATLAB的信号处理工具箱,编写程序实现f(t)和g(t)的卷积运算。
(3)结果分析:观察MATLAB仿真得到的卷积结果,分析其物理意义。
四、实验结果与分析1. 实验一:连续时间信号卷积实验(1)实验结果:通过计算得到f(t)和g(t)的卷积F(t)的波形。
卷积信号实验报告

信号与系统上机实验报告一连续时间系统卷积的数值计算140224 班张鑫学号 14071002 一、实验原理计算两个函数的卷积卷积积分的数值运算实际上可以用信号的分段求和来实现,即:如果我们只求当 t = n∆ t1 是r ( t )的值,则由上式可以得到:∆t足够小时,r(t2)就是e(t)和f(t)卷积积分的数值近似值由上面的公式可当1以得到卷积数值计算的方法如下:(1)将信号取值离散化,即以为周期,对信号取值,得到一系列宽度间隔为的矩形脉冲原信号的离散取值点,用所得离散取值点矩形脉冲来表示原来的连续时间信号;(2)将进行卷积的两个信号序列之一反转,与另一信号相乘,并求积分,所得为t=0时的卷积积分的值。
以为单位左右移动反转的信号,与另一信号相乘求积分,求的t<0和t>0时卷积积分的值;(3)将所得卷积积分值与对应的t标在图上,连成一条光滑的曲线,即为所求卷积积分的曲线。
1信号与系统上机实验报告一二、处理流程图三、C程序代码#include"stdafx.h"#include"stdio.h"//#include "stdilb.h"float u(float t){while (t>= 0) return(1);while (t<0) return(0);}float f1(float t){return(u(t+2)-u(t-2));}float f2(float t){return(t*(u(t)-u(t-2))+(4-t)*(u(t-2)-u(t-4)));}int_tmain(int argc, _TCHAR* argv[]){FILE *fp;fp=fopen("juanji.xls","w+");float t,i,j,result=0;for(i=-2;i<=6;i=i+0.1){result=0;for(j=0;j<=4;j=j+0.1)result+=f2(j)*f1(i-j)*0.1;printf("%.1f\t%.2f\t",i,result);fprintf(fp,"%.1f\t%.2f\n",i,result);}printf ("\n");return 0;}四、运行结果五、卷积曲线六、感想与总结卷积是信号与系统时域分析的基本手段,主要用于求解系统的零状态响应。
实验二连续时间信号、离散信号卷积运算

实验二 连续时间信号、离散信号卷积运算一、实验目的⑴熟悉卷积的定义和表示;⑵掌握利用计算机进行卷积运算的原理和方法;⑶熟悉连续时间信号、离散信号的相关计算方法;⑷熟悉连续时间信号卷积运算、离散信号卷积运算函数c o nv 、反卷积de conv 函数等的应用。
二、实验原理1.卷积的定义:卷积是一种特殊函数与函数之间的计算。
连续时间信号卷积积分可以表示为:f(t)=f 1(t)*f 2(t)= τττd t f f )()(21-⎰∞∞-=τττd f t f )()(12⎰∞∞--离散信号卷积积分可以表示为:f 1(k)*f 2(k)=)()(21m k f m f n -∑∞-∞= ∞-<k<∞2.卷积计算的几何解法卷积积分计算从几何上可以分为四个步骤: 翻转 → 平移 → 相乘 → 叠加(积分)3.卷积积分的应用卷积积分是信号与系统时域分析的基本手段,主要应用于求系统零状态响应。
它将输入信号分解为众多的冲激函数之和,利用冲激响应可以很方便求解LT I 系统对任意激励的零状态响应。
设一个线性零状态响应系统,已知系统的单位冲激响应为h1(t ),当系统的激励信号为x (t )时,系统的零状态响应为y z s (t)=τττd t h x t )()(0-⎰=τττd h t x t)()(0⎰- 可以简记为:y zs (t)=x(t)*h(t) 三、程序设计实验①采用函数c o nv 编程,实现离散时间序列的卷积和运算,完成两序列的卷积和,其中:f1(k )={1,2,1},对应的k1={-1,0,-1};f2(k )={1,1,1,1,1},对应的k2={-2,-1,0,1,2}。
程序代码:k1=[-1,0,1];f1=[1,2,1];subpl o t(3,1,1)stem(k1,f1);title ('f1(k)');k2=[-2,-1,0,1,2];f2=[1,1,1,1,1];subpl o t(3,1,2)stem(k2,f2);title ('f2(k)');k3=k1(1)+k2(1):k1(end)+k2(end);f3=conv(f1,f2);subplo t(3,1,3)stem(k3,f3); title('f3(k)');程序运行结果的对应信号波形图:②求f1(t)=u(t)-u(t-2),f2(t)=e^(-3t)u(t)的卷积。
连续信号卷积
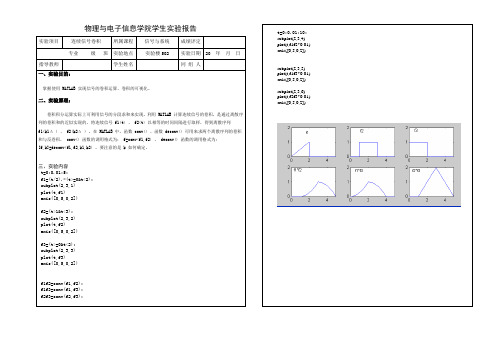
物理与电子信息学院学生实验报告t=0:0.01:10; subplot(2,3,4) plot(t,f1f2*0.01) axis([0,5,0,2])subplot(2,3,5) plot(t,f1f3*0.01) axis([0,5,0,2])subplot(2,3,6) plot(t,f2f3*0.01) axis([0,5,0,2])实验项目连续信号卷积所属课程信号与系统 成绩评定专业 级 班 实验地点 实验楼502实验日期 20 年 月 日 指导教师 学生姓名同 组 人一、实验目的:掌握使用 MATLAB 实现信号的卷积运算、卷积的可视化。
二、实验原理:卷积积分运算实际上可利用信号的分段求和来实现。
利用 MATLAB 计算连续信号的卷积,是通过离散序列的卷积和的近似实现的,将连续信号 f1(t) 、 f2(t) 以相等的时间间隔进行取样,得到离散序列 f1(k1Δ ) 、 f2(k2Δ ) 。
在 MATLAB 中,函数 conv() 、函数 deconv() 可用来求两个离散序列的卷积和与反卷积, conv() 函数的调用格式为: f=conv(f1,f2) 、 deconv() 函数的调用格式为: [f,k]=deconv(f1,f2,k1,k2) 。
要注意的是 k 如何确定。
三、实验内容 t=0:0.01:5;f1=(t/2).*(t>=0&t<2); subplot(2,3,1) plot(t,f1)axis([0,5,0,2])f2=(t>1&t<3); subplot(2,3,2) plot(t,f2)axis([0,5,0,2])f3=(t>=0&t<2); subplot(2,3,3) plot(t,f3)axis([0,5,0,2])f1f2=conv(f1,f2); f1f3=conv(f1,f3); f2f3=conv(f2,f3);四、实验总结(实验中所遇问题的原因分析及解决措施;本实验未解决的问题;对实验的改进;个人的收获等)。
连续时间信号的卷积及信号的频域分析 实验报告

课程实验报告题目:连续时间信号的卷积及信号的频域分析学院学生姓名班级学号指导教师开课学院日期实验内容:(一)连续时间信号的卷积问题1:用计算机算卷积是把连续信号进行采样,得到一个个离散数值,然后用数值计算代替连续信号的卷积,请推导数值计算与连续信号的卷积之间的关系。
(学生回答问题)上机题1.已知两个信号)2()1()(1---=t t t x εε和)1()()(2--=t t t x εε,试分别画出)(),(21t x t x 和卷积)()()(21t x t x t y *=的波形。
(上机原程序及所画出的波形图)T=0.01t1=1; t2=2;t3=0; t4=1;t=0:T: t2+t4x1=ones(size(t)).*((t>t1)-(t>t2));x2=ones(size(t)).*((t>t3)-(t>t4));y=conv(x1, x2)*T;subplot(3, 1, 1),plot(t, x1);ylabel('x1(t)');subplot(3, 1, 2),plot(t, x2);ylabel(‘x2(t)’);subplot(3, 1, 3),plot(t,y(1: (t2+t4)/T+1));ylabel (‘y(t)=x1*x2’);xlabel(‘----t/s ’);上机题2.已知两个信号)()(t e t x t ε-=和)()(2/t te t h t ε-=,试用数值计算法求卷积,并分别画出)(),(t h t x 和卷积)()()(t h t x t y *=的波形。
(上机原程序及所画出的波形图)t2=3,t4=11;T=0.01;t=0: T: t2+t4;x=exp(-t).*((t>0)-(t>t2));h=t.*exp(-t/2).*((t>0)-(t>t4));y=conv(x,h)*T;yt=4*exp(-t)+2*t.*exp(-1/2*t)-4*exp(-1/2*t);subplot(3, 1, 1),plot(t, x);ylabel(‘x(t)’);subplot(3, 1, 2),plot(t, h);ylabel(‘h(t)’);subplot(3, 1, 3),plot(t, y(1: (t2+t4)/T+1),t ,yt,'--r');legend(‘by numerical ’,’Theoretical ’);ylable(‘y=x*h ’);xlable(‘---t/s ’);实验内容:(二)信号的频域分析上机题3.求周期矩形脉冲信号的频谱图,已知s T s A 5.0,1.0,1===τ (上机原程序及所画出的波形图)a=1; tao=0.1; t=0.5;n0=t/tao;n=0: 2*n0;fn_p=a*tao/t*(sin(n*pi*tao/t+eps*(n==0)))./(n*pi*tao/t+eps*(n==0)); fn_pabs=abs(fn_p);fn_pang=angle(fn_p);fn_mabs=fliplr(fn_pabs(2: 11));fn_mang=-fliplr(fn_pang(2: 11));fnabs=[fn_mabs fn_pabs];fnang=[fn_mang fn_pang];subplot(2, 1, 1),stem((-2*n0: 2*n0), fnabs);text(4, 0.11, ‘amplitude spectrum ’);subplot(2, 1, 2),stem((-2*n0: 2*n0), fnang);text(-2, 2, ‘phase spectrum ’);xlable(‘n ’);grid问题2:改变信号的周期,比较他们的计算结果。
实验5 连续时间信号的卷积运算

实验5 连续时间信号的卷积运算一、实验目的(1)熟悉卷积的定义和表示;(2)掌握相利用计算机进行卷积运算的原理和方法;(3)熟悉连续信号卷积运算函数conv的应用。
二、涉及的MATLAB函数1.conv函数功能:实现信号的卷积运算。
调用格式:w=conv(f1,f2)*dt其中,dt为采样周期(步长);当f1,f2其中之一为冲激信号δ(t)时,w=conv(f1,f2)2.stepfun函数调用格式:Stepfun(t,t0)其中,t是时间区间,在该区间内阶跃信号一定会产生;t0是信号发生从0到1跳跃的时刻三、实验内容实验①%函数卷积a=1000;t1=-5:1/a:5;f1=stepfun(t1,0); %产生阶跃信号f2=stepfun(t1,-1/a)-stepfun(t1,1/a); %产生冲激信号subplot(231);plot(t1,f1);axis([-5,5,0,1.2]);title('f1');ylabel('f1(t)');title('单位阶跃新函数');subplot(232);plot(t1,f2);title('f2');f12=conv(f1,f2);t=-10:1/a:10;subplot(233);plot(t,f12);axis([-10,10,0,1.2]);title('f1*f2');f21=conv(f2,f1);subplot(234);plot(t,f21);axis([-10,10,0,1.2]);title('f2*f1');ylabel('y(t)');f11=conv(f1,f1)*1/a;f22=conv(f2,f2);subplot(235);plot(t,f11);title('f1*f1');subplot(236);plot(t,f22);title('f2*f2');实验②%连续函数卷积s=0.01;k1=0:s:2; %生成k1的时间向量k2=k1; %生成k2的时间向量f1=3*k1; %生成f1的样值向量f2=3*k2; %生成f2的样值向量f=conv(f1,f2);f=f*s;k0=k1(1)+k2(1); %序列f非零样值的起点k3=k1(end)+k2(end); %序列f非零样值的终点k=k0:s:k3;subplot(3,1,1);plot(k1,f1);title('f1(t)');subplot(3,1,2);plot(k2,f2);title('f2(t)');subplot(3,1,3);plot(k,f);title('f(t)');实验③%函数卷积a=1000;t1=-5:1/a:5;f1=stepfun(t1,-1/a)-stepfun(t1,1/a);%产生冲激信号f2=stepfun(t1,0);%产生阶跃信号u(t)f3=stepfun(t1,0)-stepfun(t1,4);subplot(231);plot(t1,f1);axis([-5,5,0,1.2]);title('f1'); subplot(232);plot(t1,f2);axis([-5,5,0,1.2]);title('f2'); subplot(233);plot(t1,f3);axis([-5,5,0,1.2]);title('f3'); f4=conv(f1,f2+f3);f5=conv(f1,f2)+conv(f1,f3);t=-10:1/a:10;subplot(234);plot(t,f4);axis([-10,10,0,3]);title('f4*f1');subplot(235);plot(t,f5);axis([-10,10,0,3]);title('f5');四、实验结论1、卷积积分的计算从几何上可以分为四个步骤:翻转→平移→相乘→叠加(积分)。
连续时间信号的卷积运算

实验二连续时间信号的卷积运算与LTI系统的时域分析实验人:Mr.yan1 实验目的(1)熟悉卷积的定义和表示;(2)掌握利用计算机进行卷积运算的原理和方法;(3)熟悉连续信号卷积运算函数conv的应用。
(4)熟悉连续LTI系统在典型激励信号下的响应及其特征;(5)掌握连续LTI系统单位冲激响应的求解方法;(6)掌握用卷积法计算连续时间系统的零状态响应;(7)能够应用Matlab对系统进行时域分析。
2 实验原理(1)卷积的定义、卷积的几何解法、卷积积分的应用(求系统的零状态响应)(2)对于一般的n阶LTI连续系统,如果n的数值比较小时,可以通过解析的方法得到响应。
但是,对于高阶系统,手工运算比较困难,要利用一些计算工具软件。
3 涉及的Matlab函数(1)conv函数:实现信号的卷积运算。
调用格式:w=conv(u,v)计算两个有限长度序列的卷积。
说明:该函数假定两个序列都从零开始。
(2)lsim函数:计算并画出系统在任意输入下的零状态响应。
调用格式:lsim(b,a,x,t)其中:a和b是由描述系统的微分方程系数决定的表示该系统的两个行向量;x和t是表示输入信号的行向量。
该调用格式将会绘出由向量a和b所定义的连续系统在输入为向量x 和t所定义的信号时,系统的零状态响应的时域仿真波形,且时间范围与输入信号相同。
(3)impulse函数:计算并画出系统的冲激响应。
调用格式:impulse(b,a)该调用格式以默认方式绘出向量a和b定义的连续系统的冲激响应的时域波形。
impulse(b,a,t)该调用格式将绘出向量a和b定义的连续系统在0-t时间范围内的冲激响应波形。
impulse(b,a,t1:p:t2)该调用格式将绘出向量a和b定义的连续系统在t1-t2时间范围内,且以时间间隔p均匀取样的冲激响应波形。
(4)step函数:计算并画出系统阶跃响应曲线调用格式:该函数与函数impulse()一样,也有相似的调用格式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
连续时间信号
的卷积计算实验报告
一、实验目的
1.学会运用MATLAB实现连续时间信号的卷积。
2.学会运用MATLAB符号运算法求连续时间信号的卷积。
3.学会运用MATLAB数值计算法求连续时间信号的卷积。
二、实验原理
卷积积分是信号与系统时域分析中的重要方法之一。
连续时间信号的卷积积分定义为f(t)=f1(t)*f2(t)=从负无穷到正无穷f1(tao)f2(tao)d(tao)的积分。
MATLAB进行卷积计算可以通过符号运算方法和数值计算方法来实现。
三、实验内容
1.MATLAB符号运算法求连续时间信号(课本P32题一)的卷积。
2.MATLAB数值计算法求连续时间信号(课本P32题一)的卷积。
四、实验结果
1.MATLAB符号运算法求连续时间信号(课本P32题一)的卷积。
(1)代码
(2)结果
(3)图片
2.MATLAB数值计算法求连续时间信号(课本P32题一)的卷积。
(1)代码
(2)结果
(3)图片
五、心得体会。
