流密码与分组密码编程
分组密码(全)

7
分组密码的发展历史
二十世纪之前的密码算法
算法、密钥保密
二十世纪之后的密码算法
Kerckhoffs假设:密码分析者已有密码算法 及实现的全部详细资料. Kerckhoff假设蕴涵着密码的安全性完全依赖 于密钥.
8
分组密码的发展历史
民用 不存在陷门 足够的安全强度 标准化通信需求
12
分组密码的发展历史
1999年,NIST从提交的15个候选草案中 选取了5个优良的算法作为AES的候选算法: MARS、RC6、Rijndael、Serpent和 Twofish, 综合评价最终确定Rijndael算法为新的数据 加密标准,2001年12月正式公布FIPS197标准。 /aes
定义 一个分组密码体制(P, K, C, E, D), 其中P=C={0,1}l ;K={0,1}t. 加密变换: E:P×K→C, 当k ∈K确定时,
Ek为P →C的一一映射.
解密变换: D: C×K →P, 当k ∈K确定时,
Dk为C →P的一一映射.
Dk·Ek=I
6
特点 明文、密文组长度为n,密钥长度为t,密钥量 为 2t 密文中的任一位数字与该组明文所有的数字均 有关 每组明文使用相同密钥加密 本质是{0,1,…,2n-1}集合上的自映射或置 换
22
保密系统的安全性分析 及分组密码攻击手段
主动攻击:主动出击,先发制人
3. 选择明文攻击:密码分析者可得到所需要的任何 明文所对应的密文,这些密文与待解的密文是用同 一个密钥加密得来的. 4. 选择密文攻击:密码分析者可得到所需要的任何 密文所对应的明文,解密这些密文所使用的密钥与 解密待解的密文的密钥是一样的.
密码学专业代码

密码学专业代码密码学是一门研究信息安全和保密的科学,它涉及到数学、计算机科学、工程、物理等多个领域。
密码学专业代码是指在密码学领域中使用的一些专业术语、符号、算法、协议等,它们有助于描述、分析、设计、实现和评估各种密码学系统和应用。
密码学基本概念在密码学中,有一些基本的概念和定义,它们是理解和使用密码学专业代码的基础。
以下是一些常见的密码学基本概念:明文:明文是指未经加密或变换的原始信息,它可以是任何形式的数据,如文本、图像、音频、视频等。
明文通常用字母P表示。
密文:密文是指经过加密或变换后的信息,它通常无法直接被人或机器理解,需要通过解密或逆变换才能恢复成明文。
密文通常用字母C表示。
密钥:密钥是指用于加密或解密信息的一些参数或数据,它可以是一个数字、一个字符串、一个矩阵等。
密钥通常用字母K表示。
加密:加密是指将明文通过某种算法或函数,结合密钥,变换成密文的过程。
加密通常用符号E表示,例如E(K,P)=C表示用密钥K对明文P进行加密得到密文C。
解密:解密是指将密文通过某种算法或函数,结合密钥,逆变换成明文的过程。
解密通常用符号D表示,例如D(K,C)=P表示用密钥K对密文C进行解密得到明文P。
密码系统:密码系统是指一个完整的加密和解密方案,它包括了加密算法、解密算法、密钥生成方法、密钥分配协议等。
密码系统通常用符号S表示。
密码分析:密码分析是指对密码系统进行研究和攻击的过程,目的是为了破译出明文或者找出密钥。
密码分析通常分为两类:无条件安全和计算安全。
无条件安全是指即使攻击者拥有无限的计算能力和时间,也无法破译出明文或者找出密钥的密码系统。
计算安全是指即使攻击者拥有很强的计算能力和时间,也需要付出非常大的代价才能破译出明文或者找出密钥的密码系统。
攻击模型:攻击模型是指描述攻击者拥有什么样的信息和能力来进行密码分析的一种假设。
不同的攻击模型对应不同的难度和安全性。
以下是一些常见的攻击模型:唯密文攻击:唯密文攻击是指攻击者只知道一些密文,不知道任何明文或者密钥的情况下进行的攻击。
02分组密码—DES算法及AES简介

分组密码和流密码的比较
• 基本区别
– 粒度 8字节分组 vs. 1比特或1字节
各自适应不同的应用数据格式 – 分组密码对相同的明文分组,总是输出相同的密文分组;
而流密码却输出不同的密文比特
– 流密码一般快很多
• 分组密码多些,是商用密码的主流
– 分组密码也可以用作流模式
• 安全性对比
– 流密码是核心密码的主流
L1 =R2⊕F(k2,R1) =L1⊕F(k2,R1)⊕F(k2,R1) =L1
L0 =R1⊕F(k1,R0) =L0⊕F(k1,R0)⊕F(k1,R0) =L0
kpwang@
Copyright by © 王鲲鹏
Feistel伪代码
明文m – 长度n=2t,记为m0m1,每个长度为t 密钥k – 产生r个子密钥k1,k2 ,...,kr 加密E m: for i=2 to r+1 do 0, 1 mi=mi-2 XOR f(mi-1, ki-1) i, i+1 <- ki 得密文(mr,mr+1) r, r+1 <- kr 解密D for i=r to 1 do mi-1=mi+1 XOR f(mi, ki) 或 for i=r-1 to 0 do mi=mi+2 XOR f(mi+1, ki+1) =mi XOR f(mi+1, ki+1) XOR f(mi+1, ki+1) =mi
– 密文分组和明文分组同样长 • 对某个密钥可以构造一个明密文对照表
– 电码本 (Substitution Table) – 所以分组的长得至少64比特才好
– 密钥空间2 << 可逆映射个数(2 )!
分析比较分组密码AES-CFB或OFB与流密码RC4的特点

作业二、分析比较分组密码AES-CFB 或 OFB与流密码RC4的特点一、RC4算法介绍RC4是一种对称密码算法,它属于对称密码算法中的序列密码(streamcipher,也称为流密码),它是可变密钥长度,面向字节操作的流密码。
RC4是流密码streamcipher中的一种,为序列密码。
RC4加密算法是Ron Rivest在1987年设计出的密钥长度可变的加密算法簇。
起初该算法是商业,直到1994年,它才公诸于众。
由于RC4具有算法简单,运算速度快,软硬件实现都十分容易等优点,使其在一些协议和标准里得到了广泛应用。
流密码也属于对称密码,但与分组加密算法不同的是,流密码不对明文数据进行分组,而是用密钥生成与明文一样长短的密码流对明文进行加密,加解密使用相同的密钥。
RC4算法特点:(1)、算法简洁易于软件实现,加密速度快,安全性比较高;(2)、密钥长度可变,一般用256个字节。
对称密码的工作方式有四种:电子密码本(ECB, electronic codebook)方式、密码分组(CBC, cipherblock chaining)方式、密文反馈(CFB, cipher-feedback)方式、输出反馈(OFB, output-feedback)方式。
RC4算法采用的是输出反馈工作方式,所以可以用一个短的密钥产生一个相对较长的密钥序列。
OFB方式的最大的优点是消息如果发生错误(这里指的是消息的某一位发生了改变,而不是消息的某一位丢失),错误不会传递到产生的密钥序列上;缺点是对插入攻击很敏感,并且对同步的要求比较高。
RC4的执行速度相当快,它大约是分块密码算法DES的5倍,是3DES的15倍,且比高级加密算法AES也快很多。
RC4算法简单,实现容易。
RC4的安全保证主要在于输入密钥的产生途径,只要在这方面不出现漏洞,采用128bit的密钥是非常安全的。
RC4算法加密流程:包括密钥调度算法KSA和伪随机子密码生成算法PRGA两大部分(以密钥长度为256个字节为例)。
04流密码-CIW

怎么解决?
• RSA公钥 • DH密钥交换 • MD5单向HASH函数
且听下回分解
是它的特征多项式为一个n次本原多项式
本原多项式
•若一个n次多项式f(x)的阶为2n-1,即满足条件:
•f(x)为既约多项式 •f(x)可整除(x2n-1+1) •f(x)不能整除(xp+1),其中p < 2n-1
eg. n=4,周期为24-1=15,其特征多项式是能整除 (x15+1)的4次本原多项式 x15+1=(x+1)(x2+x+1)(x4+x+1)(x4+x3+1)(x4+x3+x2+x+1) 由于x4+x3+x2+x+1|x5+1,所以本原多项式为,x4+x+1 和x4+x3+1,选择f(x)= x4+x+1,即c4=c1=c0=1
•The source host encrypts the data. •The destination host decrypts it. •The packet head is in the clear. •The user data are secure. •The traffic pattern is insecure. •Require one key per user pair •A degree of user authentication. •在较高的网络层次上实现
失去同步
恢复同步
*** ci ci+1 *** ci+n ci+n+1 ***
错误发生
错误解密
自同步序列密码的错误传播
分组密码算法和流密码算法的安全性分析

分组密码算法和流密码算法的安全性分析当今是一个网络时代,人们的生活方式与过去相比发生了很大的变化,足不出户就可以通过网络解决衣食住行中的绝大多数需求,例如,用淘宝网购买所需、用支付宝进行日常支付、用电子银行转账等等。
生活变得快捷而又方便。
然而,事物都有两面性,伴随着生活的便捷而来的是财产安全和个人隐私的保障问题。
这时,密码的使用就是在网络上对我们进行保护的一个关键技术点。
它是类似防火墙似的存在,是一切网络活动的基石。
在网络传输时一般使用的是对称加密算法来进行加密操作,如流密码算法和分组密码算法。
因此,对现有的被广泛重视和使用的分组密码算法和流密码算法的安全性进行研究和分析是非常有必要的。
在本文中,首先,我们针对分组密码算法建立统计积分区分器和多结构体统计积分区分器新模型,并将模型应用于实际算法中;其次,基于MILP方法首次将S盒的差分特征和线性特征考虑进不可能差分路线和零相关路线的自动化搜索中,首次给出ARX算法通用的不可能差分路线和零相关路线的自动化搜索方法,并将该方法应用于实际算法中;最后,在相关密钥场景下利用不可能差分方法给出流密码算法Lizard的安全性分析结果。
具体结果如下。
提出分组密码算法统计积分区分模型,并利用该模型理论破解Skipjack变种算法、给出CAST-256的最优攻击结果和IDEA的最优积分攻击结果:积分攻击是对称密码领域最强大的分析方法之一,被广泛的应用于分组密码算法的安全性分析中。
它是基于概率为1的平衡特性来构建区分器。
攻击者可以通过固定输入的一部分比特而遍历剩下的所有比特的可能取值,观察相应的输出值在某些比特上是否为均匀分布来区分真实算法和随机置换。
为了增加积分区分器的覆盖轮数,攻击者通常会在整个明文空间的限制条件下以特定的结构来遍历更多的明文比特以使得平衡特性依然成立。
然而这一要求限制了积分攻击在很多算法分析中的应用。
在本文中,为降低积分分析中使用的数据复杂度,我们基于超几何分布和多项分布为算法和随机置换构造不同的概率分布来进行区分,从而构建了统计积分这一新模型。
密码学算法

密码学算法密码学是一门应用数学学科,主要研究的是保护信息的技术和方法。
密码学算法是密码学的核心,是密码系统实现的基础。
密码学算法可以分成对称加密算法和非对称加密算法。
对称加密算法对称加密算法是指加密密钥和解密密钥相同的加密算法。
对称加密算法一般分为分组密码和流密码两种。
1. 分组密码分组密码是指把明文分成一定长度的组,然后分组加密的一种方法。
目前广泛使用的分组密码有DES、AES和Blowfish等。
DES是一种密钥长度为56位的标准分组密码算法。
它是一种基于替换和置换的Feistel密码体制。
Feistel密码体制会把明文加密或解密成为两部分,通常称为左半边和右半边。
AES是一种密钥长度为128位的分组密码算法。
它被广泛应用于网络和存储系统中。
AES加密算法采用分组密码结构,分为128、192和256三种密钥长度。
目前256是最安全的长度。
Blowfish是一种由Bruce Schneier开发的对称密钥分组密码算法,它采用的是64位的数据块,这种算法的密钥可以变化的长度,从32位到448位不等。
Blowfish算法安全性在当前的密码学中排名较高。
流密码是一种将明文连续地与密钥流使用异或运算一次一位地加密的加密方式。
流密码算法有RC4、Salsa20和ChaCha20等。
RC4是一种流密码算法,它广泛应用于网络安全和无线电波传输。
RC4是一种密钥长度变化的算法,密钥长度可以是1到256位不等。
非对称加密算法也被称为公钥密码算法,它比对称加密算法更加复杂。
非对称加密算法使用两个密钥,一个称为公钥,另一个称为私钥。
公钥可以自由发布,供任何人使用,而私钥只能保存在其所有者的设备中。
非对称加密算法中,用公钥加密的消息可以用私钥解密,用私钥加密的消息可以用公钥解密。
1. RSA加密算法RSA是一种非对称加密算法,它由Ron Rivest、Adi Shamir和Leonard Adleman三位MIT的数学家于1977年发明,并由RSA公司商业化。
流密码与分组密码
流密码和分组密码按照密钥的特征不同,密码体制分为对称密码体制和非对称密码体制。
按照对明文消息加密方式的不同,密码体制分为流密码(Stream Cipher )和分组密码(Block Cipher )[1]。
非对称密码体制均为分组密码[2]。
1 流密码流密码也称为序列密码。
在流密码中,明文以序列的方式表示,称为明文流。
在对明文流进行加密时,先由种子密钥生成一个密钥流。
然后,利用加密算法把明文流和密钥流加密,产生密文流。
流密码每次只对明文中的单个bit 位进行加密变换,加密过程所需的密钥流由种子密钥通过密钥流生成器产生。
流密码的主要原理是通过随机数发生器产生性能优良的伪随机序列(密钥流),使用该序列加密明文流(逐bit 位加密),得到密文流。
由于每一个明文都对应一个随机的加密密钥,因此流密码在理论上属于无条件安全的密码体制(一次一密密码)[3]。
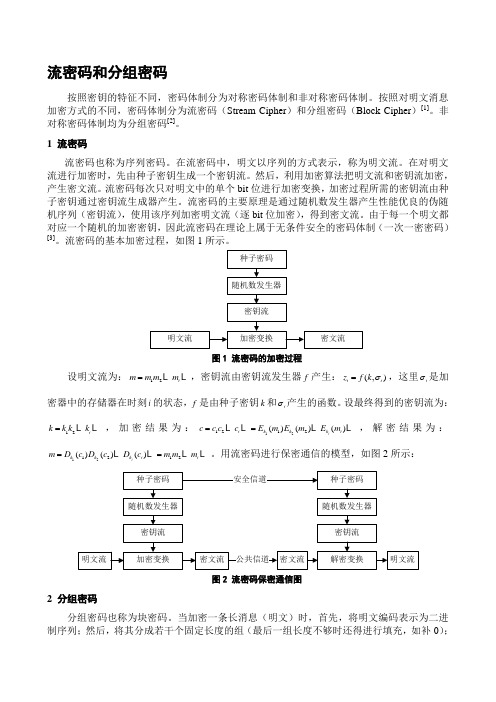
流密码的基本加密过程,如图1所示。
图1 流密码的加密过程设明文流为:12i m m m m = ,密钥流由密钥流发生器f 产生:(,)i i z f k σ=,这里i σ是加密器中的存储器在时刻i 的状态,f 是由种子密钥k 和i σ产生的函数。
设最终得到的密钥流为:12i k k k k = ,加密结果为:121212()()()i i k k k i c c c c E m E m E m == ,解密结果为:121212()()()i k k k i i m D c D c D c m m m == 。
用流密码进行保密通信的模型,如图2所示:图2 流密码保密通信图2 分组密码分组密码也称为块密码。
当加密一条长消息(明文)时,首先,将明文编码表示为二进制序列;然后,将其分成若干个固定长度的组(最后一组长度不够时还得进行填充,如补0);最后,再对逐个分组依次进行加密操作。
分组长短决定着密码的强度。
从算法的安全性考虑,分组长度不能太短,应该保证加密算法能够应付密码分析;从实用性考虑,分组长度又不能太长,要便于操作和运算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4、密钥K:长度为1-256字节,注意密钥的长度keylen与明文长度、钥流的长度没有必然关系,通常密钥的长度趣味16字节(128比特)。
RC4的原理分为三步:
srand((unsigned)time(NULL));
for(int i=0;i<kl;++i){ //随机生产长度为keylen字节的密钥
int tmp=rand()%256;
K.push_back(char(tmp));
}
}
/*
由明文产生密文
*/
void encryption(const string &,const string &,const string &);
j := (j + S[i] + key[i mod keylength]) mod 256
swap values of S[i] and S[j]
endfor
第二步利用上面重新排列的数组S来产生任意长度的密钥流,算法为
i := 0
j := 0
while GeneratingOutput:
i := (i + 1) mod 256
1、初始化S和T
for i=0 to 255 do
S[i] =i;
T[i]=K[ imodkeylen ];
2、初始排列S
for i=0 to 255 do
j= ( j+S[i]+T[i])mod256;
swap(S[i],S[j]);
3、产生密钥流
for r=0 to len do //r为明文长度,r字节
RC4算法的特点是算法简单,运行速度快,而且密钥长度是可变的,可变围为1-256字节(8-2048比特),在如今技术支持的前提下,当密钥长度为128比特时,用暴力法搜索密钥已经不太可行,所以可以预见RC4的密钥围任然可以在今后相当长的时间里抵御暴力搜索密钥的攻击。实际上,如今也没有找到对于128bit密钥长度的RC4加密算法的有效攻击方法。
private:
unsigned char S[256]; //状态向量,共256字节
i=(i+1) mod 256;
j=(j+S[i])mod 256;
swap(S[i],S[j]);
t=(S[i]+S[j])mod 256;
k[r]=S[t];
下面给出RC4加密解密的C++实现:
加密类:
/*
加密类
*/
class RC4 {
public:
/*
构造函数,参数为密钥长度
*/
RC4(int kl):keylen(kl) {
【上机容及要求】
1、分别利用RC4算法(或其它任一种标准流密码算法)和DES算法(或AES算法等其它任一种标准分组密码算法)对数据进行加解密操作
2、代码分析及注释
3、代码调试
4、代码修改及测试(选做)
备注:可借鉴网上相关法的开源代码进行编程实现,编程语言不限。
【上机报告】
1、提交关键功能有注释的源码。
2、提交运行测试结果(运行截图及说明)。
3、运行测试结果分析。
4、上机总结(任务完成情况、出现或待解决的问题、收获、体会等)。
流密码
流密码就是使用较短的一串数字(叫它密钥吧),来生成无限长的伪随码流,当然事实上只需要生成和明文长度一样的密码流就够了。一个非常简单的流密码算法是,用6个比特位101100做密钥,将它不断重复得到密码流0. ...直到和明文长度相等,然后将密码流和明文“相加”就得到密文了,解密就是将这个密码流和密文“相加”。流密码算法有个特殊的名称——维吉尼亚密码,当然这里密钥长度可以不是6。用较短的密钥产生无限长的密码流的方法非常多,其中有一种就叫做RC4。
上机一:流密码与分组密码编程
【上机目的】
熟悉流密码和分组密码加密/解密算法的基本原理,通过编程/开源代码分析分别了解一种标准流密码算法和一种标准分组密码算法的运行原理。
【上机环境】
1、硬件PC机一台。
2、系统配置:操作系统windows XP以上。
3、编程语言:C/C++/C#/Java/Python
在介绍RC4算法原理之前,先看看算法中的几个关键变量:
1、密钥流:RC4算法的关键是根据明文和密钥生成相应的密钥流,密钥流的长度和明文的长度是对应的,也就是说明文的长度是500字节,那么密钥流也是500字节。当然,加密生成的密文也是500字节,因为密文第i字节=明文第i字节^密钥流第i字节;
2、状态向量S:长度为256,S[0],S[1].....S[255]。每个单元都是一个字节,算法运行的任何时候,S都包括0-255的8比特数的排列组合,只不过值的位置发生了变换;
RC4用两步来生成密码流
首先你指定一个短的密码,储存在key[MAX]数组里,还有一个数组S[256],令S[i]=i。然后利用数组key来对数组S做一个置换,也就是对S数组里的数重新排列,排列算法为
for i from 0 to 255
S[i] := i
endfor
j := 0
for i from 0 to 255
j := (j + S[i]) mod 256
swap values of S[i] and S[j]
K := S[(S[i] + S[j]) mod 256]
output K
endwhile
output K一次产生一字符长度(8bit)的密钥流数据,一直循环直到密码流和明文长度一样为止。
产生密钥流之后,对信息进行加密和解密就只是做个“相加”的运算。
把明文的信息限制在ascii码字符集(它已经能表示所有的英文资料了哈哈),每个字符是一个比特,占8位。假设明文是abc,a、b、c的ascii值分别为97、98、99。二进制形式为01100001、01100010、01100011。密钥流和明文长度一样,假设是sdf,同样可以得到二进制流01110011、01100100、01100110,让他们在对应位做异或运算就可以得到密文了,c语言有^运算符来实现“相加”的操作。我们就直接对字符进行“相加”即a^s, b^d, c^f。得到的结果的二进制形式为00010010、00000110、00000101,它们分别表示ascii码值为18、6、5的字符
