一定是直角三角形吗(优质课)获奖课件
合集下载
北师大版八年级数学上册第1章《一定是直角三角形吗》课件
1.2 一定是直角三角形吗
问题1 在一个直角三角形中三条边满足什么样 的关系呢?
直角三角形两直角边的平方和等于斜边的平方
问题2 如果一个三角形中有两边的平方和等于 第三边的平方,那么这个三角形是否就是直角 三角形呢?
下面有三组数分别是一个三角形的三边 长a,b,c:
①5,12,13; ②7,24,25; ③8,15,17.
C
13
C
D
D
5
(a)
4
12 (b)
解:A在△AB BD中,AB2+AD2=9+16A=235=BBD2,
所以△ABD是直角三角形,∠A是直角。
在△BCD中,BD2+BC2=25+144=169=CD2,所以△BCD是
直角三角形,∠DBC是直角。
因此这个零件符合要求。
1.如图,在正方形ABCD中,AB=4,AE=2,DF=1
选择题:
• 三角形的三边分别是a,b,c, 且满足等式
(a+b)2-c2=2ab, 则此三角形是 ( B )
A. ห้องสมุดไป่ตู้角三角形;
B.直角三角形;
C. 钝角三角形;
D. 等腰三角形.
例.一个零件的形状如图(a)所示,按规定这个零件中∠A和
∠DBC都应为直角,工人师傅量得这个零件各边尺寸如图(b)所
示,这个零件合格吗?
C
13
C
D
D
5
(a)
4
12 (b)
解:A在△AB BD中,AB2+AD2=9+16A=235=BBD2,
所以△ABD是直角三角形,∠A是直角。
在△BCD中,BD2+BC2=25+144=169=CD2,所以△BCD是
问题1 在一个直角三角形中三条边满足什么样 的关系呢?
直角三角形两直角边的平方和等于斜边的平方
问题2 如果一个三角形中有两边的平方和等于 第三边的平方,那么这个三角形是否就是直角 三角形呢?
下面有三组数分别是一个三角形的三边 长a,b,c:
①5,12,13; ②7,24,25; ③8,15,17.
C
13
C
D
D
5
(a)
4
12 (b)
解:A在△AB BD中,AB2+AD2=9+16A=235=BBD2,
所以△ABD是直角三角形,∠A是直角。
在△BCD中,BD2+BC2=25+144=169=CD2,所以△BCD是
直角三角形,∠DBC是直角。
因此这个零件符合要求。
1.如图,在正方形ABCD中,AB=4,AE=2,DF=1
选择题:
• 三角形的三边分别是a,b,c, 且满足等式
(a+b)2-c2=2ab, 则此三角形是 ( B )
A. ห้องสมุดไป่ตู้角三角形;
B.直角三角形;
C. 钝角三角形;
D. 等腰三角形.
例.一个零件的形状如图(a)所示,按规定这个零件中∠A和
∠DBC都应为直角,工人师傅量得这个零件各边尺寸如图(b)所
示,这个零件合格吗?
C
13
C
D
D
5
(a)
4
12 (b)
解:A在△AB BD中,AB2+AD2=9+16A=235=BBD2,
所以△ABD是直角三角形,∠A是直角。
在△BCD中,BD2+BC2=25+144=169=CD2,所以△BCD是
初中数学《一定是直角三角形吗》_PPT完整版【北师大版】1

只要看两条较 小边的平方和 是否等于最大
边的平方。
④ ⑥
⑤
初 中 数 学 《 一定是 直角三 角形吗 》教学 分析北 师大版 1-精品 课件pp t(实用 版)
初 中 数 学 《 一定是 直角三 角形吗 》教学 分析北 师大版 1-精品 课件pp t(实用 版)
•例6:在正方形ABCD中,F是CD的中点 ,E为BC上一点,且CE= 1 CB,试判 断AF与EF的位置关系,并说4 明理由.
例2.一个零件的形状如图(a)所示,按规定
这个零件中∠A和∠DBC都应为直角,工人师傅
量得这个零件各边尺寸如图(b)所示,这个
零件合格吗?
C
13
C
D
D
5
4
12
A
B
(a)
A3B (b)
初 中 数 学 《 一定是 直角三 角形吗 》教学 分析北 师大版 1-精品 课件pp t(实用 版)
初 中 数 学 《 一定是 直角三 角形吗 》教学 分析北 师大版 1-精品 课件pp t(实用 版)
角形吗?
B
ac
Cb A
问题情景
•古埃及人曾用下面的方法得到直角:
用13个等距的结,把一根绳子 分成等长的12段,然后以3个结, 4个结,5个结的长度为边长, 用木桩钉成一个三角形,其中 一个角便是直角。
按照这种做法真能得到一个 直角三角形吗?
合作探究
下面有三组数分别是一个三角形的三边长
a,b,c:
初 中 数 学 《 一定是 直角三 角形吗 》教学 分析北 师大版 1-精品 课件pp t(实用 版)
初 中 数 学 《 一定是 直角三 角形吗 》教学 分析北 师大版 1-精品 课件pp t(实用 版)
一定是直角三角形吗 大赛获奖教学课件
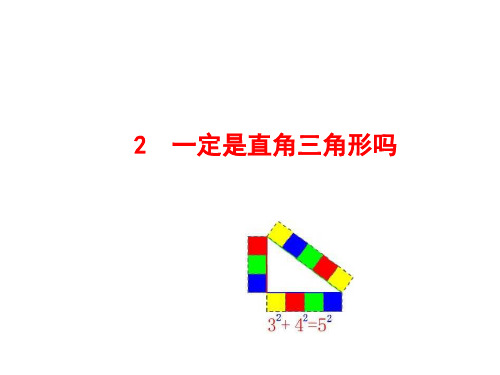
满足a2+b2=c2 的三个正整数,称为勾股数.
古埃及人曾用下面的方法得到直角:
现在明白古埃及人 的这种做法有道理 了吧!
【例题】
【例】一个零件的形状如图1所示,按规定这个零件中∠A 和∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如 图2所示,你说这个零件符合要求吗? D C D 4 A B 图1 A 3 5 12 B 图2
2.(眉山·中考)如图,每个小正方形的边长为1,A, B,C是小正方形的顶点,则∠ABC的度数为( A.90° B.60° C.45° D.30°
A B C
)
【解析】选C.根据勾股定理可知AC2=5, BC2=5,AB2=10,因为AC=BC,
而且AC2+BC2=5+5=10=AB2 ,
所以△ABC是等腰直角三角形且∠ACB=90°, 所以∠ABC=∠BAC=45°.
【跟踪训练】
1.如果线段a,b,c能组成直角三角形,则它们的比可以 是( B )
A.3:4:7
B.5:12:13
C.1:2:4
D.1:3:5
2. 将直角三角形的三边长扩大同样的倍数,则得到的 三角形 ( A )
A.是直角三角形
C.可能是钝角三角形
B.可能是锐角三角形
D.不可能是直角三角形
3.以△ABC的三条边为边长向外作正方形, 积是25, 144 , 169,
2
一定是直角三角形吗
1.经历直角三角形的判别条件(即勾股定理的逆定理)的探究 过程,发展推理论证能力. 2.掌握勾股定理的逆定理及勾股数的定义,并能进行简单的应
用.
古埃及人曾用下面的方法得到直角: 用13个等距的结把一根绳子分成等长的12段,一个工匠 同时握住绳子的第1个结和第13个结,两个助手分别握住第4
一定是直角三角形吗PPT教学课件

在日常生活中经常会碰到这样的情况,你能帮助他们吗?
情境1:农村建房时,常需要在现场画出直角
情境2:在没有测量角的仪器的情况下,工人 怎样检验所生产的零件是直角呢?
情景3:小明想要检测桌面ABCD的ADBC边 是否分别垂直于AB,他该怎么做呢?
2020/12/101 Nhomakorabea八年级数学(上册)• 北师版
1.2一定是直角三角形吗
2020/12/10
按照这种做法真能得到一个直角 三角形吗?
4
探索二
• 任意想出三个数,要求:其中两个数的平方和等 于 • 第动三手个画数:的以平上方题。中你想出来的三个数为边长,画一
个三角形。
• 以上题中的两条较短边长为直角边,画一个直角 三角形。
• 把上述你所画的两个三角形分别剪下来,叠合一起, 你发现了什么?
满足a2+b2=c2的三个 正整数,称为勾股数。
2020/12/10
7
检测:小明想要检测桌面ABCD的CD边、AB 边是否分别垂直于AC,他该怎么做呢?
C
E
D
F
A
B
2020/12/10
8
合
M
作
探 练1、如果给你一把带刻度的直尺, 你能否检验∠MPN是不是直角
P
究 A
练2、如图在△ABD中,∠A是直角,AB=3,AD=4, BC=12,DC=13,△DBC是直角三角形吗? 你能计算四边形的面积吗?
2020/12/10
5
①3、4、5 ②5、12、13
③8、15、17 ④9、40、41
注意:⑴、一组勾股数中各数的相同的整数倍的一 组新数也是勾股数。如:6、8、10; 9、12、15。
⑵、记住常用的勾股数可以提高作题速度。
情境1:农村建房时,常需要在现场画出直角
情境2:在没有测量角的仪器的情况下,工人 怎样检验所生产的零件是直角呢?
情景3:小明想要检测桌面ABCD的ADBC边 是否分别垂直于AB,他该怎么做呢?
2020/12/101 Nhomakorabea八年级数学(上册)• 北师版
1.2一定是直角三角形吗
2020/12/10
按照这种做法真能得到一个直角 三角形吗?
4
探索二
• 任意想出三个数,要求:其中两个数的平方和等 于 • 第动三手个画数:的以平上方题。中你想出来的三个数为边长,画一
个三角形。
• 以上题中的两条较短边长为直角边,画一个直角 三角形。
• 把上述你所画的两个三角形分别剪下来,叠合一起, 你发现了什么?
满足a2+b2=c2的三个 正整数,称为勾股数。
2020/12/10
7
检测:小明想要检测桌面ABCD的CD边、AB 边是否分别垂直于AC,他该怎么做呢?
C
E
D
F
A
B
2020/12/10
8
合
M
作
探 练1、如果给你一把带刻度的直尺, 你能否检验∠MPN是不是直角
P
究 A
练2、如图在△ABD中,∠A是直角,AB=3,AD=4, BC=12,DC=13,△DBC是直角三角形吗? 你能计算四边形的面积吗?
2020/12/10
5
①3、4、5 ②5、12、13
③8、15、17 ④9、40、41
注意:⑴、一组勾股数中各数的相同的整数倍的一 组新数也是勾股数。如:6、8、10; 9、12、15。
⑵、记住常用的勾股数可以提高作题速度。
《一定是直角三角形吗》示范公开课教学课件【北师大数学八年级上册】
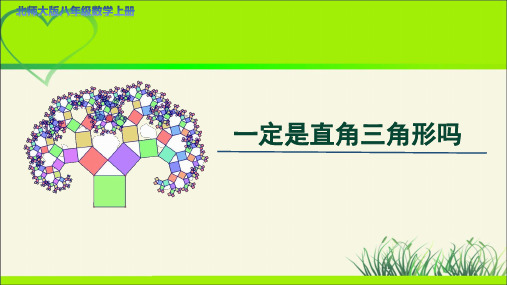
4.如图,四边形ABCD中,AB⊥AD,已知AD=3 cm,AB=4 cm, CD=12 cm,BC=13 cm,求四边形ABCD 的面积.
B
A
D
所以四边形ABCD 的面积为24 cm2.
C
一定是直角三角形吗
勾股定理的逆定理: 如果三角形的三边长a,b , c满足a2+b2=c2,那么这个三角形是直角三角形.
测量结果可能有误差,不同意 这个发现.你觉得这个发现正确吗?你能给 出一个更有说服力的理由吗?
质疑
利用量角器手工测量,结果可能有误差,有没有更有说服力的理由来验证猜想呢?
理由一
以3和4为邻边构造三角形,观察随着夹角的增加第三边的变化趋势.
测量结果可能有误差,不同意 这个发现.你觉得这个发现正确吗?你能给 出一个更有说服力的理由吗?
a
c
b
A
C
B
M
a
C1
△ABC是直角三角形.理由如下:①作一个直角∠MC1N,②在C1N上截取C1A1=b=CA,在C1M上截取C1B1=a=CB,③连接A1B1 .可证△ABC≌△A1B1C1,即可判断△ABC是直角三角形.
△ABC与△A1B1C1为何全等?
证明:在Rt△A1B1C1中, 由勾股定理得 A1B12=a2+b2=c2=AB2 .∴ A1B1=AB,在△ABC和△ A1B1C1中,∵ AB=A1B1=c,BC=B1C1=a, AC= A1C1 =b.∴ △ABC ≌△A1B1C1 . (SSS)∴ ∠C=∠C1=90°,∴ △ABC是直角三角形.
如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
勾股定理的逆定理
特别说明: 勾股定理的逆定理是直角三角形的判定定理,即已知三角形的三边长,且满足两条较小边的平方和等于最长边的平方,即可判断此三角形为直角三角形,最长边所对角为直角.
B
A
D
所以四边形ABCD 的面积为24 cm2.
C
一定是直角三角形吗
勾股定理的逆定理: 如果三角形的三边长a,b , c满足a2+b2=c2,那么这个三角形是直角三角形.
测量结果可能有误差,不同意 这个发现.你觉得这个发现正确吗?你能给 出一个更有说服力的理由吗?
质疑
利用量角器手工测量,结果可能有误差,有没有更有说服力的理由来验证猜想呢?
理由一
以3和4为邻边构造三角形,观察随着夹角的增加第三边的变化趋势.
测量结果可能有误差,不同意 这个发现.你觉得这个发现正确吗?你能给 出一个更有说服力的理由吗?
a
c
b
A
C
B
M
a
C1
△ABC是直角三角形.理由如下:①作一个直角∠MC1N,②在C1N上截取C1A1=b=CA,在C1M上截取C1B1=a=CB,③连接A1B1 .可证△ABC≌△A1B1C1,即可判断△ABC是直角三角形.
△ABC与△A1B1C1为何全等?
证明:在Rt△A1B1C1中, 由勾股定理得 A1B12=a2+b2=c2=AB2 .∴ A1B1=AB,在△ABC和△ A1B1C1中,∵ AB=A1B1=c,BC=B1C1=a, AC= A1C1 =b.∴ △ABC ≌△A1B1C1 . (SSS)∴ ∠C=∠C1=90°,∴ △ABC是直角三角形.
如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
勾股定理的逆定理
特别说明: 勾股定理的逆定理是直角三角形的判定定理,即已知三角形的三边长,且满足两条较小边的平方和等于最长边的平方,即可判断此三角形为直角三角形,最长边所对角为直角.
《一定是直角三角形吗》勾股定理PPT精品课件

是
90
120
60
150
12 13
30
180
0
5
25 24
7
15 17 8
探究新知
下面有三组数分别是一个三角形的三边长a, b, c:
①5,12,13; ②7,24,25;
③8,15,17.
问题2 这三组数在数量关系上有什么相同点? ① 5,12,13满足52+122=132,
② 7,24,25满足72+242=252,
三角形是直角三角形.
A 符号语言:
c
在△ABC中,
b
若a2 + b2 = c2
B a C 则△ABC是直角三角形.
提示:勾股定理的逆定理是直角三角形的判定定理,即已知三角
形的三边长,且满足两条较小边的平方和等于最长边的平方,即
可判断此三角形为直角三角形 ,最长边所对应的角为直角.
探究新知
素养考点 1利用勾股定理的逆定理判断直角三角形 例 下面以a,b,c为边长的三角形是不是直角三角形?如果是, 那么哪一个角是直角?
探究新知 知识点 1
勾股定理的逆定理
据说,古埃及人曾用如图所示的方法画直角.
这种方法对吗?
探究新知
三边分别为3,4,5, 满足关系:32+42=52, 则该三角形是直角三角形.
5 3
4
探究新知 做一做 下列各组数中的两数平方和等于第三数的平方,分 别以这些数为边长画出三角形(单位:cm).
① 5,12,13; ② 7,24,25; ③ 8,15,17. 问题1 用量角器量一量,它们都是直角三角形吗?
课堂小结
勾股定理 的逆定理
内容 作用 注意
如果三角形的三边长a 、b 、c满足
90
120
60
150
12 13
30
180
0
5
25 24
7
15 17 8
探究新知
下面有三组数分别是一个三角形的三边长a, b, c:
①5,12,13; ②7,24,25;
③8,15,17.
问题2 这三组数在数量关系上有什么相同点? ① 5,12,13满足52+122=132,
② 7,24,25满足72+242=252,
三角形是直角三角形.
A 符号语言:
c
在△ABC中,
b
若a2 + b2 = c2
B a C 则△ABC是直角三角形.
提示:勾股定理的逆定理是直角三角形的判定定理,即已知三角
形的三边长,且满足两条较小边的平方和等于最长边的平方,即
可判断此三角形为直角三角形 ,最长边所对应的角为直角.
探究新知
素养考点 1利用勾股定理的逆定理判断直角三角形 例 下面以a,b,c为边长的三角形是不是直角三角形?如果是, 那么哪一个角是直角?
探究新知 知识点 1
勾股定理的逆定理
据说,古埃及人曾用如图所示的方法画直角.
这种方法对吗?
探究新知
三边分别为3,4,5, 满足关系:32+42=52, 则该三角形是直角三角形.
5 3
4
探究新知 做一做 下列各组数中的两数平方和等于第三数的平方,分 别以这些数为边长画出三角形(单位:cm).
① 5,12,13; ② 7,24,25; ③ 8,15,17. 问题1 用量角器量一量,它们都是直角三角形吗?
课堂小结
勾股定理 的逆定理
内容 作用 注意
如果三角形的三边长a 、b 、c满足
一定是直角三角形吗ppt课件

和 c2 的值;③判断 a2+b2 和c2 是否相等,若相等,则是
直角三角形;若不相等,则不是直角三角形.
(2)判定一个三角形是直角三角形的方法:①有一个内
角为直角的三角形是直角三角形; ②两个内角互余的三角
形是直角三角形;③如果三角形的三边长 a,b,c 满足
a2+b2=c2, 那么这个三角形是直角三角形.
(1)确定是三个正整数;
(2)确定最大数 c;
(3)计算较小两数的平方和 a2+b2 是否等于 c2
1.2 一定是直角三角形吗
返回目录
续表
考
点
清
单
解
读
(1)记住常见的勾股数可以提高解题速度,如 3,
4,5;6,8,10;5,12,13;7,24,25;8,15,
17;9,40,41 等;
注意
(2)若三角形的三边长恰为一组勾股数,则这个
考
点
清
单
解
读
返回目录
[解题思路]
因为∠C=∠A-∠B,所以∠C+∠B=∠A,
A
因为∠C+∠A+∠B=180°,所以 2 ∠ A
不符
=180°,所以∠A=90°,所以 △ABC
合题意
是直角三角形
因为∠A∶∠B∶∠C=3∶4∶5,∠C+∠A
+ ∠B =180°,所以
B
∠C=180°×
=75°,所以△ABC
+b2=c2,所以△ABC 是直角三角形
返回目录
1.2 一定是直角三角形吗
返回目录
考 2. 勾股定理的逆定理
点
勾股定理的逆定理是判定一个三角形是不是直
直角三角形;若不相等,则不是直角三角形.
(2)判定一个三角形是直角三角形的方法:①有一个内
角为直角的三角形是直角三角形; ②两个内角互余的三角
形是直角三角形;③如果三角形的三边长 a,b,c 满足
a2+b2=c2, 那么这个三角形是直角三角形.
(1)确定是三个正整数;
(2)确定最大数 c;
(3)计算较小两数的平方和 a2+b2 是否等于 c2
1.2 一定是直角三角形吗
返回目录
续表
考
点
清
单
解
读
(1)记住常见的勾股数可以提高解题速度,如 3,
4,5;6,8,10;5,12,13;7,24,25;8,15,
17;9,40,41 等;
注意
(2)若三角形的三边长恰为一组勾股数,则这个
考
点
清
单
解
读
返回目录
[解题思路]
因为∠C=∠A-∠B,所以∠C+∠B=∠A,
A
因为∠C+∠A+∠B=180°,所以 2 ∠ A
不符
=180°,所以∠A=90°,所以 △ABC
合题意
是直角三角形
因为∠A∶∠B∶∠C=3∶4∶5,∠C+∠A
+ ∠B =180°,所以
B
∠C=180°×
=75°,所以△ABC
+b2=c2,所以△ABC 是直角三角形
返回目录
1.2 一定是直角三角形吗
返回目录
考 2. 勾股定理的逆定理
点
勾股定理的逆定理是判定一个三角形是不是直
新北师大版八年级数学上册《一定是直角三角形吗》优质课课件

北师大课标八年级 上册
同学们你们知道古埃及人用什么方法得到直角?
古埃及人曾用下面的方法得到直角: 用13个等距的结,把一根绳子分成等长的12 段,一个工匠同时握住绳子的第1个结和第13个 结,两个助手分别握住第4个结和第8个结,拉紧绳 子就得到一个直角三角形, 其直角在第4个结处.
北师大课标八年级 上册
北师大课标八年级 上册
练习
6. 四边形ABCD中已知AB=3, BC=4, CD=12, DA=13, 且∠ABC=900,求这个 四边形的面积.
A
D
B
C
7.请你写出三组勾股数;
8.一组勾股数的倍数一定是勾股数吗?为什么?
北师大课标八年级 上册
课堂小结
直角三角判别条件:
如果三角形的三边长a,b,c满足
北师大课标八年级 上册
合作讨论
例1 一个零件的形状如左图所示,按规定这 个零件中∠A和∠DBC都应为直角.工人师傅量得 这个零件各边尺寸如右图所示,这个 零件符合要 求吗? C
zxxkw
C
D
13 D 4 5
12
A
B
A 3 B
北师大课标八年级 上册
当堂检测
1. 如果线段a, b, c能组成直角三角形, 则它们的 比可能是 ( B) A. 3:4:7; B. 5:12:13; C. 1:2:4; D. 1:3:5.
a2 +b2=c2,
那么这个三角形是直角三角形
勾股数: 满足a2 +b2=c2的三个正整数,称为勾股数
A. 直角三角形;
B. 是锐角三角形;
C. 是钝角三角形; D. 是等腰直角三角形. 4. 已知∆ABC中BC=41, AC=40, AB=9, 则此三 直角 三角形, ______ ∠A 是最大角. 角形为_______ 5. 以∆ABC的三条边为边长向外作正方形, 依次 得到的面积是25, 144 , 169, 则这个三角形是 直角 三角形. ______
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1,这样的方程叫做一元一次方程.
如: 2x+3=5, y+6=8. 3.解下列方程:
(1)3x+2=14 (2)2x-4=14-x
累死我了!
你还累?这么大的 个,才比我多驮 了2个.
哼,我从你背上拿来 1个,我的包裹数就 是你的2倍!
真的?!
我从你背上拿来 1个,我的包裹数 就是你的 2 倍!
–2
【解析】A(0,2 3 ) B(-2,0)
–3
C(2,0)
–4
3.在一次“寻宝”游戏中,寻宝人已经找到了坐标为(3,2) 和(3,-2)的两个标志点,并且知道藏宝地点的坐标为(4, 4),如何确定直角坐标系找到“宝藏”?
y
5
4
·(4,4)
3
2
·(3,2)
1
· -4
-3
-2
-1
O
-1
12345
x
【例题】
【例2】如图是某市旅游景点的示意图. (1)“大成殿”在“中心广场”的 西、南各多少格?碑林在“中心广 场”的东、北各多少格?
【解析】(1) “大成殿”在 “中心广场”的西、南各2格, 碑林在“中心广场”的东3格, 北1格.
(2)如果中心广场处定为(0,0)一个小格的边长为1,
你能表示“碑林”的位置吗? y
y 【解析】形状为
等腰直角三角形,
直角边的长为
6
面积(4为 1)2 4 2 41
2
-6
-2
o
-1
2
1 41 41 41 20.5
2
2
6x
【跟踪训练】
在下图的直角坐标系中描出下列各点,并把各点用线段依次
连接起来,观察它的形状并计算其面积.
(2,2)(5,6)
(-4,6)(-7,2)
满足a2+b2=c2 的三个正整数,称为勾股数.
古埃及人曾用下面的方法得到直角:
现在明白古埃及人 的这种做法有道理 了吧!
【例题】
【例】一个零件的形状如图1所示,按规定这个零件中∠A 和∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如 图2所示,你说这个零件符合要求吗?
D
A
B
图1
CD
13
C
5 4
上面所列方程各含有几个未知数? 答:2个未知数 含有未知数的项的次数是多少? 答:次数是1
含有两个未知数,并且所含未知数的项的次数都是1 的方程叫做二元一次方程.
【跟踪训练】
下列方程中哪些是二元一次方程
(1) x+y+z=9
(2) x=6
(3) 2x+6y=14 √
(4) xy+y=7
(5) 7x+6y+4=16 √
A.90° B.60° C.45° D.30°
【解析】选C.根据勾股定理可知AC2=5,
A
BC2=5,AB2=10,因为AC=BC,
B
而且AC2+BC2=5+5=10=AB2 , 所以△ABC是等腰直角三角形且∠ACB=90°, C
所以∠ABC=∠BAC=45°.
3.如图,在四边形ABCD中,AC⊥DC,△ADC的面积为30 cm2, DC=12 cm,AB=3 cm,BC=4 cm,求△ABC的面积.
-2
·(3,-2)
-3
-4
通过本课时的学习,需要我们掌握: 建立适当的直角坐标系,描述物体的位置:关键是选好原点.
智慧的可靠标志就是能够在平凡中发现奇迹. ——爱默生
第五章 二元一次方程组
1 认识二元一次方程组
1.了解二元一次方程、二元一次方程组及其解等有关概 念,并会判断一组数是不是某个二元一次方程组的解.
【跟踪训练】
1.如果线段a,b,c能组成直角三角形,则它们的比可以 是( B ) A.3:4:7 B.5:12:13 C.1:2:4 D.1:3:5
2. 将直角三角形的三边长扩大同样的倍数,则得到的
三角形 ( A )
A.是直角三角形
B.可能是锐角三角形
C.可能是钝角三角形
D.不可能是直角三角形
3.以△ABC的三条边为边长向外作正方形, 依次得到的面 积是25, 144 , 169, 则这个三角形是_直__角___三角形.
每张成人票 5 元, 每张儿童票 3 元, 他们到底去了几个成 人,几个儿童呢?
设他们中有 x 个成人,y个儿童. 你能得到怎样的方程?
【解析】 8 个人去看电影 x+y=8 每张成人票 5 元 每张儿童票 3 元 买票花了 34 元 5x+3y=34
定义:
x-y=2 x+1=2(y-1)
x+y=8 5x+3y=34
xy-x=4
(1)
x+y =5
x-y =2
(2)
√
x+1 =2(y-1)
x +y + z =9
(3)
3x-2y =6
(1)x=6 , y=2适合方程x+y=8吗 ? x=5 , y=3呢? x=4, y=4呢?
你还能找到其他x , y的值适合方程x+y=8吗 ?
(2) x=5 , y=3适合方程5x+3y=34吗? x=2 , y=8呢?
y
【解析】如图,是 平行四边形,它的 面积为(7+2)× (6-2)=36
6
2
-6
-2 -1 o 2
6x
【跟踪训练】
在下图的直角坐标系中描出下列各组点,并将各组内的 线段依次连接起来.
1.(2,0), (4,0), (6,2), (6,6), (5,8), (4,6), (2,6), (1,8), (0,6), (0,2), (2,0);
{ 例如
x=5 就是二元一次方程组 y=3
{ x+y=8
的解
5x+3y=34
【例题】
【例】检验下列各对数是不是方程组
x 4y 6, ① 3x 2y 11 ②
的解.
(1)
x y
2, 1.
(2)
x
y
3, 1.
(3)
x y
4, 1. 2
1 AB BC 2
1 2
3 4
6(cm2 ).
通过本课时的学习,需要我们掌握: 1.勾股定理的逆定理: 如果三角形两边的平方和等于第三边的平方, 那么这个三角形是直角三角形. 2.勾股数: 满足a2+b2=c2的三个正整数,称为勾股数.
努力不一定成功;但是放弃必定会失败.
2 平面直角坐标系
下面的三组数分别是一个三角形的三边长a ,b, c: ①5, 12, 13; ②7, 24, 25; ③8, 15, 17.
(1)这三组数都满足a2+b2=c2吗? 都满足. (2)分别以每组数为三边作出三角形, 用量角器量一量. 它们都是直角三角形吗? 都是直角三角形.
勾股定理的逆定理:如果三角形的三边长a,b,c 满足a2+b2=c2,那么这个三角形是直角三角形.
2 一定是直角三角形吗
1.经历直角三角形的判别条件(即勾股定理的逆定理)的探究 过程,发展推理论证能力. 2.掌握勾股定理的逆定理及勾股数的定义,并能进行简单的应 用.
古埃及人曾用下面的方法得到直角: 用13个等距的结把一根绳子分成等长的12段,一个工匠
同时握住绳子的第1个结和第13个结,两个助手分别握住第4 个结和第8个结,拉紧绳子就得到一个直角三角形, 其直角 在第4个结处.
y
A
2
D
x
-3
Байду номын сангаас
0
3
B
-2
C
【解析】以长方形的中心为坐标原点,平行于BC、BA的直 线为x轴、y轴,建立直角坐标系.坐标分别为A(-3,2), B(-3,-2),C(3,-2),D(3,2)
1. (南通·中考)在平面直角坐标系xOy中,已知点P (2,2),点Q在y轴上,△PQO是等腰三角形,则满足条 件的点Q共有( ) A.5个 B.4个 C.3个 D.2个
C D
B 【解析】因为△ADC的面积为30 cm2,DAC=12 cm.
1
1
SACD 2 CD AC 2 12 AC 30,
所以AC=5 cm,
又因为 AB2 BC 2 32 4 2 52 AC 2 ,
所以△ABC是直角三角形, ∠B是直角.
所以
SABC
【解析】选B.如图所示,当以OP为腰时, 分别以O、P为圆心OP为半径画弧,与y轴 有三个交点Q2,Q4,Q3,当以OP为底时, OP的垂直平分线与y轴有一个交点Q1.
2.对于边长为4的正三角形△ABC,建立适当的直角坐标系,写出
各个顶点的坐标
y A
3
2
1
B
–4 –3 –2 –1 O –1
C 1 2 3 4x
你还累?这么大 的个,才比我 多驮了2个.
它们各驮了多少包裹呢?
【解析】设老牛驮了 x 个包裹 , 小马驮了 y个包裹. 老牛的包裹数比小马的多2个, 由此你能得到怎样的方程呢?
x-y=2 若老牛从小马的背上拿来1个包裹,这时它们各有几个包裹? 由此你又能得到怎样的方程呢?
x+1=2(y-1)
昨天,我们8个人 去看电影买电影票 花了34元
12 A3 B
图2
【解析】在△ABD中,
AB2 AD2 32 42 25 52 BD2,
所以△ABD 是直角三角形,∠A是直角.
在△BCD中,
BD2 BC2 52 122 169 132 CD2,
所以△BCD 是直角三角形,∠DBC是直角. 因此,这个零件符合要求.
如: 2x+3=5, y+6=8. 3.解下列方程:
(1)3x+2=14 (2)2x-4=14-x
累死我了!
你还累?这么大的 个,才比我多驮 了2个.
哼,我从你背上拿来 1个,我的包裹数就 是你的2倍!
真的?!
我从你背上拿来 1个,我的包裹数 就是你的 2 倍!
–2
【解析】A(0,2 3 ) B(-2,0)
–3
C(2,0)
–4
3.在一次“寻宝”游戏中,寻宝人已经找到了坐标为(3,2) 和(3,-2)的两个标志点,并且知道藏宝地点的坐标为(4, 4),如何确定直角坐标系找到“宝藏”?
y
5
4
·(4,4)
3
2
·(3,2)
1
· -4
-3
-2
-1
O
-1
12345
x
【例题】
【例2】如图是某市旅游景点的示意图. (1)“大成殿”在“中心广场”的 西、南各多少格?碑林在“中心广 场”的东、北各多少格?
【解析】(1) “大成殿”在 “中心广场”的西、南各2格, 碑林在“中心广场”的东3格, 北1格.
(2)如果中心广场处定为(0,0)一个小格的边长为1,
你能表示“碑林”的位置吗? y
y 【解析】形状为
等腰直角三角形,
直角边的长为
6
面积(4为 1)2 4 2 41
2
-6
-2
o
-1
2
1 41 41 41 20.5
2
2
6x
【跟踪训练】
在下图的直角坐标系中描出下列各点,并把各点用线段依次
连接起来,观察它的形状并计算其面积.
(2,2)(5,6)
(-4,6)(-7,2)
满足a2+b2=c2 的三个正整数,称为勾股数.
古埃及人曾用下面的方法得到直角:
现在明白古埃及人 的这种做法有道理 了吧!
【例题】
【例】一个零件的形状如图1所示,按规定这个零件中∠A 和∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如 图2所示,你说这个零件符合要求吗?
D
A
B
图1
CD
13
C
5 4
上面所列方程各含有几个未知数? 答:2个未知数 含有未知数的项的次数是多少? 答:次数是1
含有两个未知数,并且所含未知数的项的次数都是1 的方程叫做二元一次方程.
【跟踪训练】
下列方程中哪些是二元一次方程
(1) x+y+z=9
(2) x=6
(3) 2x+6y=14 √
(4) xy+y=7
(5) 7x+6y+4=16 √
A.90° B.60° C.45° D.30°
【解析】选C.根据勾股定理可知AC2=5,
A
BC2=5,AB2=10,因为AC=BC,
B
而且AC2+BC2=5+5=10=AB2 , 所以△ABC是等腰直角三角形且∠ACB=90°, C
所以∠ABC=∠BAC=45°.
3.如图,在四边形ABCD中,AC⊥DC,△ADC的面积为30 cm2, DC=12 cm,AB=3 cm,BC=4 cm,求△ABC的面积.
-2
·(3,-2)
-3
-4
通过本课时的学习,需要我们掌握: 建立适当的直角坐标系,描述物体的位置:关键是选好原点.
智慧的可靠标志就是能够在平凡中发现奇迹. ——爱默生
第五章 二元一次方程组
1 认识二元一次方程组
1.了解二元一次方程、二元一次方程组及其解等有关概 念,并会判断一组数是不是某个二元一次方程组的解.
【跟踪训练】
1.如果线段a,b,c能组成直角三角形,则它们的比可以 是( B ) A.3:4:7 B.5:12:13 C.1:2:4 D.1:3:5
2. 将直角三角形的三边长扩大同样的倍数,则得到的
三角形 ( A )
A.是直角三角形
B.可能是锐角三角形
C.可能是钝角三角形
D.不可能是直角三角形
3.以△ABC的三条边为边长向外作正方形, 依次得到的面 积是25, 144 , 169, 则这个三角形是_直__角___三角形.
每张成人票 5 元, 每张儿童票 3 元, 他们到底去了几个成 人,几个儿童呢?
设他们中有 x 个成人,y个儿童. 你能得到怎样的方程?
【解析】 8 个人去看电影 x+y=8 每张成人票 5 元 每张儿童票 3 元 买票花了 34 元 5x+3y=34
定义:
x-y=2 x+1=2(y-1)
x+y=8 5x+3y=34
xy-x=4
(1)
x+y =5
x-y =2
(2)
√
x+1 =2(y-1)
x +y + z =9
(3)
3x-2y =6
(1)x=6 , y=2适合方程x+y=8吗 ? x=5 , y=3呢? x=4, y=4呢?
你还能找到其他x , y的值适合方程x+y=8吗 ?
(2) x=5 , y=3适合方程5x+3y=34吗? x=2 , y=8呢?
y
【解析】如图,是 平行四边形,它的 面积为(7+2)× (6-2)=36
6
2
-6
-2 -1 o 2
6x
【跟踪训练】
在下图的直角坐标系中描出下列各组点,并将各组内的 线段依次连接起来.
1.(2,0), (4,0), (6,2), (6,6), (5,8), (4,6), (2,6), (1,8), (0,6), (0,2), (2,0);
{ 例如
x=5 就是二元一次方程组 y=3
{ x+y=8
的解
5x+3y=34
【例题】
【例】检验下列各对数是不是方程组
x 4y 6, ① 3x 2y 11 ②
的解.
(1)
x y
2, 1.
(2)
x
y
3, 1.
(3)
x y
4, 1. 2
1 AB BC 2
1 2
3 4
6(cm2 ).
通过本课时的学习,需要我们掌握: 1.勾股定理的逆定理: 如果三角形两边的平方和等于第三边的平方, 那么这个三角形是直角三角形. 2.勾股数: 满足a2+b2=c2的三个正整数,称为勾股数.
努力不一定成功;但是放弃必定会失败.
2 平面直角坐标系
下面的三组数分别是一个三角形的三边长a ,b, c: ①5, 12, 13; ②7, 24, 25; ③8, 15, 17.
(1)这三组数都满足a2+b2=c2吗? 都满足. (2)分别以每组数为三边作出三角形, 用量角器量一量. 它们都是直角三角形吗? 都是直角三角形.
勾股定理的逆定理:如果三角形的三边长a,b,c 满足a2+b2=c2,那么这个三角形是直角三角形.
2 一定是直角三角形吗
1.经历直角三角形的判别条件(即勾股定理的逆定理)的探究 过程,发展推理论证能力. 2.掌握勾股定理的逆定理及勾股数的定义,并能进行简单的应 用.
古埃及人曾用下面的方法得到直角: 用13个等距的结把一根绳子分成等长的12段,一个工匠
同时握住绳子的第1个结和第13个结,两个助手分别握住第4 个结和第8个结,拉紧绳子就得到一个直角三角形, 其直角 在第4个结处.
y
A
2
D
x
-3
Байду номын сангаас
0
3
B
-2
C
【解析】以长方形的中心为坐标原点,平行于BC、BA的直 线为x轴、y轴,建立直角坐标系.坐标分别为A(-3,2), B(-3,-2),C(3,-2),D(3,2)
1. (南通·中考)在平面直角坐标系xOy中,已知点P (2,2),点Q在y轴上,△PQO是等腰三角形,则满足条 件的点Q共有( ) A.5个 B.4个 C.3个 D.2个
C D
B 【解析】因为△ADC的面积为30 cm2,DAC=12 cm.
1
1
SACD 2 CD AC 2 12 AC 30,
所以AC=5 cm,
又因为 AB2 BC 2 32 4 2 52 AC 2 ,
所以△ABC是直角三角形, ∠B是直角.
所以
SABC
【解析】选B.如图所示,当以OP为腰时, 分别以O、P为圆心OP为半径画弧,与y轴 有三个交点Q2,Q4,Q3,当以OP为底时, OP的垂直平分线与y轴有一个交点Q1.
2.对于边长为4的正三角形△ABC,建立适当的直角坐标系,写出
各个顶点的坐标
y A
3
2
1
B
–4 –3 –2 –1 O –1
C 1 2 3 4x
你还累?这么大 的个,才比我 多驮了2个.
它们各驮了多少包裹呢?
【解析】设老牛驮了 x 个包裹 , 小马驮了 y个包裹. 老牛的包裹数比小马的多2个, 由此你能得到怎样的方程呢?
x-y=2 若老牛从小马的背上拿来1个包裹,这时它们各有几个包裹? 由此你又能得到怎样的方程呢?
x+1=2(y-1)
昨天,我们8个人 去看电影买电影票 花了34元
12 A3 B
图2
【解析】在△ABD中,
AB2 AD2 32 42 25 52 BD2,
所以△ABD 是直角三角形,∠A是直角.
在△BCD中,
BD2 BC2 52 122 169 132 CD2,
所以△BCD 是直角三角形,∠DBC是直角. 因此,这个零件符合要求.
