偏心受压构件计算长度的计算公规院
偏心受压构件验算+受弯裂缝宽度验算JTG3362-2018

计算结果部分
40004200985095000.80.790.03720.426
1.0000
54.0
200000501.01.4760.750
准永久组合计算轴向力值 N l =
裂缝宽度计算 (JTG3362-2018 第6.4条)
构件截面半径 r=频遇组合计算的轴向力值 Ns=钢筋弹性模量 Es=
使用阶段轴向力偏心距增大系数准永久组合计算弯矩值 Ml=纵向钢筋所在圆周半径 rs =钢筋应力
偏心距 e0=Ms/Ns=
与构件受力性质有关的系数 C3=
频遇组合计算弯矩值 Ms=钢筋表面形状系数 C1=
作用长期效应影响系数 =
纵向受拉钢筋有效配筋率最外侧受拉钢筋保护层厚度 c=210.5l s
M C M =+=/te s te A A ρ=
2
00
11240002s
s
l e
r r a η⎛⎫=+
= ⎪⎝⎭
-3
020
0.60.10.450.260.2s s ss s s s e N r A r e r r ηση⎛⎫- ⎪
⎝⎭==⎛⎫⎛⎫++ ⎪
⎪⎝⎭⎝⎭
28
0.055
Ⅳ类0.15
最大裂缝宽度
最大裂缝宽度限值 :
钢筋混凝土构件所在的环境类别 :
纵向钢筋直径 d=
123
0.36 1.7ss cr s te c d W C C C E σρ⎛⎫+== ⎪+⎝⎭
数
据
输
入
部
分
下表格中的蓝色数据。
黄色格未被
引用
e0/r0.532995。
偏心受压构件计算

说明:1、本表根据《桥梁混凝土结构设计原理计算示例》(2006)编写。
2、本表用于已知截面、配筋及设计轴力求极限弯矩。
3、本表仅用配普通通钢时矩形截面偏心受压计算。
4、计算时,点击“开始计算”按钮,该按钮用于逼近法求偏心矩增大系数。
5、中间结果右侧的黄色区域可以强制修改对应值,以用于特殊计算或与其它程序对比计算,正常计算时注意对该区域(Q列)清空。
6、当混凝土强度等级高于C50或钢筋为不为HRB335时,请注意修界限受压区高度值,见桥规P25,表5.2.1。
7、本计算假定箍筋足够,不发生剪切破坏。
8、设计轴力(J5)在裂缝计算和承载力计算注意区分。
无条件输入翼板有效宽度bf'(m): 1.3翼板厚度hf'(m):0.1腹板宽b(m):0.225梁高h(m):0.5第一层受拉钢筋直径(mm):22第一层受拉钢筋根数:5第一层受拉钢筋到结构受拉边缘的距离a s1(m):0.07混凝土强度等级C:30第一层受压钢筋直径(mm):28第一层受压钢筋根数:0第一层受压钢筋到结构受压边缘的距离a s1'(m):0.05设计弯矩Md(kN):150#REF!#REF!2006)编写。
钮用于逼近法求偏心矩增大系数。
对应值,以用于特殊计算或与其它程序对比计算,为HRB335时,请注意修界限受压区高度值,见桥规P25,表5.2.1。
第一排受拉钢筋面积(m2):0.0019005第二排受拉钢筋面积(m2):0第三排受拉钢筋面积(m2):0总受拉钢筋面积(m2):0.0019005受拉钢筋到结构受拉边缘的距离as(m):0.07第一排受压钢筋面积(m2):0第二排受压钢筋面积(m2):0第三排受压钢筋面积(m2):0总受压钢筋面积(m2):0受压钢筋到结构受拉边缘的距离as'(m):#REF!混凝土抗压设计强度fcd(MPa):#REF!混凝土相对受压高度x(m):#REF!有效高度h0(m):#REF!M du3(kN):#REF!。
钢筋混凝土受压构件和受拉构件—偏心受压柱计算
① 当同一主轴方向的杆端弯矩比: M1 0.9
M2
② 轴压比:
N 0.9
fc A
③ 构件的长细比满足要求: l0 34 12( M1 )
i
M2
M1、M2:分别为已考虑侧移影响的偏心受压构件两端截面按结构弹性
分析确定的对同一主轴的组合弯矩设计值,绝对值较大端为M2,绝对值较小 端为 M1;当构件按单曲率弯曲时, M1/M2取正值,否则取负值。
α1fc
α1fcbx x=ξh0
f 'yA's A's
b
h0用平面的受压承载力计算
可能垂直弯矩作用平面先破坏,按非偏心方向的轴心受 压承载力计算
N Nu 0.9 ( fc A f yAs )
2.对称配筋矩形截面小偏压构件的截面设计
对称配筋,即As=As',fy = fy',as = as ' 截面设计:已知:截面尺寸、内力设计值M及N、材料强度等级、构件计算长度,
Ne f y As (h0 as ')
e
ei
h 2
as
e ei
N e’
fyAs As
α1fcbx x
α1fc
f 'yA's A's
b
as
h0
a's
h
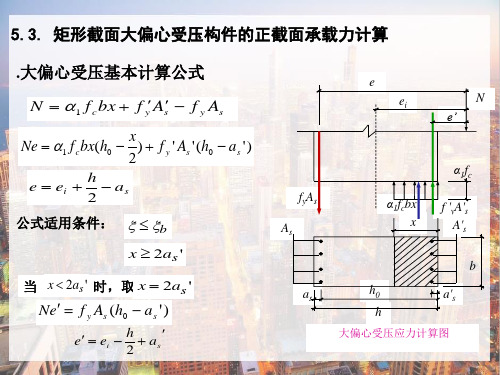
大偏心受压应力计算图
2.对称配筋矩形截面大偏压构件的截面设计
对称配筋,即As=As',fy = fy',as = as ' 截面设计:已知:截面尺寸、内力设计值M及N、材料强度等级、构件计算长度,
5.3. 矩形截面大偏心受压构件的正截面承载力计算
.大偏心受压基本计算公式
N 1 f cbx f y As f y As
《公预规》提供的附录C表C.0.2“圆形截面钢筋混凝土偏压构件正截面抗压承载力计算系数”表

C.O.2沿用边均匀配筋的圆形截面钢筋混凝土偏心受压构件,其正截面抗压承载力可用查表法(表C.0.2)并按下列规定计算求得:1当对构件承载力进行复核验算时1)由本规范公式(5.3.9-1)和(5.3.9-2)解得轴向力的偏心距:'0'g cd sd cd sd Bf D f e r Af C f ρρ+=+(C.0.2-1)2)已知cd f 、'sd f 、ρ、r ,设定ξ值,查表C.0.2,将查得的系数A、B、C、D值代入公式(C.0.2-1)计算0e 值。
若此0e 值与实际计算偏心距/d d M N η相符(允许偏差在2%以内),则设定的ξ值为所求者;若不相符,重新设定ξ值,重复上述计算,直到相符为止;3)将最后确定的ξ相应的A、B、C、D值代入规范公式(5.3.9-1)或(5.3.9-2)进行构件正截面承载力的复核验算。
2当对构件进行配筋设计时1)由公式(C.0.2-1)变换得截面配筋率:0'cd sd o f Br Ae f Ce Dgr ρ−=•−(C.0.2-2)2)已知cd f 、'sd f 、0e 、r ,设定ξ值,查表C.0.2,将查得的系数A、B、C、D值代入公式( C.0.2-2)计算ρ值,计算时式中的0e 应乘以偏心距增大系数η;再再把ρ和A、C值直代入规范公式(5.3.9-1)算得轴向力值。
若此轴向力值与实际作用的轴向力设计值相符(允许偏差在2%以内),则该ξ值及依此计算的ρ值为所求者;若不相符,重新设定ξ值,重复上述计算,直至相符为止。
3)以最后确定的ρ值代入下列公式计算纵向钢筋截面面积:2s A r ρπ=(C.0.2-3)所得钢筋配筋率应符合最小配筋率的要求。
表C.O.2圆形截面钢筋混凝土偏压构件正截面抗压承载力计算系数ξA B C D ξA B C DξA B C D0.200.32440.2628-1.52961.4216 0.210.34810.2787-1.46761.4623 0.220.37230.2945-1.40741.5004 0.230.39690.3103-1.34861.5361 0.240.42190.3259-1.29111.5697 0.250.44730.3413-1.23481.6012 0.260.47310.3566-1.17961.6307 0.270.49920.3717-1.12541.6584 0.280.52580.3865-1.07201.6843 0.290.55260.4011-1.01941.7086 0.300.57980.4155-0.96751.7313 0.310.60730.4295-0.91631.7524 0.320.63510.4433-0.86561.7721 0.330.66310.4568-0.81541.7903 0.340.69150.4699-0.76571.8071 0.350.72010.4828-0.71651.8225 0.360.74890.4952-0.66761.8366 0.370.77800.5073-0.61901.8494 0.380.80740.5191-0.57071.8609 0.390.83690.5304-0.52271.8711 0.400.86670.5414-0.47491.8801 0.410.89660.5519-0.42731.8878 0.420.92680.5620-0.379818943 0.430.95710.5717-0.33231.8996 0.440.98760.5810-0.28501.9036 0.451.01820.5898-0.23771.9065 0.461.04900.5982-0.19031.9081 0.471.07990.6061-0.14291.9084 0.481.11100.6136-0.09541.9075 0.491.14220.6206-0.04781.9053 0.501.17350.6271-0.00001.9018 0.51 1.20490.63310.0480 1.8971 0.52 1.23640.63860.0963 1.8909 0.53 1.26800.64370.1450 1.8834 0.54 1.29960.64830.1941 1.8744 0.55 1.33140.65230.2436 1.8639 0.56 1.36320.65590.2937 1.8519 0.57 1.39500.65890.3444 1.8381 0.58 1.42690.66150.3960 1.8226 0.59 1.45890.66350.44851,8052 0.60 1.49080.66510.5021 1.78560.64 1.61880.66610.7373 1.67630.65 1.65080.66510.8080 1.63430.66 1.68270.66350.8766 1.59330.67 1.71470.66150.9430 1.55340.68 1.74660.6589 1.0071 1.51460.691.77840.6559 1.06921.47690.70 1.81020.6523 1.1294 1.44020.71 1.84200.6483 1.1876 1.40450.72 1.87360.6437 1.2440 1.36970.73 1.90520.6386 1.2987 1.33580.74 1.93670.6331 1.3517 1.30280.75 1.96810.6271 1.4030 1.27060.76 1.99940.6206 1.4529 1.23920.77 2.03060.6136 1.5013 1.20860.78 2.06170.6061 1.5482 1.17870.79 2.09260.5982 1.5938 1.14960.80 2.12340.5898 1.6381 1.12120.81 2.15400.5810 1.6811 1.09340.82 2.18450.5717 1.7228 1.06630.83 2.21480.5620 1.7635 1.03980.84 2.24500.5519 1.8029 1.01390.85 2.27490.5414 1.84130.98860.86 2.30470.5304 1.87860.96390.87 2.33420.5191 1.91490.93970.88 2.36360.5073 1.95030.91610.89 2.39270.4952 1.98460.89300.90 2.42150.4828 2.01810.87040.91 2.45010.4699 2.05070.84830.92 2.47850.4568 2.08240.82660.93 2.50650.4433 2.11320.80550.94 2.53430.4295 2.14330.78470.95 2.56180.4155 2.17260.76450.96 2.58900.4011 2.20120.74460.97 2.61580.3865 2.22900.72510.98 2.64240.3717 2.25610.70610.99 2.66850.3566 2.28250.68741.002.69430.3413 2.30820.66921.012.71120.3311 2.33330.65131.022.72770.3209 2.35780.63371.032.74400.3108 2.38170.61651.042.75980.3006 2.40490.59971.082.82000.26092.49240.53561.092.83410.25112.51290.52041.102.84800.24152.53300.50551.112.86150.23192.55250.49081.122.87470.22252.57160.47651.132.88760.21322.59020.46241.142.90010.20402.60840.44861.152.91230.19492.62610.43511.162.92420.18602.64340.42191.172.93570.17722.66030.40891.182.94690.16852.67670.39611.192.95780.16002.69280.38361.202.96840.15172.70850.37141.212.97870.14352.72380.35941.222.9886O.13552.73870.34761.232.99820.12772.75320.33611.243.00750.12012.76750.32481.253.01650.11262.78130.31371.263.02520.10532.79480.30281.273.03360.09822.80800.29221.283.04170.09142.82090.28181.293.04950.08472.83350.27151.303.05690.07822.84570.26151.313.06410.07192.85760.25171.323.07090.06592.86930.24211.333.07750.06002.88060.23271.343.08370.05442.89170.22351.353.08970.04902.90240.21451.363.09540.04392.91290.20571.373.10070.03892.92320.19701.383.10580.03432.93310.18861.393.11060.02982.94280.18031.403.11500.02562.95230.17221.413.11920.02172.96150.16431.423.12310.01802.97040.15661.433.12660.01462.97910.14911.443.12990.01152.98760.14171.453.13280.00862.99580.13451.463.13540.00613.00380.12751.473.13760.00393.01150.12061.483.13950.00213.01910.11400.61 1.52280.66610.5571 1.76360.62 1.55480.66660.6139 1.73870.63 1.58680.66660.6734 1.7103 1.05 2.77540.2906 2.42760.58321.06 2.79060.2806 2.44970.56701.07 2.80540.2707 2.47130.5512 1.49 3.14080.007 3.02640.10751.503.14160.00003.03340.10111.513.14160.00003.04030.09505.3.9沿周边均匀配置纵向钢筋的圆形截面钢筋混凝土偏心受压构件(图5.3.9),其正截面抗压承载力计算应符合下列规定:图5.3.9沿周边均匀配筋的圆形截面偏心受压构件计算22'0d cd sdN Ar f C r f γρ≤+(5.3.9-1)33'00d cd sd N e Br f D gr f γρ≤+(5.3.9-2)式中0e ——轴向力的偏心距,0/d d e M N =,应乘以偏心距增大系数η,η可按第5.3.10条的规定计算;A、B——有关混凝土承载力的计算系数,按附录C 的迭代法由表C.O.2查得;C、D——有关纵向钢筋承载力的计算系数,按附录C 的迭代法由表C.O.2查得;r ——圆形截面的半径;g ——纵向钢筋所在圆周的半径s r 与圆截面半径之比,/s g r r =;ρ——纵向钢筋配筋率,2/s A r ρπ=。
第八章 偏心受压构件承载力计算公式

第8章 偏心受压构件正截面承载力知 识 点 回 顾•破坏形式及特点 •大小偏心划分 •大偏心算法第8章 偏心受压构件正截面承载力8.1.4 矩形截面偏心受压构件正截面承载力 1. 大偏心受压x £ xb 正截面破坏åN =0g 0 N £ N u = a1 f c bx + f y¢ As¢ - f y Asxö æ ¢ g 0 Ne £ N u e = a1 f c bx ç h0 - ÷ + f y¢ As¢ ( h0 - as ) 2ø èå M As = 0适用条件: x £ xb ¢ x ³ 2 as As 配筋率: r= ³ r min = max ( 0.45 ft fy, 0.2% ) bh第8章 偏心受压构件正截面承载力¢ 当 x < 2as 时,受压钢筋(此时不屈服)计算, 有两种处理方式: (1)规范算法设混凝土合力中心与 As¢ 形心重合。
åM¢ As=0¢ Ne¢ £ N u e¢ = f y As ( h0 - as )(2)平截面假定算法¢ s s¢ = Ese cu (1 - b1 as x )第8章 偏心受压构件正截面承载力2. 小偏心受压构件 (1)基本计算公式 x > xb矩形截面小偏心受压构件承载力计算简图第8章 偏心受压构件正截面承载力小偏心受压构件计算公式:åN =0åMAsg 0 N £ N u = a1 f c bx + f y¢ As¢ - s s Asxö æ ¢ g 0 Ne £ N u e = a1 f c bx ç h0 - ÷ + f y¢ As¢ ( h0 - as ) 2ø è=0依据平截面假定( b1 = 0.8 ):æ b1hoi ö s si = Ese cu ç - 1÷ è x ø公路桥规:æ b1 - x ö s si = ç ÷ fy è b1 - xb øxb < x £ 2 b1 - xb第8章 偏心受压构件正截面承载力依据平截面假定:公路桥规:第8章 偏心受压构件正截面承载力(2) “反向破坏”的计算公式 偏心距很小,且远离轴向压力一侧的钢筋配置得 不够多,偏心压力有可能位于换算截面形心轴和 截面几何中心之间。
偏心受压构件

▲分析:三个未知数,As、 A’s和 x,怎么办?
▲措施:令x=bh0
▲求解:利用两个基本公式可得
As
Ne 1 fcbh02b (1
f y (h0 as' )
0.5b )
As
1 fcbh0b
fy
f y As
N
h 式中e = ei + 2 -as
▲验算最小配筋率
As 0.002bh; A's 0.002bh
M Cmns M 2
ns
1
1300(M 2
1 /N
ea
)
/
h0
lc h
2
c
Cm
0.7 0.3 M1 M2
0.7
ea (20, h / 30)max
h为长边长度
c
0.5 fc A N
:截面曲率修正系数,当计算值大于1.0时取1.0
c
其中,当 Cmns 1.0 时取1.0
对剪力墙肢及核心筒墙肢类构件,取1.0
第五章 受压构件
(2) As 、A’s应满足最小配筋率:
As 0.002bh; A's 0.002bh
As + A's ρminbh (3) As 、A’s应满足最大配筋率:
As + A's 0.05bh
1.材料强度及几何参数
截面设计时, h0 = h - as
混凝土等级不超过C25时as‘= as =45mm 混凝土等级超过C25时as‘= as =40mm
l0
eeii
N
yy
N
y f ?sin x
le
ff
N
l0le
桥梁新规范偏心受压构件计算

圆形截面沿周边均匀配筋偏心受压构件承载力计算
圆形截面沿周边均匀配筋偏心受压构件承载力计算
说明:1、本表根据规范JTG D62-2004 5.3.9及附录C编写。
2、规范对相对受压区高度精度要求为0.02。
3、当偏心很大或很小时可改精度(Q23处)。
4、计算时,填入R列相应数据,点击“开始计算”按钮。
5、计算可以选择查表计算和按公式计算,由于查表计算未考虑g对C,D的影响,
两者将有所差别,但经测试对结果影响很小。
6、公式计算的ε增量为0.001,查表计算ε增量为0.01,故公式计算更容易找到满足要求的ε值。
桥梁设计中桥墩计算长度系数的分析

桥梁设计中桥墩计算长度系数的分析发布时间:2022-10-28T10:44:20.275Z 来源:《工程建设标准化》2022年6月第12期作者:燕孟飞张少龙[导读] 下部结构桥墩承受恒载、制动力、温度效应、风荷载、地震力等多种荷载,一般作为偏心受压构件分析。
燕孟飞张少龙河南海威路桥工程咨询有限公司河南郑州 450000摘要:下部结构桥墩承受恒载、制动力、温度效应、风荷载、地震力等多种荷载,一般作为偏心受压构件分析。
关于桥墩计算长度系数的取值,钢筋混凝土及预应力混凝土桥涵设计规范中提出,当两端均为不移动的铰,系数取1.0,当一端固定一段自由时,系数取2.0。
对于实际工程中绝大部分桥墩,往往可认为一端固定、一端有转动和水平弹性约束的构件,计算长度系数问题,其本质是压杆稳定问题。
当细长的受压杆,压力达到一定值,即Fcr时,受压杆可能突然弯曲而破坏,即发生失稳的现象。
同时杆端的支承,会对杆件的变形起到一定的约束作用,不同的支承形式对杆件变形的约束作用也不同。
故同一受压杆,当其两端的支承情况不同时,杆件所能承受的临界力值也必不相同。
基于此,本篇文章对桥梁设计中桥墩计算长度系数进行研究,以供参考。
关键词:桥梁设计;桥墩计算;长度系数分析引言项目所在区域地震发生频率较高,桥梁设计位置河谷较深,山谷内弯道数量多、地势高差较大,初期进行桥梁规划设计时,秉承结构安全、项目耐久两个设计原则开展桥梁的整体设计。
该项目应侧重关注桥位的设计方案,考量结构安全性。
结合环境因素形成的限制作用,综合选出安全性较高的位置。
如果桥位地势含不利因素,需及时给出补救措施,消除不利影响。
同时,桥梁设计应侧重落实抗震设计工作,积极采取抗震措施,切实增强项目整体的抗震效果。
桥梁设计需结合桥位周边的环境特点,如地势、河床宽度等,以此保障方案的可行性。
如果桥位周边环境比较复杂、施工难度大,可采用大跨径结构。
1桥梁设计的原则结合目前我国大量的桥梁建设的案例分析,此领域中包含各种类型的桥梁形式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2. 一端固结一端转动约束和水平约束弹簧支撑杆件
表解法
k Bw k Bt
0 0.025 0.05 0.1 0.2 0.3 0.4 0.5 0.75
1 1.5 2 5 10
0 0.025 0.05 0.1 0.2 0.3 0.4 0.5 0.75 1 1.5 2 5 10
2.00 1.93 1.86 1.75 1.60 1.50 1.41 1.37 1.28 1.22 1.16 1.12 1.05 1.03 1.91 1.84 1.79 1.69 1.55 1.46 1.39 1.34 1.25 1.20 1.14 1.10 1.04 1.01 1.83 1.77 1.72 1.63 1.51 1.42 1.36 1.31 1.23 1.18 1.12 1.09 1.02 1.00 1.70 1.65 1.61 1.53 1.43 1.35 1.30 1.26 1.18 1.14 1.08 1.05 1.00 0.98 1.50 1.47 1.44 1.38 1.30 1.24 1.20 1.16 1.10 1.07 1.02 1.00 0.95 0.93 1.36 1.34 1.31 1.27 1.20 1.16 1.12 1.09 1.04 1.01 0.97 0.95 0.91 0.89 1.26 1.24 1.22 1.18 1.13 1.09 1.05 1.03 0.99 0.96 0.93 0.91 0.87 0.86 1.18 1.16 1.14 1.11 1.06 1.03 1.00 0.98 0.94 0.92 0.89 0.87 0.84 0.83 1.03 1.02 1.00 0.98 0.95 0.92 0.90 0.88 0.85 0.83 0.81 0.80 0.78 0.77 0.94 0.93 0.92 0.90 0.87 0.84 0.82 0.81 0.78 0.77 0.75 0.74 0.72 0.72 0.83 0.82 0.81 0.79 0.77 0.75 0.73 0.71 0.69 0.68 0.66 0.66 0.65 0.64 0.78 0.77 0.76 0.74 0.72 0.70 0.68 0.67 0.64 0.62 0.61 0.60 0.59 0.59 0.72 0.71 0.70 0.69 0.67 0.66 0.64 0.63 0.61 0.59 0.57 0.56 0.52 0.51 0.71 0.70 0.70 0.69 0.67 0.65 0.64 0.63 0.61 0.59 0.57 0.56 0.52 0.51
1. 问题的提出 2. 一端固结一端水平和转动约束弹簧支撑杆件 3. 连续刚构双薄壁墩计算长度系数 4. 梁式桥桥墩考虑墩顶水平刚度的计算长度系
数 5. 结语
y ·h
2. 一端固结一端转动约束和水平约束弹簧支撑杆件 计算图式
A 端:固结 B 端:设置转动约束弹簧、水、
平约束、弹簧 荷载:柱顶作用轴向荷载P。
y ·h
3. 连续刚构双薄壁墩计算长度系数
分析工况
情况一:两薄壁墩受到同样大的竖 向力,同时出现失 稳。
主要出现在:
施工阶段正在平衡 悬浇混凝土,当不 考虑或较少考虑不 平衡弯矩时的情况。
挠曲线微分方程
边界条件
B端: 水平位移=水平力÷水平弹簧刚度 转角=弯矩÷转动弹簧刚度
A端: 水平位移为0 转角为0
y ·h
2. 一端固结一端转动约束和水平约束弹簧支撑杆件
挠曲线微分方程
v''
k 2v
k 2 (vB
QB P
(L
x)
MB P
)
根据边界条件可得挠曲线微分方程为:
EI t 2EI
t 2EI t 4E 2I 2
弯矩增大系数计算公式
荷载
计算长度
杆件自
横向
边界
身荷载
荷载
条件
y ·h
1. 问题的提出
标准的边界条件
弹簧约束边界条件 由于构件件的相互作用,一 般均可视为转动约束弹簧、 水平约束弹簧作用,或者两 者的共同作用。
y ·h
1. 问题的提出
一般问题分析 连续刚构双壁墩分析 水平约束弹簧柱分析
y ·h
提纲
L
k Bt
kB 12EI
水平刚度比
L3
y ·h
2. 一端固结一端转动约束和水平约束弹簧支撑杆件
表解法
( EI
L B
t 2EI L3kB
1)t
sin
t
(t 2EI
L B
t4E2I 2
L4 BkB
2) cos t
2
0
1 4kBw
t2 12kBt
t2 4kBw
t4 48kBwkBt
t
(12kBt 4kBwt 2 48kBtkBw)t sin t (12kBtt 2 t 4 96kBtkBw) cos t 96kBtkBw 0
偏心受压构件计算长度的 确定
袁洪
2005年11月18日
提纲
1. 问题的提出 2. 一端固结一端水平和转动约束弹簧支撑杆件 3. 连续刚构双薄壁墩计算长度系数 4. 梁式桥桥墩考虑墩顶水平刚度的计算长度系数 5. 结语
y ·h
1. 问题的提出
柱形构件
弯矩
轴力
二次弯矩
弯矩增大系数计算公式
y ·h
1. 问题的提出
计算图式
y ·h
2. 一端固结一端转动约束和水平约束弹簧支撑杆件
挠曲线微分方程
v'' M (x) EI
v''
P EI
v
P EI
(vB
QB P
(L
x)
MB P
)
k2 P EI
v''
k 2v
k 2 (vB
QB P
(L
x)
MB P
)
计算图式
y ·h
2. 一端固结一端转动约束和水平约束弹簧支撑杆件
(
L B
L3kB
1)t sin
t
(
L B
L4 BkB
2) cos t
2
0
计算长度系数:
t
y ·h
2. 一端固结一端转动约束和水平约束弹簧支撑杆件
表解法
EI (
L B
t 2EI L3kB
1)t sin
t
(t 2EI
L B
t4E2I 2
L4 BkB
2) cos t
2
0
设定Biblioteka kBwB4EI
转动刚度比
y ·h
2. 一端固结一端转动约束和水平约束弹簧支撑杆件 结论
边界 条件
弹簧约 束刚度
弹簧约束刚度比
kBw kBt
查表求得计 算长度系数
y ·h
提纲
1. 问题的提出 2.一端固结一端水平和转动约束弹簧支撑杆件 3. 连续刚构双薄壁墩计算长度系数 4.梁式桥桥墩考虑墩顶水平刚度的计算长度系
数 5. 结语
