《材料力学》课后习题答案详细
材料力学课后答案.doc

材料力学课后答案第一章材料单向静拉伸载荷下的力学性能一、解释下列名词滞弹性:在外加载荷作用下,应变落后于应力现彖。
静力韧度:材料在静拉仲时单位体积材科从变形到断裂所消耗的功。
弹性极限:试样加载后再卸裁,以不出现残留的永久变形为标准,材料能够完全弹性恢复的最高应力。
比例极限:应力一应变曲线上符合线性关系的最高应力。
包中格效应:指原先经过少量塑性变形,卸载后同向加载,弹性极限(。
P)或屈服强度(。
S)增加;反向加载时弹性极限(。
P)或屈服强度3 s)降低的现象。
解理断裂:沿一定的晶体学平面产生的快速穿晶断裂。
晶体学平面一一解理面,一般是低指数,表面能低的晶面。
解理而:在解理断裂屮具冇低指数,表而能低的品体淫平而。
韧脆转变:材料力学性能从韧性状态转变到脆性状态的现象(冲击吸收功明显下降,断裂机理由微孔聚集型转变微穿晶断裂,断口特征出纤维状转变为结晶状)。
静力韧度:材料在静拉伸时单位体积材料从变形到断裂所消耗的功叫做静力韧度。
是一个强度与塑性的综合指标,是表示静载下材料强度与塑性的最佳配合。
二、金属的弹性模量主要取决于什么?为什么说它是一个对结构不敏感的力学姓能?答案:金屈的弹性模量主要取决于金屈键的本性和原子间的结合力,而材料的成分和组织对它的影响不大,所以说它是一个对组织不皱感的性能指标,这是弹性模量在性能上的主要特点。
改变材料的成分和组织会对材料的强度(如屈服强度、抗拉强度)有显著影响,但对材料的刚度影响不大。
三、什么是包辛格效应,如何解释,它冇什么实际意义?答案:包辛格效应就是指原先经过变形,然后在反向加载时弹性极限或屈服强度降低的现象。
特别是弹性极限在反向加载时几乎下降到零,这说明在反向加载吋犁性变形立即开始了。
包辛格效应可以用位错理论解释。
第一,在原先加载变形时,位错源在滑移而上产生的位错遇到障碍,塞积后便产生了背应力,这背应力反作用于位错源,当背应力(取决于塞积时产生的应力集中)足够大时,可使位错源停止开动。
材料力学第3版习题答案

材料力学第3版习题答案第一章:应力分析1. 某材料在单轴拉伸下的应力-应变曲线显示,当应力达到200 MPa 时,材料发生屈服。
若材料在该应力水平下继续加载,其应力将不再增加,但应变继续增加。
请解释这一现象,并说明材料的屈服强度是多少?答案:这种现象表明材料进入了塑性变形阶段。
在单轴拉伸试验中,当应力达到材料的屈服强度时,材料的晶格结构开始发生滑移,导致材料的变形不再需要额外的应力增加。
因此,即使继续加载,应力保持不变,但应变会因为材料内部结构的重新排列而继续增加。
在本例中,材料的屈服强度是200 MPa。
第二章:材料的弹性行为2. 弹性模量是描述材料弹性行为的重要参数。
若一块材料的弹性模量为210 GPa,当施加的应力为30 MPa时,其应变是多少?答案:弹性模量(E)与应力(σ)和应变(ε)之间的关系由胡克定律描述,即σ = Eε。
要计算应变,我们可以使用公式ε =σ/E。
将给定的数值代入,得到ε = 30 MPa / 210 GPa =1.43×10^-4。
第三章:材料的塑性行为3. 塑性变形是指材料在达到屈服点后发生的永久变形。
如果一块材料在单轴拉伸试验中,其屈服应力为150 MPa,当应力超过这个值时,材料将发生塑性变形。
请解释塑性变形与弹性变形的区别。
答案:塑性变形与弹性变形的主要区别在于材料在去除外力后是否能够恢复原状。
弹性变形是指材料在应力作用下发生的形状改变,在应力移除后能够完全恢复到原始状态,不留下永久变形。
而塑性变形是指材料在应力超过屈服点后发生的不可逆的永久变形,即使应力被移除,材料的形状也不会恢复到原始状态。
第四章:断裂力学4. 断裂韧性是衡量材料抵抗裂纹扩展的能力。
如果一块材料的断裂韧性为50 MPa√m,试样的尺寸为100 mm×100 mm×50 mm,试样中存在一个长度为10 mm的初始裂纹。
请计算在单轴拉伸下,材料达到断裂的临界应力。
第四版单辉祖材料力学课后答案

第四版单辉祖材料力学课后答案引言《材料力学》是材料科学与工程专业的一门基础课程,主要介绍了材料的力学性质和力学行为。
本文以《材料力学》第四版的单辉祖所编写的课后习题为题,给出了相应的答案。
通过对这些习题的解答,帮助学生巩固课堂所学的知识,并提供了一些解题思路和方法。
目录•第一章引言•第二章物质的内部力和应力•第三章弹性和塑性力学基础第一章引言1. 什么是材料力学?答案:材料力学是研究物质响应外力作用下的变形和破坏行为的科学。
2. 材料力学的主要内容有哪些?答案:材料力学的主要内容包括静力学、动力学、弹性力学、塑性力学、断裂力学等。
第二章物质的内部力和应力1. 什么是内力?答案:内力是物质内部分子间相互作用所产生的力。
2. 什么是应力?答案:应力是单位面积上的力,表示为单位面积上的力的矢量。
3. 应力的分类有哪些?答案:应力可分为法向应力和切应力两种,法向应力垂直于截面,切应力与截面垂直。
4. 弹性应力-应变关系有哪些?答案:弹性应力-应变关系有胡克定律,即应力与应变成正比。
第三章弹性和塑性力学基础1. 弹性和塑性的区别是什么?答案:弹性是指物体在受到外力作用下发生变形后,外力去除后恢复原状的能力;塑性是指物体在受到外力作用下发生变形后,即使外力去除,物体也不能恢复原状。
2. 什么是弹性模量?答案:弹性模量是描述物质抵抗压缩和拉伸变形能力的指标,表示为物质单位应力与应变的比值。
3. 什么是屈服强度?答案:屈服强度是材料在拉伸过程中,在产生明显塑性变形或显著应力减小时的应力值。
4. 什么是塑性应变?答案:塑性应变是指材料在超过屈服点后产生的应变。
结论本文为《材料力学》第四版单辉祖所编写的课后习题的答案,涵盖了材料力学的部分基础知识。
通过对这些习题的解答,希望能够帮助学生深入理解材料力学的概念和原理,并提供一些解题思路和方法。
通过不断练习,学生能够对材料力学有更深入和全面的认识,为日后的学习和研究打下坚实的基础。
材料力学第四版课后习题答案

材料力学第四版课后习题答案1. 引言。
材料力学是材料科学与工程中的重要基础课程,通过学习材料力学,可以帮助我们更好地理解材料的性能和行为。
本文档将针对材料力学第四版的课后习题进行答案解析,帮助学习者更好地掌握课程内容。
2. 第一章。
2.1 课后习题1。
答,根据受力分析,可以得到杆件的受力情况。
然后利用杆件的受力平衡条件,可以得到杆件的应力状态。
最后,根据应力状态计算应变和变形。
2.2 课后习题2。
答,利用受力分析,可以得到杆件的受力情况。
然后利用杆件的受力平衡条件,可以得到杆件的应力状态。
最后,根据应力状态计算应变和变形。
3. 第二章。
3.1 课后习题1。
答,利用受力分析,可以得到梁的受力情况。
然后利用梁的受力平衡条件,可以得到梁的应力状态。
最后,根据应力状态计算应变和变形。
3.2 课后习题2。
答,利用受力分析,可以得到梁的受力情况。
然后利用梁的受力平衡条件,可以得到梁的应力状态。
最后,根据应力状态计算应变和变形。
4. 第三章。
4.1 课后习题1。
答,利用受力分析,可以得到薄壁压力容器的受力情况。
然后利用薄壁压力容器的受力平衡条件,可以得到薄壁压力容器的应力状态。
最后,根据应力状态计算应变和变形。
4.2 课后习题2。
答,利用受力分析,可以得到薄壁压力容器的受力情况。
然后利用薄壁压力容器的受力平衡条件,可以得到薄壁压力容器的应力状态。
最后,根据应力状态计算应变和变形。
5. 结论。
通过对材料力学第四版课后习题的答案解析,我们可以更好地掌握材料力学的基本原理和方法。
希望本文档能够对学习者有所帮助,促进大家对材料力学的深入理解和应用。
材料力学课后答案

材料力学课后答案材料力学是一门研究材料的结构和性质以及力学行为的学科。
以下是材料力学课后习题的答案。
1. 对于一个材料试验样品的拉伸测试,如何计算应力和应变?答:应力是试样受到的外部力除以其截面积,应变是试样的长度变化除以其原始长度。
2. 当一根钢条受到拉伸力时,它的截面积会变大还是变小?为什么?答:当钢条受到拉伸力时,它的截面积会减小。
这是因为外部力导致钢条内部发生塑性变形,使其截面积减小。
3. 什么是杨氏模量?如何计算?答:杨氏模量是表征材料在受到应力时的变形能力的物理量。
它可以通过应力与应变之间的比率来计算,即杨氏模量=应力/应变。
4. 什么是泊松比?如何计算?答:泊松比是一个无量纲的物理量,它描述了材料在拉伸或压缩时的横向收缩量与纵向伸长量之间的比例关系。
它可以通过横向应变与纵向应变之间的比率来计算,即泊松比=横向应变/纵向应变。
5. 什么是屈服强度?如何确定屈服强度?答:屈服强度是材料在受到应力时开始产生塑性变形的应力值。
它可以通过拉伸测试或压缩测试中的应力-应变曲线来确定,屈服强度对应于曲线上的屈服点。
6. 材料的断裂强度是什么?如何计算?答:材料的断裂强度是指材料在受到拉伸或压缩的最大应力值。
它可以通过拉伸测试或压缩测试中的应力-应变曲线来确定,断裂强度对应于曲线上的断裂点。
7. 什么是韧性?如何评价材料的韧性?答:韧性是材料在受力过程中吸收能量的能力。
可以通过材料的断裂能量来评价韧性,断裂能量是在材料断裂前吸收的总能量。
8. 什么是冷加工和热加工?它们对材料性能有何影响?答:冷加工是在室温下对材料进行塑性变形,而热加工是在高温下对材料进行塑性变形。
冷加工会使材料变硬和脆化,而热加工则会使材料变软和韧性增加。
以上是材料力学课后习题的答案,希望对你的学习有所帮助。
如果有任何疑问,请随时向我提问。
材料力学课后习题答案

材料力学课后习题答案欢迎大家来到大学网,小编搜集整理了材料力学课后习题答案供大家查阅,希望大家喜欢。
1、解释下列名词。
1弹性比功:金属材料吸收弹性变形功的能力,一般用金属开始塑性变形前单位体积吸收的最大弹性变形功表示。
2.滞弹性:金属材料在弹性范围内快速加载或卸载后,随时间延长产生附加弹性应变的现象称为滞弹性,也就是应变落后于应力的现象。
3.循环韧性:金属材料在交变载荷下吸收不可逆变形功的能力称为循环韧性。
4.包申格效应:金属材料经过预先加载产生少量塑性变形,卸载后再同向加载,规定残余伸长应力增加;反向加载,规定残余伸长应力降低的现象。
5.解理刻面:这种大致以晶粒大小为单位的解理面称为解理刻面。
6.塑性:金属材料断裂前发生不可逆永久(塑性)变形的能力。
韧性:指金属材料断裂前吸收塑性变形功和断裂功的能力。
7.解理台阶:当解理裂纹与螺型位错相遇时,便形成1个高度为b 的台阶。
8.河流花样:解理台阶沿裂纹前端滑动而相互汇合,同号台阶相互汇合长大,当汇合台阶高度足够大时,便成为河流花样。
是解理台阶的1种标志。
9.解理面:是金属材料在一定条件下,当外加正应力达到一定数值后,以极快速率沿一定晶体学平面产生的穿晶断裂,因与大理石断裂类似,故称此种晶体学平面为解理面。
10.穿晶断裂:穿晶断裂的裂纹穿过晶内,可以是韧性断裂,也可以是脆性断裂。
沿晶断裂:裂纹沿晶界扩展,多数是脆性断裂。
11.韧脆转变:具有一定韧性的金属材料当低于某一温度点时,冲击吸收功明显下降,断裂方式由原来的韧性断裂变为脆性断裂,这种现象称为韧脆转变12.弹性不完整性:理想的弹性体是不存在的,多数工程材料弹性变形时,可能出现加载线与卸载线不重合、应变滞后于应力变化等现象,称之为弹性不完整性。
弹性不完整性现象包括包申格效应、弹性后效、弹性滞后和循环韧性等决定金属屈服强度的因素有哪些?答:内在因素:金属本性及晶格类型、晶粒大小和亚结构、溶质元素、第二相。
材料力学完整课后习题答案

习题2-2一打入基地内的木桩如图所示,杆轴单位长度的摩擦力fkx2,试做木桩的后力图。
解:由题意可得:l 1 0 fdx F 有kl 3 F k 3F / l 3 3 l FN x1 3Fx 2 / l 3dx F x1 / l 3 0习题2-3 石砌桥墩的墩身高l 10m ,其横截面面尺寸如图所示。
荷载 F 1000kN ,材料的密度2.35kg / m 3 ,试求墩身底部横截面上的压应力。
解:墩身底面的轴力为:N F G F Alg 2-3 图1000 3 2 3.14 12 10 2.35 9.8 3104.942kN 墩身底面积: A 3 2 3.14 12 9.14m 2 因为墩为轴向压缩构件,所以其底面上的正应力均匀分布。
N 3104.942kN 339.71kPa 0.34MPa A 9.14m 2习题2-7 图示圆锥形杆受轴向拉力作用,试求杆的伸长。
2-7 图解:取长度为dx 截离体(微元体)。
则微元体的伸长量为:Fdx l F F l dx d l ,l dx EA x 0 EA x E 0 A x r r1 x r r d d1 d ,r 2 1 x r1 2 x 1 ,r2 r1 l l 2l 2 d d1 d d1 d d1 2 d d A x 2 x 1 u2 ,d 2 x 1 du 2 dx 2l 2 2l 2 2l 2l 2l dx d d 2l du dx du ,2 2 1 du 2 d 2 d1 A x u d1 d 2 u l F F l dx 2 Fl l du 因此,l dx 0 u 2 0 EA x E 0 A x E d1 d 2 l 2 Fl 1 l 2 Fl 1 u E d d d d E d1 d 2 0 2 2 d 1 1 x 1 2l 2 0 2 Fl 1 1 E d1 d 2 d 2 d 1 dd1 l 1 2l 2 2 2 Fl 2 2 4 Fl E d1 d 2 d 2 d1 Ed 1 d 2习题2-10 受轴向拉力 F 作用的箱形薄壁杆如图所示。
(完整版)材料力学课后习题答案
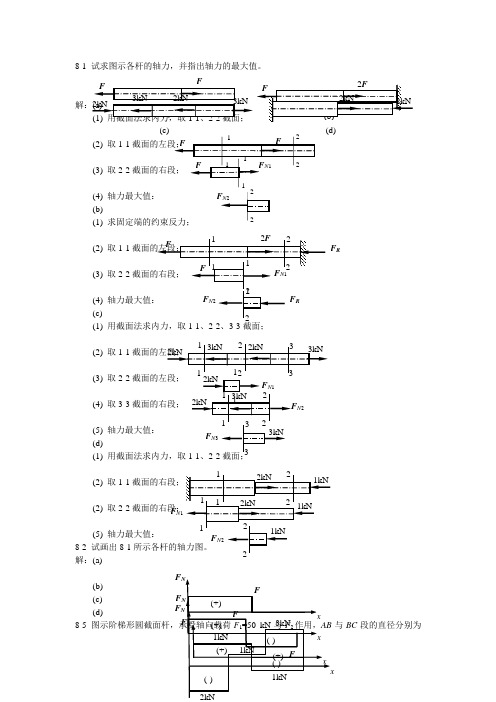
8-1 试求图示各杆的轴力,并指出轴力的最大值。
(2) 取1-1(3) 取2-2(4) 轴力最大值: (b)(1) 求固定端的约束反力; (2) 取1-1(3) 取2-2(4) (c)(1) 用截面法求内力,取1-1、2-2、3-3截面;(2) 取1-1(3) 取2-2 (4) 取3-3截面的右段;(5) 轴力最大值: (d)(1) 用截面法求内力,取1-1、(2) 取1-1(2) 取2-2(5) 轴力最大值: 8-2 试画出8-1解:(a) (b) (c) (d) 8-5与BC 段的直径分别为(c) (d)F RN 2F N 3 F N 1F F Fd 1=20 mm 和d 2=30 mm ,如欲使AB 与BC 段横截面上的正应力相同,试求载荷F 2之值。
解:(1) 用截面法求出(2) 求1-1、2-28-6 题8-5段的直径d 1=40 mm ,如欲使AB 与BC 段横截面上的正应力相同,试求BC 段的直径。
解:(1)用截面法求出1-1、2-2截面的轴力;(2) 求1-1、2-2截面的正应力,利用正应力相同;8-7 图示木杆,承受轴向载荷F =10 kN 作用,杆的横截面面积A =1000 mm 2,粘接面的方位角θ= 450,试计算该截面上的正应力与切应力,并画出应力的方向。
解:(1) (2) 8-14 2=20 mm ,两杆F =80 kN 作用,试校核桁架的强度。
解:(1) 对节点A(2) 列平衡方程 解得: (2) 8-15 图示桁架,杆1A 处承受铅直方向的载荷F 作用,F =50 kN ,钢的许用应力[σS ] =160 MPa ,木的许用应力[σW ] =10 MPa 。
解:(1) 对节点A (2) 84 mm 。
8-16 题8-14解:(1) 由8-14得到的关系;(2) 取[F ]=97.1 kN 。
8-18 图示阶梯形杆A 2=100 mm 2,E =200GPa ,试计算杆AC 的轴向变形 解:(1) (2) AC 8-22 图示桁架,杆1与杆2的横截面面积与材料均相同,在节点A 处承受载荷F 作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
N(x) F F x a
x (a,0]
轴力图如图所示。
[习题 2-2] 试求图示等直杆横截面 1-1、2-2 和平 3-3 上的轴力,并作轴
力图。若横截面面积 A 400mm2 ,试
求各横截面上的应力。
解:(1)求指定截面上的轴力
N11 20kN N 22 10 20 10(kN )
10000 100
0
100 100.0 0.0
10000 100
30
100 75.0 43.3
10000 100
45
100 50.0 50.0
10000 100
60
100 25.0 43.3
10000 100
90
100
0.0
0.0
[习题 2-7] 一根等直杆受力如图所 示。已知杆的横截面面积 A 和材料 的弹性模量 E。试作轴力图,并求杆 端点 D 的位移。 解:(1)作轴力图
N33 F 2F 2F F
轴力图如图所示。
1
(c)
解:(1)求指定截面上的轴力
N11 2F N22 F 2F F
(2)作轴力图
N33 2F F 2F 3F
轴力图如图所示。
(d)
解:(1)求指定截面上的轴力
N11 F
N 22
2F
qa
F
2F
F a
a
F
2F
(2)作轴力图
中间段的轴力方程为:
解:墩身底面的轴力为:
N (F G) F Alg
1000 (3 2 3.14 12 ) 10 2.35 9.8 3104.942(kN )
1000 (3 2 3.14 12 ) 10 2.35 9.8
3104.942(kN )
墩身底面积: A (3 2 3.14 12 ) 9.14(m2 )
材料可认为符合胡克定律,其弹性模量 E 10GPa 。如不计柱的自重,试求:
(1)作轴力图;
(2)各段柱横截面上的应力;
(3)各段柱的纵向线应变;
(4)柱的总变形。
解:(1)作轴力图
N AC 100kN NCB 100 160 260(kN )
轴力图如图所示。
(2)计算各段上的应力
AC
N AC A
N AB N1 18.117kN
;
N AC N 2 25.621kN
11
(2)由变形能原理求 A 点的铅垂方向的位移
1 2
F A
N
2 1
l1
2EA1
N 22l2 2EA2
A
1 F
( N12l1 EA1
N
2 2
l2
比 0.3。当其轴向拉伸时,已知纵向线应变 0.001,试求其变形后的壁厚。
解:(1)证明 s d
8
在圆形截面上取一点 A,连结圆心 O 与 A 点,则 OA 即代表直径方向。
过 A 点作一条直线 AC 垂直于 OA,则 AC 方向代表圆周方向。
s AC (泊松比的定义式),同理,
解:(1)求 AB、AC 杆的轴力
以节点 A 为研究对象,其受力图如图所
示。
由平衡条件得出:
X 0 : N AC sin 30o N AB sin 45o 0
N AC 2N AB ………………………(a)
Y 0 : N AC cos 30o N AB cos 45o 35 0
3N AC 2N AB 70 ………………(b) (a) (b)联立解得:
d OA
故有: s d 。
(2)求轴向力 F
d 0.0025mm
' d 0.0025 2.5 104
d
10
'
'
2.5 104 0.3
25 104 3
E F E A F AE 0.25 3.14 102 210 103 25 104 13737.5(N ) 13.74kN
N CD F N BC 2F F F N AB 2F 2F F F
6
AD 杆的轴力图如图所示。
(2)求 D 点的位移
D
l AD
N ABl AB EA
N BC lBC EA
N CD lCD EA
Fl / 3 Fl / 3 Nl / 3 EA EA EA
Fl (→)
3EA
[习题 2-8] 一木桩受力如图所示。柱的横。截面为边长 200mm 的正方形,
上的正应力和切应力,并用图表示其方
向。
解:斜截面上的正应力与切应力的公式
为:
5
0 cos 2
0 2
sin 2
式中, 0
N A
10000 N 100mm 2
100MPa ,把
的数值代入以上二式得:
题目 编号 习题 2-6
轴向拉/压杆斜截面上的应力计算
N (N ) A(mm 2 ) (o ) 0 (MPa) (MPa) (MPa)
为两个 75mm 8mm 的等边角钢。已知屋面承受集度为
q 20kN / m 的竖直均布荷载。试求拉杆 AE 和 EC 横截面
上的应力。
解:(1)求支座反力
由结构的对称性可知:
RA
RB
1 ql 2
0.5 20 (2 4.37 9)
177.4(kN )
(2)求 AE 和 EG 杆的轴力
① 用假想的垂直截面把 C 铰和 EG 杆同时切断,取左部分为研究
10000N 1000mm 210000N / mm2 100mm2
0.476mm
B 点的铅垂位移: l2
N2l EA2
10000N 1000mm 210000N / mm2 100mm2
0.476mm
1、2、3 杆的变形协(谐)调的情况如图所示。由 1、2、3 杆的
变形协(谐)调条件,并且考虑到 AB 为刚性杆,可以得到:
解:(1)求各杆的轴力
以 AB 杆为研究对象,其受力图如图
所示。
因为 AB 平衡,所以
X 0
N3 cos 45o 0 N3 0
由对称性可知,受力CH图 0
N1 N 2 0.5F 0.5 20 10(kN )
10
(2)求 C 点的水平位移与铅垂位移。 变形协调图
A
点的铅垂位移:l1
N1l EA1
C 点的水平位移: CH AH BH l1 tan 45o 0.476(mm) C 点的铅垂位移: C l1 0.476(mm) [习题 2-13] 图示实心圆杆 AB 和 AC 在 A 点以铰相连接,在 A 点作用有铅垂
向下的力 F 35kN 。已知杆 AB 和 AC 的直径分别为 d1 12mm 和 d2 15mm ,钢 的弹性模量 E 210GPa 。试求 A 点在铅垂方向的位移。
6.5 104
(4)计算柱的总变形
l AC AC l AC CB lCB (2.5 1500 6.5 1500) 104 1.35(mm)
[ 习 题 2-9] 一 根 直 径 d 16mm 、 长 l 3m 的 圆 截 面 杆 , 承 受 轴 向 拉 力
F 30kN ,其伸长为 l 2.2mm 。试求杆横截面上的应力与材料的弹性模量
2
N33 20 10 20 10(kN )
(2)作轴力图
轴力图如图所示。
(3)计算各截面上的应力
11
N11 A
20 103 N 400mm 2
50MPa
22
N 22 A
10 103 N 400mm 2
25MPa
33
N 33 A
10 103 N 400mm 2
25MPa
[习题 2-3] 试求图示阶梯状直杆横截面 1-1、2-2 和平 3-3 上的轴力,并作
对象,其受力图如图所示。由平衡条件可知:
MC (F) 0
N EG
(1 1.2)
20
(4.37
4.5)
8.87 2
177.4
8.87
0
N EG
1 [20 (4.37 4.5) 8.87
2.2
2
177.4 8.87] 357.62(kN )
② 以 C 节点为研究对象,其受力图如图所
因为墩为轴向压缩构件,所以其底面上的正应力
均匀分布。
N A
3104.942kN 9.14m 2
339.71kPa
0.34MPa
[习题 2-6] 图示拉杆承受轴向拉力 F 10kN ,杆的横截面面积 A 100mm2 。
如以 表示斜截面与横截面的夹角,试求当 0o ,30o ,45o ,60o ,90o 时各斜截面
轴力图。若横截面面积 A1 200mm2 , A2 300mm2 , A3 400mm2 ,并求各横截 面上的应力。
解:(1)求指定截面上的轴力
N11 20kN N 22 10 20 10(kN ) N33 20 10 20 10(kN )
(2)作轴力图
轴力图如图所示。
(3)计算各截面上的应力
示。
由平平衡条件可得:
X 0
N EG N EA cos 0
N EA
N EG cos
357.62 4.37
366.86(kN )
4.37 2 12
4
(3)求拉杆 AE 和 EG 横截面上的应力
查 型 钢 表 得 单 个 75mm 8mm 等 边 角 钢 的 面 积 为 :
A1 11.503cm2 1150.3mm2
常数为 E, ,试求 C 与 D 两点间的距离改
变量 CD 。
9
解: ' F / A F
E
EA
式中, A (a )2 (a )2 4a ,故:
